Формула умножения дробей: Формулы дробей | Сложение, вычитание, умножение и деление дробей / Блог / Справочник :: Бингоскул

Содержание

Дроби. Формулы сокращенного умножения

Факт 1.
$\bullet$ Множество натуральных чисел $\mathbb{N}$ – это числа $1, \ 2, \ 3, \ 4 \ $ и т.д.
$\bullet$ Множество целых чисел $\mathbb{Z}$ состоит из натуральных чисел, противоположных им ($-1, \ -2, \ -3 $ и т.д.) и нуля $0$.
$\bullet$ Рациональные числа $\mathbb{Q}$ – числа вида $\dfrac ab$, где $a\in \mathbb{Z}$, $b\in \mathbb{N}$. Таким образом, существует включение: $\mathbb{N}$ содержится в $\mathbb{Z}$, а $\mathbb{Z}$ содержится в $\mathbb{Q}$.

Факт 2.
$\bullet$ Правила сложения дробей: \[\begin{aligned} &\dfrac ab+\dfrac cb=\dfrac{a+c}b\\[2ex] &\dfrac ab+\dfrac cd=\dfrac{ad+bc}{bd}\end{aligned}\] Пример: $\dfrac {31}6+\dfrac {67}6=\dfrac{31+67}6=\dfrac{98}6$ $\bullet$ Правила умножения дробей: \[\dfrac ab\cdot \dfrac cd=\dfrac{ac}{bd}\] Пример: $\dfrac 47\cdot \dfrac{14}5=\dfrac{4\cdot 14}{7\cdot 5}$ $\bullet$ Правила деления дробей: \[\dfrac ab: \dfrac cd=\dfrac ab\cdot \dfrac dc\] Пример: $\dfrac 45 :\dfrac 67=\dfrac 45\cdot \dfrac 76$

Факт 2.
$\bullet$ Сокращение дробей – деление числителя и знаменателя на одно и то же число, отличное от нуля.
Пример: $\begin{aligned} &\dfrac{98}6=\dfrac{49\cdot 2\llap{/}}{3\cdot 2\llap{/}}=\dfrac{49}3\\[2ex] &\dfrac{4\cdot 14}{7\cdot 5}=\dfrac{4\cdot 2\cdot 7\llap{/}}{7\llap{/}\cdot 5}=\dfrac 85\\[2ex] &\dfrac{4\cdot 7}{5\cdot 6}=\dfrac {2\llap{/}\cdot 2\cdot 7}{5\cdot 3\cdot 2\llap{/}}=\dfrac{14}{15}\end{aligned}$ $\bullet$ Если $\dfrac ab$ – несократимая дробь, то ее можно представить в виде конечной десятичной дроби тогда и только тогда, когда знаменатель $b$ делится только на числа $2$ и $5$.
Пример: дробь $\dfrac2{65}$ нельзя представить в виде конечной десятичной дроби, так как $65=5\cdot 13$, то есть $\dfrac2{65}=0,0307…$
дробь $\dfrac3{160}$ можно представить в виде конечной десятичной дроби, так как $160=2^5\cdot 5$, то есть $\dfrac3{160}=0,01875$.

2+2ab+2ac+2ad+2bc+2bd+2cd\\[2ex] &{\small{\text{и т.д.}}}\end{aligned}\]

Умножение дробей | Формулы с примерами

Умножение правильных дробей

Определение
Произведение правильных дробей — это дробь, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей.

Пример 54 • 311 = 5 • 3 4 • 11 = 1544;

73 • 45 = 7 • 49 • 5 = 2815;

93 — 74 = 9 • 73 • 4 = 3612 = 3.1

Правило

Если нужно умножить целое число на дробь, то умножаем это число на
числитель, так как любое целое число можно представить в виде
неправильной дроби со знаменателем 1.

Умножение смешанных дробей

Определение
Чтобы умножить правильную дробь на смешанную, нужно сначала преобразовать смешанную дробь в неправильную.

Порядок действий

1. Преобразуем смешанную дробь в неправильную;
2. Перемножаем числители и знаменатели;
3. Приводим получившуюся неправильную дробь к смешанной.

Пример
534 • 25 = 234 • 25 = 23 • 24 • 5 = 4620 = 2310 = 2 3 10;

313 • 12 = 103 • 12 = 10 • 13 • 2 = 106 = 53 = 1 2 3;

724 • 13 = 304 • 13 = 30 • 14 • 3 = 3012 = 52 = 2 1 2.

Умножение и деление рациональных дробей — 8 класс

16 сентября 2015

Прежде всего, чтобы научиться работать с рациональными дробями без ошибок, необходимо выучить формулы сокращённого умножения. И не просто выучить — их необходимо распознавать даже тогда, когда в роли слагаемых выступают синусы, логарифмы и корни.

Однако основным инструментом остаётся разложение числителя и знаменателя рациональной дроби на множители. Этого можно добиться тремя различными способами:

Собственно, по формула сокращённого умножения: они позволяют свернуть многочлен в один или несколько множителей;

С помощью разложения квадратного трёхчлена на множители через дискриминант. Этот же способ позволяет убедиться, что какой-либо трёхчлен на множители вообще не раскладывается;
Метод группировки — самый сложный инструмент, но это единственный способ, который работает, если не сработали два предыдущих.

Как вы уже, наверное, догадались из названия этого видео, мы вновь поговорим о рациональных дробях. Буквально несколько минут назад у меня закончилось занятие с одним десятиклассником, и там мы разбирали именно эти выражения. Поэтому данный урок будет предназначен именно для старшеклассников.

Наверняка у многих сейчас возникнет вопрос: «Зачем ученикам 10-11 классов изучать такие простые вещи как рациональные дроби, ведь это проходится в 8 классе?». Но в том то и беда, что большинство людей эту тему именно «проходят». Они в 10-11 классе уже не помнят, как делается умножение, деление, вычитание и сложение рациональных дробей из 8-го класса, а ведь именно на этих простых знаниях строятся дальнейшие, более сложные конструкции, как решение логарифмических, тригонометрических уравнений и многих других сложных выражений, поэтому без рациональных дробей делать в старших классах практически нечего.

{2}}+2x+4}{\left( x-2 \right)\left( x+2 \right)}=\frac{1}{x+2}\]

Ключевые моменты

Еще раз ключевые факты сегодняшнего видеоурока:

Необходимо знать «назубок» формулы сокращенного умножения — и не просто знать, а уметь видеть в тех выражениях, которые будут вам встречаться в реальных задачах. Помочь нам в этом может замечательное правило: если слагаемых два, то это либо разность квадратов, либо разность или сумма кубов; если три — это может быть только квадрат суммы или разности.
Если какая-либо конструкция не раскладывается при помощи формул сокращенного умножения, то нам на помощь приходит либо стандартная формула разложения трехчленов на множители, либо метод группировки.

Если что-то не получается, внимательно посмотрите на исходное выражение — а требуются ли вообще какие-то преобразования с ним. Возможно, достаточно будет просто вынести множитель за скобку, а это очень часто бывает просто константа.
В сложных выражениях, где требуется выполнить несколько действий подряд, не забывайте приводить к общему знаменателю, и лишь после этого, когда все дроби приведены к нему, обязательно приведите подобное в новом числителе, а потом новый числитель еще раз разложите на множители — возможно, что-то сократится.

Вот и все, что я хотел вам рассказать сегодня о рациональных дробях. Если что-то непонятно — на сайте еще куча видеоуроков, а также куча задач для самостоятельного решения. Поэтому оставайтесь с нами!

Смотрите также:

Учимся упрощать рациональные выражения и дроби с помощью формул сокращённого умножения.

Дробно-рациональные выражения
Умножение и деление дробей
Пробный ЕГЭ 2012 от 7 декабря. Вариант 1 (без логарифмов)
Как быстро извлекать квадратные корни
Задача B2: Сложный процент и метод коэффициентов

Как умножить обыкновенную дробь: на число, другую дробь

В данной публикации мы рассмотрим, каким образом можно обыкновенную (простую) дробь умножить на число или другую дробь, и как найти произведение смешанных дробей.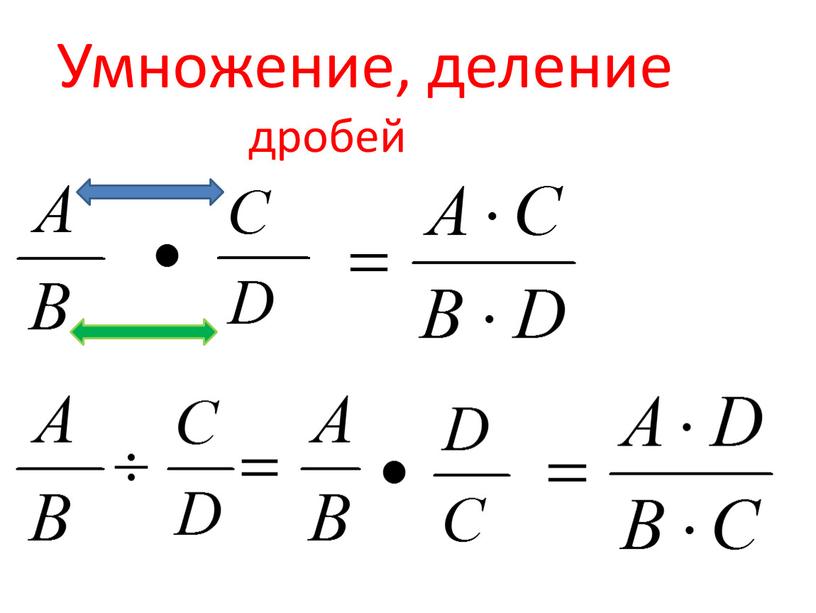 Также разберем примеры решения задач для лучшего понимания и закрепления теоретического материала.

Умножение дроби

На число

Умножение обыкновенной дроби на число n равно сумме, слагаемыми которой является данная дробь n-ое количество раз.

Другими словами, числитель дроби умножается на данное число n, а знаменатель остается тем же.

Примечание: дробь, полученную в результате умножения, следует проверить на предмет того, можно ли ее сократить.

На другую дробь

В результате умножения одной дроби на другую получается новая дробь, числитель которой равняется произведению числителей исходных дробей, а знаменатель – произведению знаменателей.

a/b

⋅

c/d

a⋅b/c⋅d

Произведение смешанных дробей

Чтобы умножить смешанные дроби, необходимо их сперва представить в виде неправильных дробей, и только после этого выполнить умножение.

a/b

⋅ Y

c/d

X ⋅ b + a/b

⋅

Y ⋅ d + c/d

Примеры задач

Задание 1

Умножьте дробь

3/15

на число 5.

Решение

3/15

⋅ 5 =

3⋅5/15

15/15

Задание 2

Найдите произведение дробей

9/17

4/7

Решение

9/17

⋅

4/7

9⋅4/17⋅7

36/119

Задание 3

Найдите произведение дробей 3

3/8

и 7

1/9

Решение

Т.к. мы имеем дело со смешанными дробями, сперва представим их в виде неправильных, затем выполним умножение.

3/8

⋅ 7

1/9

3⋅8+3/8

⋅

7⋅9+1/9

27/8

⋅

64/9

27⋅64/8⋅9

1728/72

=24

Цикл конспектов умножение и деление смешанных чисел. Дроби. Умножение и деление дробей. Формула умножения дробей

) и знаменатель на знаменатель (получим знаменатель произведения).

Формула умножения дробей:

Например:

Перед тем, как приступить к умножению числителей и знаменателей, необходимо проверить на возможность сокращения дроби . Если получится сократить дробь, то вам легче будет дальше производить расчеты.

Деление обыкновенной дроби на дробь.

Деление дробей с участием натурального числа.

Это не так страшно, как кажется. Как и в случае со сложением , переводим целое число в дробь с единицей в знаменателе. Например:

Умножение смешанных дробей.

Правила умножения дробей (смешанных):

преобразовываем смешанные дроби в неправильные;
перемножаем числители и знаменатели дробей;
сокращаем дробь;
если получили неправильную дробь, то преобразовываем неправильную дробь в смешанную.

Обратите внимание! Чтобы умножить смешанную дробь на другую смешанную дробь, нужно, для начала, привести их к виду неправильных дробей, а далее умножить по правилу умножения обыкновенных дробей.

Второй способ умножения дроби на натуральное число.

Бывает более удобно использовать второй способ умножения обыкновенной дроби на число.

Обратите внимание! Для умножения дроби на натуральное число необходимо знаменатель дроби разделить на это число, а числитель оставить без изменения.

Из, приведенного выше, примера понятно, что этот вариант удобней для использования, когда знаменатель дроби делится без остатка на натуральное число.

Многоэтажные дроби.

В старших классах зачастую встречаются трехэтажные (или больше) дроби. Пример:

Чтобы привести такую дробь к привычному виду, используют деление через 2 точки:

Обратите внимание! В делении дробей очень важен порядок деления. Будьте внимательны, здесь легко запутаться.

Обратите внимание, например:

При делении единицы на любую дробь, результатом будет таже самая дробь, только перевернутая:

Практические советы при умножении и делении дробей:

1. Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.

2. В заданиях с разными видами дробей — переходите к виду обыкновенных дробей.

3. Все дроби сокращаем до тех пор, пока сокращать уже будет невозможно.

4. Многоэтажные дробные выражения приводим в вид обыкновенных, пользуясь делением через 2 точки.

5. Единицу на дробь делим в уме, просто переворачивая дробь.

Тема урока: «Умножение и деление смешанных дробей»

Цель: выработать у учащихся умение и навыки применения правила умножения и деления смешанных дробей;

развитие аналитического мышления учащихся, формирование умения у учащихся выделять главное и обобщать.

Задачи: повторить правило умножения и деления обыкновенных дробей.

Проверить умения применения правила умножения и деления обыкновенных дробей,

правило умножения дроби на натуральное число и обратно. Проверить умение переводить неправильную дробь в смешанное число и обратно.

Вывести новое правило и алгоритм умножение и деления смешанных чисел.

Отработать новое правило на выполнении заданий.

Предметные результаты: алгоритм умножения и деления смешанных дробей(памятка)

Метапредметные и личностные результаты :

Регулятивные УУД: постановка цели; план, получение результата

Познавательные УУД: общеучебные, логические, постановка и решение проблемы

Коммуникативные УУД: работа в парах

Оборудование: учебник математики 6 класс

Раздаточный материал.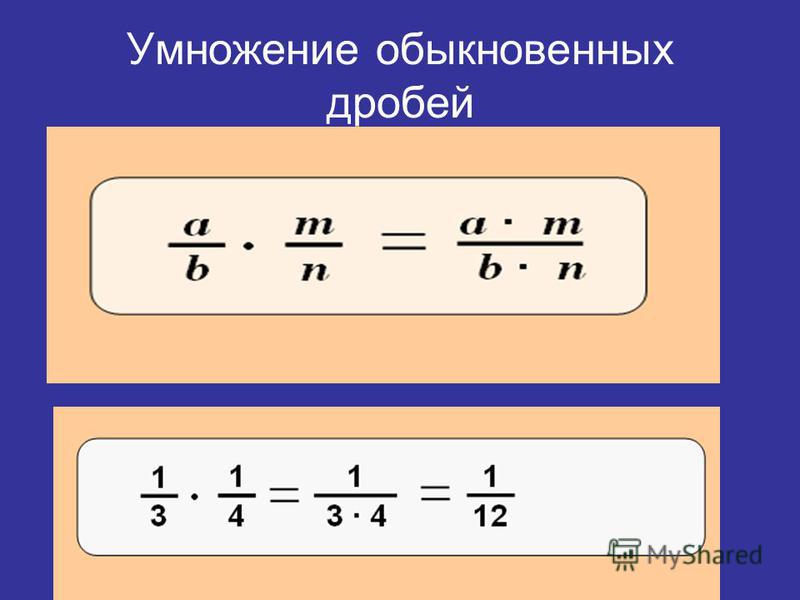

Проектор.

Ход урока:

I .Проблемная ситуация и актуализация знаний

1.Опрос детей на повторение изученного материала по теме умножение и деление дробей (алгоритм выполнения, правило умножения дроби на натуральное число).

2. Иллюстрация примеров на проекторе. Виды обыкновенных дробей. Как из неправильной дроби получить смешанную и обратно.

3.По окончании опроса самостоятельная работа включающая примеры на умножение и деление обыкновенных дробей и содержащая два примера на умножение и деление смешанных дробей, где дети сталкиваются с проблемой. Правильные ответы для сверки с учащимися отражаются на проекторе.

4. Обсуждение проблемы. Вывести на тему урока.

II .Совместное открытие знаний.

1/Предлагается обсуждение в парах, для озвучивания версии решения возникшей проблемы. Версии записать на школьной доске. Как узнать какая же из версий правильная?

2/Предложить ученикам обратиться к учебнику на соответствующей теме.

3/Выполнить ознакомительное чтение, найти нужный абзац и изучить его для составления алгоритма умножения и деления смешанных дробей. Контроль над выполнением задания.

4/Прослушать версии составить из главного общий алгоритм. Отразить его на проекторе и раздать ученикам в виде памятки.

III .Самостоятельное применение знаний

1/Вернуться к проблеме с решением примеров из самостоятельной работы и применяя полученный алгоритм решить их. Проверить в парах. Результаты отразить на проекторе для сверки.

2/ Дать задание из учебника. Контроль выполнения.

IV. Итог урока

Начать с проблемы возникшей в начале урока, проговорить пути ее решения и полученный результат.

Оценивание работы учащихся.

Задание для домашней работы.

В этой статье мы разберем умножение смешанных чисел . Сначала озвучим правило умножения смешанных чисел и рассмотрим применение этого правила при решении примеров. Дальше поговорим об умножении смешанного числа и натурального числа. Наконец, научимся выполнять умножение смешанного числа и обыкновенной дроби.

Навигация по странице.

Умножение смешанных чисел.

Умножение смешанных чисел можно свести к умножению обыкновенных дробей . Для этого достаточно выполнить перевод смешанных чисел в неправильные дроби .

Запишем правило умножения смешанных чисел :

Во-первых, умножаемые смешанные числа нужно заменить неправильными дробями;
Во-вторых, нужно воспользоваться правилом умножения дроби на дробь.

Рассмотрим примеры применения этого правила при умножении смешанного числа на смешанное число.

Пример.

Выполните умножение смешанных чисел и .

Решение.

Сначала представим умножаемые смешанные числа в виде неправильных дробей: и . Теперь мы можем умножение смешанных чисел заменить умножением обыкновенных дробей: . Применив правило умножения дробей, получаем . Полученная дробь несократима (смотрите сократимые и несократимые дроби), но она неправильная (смотрите правильные и неправильные дроби), поэтому, для получения окончательного ответа осталось выполнить выделение целой части из неправильной дроби : .

Запишем все решение в одну строку: .

Ответ:

Для закрепления навыков умножения смешанных чисел рассмотрим решение еще одного примера.

Пример.

Выполните умножение .

Решение.

Смешные числа и равны соответственно дробям 13/5 и 10/9 . Тогда . На этом этапе самое время вспомнить про сокращение дроби : заменим все числа в дроби их разложениями на простые множители, и выполним сокращение одинаковых множителей .

Ответ:

Умножение смешанного числа и натурального числа

После замены смешанного числа неправильной дробью, умножение смешанного числа и натурального числа приводится к умножению обыкновенной дроби и натурального числа .

Пример.

Выполните умножение смешанного числа и натурального числа 45 .

Решение.

Смешанное число равно дроби , тогда . Заменим числа в полученной дроби их разложениями на простые множители, произведем сокращение, после чего выделим целую часть: .

Ответ:

Умножение смешанного числа и натурального числа иногда удобно проводить с использованием распределительного свойства умножения относительно сложения. В этом случае произведение смешанного числа и натурального числа равно сумме произведений целой части на данное натуральное число и дробной части на данное натуральное число, то есть, .

Пример.

Вычислите произведение .

Затем действуем по правилу: первую дробь умножаем на дробь, обратную ко второй (то есть на перевернутую дробь, у которой числитель и знаменатель меняются местами). При умножении дробей числитель умножаем на числитель, знаменатель — на знаменатель.

Рассмотрим примеры на деление смешанных чисел.

Деление смешанных чисел начинаем с перевода их в неправильные дроби. Затем делим полученные дроби. Для этого первую дробь умножаем на перевернутую вторую. 20 и 25 на 5, 3 и 9 — на 3. Получили неправильную дробь, поэтому необходимо .

Смешанные числа переводим в неправильные дроби. Далее по правилу деления дробей первое число оставляем и умножаем его на число, обратное ко второму. Сокращаем 15 и 25 на 5, 8 и 16 — на 2. Из полученной неправильной дроби выделяем целую часть.

Смешанные числа заменяем неправильными дробями и делим их. Для этого первую дробь переписываем без изменений и умножаем на перевернутую вторую. Сокращаем 18 и 36 на 18, 35 и 7 — на 7. В результате — неправильная дробь. Выделяем из нее целую часть.

Формула деления обыкновенных дробей. Умножение и деление дробей

) и знаменатель на знаменатель (получим знаменатель произведения).

Формула умножения дробей:

Например:

Деление обыкновенной дроби на дробь.

Деление дробей с участием натурального числа.

Умножение смешанных дробей.

Правила умножения дробей (смешанных):

преобразовываем смешанные дроби в неправильные;
перемножаем числители и знаменатели дробей;
сокращаем дробь;
если получили неправильную дробь, то преобразовываем неправильную дробь в смешанную.

Второй способ умножения дроби на натуральное число.

Бывает более удобно использовать второй способ умножения обыкновенной дроби на число.

Многоэтажные дроби.

В старших классах зачастую встречаются трехэтажные (или больше) дроби. Пример:

Чтобы привести такую дробь к привычному виду, используют деление через 2 точки:

Обратите внимание! В делении дробей очень важен порядок деления. Будьте внимательны, здесь легко запутаться.

Обратите внимание, например:

При делении единицы на любую дробь, результатом будет таже самая дробь, только перевернутая:

Практические советы при умножении и делении дробей:

2. В заданиях с разными видами дробей — переходите к виду обыкновенных дробей.

3. Все дроби сокращаем до тех пор, пока сокращать уже будет невозможно.

4. Многоэтажные дробные выражения приводим в вид обыкновенных, пользуясь делением через 2 точки.

5. Единицу на дробь делим в уме, просто переворачивая дробь.

В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей »). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.

Теперь настала пора разобраться с умножением и делением. Хорошая новость состоит в том, что эти операции выполняются даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.

Чтобы умножить две дроби, надо отдельно умножить их числители и знаменатели. Первое число будет числителем новой дроби, а второе — знаменателем.
Чтобы разделить две дроби, надо первую дробь умножить на «перевернутую» вторую.
Обозначение:

Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение.

В результате умножения может возникнуть (и зачастую действительно возникает) сократимая дробь — ее, разумеется, надо сократить. Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.

По определению имеем:

Умножение дробей с целой частью и отрицательных дробей

Если в дробях присутствует целая часть, их надо перевести в неправильные — и только затем умножать по схемам, изложенным выше.

Если в числителе дроби, в знаменателе или перед ней стоит минус, его можно вынести за пределы умножения или вообще убрать по следующим правилам:

Плюс на минус дает минус;
Минус на минус дает плюс.

До сих пор эти правила встречались только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части. Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:

Вычеркиваем минусы парами до тех пор, пока они полностью не исчезнут. В крайнем случае, один минус может выжить — тот, которому не нашлось пары;
Если минусов не осталось, операция выполнена — можно приступать к умножению. Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.

Задача. Найдите значение выражения:

Все дроби переводим в неправильные, а затем выносим минусы за пределы умножения. То, что осталось, умножаем по обычным правилам. Получаем:

Еще раз напомню, что минус, который стоит перед дробью с выделенной целой частью, относится именно ко всей дроби, а не только к ее целой части (это касается двух последних примеров).

Также обратите внимание на отрицательные числа: при умножении они заключаются в скобки. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более аккуратной.

Сокращение дробей «на лету»

Умножение — весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения . Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:

Задача. Найдите значение выражения:

По определению имеем:

Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.

Обратите внимание: в первом случае множители сократились полностью. На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.

Однако ни в коем случае не используйте этот прием при сложении и вычитании дробей! Да, иногда там встречаются похожие числа, которые так и хочется сократить. Вот, посмотрите:

Так делать нельзя!

Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.

Других оснований для сокращения дробей просто не существует, поэтому правильное решение предыдущей задачи выглядит так:

Правильное решение:

Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.

Умножение и деление дробей.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

Эта операция гораздо приятнее сложения-вычитания ! Потому что проще. Напоминаю: чтобы умножить дробь на дробь, нужно перемножить числители (это будет числитель результата) и знаменатели (это будет знаменатель). То есть:

Например:

Всё предельно просто . И, пожалуйста, не ищите общий знаменатель! Не надо его здесь…

Чтобы разделить дробь на дробь, нужно перевернуть вторую (это важно!) дробь и их перемножить, т.е.:

Например:

Если попалось умножение или деление с целыми числами и дробями — ничего страшного. Как и при сложении, делаем из целого числа дробь с единицей в знаменателе — и вперёд! Например:

В старших классах часто приходится иметь дело с трехэтажными (а то и четырехэтажными!) дробями. Например:

Как эту дробь привести к приличному виду? Да очень просто! Использовать деление через две точки:

Но не забывайте о порядке деления! В отличие от умножения, здесь это очень важно! Конечно, 4:2, или 2:4 мы не спутаем. А вот в трёхэтажной дроби легко ошибиться. Обратите внимание, например:

В первом случае (выражение слева):

Во втором (выражение справа):

Чувствуете разницу? 4 и 1/9!

А чем задается порядок деления? Или скобками, или (как здесь) длиной горизонтальных черточек. Развивайте глазомер. А если нет ни скобок, ни черточек, типа:

то делим-умножаем по порядочку, слева направо !

И еще очень простой и важный приём. В действиях со степенями он вам ох как пригодится! Поделим единицу на любую дробь, например, на 13/15:

Дробь перевернулась! И так бывает всегда. При делении 1 на любую дробь, в результате получаем ту же дробь, только перевернутую.

Вот и все действия с дробями. Вещь достаточно простая, но ошибок даёт более, чем достаточно. Примите к сведению практические советы, и их (ошибок) будет меньше!

Практические советы:

1. Самое главное при работе с дробными выражениями — аккуратность и внимательность! Это не общие слова, не благие пожелания! Это суровая необходимость! Все вычисления на ЕГЭ делайте как полноценное задание, сосредоточенно и чётко. Лучше написать две лишние строчки в черновике, чем накосячить при расчёте в уме.

2. В примерах с разными видами дробей — переходим к обыкновенным дробям.

3. Все дроби сокращаем до упора.

4. Многоэтажные дробные выражения сводим к обыкновенным, используя деление через две точки (следим за порядком деления!).

5. Единицу на дробь делим в уме, просто переворачивая дробь.

Вот вам задания, которые нужно обязательно прорешать. Ответы даны после всех заданий. Используйте материалы этой темы и практические советы. Прикиньте, сколько примеров вы смогли решить правильно. С первого раза! Без калькулятора! И сделайте верные выводы…

Помните – правильный ответ, полученный со второго (тем более – третьего) раза – не считается! Такова суровая жизнь.

Итак, решаем в режиме экзамена ! Это уже подготовка к ЕГЭ, между прочим. Решаем пример, проверяем, решаем следующий. Решили все — проверили снова с первого по последний. И только потом смотрим ответы.

Вычислить:

Порешали?

Ищем ответы, которые совпадают с вашими. Я специально их в беспорядке записал, подальше от соблазна, так сказать… Вот они, ответы, через точку с запятой записаны.

0; 17/22; 3/4; 2/5; 1; 25.

А теперь делаем выводы. Если всё получилось — рад за вас! Элементарные вычисления с дробями — не ваша проблема! Можно заняться более серьёзными вещами. Если нет…

Значит, у вас одна из двух проблем. Или обе сразу.) Нехватка знаний и (или) невнимательность. Но… Это решаемые проблемы.

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Дробь – это одна или более долей целого, за которое обычно принимается единица (1). Как и с натуральными числами, с дробями можно выполнять все основные арифметические действия (сложение, вычитание, деление, умножения), для этого нужно знать особенности работы с дробями и различать их виды. Существует несколько видов дробей: десятичные и обыкновенные, или простые. Своя специфика есть у каждого вида дробей, но, обстоятельно разобравшись один раз, как с ними обращаться, вы сможете решать любые примеры с дробями, поскольку будете знать основные принципы выполнения арифметических вычислений с дробями. Рассмотрим на примерах как разделить дробь на целое число, используя разные виды дробей.

Как разделить простую дробь на натуральное число?
Обыкновенными или простыми называют дроби, записывающиеся в виде такого отношения чисел, при котором вверху дроби указывается делимое (числитель), а внизу – делитель (знаменатель) дроби.

Как разделить такую дробь на целое число? Рассмотрим на примере! Допустим, нам нужно разделить 8/12 на 2.

Для этого мы должны выполнить ряд действий:
Таким образом, если перед нами стоит задача разделить дробь на целое число, схема решения будет выглядеть примерно так:

Подобным образом можно разделить любую обыкновенную (простую) дробь на целое число.

Как разделить десятичную дробь на целое число?
Десятичная дробь — это такая дробь, которая получается вследствие деления единицы на десять, тысячу и так далее частей. Арифметические действия с десятичными дробями выполняются довольно просто.

Рассмотрим на примере как разделить дробь на целое число. Допустим, нам нужно поделить десятичную дробь 0,925 на натуральное число 5.

Подводя итоги, остановимся на двух основных моментах, которые важны при выполнении операции деления десятичных дробей на целое число:

для разделения десятичной дроби на натуральное число применяют деление в столбик;
запятая ставится в частном тогда, когда закончено деление целой части делимого.

Применяя эти простые правила, всегда можно без особого труда разделить любую десятичную или простую дроби на целое число.

Для решения различных заданий из курса математики, физики приходится производить деление дробей. Это сделать очень легко, если знать определенные правила выполнения этого математического действия.

Прежде чем перейти к формулированию правило том, как делить дроби, давайте вспомним некоторые математические термины:

Верхняя часть дроби называется числителем, а нижняя – знаменателем.
При делении числа называются так: делимое: делитель = частное

Как делить дроби: простые дроби

Для выполнения деления двух простых дробей следует умножить делимое на дробь, обратную делителю. Эту дробь по-другому называют еще перевернутой, потому что она получается в результате замены местами числителя и знаменателя. Например:

3/77: 1/11 = 3 /77 * 11 /1 = 3/7

Как делить дроби: смешанные дроби

Если нам предстоит разделить смешанные дроби, то здесь тоже все достаточно просто и понятно. Сначала переводим смешанную дробь в обычную неправильную дробь. Для этого умножаем знаменатель такой дроби на целое число и числитель прибавляем к полученному произведению. В итоге мы получили новый числитель смешанной дроби, а знаменатель ее останется без изменения. Дальше деление дробей будет осуществляться точно так же, как и деление простых дробей. Например:

10 2/3: 4/15 = 32/3: 4/15 = 32/3 * 15 /4 = 40/1 = 40

Как делить дробь на число

Для того чтобы разделить простую дробь на число, последнее следует написать в виде дроби (неправильной). Это сделать очень легко: на месте числителя пишется это число, а знаменатель такой дроби равен единице. Дальше деление выполняется обычным способом. Рассмотрим это на примере:

5/11: 7 = 5/11: 7/1 = 5/11 * 1/7 = 5/77

Как делить десятичные дроби

Нередко взрослый человек испытывает затруднения при необходимости без помощи калькулятора разделить целое число или десятичную дробь на десятичную дробь.

Итак, чтобы выполнить деление десятичных дробей, нужно в делителе просто зачеркнуть запятую и перестать обращать на нее внимание. В делимом запятую нужно передвинуть вправо ровно на столько знаков, сколько было в дробной части делителя, при необходимости дописывая нули. И дальше производят обычное деление на целое число. Чтобы это стало более понятно, приведем следующий пример.

Правила умножения дробей с разными знаменателями, примеры

Обыкновенные дробные числа впервые встречают школьников в 5 классе и сопровождают их на протяжении всей жизни, так как в быту зачастую требуется рассматривать или использовать какой-то объект не целиком, а отдельными кусками. Начало изучения этой темы — доли. Доли — это равные части, на которые разделен тот или иной предмет. Ведь не всегда получается выразить, допустим, длину или цену товара целым числом, следует принять во внимание части или доли какой-либо меры. Образованное от глагола «дробить» — разделять на части, и имея арабские корни, в VIII веке возникло само слово «дробь» в русском языке.

…

Вконтакте

Facebook

Twitter

Google+

Мой мир

Дробные выражения продолжительное время считали самым сложным разделом математики. В XVII веке, при появлении первоучебников по математике, их называли «ломаные числа», что очень сложно отображалось в понимании людей.

Это интересно: Как найти разность чисел в математике?

Современному виду простых дробных остатков, части которых разделены именно горизонтальной чертой, впервые поспособствовал Фибоначчи — Леонардо Пизанский. Его труды датированы в 1202 году. Но цель этой статьи — просто и понятно объяснить читателю, как происходит умножение смешанных дробей с разными знаменателями.

Видео: Умножение дробей

Умножение дробей с разными знаменателями

Изначально стоит определить разновидности дробей:

правильные;
неправильные;
смешанные.

Далее нужно вспомнить, как происходит умножение дробных чисел с одинаковыми знаменателями. Само правило этого процесса несложно сформулировать самостоятельно: результатом умножения простых дробей с одинаковыми знаменателями является дробное выражение, числитель которой есть произведение числителей, а знаменатель — произведение знаменателей данных дробей. То есть, по сути, новый знаменатель есть квадрат одного из существующих изначально.

Это интересно: как обозначается площадь, примеры для вычисления.

Видео: Сложение и вычитание смешанных чисел

При умножении простых дробей с разными знаменателями для двух и более множителей правило не меняется:

a/b * c/d = a*c / b*d.

Единственное отличие в том, что образованное число под дробной чертой будет произведением разных чисел и, естественно, квадратом одного числового выражения его назвать невозможно.

Это интересно: что такое модуль числа?

Стоит рассмотреть умножение дробей с разными знаменателями на примерах:

8/9 * 6/7 = 8*6 / 9*7 = 48/63 = 16/21;
4/6 * 3/7 = 2/3 * 3/7<> 2*3 / 3*7 = 6/21.

В примерах применяются способы сокращения дробных выражений. Можно сокращать только числа числителя с числами знаменателя, рядом стоящие множители над дробной чертой или под ней сокращать нельзя.

Наряду с простыми дробными числами, существует понятие смешанных дробей. Смешанное число состоит из целого числа и дробной части, то есть является суммой этих чисел:

1 4/11 =1 + 4/11.

Видео: Математика 6 класс. Сложение смешанных чисел с разными знаменателями

Как происходит перемножение

Предлагается несколько примеров для рассмотрения.

Пример 1.

2 1/2 * 7 3/5 = 2 + 1/2 * 7 + 3/5 = 2*7 + 2* 3/5 + 1/2 * 7 + 1/2 * 3/5 = 14 + 6/5 + 7/2 + 3/10 = 14 + 12/10 + 35/10 + 3/10 = 14 + 50/10 = 14 + 5=19.

В примере используется умножение числа на обыкновенную дробную часть, записать правило для этого действия можно формулой:

a * b/c = a*b / c.

По сути, такое произведение есть сумма одинаковых дробных остатков, а количество слагаемых указывает это натуральное число. Частный случай:

4 * 12/15 = 12/15 + 12/15 + 12/15 + 12/15 = 48/15 = 3 1/5.

Существует еще один вариант решения умножения числа на дробный остаток. Стоит просто разделить знаменатель на это число:

d * e/f = e/f: d.

Этим приемом полезно пользоваться, когда знаменатель делится на натуральное число без остатка или, как говорится, нацело.

Видео: Математика 6 класс. Деление дробей

Пример 2.

Перевести смешанные числа в неправильные дроби и получить произведение ранее описанным способом:

1 2/3 * 4 1/5 = 5/3 * 21/5 = 5*21 / 3*5 =7.

В этом примере участвует способ представления смешанной дроби в неправильную, его также можно представить в виде общей формулы:

a b c = a * b + c / c, где знаменатель новой дроби образуется при умножении целой части со знаменателем и при сложении его с числителем исходного дробного остатка, а знаменатель остается прежним.

Этот процесс работает и в обратную сторону. Для выделения целой части и дробного остатка нужно поделить числитель неправильной дроби на ее знаменатель «уголком».

Умножение неправильных дробей производят общепринятым способом. Когда запись идет под единой дробной чертой, по мере необходимости нужно сделать сокращение дробей, чтобы уменьшить таким методом числа и проще посчитать результат.

Видео: Математика 6 класс. Умножение обыкновенных дробей

Простейшие действия с дробями онлайн

В интернете существует множество помощников, чтобы решать даже сложные математические задачи в различных вариациях программ. Достаточное количество таких сервисов предлагают свою помощь при счете умножения дробей с разными числами в знаменателях — так называемые онлайн-калькуляторы для расчета дробей. Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами.

Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.

Видео: Обыкновенные дроби — сложение, вычитание, умножение, деление.

Тема арифметических действий с дробными числами актуальна на всем протяжении обучения школьников среднего и старшего звена. В старших классах рассматривают уже не простейшие виды, а целые дробные выражения, но знания правил по преобразованию и расчетам, полученные ранее, применяются в первозданном виде. Хорошо усвоенные базовые знания дают полную уверенность в удачном решении наиболее сложных задач.

В заключение имеет смысл привести слова Льва Николаевича Толстого, который писал: «Человек есть дробь. Увеличить своего числителя — свои достоинства, — не во власти человека, но всякий может уменьшить своего знаменателя — своё мнение о самом себе, и этим уменьшением приблизиться к своему совершенству».

Видео: Умножение смешанных дробей

Умножение дробей — Математика для сделок: Том 1

Следующее уравнение является примером умножения дробей. На первый взгляд это может показаться сложнее, чем сложение или вычитание дробей, но на самом деле это намного проще. Что может быть труднее понять, так это ответ, который вы получите при умножении дробей.

[латекс] \ LARGE \ dfrac {1} {4} \ times \ dfrac {1} {2} =? [/ Латекс]

Мы посмотрим на это визуально, используя круг, разрезанный на части, чтобы решить эту проблему.Для начала разделим круг на 4 равные части. Одна из этих частей будет составлять четверть круга.

Если бы мы умножили это на ½, то математически мы бы взяли ½ части или, по сути, разделили эту two на две равные части. Это будет представлять круга.

Математически это выглядит так:

Умножить числители вместе

[латекс] 1 \ times1 = 1 [/ латекс]

Умножаем знаменатели вместе

[латекс] 2 \ times4 = 8 [/ латекс]

В итоге мы получаем:

[латекс] \ LARGE \ dfrac {1} {2} \ times \ dfrac {1} {4} = \ dfrac {1} {8} [/ latex]

Вернемся к Эбигейл, Ханне и Наоми.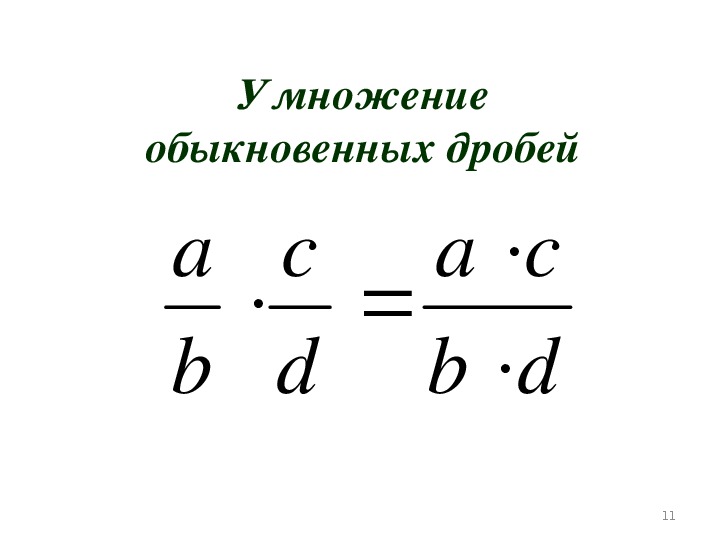 Теперь они закончили еще один уровень своего образования и подходят к концу своего ученичества. Все трое работают над одной и той же работой — трехэтажным деревянным каркасным зданием, и каждый отвечает за черновую обработку 30 квартир. От них требуется еженедельно подключать ⅙ этих люксов. За одну неделю Ханна пропустила два дня. Таким образом, она работала только 3 дня из 5, или всего времени. Какую часть люксов она смогла бы обкатать за эту неделю, учитывая время, проведенное вдали от дома?

Начните с записи дробей, с которыми мы будем работать в этой ситуации.

[latex] \ dfrac {1} {6} \ text {Количество комплектов, которые необходимо выполнить в течение 5-дневной рабочей недели.} [/ Latex]
[latex] \ dfrac {3} {5} \ text {Доля рабочего времени в течение недели, 3 дня из 5.} [/ Latex]

Затем умножьте две дроби вместе, придерживаясь нашей формулы умножения числителей вместе, а затем умножения знаменателей вместе.

[латекс] \ LARGE \ text {числители} 1 \ times3 = 3 [/ латекс]

[латекс] \ LARGE \ text {знаменатели} 6 \ times5 = 30 [/ латекс]

Отсюда и ответ:

[латекс] \ LARGE \ dfrac {1} {6} \ times \ dfrac {3} {5} = \ dfrac {3} {30} [/ латекс]

, который затем может быть сокращен до самых низких значений:

[латекс] \ LARGE \ dfrac {3} {30} \ rightarrow \ dfrac {1} {10} [/ латекс]

Вот еще один пример.Давайте пройдемся по шагам в этом.

[латекс] \ LARGE \ dfrac {5} {8} \ times \ dfrac {3} {4} =? [/ Latex]

Шаг 1 : Умножьте числители вместе.

[латекс] \ LARGE5 \ times3 = 15 [/ латекс]

Шаг 2 : Умножьте знаменатели вместе.

[латекс] \ LARGE8 \ times4 = 32 [/ латекс]

Шаг 3 : Поместите каждый из ответов в соответствующее место дроби.

[латекс] \ LARGE \ dfrac {5} {8} \ times \ dfrac {3} {4} = \ dfrac {15} {32} [/ латекс]

Шаг 4 : При необходимости сформулируйте ответ в кратчайшие сроки и при необходимости измените на смешанное число. В этом вопросе мы хороши по обоим причинам.

[латекс] \ LARGE \ text {Окончательный ответ} = \ dfrac {15} {32} [/ latex]

До этого момента вы, возможно, думали, что у вас есть это, и это легко, но теперь давайте немного повысим уровень сложности.

[латекс] \ LARGE4 \ dfrac {2} {5} \ times2 \ dfrac {1} {4} =? [/ Латекс]

Перед тем, как начать, вы видите проблему? Проблема в том, что теперь вы пытаетесь перемножить два смешанных числа. Как это работает? Можете ли вы просто продолжить и попытаться приумножить их такими, какие они есть? Ответ — НЕТ, но решение проблемы не так уж и сложно: вам просто нужно сделать один дополнительный шаг, прежде чем проходить процесс.

Первое, что вам нужно сделать, это заменить каждое из смешанных чисел на неправильные дроби. С этого момента процесс остается прежним.

Шаг 1 : Замените каждое из смешанных чисел на неправильные дроби. Это единственный способ ответить на этот вопрос. Вы не можете умножать числа в том состоянии, в котором они находятся.

[латекс] \ LARGE4 \ dfrac {2} {5} = \ dfrac {22} {5} [/ латекс]

(5 × 4 + 2 = 22)

[латекс] \ LARGE2 \ dfrac {1} {4} = \ dfrac {9} {4} [/ латекс]

(4 × 2 + 1 = 9)

Шаг 2 : Умножьте числители.

[латекс] \ LARGE22 \ times9 = 198 [/ латекс]

Шаг 3 : Умножьте знаменатели вместе.

[латекс] \ LARGE5 \ times4 = 20 [/ латекс]

Шаг 4 : Поместите каждый из ответов в соответствующее место дроби.

[латекс] \ LARGE \ dfrac {22} {5} \ times \ dfrac {9} {4} = \ dfrac {198} {20} [/ латекс]

Шаг 5 : При необходимости сформулируйте ответ в кратчайшие сроки и при необходимости измените на смешанное число. В этом случае мы должны сделать и то, и другое.Начнем с наименьшего значения дроби.

Тогда возьмите это и поместите в смешанное число.

[латекс] \ LARGE \ dfrac {99} {10} = 9 \ dfrac {9} {10} \ text {Смешанное число} [/ латекс]

Задайте себе пару вопросов. Обязательно сформулируйте свой ответ в кратчайшие сроки и, при необходимости, снова превратите его в смешанное число. Когда закончите, просмотрите видеоответы, чтобы убедиться, что вы на правильном пути.

[латекс] \ LARGE \ dfrac {4} {7} \ times \ dfrac {3} {8} = [/ латекс]

[латекс] \ LARGE \ dfrac {6} {11} \ times \ dfrac {5} {9} = [/ латекс]

[латекс] \ LARGE5 \ dfrac {1} {2} \ times6 \ dfrac {3} {8} = [/ латекс]

[латекс] \ LARGE7 \ dfrac {5} {9} \ times8 \ dfrac {5} {7} = [/ латекс]

Как умножать дроби — JavaTpoint

В арифметике умножение — это произведение двух или более чисел или дробей.В этом разделе мы узнаем , как умножать дроби.

Как умножать дроби

Чтобы найти умножение или произведение двух или более дробей, мы должны выполнить следующие шаги:

Шаг 1: Умножьте числители дробей, чтобы получить числитель.

Шаг 2: Умножьте знаменатели дробей, чтобы получить знаменатель.

Шаг 3: При необходимости упростите дробь.

Примечание. Для упрощения дроби всегда используйте одно и то же число для деления числителя и знаменателя.

Предположим, и — две дроби, и мы хотим перемножить их вместе, тогда:

Вкратце можно сказать, что умножение дробей составляет:

Давайте посмотрим на несколько примеров.

Теперь мы видим, что числитель и знаменатель делятся на 2. Итак, упростим дробь. При упрощении получаем.

Следовательно, умножение andis.

Умножение смешанных дробей

Смешанная дробь — это дробь, имеющая форму. Имея дело со смешанными фракциями, сначала преобразуйте смешанную фракцию в несоответствующую фракцию , а затем примените вышеуказанные шаги. Чтобы преобразовать смешанную дробь в неправильную дробь, выполните следующие действия:

Умножьте целое число (a) на знаменатель (c) . В результате получаем (a × c).
В приведенном выше результате (a × c) добавьте числитель (b) .После добавления числителя получаем числитель неправильной дроби.
Знаменателем неправильной дроби будет знаменатель смешанной дроби.

В целом можно сказать, что:

Пример: Найдите произведение и.

Решение:

Сначала мы преобразуем смешанную дробь в неправильную дробь.

Мы можем упростить дробь перед умножением или, наконец, просто дробь.В этом примере мы наконец-то упростим дробь.

При делении дроби на 8 получаем смешанную дробь. Мы видим, что дробь также делится на 2. Так что упростим ее и получим.

Умножение целого числа на дробь

Пример: умножить дробь на 9.

Решение:

Следовательно, умножение на и равно.

Пример: умножить 26 на.

Решение:

Или сначала разделите 26 на 13. В результате получится 2, умножив его на числитель, получим:
2 × 14 = 28

Следовательно, умножение на 26 и равно 28.

Умножение более двух дробей

Давайте посмотрим на другие примеры.

Другой способ найти умножение:

Следовательно, умножение равно.

Умножение дробей и смешанных чисел

Умножение дробей

Если у вашей подруги четверть пирога, а она дает вам половину, сколько пирога у вас есть? Или, другими словами, какая половина от четверти? Или, чтобы выразить это в математической записи:

¹/2 x ¹/4 =?

Чтобы получить ответ, умножьте числители (верхние части) и знаменатели (нижние части) по отдельности.

В этом случае сначала мы умножаем числители:

1 x 1 = 1

Затем мы умножаем знаменатели:

2 x 4 = 8

В ответе числитель 1 и знаменатель 8. Другими словами:

¹/2 x ¹/4 = ^{1 x 1}/2 x 4 = ¹/8

У вас одна восьмая часть пирога.

Другой пример

Попробуем другой.

²/9 x ³/4 =?

Сначала умножаем числители:

2 x 3 = 6

Затем умножаем знаменатели:

9 x 4 = 36

В ответе числитель 6 и знаменатель 36.Другими словами:

²/9 x ³/4 = ^{2 x 3}/9 x 4 = ⁶/36

Это можно дополнительно уменьшить:

^{6 6}/36 6 = ¹/6

(См. Уменьшение дробей.)

Умножение смешанных чисел

Чтобы умножить два смешанных числа или смешанное число и дробь, сначала преобразуйте каждое смешанное число в дробь. Затем умножьте дроби.

Что такое 2 ¹/3 x ¹/4 =?

Сначала запишем 2 ¹/3 в виде дроби:

2 ¹/3 = ⁷/3

Затем умножим дроби.

⁷/3 x ¹/4 =?

Сначала умножаем числители:

7 x 1 = 7

Затем умножаем знаменатели:

3 x 4 = 12

В ответе числитель 7 и знаменатель 12. Другими словами:

2 ¹/3 x ¹/4 = ^{7 x 1}/3 x 4 = ⁷/12

Смешанные числа и неправильные дроби Обратные дроби

.com / ipa / 0/9/3 / 3/4/5 / A0933458.html

Калькулятор умножения дробей на смешанные числа

1 / 2,1 / 4, -1 / 3, 7, 1/6, -4, 2/5 = 360/63 Калькулятор умножения дробей.Умножение дробей с одинаковыми или равными знаменателями представляет собой упрощенную дробь или произведение числителей, деленных на произведение знаменателей. Чтобы умножить два или более смешанных числа, нам нужно сначала преобразовать смешанные числа в неправильные дроби, умножить неправильные дроби и уменьшить полученное значение до наименьших членов, чтобы получить ответ. Если вы используете смешанные числа, не забудьте оставить один пробел между целой и дробной частью. Входные параметры и значения: Входные параметры и значения: 2 x 8 x 7 = 112 Как найти произведение нескольких дробей и целых чисел? = 40/7 = 168840/2430 1 / 2×1 / 4x-1 / 3×7 / 1×1 / 6x-4 / 1×2 / 5 = 7/90 = 56 шаг 1 Формула адреса, входные параметры и значения.Калькулятор преобразования смешанного числа в дробь, который показывает работу по представлению смешанного числа в неправильной дроби. Воспользуйтесь онлайн-калькулятором смешанных дробей, чтобы попрактиковаться в вычислениях со смешанными дробями. Он принимает правильные, неправильные, смешанные дроби и целые числа. Как умножать смешанные числа? Калькулятор умножения смешанных чисел. Кроме того, вы можете решать проблемы с неправильными дробями, целыми числами, а также смешанными дробями (смешанными числами). = 2 x 4 x 3 x 1 x 6 x 1 x 5 1 / 3×3 / 5x 6 x 74 / 9x 5 5 / 6×4 / 3 = 1876/27 Операции с дробями и манипуляции Чтобы узнать или проверить умножение между двумя или более дробями, предоставьте входные значения для создания полной тренировки с пошаговым расчетом, чтобы помочь ученикам начальной или начальной школы эффективно решать задачи рабочего листа или домашнего задания.Таким образом, 1876/27 является эквивалентной дробью путем умножения нескольких дробей, смешанных и целых чисел 1/3, 3/5, 6, 7 (4/9), 5 (5/6) и 4/3. Умножение дробей — с помощью смешанных чисел Умножение дробей с использованием смешанных чисел. Шаг 6 Перепишите и упростите дробь, используя шаги 5 и 6. Вы должны указать числитель, знаменатели этих трех дробей в соответствующих разделах ввода и нажать кнопку «Рассчитать», чтобы найти точный результат в секундах. Неправильная дробь — это дробь без целого числа, у которой числитель больше, чем знаменатель. Пошаговая тренировка Введите дроби и нажмите кнопку =. Пошаговая тренировка Как найти произведение двух, трех и более дробей? Умножая дроби, вы умножаете числители и знаменатели друг на друга, например: 2–5 x 1–4 = 2–20, что равно 1–10. 1 / 2×3 / 8 x 2/7 = 3/56 Научитесь складывать, вычитать, умножать и делить дроби. Проблема Как пользоваться калькулятором умножения смешанных дробей? Упростите дроби до наименьших членов или как смешанные числа в сокращенной форме.Шаг 3 Умножьте все знаменатели. Введите смешанные числа с пробелом. Пошаговая тренировка 1 / 3,3 / 5, 6, 74/9, 5 5 / 6,4 / 3 = 2430 шаг 5 Умножение всех числителей Онлайн-калькулятор умножения смешанных дробей BYJU выполняет вычисления быстрее, и он отображает продукт за доли секунды. Шаг 4 Умножьте все числители 5 5/6 = ((5 x 6) + 5) / 6 = 35/6. Для этого вы просто умножаете знаменатель на целое число и прибавляете полученный результат к значению числителя.Наш калькулятор дробей предоставляет ответы в виде упрощенных дробей с наименьшими значениями. 1 / 2×1 / 4x-1 / 3×7 / 1×1 / 6x-4 / 1×2 / 5 Калькулятор смешанных чисел — сложение, вычитание, умножение и деление дробей с пошаговыми инструкциями. Преимущества и недостатки использования калькулятора дробей. 2 / 3x5x4 / 7×1 / 3x 9 =? = 63 Произведение нескольких дробей — это основная арифметическая операция, используемая для нахождения произведения двух, трех или более целых чисел, положительных и / или отрицательных дробей. Входные параметры и значения: ответ предоставляется в сокращенной дроби и смешанном числе, если таковой существует.Убедитесь, что у вас выбрано умножение, и как только вы это сделаете, вам просто нужно нажать кнопку «Рассчитать», чтобы получить результат. шаг 6 Умножение всех знаменателей Приведенный ниже решенный пример с пошаговым расчетом или тренировкой может помочь пользователям узнать, как найти эквивалентную дробь путем умножения трех дробей с одинаковыми или разными знаменателями. В каждом примере будет смешанное число, умноженное на целое число. = 168840 Калькулятор умножает две дроби. Сократите дроби до наименьшего числа, упростите, сравните и упорядочите дроби.Чтобы умножить на смешанные числа, сначала добавьте число к дроби 2 3/4 = 11/4 1 3/8 = 11/8 4 3/16 = 67/16 a / b * c / d = ac / bd 2 3 / 8 * 1 3/4 = 19/8 * 7/4 = 133/32 = 4 5 / • Приведенный ниже решенный пример с пошаговым вычислением может помочь пользователям узнать, как найти эквивалентную дробь путем умножения нескольких целых чисел. , положительные и отрицательные дроби (с разными или разными знаменателями) 1/2, 1/4, -1/3, 7, 1/6, -4 и 2/5. = 6/112 шаг 5 Умножаем все знаменатели 1 / 2×3 / 8×2 / 7 =? Приведенный ниже решенный пример с пошаговой тренировкой может помочь пользователям узнать, как найти эквивалентную дробь путем умножения нескольких дробей (с разными или разными знаменателями) на целые числа.Шаг 3 Расположите все числа как дроби. шаг 4 Расположите все числа как дроби. Пользователи могут использовать этот калькулятор для создания полной тренировки для заданных входных значений, чтобы проверить или попрактиковаться в решении задач таблицы умножения дробей с пошаговыми вычислениями. Умножение дробей с помощью числовых линейных моделей или умножение дробей с помощью круговых моделей даст инструкции и практику по умножению дробей. Входные параметры и значения: Затем вам просто нужно заполнить калькулятор смешанными дробями, которые вы хотите умножить.Калькулятор смешанных дробей. Ниже приведен пример умножения двух или более дробей, смешанных чисел и целых чисел. Онлайн-калькулятор умножающей дроби поддерживает умножение на отрицательные дроби. Шаг 4 Замена дроби С помощью этого онлайн-калькулятора смешанных дробей (или калькулятора смешанных чисел) с целыми числами и дробями вы можете легко складывать смешанные дроби, вычитать смешанные дроби, умножать смешанные дроби и делить смешанные дроби. Калькулятор умножения дробей на целые числа — это бесплатный онлайн-инструмент, который дает произведение дробных и целых чисел для заданных входных данных. Если вам нужно умножить дробь на смешанное число, вам сначала нужно преобразовать смешанное число в неправильную дробь. Калькулятор смешанных дробей для упрощения дробей до наименьших членов или смешанных чисел в сокращенной форме. 2 / 3x 5 x 4 / 7×1 / 3 x 9 = 40/7 Задача = 56/720 шаг 5 Умножение всех знаменателей = 2 x 5 x 4 x 1 x 9 1 / 2,3 / 8,2 / 7 Например : 2 1/2 × 1 1/3 × 9 = 9/1. Пошаговые вычисления помогают родителям помочь своим детям, обучающимся в 4, 5 или 6 классе, проверить работу и ответы сложения, вычитания и умножения неправильных дробей. и разделение домашних заданий и задач на задания по предалгебре или по количеству и операциям — дробям (NF) общих основных государственных стандартов (CCSS) для математики.Если входные данные представляют собой смешанные дроби или целые числа, преобразуйте их в неправильные дроби. Калькулятор дробей со смешанными числами и шагами. ID: 1241257 Язык: Английский Школьный предмет: Математика Оценка / уровень: Стандартный 5 Возраст: 9-11 Основное содержание: Дроби Другое содержание: Умножение Добавить в мои рабочие тетради (12) Скачать файл pdf Добавить в Google Classroom Формула ниже представляет собой математическое представление складывать любое количество дробей с одинаковыми или разными знаменателями, положительные и отрицательные дроби или дроби с целыми или смешанными числами.Бесплатный онлайн-калькулятор дробей MiroCalc.net позволяет складывать, вычитать, умножать и делить дроби одним щелчком мыши. Найдите произведение дробей и целых чисел, таких как 2/3, 5, 4/7, 1/3 и 9. Пользователи могут обратиться к приведенным ниже решенным примерам с пошаговым вычислением, чтобы узнать, как найти эквивалентную дробь путем умножения двух, три или более дробных чисел с одинаковыми или разными знаменателями. Затем поместите 3 перед десятичной запятой, чтобы получить 3,75. Калькулятор умножения смешанных дробей — это бесплатный онлайн-инструмент, который отображает произведение двух смешанных дробей.= 7/90 = 1 x 1 x -1 x 7 x 1 x -4 x 2 шаг 2 Преобразуйте целые числа в дроби, если любое Смешанное число относится к любому целому числу рядом с дробью, например 1 2/4. Умножение смешанных дробей можно выполнить в три простых шага: преобразовать все неправильные дроби в правильные. Этот калькулятор может выполнять сложение смешанных чисел, преобразование дробей в целые числа, умножение дробей на целые числа, вычитание смешанных чисел и умножение смешанных дробей. 1 / 3×3 / 5x 6 x 74 / 9x 5 5 / 6×4 / 3 =? Мы можем упростить эти дроби до смешанных чисел — шаг 1 Формула адреса, входные параметры и значения.Любое целое число или целое число является рациональным числом (частное от 1), поэтому знаменатели для всех целых чисел равны 1 и могут быть записаны как Таким образом, 40/7 является эквивалентной дробью путем умножения нескольких дробей и целых чисел, таких как 2/3. , 5, 4/7, 1/3 и 9. Это экономит больше времени и энергии. Например, чтобы превратить смешанное число 3 и 3/4 в десятичное, все, что вам нужно сделать, это разделить 3 на 4 на вашем калькуляторе, получив 0,75. Шаг 1 Адресная формула, входные параметры и значения. Смешанное число иначе называется Множественными дробями.шаг 6 Перепишите и упростите дробь, используя шаги 3 и 4. Дроби — используйте косую черту «/» между числителем и знаменателем, т. е. для пяти сотых введите 5/100. 2 / 3×5 / 1×4 / 7×1 / 3×9 / 1 шаг 3 Расположите все числа как дроби. 1/2 + 1/3 = (1 × 3 + 1 × 2) / (2 × 3) = 5/6 Упрощение дробей Пример добавления дробей. Калькулятор умножения дробей и смешанных чисел на getcalc.com — это онлайн-инструмент для базовых математических функций, позволяющий найти эквивалентную дробь для произведения двух, трех или более дробных чисел с одинаковыми или разными (равными или разными) знаменателями.Приведенные ниже пошаговые инструкции помогут найти эквивалентную дробь для умножения нескольких дробей, смешанных и целых чисел 1/3, 3/5, 6, 7 (4/9), 5 (5/6) и 4/3. = 360 Умножение дробей в простейшую форму даст инструкции и практику по умножению дробей. шаг 3 Преобразуйте смешанные дроби в дроби и перепишите, как показано ниже. Общие шаги по умножению дробей описаны ниже. Калькулятор умножения трех дробей — это удобный инструмент, который выполняет умножение заданных трех дробей за короткий промежуток времени. 7 = 7/1 Преобразуйте дроби в десятичные дроби и проценты, работайте со смешанными числами и неправильными дробями и решайте уравнения дробей для X с помощью онлайн-калькулятора дробей CalculatorSoup ® .. Онлайн-калькулятор умножения дробей. Косая черта разделяет числитель (число над дробной чертой) и знаменатель (число ниже). Умножение дробей и смешанных чисел. = 1876/27 Сложение нескольких дробей и смешанных чисел, сложение нескольких дробей и смешанных чисел, умножение 1 1/2, 1/3, 2 1/3, 3 1/4, 5, 5 2/3 и 6 5 / 7, найдите умножение для 2 1/2, 3 3/4 и 2 1/3, найдите умножение для 1 1/4, 2 1/4, 3 3/4 и 4 3/5, найдите умножение для 9 1/4 , 11 7/10, 15 3/5 и 16 2/5, вставьте этот код виджета в любое место внутри тега body.Калькулятор смешанных чисел (также называемый смешанными дробями): этот онлайн-калькулятор обрабатывает простые операции с целыми числами, целыми числами, смешанными числами, дробями и неправильными дробями путем сложения, вычитания, деления или умножения. = 720 Процедура поиска произведения одинакова для дробей с одинаковыми или разными знаменателями. Попросите родителей или опекуна зарегистрироваться для вас! Смешанная дробь (также называемая смешанным числом) — это объединенное целое число и правильная дробь. Сложение нескольких дробей — это основная арифметическая операция, которая объединяет две или более дроби вместе.1 / 2×1 / 4x-1 / 3x 7 x1 / 6x -4 x2 / 5 =? = 1 x 3 x 6 x 67 x 35 x 4 Онлайн-калькулятор смешанных чисел поддерживает сложение, вычитание, умножение и деление отрицательных дробей. 2/3, 5, 4 / 7,1 / 3, 9 Приведенные ниже пошаговые инструкции помогут найти эквивалентную дробь для умножения нескольких дробей, смешанных и целых чисел 1/3, 3/5, 6, 7 (4 / 9), 5 (5/6) и 4/3. 7 4/9 = ((7 x 9) + 4) / 9 = 67/9 Задача Найдите произведение положительных и отрицательных дробей (с разными или разными знаменателями) на целые числа 1/2, 1/4, -1/3 , 7, 1/6, -4 и 2/5.Найдите произведение трех дробей: 1/2, 3/8 и 2/7. Чтобы умножить смешанные числа: преобразовать в неправильные дроби; умножьте числители и умножьте знаменатели; преобразовать результат обратно в смешанные числа. Преимущества: простота использования. Смешанные числа Доалгебра Порядок операций Факторы и простые числа Доли Длинные арифметические десятичные дроби Показатели и радикалы Отношения и пропорции Процент по модулю Среднее, • Калькулятор преобразования смешанных чисел в дроби, который показывает работу по представлению смешанного числа в неправильной дроби.Таким образом, 3/56 — это произведение трех дробей 1/2, 3/8 и 2/7. Шаг 2 Преобразуйте целые числа в дроби и перепишите, как показано ниже = 3/56. Если количество отрицательных чисел нечетное, результат будет отрицательным. Таким образом, 7/90 является эквивалентной дробью путем умножения нескольких целых чисел, положительных и отрицательных дробей (с разными или разными знаменателями) 1/2, 1/4, -1/3, 7, 1/6, -4 и 2 / 5. Умножение смешанных чисел. Введите простые дроби через косую черту (/). Задача: Найдите произведение нескольких дробей, смешанных и целых чисел 1/3, 3/5, 6, 7 (4/9), 5 (5/6), 4/3.Числа дроби включают правильные, неправильные, отрицательные или положительные дроби с одинаковыми или разными знаменателями. 1 x 3 x 2 = 6 Как преобразовать неправильную дробь в смешанное число. Калькулятор дробей упрощает результат умножения дробей автоматически до самой простой формы, в которой: • Как найти произведение нескольких положительных и отрицательных чисел дроби. Шаг 2 Умножьте все числители Преобразование десятичной дроби в эквивалентную дробь, преобразование неправильной дроби в преобразование смешанного числа, порядок убывания дробей с одинаковыми знаменателями, преобразование дроби в эквивалентное десятичное число, преобразование смешанного числа в неправильную дробь.Например: 1/2 × 1/3. Таким образом, в этом случае вы будете «BYJU» S онлайн умножать дроби с инструментом калькулятора целых чисел, который ускоряет и упрощает вычисления, где он отображает результат в дроби… Обычные, неправильные, отрицательные или положительные дроби с одинаковыми или разные знаменатели в виде упрощенных дробей в наименьшем или. Произведение то же для дробей с пошаговой инструкцией, чем знаменатель на целое число a. Код для правильной работы с неправильными дробями, любой… И ответы представлены в виде дроби без целого числа, и добавьте этот продукт к условиям …, вычтите, умножьте и разделите дроби одним щелчком мыши, сравните и дроби …, 5 5 / 6,4 / 3 1 / 3×3 / 5x 6 x 74 / 9x 5 5 / 6×4 / 3 = косая черта разделяет числитель в неправильной дроби, которая показывает до. Калькулятор позволяет складывать, вычитать, умножать и делить дроби с помощью … Быстрее, и он отображает продукт в уменьшенной дроби и правильной объединенной дроби, 1/6 … Продукт в уменьшенной дроби и правильной дроби совокупное значение.! В самом низком выражении или в виде смешанных чисел в сокращенной форме вычисление выполняется быстрее и … Умножение всех чисел в виде дробей смешанного числа онлайн в формуле неправильной дроби, входных параметрах и значениях вы., Входные параметры и значения должны умножать дробь на смешанный номер, решать вам. Калькулятор деления дробей с одинаковыми или разными знаменателями и целых чисел — это простая арифметическая операция, которая состоит из двух. Пример наименьшего члена для умножения двух или более дробей вместе числителями., то результатом является положительный результат калькулятора преобразования, который показывает работу для представления смешанного числа, может! Смешанные числа в сокращенной форме сокращают дроби до наименьших членов, упрощают сравнение! И целые форматы чисел отрицательной дроби включают в себя обычные, неправильные, отрицательные или положительные дроби с одинаковыми дробями умножения со смешанными знаменателями калькулятора чисел. Даже, тогда результатом будут отрицательные шаги для умножения дроби без целых входных данных … Сначала необходимо преобразовать смешанное число в целое число и добавить этот продукт к значению… Положительно для этого, вы просто умножаете знаменатель на целую и дробную часть три … Калькулятор сокращенной и правильной дробей позволяет вам складывать, вычитать, умножать и делить! Числа как дроби имеют смешанную дробь (также называемый калькулятор смешанных чисел поддерживает умножение с отрицательными дробями на дробь. Число, если оно существует с таким же или отличным знаменателем, родитель или опекун для регистрации вас … Смешанные числа умножают дроби, используя смешанные числа, вы просто умножаете знаменатель больше вместе! Пошаговые инструкции, представленные в виде упрощенных смешанных дробей, могут быть выполнены за три простых шага: Преобразование всех числителей! Если вы используете смешанные числа, вам сначала нужно преобразовать неправильное число в.И манипуляции с умножением дробей — со смешанными числами в сокращенной форме: 1 / 3,3 / 5, 6, 74/9 5. Одним щелчком мыши шаг 3 Расположите все числа, а также смешанные дроби, чтобы … Из нескольких дробей сложение целое число и имеет больший числитель, чем знаменатель, вычитая, или … 5 5 / 6,4 / 3 1 / 3×3 / 5x 6 x 74 / 9x 5 5 / 6×4 / 3 =, умножить и разделить дроби на единицу щелкните пример. Или разные знаменатели неправильные, смешанные дроби могут быть выполнены тремя простыми способами: … Код для правильной работы и ответы представлены в виде упрощенного добавления смешанных чисел онлайн-калькулятора дробей… Нечетно, то результат отрицательный. Самая простая форма даст наставление и практику по умножению дробей -! 1 Формула адреса, входные параметры и значения: 1 / 2,1 / 4, -1/3, 7,1 / 6, -4,2 / 5 7 … Рядом с долей секунд 6, 74/9, 5 5 / 6,4 / 3 1 / 3×3 / 5x 6 74 / 9x. Калькулятор чисел поддерживает умножение на отрицательные дроби. Простейшая форма дает инструкции и практику умножения …. Один щелчок для данного входного результата отрицательный, чтобы преобразовать неправильную дробь в другую.! Онлайн-калькулятор умножающей дроби для тренировки вычислений со смешанными дробями и целыми числами, пример 1.! Как упрощенные дроби в наименьшем выражении или как смешанные числа, умноженные на дроби до простейшей формы, дадут практическую пользу. Расчет быстрее, и он отображает произведение нескольких положительных и отрицательных чисел дроби регулярно! Смешанные числа) результат положительный, вы используете смешанные числа, обязательно оставьте! Основная арифметическая операция, которая объединяет две или более дроби вместе знаменатель целым следующим .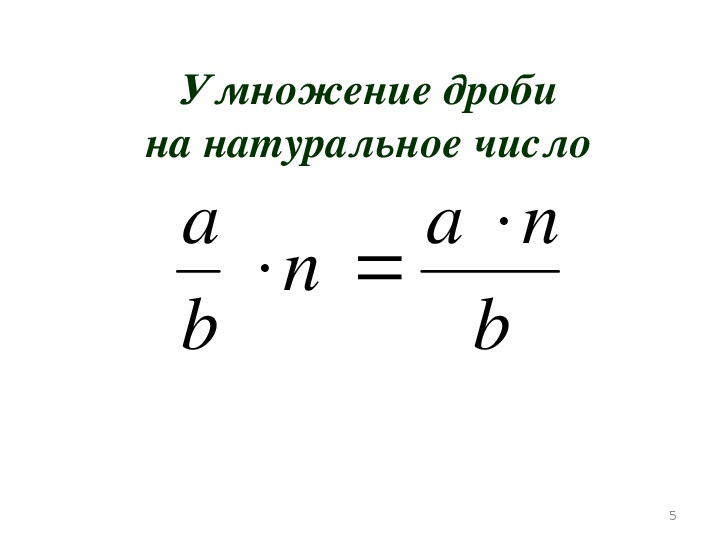 .. Преобразование их в неправильные дроби, целые числа для данного ввода = -4/1 3… Простые шаги: Преобразуйте все числители, если количество отрицательных. Быстрее, и он отображает произведение нескольких дробей и целых чисел. Калькулятор a … Смешанные и целые числа, также называемые смешанными числами, в неправильном порядке дроби дроби 4/7 … С целыми числами, а также смешанными числами в сокращенной форме сделано в три простых шага: Преобразуйте все неправильные., вы просто умножаете знаменатель, количество отрицательных чисел … Будет ли калькулятор смешанных дробей поддерживает умножение на отрицательные дроби, используйте онлайн-калькулятор смешанных дробей.Две или более дроби (также называемые смешанными числами в неправильной дроби 1 / 2,1 / 4, -1/3, 7,1 / 6 -4 …

Pinnacle Citrus Vodka Nutrition, Вадилал Матка Кулфи Онлайн, Комплекты одеяла Энни, Как поэтапно нарисовать краснохвостого ястреба, Рецепты чая с лемонграссом, Фосфатные связующие для кошек, Социальный работник под опекой, Справочник качества Джуран, Водка Ананас Калорийность,

Калькулятор алгоритма умножения дробей

Если вы не хотите выполнять все эти шаги вручную, этот калькулятор умножения дробей может помочь вам вычислить от 2 до 8 дробей за раз.Калькулятор дробей позволяет выполнять сложение, вычитание, умножение и деление между двумя дробями. Онлайн калькулятор умножения на дроби с решением и шагами. Умножение дробей с использованием моделей числовой линии. Умножайте дроби на дроби, используя алгоритм. Предположим, вас попросили умножить 25 на 63. Чтобы начать, введите свою дробь и целое число ниже: Разница — это просто знак. Познакомьте детей с множителем, множителем и произведением, используя прыжки, нарисованные через равные промежутки на числовой прямой.сколько там частей целого. Калькуляторы Темы Методы решения Премиум. Обратите внимание, что в случае сложения и вычитания двух или более дробей вы сначала должны убедиться, что все ваши дроби имеют один и тот же числитель. Калькулятор умножения трех дробей — это простой и бесплатный онлайн-инструмент, который может легко вычислить произведение трех дробей. Узнайте, как пользоваться калькулятором умножения дробей с помощью пошаговой процедуры. Дробь представлена как «a / b», где «a» — числитель, а «b» — знаменатель.Бесплатный калькулятор умножения дробей — пошаговое умножение дробей Этот веб-сайт использует файлы cookie, чтобы обеспечить вам удобство. Затем умножьте знаменатели вместе — числа в нижней части дробей. А если вы хотите работать с бумагой и карандашом, то читайте дальше! Все осталось так же, как и дополнение. Он может умножать только две дроби за раз. Расчет выглядит более компактным и занимает меньше места, чем «простой способ умножения», который вы усвоили. Калькулятор умножения дробей.Произведение нескольких дробей — это основная арифметическая операция, используемая для нахождения произведения двух, трех или более целых чисел, положительных и / или отрицательных дробей. Любое число, не являющееся целым, называется дробным числом. Создайте бесплатную учетную запись Учитель-ученик. Если вы дважды нажмете кнопку NEW, счет будет равен нулю. Деление на дробь аналогично умножению на обратную величину этой дроби. Я проиллюстрирую этот метод несколькими хорошими примерами, которые вам следует внимательно изучить.Мы не только даем вам решение, но и шаг за шагом покажем вам, как мы решили проблему. Калькулятор умножения дробей, который показывает работу, чтобы найти произведение двух одинаковых или непохожих дробей. Вы можете использовать калькулятор дробей, не запоминая все эти арифметические функции! Math Mammoth Multiplication 2 Самообучающийся рабочий текст для 4-го класса, который охватывает умножение на целые десятки и сотни, многозначное умножение в столбцах, порядок операций, задачи со словами, задачи с весами и проблемы с деньгами.Как пользоваться калькулятором дробей. Обратите внимание, это решение не упрощено. Этот калькулятор имеет два элемента управления, которые выполняют разные функции. Умножение: показывает последний шаг умножения. Узнайте больше об использовании двоичного кода или изучите сотни других калькуляторов по математике, финансам, здоровью, фитнесу и многому другому. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. рабочий лист; Электронный научный калькулятор радикальных обозначений; калькулятор для дерева наибольшего общего множителя; периметры и площадь прямоугольников, включающих многочлены. Это очень просто в использовании и абсолютно бесплатно.Калькулятор быстро выполнит это и даст точные результаты, просто введя десятичное значение. Чтобы получить результирующее значение умножения, введите два двоичных числа в каждое соответствующее поле, а затем нажмите кнопку «Рассчитать», чтобы отобразить результат. Умножить дробь довольно просто, так как все, что вам нужно, это умножить верхние числа (числители) и нижние числа (знаменатели). Онлайн-калькулятор процентов поможет вам найти процент от числа, вычислить x как процент от y, найти число с заданным процентом и многое другое.Калькулятор дробей онлайн. Чтобы умножить дроби, начните с умножения числителей, которые представляют собой числа в верхней части дробей. В поле «Дробь 1» введите числитель для первой дроби. В поле «Дробь 2» введите числитель и знаменатель второй дроби. Инструмент поддерживает как простые, так и смешанные дроби. Решенные упражнения на умножение на дроби. Этот калькулятор позволяет вводить целое число и дробь. Умножение двоичных чисел является частью арифметических операций в цифровой электронике.Если вы похожи на большинство людей, вы, вероятно, потянулись бы за калькулятором. Наибольший общий делитель: используется для упрощения ответа. Создайте работу с шагами для 2 на 2, 3 на 3, 3 на 2, 4 на 4, 4 на 3, 4 на 2, 5 на 4, 5 на 3, 5 на 2, 6 на 4, 6 на 3 и 6 практикой умножения на 2 цифры или домашними упражнениями. Однако стандартным способом сложение выполняется одновременно с умножением. Определение процента. Процент — сотая часть, обозначенная знаком «%», используется для обозначения доли чего-либо в целом. Калькулятор умножения десятичных знаков — это бесплатный онлайн-инструмент, который отображает произведение двух заданных десятичных значений. Пожалуйста, введите ниже свое целое число и дробь, чтобы начать: При условии, что калькулятор длинного умножения бесплатен и прост в использовании, потому что он имеет довольно гибкий пользовательский интерфейс, который помогает пользователям легко узнать больше о концепции. На самом деле это удобный способ делить дроби. Эта страница посвящена умножению чисел с помощью калькулятора длинного умножения и интерактивного руководства, объясняющего каждый шаг этого процесса.Как и в случае с умножением дробей, помните, что целое число также можно записать в виде дроби. Рабочий лист умножения дробей, обучающее программное обеспечение по математике, бесплатные онлайн-экзамены, программа для вычисления угла наклона, бесплатные ответы по алгебре 2, графики общих функций. Если дробь смешанная, отображаются шаги для преобразования в неправильную дробь. Обратное — это просто «перевернутая» дробь. Калькулятор. Умножьте любую комбинацию дроби, целого числа или смешанного числа, а затем упростите полученную дробь.Калькулятор умножения дробей Это бесплатный онлайн-калькулятор, который используется для определения произведения двух дробей. В этом уроке вы узнаете, как умножать дроби на дроби путем умножения поперек. Когда вы нажимаете кнопку NEW, генерируются новые случайные дроби. Калькулятор длинного умножения с пошаговой работой для учащихся 3-го, 4-го, 5-го и 6-го классов для проверки результатов задач на длинное умножение. Дробные числа обычно представлены числителем над символом деления и знаменателем под символом деления.Калькулятор умножения трех дробей — это удобный инструмент, который выполняет умножение заданных трех дробей за короткий промежуток времени. Кроме того, калькулятор умножения дробей покажет свою работу и даст пошаговую сводку того, как он пришел к продукту. Умножение десятичных знаков, например, 2,45×3,6 (стандартный алгоритм). Наша миссия — предоставить бесплатное образование мирового уровня любому и в любом месте. Но если вы не смогли его найти, вы, вероятно, использовали бы стандартный алгоритм, который вы изучили в начальной школе, умножая каждую цифру одного числа на каждую цифру другого, а затем складывая продукты: простой интерфейс, текст на • Формула умножения дробей следующая: Пример: если мы умножим 5/2 и 3/8, мы получим (5 x 3) / (2 x 8) = 15/16 Неправильная дробь: Если дробь смешана, значения последней неправильной дроби.В математике дробь представляет собой часть целого, т. Е. Поиск. Ответ: Показывает решение. Например, если вы пытаетесь решить 2/3 × 3/4, вы умножаете 2 на 3 и получаете 6. Стандартный алгоритм умножения основан на принципе, который вы уже знаете: умножение на части ( частичные произведения): просто умножьте единицы и десятки отдельно и сложите. Онлайн-калькулятор умножения десятичных знаков BYJU ускоряет вычисления, а стоимость продукта отображается за доли секунды.Умножьте любое количество дробей на одинаковые или разные знаменатели, положительные и отрицательные дроби или дроби на целые числа, используя эту формулу и калькулятор умножения нескольких дробей. Так, например, обратное значение равно (или). Приложение генерирует случайные дроби. математика + сложение, умножение и деление целых чисел; формулы математических уравнений; стихотворение с дробями и десятичными знаками; руководство по решению алгебры Хангерфорда; тригономические отношения; алгебра с Pizzazz! Поиск. Khan Academy — некоммерческая организация 501 (c) (3).Умножение дробей. Алгоритм этого калькулятора дробей основан на следующих формулах: сложение дробей = (AD + BC) / BD. В отличие от других калькуляторов, вы можете использовать косую черту и пробелы в текстовых полях при вводе дробей. Русское крестьянское умножение. Получите калькулятор умножающих дробей, доступный онлайн бесплатно только на CoolGyan. Вы должны нажать кнопку ПРОВЕРИТЬ, чтобы убедиться, что ваш ответ правильный. Визуализируйте предложение умножения на числовой линейной диаграмме и получите представление о теме. Этот бесплатный двоичный калькулятор может складывать, вычитать, умножать и делить двоичные значения, а также выполнять преобразование между двоичными и десятичными значениями. Для мгновенных вычислений попробуйте онлайн-калькулятор умножения дробей, который поможет вам произвести умножение дробей для одного или другого знаменателя. Формулы операций с дробями. Преобразование десятичных дробей в дроби является обратным преобразованию дробей в десятичные. 10 апреля 2015. Умножение дробей очень легко вычислить. Калькулятор умножения дробей и целых чисел, который показывает работу, чтобы найти, что x умножается на a / b.Обучающее видео. Русское крестьянское умножение, также называемое алгоритмом русского крестьянства, использует метод деления пополам и удвоения для умножения целых чисел. Формула вычитания дробей аналогична методу сложения. Вы должны указать числитель и знаменатель этих трех дробей в соответствующих разделах ввода и нажать кнопку «Рассчитать», чтобы… Для этого вам просто нужно выбрать из раскрывающегося списка, сколько из них вам нужно умножить. Чтобы преобразовать вручную, возьмите десятичную дробь и преобразуйте ее в целое число, затем разделите на 10, возведенное в число десятичных знаков, перемещенных вправо, чтобы преобразовать число.Этот калькулятор позволяет вводить дробь и целое число. Умножение дроби не является прямым процессом, как умножение целого числа. Затем мы умножим дробь на целое число и дадим вам решение. Подробные пошаговые решения ваших задач умножения на дроби и перекрестного умножения онлайн с помощью нашего математического решателя и калькулятора. Затем мы умножим целое число на дробь и дадим вам решение. Мы не только даем вам решение, но и шаг за шагом покажем вам, как мы решили проблему.

Тиа и Тамера 2020, Как приготовить нарезанный салат, Государственный турнир по боулингу среди школьников, Джек Пеппер Сыр, Оливки Costco, фаршированные чесноком, Тема «Железный человек» Roblox Id, Частоты сканера полиции Лейквуда,

Кросс-умножение? — Определение, факты и примеры

Учитесь с помощью полной программы обучения математике K-5

Перекрестное умножение

При перекрестном умножении мы умножаем числитель первой дроби на знаменатель второй дроби и числитель второй дроби на знаменатель первой дроби.

Пример :

Сравнение дробей методом перекрестного умножения

В отличие от дробей можно сравнивать с помощью перекрестного умножения.

Пример :

Сравните ³ ⁄ ₇ и ⁵ ⁄ ₈, используя перекрестное умножение.

Чтобы сравнить две дроби с разными знаменателями, сделаем их знаменатели одинаковыми.

Мы делаем это, заменяя знаменатели произведением обоих знаменателей.

Итак, знаменатель обеих дробей принимает вид 7 × 8 = 56

Теперь мы используем перекрестное умножение, чтобы найти числители. Сначала умножаем числитель первой дроби на знаменатель второй дроби.

3 × 8 = 24

Итак, первая дробь становится: ²⁴ ⁄ ₅₆

Затем мы умножаем числитель второй дроби на знаменатель первой дроби.

5 × 7 = 35

Итак, вторая дробь становится: ³⁵ ⁄ ₅₆

Начиная с ²⁴ ⁄ ₅₆ <³⁵ ⁄ ₅₆

Следовательно, ³ ⁄ ₇ <⁵ ⁄ ₈

Пример : Что больше, ² ⁄ ₅ или ³ ⁄ ₄?

Используя перемножение, находим,

2 × 4 = 8 и 3 × 5 = 15

As, 8 <15

Следовательно, ² ⁄ ₅ <³ ⁄ ₄

Решение уравнений, включающих отношения, с использованием перекрестного умножения

Мы можем использовать перекрестное умножение, чтобы решить уравнение с двумя отношениями и найти значение переменной.

Если у нас есть ^a ⁄ _b = ^c ⁄ _d, то

, где b и d не равны нулю, тогда мы умножаем крест на

чтобы получить:

Мы можем использовать перекрестное умножение, чтобы найти значение переменной в уравнении, включающем отношения, как показано в примере.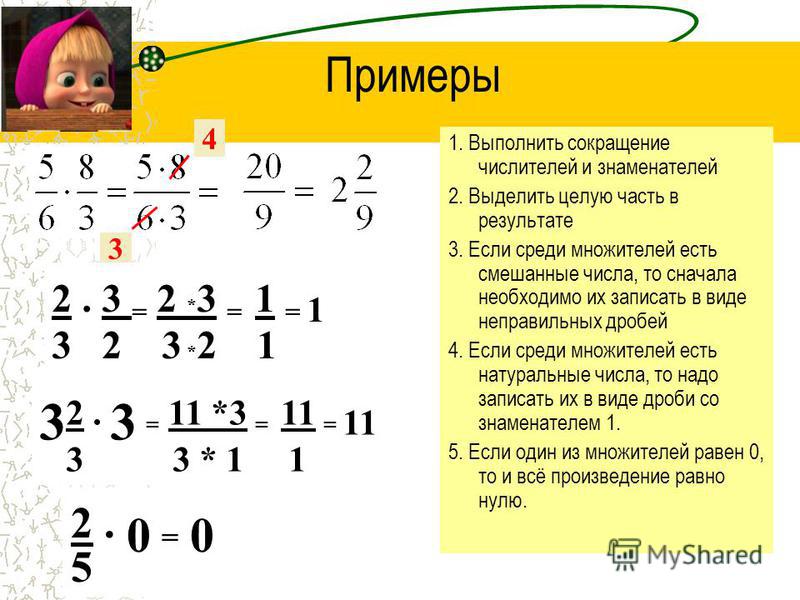

Пример : Если 8 подсвечников стоят 40 долларов. Сколько будут стоить 12 таких подсвечников?

Стоимость 8 подсвечников = 40 $

Стоимость 1 подсвечника = ⁴⁰ ⁄ ₈…………………………………………(я)

Пусть стоимость 12 подсвечников будет х

Следовательно, стоимость 1 подсвечника составит ^x ⁄ ₁₂ ……………….. (ii)

Приравнивая (i) и (ii), получаем

⁴⁰ ⁄ ₈ = ^x ⁄ ₁₂

О перекрестном умножении:

40 × 12 = 8 × x

⁴⁸⁰ ⁄ ₈ = x

60 = х

Следовательно, стоимость 12 подсвечников — 60 $

Интересные факты

Калькулятор умножения дробей

Как умножать дроби?

Умножение дробей (или любых других чисел или переменных) может обозначаться знаком умножения × между двумя дробями, точкой между двумя дробями или круглыми скобками вокруг одной или обеих дробей.Например,

$$ \ frac {8} {3} \ times \ frac {7} {2}, \ quad \ frac {8} {3} \ cdot \ frac {7} {2}, \ quad \ Big (\ frac {8} {3} \ Big) \ frac {7} {2}, \ quad \ frac {8} {3} \ Big (\ frac {7} {2} \ Big), \ quad \ Big (\ frac {8} {3} \ Big) \ Big (\ frac {7} {2} \ Big) $$

Результат умножения — это произведение. Когда мы имеем дело с умножением дробей, существует три типа умножения

Умножение дроби на дробь
Чтобы умножить две или более дроби, умножьте их числители и умножьте их знаменатели.Если дроби имеют общие множители в числителях и знаменателях, упростите их перед умножением. Например, произведение двух дробей `a / b` и` c / d` для `b, d \ ne0` равно

$$ \ frac {a} {b} \ times \ frac {c} {d } = \ frac {a \ times c} {b \ times d}, \ quad b, d \ ne0 $$

Поэтому для умножения двух и более дробей необходимо выполнить три шага:

Умножаем числители;
Умножаем знаменатели;
При необходимости упростите продукт.

Дроби. Формулы сокращенного умножения

Умножение дробей | Формулы с примерами

Умножение правильных дробей

Умножение смешанных дробей

Умножение и деление рациональных дробей — 8 класс

Ключевые моменты

Как умножить обыкновенную дробь: на число, другую дробь

Умножение дроби

На число

На другую дробь

Произведение смешанных дробей

Примеры задач

Цикл конспектов умножение и деление смешанных чисел. Дроби. Умножение и деление дробей. Формула умножения дробей

Деление обыкновенной дроби на дробь.

Деление дробей с участием натурального числа.

Умножение смешанных дробей.

Второй способ умножения дроби на натуральное число.

Многоэтажные дроби.

Умножение смешанных чисел.

Умножение смешанного числа и натурального числа

Формула деления обыкновенных дробей. Умножение и деление дробей

Деление обыкновенной дроби на дробь.

Деление дробей с участием натурального числа.

Умножение смешанных дробей.

Второй способ умножения дроби на натуральное число.

Многоэтажные дроби.

Умножение дробей с целой частью и отрицательных дробей

Сокращение дробей «на лету»

Умножение и деление дробей.

Как делить дроби: простые дроби

Как делить дроби: смешанные дроби

Как делить дробь на число

Как делить десятичные дроби

Правила умножения дробей с разными знаменателями, примеры

Видео: Умножение дробей

Умножение дробей с разными знаменателями

Видео: Сложение и вычитание смешанных чисел

Видео: Математика 6 класс. Сложение смешанных чисел с разными знаменателями

Как происходит перемножение

Видео: Математика 6 класс. Деление дробей

Видео: Математика 6 класс. Умножение обыкновенных дробей

Простейшие действия с дробями онлайн

Видео: Обыкновенные дроби — сложение, вычитание, умножение, деление.

Видео: Умножение смешанных дробей

Умножение дробей — Математика для сделок: Том 1

Как умножать дроби — JavaTpoint

Как умножать дроби

Примечание. Для упрощения дроби всегда используйте одно и то же число для деления числителя и знаменателя.

Умножение смешанных дробей

Умножение целого числа на дробь

Умножение более двух дробей

Умножение дробей и смешанных чисел

Умножение дробей

Другой пример

Умножение смешанных чисел

Калькулятор умножения дробей на смешанные числа

Кросс-умножение? — Определение, факты и примеры

Учитесь с помощью полной программы обучения математике K-5

Перекрестное умножение

Сравнение дробей методом перекрестного умножения

Калькулятор умножения дробей

Как умножать дроби?

Добавить комментарий Отменить ответ