Как правильно сравнивать дроби?
Сравнение дробей с одинаковыми знаменателями
Как и при любом другом сравнении, суть сравнения дробей — в том, чтобы определить меньшую и большую дроби.
Нет ситуации более благоприятной для сравнения, чем дроби с одинаковыми знаменателями. Если вся разница между дробями только в числителях, пользуемся следующим правилом:
Из двух дробей с одинаковыми знаменателями больше дробь с большим числителем. А меньше будет та дробь, числитель которой меньше. |
А теперь на примерах.
Пример 1. Сравните дроби:
- Мы видим, что знаменатели дробей — равны. Значит сравниваем числители:
8 < 12
12 > 8 - Это значит, что < Изи!
Пример 2. Сравните дроби:
- Как и в прошлом примере, знаменатели дробей — равны. Сравниваем числители:
9 > 10
1 < 10 - Это значит, что >
Пример 3.
- Знаменатели дробей снова равны. Сравниваем числители:
3 > 1
1 < 3 - Это значит, что >
Как видите, нет ничего сложного в сравнении дробей, если знаменатели равны. Вся задача заключается в том, чтобы определить больший и меньший числитель.
Давайте разберем наглядный пример сравнения дробей. Еще больше наглядных примеров — на курсах по математике в онлайн-школе Skysmart!
Допустим, в торте 6 кусков. Если от целого торта отрезать один кусок — в торте останется 5 кусков.
- Запишем в виде дробей: и
- А теперь сравним полученные дроби: знаменатели — равны, сравниваем числители:
6 > 5
5 < 6. - Это значит, что >
Понять, что целый торт больше, чем торт без одного куска, можно и без сравнения дробей. Но это же самое правило можно применить и при менее очевидных сравнениях, которые часто встречаются в повседневной жизни.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Запишитесь и участвуйте в розыгрыше 8 уроков
Сравнение дробей с одинаковыми числителями
Вы уже разобрались со сравнением дробей с одинаковыми знаменателями. Теперь задача чуть усложняется — научимся сравнивать дроби с разными знаменателями, но с одинаковыми числителями.
Запомните правило:
Если у двух дробей одинаковые числители, то больше будет та дробь, чей знаменатель меньше. А меньше будет дробь с большим знаменателем. |
А теперь наши любимые примеры. Погнали!
Пример 1. Сравните дроби:
- У дробей разные знаменатели и одинаковые числители. Значит, согласно правилу, нужно сравнить знаменатели:
9 > 7 - Значит, дробь с меньшим знаменателем — больше:
Пример 2. Сравните дроби:
- У дробей разные знаменатели и одинаковые числители. Значит, согласно правилу, нужно сравнить знаменатели:
10 < 11
11 > 10 - Значит дробь с меньшим знаменателем — больше:
Пример 3. Сравните дроби:
Сравните дроби:
- У дробей разные знаменатели и одинаковые числители. Значит, согласно правилу, нужно сравнить знаменатели:
6 > 3
3 < 6 - Значит, дробь с меньшим знаменателем — больше.
Для наглядности представим ситуацию, в которой вам предстоит разделить торт между тремя друзьями. Это значит, что 6 кусков торта равномерно распределяются по 3 людям: каждому достается 6:3 = 2 по 2 кусочка.
А теперь представим более приятную ситуацию: кусков торта по-прежнему 6, а друзей уже только 2. Тогда каждому достанется по 3 вкуснейших кусочка:
Как видите, сравнение дробей может вам пригодиться в самых неожиданных ситуациях. Теперь, когда снова придется хорошенько задуматься о соотношении кусков торта и приглашенных гостях, изученная тема поможет вам принять верное решение😉.
Сравнение дробей с разными числителями и разными знаменателями
Нет ничего хитрого в сравнении дробей с одинаковыми числителями или знаменателями. Чуть больше усилий потребуется при сравнении дробей, в которых нет ничего одинакового.
Чуть больше усилий потребуется при сравнении дробей, в которых нет ничего одинакового.
Запоминаем
Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю, а затем сравнить числители.
Сначала вспомним, как привести дроби к общему знаменателю.
Рассмотрим пример дробей с разными знаменателями.
- Нужно подобрать число, которое будет делиться на 7 и на 2, например, 14. Проверим:
14:7 = 2 - Первую дробь умножаем на дополнительный множитель 2:
- Вторую дробь умножаем на дополнительный множитель 7:
- Дроби приведены к общему знаменателю:
Давайте потренируемся в сравнении дробей.
Пример 1. Сравните дроби:
- Приведем дроби к общему знаменателю. 30 делится на 15 и на 2.
30 : 15 = 2
30 : 2 = 15 - Первую дробь умножаем на дополнительный множитель 2:
- Вторую дробь умножаем на дополнительный множитель 15:
- Дроби приведены к общему знаменателю:
- Если две дроби имеют одинаковые знаменатели, то, согласно правилу, больше та дробь, чей числитель больше:
При сравнении неправильных дробей с правильными помните, что неправильная дробь всегда больше правильной.
Пример 2: Сравните дроби:
- 6/5 — неправильная дробь.
- Выделим целую часть:
- Значит, что
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.
Вычитание смешанных чисел
Вычитание проходит гладко, когда уменьшаемое больше вычитаемого.
- 12 — 7 = 6
12 — уменьшаемое
7 — вычитаемое
5 — разность
В случае, если вычитаемое больше уменьшаемого, разность оказывается отрицательной. В этом нет ничего страшного. Но математика в 5 классе — «положительная», поэтому научимся находить разность смешанных чисел, не скатываясь «в минусы».
При вычитании дробей действует тот же самый принцип: вычитаемое должно быть меньше уменьшаемого. Вот здесь то вам и пригодится навык сравнивать дроби.
Пример 1. Вычислите:
Вычитаемая дробь меньше уменьшаемой
- Выполняем вычитание:
Пример 2.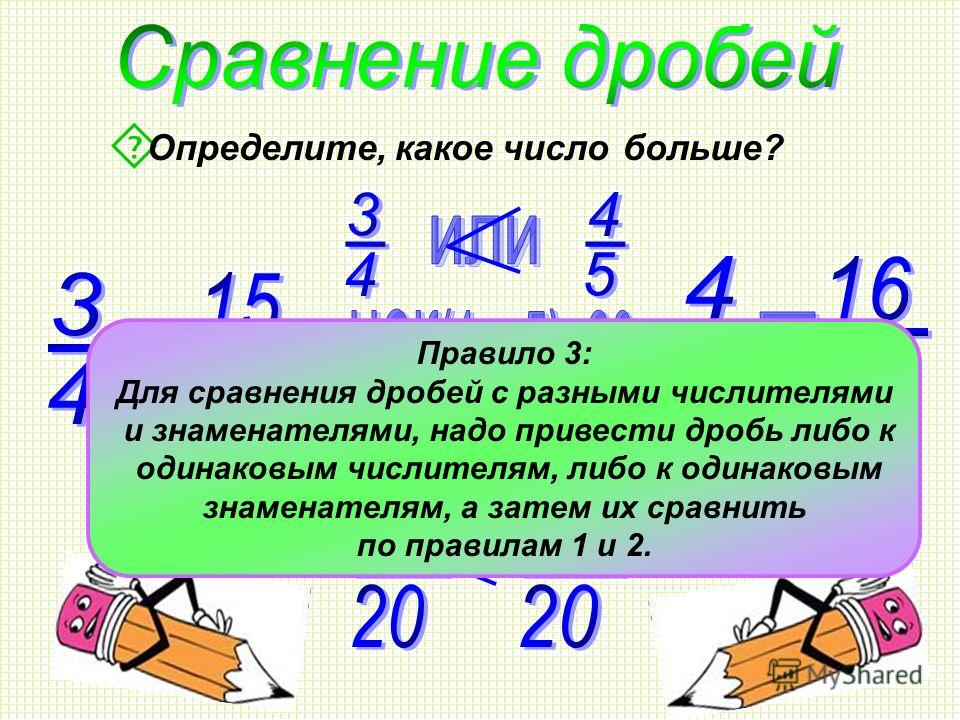 Найдите разность:
Найдите разность:
- Смешанные дроби превращаем в неправильные:
- Чтобы найти разность дробей с разными числителями и знаменателями, нужно привести их к общему знаменателю:
- Наименьшее общее кратное — 40
40 : 8 = 5
40 : 5 = 8 - Умножаем первую дробь на дополнительный множитель 5:
- Умножаем вторую дробь на дополнительный множитель 8:
- Дроби приведены к общему знаменателю:
Примеры для самопроверки
Теория — это, конечно, хорошо. Но без практики — никуда. Пора потренироваться в решении примеров и закрепить тему сравнения дробей.
Пример 1. Сравните дроби:
Ответ: по правилу сравнения дробей с одинаковыми знаменателями, больше та дробь, у которой числитель больше. Это значит, что
Пример 2. Сравните дроби:
Ответ: по правилу сравнения дробей с разными знаменателями и одинаковыми числителями, больше та дробь, чей знаменатель меньше.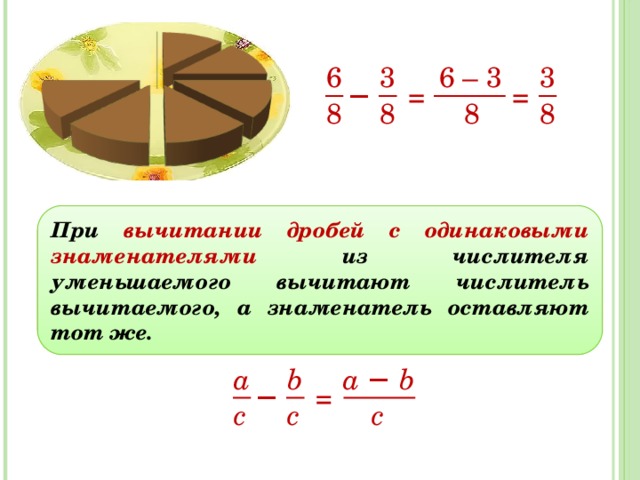 Это значит, что
Это значит, что
Пример 3. Сравните дроби:
Как решаем:
Ответ:.
- По правилу сравнения дробей с разными числителями и знаменателями, сначала нужно привести дроби к общему знаменателю:
- Наименьшее общее кратное — 15:
15 : 15 = 1
15 : 5 = 3 - Умножаем первую дробь на дополнительный множитель 1:
- Умножаем вторую дробь на дополнительный множитель 3:
- Дроби приведены к общему знаменателю:
- Сравниваем числители получившихся дробей: 3 < 6
Пример 4. Найдите разность:
Как решаем:
- Смешанные дроби превращаем в неправильные:
- Чтобы найти разность дробей с разными числителями и знаменателями, нужно привести их к общему знаменателю.
- Наименьшее общее кратное — 42:
42 : 7 = 6
42 : 6 = 7 - Умножаем первую дробь на дополнительный множитель 6:
- Умножаем вторую дробь на дополнительный множитель 7:
- Дроби приведены к общему знаменателю.

- Теперь можно вычитать:
Ответ:
правила, примеры, решения, как сравнить дроби с разными знаменателями
Данная статья рассматривает сравнение дробей. Здесь мы выясним, какая из дробей больше или меньше, применим правило, разберем примеры решения. Сравним дроби как с одинаковыми, так и разными знаменателями. Произведем сравнение обыкновенной дроби с натуральным числом.
Сравнение дробей с одинаковыми знаменателями
Когда производится сравнение дробей с одинаковыми знаменателями, мы работаем только с числителем, а значит, сравниваем доли числа. Если имеется дробь 37, то она имеет 3 доли 17, тогда дробь 87 имеет 8 таких долей. Иначе говоря, если знаменатель одинаковый, производится сравнение числителей этих дробей, то есть 37 и 87 сравниваются числа 3 и 8.
Отсюда следует правило сравнения дробей с одинаковыми знаменателями: из имеющихся дробей с одинаковыми показателями считается большей та дробь, у которой числитель больше и наоборот.
Это говорит о том, что следует обратить внимание на числители. Для этого рассмотрим пример.
Пример 1Произвести сравнение заданных дробей 65126 и 87126.
Решение
Так как знаменатели дробей одинаковые, переходим к числителям. Из чисел 87 и 65 очевидно, что 65 меньше. Исходя из правила сравнения дробей с одинаковыми знаменателями имеем, что 87126 больше 65126.
Ответ: 87126>65126.
Сравнение дробей с разными знаменателями
Сравнение таких дробей можно соотнести со сравнением дробей с одинаковыми показателями, но имеется различие. Теперь необходимо дроби приводить к общему знаменателю.
Если имеются дроби с разными знаменателями, для их сравнения необходимо:
- найти общий знаменатель;
- сравнить дроби.
Рассмотрим данные действия на примере.
Пример 2Произвести сравнение дробей 512 и 916.
Решение
В первую очередь необходимо привести дроби к общему знаменателю. Это делается таким образом: находится НОК, то есть наименьший общий делитель, 12 и 16. Это число 48. Необходимо надписать дополнительные множители к первой дроби 512 , это число находится из частного 48:12=4, для второй дроби 916– 48:16=3. Запишем получившееся таким образом: 512=5·412·4=2048 и 916=9·316·3=2748.
Это делается таким образом: находится НОК, то есть наименьший общий делитель, 12 и 16. Это число 48. Необходимо надписать дополнительные множители к первой дроби 512 , это число находится из частного 48:12=4, для второй дроби 916– 48:16=3. Запишем получившееся таким образом: 512=5·412·4=2048 и 916=9·316·3=2748.
После сравнения дробей получаем, что 2048<2748. Значит, 512 меньше 916.
Ответ: 512<916.
Имеется еще один способ сравнения дробей с разными знаменателями. Он выполняется без приведения к общему знаменателю. Рассмотрим на примере. Чтобы сравнить дроби ab и cd, приводим к общему знаменателю, тогда b·d, то есть произведение этих знаменателей. Тогда дополнительные множители для дробей будут являться знаменатели соседней дроби. Это запишется так a·db·d и c·bd·b. Используя правило с одинаковыми знаменателями, имеем, что сравнение дробей свелось к сравнениям произведений a·d и c·b. Отсюда получаем правило сравнения дробей с разными знаменателями: если a·d>b·c, тогда ab>cd, но если a·d<b·c, тогдаab<cd. Рассмотрим сравнение с разными знаменателями.
Рассмотрим сравнение с разными знаменателями.
Произвести сравнение дробей 518 и 2386.
Решение
Данный пример имеет a=5, b=18, c=23 и d=86. Тогда необходимо вычислить a·d и b·c. Отсюда следует, что a·d=5·86=430 и b·c=18·23=414. Но 430>414, тогда заданная дробь 518 больше, чем 2386.
Ответ: 518>2386.
Сравнение дробей с одинаковыми числителями
Если дроби имеют одинаковые числители и разные знаменатели, тогда можно выполнять сравнение по предыдущему пункту. Результат сравнения возможет при сравнении их знаменателей.
Имеется правило сравнения дробей с одинаковыми числителями: из двух дробей с одинаковыми числителями больше та дробь, которая имеет меньший знаменатель и наоборот.
Рассмотрим на примере.
Пример 4Произвести сравнение дробей 5419 и 5431.
Решение
Имеем, что числители одинаковые, значит, что дробь, имеющая знаменатель 19 больше дроби, которая имеет знаменатель 31. Это понятно, исходя из правила.
Это понятно, исходя из правила.
Ответ: 5419>5431.
Иначе можно рассмотреть на примере. Имеется две тарелки, на которых 12 пирога, анна другой 116. Если съесть 12 пирога, то насытишься быстрей, нежели только 116. Отсюда вывод, что наибольший знаменатель при одинаковых числителях является наименьшим при сравнении дробей.
Сравнение дроби с натуральным числом
Сравнение обыкновенной дроби с натуральным числом идет как и сравнение двух дробей с записью знаменателей в виде 1. Для детального рассмотрения ниже приведем пример.
Пример 4Необходимо выполнить сравнение 638 и 9.
Решение
Необходимо представить число 9 в виде дроби 91. Тогда имеем необходимость сравнения дробей 638 и 91. Далее следует приведение к общему знаменателю путем нахождения дополнительных множителей. После этого видим, что нужно сравнить дроби с одинаковыми знаменателями 638 и 728. Исходя из правила сравнения, 63<72, тогда получаем 638<728. Значит, заданная дробь меньше целого числа 9, то есть имеем 638<9.
Значит, заданная дробь меньше целого числа 9, то есть имеем 638<9.
Ответ: 638<9.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Онлайн урок: Сравнение дробей с разными знаменателями по предмету Математика 6 класс
- Урок 11.Сравнение дробей с разными знаменателями
На этом уроке мы научимся сравнивать дроби с одинаковыми знаменателями, с одинаковыми числителями, с разными числителями и знаменателями. А также закрепим навыки, решив несколько примеров и упражнений.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis
dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore
voluptate!
Adipisci autem beatae consectetur corporis
dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore
voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Сравним дроби \(\mathbf{\frac{2}{5}}\) и \(\mathbf{\frac{2}{7}}\)
Дробная черта заменяет знак деления.
Представьте, что торт разделили в первом случае на пять частей, а во втором случае на семь.
Понятно, что если пришло пятеро гостей, то в первом случае каждому гостю достанется больший кусок торта, чем во втором случае.
Следовательно, \(\mathbf{\frac{2}{5}>\frac{2}{7}}\)
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis
dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore
voluptate!
Adipisci autem beatae consectetur corporis
dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore
voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Если дроби имеют одинаковые числители, то больше та дробь, у которой меньше знаменатель.
Пример 1
Сравните дроби:
А) \(\mathbf{\frac{3}{4}}\) и \(\mathbf{\frac{3}{8}}\)
Б) \(\mathbf{\frac{5}{6}}\) и \(\mathbf{\frac{5}{9}}\)
В) \(\mathbf{\frac{4}{11}}\) и \(\mathbf{\frac{4}{17}}\)
Г) \(\mathbf{\frac{60}{77}}\) и \(\mathbf{\frac{60}{133}}\)
Решение:
А) \(\mathbf{\frac{3}{4}>\frac{3}{8}}\), т. к. \(\mathbf{4 < 8}\)
к. \(\mathbf{4 < 8}\)
Б) \(\mathbf{\frac{5}{6}>\frac{5}{9}}\), т.к. \(\mathbf{6 < 9}\)
В) \(\mathbf{\frac{4}{11}>\frac{4}{17}}\), т.к. \(\mathbf{11 < 17}\)
Г) \(\mathbf{\frac{60}{77}>\frac{60}{133}}\), т.к. \(\mathbf{77 < 133}\)
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Сравним дроби \(\mathbf{\frac{1}{8}}\) и \(\mathbf{\frac{4}{7}}\)
По иллюстрации видно, что \(\mathbf{\frac{1}{8}}\) меньше половины, а \(\mathbf{\frac{4}{7}}\)- больше половины. Следовательно, \(\mathbf{\frac{1}{8}}\) < \(\mathbf{\frac{4}{7}}\)
Следовательно, \(\mathbf{\frac{1}{8}}\) < \(\mathbf{\frac{4}{7}}\)
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Если рассуждать логически и вспомнить, что дробная черта заменяет знак деления, то можно сравнить дроби следующим образом:
- меньшее число 1 делят на большее количество частей (на 8)
- большее число 4 делят на меньшее количество частей (на 7)
Действительно, получится, что \(\mathbf{1:8 < 4:7}\)
Итак, чтобы сравнить дроби с разными знаменателями, надо:
- привести данные дроби к наименьшему общему знаменателю
- сравнить полученные дроби
Например, сравним дроби \(\mathbf{\frac{3}{4}}\) и \(\mathbf{\frac{1}{2}}\)
Приведем к наименьшему общему знаменателю дроби \(\mathbf{\frac{3}{4}}\) и \(\mathbf{\frac{1}{2}}\)
Найдем наименьшее общее кратное знаменателей дробей:
\(\mathbf{НОК (4,2) = 4}\)
\(\mathbf{\frac{3}{4} = \frac{3\cdot1}{4\cdot1} = \frac{3}{4}}\)
\(\mathbf{\frac{1}{2} = \frac{1\cdot2}{2\cdot2} = \frac{2}{4}}\)
\(\mathbf{\frac{3}{4}}\) > \(\mathbf{\frac{2}{4}}\), следовательно, и \(\mathbf{\frac{3}{4}}\) > \(\mathbf{\frac{1}{2}}\)
Пример 1
Сравните дроби:
А) \(\mathbf{\frac{4}{15}}\) и \(\mathbf{\frac{14}{21}}\)
Б) \(\mathbf{\frac{7}{12}}\) и \(\mathbf{\frac{4}{15}}\)
В) \(\mathbf{\frac{5}{11}}\) и \(\mathbf{\frac{7}{10}}\)
Г) \(\mathbf{\frac{2}{9}}\) и \(\mathbf{\frac{3}{8}}\)
Решение:
А)
\(\mathbf{НОК (15,21) = 105}\)
\(\mathbf{\frac{4}{15} = \frac{4\cdot7}{15\cdot7} = \frac{28}{105}}\)
\(\mathbf{\frac{14}{21} = \frac{14\cdot5}{21\cdot5} = \frac{70}{105}}\)
\(\mathbf{\frac{28}{105}}\) < \(\mathbf{\frac{70}{105}}\), следовательно, и \(\mathbf{\frac{4}{15}}\) < \(\mathbf{\frac{14}{21}}\)
Б)
\(\mathbf{НОК (12,15) = 60}\)
\(\mathbf{\frac{7}{12} = \frac{7\cdot5}{12\cdot5} = \frac{35}{60}}\)
\(\mathbf{\frac{4}{15} = \frac{4\cdot4}{15\cdot4} = \frac{16}{60}}\)
\(\mathbf{\frac{35}{60}}\) > \(\mathbf{\frac{16}{60}}\), следовательно, и \(\mathbf{\frac{7}{12}}\) > \(\mathbf{\frac{4}{15}}\)
В)
\(\mathbf{НОК (11,10) = 110}\)
\(\mathbf{\frac{5}{11} = \frac{5\cdot10}{11\cdot10} = \frac{50}{110}}\)
\(\mathbf{\frac{7}{10} = \frac{7\cdot11}{10\cdot11} = \frac{77}{110}}\)
\(\mathbf{\frac{50}{110}}\) < \(\mathbf{\frac{77}{110}}\), следовательно, и \(\mathbf{\frac{5}{11}}\) < \(\mathbf{\frac{7}{10}}\)
Г)
\(\mathbf{НОК (9,8) = 72}\)
\(\mathbf{\frac{2}{9} = \frac{2\cdot8}{9\cdot8} = \frac{16}{72}}\)
\(\mathbf{\frac{3}{8} = \frac{3\cdot9}{8\cdot9} = \frac{27}{72}}\)
\(\mathbf{\frac{16}{72}}\) < \(\mathbf{\frac{27}{72}}\), следовательно, и \(\mathbf{\frac{2}{9}}\) < \(\mathbf{\frac{3}{8}}\)
Пример 2
Расположите в порядке возрастания дроби:
А) \(\mathbf{\frac{7}{50}, \frac{11}{5}, \frac{9}{10}, \frac{13}{25}}\)
Б) \(\mathbf{\frac{9}{10}, \frac{19}{20}, \frac{7}{100}, \frac{3}{50}}\)
Решение:
А) Приведем все дроби к общему знаменателю.
\(\mathbf{НОК (50,5,10,25) = 50}\)
\(\mathbf{\frac{11}{5} = \frac{11\cdot10}{5\cdot10} = \frac{110}{50}}\)
\(\mathbf{\frac{9}{10} = \frac{9\cdot5}{10\cdot5} = \frac{45}{50}}\)
\(\mathbf{\frac{13}{25} = \frac{13\cdot2}{25\cdot2} = \frac{26}{50}}\)
\(\mathbf{\frac{7}{50} < \frac{26}{50} < \frac{45}{50} < \frac{110}{50}}\), следовательно, \(\mathbf{\frac{7}{50} < \frac{13}{25} < \frac{9}{10} < \frac{11}{5}}\)
Б) Приведем все дроби к общему знаменателю.
\(\mathbf{НОК (10,20,100,50) = 100}\)
\(\mathbf{\frac{9}{10} = \frac{9\cdot10}{10\cdot10} = \frac{90}{100}}\)
\(\mathbf{\frac{19}{20} = \frac{19\cdot5}{20\cdot5} = \frac{95}{100}}\)
\(\mathbf{\frac{3}{50} = \frac{3\cdot2}{50\cdot2} = \frac{6}{100}}\)
\(\mathbf{\frac{6}{100} < \frac{7}{100} < \frac{90}{100} < \frac{95}{100}}\), следовательно, \(\mathbf{\frac{3}{50} < \frac{7}{100} < \frac{9}{10} < \frac{19}{20}}\)
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis
dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore
voluptate!
Adipisci autem beatae consectetur corporis
dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore
voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Мы рассмотрели все возможные способы сравнения обыкновенных дробей, познакомились с универсальным способом сравнения дробей с разными знаменателями: приведением дробей к общему знаменателю.
В качестве дополнительного множителя всегда подойдет знаменатель другой дроби.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Сегодня мы с вами занимались сравнением дробей. Например, мы сравнивали дроби с одинаковыми числителями. Особое место среди них занимают египетские дроби. Их свойство заключается в том, что они записываются в виде суммы нескольких дробей, у которых в числителе стоит 1.
$$\mathbf{\frac{1}{2}+\frac{1}{5}+\frac{1}{7}}$$
Из названия понятно, что изобрели их в Египте в глубокой древности. Из старых свитков и математических папирусов современники узнали, что египтяне пользовались своей таблицей дробей для чисел вида \(\mathbf{\frac{2}{n}}\)
Кроме самой таблицы были обнаружены 64 задачи, решённые с помощью них.
Для обозначения единицы египтяне использовали значок, похожий на глаз. Он назывался ер (один из) или рот. Довольно интересную запись привычных нам дробей можно увидеть на рисунке ниже.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Разложенные таким образом дроби не всегда удобно будет сравнивать. В сумме может быть много слагаемых и можно легко запутаться, поэтому проще пользоваться посчитанными суммами.
В бесплатной версии урока недоступны:
- Видео
- Изображения
- Дополнительная информация
- Таблицы
- Тесты
Получить доступ
Сравнение дробей — Помощник для школьников Спринт-Олимпик.
 ру
руПродолжаем изучать дроби. Сегодня мы поговорим об их сравнении. Тема интересная и полезная. Она позволит новичку почувствовать себя учёным в белом халате.
Суть сравнения дробей заключается в том, чтобы узнать какая из двух дробей больше или меньше.
Чтобы ответить на вопрос какая из двух дробей больше или меньше, пользуются операциями отношения, такими как больше (>) или меньше (<).
Ученые-математики уже позаботились о готовых правилах, позволяющие сразу ответить на вопрос какая дробь больше, а какая меньше. Эти правила можно смело применять.
Мы рассмотрим все эти правила и попробуем разобраться, почему происходит именно так.
Содержание
- Сравнение дробей с одинаковыми знаменателями
- Сравнение дробей с одинаковыми числителями
- Сравнение дробей с разными числителями и разными знаменателями
- Вычитание смешанных чисел. Сложные случаи.
Дроби, которые нужно сравнить, попадаются разные. Самый удачный случай это когда у дробей одинаковые знаменатели, но разные числители. В этом случае применяют следующее правило:
Самый удачный случай это когда у дробей одинаковые знаменатели, но разные числители. В этом случае применяют следующее правило:
Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше. И соответственно меньше будет та дробь, у которой числитель меньше.
Например, сравним дроби
и и ответим, какая из этих дробей больше. Здесь одинаковые знаменатели, но разные числители. У дроби числитель больше, чем у дроби . Значит дробь больше, чем . Так и отвечаем. Отвечать нужно с помощью значка больше (>)
Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на четыре части.
пиццы больше, чем пиццы:
Каждый согласится с тем, что первая пицца больше, чем вторая.
Сравнение дробей с одинаковыми числителямиСледующий случай, в который мы можем попасть, это когда числители дробей одинаковые, но знаменатели разные. Для таких случаев предусмотрено следующее правило:
Для таких случаев предусмотрено следующее правило:
Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше. И соответственно меньше та дробь, у которой знаменатель больше.
Например, сравним дроби
и . У этих дробей одинаковые числители. У дроби знаменатель меньше, чем у дроби . Значит дробь больше, чем дробь . Так и отвечаем:
Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на три и четыре части.
пиццы больше, чем пиццы:
Каждый согласится с тем, что первая пицца больше, чем вторая.
Сравнение дробей с разными числителями и разными знаменателями
Нередко случается так, что приходиться сравнивать дроби с разными числителями и разными знаменателями.
Например, сравнить дроби
и . Чтобы ответить на вопрос, какая из этих дробей больше или меньше, нужно привести их к одинаковому (общему) знаменателю. Затем можно будет легко определить какая дробь больше или меньше.
Затем можно будет легко определить какая дробь больше или меньше.
Приведём дроби
и к одинаковому (общему) знаменателю. Найдём наименьшее общее кратное (НОК) знаменателей обеих дробей. НОК знаменателей дробей и это число 6.
Теперь находим дополнительные множители для каждой дроби. Разделим НОК на знаменатель первой дроби
. НОК это число 6, а знаменатель первой дроби это число 2. Делим 6 на 2, получаем дополнительный множитель 3. Записываем его над первой дробью:
Теперь найдём второй дополнительный множитель. Разделим НОК на знаменатель второй дроби
. НОК это число 6, а знаменатель второй дроби это число 3. Делим 6 на 3, получаем дополнительный множитель 2. Записываем его над второй дробью:
Умножим дроби на свои дополнительные множители:
Мы пришли к тому, что дроби, у которых были разные знаменатели, превратились в дроби, у которых одинаковые знаменатели. А как сравнивать такие дроби мы уже знаем. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше:
А как сравнивать такие дроби мы уже знаем. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше:
Правило правилом, а мы попробуем разобраться почему
больше, чем . Для этого выделим целую часть в дроби . В дроби ничего выделять не нужно, поскольку эта дробь уже правильная.
После выделения целой части в дроби
, получим следующее выражение:
Теперь можно легко понять, почему
больше, чем . Давайте нарисуем эти дроби в виде пицц:
2 целые пиццы и
пиццы, больше чем пиццы.
Вычитание смешанных чисел. Сложные случаи.Вычитая смешанные числа, иногда можно обнаружить, что всё идёт не так гладко, как хотелось бы. Часто случается так, что при решении какого-нибудь примера ответ получается не таким, каким он должен быть.
При вычитании чисел уменьшаемое должно быть больше вычитаемого.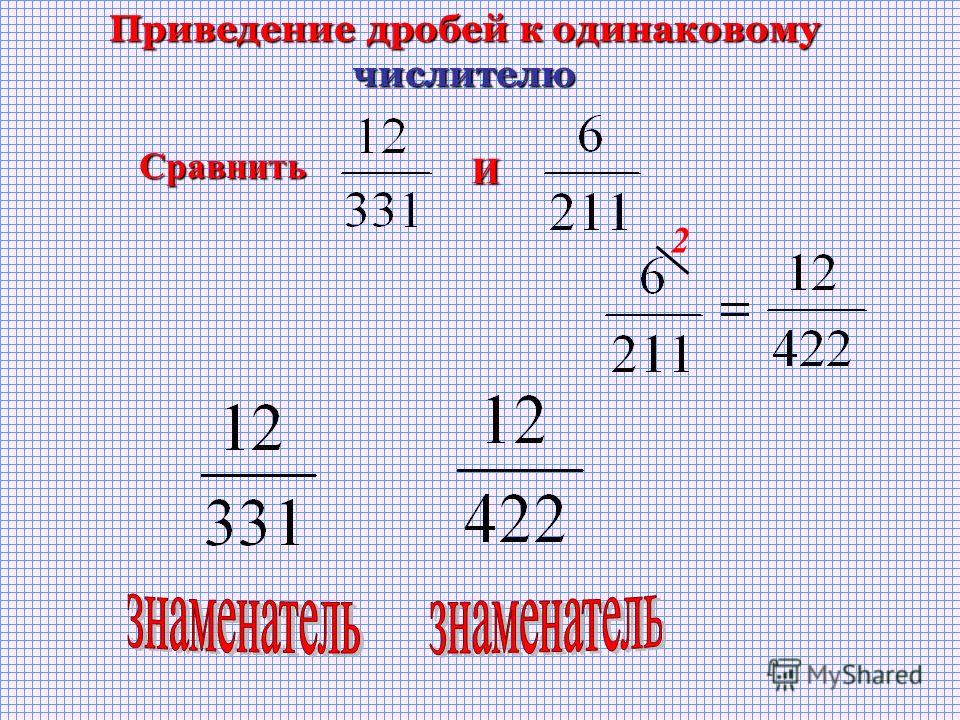 Только в этом случае будет получен нормальный ответ.
Только в этом случае будет получен нормальный ответ.
Например, 10−8=2
10 — уменьшаемое
8 — вычитаемое
2 — разность
Уменьшаемое 10 больше вычитаемого 8, поэтому мы получили нормальный ответ 2.
А теперь посмотрим, что будет если уменьшаемое окажется меньше вычитаемого. Пример 5−7=−2
5 — уменьшаемое
7 — вычитаемое
−2 — разность
В этом случае мы выходим за пределы привычных для нас чисел и попадаем в мир отрицательных чисел, где нам ходить пока рано, а то и опасно. Чтобы работать с отрицательными числами, нужна соответствующая математическая подготовка, которую мы ещё не получили.
Если при решении примеров на вычитание вы обнаружите, что уменьшаемое меньше вычитаемого, то можете пока пропустить такой пример. Работать с отрицательными числами допустимо только после их изучения.
С дробями ситуация та же самая. Уменьшаемое должно быть больше вычитаемого. Только в этом случае можно будет получить нормальный ответ. А чтобы понять больше ли уменьшаемая дробь, чем вычитаемая, нужно уметь сравнить эти дроби.
Например, решим пример
.
Это пример на вычитание. Чтобы решить его, нужно проверить больше ли уменьшаемая дробь, чем вычитаемая.
больше чем
поэтому смело можем вернуться к примеру и решить его:
Теперь решим такой пример
Проверяем больше ли уменьшаемая дробь, чем вычитаемая. Обнаруживаем, что она меньше:
В этом случае разумнее остановиться и не продолжать дальнейшее вычисление. Вернёмся к этому примеру, когда изучим отрицательные числа.
Смешанные числа перед вычитанием тоже желательно проверять. Например, найдём значение выражения
.
Сначала проверим больше ли уменьшаемое смешанное число, чем вычитаемое. Для этого переведём смешанные числа в неправильные дроби:
Получили дроби с разными числителями и разными знаменателями. Чтобы сравнить такие дроби, нужно привести их к одинаковому (общему) знаменателю. Не будем подробно расписывать, как это сделать. Если испытываете затруднения, обязательно повторите действия с дробями.
Не будем подробно расписывать, как это сделать. Если испытываете затруднения, обязательно повторите действия с дробями.
После приведения дробей к одинаковому знаменателю, получаем следующее выражение:
Теперь нужно сравнить дроби
и . Это дроби с одинаковыми знаменателями. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.
У дроби
числитель больше, чем у дроби . Значит дробь больше, чем дробь .
А это значит, что уменьшаемое
больше, чем вычитаемое
А значит мы можем вернуться к нашему примеру и смело решить его:
Пример 3. Найти значение выражения
Проверим больше ли уменьшаемое, чем вычитаемое.
Переведём смешанные числа в неправильные дроби:
Получили дроби с разными числителями и разными знаменателями. Приведем данные дроби к одинаковому (общему) знаменателю:
Теперь сравним дроби
и . У дроби числитель меньше, чем у дроби , значит дробь меньше, чем дробь
У дроби числитель меньше, чем у дроби , значит дробь меньше, чем дробь
А это значит, что и уменьшаемое
меньше, чем вычитаемое
А это гарантировано приведёт нас в мир отрицательных чисел. Поэтому разумнее остановиться на этом месте и не продолжать вычисление. Продолжим его, когда изучим отрицательные числа.
Пример 4. Найти значение выражения
Проверим больше ли уменьшаемое, чем вычитаемое.
Переведём смешанные числа в неправильные дроби:
Получили дроби с разными числителями и разными знаменателями. Приведем их к одинаковому (общему) знаменателю:
Теперь нужно сравнить дроби
и . У дроби числитель больше, чем у дроби . Значит дробь больше, чем дробь .
А это значит, что уменьшаемое
больше, чем вычитаемое
Поэтому мы смело можем продолжить вычисление нашего примера:
Сначала мы получили ответ
. Эту дробь мы сократили на 2 и получили дробь , но такой ответ нас тоже не устроил и мы выделили целую часть в этом ответе. В итоге получили ответ .
Эту дробь мы сократили на 2 и получили дробь , но такой ответ нас тоже не устроил и мы выделили целую часть в этом ответе. В итоге получили ответ .
Предыдущая
Математика с нуляСмешанные числа
СледующаяМатематика с нуляЕдиницы измерения
Сравнение дробей. Как сравнивать дроби с разными знаменателями?
Не только простые числа можно сравнивать, но и дроби тоже. Ведь дробь — это такое же число как, к примеру, и натуральные числа. Нужно знать только правила, по которым сравнивают дроби.
Сравнение дробей с одинаковыми знаменателями.
Если у двух дробей одинаковые знаменатели, то такие дроби сравнить просто.
Чтобы сравнить дроби с одинаковыми знаменателями, нужно сравнить их числители. Та дробь больше у которой больше числитель.
Рассмотрим пример:
Сравните дроби \(\frac{7}{26}\) и \(\frac{13}{26}\).
Знаменатели у обоих дробей одинаковые равны 26, поэтому сравниваем числители. Число 13 больше 7. Получаем:
\(\frac{7}{26} < \frac{13}{26}\)
Сравнение дробей с равными числителями.

Если у дроби одинаковые числители, то больше та дробь, у которой знаменатель меньше.
Понять это правило можно, если привести пример из жизни. У нас есть торт. К нам в гости могут прийти 5 или 11 гостей. Если придут 5 гостей, то мы разрежем торт на 5 равных кусков, а если придут 11 гостей, то разделим на 11 равных кусков. А теперь подумайте в каком случаем на одного гостя придется кусок торта большего размера? Конечно, когда придут 5 гостей, кусок торта будет больше.
Или еще пример. У нас есть 20 конфет. Мы можем поровну раздать конфеты 4 друзьям или поровну поделить конфеты между 10 друзьями. В каком случае у каждого друга будет конфет больше? Конечно, когда мы разделим только на 4 друзей, количество конфет у каждого друга будет больше. Проверим эту задачу математически.
\(\frac{20}{4} > \frac{20}{10}\)
Если мы до решаем эти дроби, то получим числа \(\frac{20}{4} = 5\) и \(\frac{20}{10} = 2\). Получаем, что 5 > 2
В этом и заключается правило сравнения дробей с одинаковыми числителями.
Рассмотрим еще пример.
Сравните дроби с одинаковым числителем \(\frac{1}{17}\) и \(\frac{1}{15}\) .
Так как числители одинаковые, больше та дробь, где знаменатель меньше.
\(\frac{1}{17} < \frac{1}{15}\)
Сравнение дробей с разными знаменателями и числителями.
Чтобы сравнить дроби с разными знаменателями, необходимо дроби привести к общему знаменателю, а потом сравнить числители.
Пример:
Сравните дроби \(\frac{2}{3}\) и \(\frac{5}{7}\).
Сначала найдем общий знаменатель дробей. Он будет равен числу 21.
\(\begin{align}&\frac{2}{3} = \frac{2 \times 7}{3 \times 7} = \frac{14}{21}\\\\&\frac{5}{7} = \frac{5 \times 3}{7 \times 3} = \frac{15}{21}\\\\ \end{align}\)
Потом переходим к сравнению числителей. Правило сравнения дробей с одинаковыми знаменателями.
\(\begin{align}&\frac{14}{21} < \frac{15}{21}\\\\&\frac{2}{3} < \frac{5}{7}\\\\ \end{align}\)
Неправильная дробь всегда больше правильной. Потому что неправильная дробь больше 1, а правильная дробь меньше 1.
Потому что неправильная дробь больше 1, а правильная дробь меньше 1.
Пример:
Сравните дроби \(\frac{11}{13}\) и \(\frac{8}{7}\).
Дробь \(\frac{8}{7}\) неправильная и она больше 1.
\(1 < \frac{8}{7}\)
Дробь \(\frac{11}{13}\) правильная и она меньше 1. Сравниваем:
\(1 > \frac{11}{13}\)
Получаем, \(\frac{11}{13} < \frac{8}{7}\)
Вопросы по теме:
Как сравнить дроби с разными знаменателями?
Ответ: надо привести к общему знаменателю дроби и потом сравнить их числители.
Как сравнивать дроби?
Ответ: сначала нужно определиться к какой категории относятся дроби: у них есть общий знаменатель, у них есть общий числитель, у них нет общего знаменателя и числителя или у вас правильная и неправильная дробь. После классификации дробей применить соответствующее правило сравнения.
Что такое сравнение дробей с одинаковыми числителями?
Ответ: если у дробей одинаковые числители, та дробь больше у которой знаменатель меньше.
Пример №1:
Сравните дроби \(\frac{11}{12}\) и \(\frac{13}{16}\).
Решение:
Так как нет одинаковых числителей или знаменателей, применяем правило сравнения с разными знаменателями. Нужно найти общий знаменатель. Общий знаменатель будет равен 96. Приведем дроби к общему знаменателю. Первую дробь \(\frac{11}{12}\) умножим на дополнительный множитель 8, а вторую дробь \(\frac{13}{16}\) умножим на 6.
\( \begin{align}&\frac{11}{12} = \frac{11 \times 8}{12 \times 8} = \frac{88}{96}\\\\&\frac{13}{16} = \frac{13 \times 6}{16 \times 6} = \frac{78}{96}\\\\ \end{align}\)
Сравниваем дроби числителями, та дробь больше у которой числитель больше.
\( \begin{align}&\frac{88}{96} > \frac{78}{96}\\\\&\frac{11}{12} > \frac{13}{16}\\\\ \end{align}\)
Пример №2:
Сравните правильную дробь с единицей?
Решение:
Любая правильная дробь всегда меньше 1.
Задача №1:
Сын с отцом играли в футбол. Сын из 10 подходов в ворота попал 5 раз. А папа из 5 подходов попал в ворота 3 раза. Чей результат лучше?
Решение:
Сын попал из 10 возможных подходов 5 раз. Запишем в виде дроби \(\frac{5}{10} \).
Папа попал из 5 возможных подходов 3 раз. Запишем в виде дроби \(\frac{3}{5} \).
Сравним дроби. У нас разные числители и знаменатели, приведем к одному знаменателю. Общий знаменатель будет равен 10.
\(\begin{align}&\frac{3}{5} = \frac{3 \times 2}{5 \times 2} = \frac{6}{10}\\\\&\frac{5}{10} < \frac{6}{10}\\\\&\frac{5}{10} < \frac{3}{5}\\\\ \end{align}\)
Ответ: у папы результат лучше.
правила и преобразования обыкновенных дробных выражений в 5 классе
Математика
12.11.21
12 мин.
Существует определенный класс задач, в которых требуется произвести сравнение дробей с разными знаменателями. Очень часто операция выполняется неверно, поскольку учащийся не знает алгоритма ее выполнения, а источники в интернете не всегда предоставляют достоверную информацию. Специалисты-математики рекомендуют изучить теорию и разобраться в ключевых методиках, а затем переходить к практике.
Очень часто операция выполняется неверно, поскольку учащийся не знает алгоритма ее выполнения, а источники в интернете не всегда предоставляют достоверную информацию. Специалисты-математики рекомендуют изучить теорию и разобраться в ключевых методиках, а затем переходить к практике.
Оглавление:
- Правила конвертации
- Смешанные числа
- Приведение к общему знаменателю
- Множитель и произведение
- Простые значения
- Составные элементы
Общие сведения
Дроби — действительные числа, состоящие из целой и дробной частей.
Они классифицируются на два вида:
- Десятичные.
- Обыкновенные.
Каждый из типов возможно переводить в другой, т. е. обыкновенную можно переконвертировать в десятичную и наоборот. Десятичная — дробь, целая и дробная часть которой отделены между собой точкой или запятой (2,36 и т. д. ). Обыкновенная — дробное выражение, состоящее из числителя и знаменателя (2/3). Первый расположен в верхней части, а второй — в нижней.
д. ). Обыкновенная — дробное выражение, состоящее из числителя и знаменателя (2/3). Первый расположен в верхней части, а второй — в нижней.
В математике принято записывать дробное значение в десятичной форме, когда операция деления не дает бесконечную величину или для ведения расчетов. Обыкновенная применяется при вычислениях или для окончательной записи результата. Например, лучше записать 1/3, чем бесконечное число 0,333333333333333333333333333333333… и т. д.
Операция деления состоит из следующих элементов: делимого, делителя и частного. Первое — величина, которую требуется разделить, второе — коэффициент, делящий первое значение и третий — результат вычисления.
Правила конвертации
Для представления десятичной дроби в виде обыкновенной математики разработали определенную методику. Она имеет такой вид:
- Записать искомое выражение: 1,26.
- Умножить его на 100 (выбирается исходя из количества разрядов после запятой) и сформировать числитель: 126.

- Провести операции по сокращению и записать искомое выражение: 126/100=1 (26/100)=1 (13/50).
Результат, который получился в последнем пункте, называется смешанным числом. Следует подробно разобрать операции с ним, поскольку при сравнении также используется такая форма записи.
Смешанные числа
Смешанным значением является обыкновенное дробное выражение, полученное в результате преобразования неправильной формы с выделенной целой частью.
Следует отметить, что дроби бывают двух типов: правильными и неправильными. У первых всегда числитель меньше знаменателя, а у вторых — больше.
Математики рекомендуют сравнивать дроби в смешанном формате, когда они представлены в неправильной форме. Существует определенный алгоритм преобразования для этих целей:
- Записать величину: 29/6.
- Выделить целое методом подбора: 4 (6*4=24).
 Если взять 5, она не подойдет, поскольку не выполняется неравенство 29<6*5.
Если взять 5, она не подойдет, поскольку не выполняется неравенство 29<6*5. - Отнять от 29 число 24, а затем записать искомую величину: 4 ((29−6*4)/6)=4 (5/6).
Для выполнения обратной операции методику нужно выполнить в обратном порядке.
Она примет такой вид:
- Записывается смешанная форма: 4 (5/6).
- Перемножается знаменатель и целая часть, а затем прибавляется значение, находящееся в числителе: (6*4+5)/6=29/6.
Однако эта методика используется, когда требуется сравнить дроби с одинаковыми знаменателями. Если они разные, нужны дополнительные знания.
Приведение к общему знаменателю
Чтобы сравнить 2 дроби, нужно привести их к общему знаменателю. Существует 3 случая, которые реализуются посредством различных алгоритмов. К ним относятся:
- Произведение и множитель.

- Простые величины.
- Составные элементы.
В первом случае знаменатель одной дроби является множителем другой. Однако это является самым простым вариантом. Задачи такого типа встречаются редко.
Если знаменатели являются простыми числами (делятся на 1 и сами себя), алгоритм приведения будет существенно отличаться от предыдущего.
В последнем случае нужно уметь разложить число на множители или простые элементы.
Множитель и произведение
Для приведения обыкновенных дробей с разными знаменателями, один из которых является множителем другого, требуется воспользоваться простым правилом. Оно имеет следующий вид:
- Записать две дроби: 1 (2/8) и 1 (¾).
- Переконвертировать их в неправильные обыкновенные: (8*1+2)/8=10/8 и (4*1+¾)=7/4.
- Определить результирующую величину или окончательный знаменатель: 8.
- Умножить на соответствующие коэффициенты, полученные при делении результата в 3 пункте на текущий: [10*(8/8)]/8=10/8 и [7*(8/4)]/8=14/8.

Из методики можно сделать вывод, какой должен быть общий знаменатель для результирующей дроби. На основании этого формируется правило: он равен эквивалентному большему значению, которое делится на второе. Иногда для удобства при выполнении арифметической операции (например, сложения) возможно записать выражение в таком виде: [10*(8/8) + 7*(8/4)]/8=24/8=3.
Если нужно просто сравнить 2 величины, последний оптимизирующий метод использовать нет необходимости.
Простые значения
Если знаменатели двух дробей не равны между собой и являются простыми числами, требуется использовать перекрестный метод. Его суть в том, что для нахождения общего делителя нужно перемножить элементы дробных выражений между собой. Алгоритм имеет такой вид:
- Записать искомые величины.
- При необходимости выполнить преобразования из смешанного числа.

- Для получения результирующего значения требуется перемножить знаменатели.
- Разделить полученную величину на текущие знаменатели.
- Умножить числители на множители, полученные в 4 пункте.
Для понимания алгоритма требуется решить пример. Методика для чисел 5/7 и 2/3 имеет такой вид:
- Записать дроби: 5/7 и 2/3.
- Преобразовывать не требуется.
- Общий знаменатель: 7*3=21.
- Множители: 3 и 7 соответственно.
- Умножение числителей: 5*3/21=15/21 и 2*7/21=14/21.
После преобразования дробных величин возможно осуществлять любые арифметические и логические (сравнения) операции. Следующий случай является сложным, поскольку требуется умение, позволяющее разложить число на множители.
Составные элементы
Самый сложный случай — знаменатели дроби не являются простыми числами и один из них — не множитель другого.
Для приведения дробей к общему знаменателю требуется отдельные значения разложить на множители, затем найти наименьшее общее значение. Математики называют его наименьшим общим кратным (НОК). Алгоритм имеет такой вид:
- Разложить знаменатель первой дроби на множители.
- Выполнение первого пункта для второго.
- Вывод общего значения на основе анализа элементов.
- Определение нужных коэффициентов для числителей.
- Записать результирующие дроби.
Работу методики следует разобрать на примере двух обыкновенных дробей: 7/12 и 13/16. Реализация имеет такой вид:
- Разложение 12 на простые элементы: 12 = 2*2*3.
- Простые множители для 16: 16 = 2*2*2*2.
- Анализ элементов: общие — 2*2=4, недостающие — 3*2*2=12. НОК=общие*недостающие для первого знаменателя, т. е. 12*4=48).
- Коэффициенты: [7*(48/12)]/48 и [13*(48/16)]/48.
- Результирующие величины: 7*4/48=28/48 и 13*3/48=39/48.
Можно брать также за основу первый знаменатель, а уже потом искать дополнительные элементы. Математики не рекомендуют использовать последнюю методику, поскольку можно сделать больше ошибок при расчетах. После рассмотрения всех случаев приведения дробей можно перейти к их сравнению.
Математики не рекомендуют использовать последнюю методику, поскольку можно сделать больше ошибок при расчетах. После рассмотрения всех случаев приведения дробей можно перейти к их сравнению.
Сравнение дробей
Сравнить две дроби с разными знаменателями довольно просто.
Условно задачи можно классифицировать таким образом:
- Одинаковые числители и разные знаменатели.
- Разные элементы.
- Отрицательные и положительные.
В первом случае знак больше «>» или меньше «<» ставится в сторону той дробной величины, у которой знаменатель меньше или больше. Например, 5/8 > 5/12, т. к. 8>12. Если у дробных величин разные числители и знаменатели, требуется привести их к общему значению, а затем сравнить. При сравнении отрицательного значения и положительно «<» ставится в сторону первого. В этом случае нет смысла приводить какие-либо преобразования.
Таким образом, для сравнения дробей нужно знать основные алгоритмы приведения с разными знаменателями и уметь преобразовывать смешанные числа.
Сравнение дробей – методы, пояснения и примеры
Сравнение дробей означает определение большей и меньшей дроби между любыми двумя или более дробями. Поскольку дроби состоят из двух частей — числителя и знаменателя, их сравнивают по определенному набору правил. Давайте узнаем больше о сравнении дробей на этой странице.
| 1. | Как сравнивать дроби? |
| 2. | Сравнение дробей с одинаковыми знаменателями |
| 3. | Сравнение дробей с разными знаменателями |
| 4. | Десятичный метод сравнения дробей |
| 5. | Сравнение дробей с помощью визуализации |
| 6. | Сравнение дробей с помощью перекрестного умножения |
7. | Часто задаваемые вопросы о сравнении дробей |
Как сравнивать дроби?
Сравнение дробей включает набор правил, связанных с числителем и знаменателем. При сравнении любых двух дробей мы узнаем большую и меньшую дробь. Нам нужно сравнивать дроби в нашей повседневной жизни. Например, когда нам нужно сравнить соотношение ингредиентов при соблюдении рецепта или сравнить результаты экзаменов и т. д. Итак, давайте рассмотрим различные методы сравнения дробей, чтобы лучше понять концепцию.
Что такое дробь?
Прежде чем исследовать концепцию сравнения дробей, давайте вспомним дроби. Дробь является частью целого и состоит из двух частей — числителя и знаменателя. Числитель — это число в верхней части дробной черты, а знаменатель расположен под дробной чертой.
Теперь давайте поговорим подробнее о сравнении дробей.
Сравнение дробей с одинаковыми знаменателями
При сравнении дробей с одинаковыми знаменателями становится легче определить большую или меньшую дробь. Проверив, совпадают ли знаменатели, мы можем просто найти дробь с большим числителем. Если и числители, и знаменатели равны, дроби также равны. Например, сравним 6/17 и 16/17
Проверив, совпадают ли знаменатели, мы можем просто найти дробь с большим числителем. Если и числители, и знаменатели равны, дроби также равны. Например, сравним 6/17 и 16/17
- Шаг 1: Обратите внимание на знаменатели данных дробей: 6/17 и 16/17. Знаменатели одинаковы.
- Шаг 2: Теперь сравните числители. Мы видим, что 16 > 6,
- Шаг 3: Дробь с большим числителем является большей дробью. Следовательно, 6/17 < 16/17.
Сравнение дробей с разными знаменателями
Для сравнения дробей с разными знаменателями нам нужно преобразовать их в одинаковые знаменатели, для чего мы должны найти наименьшее общее кратное (НОК) знаменателей. Когда знаменатели сделаны одинаковыми, мы можем легко сравнивать дроби. Например, сравним 1/2 и 2/5.
- Шаг 1: Обратите внимание на знаменатели данных дробей: 1/2 и 2/5. Они разные. Итак, найдем НОК 2 и 5. НОК(2, 5) = 10, .
- Шаг 2: Теперь переведем их так, чтобы знаменатели стали одинаковыми. Умножим первую дробь на 5/5, то есть 1/2 × 5/5 = 5/10.
- Шаг 3: Теперь умножим вторую дробь на 2/2, то есть 2/5 × 2/2 = 4/10.
- Шаг 4: Сравните дроби: 5/10 и 4/10. Поскольку знаменатели одинаковы, мы сравним числители и увидим, что 5 > 4 .
- Шаг 5: Дробь с большим числителем является большей дробью, то есть 5/10 > 4/10. Следовательно, 1/2 > 2/5

Следует отметить, что если знаменатели разные, а числители одинаковые, то мы можем легко сравнивать дроби, глядя на их знаменатели. Дробь с меньшим знаменателем имеет большее значение, а дробь с большим знаменателем имеет меньшее значение. Например, 2/3 > 2/6.
Десятичный метод сравнения дробей
В этом методе мы сравниваем десятичные значения дробей. Для этого числитель делится на знаменатель и дробь преобразуется в десятичную. Затем сравниваются десятичные значения. Например, давайте сравним 4/5 и 6/8.
Затем сравниваются десятичные значения. Например, давайте сравним 4/5 и 6/8.
- Шаг 1: Запишите 4/5 и 6/8 десятичными знаками. 4/5 = 0,8 и 6/8 = 0,75.
- Шаг 2: Сравните десятичные значения. 0,8 > 0,75
- Шаг 3: Дробь с большим десятичным значением будет большей дробью. Следовательно, 4/5 > 6/8
Сравнение дробей с помощью визуализации
Мы можем использовать различные графические методы и модели для визуализации более крупных фракций. Обратите внимание на приведенный ниже рисунок, на котором показаны модели A и B, представляющие две дроби. Мы можем легко определить, что 4/8 < 4/6, потому что 4/6 покрывает большую заштрихованную область, чем 4/8. Обратите внимание, что меньшая часть занимает меньшую площадь того же целого. Здесь следует принять во внимание, что размер моделей A и B должен быть точно таким же, чтобы сравнение было достоверным. Затем каждая модель делится на равные части, соответствующие их соответствующим знаменателям.
Сравнение дробей с помощью перекрестного умножения
Для сравнения дробей методом перекрестного умножения мы умножаем числитель одной дроби на знаменатель другой дроби. Давайте разберемся в этом с помощью примера. Сравните 1/2 и 3/4. Обратите внимание на приведенный ниже рисунок, который лучше объясняет это.
- Шаг 1: Когда мы умножаем данные дроби крестом для их сравнения, мы должны иметь в виду, что если мы умножаем числитель первой дроби на знаменатель второй дроби, мы должны записать произведение следующим к первой дроби. Здесь 1 × 4 = 4, и мы будем писать 4 рядом с первой дробью. (Напишите произведение рядом с выбранным числителем)
- Шаг 2: Аналогично, когда мы умножаем числитель второй дроби на знаменатель первой дроби, мы должны писать произведение рядом со второй дробью. Здесь 3 × 2 = 6, и мы будем писать 6 возле второй дроби.
- Шаг 3: Теперь сравним произведения 4 и 6.
 Поскольку 4 < 6, можно легко сравнить соответствующие дроби, то есть 1/2 < 3/4. Следовательно, 1/2 < 3/4
Поскольку 4 < 6, можно легко сравнить соответствующие дроби, то есть 1/2 < 3/4. Следовательно, 1/2 < 3/4
☛ Похожие темы
- Типы дробей
- Калькулятор сравнения дробей
- Умножение дробей
- Деление дробей
- Десятичные числа и дроби
Примеры сравнения дробей
Пример 1: Почему 5/11 > 4/11? Вы можете объяснить?
Решение:
Сравнивать дроби становится легче, если знаменатели совпадают. 5/11 и 4/11 имеют одинаковые знаменатели; следовательно, мы можем просто сравнивать дроби, наблюдая за числителями. Дробь с большим числителем и будет большей дробью. 5 > 4. Следовательно, 5/11 > 4/11.
Пример 2: Райана попросили доказать, что данные дроби: 4/6 и 6/9 равны. Можете ли вы доказать это, используя метод LCM?
Решение:
Мы можем сделать знаменатели одинаковыми, найдя НОК знаменателей данных дробей.
 НОК 6 и 9 равно 18. Итак, мы умножим 4/6 на 3/3, (4/6) × (3/3) = 12/18 и 6/9 на 2/2, (6/ 9) × (2/2) = 12/18, что преобразует их в одинаковые дроби с одинаковыми знаменателями. Новые дроби с теми же знаменателями будут 12/18 и 12/18. Следовательно, обе дроби равны: 4/6 = 6/9.. Следовательно, 4/6 = 6/9.
НОК 6 и 9 равно 18. Итак, мы умножим 4/6 на 3/3, (4/6) × (3/3) = 12/18 и 6/9 на 2/2, (6/ 9) × (2/2) = 12/18, что преобразует их в одинаковые дроби с одинаковыми знаменателями. Новые дроби с теми же знаменателями будут 12/18 и 12/18. Следовательно, обе дроби равны: 4/6 = 6/9.. Следовательно, 4/6 = 6/9.Пример 3: Сравните дроби 5/8 и 7/12.
Решение: Для сравнения дробей с разными знаменателями нам нужно найти НОК знаменателей. НОК 8 и 12 равно 24. Итак, давайте умножим 5/8 на 3/3, то есть 5/8 × 3/3 = 15/24. Теперь умножим 7/12 на 2/2, то есть 14/24. Теперь, когда у нас есть похожие дроби 15/24 и 14/24, мы можем легко их сравнить. Так как 15 > 14, 5/8 > 7/12. Следовательно, 5/8 > 7/12.
перейти к слайдуперейти к слайдуперейти к слайду
Хотите создать прочную основу в математике?
Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.
Записаться на бесплатный пробный урок
Практические вопросы по сравнению дробей
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы о сравнении дробей
Что означает сравнение дробей?
Сравнение дробей означает сравнение заданных дробей, чтобы определить, является ли одна дробь меньше, больше или равна другой дроби. Как и целые числа, мы можем сравнивать дроби, используя одни и те же символы: <,> и =. Существуют различные методы и правила сравнения дробей в зависимости от числителя и знаменателя, а также от вида дробей.
Каково правило сравнения дробей с одинаковым знаменателем?
Когда знаменатели данного набора дробей одинаковы, дробь с меньшим числителем является меньшей дробью, а дробь с большим числителем — большей дробью. При равенстве числителей дроби считаются равными. Например, если нам нужно сравнить 2/5 и 4/5, нам просто нужно проверить и сравнить числители. Поскольку 2 < 4, можно сказать, что 2/5 < 4/5.
Поскольку 2 < 4, можно сказать, что 2/5 < 4/5.
По какому правилу сравнивать дроби с одинаковым числителем?
Если дроби имеют одинаковый числитель, то дробь с меньшим знаменателем больше. Например, сравним дроби с одним и тем же числителем. Даны дроби 1/2 и 1/6. Теперь из них дробь с меньшим знаменателем равна 1/2. Таким образом, 1/2 является большей из данных дробей.
Что такое эквивалентные дроби?
Дроби, имеющие разные числители и знаменатели, но равные по своим значениям, называются эквивалентными дробями. Например, 5/10 и 6/12 являются эквивалентными дробями, поскольку обе они в упрощенном виде равны 1/2.
Как проще всего сравнивать дроби?
Самый простой и быстрый способ сравнения дробей — преобразовать их в десятичные числа. Дробь с большим десятичным значением является большей дробью.
Зачем нужно сравнивать дроби?
Сравнение дробей является важным компонентом, который помогает учащимся развивать свое числовое представление о размере дроби. Это помогает им понять, что стратегии, которые они используют для сравнения целых чисел, не обязательно применимы при сравнении дробей. Например, 1/4 больше 1/8, хотя целое число 8 больше 4.
Это помогает им понять, что стратегии, которые они используют для сравнения целых чисел, не обязательно применимы при сравнении дробей. Например, 1/4 больше 1/8, хотя целое число 8 больше 4.
Как сравнивать дроби с разными знаменателями?
Чтобы сравнивать дроби с разными знаменателями, нам нужно найти наименьшее общее кратное (НОК) знаменателей и преобразовать данные дроби в подобные дроби, сделав их знаменатели одинаковыми, и тогда числители можно будет легко сравнить. Например, давайте сравним 7/12 и 9/16.
- Шаг 1: Поскольку данные дроби имеют разные знаменатели, мы найдем НОК знаменателей. LCM 12 и 16 = 48,
- Шаг 2: Теперь переведем дроби так, чтобы знаменатели стали одинаковыми. Умножим первую дробь на 4/4, то есть 7/12 × 4/4 = 28/48.
- Шаг 3: Теперь давайте умножим вторую дробь на 3/3, то есть 9/16 × 3/3 = 27/48.
- Шаг 4: Сравните дроби: 28/48 и 27/48. Поскольку знаменатели одинаковые, сравним числители и увидим, что 28 > 27.

- Шаг 5: Дробь с большим числителем является большей дробью, то есть 28/48 > 27/48. Следовательно, 7/12 > 9/16
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочие листы по сравнению дробей
Как сравнивать разные дроби
Чем отличаются дроби?
В отличие от дробей две или более дроби имеют разные знаменатели. Это означает, что числа в нижней части разных дробей различны. В отличие от дробей, каждая из них делится на части разного размера, поэтому их нельзя легко сравнивать или добавлять.
Например, 1 / 4 и 1 / 3 не являются дробями, потому что у них разные знаменатели. Первая фракция делится на 3 части, а вторая фракция делится на 4 части.
Подобные дроби — это дроби, у которых знаменатели в нижней части совпадают. Например, 1 / 4 и 3 / 4 . Обе эти дроби имеют одинаковый знаменатель, равный 4.
Мы видим, что 3 / 4 больше, чем 1 / 4 , потому что у нас есть 3 квартала по сравнению с 1 кварталом. Мы сравниваем детали одинакового размера.
Мы сравниваем детали одинакового размера.
Однако сразу не ясно, какая из разнородных дробей 2 / 3 и 3 / 5 больше.
Как сравнивать дроби с разными знаменателями
Чтобы сравнить дроби с разными знаменателями, выполните следующие действия:
- Найдите первое число, которое появится в таблице умножения каждого знаменателя. Это общий знаменатель.
- Запишите каждую дробь в виде эквивалентной дроби, имеющей этот общий знаменатель.
- Чем больше числитель этих дробей, тем больше дробь.
В качестве примера сравним неодинаковые дроби 1 / 4 и 2 / 6 .
Шаг 1 — найти первое число, которое появится в таблице умножения обоих знаменателей. Таблица умножения на 4 — это 4, 8, 12, 16, 20, 24. Таблица умножения на 6 — это 6, 12, 18, 24.
Нам нужно только перечислить числа до 24, потому что 4 × 6 = 24. Однако мы видим, что 12 — это число, которое появляется первым. Мы будем использовать 12 в качестве общего знаменателя.
Мы будем использовать 12 в качестве общего знаменателя.
Шаг 2 — записать обе дроби как эквивалентные дроби с общим знаменателем. Запишем обе дроби от 12.
1 / 4 = 3 / 12 и 2 / 6 = 4 / 12 12
Шаг 3 — сравнить дроби по их числителю.
3 меньше 4, поэтому 4 / 12 меньше 3 / 12 .
Это позволяет нам сравнивать исходные дроби.
1 / 4 меньше 2 / 6 .
Мы можем записать это как 1 / 4 2 / 6 .
Мы можем использовать знаки неравенства большего меньшего и меньшего для сравнения дробей. Знак » всегда открывается в сторону большей дроби и указывает на меньшую дробь.
Вот еще один пример сравнения дробей с разными знаменателями. У нас есть 3 / 4 и 7 / 8 .
Мы видим, что 8 — это первое число в таблице умножения на 4 и 8. Мы удваиваем числа в первой дроби, так что 3 / 4 = 6 / 8 .
Мы можем оставить 7 / 8 такими же.
Теперь, когда обе дроби не равны 8, мы можем их сравнить.
6 меньше 7, поэтому 6 / 8 меньше 7 / 8 .
Поэтому мы можем сказать, что 3 / 4 меньше, чем 7 / 8 .
Пишем 3 / 4 7 / 8 . Стрелка знака указывает на меньшую дробь.
Как сравнивать неправильные дроби с разными знаменателями
Чтобы сравнить неправильные дроби с разными знаменателями, сначала запишите каждую дробь как эквивалентную ей дробь, чтобы обе они имели одинаковый знаменатель. Теперь самая большая неправильная дробь будет иметь наибольший числитель. Две неправильные дроби можно сравнивать только в том случае, если у них один и тот же знаменатель в нижней части.
Например, вот неправильные дроби 5 / 4 и 6 / 5 . Неправильные дроби — это просто дроби, у которых числитель сверху больше, чем знаменатель снизу.
Общий знаменатель этих дробей равен 20. 20 — первое число как в таблице умножения на 4, так и в таблице умножения на 5.
Запись дробей в виде эквивалентных дробей со знаменателями 20, 5 / 4 = 25 / 20 и 6 / 5 = 24 / 20 .
25 больше числителя 24, поэтому 25 / 20 больше 24 / 20 .
Следовательно, 5 / 4 больше, чем 6 / 5 .
Вот еще один пример сравнения размера двух неправильных дробей.
У нас есть 10 / 3 и 9 / 2 .
Пишем 10 / 3 = 20 / 6 и 9 / 2 = 02 27 / 90.
Обе дроби имеют одинаковый знаменатель, и теперь их можно заказать.
20 меньше 27, поэтому 20 / 6 меньше 27 / 6 .
Следовательно, 10 / 3 меньше 9 / 2 .
Сравнение дробей с использованием десятичных дробей
Преобразование различных дробей в десятичные — это метод, который можно использовать для сравнения их размера. Дроби можно превратить в десятичные, разделив числитель на знаменатель. Чем больше десятичное число, тем больше дробь.
Например, здесь у нас есть дроби 2 / 5 и 3 / 4 .
Превратим 2 / 5 в десятичную дробь, разделив 2 на 5.
2 ÷ 5 = 0,4.
Превратим 3 / 4 в десятичную дробь, разделив 3 на 4.
3 ÷ 4 = 0,75.
Наибольшее десятичное число равно 0,75. Следовательно, большая часть равна 3 / 4 .
Мы говорим, что 2 / 5 меньше 3 / 4
Сравнение дробей – определение, методы, примеры, часто задаваемые вопросы
« Сравнение дробей » относится к определению большей и меньшей дроби в заданном наборе дробей. При сравнении дробей соблюдается ряд правил для сравнения числителя и знаменателя дроби, где числитель — это число над дробной чертой, а знаменатель — число под дробной чертой. Мы можем определить большую и меньшую дроби, сравнивая любые две дроби. Дроби можно сравнивать, даже если у них разные числители и знаменатели. Чтобы лучше понять концепцию, давайте рассмотрим различные способы сравнения дробей.
Дробь
Перед тем, как перейти к понятию сравнения двух дробей, давайте вспомним, что такое дробь. Дробь определяется как часть целого, состоящая из двух частей: числителя и знаменателя, где числитель — это число над дробной чертой, а знаменатель — число под дробной чертой.
Как сравнить две дроби в числах?
Чтобы определить, какая из двух дробей больше или меньше, нужно их сравнить. В зависимости от числителя, знаменателя и вида дробей существуют разные методы и правила сравнения дробей. Их:
- Сравнение фракций с теми же знаменателями
- Сравнение фракций с непоходом на знаменатели
- Сравнивая фракции с использованием десятичного метода
- Сравнивая фракции с использованием визуализации
- Сравнение фракций с использованием неполноценного метода
- Сравнение дробей с одинаковыми числителями
- По убыванию
- Сложение и вычитание дробей с одинаковыми или одинаковыми числителями
- Использование моделей для сравнения фракций: тот же знаменатель
- Модели использования для сравнения фракций: Тот же числовой
- Знаменатель — это нижнее число в дроби.

- Показывает, на сколько равных частей делится предмет.
- Число в знаменателе увеличивается
- Один и тот же числитель равен тому же количеству частей, о которых идет речь
- Итак, если дроби относятся к одному и тому же целому, а числители одинаковы, то количество по сравнению — то же самое.

- Рани читает 1/6 книги утром; днем она читает 4/6 книги. Какую часть книги она читает?
- Чему равна дробь 3/4 со знаменателем 20?
- У Раджа 26 ирисок. Половину отдал другу. Сколько ирисок он дал своему другу?
- Напишите два оператора сравнения дробей, показанных ниже.

- Как сравнивать дроби, относящиеся к одному и тому же целому числу и имеющие один и тот же знаменатель, путем сравнения их числителей
- Как сравнивать дроби, относящиеся к одному и тому же целому числу и имеющие один и тот же числитель путем сравнения их знаменателей
- Как использовать символы (>, <, =) для сравнения дробей с разными числителями и знаменателями
- Знать, что для сравнения двух дробей обе должны относиться к одному и тому же целому
- Как рисовать модели площадей для сравнения двух дробей
- Как сравнивать дроби, относящиеся к одному и тому же целому числу и имеющие одинаковый знаменатель, путем сравнения их числителей
- Как сравнивать дроби, относящиеся к одному и тому же целому числу и имеют один и тот же числитель, сравнивая их знаменатели
- Как использовать символы (>, <, =) для сравнения дробей с разными числителями и знаменателями
- Знать, что для сравнения двух дробей обе должны относиться к одному и тому же целому
- Как рисовать модели площадей для сравнения двух дробей
Ранее мы видели, что дроби состоят из двух частей.
Одна часть является старшим числом, или числитель .
Другим является нижнее число, или знаменатель .
Знаменатель говорит нам, сколько частей в целом.
Числитель говорит нам, сколько таких частей у нас есть.
Если дроби имеют одинаковый знаменатель, это означает, что они разделены на одинаковое количество частей.
Это означает, что мы можем сравнить этих дробей, просто взглянув на числитель.

Здесь 5 больше 4…
Здесь 5 больше 4… так что мы можем сказать, что 5/6 больше 4/6.
Давайте рассмотрим другой пример. Какой из них больше: 2/8 или 6/8?
Если вы думали, что 6/8 больше, вы были правы!
Обе дроби имеют одинаковый знаменатель.
Итак, мы сравнили числители. 6 больше 2, поэтому 6/8 больше 2/8.
Сравним эти дроби: 5/8 и 4/6.
Прежде чем мы их сравним, нам нужно изменить обе дроби так, чтобы они имели одинаковый знаменатель или нижний номер.
Сначала найдем наименьшее число, которое можно разделить на оба знаменателя. Мы называем это наименьшим общим знаменателем .
Наш первый шаг — найти числа, которые можно без остатка разделить на 8.
Это легко сделать с помощью таблицы умножения. Все числа в 8-й строке можно разделить на 8 без остатка.
Теперь давайте посмотрим на наш второй знаменатель: 6.
Мы снова можем использовать таблицу умножения.
 Все числа в 6-й строке можно разделить на 6 без остатка.
Все числа в 6-й строке можно разделить на 6 без остатка.Сравним две строки. Похоже, есть несколько чисел, которые можно разделить на 6 и 8 без остатка.
24 — это наименьшее число, которое встречается в обеих строках, поэтому это наименьший общий знаменатель .
Теперь мы изменим наши дроби так, чтобы они имели одинаковый знаменатель: 24.
Для этого нам нужно изменить числители так же, как мы изменили знаменатели.
Давайте еще раз посмотрим на 5/8. Чтобы изменить знаменатель на 24…
Давайте снова посмотрим на 5/8. Чтобы изменить знаменатель на 24… нам пришлось умножить 8 на 3.
Поскольку мы умножили знаменатель на 3, мы также умножим числитель, или верхнее число, на 3.
5 умножить на 3 равно 15. Таким образом, мы изменили 5/8 на 15/24.
Мы можем это сделать, потому что любое число равно 1.
Итак, когда мы умножаем 5/8 на 3/3.
 ..
..Итак, когда мы умножаем 5/8 на 3/ 3… на самом деле мы умножаем 5/8 на 1.
Поскольку любое число, умноженное на 1, равно самому себе…
Поскольку любое число, умноженное на 1, равно самому себе… мы можем сказать что 5/8 равно 15/24.
Теперь проделаем то же самое с другой дробью: 4/6. Мы также изменили его знаменатель на 24,9.0005
Наш старый знаменатель был 6. Чтобы получить 24, мы умножили 6 на 4.
Итак, мы также умножим числитель на 4.
равно 16/24.
Теперь, когда знаменатели совпадают, мы можем сравнить две дроби, взглянув на их числители.
16/24 больше 15/24…
16/24 больше 15/24… поэтому 4/6 больше 5/8.
Попробуем уменьшить эту дробь: 16/20.
Так как числитель и знаменатель четные числа , вы можете разделить их на 2, чтобы уменьшить дробь.
Сначала мы разделим числитель на 2. 16 разделить на 2 будет 8.
Затем мы разделим знаменатель на 2. 20 разделить на 2 равно 10.
Мы’ ve уменьшил 16/20 до 8/10. Мы могли бы также сказать, что 16/20 равно 8/10.
Если числитель и знаменатель все еще можно разделить на 2, мы можем продолжить сокращение дроби.
8 разделить на 2 равно 4.
10 разделить на 2 равно 5.
Поскольку не существует числа, на которое можно разделить 4 и 5, мы не можем больше сокращать 4/5.
Это означает, что 4/5 является простейшим формой от 16/20.
Попробуем сократить другую дробь: 6/9.
Хотя числитель четный, знаменатель нечетное число , поэтому мы не можем уменьшить путем деления на 2.

Вместо этого нам нужно найти число, которое 6 и 9можно разделить на. Таблица умножения поможет найти это число.
Найдем 6 и 9 в той же строке . Как видите, 6 и 9 можно разделить на 1 и 3.
Деление на 1 не изменит эти дроби, поэтому мы будем использовать наибольшее число , на которое можно разделить 6 и 9.
Это 3. Это называется наибольшим общим делителем или НОД . (Вы также можете назвать это наибольший общий делитель или GCF .)
3 — это НОД 6 и 9, потому что это наибольшее число, на которое они могут делиться.
Итак, мы разделим числитель на 3. 6 разделить на 3 равно 2.
Затем мы разделим знаменатель на 3. 9 разделить на 3 равно 3.
Теперь у нас есть уменьшено 6/9 до 2/3, что является его простейшей формой.
 Мы могли бы также сказать, что 6/9 равно 2/3.
Мы могли бы также сказать, что 6/9 равно 2/3.Преобразуем 1 1/4 в неправильную дробь.
Во-первых, нам нужно выяснить, сколько частей составляют целое число: 1 в этом примере.
Для этого умножим целое число , 1, на знаменатель, 4.
1 умножить на 4 равно 4.
Теперь добавим к этому числу 4. числитель 1.
4 плюс 1 равно 5.
Знаменатель остается прежним.

Наша неправильная дробь — 5/4, или пять четвертых. Таким образом, мы могли бы сказать, что 1 1/4 равно 5/4.
Это означает, что в 1 1/4 содержится пять 1/4.
Преобразуем другое смешанное число: 2 2/5.
Сначала умножим целое число на знаменатель. 2 умножить на 5 равно 10.
Далее мы добавим 10 к числителю. 10 плюс 2 равно 12.
Как всегда, знаменатель останется прежним.
Итак, 2 2/5 равно 12/5.
Превратим 10/4 в смешанное число.
Любую дробь можно представить как деление задачу . Просто относитесь к линии между числами как к знаку деления (/).
Итак, разделим числитель, 10 на знаменатель, 4.
10 разделить на 4 равно 2… остаток от 2.
Ответ 2 станет нашим целым числом, потому что 10 можно разделить на 4 дважды .
И остаток , 2 станет числителем дроби, потому что у нас осталось 2 части.
Знаменатель остается прежним.
Итак, 10/4 равно 2 2/4.
Возьмем другой пример: 33/3.
Разделим числитель 33 на знаменатель 3.
33 разделить на 3…
33 разделить на 3… равно 11 без остатка.

060606073. легко найти большую или меньшую дробь, если дроби имеют одинаковые знаменатели. При сравнении дробей проверяйте, совпадают ли знаменатели. Если знаменатели равны, то больше та дробь, у которой числители больше. Дроби равны, если равны числители и знаменатели обеих дробей.
Пример: Сравните: 12.05 и 17.12.
Решение:
Шаг 1: Сначала обратите внимание на знаменатели данных дробей, то есть 5/12 и 17/12.
Здесь знаменатели одинаковы для обеих дробей.
Шаг 2: Теперь сравним числители данных дробей. Мы можем заметить, что 17 > 5.
Шаг 3: Мы знаем, что дробь с большим числителем больше. Следовательно, 5/12 < 17/12.
Сравнение дробей с разными знаменателями
Чтобы сравнить дроби с разными знаменателями, мы должны преобразовать их в одинаковые знаменатели, для которых мы должны найти наименьшее общее кратное (НОК) знаменателей. Поскольку знаменатели равны, мы можем легко сравнивать дроби.
Пример: Сравните: 1/4 и 2/3.
Решение:
Шаг 1: Сначала обратите внимание на знаменатели данных дробей, то есть 1/4 и 2/3. Поскольку знаменатели разные, сделайте их равными, найдя НОК 4 и 3. НОК(4,3) = 12,
Шаг 2: Теперь преобразуем данную дробь так, чтобы у них были одинаковые знаменатели. Итак, умножьте первую дробь на 3/3, т.
е. 1/4 × 3/3 = 4/12.
Шаг 3: Точно так же умножьте вторую дробь на 4/4, т. е. 2/3 × 4/4 = 8/12. Таким образом, первая дробь становится 4/12, а другая — 8/12.
Шаг 4: Сравните полученные новые дроби, т. е. 4/12 и 8/12. Так как знаменатели одинаковые, сравним числители. Мы можем заметить, что 4 < 8,
Шаг 5: Дробь с большим числителем является большей дробью. Итак, 8/12 > 4/12. Итак, 1/4 > 2/3.
Примечание: Обратите внимание, что если данные дроби имеют одинаковые числители и разные знаменатели, то мы можем легко сравнить их, глядя на их знаменатели. Дробь, у которой знаменатель меньше, имеет большее значение, а дробь, у которой знаменатель больше, имеет меньшее значение. Например 6/2 > 6/5.
Сравнение дробей десятичным методом
В этом методе можно сравнивать дроби, находя десятичные значения дробей и сравнивая их. Для этого делим числитель на знаменатель, и таким образом дробь преобразуется в десятичную. Наконец, сравните их десятичные значения. Давайте разберемся в этом на примере.
Наконец, сравните их десятичные значения. Давайте разберемся в этом на примере.
Пример: Сравните 3/5 и 2/4.
Решение:
Шаг 1: Чтобы записать 3/5 и 2/4 десятичными знаками, разделите числитель на знаменатель. Разделите 3 на 5 и 2 на 4.
Шаг 2: Полученные десятичные значения равны 0,6 и 0,5.
Шаг 3: Наконец, сравните десятичные значения. 0,6 > 0,5. Дробь с большим десятичным значением будет больше. Следовательно, 3/5 > 2/4.
Сравнение дробей с помощью визуализации
По сравнению с любым другим методом сравнение дробей с помощью визуализации проще. Сделайте два ящика так, чтобы длина и ширина обоих были одинаковыми. На приведенном ниже рисунке показаны модели А и В, которые представляют собой две фракции. Затем разделите каждую модель на равные части, соответствующие их соответствующим знаменателям. Теперь мы можем легко обнаружить, что 2/6 < 2/4, так как 2/4 покрывает большую заштрихованную область по сравнению с 2/6. Меньшая фракция занимает меньшую площадь того же целого, а большая фракция занимает большую площадь того же целого.
Меньшая фракция занимает меньшую площадь того же целого, а большая фракция занимает большую площадь того же целого.
Сравнение дробей методом перекрестного умножения
Чтобы сравнивать дроби методом перекрестного умножения, мы должны умножить числитель одной дроби на знаменатель другой дроби. Давайте разберемся в этом на примере.
Пример: Сравните 3/8 и 4/5.
Обратите внимание на приведенный ниже рисунок, который лучше объясняет концепцию перекрестного умножения.
Шаг 1: Обратите внимание, что когда мы выполняем перекрестное умножение для сравнения двух дробей, мы должны умножить числитель первой дроби на знаменатель второй дроби. Мы должны написать произведение на стороне выбранного числителя. Здесь произведение 3 × 5 = 15, которое мы пишем рядом с первой дробью.
Шаг 2: Аналогично, при умножении числителя второй дроби на знаменатель первой дроби мы должны записать произведение рядом со второй дробью.
Здесь произведение 4 × 8 = 32, которое мы запишем возле второй дроби.
Шаг 3: Теперь сравните оба произведения, т. е. 15 и 32. Поскольку 15 < 32, можно легко сравнить соответствующие дроби, т. е. 3/8 < 4/5. Следовательно, 3/8 < 4/5.
Решенные примеры на сравнение дробей
Пример 1: Какая из следующих дробей больше: 6/11 или 8/15?
Решение:
Даны дроби: 6/11 и 8/15
Знаменатели данных дробей различны. Итак, найдите НОК знаменателей, т. е. НОК(11, 15) = 165.
Теперь умножьте 6/11 на 15/15 и 8/15 на 11.
6/11 × 15/15 = 90/165
8/15 × 11/11 = 88/165
Теперь сравните числители, так как знаменатели одинаковы.
Итак, 90 > 88, т. е. 90/165 > 88/165.
Следовательно, 6/11 > 8/15, т. е. 6/11 — большая дробь.
Пример 2: Какая из данных дробей меньше: 13/85 или 21/85?
Решение:
Даны дроби: 13/85 и 21/85.
Знаменатели данных дробей совпадают. Итак, сравните числители данных дробей.
13 < 21.
Итак, 13/85 < 21/85.
Следовательно, 13/85 — меньшая дробь.
Пример 3: Сравните дроби 4/25 и 33/100.
Решение:
Чтобы сравнить данные дроби, найдите их десятичные значения. Итак, делим 4 на 25 и 33 на 100.
4/25 = 0,16
33/100 = 0,33
Из десятичных значений можно сделать вывод, что 0,33 > 0,16. Итак, 33/100 больше, чем 4/25.
Следовательно, 33/100 больше, чем 4/25.
Пример 4: Мрунала попросили доказать равенство данных дробей: 30/90 и 25/75. Можете ли вы доказать данное утверждение, используя метод НОК?
Решение:
Даны дроби: 30/90 и 25/75.
Знаменатели данных дробей различны. Итак, найдите НОК знаменателей, т. е. НОК(90, 75) = 450.
Теперь умножьте 30/90 на 5/5 и 25/75 на 6/6.
30/90 × 5/5 = 150/450
25/75 × 6/6 = 150/450
Теперь сравните числители, так как знаменатели одинаковы.
Итак, 150 = 150, т. е. 150/450 = 150/450.
Таким образом, 30/90 = 25/75, т. е. обе указанные дроби равны.
Значит, доказано.
Пример 5: Какая из следующих дробей больше: 27/41 или 27/67?
Решение:
Даны дроби: 27/41 и 27/67.
Здесь числители обеих дробей одинаковы, но знаменатели разные.
Мы знаем, что дробь с меньшим знаменателем имеет большее значение, а дробь с большим знаменателем имеет меньшее значение.
Здесь 41 < 67.
Итак, 27/41 > 27/67
Следовательно, 27/41 — большая дробь.
Часто задаваемые вопросы о сравнении дробей
Вопрос 1: Что подразумевается под сравнением дробей?
Ответ:
«Сравнение дробей» относится к определению большей и меньшей дроби в заданном наборе дробей.
Мы можем определить большую, меньшую или эквивалентную дробь, сравнив любые две дроби. В зависимости от числителя, знаменателя и вида дробей существуют разные методы и правила сравнения дробей.
Вопрос 2: По какому правилу сравнивать дроби с одинаковыми знаменателями?
Ответ:
Если данный набор дробей имеет одинаковый знаменатель, то дробь, у которой числитель меньше, является меньшей дробью, а дробь, у которой числитель больше, является большей дробью. Если числители равны, то дроби считаются равнозначными дробями. Например, если нам нужно сравнить 2/3 и 5/3, нам просто нужно проверить их числители и сравнить их. Поскольку 2 < 5, значит, 2/3 < 5/3.
Вопрос 3: Каково правило сравнения дробей с одинаковым числителем?
Ответ:
Если данный набор дробей имеет одинаковый числитель, то дробь, у которой знаменатель меньше, является большей дробью, а дробь, у которой знаменатель больше, является меньшей дробью.
Например, если нам нужно сравнить 4/3 и 4/9, нам просто нужно проверить их знаменатели и сравнить их. Теперь из 4/3 и 4/9 дробь с меньшим знаменателем равна 4/3. Следовательно, 4/3 является большей частью данных дробей.
Вопрос 4: Что такое эквивалентные дроби?
Ответ:
Равные дроби — это те, которые имеют разные числители и знаменатели, но имеют одинаковые значения при упрощении. Например, 3/12 и 5/20 являются эквивалентными дробями, так как обе они равны 1/4 в упрощенном виде.
Вопрос 5: Как сравнивать дроби с разными знаменателями?
Ответ:
Чтобы сравнить дроби с разными знаменателями, мы должны преобразовать их в одинаковые знаменатели, для которых мы должны найти наименьшее общее кратное (НОК) знаменателей. Поскольку знаменатели равны, мы можем легко сравнивать дроби. Например, сравним 1/4 и 2/3.
Шаг 1: Сначала обратите внимание на знаменатели данных дробей, то есть 1/4 и 2/3.
Поскольку знаменатели разные, сделайте их равными, найдя НОК 4 и 3. НОК(4,3) = 12.
Шаг 2: Теперь давайте преобразуем данную дробь так, чтобы у них были одинаковые знаменатели. Итак, умножьте первую дробь на 3/3, т. е. 1/4 × 3/3 = 4/12.
Шаг 3: Точно так же умножьте вторую дробь на 4/4, т. е. 2/3 × 4/4 = 8/12. Таким образом, первая дробь становится 4/12, а другая — 8/12.
Шаг 4: Сравните полученные новые дроби, т. е. 4/12 и 8/12. Так как знаменатели одинаковые, сравним числители. Мы можем заметить, что 4 < 8.
Шаг 5: Дробь с большим числителем является большей дробью. Итак, 8/12 > 4/12. Итак, 1/4 > 2/3.
Сравнение дробей с одинаковыми числителями? Определение, метод
Что такое числитель?
Когда числа записываются в виде дроби, их можно представить как a/b, где a — числитель, а b — знаменатель. Числитель — это часть дроби, которая находится над чертой и представляет собой количество частей от целого. С другой стороны, знаменатель — это общее количество частей.
Например: в дроби $\frac{3}{5}$ числитель равен 3.
На изображении выше количество заштрихованных частей от общего числа частей равно 5. Таким образом, числитель равен 5 и знаменатель равен 6.
Определение
Давайте посмотрим на две дроби, то есть $\frac{5}{7}$ и $\frac{5}{9}$. Мы видим, что числители одинаковы, т. е. 5. Такие числители называются , как и числители . Другими словами, когда числители двух или более дробей одинаковы, а знаменатели разные, их называют одинаковыми или подобными числителями .
Рассмотрим еще один пример:
В приведенном выше примере первая фигура разделена на 3 части и только 1 закрашена, тогда как во второй фигуре 4 равные части и только 1 закрашена. В детстве вы помните, что считали единичные дроби. Единичные дроби — это дроби, в которых дроби имеют числитель 1.
Сравнение дробей с одинаковыми или одинаковыми числителями — простая задача.
Сравним $\frac{3}{5}$ и $\frac{3}{7}$.
Из моделей видно, что $\frac{3}{5}>\frac{3}{7}$.
Чтобы сравнить две или более дроби с такими же или подобными числителями , нам достаточно сравнить их знаменатели . Меньше та дробь, у которой знаменатель больше.
Если мы сравним $\frac{9}{11}$ и $\frac{9}{17}$, то увидим, что знаменатель 17 больше знаменателя 11. Итак, $\frac{9}{11 }>\frac{9}{17}$. Упорядочивание дробей с одинаковыми числителями Поэтому, когда числа имеют значения от наименьшего к наибольшему, мы говорим, что они расположены в порядке возрастания. Упорядочить по возрастанию дроби с одинаковыми числителями довольно просто. Чем больше знаменатель, тем меньше дробь.
Например: Запишите числа в порядке возрастания: $\frac{1}{33},\frac{1}{45},\frac{1}{27},\frac{1}{19} $.
Как известно, чем больше знаменатель, тем меньше дробь.
45 > 33 > 27 > 19
$\Rightarrow\frac{1}{45}<\frac{1}{33}<\frac{1}{27}<\frac{1}{19}$
По убыванию также известно как по убыванию . Итак, когда числа имеют свои значения от наибольшего к наименьшему, мы говорим, что они расположены в порядке убывания. Порядок убывания прямо противоположен порядку возрастания. Чем меньше знаменатель, тем больше дробь.
Итак, когда числа имеют свои значения от наибольшего к наименьшему, мы говорим, что они расположены в порядке убывания. Порядок убывания прямо противоположен порядку возрастания. Чем меньше знаменатель, тем больше дробь.
Например: Запишите числа в порядке убывания: $\frac{1}{33},\frac{1}{45},\frac{1}{27},\frac{1}{19} $.
Как известно, чем больше знаменатель, тем меньше дробь.
19 < 27 < 33 < 45
$\Rightarrow\frac{1}{19}>\frac{1}{27}>\frac{1}{33}>\frac{1}{45}$
Сложение или вычитание дробей с одинаковыми или одинаковыми числителями и разными знаменателями аналогично сложению или вычитанию дробей с разными знаменателями.
Предположим, у нас есть $\frac{2}{3}$ и $\frac{2}{5}$. Чтобы их сложить, нужно сначала сделать знаменатели равными.
НОК (3, 5) = 15
$\frac{2\times5}{3\times5}=\frac{10}{15} $and$\frac{2\times3}{5\times3}= \frac{6}{15}$
$\frac{10}{15}+\frac{6}{15}=\frac{16}{15}$
Вычтем их.
$\frac{10}{15}-\frac{6}{15}=\frac{4}{15}$
Как сделать одинаковые числители?
Чтобы сделать числители двух или более дробей одинаковыми или похожими, мы можем узнать НОК числителей, а затем умножить числители на соответствующие числа. Становится легко сравнивать, есть ли одинаковые или одинаковые числители.
Например: Мы должны сравнить $\frac{3}{4}$ и $\frac{9}{11}$.
Найдя НОК, можно найти общие числители.
НОК (3, 9) = 9
$\frac{3\times3}{4\times3}=\frac{9}{12}$ и $\frac{9}{11}$
Для сравнения $\frac{9}{12}$ и $\frac{9}{11}$, нам просто нужно посмотреть на знаменатель.
Начиная с 12 > 11
$\frac{9}{12}< \frac{9}{11}\Rightarrow\frac{3}{4}<\frac{9}{11}$
Решенные примеры
Пример 1: Запишите следующие дроби в порядке убывания.
$\frac{7}{20},\frac{7}{9},\frac{7}{11},\frac{7}{19}$ и $\frac{7}{ 25}$
Решение: Чем меньше знаменатель, тем больше дробь, если дроби имеют одинаковые или одинаковые числители.
9 < 11 < 19 < 20 25
$\frac{7}{9}>\frac{7}{11}>\frac{7}{19}>\frac{7}{20}>\ frac{7}{25}$
Пример 2. Найдите дроби с одинаковыми или одинаковыми числителями из следующей группы дробей.
$\frac{3}{5},\frac{3}{10},\frac{1}{6},\frac{3}{8},\frac{3}{19},\ frac{8}{13}$
Решение:
Дроби с одинаковыми или одинаковыми числителями: $\frac{3}{5},\frac{3}{10},\frac{3} {8},\frac{3}{19}$.
Пример 3. Добавьте $\frac{1}{3}+\frac{1}{5}+\frac{1}{9}$ .
Решение: НОК(3, 5 и 9) = 45
$\frac{1\times15}{3\times15}=\frac{15}{45};\frac{1\times9}{ 5\times9}=\frac{9}{45};\frac{1\times5}{9\times5}=\frac{5}{45}$
$\frac{15}{45}+\frac{9}{45}+\frac{5}{45} = \frac{29}{45 }$
Пример 4. Запишите следующие дроби в порядке возрастания:
$\frac{135}{178},\frac{135}{199},\frac{135}{101},\frac{ 135}{119}$ и $\frac{135}{229}$
Решение: Чем больше знаменатель, тем меньше дробь, если дроби имеют одинаковые или одинаковые числители.
229 > 199 > 178 > 119 > 101
$\frac{135}{229}<\frac{135}{199}<\frac{135}{178}<\frac{135}{119}<\frac{135}{101}$
Практические задачи
$\frac{13} {35}\gt\frac{13}{34}$
$\frac{15}{17}\gt\frac{15}{13}$
$\frac{11}{34}\gt\ frac{11}{49}$
$\frac{21}{34}\lt\frac{21}{49}$
Правильный ответ: $\frac{11}{34}\gt\frac{ 11}{49}$
Чем больше знаменатель, тем меньше дробь, если дроби имеют одинаковые или одинаковые числители.
$\gt$
$\lt$
=
Ни один из этих
Правильный ответ: $\lt$
Давайте сделаем числитель таким же или подобным.
НОК(2, 4) = 4
$\frac{2\times2}{7\times2}=\frac{4}{14}$ и $\frac{4}{13}$
Так как, $14 \gt 13$
$27 \lt \frac{4}{13}$
Неправильная дробь
Эквивалентная дробь
Подобная дробь
Дробь с одинаковыми числителями
Правильный ответ: Дробь с одинаковыми числителями
LCM) = 12$\frac{1\times4}{3\times4}=\frac{4}{12};\frac{1\times3}{4\times3}=\frac{3}{12}$
$\frac{4}{12}-\frac{3}{12}=\frac{1}{12}$
НОК (5, 6) = 30
$\frac{1\times6}{5 \times6}=\frac{6}{30};\frac{1\times5}{6\times5}=\frac{5}{30}$
$\frac{6}{30}-\frac{5 }{30}=\frac{1}{30}$
$\frac{1}{12}$ и $\frac{1}{30}$ – дроби с одинаковыми или одинаковыми числителями.
Часто задаваемые вопросы
В чем разница между одинаковыми числителями и одинаковыми знаменателями?
Когда числители двух или более дробей одинаковы, а знаменатели разные, они называются такие же или одинаковые числители . Принимая во внимание, что когда знаменатели двух или более дробей одинаковы, они называются с одинаковыми или одинаковыми знаменателями .
Дроби с одинаковыми или одинаковыми числителями называются одинаковыми?
Нет, дроби с одинаковыми или одинаковыми знаменателями называются одинаковыми дробями.
Как сравнивать дроби с одинаковыми или одинаковыми числителями?
Мы должны сверить знаменатели дробей с одинаковыми или одинаковыми числителями. Чем больше знаменатель, тем меньше дробь.
Сравнение фракций: тот же метод числителя и знаменателя
Ключевые концепции
Когда две дроби имеют одинаковый знаменатель, их легко сравнивать:
Например, 4/9 меньше, чем 5/9 (поскольку 4 < 5)
4/9 равно 4-кратной доле единицы1/9
5/9 равно 5-кратной доле единицы1/9
Нарисуйте 𝟏/𝟗 полосы,
Здесь мы можем заметить, что знаменатели одинаковы в обеих дробях.
Итак, мы должны сравнить числители.
Числитель 4 меньше 5 (4 < 5)
∴4/9 меньше 5/9
Сравнение с использованием символов : 4/9 < 5/9
Пример
Что больше, 3/6 или 2/6 ?
3/6 равно 3 доле единицы 1/6
2/6 равно 2 доле единицы 1/6
Итак, 3/6 больше 2/6
Сравнение с использованием символов : 3/6 > 2/6
Пример из жизни
Пицца была разделена на три равные части (ломтика).
На схеме целое представлено дробью 3/3
Если убрать одну часть, оставшаяся часть будет равна 2/3
В этом примере оба знаменателя совпадают, поэтому мы должны сравнить числители.
Числитель 3 больше 2.
∴ 3/3 больше 2/3.
Использование 𝟏/𝟑 полосы:
Сравнение с использованием символов : 3/3> 2/3
13.4 Используйте модели для сравнения: тот же числоПосмотрите на модели
Каждый из них имеет 1 заштрихованную часть. Итак, все, что нам нужно сравнить, это размер каждой части
Какая часть пирога имеет самую большую заштрихованную часть? 1/2 Что происходит со знаменателем, когда ваши фигуры становятся меньше?
Пример
Том и Джерри испекли по пирогу. Пироги были одного размера. Том разрезал свой пирог на 8 ломтиков; Джерри разрезал его на 6 ломтиков. Каждый съел по 2 кусочка своего пирога. Кто съел больше?
Нарисовать модель. Запишите долю, которую каждый съел
Они съели одинаковое количество кусочков?
Числители одинаковые?
Мы используем дроби для сравнения размеров частей или сравнения знаменателей.
Шестые больше восьмых, поэтому
2/6 больше 2/8.
Итак, Джерри съел еще пирога.
Упражнение:
5. Что больше ¼ или 1/6? Нарисуйте полоски дробей, чтобы завершить схему и ответить на вопрос.
6. Мария и Нина заказали по маленькой пицце. Мария съела 3/8 своей пиццы. Нина съела 3/6 своей пиццы. Кто съел больше пиццы?
7. Объясните, почему 1/6 больше 1/8, но меньше 1/3?
8. Каждая из двух пицц была разрезана на шесть частей. Ашраф, Дрю и Кэти поровну разделили пиццу. Сколько шестых получил каждый друг?
9. Эрик и Фрэнк хотят поровну разделить 4/3 фута веревки. Какой длины веревки должен получить каждый друг? Объясните, как использовать рисунок для решения задачи.
10. Рональд целый день рисовал картину для своего друга. К концу дня Рональд закончил четвертую часть картины. Если он может закончить столько же картин каждый день, сколько времени потребуется Рональду, чтобы написать 2 целых картины?
Чему мы научились:
Концептуальная карта
Фракции: сравнение и сокращение дробей
Урок 2: сравнение и сокращение дробей
/en/fractions/introduction-to-fractions/05
/content/
Сравнение дробей В разделе «Введение в дроби» мы узнали, что дроби — это способ показать часть чего-то. Дроби полезны, поскольку они позволяют нам точно сказать, сколько у нас чего-то есть. Некоторые дроби больше других. Например, что больше: 6/8 пиццы или 7/8 пиццы?
Дроби полезны, поскольку они позволяют нам точно сказать, сколько у нас чего-то есть. Некоторые дроби больше других. Например, что больше: 6/8 пиццы или 7/8 пиццы?
На этом изображении мы видим, что 7/8 больше. Иллюстрация позволяет легко сравнивать эти дроби. Но как бы мы это сделали без картинок?
Щелкните слайд-шоу, чтобы узнать, как сравнивать дроби.
Как вы видели, если две или более дроби имеют одинаковый знаменатель, вы можете сравнить их, взглянув на их числители. Как вы можете видеть ниже, 3/4 больше, чем 1/4. Чем больше числитель, тем больше дробь.
Сравнение дробей с разными знаменателями
На предыдущей странице мы сравнили дроби, имеющие одинаковые нижних числа или знаменателя . Но вы знаете, что дроби могут иметь любого числа в качестве знаменателя. Что происходит, когда вам нужно сравнить дроби с разными нижними числами?
Например, какой из них больше: 2/3 или 1/5? Трудно сказать, просто глядя на них. В конце концов, 2 больше, чем 1, но знаменатели не совпадают.
В конце концов, 2 больше, чем 1, но знаменатели не совпадают.
Если вы посмотрите на картинку, то разница очевидна: 2/3 больше, чем 1/5. С иллюстрацией сравнить эти дроби было легко, но как это сделать без картинки?
Щелкните слайд-шоу, чтобы узнать, как сравнивать дроби с разными знаменателями.
Уменьшающие дроби
Какая из них больше: 4/8 или 1/2?
Если бы вы посчитали или просто посмотрели на картинку, то могли бы сказать, что равны . Другими словами, 4/8 и 1/2 означают одно и то же, хотя и пишутся по-разному.
Другими словами, 4/8 и 1/2 означают одно и то же, хотя и пишутся по-разному.
Если 4/8 означает то же самое, что и 1/2, почему бы просто не назвать его так? Половина легче сказать, чем четыре восьмых , и для большинства людей это также легче понять. В конце концов, когда вы едите с другом, вы делите счет на 9.0003 половина , а не восьмых .
Если вы запишете 4/8 как 1/2, вы на уменьшите . Когда мы уменьшаем на дробь, мы записываем это в более простой форме. Сокращенные дроби всегда равны исходной дроби.
Мы уже уменьшили 4/8 до 1/2. Если вы посмотрите на приведенные ниже примеры, то увидите, что и другие числа можно уменьшить до 1/2. Все эти дроби равны .
5/10 = 1/2
11/22 = 1/2
36/72 = 1/2
Все эти дроби также были приведены к более простой форме.
4/12 = 1/3
14/21 = 2/3
35/50 = 7/10
Щелкните слайд-шоу, чтобы узнать, как уменьшить дроби на , разделив .
Несократимые дроби
Не все дроби можно сократить. Некоторые из них уже настолько просты, насколько это возможно. Например, вы не можете уменьшить 1/2, потому что нет другого числа, кроме 1, на которое можно разделить и 1, и 2. (По этой причине нельзя уменьшить на любую дробь из числа , у которой числитель равен 1.)
Некоторые дроби с большими числами тоже нельзя уменьшить. Например, 17/36 нельзя уменьшить, потому что нет числа, на которое можно разделить и 17, и 36. Если вы не можете найти общие кратные для чисел в дроби, скорее всего, это неприводимое .
Попробуйте это!
Приведите каждую дробь к простейшей форме.
Смешанные числа и неправильные дроби
На предыдущем уроке вы узнали о смешанных числах . Смешанное число имеет как дробь , так и целое число . Например, 1 2/3. Вы бы прочитали 1 2/3 так: одна и две трети .
Например, 1 2/3. Вы бы прочитали 1 2/3 так: одна и две трети .
Другой способ записи: 5/3 или пять третей . Эти два числа выглядят по-разному, но на самом деле они одинаковы. 5/3 — это неправильная дробь . Это просто означает, что числитель на больше, чем знаменатель на .
Бывают случаи, когда вы предпочитаете использовать неправильную дробь вместо смешанного числа. Смешанное число легко превратить в неправильную дробь. Давайте узнаем, как:
г. Попробуйте это!
Попробуйте преобразовать эти смешанные числа в неправильные дроби.
Преобразование неправильных дробей в смешанные числа
Неправильные дроби полезны в математических задачах, в которых используются дроби, как вы узнаете позже. Однако их сложнее читать и понимать, чем смешанные числа . Например, гораздо легче представить себе 2 4/7, чем 18/7.
Просмотрите слайд-шоу, чтобы узнать, как преобразовать неправильную дробь в смешанное число.


 Если взять 5, она не подойдет, поскольку не выполняется неравенство 29<6*5.
Если взять 5, она не подойдет, поскольку не выполняется неравенство 29<6*5.



 Поскольку 4 < 6, можно легко сравнить соответствующие дроби, то есть 1/2 < 3/4. Следовательно, 1/2 < 3/4
Поскольку 4 < 6, можно легко сравнить соответствующие дроби, то есть 1/2 < 3/4. Следовательно, 1/2 < 3/4 НОК 6 и 9 равно 18. Итак, мы умножим 4/6 на 3/3, (4/6) × (3/3) = 12/18 и 6/9 на 2/2, (6/ 9) × (2/2) = 12/18, что преобразует их в одинаковые дроби с одинаковыми знаменателями. Новые дроби с теми же знаменателями будут 12/18 и 12/18. Следовательно, обе дроби равны: 4/6 = 6/9.. Следовательно, 4/6 = 6/9.
НОК 6 и 9 равно 18. Итак, мы умножим 4/6 на 3/3, (4/6) × (3/3) = 12/18 и 6/9 на 2/2, (6/ 9) × (2/2) = 12/18, что преобразует их в одинаковые дроби с одинаковыми знаменателями. Новые дроби с теми же знаменателями будут 12/18 и 12/18. Следовательно, обе дроби равны: 4/6 = 6/9.. Следовательно, 4/6 = 6/9.
 Здесь знаменатели одинаковы для обеих дробей.
Здесь знаменатели одинаковы для обеих дробей. е. 1/4 × 3/3 = 4/12.
е. 1/4 × 3/3 = 4/12. Здесь произведение 4 × 8 = 32, которое мы запишем возле второй дроби.
Здесь произведение 4 × 8 = 32, которое мы запишем возле второй дроби.

 Мы можем определить большую, меньшую или эквивалентную дробь, сравнив любые две дроби. В зависимости от числителя, знаменателя и вида дробей существуют разные методы и правила сравнения дробей.
Мы можем определить большую, меньшую или эквивалентную дробь, сравнив любые две дроби. В зависимости от числителя, знаменателя и вида дробей существуют разные методы и правила сравнения дробей. Например, если нам нужно сравнить 4/3 и 4/9, нам просто нужно проверить их знаменатели и сравнить их. Теперь из 4/3 и 4/9 дробь с меньшим знаменателем равна 4/3. Следовательно, 4/3 является большей частью данных дробей.
Например, если нам нужно сравнить 4/3 и 4/9, нам просто нужно проверить их знаменатели и сравнить их. Теперь из 4/3 и 4/9 дробь с меньшим знаменателем равна 4/3. Следовательно, 4/3 является большей частью данных дробей. Поскольку знаменатели разные, сделайте их равными, найдя НОК 4 и 3. НОК(4,3) = 12.
Поскольку знаменатели разные, сделайте их равными, найдя НОК 4 и 3. НОК(4,3) = 12.



 Все числа в 6-й строке можно разделить на 6 без остатка.
Все числа в 6-й строке можно разделить на 6 без остатка. ..
..
 Мы могли бы также сказать, что 6/9 равно 2/3.
Мы могли бы также сказать, что 6/9 равно 2/3.
