перевод на английский, синонимы, антонимы, примеры предложений, значение, словосочетания
Во многих из этих стран учетные ставки уже двузначные или близки к этому уровню, поэтому их регуляторы не окажутся в позиции догоняющих, как это произошло в 2013 г. | With policy rates at or close to double — digit levels in many of those economies, the authorities are not behind the curve the way they were in 2013. |
В первые три сезона он одерживал двузначные победы, а в 2010 году помог Сан-Франциско выиграть первый чемпионат с 1954 года. | He posted double — digit wins in his first three seasons, and in 2010 he helped San Francisco win their first championship since 1954. |
Каждый раз, когда она участвовала в крупных международных соревнованиях, она собирала двузначные средние баллы. | Every time she has competed in a major international event, she has compiled double — digit scoring averages. |
ДФЛ опубликовала двузначные результаты в обеих палатах законодательного собрания, избрала Эми Клобучар в Сенат США и увеличила число членов Конгресса в Палате представителей США на одного. | The DFL posted double — digit gains in both houses of the legislature, elected Amy Klobuchar to the U.S. Senate, and increased the party’s U.S. House caucus by one. |
Примечательно, что это позволило использовать двузначные годы и неоднозначные форматы YY-MM-DD и YYMMDD. | Notably, this allowed two — digit years to be used and the ambiguous formats YY — MM — DD and YYMMDD. |
Рост населения Уичито вырос на двузначные цифры, и окружающие пригороды являются одними из самых быстрорастущих городов в штате. | Wichita’s population growth has grown by double digits and the surrounding suburbs are among the fastest growing cities in the state. |
В течение последнего десятилетия цены на жилье в Пекине и Шанхае ежегодно увеличивались в среднем на двузначные цифры. | Over the last decade, residential prices increased every year on average by double digits in Beijing or Shanghai. |
Нет никакого назначения для Числа 9. Нумерологи анализируют двузначные числа от 10 до 99. | There is no assignment for the number 9. Numerologists analyze double — digit numbers from 10 to 99. |
Введение жесткой кредитно-денежной политики обеспечило к лету резкое сокращение инфляции до низкого двузначного уровня. | Tight monetary policy brought about a dramatic fall in inflation to low single — digit numbers in the summer. |
А. Азиатско-Тихоокеанский регион учится жить и обеспечивать дальнейшее процветание без двузначного роста экспорта. | A. Asia and the Pacific is learning how to live and continue to prosper without double — digit export growth. |
Возможно, скорость подъёма его экономики и не достигнет двузначного прказателя предыдущих лет, однако к 2010 году Китай вполне может начать расти быстрее, чем любая страна в Европе или целом западном полушарии. | Its pace of expansion may not reach the double — digit rates of recent years, but China in 2010 will probably grow more rapidly than any country in Europe or in the western hemisphere. |
Может иметь значение country:allowed или country:disallowed с добавлением двузначного кода страны по стандарту ISO 3166. | Can be country:allowed or country:disallowed accompanied by a two character country code as specified by the ISO 3166 standard. |
Как правило, развитие продвигается просто сумасшедшими темпами ради двузначного индекса роста доходов. | And development just basically going berserk, for a double figure growth index, basically. |
Сначала рассмотрим случай нахождения квадратного корня из числа Z, то есть квадрата двузначного числа XY, где X-десятичная цифра, а Y-единичная цифра. | First, consider the case of finding the square root of a number Z, that is the square of a two — digit number XY, where X is the tens digit and Y is the units digit. |
2] он изменил ход многих игр, например, когда он в одиночку вывел Шохоку из двузначного дефицита против Кайнана. | 2] He has changed the course of many games, such as when he single — handedly brought Shohoku back from a double — digit deficit against Kainan. |
Для начала нам понадобится помощь. Кто-нибудь может выбрать любое двузначное число? | Would somebody get us started by giving us a two — digit number please? |
Ну, число двузначное , неплохо. | Well, it’s double digits, sounds good. |
На тебя двузначное количество жалоб, а ты продолжаешь подливать масла в огонь. | You have double — digit complaints on you, and you just keep pouring gas on the fire. |
Ее дни сочтены. И число этих дней даже не двузначное . | Her days are numbered, and the number in question isn’t even in double digits. |
Потому что религиозное обучение это разница между 9 зачётными предметами и 10, а ты обещал мне двузначное число так что иди и позаботься об этом. | Because RE is the difference between ten GCSEs and nine and you promised me double figures, so just do one! |
Как и в случае любого основания в его системе, десять-это первое двузначное число в десятичной системе счисления и, следовательно, наименьшее число, где положение числа влияет на его значение. | As is the case for any base in its system, ten is the first two — digit number in decimal and thus the lowest number where the position of a numeral affects its value. |
Появление этой теории в то время, когда весь мир тревожился по поводу двузначной инфляции, обеспечило центральные банки тем самым поводом, в котором они так нуждались, чтобы приступить к непопулярным действиям. | The theory’s publication at a time of worldwide alarm about double — digit inflation offered central bankers exactly the pretext they needed for desperately unpopular actions. |
Конгрессмен, у вас стабильное количество голосов по консервативным вопросам и последние 5 выборов вы побеждали с двузначной разницей. | Congressman, you have a consistent voting record on conservative issues, and in the past five elections you’ve won your district by double digits. |
В ноябре 2013 года Lenovo сообщила, что впервые достигла двузначной доли рынка в Соединенных Штатах. | In November 2013 Lenovo reported that they had achieved double — digit market share in the United States for the first time. |
Четыре страны не могут классифицировать домохозяйства на двузначном уровне, например пары в консенсуальном союзе без проживающих с ними детей, пары в консенсуальном союзе с младшим проживающим с ними ребенком в возрасте до 25. | Four countries could not classify into the two — digit level, e.g. cohabiting couples without resident children, cohabiting couples, youngest child under 25. |
Рассмотрение этого тезиса привело Аристотеля к отказу от принципа двузначности для утверждений относительно будущего. | Considering this thesis led Aristotle to reject the principle of bivalence for assertions concerning the future. |
Сьюзен Хаак однажды заявила, что многозначная логика не требует ни промежуточных терминов между истинным и ложным, ни отказа от двузначности . | Susan Haack once claimed that a many — valued logic requires neither intermediate terms between true and false, nor a rejection of bivalence. |
А это двузначный прирост по всем направлениям. | Now that’s double — digit gains across the board. |
Мы получаем то, что ожидали, семизначный телефонный номер… и двузначный идентификатор звонившего, как здесь, 13. | We’re getting what you’d expect, seven digits of a telephone number. |
Баланс может очень быстро сместиться в пользу китайцев, если они продолжат двузначный ежегодный рост, в то время как американцы и их союзники сократят его. | The balance may shift to the advantage of the Chinese very quickly if they continue double digit yearly growth while the Americans and their allies cut back. |
Транклайн штата Мичиган-двузначный щит. | Michigan State Trunkline double — digit shield. |
Двузначный государственный маршрут щит, Южная Каролина. | Two — digit state route shield, South Carolina. |
Двузначный щит шоссе штата использует подсолнух, штат Канзас. | Two — digit state highway shield uses a sunflower, Kansas. |
Двузначный щит шоссе штата использует краеугольный камень, Пенсильвания. | Two — digit state highway shield uses a keystone, Pennsylvania. |
Я ненавижу утро вторника, с его собакой, с двузначным рейтингом. | I hate Tuesday mornings now. There’s that dog with his beautiful double digits. |
Этот козырь даст ему победу на праймериз с двузначным отрывом. | It’s an applause line, and he’s going to win his primary by double digits. |
В колледже юридических исследований число диссертаций, представленных по теме Zersetzung, было двузначным . | At the College of Legal Studies, the number of dissertations submitted on the subject of Zersetzung was in double figures. |
В колледже юридических исследований число диссертаций, представленных по теме Zersetzung, было двузначным . | The rule is a precautionary trivial burden required to avert the great probable gravity of precious life loss and momentous damage. |
Многим российским фирмам запретили брать в европейских банках кредиты в евро, из-за чего они были вынуждены обращаться к банковской системе России, где процент по кредитам выражается двузначными цифрами, либо вообще воздерживаться от заимствований. | Many domestic companies have also been banned from obtaining euro credit from European banks, forcing them to take on Russian double digit yield instead, or abstain from credit. |
В 2013 году электронная коммерция Бразилии быстро росла, а розничные продажи электронной коммерции, как ожидается, будут расти двузначными темпами в течение 2014 года. | In 2013, Brazil’s e — commerce was growing quickly with retail e — commerce sales expected to grow at a double — digit pace through 2014. |
Шокеры управляли таблицей с мужским баскетбольным турниром конференции долины Миссури 2014 года, выиграв все три игры двузначными числами. | The Shockers ran the table with the 2014 Missouri Valley Conference Men’s Basketball Tournament, winning all three games by double digits. |
Некоторые программы, столкнувшись с двузначными годами, не могли отличить 2000-й от 1900-го. | Some programs, when facing two digit years, could not distinguish between 2000 and 1900. |
Это неудивительно, если учесть, что рост ВВП Китая, хотя и значительно отстает от двузначных чисел в период расцвета, все еще остается больше 6 % в годовом исчислении. | This should not be surprising, given that Chinese GDP growth, though down significantly from its double — digit heyday, remains above 6%. |
На мой взгляд, здесь нет двузначных правил. | No rules kind of has a double — sided meaning to me. |
Она нужна для морально двузначных ситуаций, в которых требуется не только стрелять или не стрелять. | For morally ambiguous situations that involve more than shoot or don’t shoot. |
Лили предположила восемь, но я знаю, что мой мальчик добрался до двузначных чисел. | Lily guessed eight, but I know my boy got to double digits. |
Эта повышенная способность детей помнить свои ранние годы не начинает исчезать до тех пор, пока дети не достигнут двузначных цифр. | This increased ability for children to remember their early years does not start to fade until children reach double digits. |
Положительный, безналоговый перенос от Муни АРБ может доходить до двузначных цифр. | Positive, tax — free carry from muni arb can reach into the double digits. |
В некоторых провинциях есть один, а в других-несколько двузначных номеров. | Some provinces have one, other have several two digit numbers assigned. |
Математика Однозначные и двузначные числа. Сравнение двузначных чисел
Материалы к уроку
Конспект урока
2. Однозначные и двузначные числа. Сравнение двузначных чисел
Однозначные и двузначные числа. Сравнение двузначных чисел
1. Организационный этап
Долгожданный дан звонок –
Начинается урок.
Тут затеи и задачи,
Игры, шутки – всё для вас!
Пожелаю всем удачи –
За работу, в добрый час!
2. Этап подготовки учащихся к активному сознательному усвоению знаний
1. Целеполагание
Сегодня на уроке мы познакомимся с новыми математическими понятиями «однозначные и двузначные числа», будем учиться сравнивать двузначные числа.
2. Устный счёт
Задание 1
Отметьте закономерность составления ряда и продолжите его: 20, 17, 18, 15, 16. Два грибочка без чисел
Назовите числа, которые здесь вы видите числа 1-20
Назовите число, в котором 1 десяток и 3 единицы. 13
13
Назовите разность чисел 15 и 3. 12
Насколько 10 больше 7? 3
Найдите сумму чисел 11 и 6. 17
Уменьшите 19 на 3. 16
Насколько 3 меньше 12? 9
Увеличьте 6 на 8. 14
Задание 2
Подумайте, какие числа пропущены?
6 9 10 7
/\ /\ /\ /\
2 4 2 7 5 5 1 6
Задание 3
Какие из данных фигур являются ломаными? Z; W
Задание 4
Сколько прямоугольников можно насчитать в изображении окна? 5
Задание 5
Дед, баба, внучка, Жучка, кошка, мышка тянули-тянули, вытянули репку и смотрят. Сколько пар глаз смотрели на репку? Сколько всего глаз смотрело на репку?
Правильно, шесть пар. Значит 12 глаз.
Значит 12 глаз.
Задание 6
Пара лошадей пробежала 40 км. Сколько километров пробежала каждая лошадь?
Молодцы, 40 км.
3. Этап усвоения новых знаний
Ребята, посмотрите, вас приветствует Незнайка. Назовите число. 13
Запишите это число. 13
Сколько единиц в этом числе? 3 ед.
Сколько десятков в этом числе? 1 дес.
Запишите число, которое следует при счёте за числом 13. 14
Что обозначает каждая цифра в записи этого числа?
Назовите число. 30
Запишите число. 30
Назовите количество единиц в этом числе? 0
Назовите количество десятков в этом числе? 3
Как видим, в этом числе отсутствуют отдельные единицы. Но всего единиц в этом числе 20.
Разделите числа на 2 группы. 3, 6, 8, 9, 0. 12, 18, 20, 43.
3, 6, 8, 9, 0. 12, 18, 20, 43.
Числа 3, 6, 8, 9, 0 содержат только единицы и записываются одной цифрой – это однозначные числа.
Числа 12,18, 20,43 содержат единицы и десятки, записываются двумя цифрами – это двузначные. Такие числа обязательно содержат десятки, поэтому числа 01, 02 не являются двузначными.
4. Этап закрепления новых знаний
Задание 1
Прочитайте и запишите числа. Подчеркните одной чертой число единиц, двумя чертами число десятков.
Под каждым числом запишите следующее за ним при счёте.
Выпишите в одну строку однозначные числа, в другую строку двузначные числа.
Назовите количество единиц и десятков в двузначных числах.
Задание 2
Решите примеры, сверяясь со слайдом.
12 — 3 = 9 16 — 9 = 7 6 + 6 = 12 17 — 10 = 7 50 — 20 = 30
12 — 6 = 6 16 — 8 = 8 7 + 7 = 14 16 — 6 = 10 60 — 40 = 20
Задание 3
Неравенство: 70 … 17
Чтобы сравнить два двузначных числа, мы должны сначала сравнить десятки; если десятки равны, то мы смотрим на единицы. 70 – это 7 дес., а 17 – это 1 дес. и 7 ед., 7дес. больше 1дес., значит 70 > 17
70 – это 7 дес., а 17 – это 1 дес. и 7 ед., 7дес. больше 1дес., значит 70 > 17
Используя этот приём, сравните остальные числа.
15…50
1 дес. 5 ед.
34 …43
3 дес. 4 ед.
87…78
8 дес. 7 ед. > 7 дес. 8 ед.
2 дм…12 см
2 дм = 20 см
2 дес. см > 1 дес. 2 ед. см
8 дм… 80 см
8 дм = 80 см
8 дес. см = 8 дес. см
Задание 4
На карусели катается 10 мальчиков, а девочек на 6 меньше. Сколько девочек катается на карусели? Сколько всего детей катается на карусели?
Что известно в задаче?
Что спрашивается в задаче?
Как найти, сколько девочек катается на карусели?
Решение.
1) 10 — 6 = 4 (дев.)
Как найти, сколько всего детей катается на карусели?
2) 10 + 4 = 14 (д. )
)
Как записать ответ?
Ответ: 4 девочки, 14 детей
Самостоятельная работа
Задание 1
Запишите числа.
Проверьте себя.
2 дес. = 20 17 = 1 дес. 7 ед.
3 дес. 7 ед.= 37 48 = 4дес. 8 ед.
1 дес. 9 ед.= 19 60 = 6дес. 0 ед.
Задание 2
Решите примеры.
Проверьте себя.
11 — 2 = 9 12 — 3 = 9 13 — 4 = 9 14 — 5 = 9 15 — 6 = 9 16 — 7 = 9
/\ /\ /\ /\ /\ /\
1 1 2 1 3 1 4 1 5 1 6 1
Задание 3
У Кости 4 десятка марок. Он подарил 10 марок Арсению. Сколько марок осталось у Кости? Решите задачу.
Он подарил 10 марок Арсению. Сколько марок осталось у Кости? Решите задачу.
Проверьте себя.
Было — 4 дес. м.
Подарил — 10 м.
Осталось — ?
4 дес. = 40
40 — 10 = 30 (м.)
Ответ: 30 марок.
Задание 4
На столе лежит 8 красных карандашей, а зелёных карандашей на 3 больше. Сколько зелёных карандашей лежит на столе? Сколько всего карандашей находится на столе?
Решите задачу, пользуясь кратким условием.
Проверьте себя и оцените свои успехи.
Решение.
1) 8 + 3 = 11 (к.)
2) 8 + 11 = 19 (к.)
Ответ: 11 зелёных карандашей, 19 карандашей.
Логические задания
Задание 1
Пример 9.. 8 .. 3 .. 2.. 6 = 12.
Поставьте знаки таким образом, чтобы получилось верное равенство.
9 + 8 + 3 — 2 — 6 = 12
9 — 8 + 3 + 2 + 6
Задание 2
Нарисуйте такую же фигуру.
Зачеркните 2 палочки так, чтобы осталось 4 квадратика такой же формы.
5. Этап подведения итогов
Сколько десятков в числах 23, 14, 45, 12, 11?
Сколько цифр используют при записи однозначных чисел?
Cколько цифр используют при записи двузначных чисел?
На что нужно опираться при сравнении двузначных чисел?
Конечно же, на десятичный состав числа.
Рефлексия
Продолжите фразу:
сегодня я узнал
было интересно
было трудно
Спасибо за сотрудничество.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
| · = | ||||||||||||||||||||
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 | 48 | 51 | 54 | 57 | 60 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | 78 | 84 | 90 | 96 | 102 | 108 | 114 | 120 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 | 91 | 98 | 105 | 112 | 119 | 126 | 133 | 140 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 | 104 | 112 | 120 | 128 | 136 | 144 | 152 | 160 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | 117 | 126 | 135 | 144 | 153 | 162 | 171 | 180 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
| 11 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 | 143 | 154 | 165 | 176 | 187 | 198 | 209 | 220 |
| 12 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 | 156 | 168 | 180 | 192 | 204 | 216 | 228 | 240 |
| 13 | 13 | 26 | 39 | 52 | 65 | 78 | 91 | 104 | 117 | 130 | 143 | 156 | 169 | 182 | 195 | 208 | 221 | 234 | 247 | 260 |
| 14 | 14 | 28 | 42 | 56 | 70 | 84 | 98 | 112 | 126 | 140 | 154 | 168 | 182 | 196 | 210 | 224 | 238 | 252 | 266 | 280 |
| 15 | 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 | 150 | 165 | 180 | 195 | 210 | 225 | 240 | 255 | 270 | 285 | 300 |
| 16 | 16 | 32 | 48 | 64 | 80 | 96 | 112 | 128 | 144 | 160 | 176 | 192 | 208 | 224 | 240 | 256 | 272 | 288 | 304 | 320 |
| 17 | 17 | 34 | 51 | 68 | 85 | 102 | 119 | 136 | 153 | 170 | 187 | 204 | 221 | 238 | 255 | 272 | 289 | 306 | 323 | 340 |
| 18 | 18 | 36 | 54 | 72 | 90 | 108 | 126 | 144 | 162 | 180 | 198 | 216 | 234 | 252 | 270 | 288 | 306 | 324 | 342 | 360 |
| 19 | 19 | 38 | 57 | 76 | 95 | 114 | 133 | 152 | 171 | 190 | 209 | 228 | 247 | 266 | 285 | 304 | 323 | 342 | 361 | 380 |
| 20 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
Как умножать числа столбиком (видео по математике)
Чтобы потренироваться и быстро выучить, можно также попробовать умножать числа столбиком.
Те, кто в школе относился к урокам математики с пренебрежением, наверняка хотя бы несколько раз в жизни бывали в неловкой ситуации. Как посчитать, сколько оставить на чай или сумму коммунального платежа? Если знать пару простых приёмов, это займёт у вас буквально секунду. А уж во время экзамена знание правил умножения больших чисел может помочь сэкономить критически недостающее время. «Мел» совместно с Creu делится простыми секретами вычислений.
Для тех, кто готовится к главному школьному экзамену
1. Умножение на 11
Все мы знаем, что при умножении на десять к числу добавляется ноль, а знаете ли вы, что существует такой же простой способ умножения двузначного числа на 11? Вот он:
Возьмите исходное число и представьте промежуток между двумя знаками (в этом примере мы используем число 52): 5_2
Теперь сложите два числа и запишите их посередине: 5_(5+2)_2.
Таким образом, ваш ответ: 572.Если при сложении чисел в скобках получается двузначное число, просто запомните вторую цифру, а единицу прибавьте к первому числу: 9_(9+9)_9 (9+1)_8_9 10_8_9 1089. Это срабатывает всегда.
Это срабатывает всегда.
2. Быстрое возведение в квадрат
Этот приём поможет быстро возвести в квадрат двузначное число, которое заканчивается на пять. Умножьте первую цифру саму на себя +1, а в конце допишите 25. Вот и всё! 252 = (2x(2+1)) & 25
3. Умножение на пять
Большинству очень просто даётся таблица умножения на пять, но когда приходится иметь дело с большими числами, сделать это становится сложнее.
Этот приём невероятно прост. Возьмите любое число и поделите пополам. Если в результате получилось целое число, припишите ноль в конце. Если нет, не обращайте внимание на запятую и в конце добавьте пять. Это срабатывает всегда:
2682×5 = (2682 / 2) & 5 или 0
2682 / 2 = 1341 (целое число, поэтому добавьте 0)
Давайте попробуем другой пример:
2943,5 (дробное число, пропустите запятую, добавьте 5)
4. Умножение на девять
Это просто. Чтобы умножить любое число от одного до девяти на девять, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например, 9×3 — загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9×3 — это два), затем посчитайте после загнутого пальца (в нашем случае — семь). Ответ — 27.
Загните палец, который соответствует умножаемому числу (например, 9×3 — загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9×3 — это два), затем посчитайте после загнутого пальца (в нашем случае — семь). Ответ — 27.
5. Умножение на четыре
Это очень простой приём, хотя очевидный лишь для некоторых. Хитрость в том, что нужно просто умножить на два, а затем опять умножить на два: 58×4 = (58×2) + (58×2) = (116) + (116) = 232.
6. Подсчёт чаевых
Если вам нужно оставить 15% чаевых, есть простой способ сделать это. Высчитайте 10% (разделите число на десять), а потом добавьте получившееся число к его половине и получите ответ:
15% от $25 = (10% от 25) + ((10% от 25) / 2)
$2.50 + $1.25 = $3.75
7. Сложное умножение
Если вам нужно умножать большие числа, причём одно из них — чётное, вы можете просто перегруппировать их, чтобы получить ответ:
32×125 всё равно что:
16×250 всё равно что:
8×500 всё равно что:
8.
 Деление на пять
Деление на пятьНа самом деле делить большие числа на пять очень просто. Нужно просто умножить на два и перенести запятую:
1 . 195 * 2 = 390
2 . Переносим запятую: 39,0 или просто 39.
1 . 2978 * 2 = 5956
2 . 595,6
9. Вычитание из 1000
Чтобы выполнить вычитание из 1000, можете пользоваться этим простым правилом. Отнимите от девяти все цифры, кроме последней. А последнюю цифру отнимите от десяти:
1 . От 9 отнимите 6 = 3
2 . От 9 отнимите 4 = 5
3 . От 10 отнимите 8 = 2
10. Систематизированные правила умножения
Умножение на 5 : Умножьте на 10 и разделите на 2.
Умножение на 6 : Иногда проще умножить на 3, а потом на 2.
Умножение на 9 : Умножьте на 10 и отнимите исходное число.
Умножение на 12 : Умножьте на 10 и дважды прибавьте исходное число.
Умножение на 13 : Умножьте на 3 и 10 раз прибавьте исходное число.
Умножение на 14 : Умножьте на 7, а затем на 2.
Умножение на 15 : Умножьте на 10 и 5 раз прибавьте исходное число, как в предыдущем примере.
Умножение на 16 : Если хотите, 4 раза умножьте на 2. Или умножить на 8, а потом на 2.
Умножение на 17 : Умножьте на 7 и 10 раз прибавьте исходное число.
Умножение на 18 : Умножьте на 20 и дважды отнимите исходное число.
Умножение на 19 : Умножьте на 20 и отнимите исходное число.
Умножение на 24 : Умножьте на 8, а потом на 3.
Умножение на 27 : Умножьте на 30 и 3 раза отнимите исходное число.
Умножение на 45 : Умножьте на 50 и 5 раз отнимите исходное число.
Умножение на 90 : Умножьте на 9 и припишите 0.
Умножение на 98 : Умножьте на 100 и дважды отнимите исходное число.
Умножение на 99 : Умножьте на 100 и отнимите исходное число.
БОНУС: проценты
Вычислить 7% от 300.
Сперва нужно понять значение слова «процент» (percent). Первая часть слова — про (per). Per = для каждого. Вторая часть — цент (cent), это как 100. Например, столетие = 100 лет. 100 центов в одном долларе и так далее. Итак, процент = для каждой сотни.
Первая часть слова — про (per). Per = для каждого. Вторая часть — цент (cent), это как 100. Например, столетие = 100 лет. 100 центов в одном долларе и так далее. Итак, процент = для каждой сотни.
Итак, получается, что 7% от 100 будет семь. (Семь для каждой сотни, только одной сотни).
8% от 100 = 8.
35,73% от 100 = 35,73
Но как это может быть полезным? Вернёмся к задачке 7% от 300.
7% от первой сотни равно 7. 7% от второй сотни — то же 7, и 7% от третьей сотни — все те же 7. Итак, 7 + 7 + 7 = 21. Если 8% от 100 = 8, то 8% от 50 = 4 (половина от 8).
Дробите каждое число, если нужно вычислить проценты из 100, если же число меньше 100, просто перенесите запятую влево.
Примеры:
8%200 =? 8 + 8 = 16.
8%250 =? 8 + 8 + 4 = 20,
8%25 = 2,0 (Передвигаем запятую влево).
15%300 = 15+15+15 =45
15%350 = 15+15+15+7,5 = 52,5
Также полезно знать, что вы всегда можете поменять числа местами: 3% от 100 — то же самое, что 100% от 3. А 35% от 8 — то же самое, что и 8% от 35.
А 35% от 8 — то же самое, что и 8% от 35.
Ментальная арифметика для детей от 5 до 16 лет • Детский клуб «Классики»
Вы сможете решить этот пример за несколько секунд, без помощи калькулятора?
872+116-761+262-378=?
А ваш ребенок сможет.
Детский клуб «Классики» открывает новое направление – Ментальная Арифметика для детей от 5 до 16 лет.
Что такое ментальная арифметика?
- Ментальная – значит «мысленная». Ментальная арифметика – вычисления в уме, без помощи калькулятора, тетрадок и других вспомогательных средств
- Ментальная арифметика зародилась в древнем Китае, а в 21 веке приобрела фантастическую популярность. Завоевав азиатские страны, ментальная арифметика быстро развивается в Европе и Америке. Сейчас во всем мире работает более 5000 школ этого направления.
- На первом этапе ребенок учится считать при помощи абакуса. Это прибор, похожий на счёты.
- На следующем этапе дети откладывают настоящие абакусы в сторону и переходят на воображаемые.
 Теперь они только представляют этот прибор в уме и считают, мысленно передвигая косточки.
Теперь они только представляют этот прибор в уме и считают, мысленно передвигая косточки. - Как раз в этот момент начинается самая большая польза от занятий. Почему? Сейчас объясним.
Положительный эффект от занятий ментальной арифметикой
Собственно зачем ребенку уметь делать такие сложные вычисления в уме? Ведь удобные калькуляторы есть в любом смартфоне.
Быстрые вычисления в уме – это не самоцель.
Когда дети переходят к работе с «мысленными абакусами», в работу включается воображение, концентрация внимания. То есть, задействуется правое полушарие головного мозга.
В это же время синхронно работает и развивается левое полушарие, отвечающее за логику и счет.
Таким образом мышление ребенка с детства «привыкает» решать жизненные задачи двумя полушариями головного мозга одновременно: сконцентрироваться на вопросе, вообразить какую-то схему и логически решить эту задачу. Очень быстро возникает креативный и в то же время логический подход к решению вопросов.
Итак
- Ребенок учится делать сложные вычисления в уме и удивлять окружающих. Растет его самооценка и уверенность в себе
- Развивается кратковременная, долговременная и фотографическая память, концентрация внимания, как следствие – повышается успеваемость в школе
- Ребенок с детства учится решать жизненные задачи, задействуя оба полушария головного мозга сразу: сконцентрировался, вообразил схему решения, быстро нашел креативное и логически обоснованное решение вопроса.
Преимущества нашего курса
- Все ученики получают доступ к порталу с упражнениями, чтобы ребенок мог тренироваться каждый день самостоятельно по 10 минут, а родитель мог отслеживать прогресс
- Каждый урок всего курса прописан по минутам. Ученики получают рабочие тетради, в которых к каждому занятию предусмотрено определенное количество упражнений. Преподаватель отпускает ребенка когда убедится, что все они выполнены корректно и ребенок усвоил материал.

- Стоимость пропущенных занятий не пропадает: мы «перебрасываем» эти деньги на депозит, который можно впоследствии использовать для посещения занятий и мастер-классов творческих направлений.
Результаты детей 5-6 лет:
Через 4 месяца занятий: Дети умеют складывать и вычитать на абакусе двузначные числа, а в уме они считают легкие примеры с двузначными числами и одинаковыми цифрами, например 11+66-55+77 и т.д.
Через 8 месяцев занятий: Дети складывают и вычитают на абакусе двузначные числа, используя несложные формулы, а в уме они решают легкие примеры, такие как 11+66-55+77, 54+45-31-15, и т.д.
Через полтора года занятий: Дети складывают и вычитают на абакусе двузначные и трехзначные числа, переходят к расчету примеров с четырехзначными числами. В уме решают примеры с двузначными числами. Знают таблицу умножения на скорость.
Через 3 года занятий (к 8 годам): Ребенок в уме проводит вычисления с четырехзначными числами — сложение, вычитание, умножение, деление, извлечение квадратного корня и выведение процента.
Результаты детей 6-7 лет:
Через 2 месяца занятий: Дети складывают и вычитают на абакусе двузначные числа, а в уме считают легкие примеры с двузначными числами и одинаковыми цифрами, например 11+66-55+77 и т.д.
Через 4 месяца занятий: Дети складывают и вычитают на абакусе двузначные числа, используя несложные формулы, а в уме они решают легкие примеры, такие как 11+66-55+77, 54+45-31-15, и т.д.
Через 1 год занятий: Дети складывают и вычитают на абакусе двузначные и трехзначные числа, переходят к расчету примеров с четырехзначными числами. В уме решают примеры с двузначными числами. Знают таблицу умножения на скорость.
Через 2,5 года занятий: Ребенок в уме проводит вычисления с четырехзначными числами — сложение, вычитание, умножение, деление, извлечение квадратного корня и выведение процента.
Результаты детей старше 8 лет
Через 2 месяца занятий: Дети складывают и вычитают на абакусе двузначные числа, используя несложные формулы, а в уме решают легкие примеры, такие как 11+66-55+77, 54+45-31-15, и т. д.
д.
Через 9 месяцев занятий: Дети складывают и вычитают на абакусе двузначные и трехзначные числа, переходят к расчету примеров с четырехзначными числами. В уме решают примеры с двузначными числами. Знают таблицу умножения на скорость.
Через 2,5 года занятий: Ребенок в уме проводит вычисления с четырехзначными числами — сложение, вычитание, умножение, деление, извлечение квадратного корня и выведение процента.
Организационные моменты
Расписание: занятия проводятся 1 раз в неделю по 2 академических часа.
Общая продолжительность курса: 2,5-3 года.
Запишитесь на пробное занятие по телефону +7 495 724 19 04 или заполнив форму на этом сайте.
Сложение и вычитание двузначных чисел » «Просвещение»
Реклама
Скворцова Ирина Анатольевна
Учитель начальных классов
КГУ «СШ № 7 с ДМЦ»
Цели
урока: используя знания о десятичном составе чисел закрепить
навыки сложения и вычитания двузначных чисел устно и письменно.
Задачи урока:
-закрепить навыки учащихся при выполнении сложения и вычитания двузначных чисел,умение работать по алгоритму, при решение примеров и задач; научить анализировать, сравнивать и решать задачи, продолжить работу с геометрическим материалом;
— развивать логическое мышление, память, внимание, умения сравнивать, анализировать, обобщать, делать выводы, развивать коммуникативные умения, математическую речь, умение применять полученные знания на практике;
— воспитывать интерес и любовь к урокам математики; учить работать в коллективе, группах; воспитывать требовательность к себе, трудолюбие, дисциплинированность, аккуратность.
Тип урока: урок обобщения и закрепления полученных знаний
Методы: словесный, наглядный, частично-поисковый, практический.
Формы: фронтально-коллективные, самостоятельная работа, работа у доски.
Оборудование: интерактивная доска, слайды, учебник
«Математика2», карандаш, раздаточный материал, смайлики (для оценивания работы групп),
рабочие тетради.
ХОД УРОКА:
I.Организационный момент. Мотивация.
Парадные, нарядные,
Такие ненаглядные
И мальчики, и девочки
Внимательно глядят.
Вам всем учиться хочется?
Урок к нам в гости просится.
Пора его начать!
Долгожданный дан звонок
Начинается урок.
Но прежде чем начнем урок, давайте настроимся на успешную работу. Повторяем за мной: Я – молодец! Я все смогу! У меня все получится!
-Сделайте глубокий вдох, затем выдохните с силой. Повторите упражнение еще раз.
1.Сообщение темы и цели урока.
2.Карта оценки учащихся (подробное объяснение ученикам работы с картой).
3.Оформление тетрадей под диктовку с доски.(слайд№ )
4. Минутка каллиграфии «Пиши правильно!»
69 96 69 96 69 96 69 96
II. Актуализация:
Актуализация:
1. Назови геометрические фигуры (домик)
2. Построй мостик (прибавляя по 5 ед.) Какая закономерность наблюдается?
3. На слайде цифры вразброс от 10 до 20
4. Состав двузначного числа: что такое двузначное число? Это такое число, которое состоит из десятков и единиц.
5.– Чем отличается однозначное число от двузначного? (Для записи однозначного числа требуется один знак (цифра), для двузначного – два)
6.– Как называется цифра , стоящая справа у двузначного? (единица)
7.– Как называется цифра, стоящая слева у двузначного числа? ( десятки)
8._Как можно прочитать эти числа , разбив их на десятки и единицы? (2дес.2 ед. и т.д.)
3. Разложи число на составляющие его десятки и единицы.(Устно все по очереди) После проверки ОЦЕНКА
4. Заполни «пустые» окошки. (письменно, самостоятельно, взаимопроверка)
ОЦЕНКА
48 = 40 + …
70 + 3 = …
21 = 1 + …
96 = … + 6
5 + 80 = …
39 = … + …
5. Сравни выражения
(разноуровневое задание) 3 ученика у доски ОЦЕНКА
Сравни выражения
(разноуровневое задание) 3 ученика у доски ОЦЕНКА
III.Работа по теме урока:
– Посмотрим, как графически записан пример ( на сложение).
– Что обозначают треугольники?… (Десятки)
– Что обозначают точки?… (Единицы)
– Прочитаем пример.
Чтение с места: Двадцать четыре плюс тринадцать равно тридцать семь.
– Запишем его с помощью цифр: 24 + 13 = 37. (записывает 1 ученик на доске цифровое выражение)
– Как сложить двузначные числа?
(Дети высказывают своё мнение)
– Чтобы сложить…
ПРАВИЛО-ВЫВОД Чтобы сложить двузначные числа—единицы складываю с единицами, десятки складываю с десятками. ОЦЕНКА
– На доске графически записан следующий пример (на вычитание).
– Прочитаем его.
…Сорок пять минус четырнадцать равно
тридцать один.
– Запишем его с помощью цифр 45 –14 = 31
– Сделаем вывод: чтобы вычесть двузначные числа, нужно из единиц вычесть единицы, а из десятков – десятки. ОЦЕНКА
АЛГОРИТМ сложения и вычитания двузначных чисел (чтение правила хором)
Физкультминутка
Мы дружно потрудились
Немного устали
Быстро все сразу
За партами встали.
Руки поднимем, потом разведём.
В ладоши похлопаем, потом их встряхнём.
Направо посмотрим, налево посмотрим
И очень глубоко всей грудью вздохнём!
(Можно повторить)
Закрепление
– За время нашего отдыха к нам прибежали за помощью герои сказки «Гуси-лебеди». Это Аленушка и её братец Иванушка. Сестрица с братцем добежали до молочной реки. Видят: летят гуси-лебеди. Попросили у речки:
– Речка, матушка, спрячь нас!
Речка: Если справитесь с моим заданием, то я вас укрою.
– Ребята, поможем Аленушке с братцем,
быстро выполним задание. (решение самостоятельно в тетради, взаимопроверка)
ОЦЕНКА
(решение самостоятельно в тетради, взаимопроверка)
ОЦЕНКА
44 – 13
69 – 21
52 + 15
76 — 24
Речка укрыла их кисельным бережком. Гуси-лебеди не увидали, пролетели мимо. Девочка с братцем дальше побежала, но вот воротились гуси-лебеди. Что делать, кого просить о помощи…
… Видят яблоню…
Яблоня: Решите мою задачу, тогда спрячу! На моих ветках поспели яблоки. Вы, дети, съешьте 8 яблок, а лесные зверята съедят 14 яблок. Сколько яблок поспело на моих ветках? (на доске и в тетради записать только решение) 8 + 14 = 22 яблока ОЦЕНКА
– Ребята проверим, правильно ли мы выполнили задание, выручили детей.
Яблоня заслонила ветвями, прикрыла листами…
Пролетели гуси мимо, а девочка с братцем дальше побежали. Добежали до печки. Видят, опять гуси-лебеди летят…
Печь. Печка дала самые трудные задания. Не обойтись Аленушке с братом без нашей помощи.
1. Решить графический пример. Ответ записать
в тетрадь в виде числового выражения.ОЦЕНКА
Ответ записать
в тетрадь в виде числового выражения.ОЦЕНКА
1.Задание по учебнику с.167 №6 реши уравнения (коллективное решение под диктовку) ОЦЕНИВАНИЕ
– Мы помогли героям сказки. Печь спрятала детей. Гуси-лебеди полетали-полетали, покричали-покричали и ни с чем улетели к Бабе Яге. А нам осталось совсем немного –сгруппировать фигуры по признакам.Сестрица с братцем счастливые побегут домой, где их ждут отец с матерью и подарки.
IV.Рефлексия
– С какими числами мы работали на уроке?(С двузначными)
– Как сложить двузначные числа?
– Как вычесть двузначные числа?
V.Оценивание работы каждого ученика, подсчитывание смайликов, комментирование оценок учителем.
VI. Домашнее задание: с 166 № 3 (1,2 столбик), повторить алгоритмы
VII.Выводы: я научился….
Я смогу, если …
Теперь я умею…..
Я буду стараться, чтобы…..
VIII. Подведение итогов урока.
Подведение итогов урока.
Очень жаль, что путь недолог,
Попрощаться нам пора,
Но на следующем уроке
Вновь продолжиться игра!
– Всем спасибо! Урок окончен.
Скачать презентацию: Prezentaciya-k-uroku.zip [1.74 Mb] (cкачиваний: 83)
Урок «Деление двузначного числа». 3-й класс
Основные цели:
- Сформировать способность письменному делению двузначного числа на однозначное.
- Повторить приемы деления суммы на число.
Мыслительные операции, необходимые на этапе проектирования: анализ, сравнение, обобщение, аналогия.
Демонстрационный материал:
- графические модели
- алгоритм деления суммы на число:
- опорные схемы.
- презентация к уроку
- геометрические фигуры на магнитах: треугольники и кружки.
Раздаточный материал:
- счетный геометрический материал : треугольники и кружки;
- образцы для самопроверки примеров, задач.

Оборудование: учебник для 3 класса начальной школы (второе полугодие) (авторы М.И. Моро и др.), компьютер, мультимедийный проектор.
Ход урока
Актуализация знаний и фиксация затруднений в индивидуальной деятельности.
Цели:
- повторить таблицу умножения и деления. Однозначных чисел
- способы деления суммы на число.
- тренировать мыслительные операции: анализ, сравнение, аналогию.
- организовать выполнение учащимися самостоятельной работы №1 и самопроверку работы по готовому образцу с фиксацией учащимися своих результатов (без исправления ошибок)
Организация учебного процесса
Найди закономерность, продолжи ряд . (слайд1)
12, 20, 28, :, :, :, : .
65, 55, 45, :, :, : .
— Расскажите, как вы нашли числа. (Смотрю на
первое и второе число, думаю, как из первого
получили второе, проверяю на 3 числе. )
)
— Расскажите о числах первого ряда.
(двузначные, четные. делятся на однозначные числа 2 и 4, каждое следующее число больше первого на 8, и меньше на 8, численный ряд увеличивается. Наименьшее число 12, наибольшее число 60.
(двузначные, нечетные. делятся на однозначное число 5, каждое следующее число больше первого на 10, и меньше на 10, численный ряд уменьшается. Наименьшее число 15, наибольшее число 65. )
— Разделите первый ряд чисел на число 4.
(коллективно) (слайд 2)
12 : 4 =
20 : 4 =
36 : 4 =
44 : 4 =
52 : 4 =
60 : 4 =
— как справились с примерами?
— какие примеры вызвали затруднения?
— Какова тема нашего урока.? (деление двузначного числа на однозначное)
Построение проекта выхода из затруднений
Цели:
- организовать построения детьми нового способа
деления двузначного числа на однозначное число.

- зафиксировать в речи новый способ деления.
— что вы умеете делить? (числа из таблицы умножения, сумму чисел)
— вспомните алгоритм деления суммы на однозначное число (слайд 3)
1. Сложу сумму слагаемых и разделю.
или
1. Разделю каждое слагаемое.
2. Сложу результаты
— чтобы разделить 44 что нужно сделать, чтобы разделить 44 (представить в виде суммы слагаемых)
Воспользуемся графической моделью. (слайд 4)
-Выведение алгоритма.
-Как разделить двузначное число на однозначное?
Алгоритм деления двузначного числа
1. Представлю в виде суммы разрядных
или
суммы удобных слагаемых
2. Разделю слагаемые
3. Сложу результаты. (слайд8)
Помните , что одно из слагаемых это число из таблицы умножения.
Физкультминутка:
| Открывай скорее книжку, | (развести в стороны руки) |
В книжке мошка, мышка, Мишка. |
(переваливаться, руки в бок) |
| В книжке мячик круглый бок: | (круговые движения руками) |
| Прыг-скок! Прыг-скок! | (прыжки на месте) |
| В книжке зонт открой и пой, | |
| Лупит дождь, а ты сухой. | (постукивать пальчиками по тыльной стороне другой ладони) |
| В книжке киска близко-близко, | (погладить воображаемые усики на щеках) |
| На цветной картинке киску | |
| Долго глажу я рукой | (гладить одной рукой другую) |
| Ведь у киски мех такой теплый. | (прочесывают пальцами волосы на голове и обнимают себя) |
Первичное закрепление во внешней речи.
Цель:
- Создать условия для фиксации изученного способа деления во внешней речи.
(Устно)
Работа по учебнику 1 строка, 1 пример.(с.15)
№ 1.(устно) (слайд 9)
№2 Решение 1,2 столбики с устным объяснением.
Самостоятельная работа с самопроверкой по эталону.
Цель:
- Организовать самопроверку умения проверять изученные деления двузначного числа на однозначное.
Форма работы индивидуальная.
Решают 3,4 столбики по вариантам, проверяют самостоятельно по образцу.
-какие трудности возникли?
-у кого все получилось, поставьте себе «+» в оценочных листах.
Включение в систему знаний и повторение.
(слайд 10)
Цель:
- организовать повторение решения задач деления суммы на число.
— Задание: Решение задач № по вариантам. (Работают по памятке)
(Работают по памятке)
1 вариант. С одной грядки сняли 18 кг моркови, а с другой 54 кг. Всю морковь разложили в корзины по 8 кг в каждую. Сколько потребовалось корзин?
2 вариант. Дети собрали для питомника 25 кг каштанов и 29 кг желудей. Всё это они упаковали в пакеты, по 9 кг в каждый. Сколько потребовалось пакетов?
-Выполняем.
— Проверяем по схемам (слайд 11)
1 вариант
18 кг и 54 кг. ? — ? корз.
по 8 кг. — 1 корз.
2 вариант (слайд 12)
25 кг и 29 кг. ? — ? пак.
по 9 кг.- 1 пак.
-Обобщение:
-Какого вида была задача? (деление суммы на число)
Решение задачи № 3 (слайд 13)
Театр-3 зд. на ? зд. >
Библиотеки-? зд. в 6 раз >
Рефлексия деятельности.
Цели:
- зафиксировать в речи новый способ деления двузначных чисел.
- зафиксировать затруднения , которые остались и способы их преодоления
- оценить собственную деятельность на уроке.

-Оцените свою работу в оценочных листах.
Домашнее задание. № 4, 5 стр.15, лабиринт.
Литература:
Н.М. Куракина «Сценарии открытых уроков» УМЦ «Школа 2000-2005»
Приложение.
Числа до 2 цифр — определение, разрядное значение
В двузначных числах есть только два разряда — разряд единиц и разряд десятков. Каждое число, состоящее более чем из 1 цифры, имеет разные цифры, описываемые их разрядными значениями. Двузначные числа начинаются с 10 и заканчиваются на 99. Другими словами, наименьшее двузначное число — 10, а наибольшее двузначное число — 99.
| 1. | Что такое двузначные числа? |
| 2. | Как записывать числа до 2 цифр? |
| 3. | Общие ошибки чисел до 2 цифр |
| 4. | Часто задаваемые вопросы о номерах до 2 цифр |
Что такое двузначные числа?
Двузначные числа — это числа, состоящие из двух цифр, которые начинаются с цифры 10 и заканчиваются цифрой 99. Они не могут начинаться с нуля, потому что в этом случае это будет считаться однозначной цифрой. Цифра в разряде десятков может быть любым числом от 1 до 9. Например, 45, 78, 12 — двузначные числа.
Они не могут начинаться с нуля, потому что в этом случае это будет считаться однозначной цифрой. Цифра в разряде десятков может быть любым числом от 1 до 9. Например, 45, 78, 12 — двузначные числа.
Разрядное значение в двузначных числах
Разрядное значение — это положение каждой цифры в числе. Когда мы говорим об однозначных числах, есть только одно разрядное значение, которое является разрядом единиц. Когда мы подходим к двузначным числам, есть два разряда — единицы и десятки. Обратите внимание на следующий рисунок, на котором показано двузначное число 23, написанное вместе с его разрядными значениями. Цифра 2 стоит на месте десятков и означает 20, а цифра 3 стоит на месте единиц и означает 3.
Присвоение разрядных значений
Мы знаем, что разрядное значение числа говорит о позиции цифры. В двузначных числах единственными разрядами являются десятки и единицы.
Давайте посмотрим на следующий набор чисел, чтобы понять комбинацию единиц и десятков:
а. ) 33 ⇒ 3 десятка + 3 единицы = (3 × 10) + (3 × 1) = 30 + 3 = 33
) 33 ⇒ 3 десятка + 3 единицы = (3 × 10) + (3 × 1) = 30 + 3 = 33
б.) 18 ⇒ 1 десяток + 8 единиц = (1 × 10) + (8 × 1) = 10 + 8 = 18
в.) 27 ⇒ 2 десятка + 7 единиц = (2 × 10) + ( 7 × 1) = 20 + 7 = 27
Как записывать числа до 2 цифр?
Двузначные числа можно записывать в виде цифр, прописью и в расширенной форме. Например, 45 — это двузначное число. Давайте посмотрим, как это можно записать тремя способами.
- В цифровой форме: 45
- Прописью: сорок пять
- В развернутом виде: 40+5
Двузначные числа в словах
Когда числа записываются словами с помощью разрядных значений, это помогает нам писать их по буквам. Самое маленькое двузначное число — 10, которое записывается как десять. После этого числа от 11 до 20 записываются как 11 – одиннадцать, 12 – двенадцать, 13 – тринадцать, 14 – четырнадцать, 15 – пятнадцать, 16 – шестнадцать, 17 – семнадцать, 18 – восемнадцать, 19.- девятнадцать, а 20 — двадцать. После этого они записываются как 21 — двадцать один, 22 — двадцать два, 23 — двадцать три и так далее, пока не дойдет до 30 — тридцать, и тот же образец следует после тридцати, сорока и так далее.
После этого они записываются как 21 — двадцать один, 22 — двадцать два, 23 — двадцать три и так далее, пока не дойдет до 30 — тридцать, и тот же образец следует после тридцати, сорока и так далее.
Двузначные числа в расширенной форме
Расширенная форма числа помогает узнать о его составляющих. Развернутую форму двузначного числа можно показать по-разному. Рассмотрим двузначное число 57.
- Число 57 можно записать в одной форме как 57 = (5 × десятков) + (7 × единиц)
- По-другому это можно записать как 57 = (5 × 10) + (7 × 1)
- Третий способ записать 57 в расширенной форме: 57 = 50 + 7.
Общие ошибки чисел до 2 цифр
- Дети часто могут назвать все числа до 99 (или 100), но могут ошибаться, когда их просят найти большее число между двумя числами. Они повторяют числа от 1 до 100 так, как будто выучили буквы алфавита. Если это произойдет, то найти большее число между 14 и 15 так же сложно, как найти большую букву между С и D.
 Дети должны понимать, что, в отличие от букв, числа связаны друг с другом. 15 ровно на единицу больше, чем 14. Для этого можно использовать числовые линии и цветные счетчики, чтобы связать звук с количеством.
Дети должны понимать, что, в отличие от букв, числа связаны друг с другом. 15 ровно на единицу больше, чем 14. Для этого можно использовать числовые линии и цветные счетчики, чтобы связать звук с количеством. - Дети склонны ошибаться при работе с числами при изменении разряда десятков. Например, при переходе от 19 к 20, от 29 к 30, от 39 к 40 и т. д. Часто двузначные числа вводятся без привязки к разрядным значениям. Хотя это облегчает запоминание чисел, это может быть не лучшей стратегией, поскольку дети не видят числа, составленные из общего набора цифр от 0 до 9. В этом случае можно использовать счеты для моделирования чисел и основания. -10 блоков могут быть использованы, чтобы помочь им визуализировать числа.
- Дети делают ошибки при написании или чтении чисел словами, особенно от одиннадцати до девятнадцати. Нет никакой замены практике. Дети должны практиковаться в написании названий чисел. Как правило, при небольшой преднамеренной и целенаправленной практике эту ошибку можно легко исправить.

Советы по числам до 2 цифр
Ниже приведены некоторые советы и рекомендации по числам до 2 цифр.
- При умножении любого однозначного числа (от 1 до 9) на 10 получается двузначное число. Например, 4 × 10 = 40
- Наименьшее двузначное число, состоящее только из одной цифры, равно 11.
- Наименьшее двузначное число, состоящее из двух разных цифр, равно 10. (10 также является наименьшим двузначным числом)
- Наибольшее двузначное число, использующее только одну цифру, равно 99. (99 также является наибольшим двузначным числом).
- Наибольшее двузначное число, использующее все разные цифры, равно 98.
- В двузначных числах есть только два разряда: десятки и единицы.
- Есть девяносто «двухзначных чисел», начиная с 10-99.
Вот список всех чисел до 2 цифр от 10 до 99.
Наименьшее двузначное число
Наименьшее двузначное число — 10, поскольку предыдущее число — 9, которое является однозначным числом.
Наибольшее двузначное число
Наибольшее двузначное число — 99, поскольку следующее число — 100, которое является трехзначным числом.
Важные примечания
Ниже приведены некоторые важные примечания, связанные с числами до 2 цифр, которые мы изучали в этой статье.
- Наименьшее двузначное число — 10, а наибольшее двузначное число — 99.
- Всего девяносто двузначных чисел.
- Двузначное число не может начинаться с 0, так как в этом случае оно будет считаться однозначным.
☛ Статьи по теме
- Номера до 3 цифр
- Номера до 4 цифр
- Номера до 5 цифр
- Номера до 6 цифр
- Номера до 7 цифр
- Номера до 8 цифр
- Номера до 9 цифр
- Номера до 10 цифр
Примеры двузначных чисел
Пример 1: В чем разница между самым большим двузначным числом и числом 20?
Решение: Наибольшее двузначное число = 99
.
Разница между 99 и 20 составляет 99 — 20 = 79
Пример 2: Создайте двузначное число, в котором 7 — это разряд десятков, а 5 — разряд единиц. Запишите номер в развернутой форме и напишите его номерное название.
Решение: Если 7 в разряде десятков и 5 в разряде единиц, число равно 75.
Расширенная форма 75 = 70 + 5. Это также можно записать как (7 десятков) + (5 единиц) или (7 × 10) + (5 × 1) 9.0185 Имя числа 75 — это семьдесят пять.Пример 3: Запишите первые четыре «двузначных числа» и последние четыре «двузначных числа».
Решение: Первые четыре двузначных числа: 10, 11, 12, 13.
Последние четыре двузначных числа: 96, 97, 98, 99.
перейти к слайдуперейти к слайдуперейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Записаться на бесплатный пробный урок
Практические вопросы по числам до 2 цифр
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о номерах до 2 цифр
Что такое двузначные числа в математике?
Число называется двузначным, если оно состоит из двух цифр, в которых разряд десятков должен стоять от 1 до 9, оно не может начинаться с нуля, потому что в этом случае оно станет однозначным числом. Например, 35, 45, 60, 11 и так далее — двузначные числа.
Сколько существует двузначных чисел?
Всего существует девяносто двузначных чисел, начиная с 10 и заканчивая 99. Это означает, что наименьшее двузначное число равно 10, а самое большое двузначное число равно 99.
Какое самое большое 2- Цифровой номер?
Самое большое двузначное число — 99, а следующее число — 100, которое является трехзначным числом.
Какое самое маленькое двузначное число?
Наименьшее двузначное число — 10, поскольку предыдущее число — 9, то есть однозначное число.
Какое наибольшее двузначное число делится на 10?
Самое большое двузначное число, которое делится на 10, — это 90. Хотя самое большое двузначное число — 99, оно не делится на 10.
Какое наибольшее двузначное число можно составить из 8 и 6?
Наибольшее двузначное число, которое можно составить из 8 и 6, равно 86. Поскольку 8 больше 6, поэтому мы оставляем 8 на разряде десятков и 6 на разряде единиц. Следовательно, 86 — это самое большое двузначное число, состоящее из цифр 8 и 6.
Напишите расширенную форму данного двузначного числа 65.
Расширенную форму числа 65 можно представить как 60 + 5. Это также можно записать как 6 десятков + 5 единиц или (6 × 10) + (5 × 1).
Сколько десятков в двузначном числе 20?
В данном числе 20 цифра 2 стоит на месте десятков. Следовательно, в числе 20 2 десятка. Это можно записать как 20 = 2 десятка + 0 единиц.
Могут ли двузначные числа начинаться с 0?
Нет, двузначные числа не могут начинаться с 0. Разряд десятков в двузначном числе не может быть нулем, это может быть любое число от 1 до 9, в противном случае оно будет считаться однозначным числом. Например, 05, 06, 07 — все однозначные числа, а 56, 78, 79 — двузначные числа.
Разряд десятков в двузначном числе не может быть нулем, это может быть любое число от 1 до 9, в противном случае оно будет считаться однозначным числом. Например, 05, 06, 07 — все однозначные числа, а 56, 78, 79 — двузначные числа.
Каковы разрядные значения в числах до 2 цифр?
Значение разряда помогает определить положение цифр. В двузначных числах всего два разряда — десятки и единицы. Например, в числе 98 9 стоит на месте десятков, а 8 — на месте единиц.
Какое самое большое двузначное простое число?
Самое большое двузначное простое число — 97, потому что 97 имеет только 2 делителя, 1 и 97.
Загрузить БЕСПЛАТНЫЕ учебные материалы
Загрузить бесплатные рабочие листы KG
Рабочий лист чисел
Умножение двузначных чисел | Как умножать, методы, примеры
Введение Умножение — это одна из четырех основных математических операций, а остальные три — это сложение, вычитание и деление. Прежде чем мы перейдем к изучению того, как умножать двузначные числа, давайте вспомним, что мы подразумеваем под умножением.
Умножение определяется как процесс нахождения произведения двух или более чисел. Полученный таким образом результат называется продуктом . Предположим, вы купили 6 ручек в один день и 6 ручек на следующий день. Всего ручек, которые вы купили, теперь 2 умножить на 6 или 6 + 6 = 12.
Это также можно записать как 2 x 6 = 12
Не тот символ, который используется для умножения. Символ (x) обычно используется для обозначения умножения. Другими распространенными символами, которые используются для умножения, являются звездочка (*) и точка (.)
Символ умноженияОбратите внимание на символ, используемый в приведенном выше примере для умножения. Символ (x) обычно используется для обозначения умножения. Другими распространенными символами, которые используются для умножения, являются звездочка (*) и точка (.)
Теперь давайте рассмотрим некоторые важные термины, которые используются при умножении двух чисел.
Некоторые важные термины, используемые при умножении –
Множимое . Число, которое нужно умножить, называется множимым.
Множитель — Число, на которое мы умножаем, называется множителем.
Произведение – Результат, полученный после умножения множителя на множимое, называется произведением.
Связь между множителем, множимым и произведением может быть выражена как –
Множитель × Множитель = Произведение
Давайте разберемся с этим на примере.
Предположим, у нас есть два числа 9 и 5. Мы хотим умножить 9 на 5.
Итак, мы выражаем это как 9 x 5, что дает нам 45.
Следовательно, 9 x 5 = 45
Здесь 9 равно множимое, 5 — множитель, 45 — произведение.
Теперь, когда мы поняли, что мы подразумеваем под умножением и терминами, связанными с ним, давайте перейдем к изучению умножения однозначных чисел.
Теперь давайте разберемся, как выполнять умножение, когда у нас есть многозначные числа.
Как умножать двузначные числа?Прежде чем мы приступим к пониманию умножения двузначных чисел, важно вспомнить, что подразумевается под двузначными числами?
Напомним, что каждая цифра числа имеет разрядное значение. Например, число 5 — это однозначное число, где 5 стоит на месте единицы. Точно так же в числе 27 цифра 2 стоит на месте десятков, а цифра 7 — на месте единиц. Итак, как мы определяем двузначные числа? Двузначные числа — это числа, состоящие из 2 цифр, т. е. числа, состоящие из цифр только на разрядах единиц и десятков. Например, числа 55 и 67 двузначные.
Теперь давайте перейдем к изучению умножения двузначных чисел. Когда дело доходит до умножения двузначных чисел, есть два метода умножения чисел. Этими методами являются метод расширенной записи и метод столбца. Давайте разберемся в обоих методах.
Метод расширенной записи В методе расширенной записи мы расширяем множимое по разрядным значениям, а затем умножаем каждое число на множитель. Затем мы суммируем все полученные результаты, чтобы получить окончательный ответ. Давайте разберемся на примере.
Затем мы суммируем все полученные результаты, чтобы получить окончательный ответ. Давайте разберемся на примере.
Например, умножить 35 на 40
Решение
Мы решим это шаг за шагом.
Шаг 1 – Запишите число (множимое) в развернутом виде. Получаем,
35 = 30 + 5
Шаг 2 – Умножаем каждое число на заданное число (множитель) по одному. Получаем,
30 х 40 + 5 х 40 = 1200 + 200
Шаг 3 — Складываем полученные результаты. Получаем,
1200 + 200 = 1400
Отсюда 35 х 40 = 1400
Хотя этот метод и прост, он может не подходить для больших чисел. Но он используется для понимания основных понятий умножения.
Метод столбцаВ этом методе мы разбиваем числа на столбцы и умножаем числа на множимое одно за другим. Есть два сценария использования этого метода.
Давайте разберемся с ними один за другим
Умножение без перегруппировки Этот метод вступает в силу, когда у нас есть меньшие числа, которые не требуют переноса каких-либо чисел на разряд следующего разряда. Давайте разберемся на примере.
Давайте разберемся на примере.
Например, умножьте 21 на 32
Решение
Чтобы получить результат, выполните следующие действия.
Шаг 1. Сначала мы записываем множимое и множитель в столбцах. Здесь у нас есть 21 как множимое и 32 как множитель.
Шаг 2. Теперь умножаем число, стоящее на месте множимого, т. е. 1, на число, стоящее на месте множителя, которое в данном случае равно 2. Получаем
. Шаг 3. Теперь умножаем число в десятом месте множимого на 2. Получаем
Шаг 4. Теперь нам нужно поставить 0 на место единиц в следующей строке в качестве заполнителя. Мы получим
Шаг 5. Поскольку мы завершили умножение множимого на первую цифру множителя, мы выполняем те же действия, что и выше для умножения множимого на следующее число множителя, а затем пишем результатом будет строка напротив 0, которую мы поместили в качестве заполнителя на предыдущем шаге. Получим –
Шаг 6 Теперь, когда мы перемножили все цифры множителя с множимым, сложим полученные цифры по вертикали. мы получим
мы получим
Полученный таким образом результат является нашим ответом. Следовательно, 21 x 32 = 672
Умножение с перегруппировкойВ приведенном выше случае у нас есть небольшие умножения, которые не требуют двузначных результатов ни на одном шаге. Но в случае больших чисел потребуется перенести число на число со следующим значением разряда. Это называется умножением с перегруппировкой. Давайте разберемся на примере.
Например, умножить 25 на 34
Решение
Мы будем использовать следующие шаги, чтобы получить наш результат.
Шаг 1. Сначала мы записываем множимое и множитель в столбцах.
Шаг 2. Умножьте цифру единицы множимого на 4. У нас есть 4 x 5 = 20. Запишите 0 в столбце единиц и перенесите 2 в столбец десятков.
Шаг 3 – Умножаем десятый разряд множимого на 4. Получаем 2 x 4 = 8. Прибавляем к нему 2, которые были перенесены, чтобы получить 8 + 2 = 10. Теперь запишем 0 в столбце десятков и перенесем 1 в сто столбик.
Теперь запишем 0 в столбце десятков и перенесем 1 в сто столбик.
Шаг 4 Теперь нам нужно поставить 0 на место единиц в следующей строке в качестве заполнителя. Мы получим
Шаг 5. Поскольку мы завершили умножение множимого на первую цифру множителя, мы выполняем те же действия, что и выше для умножения множимого на следующее число множителя, а затем пишем результатом будет строка напротив 0, которую мы поместили в качестве заполнителя на предыдущем шаге. Получим –
Шаг 6 Теперь, когда мы перемножили все цифры множителя с множимым, сложим полученные цифры по вертикали. мы получим
Полученный таким образом результат является нашим ответом. Следовательно, 25 x 34 = 850
Вышеуказанные шаги могут быть обобщены для определения умножения, которое обычно известно как длинное умножение. Определим эти шаги.
Длинное умножение Длинное умножение похоже на метод столбца, за исключением того факта, что здесь мы умножаем большие числа. Этот метод используется, когда множимое больше 9, т. е. множимое больше однозначного числа. Этот метод включает в себя следующие этапы –
Этот метод используется, когда множимое больше 9, т. е. множимое больше однозначного числа. Этот метод включает в себя следующие этапы –
- Сначала запишем множимое и множитель столбцами.
- Сначала умножьте число, стоящее на месте единицы множителя, на все числа множимого и запишите их горизонтально.
- Убедитесь, что вы записываете числа справа налево и каждое число находится под соответствующим разрядом множимого.
- Теперь перейдите к следующей строке.
- Поставьте 0 на месте единицы в этой строке.
- Теперь найдите цифру в разряде десятков множителя. Умножьте число, стоящее в десятом разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили 0,9.0070
- Снова перейти на следующую строку.
- Поставьте 0 на месте единиц и десятков в этой строке.
- Теперь найдите цифру в разряде сотен множителя. Умножьте число, стоящее в сотенном разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили два нуля.

- Продолжайте в том же духе, добавляя дополнительный ноль в каждой строке, пока не дойдете до конца множителя
- Сложите числа по вертикали в соответствии с их разрядностью.
- Полученное таким образом число и есть ваш результат.
Давайте разберем это на примере
Например, Умножьте 32 на 13
Решение
- Сначала мы запишем множимое и множитель в столбцах.
- Затем умножьте число, стоящее на месте множителя, на все числа множимого и запишите их горизонтально.
- Поместите 0 на место единиц следующей строки
- Теперь найдите цифру в разряде десятков множителя. Умножьте число, стоящее в десятом разряде множителя, на все числа множимого и запишите их горизонтально в строке, где вы отметили 0.
- В множимом больше нет числа. Теперь сложите числа по вертикали в соответствии с их разрядностью.
Окончательный ответ: 416. Следовательно, 32 x 13 = 416
Следовательно, 32 x 13 = 416
Давайте посмотрим на другой пример, где мы 3 цифры в множимом.
Например, Умножить 53 на 25
Решение
1. Сначала запишем множимое и множитель в столбцы
- Затем умножим число, стоящее на месте единицы, на все числа множителя множимое и запишем их горизонтально.
- Поставьте 0 на месте единицы следующей строки
- Теперь найдите цифру в разряде десятков множителя. Умножьте десятичное число множителя на все числа множимого и запишите их горизонтально в строке, где вы отметили 0.
- Теперь, когда мы умножили все цифры множителя на множимое, мы добавит полученные цифры по вертикали. Получим
Отсюда 53 х 25 = 1325
Решенные примеры Пример 1 В кинозале 58 рядов, в каждом ряду 25 мест. Сколько человек может разместиться в зале?
Сколько человек может разместиться в зале?
Решение Нам дано, что в кинозале 58 рядов и в каждом ряду 25 мест. Нам нужно найти количество человек, которое может разместиться в зале. Подытожим предоставленную нам информацию.
Количество рядов в кинозале = 58
Количество мест в каждом ряду = 25
Количество человек, которые могут разместиться в зале = ?
Количество человек, которые могут разместиться в зале, можно найти, умножив количество рядов на количество мест в каждом ряду. Это означает, что –
Количество человек, которые могут разместиться в зале = (Количество рядов в кинозале) x (Количество мест в каждом ряду) ……………………… ( 1 )
Подставляя данное значения в приведенном выше уравнении, мы будем иметь,
Количество человек, которые могут быть размещены в зале = 58 x 25
Теперь
Отсюда количество человек, которое может разместиться в зале = 1450
Пример 2 Ресторан приобрел 81 коробку пакетов с кетчупом. В каждой коробке было 49 пакетов кетчупа. Сколько всего пакетов с кетчупом купил ресторан?
В каждой коробке было 49 пакетов кетчупа. Сколько всего пакетов с кетчупом купил ресторан?
Решение Нам сообщили, что ресторан приобрел 81 коробку пакетов с кетчупом. В каждой коробке было 49 пакетов кетчупа. Нам нужно узнать, сколько всего пакетов кетчупа купил ресторан. Подытожим предоставленную нам информацию.
Количество коробок кетчупа, купленных рестораном = 81
Количество пачек кетчупа в каждой коробке = 49
Общее количество пачек кетчупа, купленных рестораном = ?
Чтобы найти значение количества упаковок кетчупа, купленных рестораном, нам нужно будет умножить количество упаковок кетчупа, купленных рестораном, на количество упаковок кетчупа в каждой коробке. Это означает, что
Общее количество упаковок кетчупа, купленных рестораном = (Количество упаковок кетчупа, купленных рестораном) x (Количество упаковок кетчупа в каждой коробке) ……………………………. ( 1 )
Подставив данные значения в приведенное выше уравнение, мы получим,
Общее количество пакетов кетчупа, купленных рестораном = 81 x 49
Теперь,
Следовательно, общее количество пакетов кетчупа, купленных рестораном ресторан = 3969.
Пример 3 Уильям купил 60 упаковок бумажных салфеток. В каждой упаковке было 56 салфеток. Сколько салфеток купил Уильям?
Решение Нам сообщили, что Уильям купил 60 упаковок бумажных салфеток. В каждой упаковке было 56 салфеток. Нам нужно найти количество салфеток, купленных Уильямом. Подытожим предоставленную нам информацию.
Количество упаковок бумажных салфеток, купленных Уильямом = 60
Количество салфеток в каждой упаковке = 56
Общее количество салфеток, купленных Уильямом = ?
Чтобы найти общее количество салфеток, купленных Вильямом, нам нужно будет умножить количество упаковок бумажных салфеток, купленных Вильямом, на количество салфеток в каждой упаковке. Это означает, что
Общее количество салфеток, купленных Вильямом = (Количество упаковок бумажных салфеток, купленных Вильямом) x (Количество салфеток в каждой упаковке) ………. ( 1 )
Подставив данные значения в приведенное выше уравнение, мы получим,
Общее количество тканей, купленных Уильямом = 60 x 56
Теперь,
Следовательно, общее количество тканей, купленных Уильямом = 3360
Основные факты и резюме- Умножение определяется как процесс нахождения произведения двух или более чисел.

- Число, которое нужно умножить, называется множимым.
- Число, на которое мы умножаем, называется множителем.
- Результат, полученный после умножения множителя на множимое, называется произведением.
- Двузначные числа — это числа, состоящие из двух цифр, одной цифры на месте десятков и одной цифры на месте единиц.
- В методе расширенной записи мы расширяем множимое по разрядным значениям, а затем умножаем каждое число на множитель. Затем мы суммируем все полученные результаты, чтобы получить окончательный ответ.
- В методе столбца мы разбиваем числа на столбцы и умножаем числа на множимое одно за другим.
Умножение двузначных чисел (Тематика путешествий и туров) Рабочие листы
Вычитание двузначных чисел (Тематика больниц) Рабочие листы
Свойства умножения (Тема недвижимости) Рабочие листы
Просмотреть все рабочие листы Мы тратим 90 много времени, исследуя и собирая информацию на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Рабочие листы для сложения двух цифр | Что такое?, Примеры и резюме
Рабочие листы /Математика /Сложение /Таблицы сложения двух цифр
Премиум
Не готовы приобрести подписку? Нажмите, чтобы загрузить бесплатную пробную версию Загрузить образец
Содержание
После того, как мы научимся складывать однозначные числа, следующим шагом будет научиться складывать двузначные числа . Дополнение используется в быту много раз в день. Всякий раз, когда мы считаем деньги или что-то еще, мы используем сложение. Мы можем добавить столько чисел, сколько захотим.
Дополнительную информацию о сложении двух цифр см. в файле фактов ниже или, в качестве альтернативы, вы можете загрузить наш 28-страничный пакет рабочих листов на сложение двух цифр для использования в классе или дома. Этот рабочий лист разбит на начальный, средний и продвинутый, что означает, что вы можете выбрать уровень сложности для своего ученика.
Этот рабочий лист разбит на начальный, средний и продвинутый, что означает, что вы можете выбрать уровень сложности для своего ученика.
Ключевые факты и информация
Резюме:
- Сложение чисел означает нахождение общего значения или суммы этих чисел вместе взятых.
Пример: 2 + 1 = 3 - Сложение двузначных чисел: 21+ 31 = 52
- Когда мы добавляем ноль к числу, число остается неизменным.
Пример: 20 + 0 = 20 - Сложение — одна из самых основных операций, которая поможет нам понять все остальные операции.
Что такое сложение?
- После развития чувства числа дети знакомятся со сложением. Сложение — одна из четырех основных операций, которым обучают в математике.
- Четыре основных действия: сложение, вычитание, умножение и деление. Сложение двух чисел дает их общее значение.
- Это означает, что путем сложения двух чисел мы находим их сумму. Дополнение используется в быту много раз в день.

- Всякий раз, когда мы считаем деньги или что-то еще, мы используем сложение. Мы можем добавить столько чисел, сколько захотим.
- Дополнение имеет специальный символ «+».
- Вот примеры простого сложения одной цифры:
1 + 4 = 5
7 + 2 = 9
5 + 3 = 8
6 + 0 = 6
0 + 3 = 3
Сложение двух цифр
- Сложение отдельных цифр очень просто и похоже на счет.
- Как только мы научимся складывать однозначные числа, следующим шагом будет научиться складывать двузначные числа.
- Нам просто нужно выполнить простую процедуру.
- У нас может быть два случая. Добавление либо создаст перенос, либо не создаст перенос.
- Сначала мы объясним сценарий, в котором нет переноса. Это относительно проще и похоже на сложение одной цифры.
Case I (No carry)
- Suppose we add the following two numbers:
24 + 34
- We start by arranging these two numbers vertically as shown below:
24
34
- Мы делаем это так, чтобы единицы и десятки в обоих числах совпадали.

- В нашем примере для числа 24 4 стоит на месте единиц, а 2 — на десятках. Точно так же для 34 4 на месте единиц и 3 на десятках.
- Расположив числа по вертикали, мы получим единицы над единицами и десятки над десятками.
- После упорядочивания мы рисуем линию под этими числами и ставим знак сложения слева, как показано на рисунке:
- Далее мы начинаем складывать числа. Мы начинаем справа и добавляем два числа в одном месте.
4 + 4 = 8
- Ответ пишем под чертой на одном месте.
- Затем мы добавляем два числа в разряде десятков.
2 + 3 = 5
- Мы записываем ответ под линией на Tens Place, как показано ниже:
SO, 24 + 34 = 58
Case II (с переносом)
= 58.
- Предположим, мы хотим сложить следующие числа:
47 + 35
- Мы снова расположим их вертикально, как в предыдущем примере:
- Начнем со сложения цифр на единицу.

7 + 5 = 12
- Сложив, мы получаем двузначное число 12.
- В этом двузначном числе 2 стоят на разряде единиц и 1 — на разряде десятков.
- Мы пишем 2 под чертой на месте единиц и используем 1 как перенос и помещаем его поверх 4, как показано ниже:
- Теперь мы добавляем две цифры на разряде десятков вместе с цифрой переноса.
4 + 3 + 1 = 8
- Ответ пишем на десятках под чертой.
Итак, 47 + 35 = 82
Важность сложения
- Сложение помогает развивать умственные способности и чувство числа у детей.
- Он используется в повседневной жизни, потому что мы ежедневно складываем числа, предметы, деньги и т. д.
- Он служит основой для изучения новых концепций.
Пример:
- Добавьте следующие цифры:
14 + 22
- Мы сначала добавляем обе цифры в одном месте:
4 + 2 = 6
- Затем мы добавим цифровые цифры в Tens Place: 795 9007 9007 9007 9007
- .
 Затем мы добавим Digits At Tens Place: 795 9007 29007
Затем мы добавим Digits At Tens Place: 795 9007 29007 - . + 2 = 3
SO, 14 + 22 = 36
Пример:
- Добавить следующие цифры:
34 + 19
- Мы добавим Два Дикопа.
4 + 9 = 13
- Мы пишем 3 на месте единиц под синей линией и используем 1 как цифру переноса.
- Теперь складываем две цифры и перенос в разряде десятков:
3 + 1 + 1 = 5
- Пишем 5 в разряде десятков под синей линией.
Итак, 34 + 19 = 53
Пример:
- Предположим, что Ник купил 10 розовых и 16 фиолетовых шариков на день рождения Сары. Сколько всего воздушных шаров он купил?
Розовые воздушные шары = 10
Фиолетовые воздушные шары = 16
Тотальные воздушные шары = розовые воздушные шары + фиолетовые шарики
Всего воздушных шаров = 10 +9000 2 5 .
- Добавляя цифры в десять мест.0004
Это фантастический набор, который включает в себя все, что вам нужно знать о сложении двух цифр на 28 подробных страницах. Это готовых к использованию рабочих листов для сложения двух цифр, которые идеально подходят для обучения студентов сложению двух цифр. Как только мы научимся складывать однозначные числа, следующим шагом будет научиться складывать двузначные числа. Дополнение используется в быту много раз в день. Всякий раз, когда мы считаем деньги или что-то еще, мы используем сложение. Мы можем добавить столько чисел, сколько захотим.
Полный список включенных рабочих листов
- Рабочий лист 1 (начинающий)
- Рабочий лист 2 (начинающий)
- Рабочий лист 3 (начинающий)
- Рабочий лист 4 (начинающий
- . )
- Рабочий лист 7 (средний)
- Рабочий лист 8 (средний)
- Рабочий лист 9 (дополнительный)
- Рабочий лист 10 (дополнительный)
- Рабочий лист 11 (дополнительный)
- Рабочий лист 12 (Дополнительно)
Ссылка/цитирование этой страницы
Если вы ссылаетесь на какой-либо контент на этой странице на своем собственном веб-сайте, используйте приведенный ниже код, чтобы указать эту страницу как первоисточник.

Рабочие листы для сложения двух цифр: https://kidskonnect.com – KidsKonnect, 6 марта 2019 г.
Ссылка появится в виде рабочих листов для сложения двух цифр: https://kidskonnect.com — KidsKonnect, 6 марта 2019 г.
Используйте с любой учебной программой
Эти рабочие листы были специально разработаны для использования с любой международной учебной программой. Вы можете использовать эти рабочие листы как есть или отредактировать их с помощью Google Slides, чтобы сделать их более конкретными для ваших собственных уровней способностей учащихся и стандартов учебной программы.
Умножение на двузначные числа — подход к ментальной математике
Уловки в ментальной арифметике, чтобы стать человеком-калькулятором
Техника умножения на двузначные числа, описанная в этом разделе, вдохновлена ведической математикой.
 Этот трюк поможет вам умножить любое двузначное число в уме. Это обобщенный подход, вы можете получить решение еще до того, как узнаете его. То есть, применяя метод умножения на двузначное число, описанный в этом посте, вы можете вычислить результат слева направо.
Этот трюк поможет вам умножить любое двузначное число в уме. Это обобщенный подход, вы можете получить решение еще до того, как узнаете его. То есть, применяя метод умножения на двузначное число, описанный в этом посте, вы можете вычислить результат слева направо.Эта техника отличается от того, чему мы научились в детстве. В этом вам нужно умножать двузначное число справа налево, что включает в себя запоминание или запись переноса. Это значительные накладные расходы в подходе к ментальной математике. Умножение на 2-значное число с использованием подхода слева направо, вы можете вычислить произведение в уме, не беспокоясь о переносе.
К концу этого поста вы научитесь следующим трюкам
- Умножение 2 цифр на 1 цифру
- Умножение 2 цифр на 2 цифры
В следующем уроке по умножению трех цифр мы расширили прием умножения двух цифр из этого урока и использовали его для умножения 3 цифр на 2 цифры.
Умножение двузначных чисел — Видео
Подход к умножению трехзначных чисел объясняется в видеороликах ниже с помощью двух примеров.
 В первом примере основное внимание уделяется умножению двузначных чисел без переноса, а во втором — с переносом.
В первом примере основное внимание уделяется умножению двузначных чисел без переноса, а во втором — с переносом.Пример 1
Пример 2
Умножение на 2 цифровых числа — подход
as объяснены в видео умножать двузначные числа. Этот метод помогает нам легко умножать двузначные числа в уме.
 Мы рассмотрим этот трюк с умножением, разделив подход к умножению на двузначные числа на следующие разделы:
Мы рассмотрим этот трюк с умножением, разделив подход к умножению на двузначные числа на следующие разделы:- Как умножать два двузначных числа
- Как умножать двузначные числа на однозначные числа
Умножение двухзначных чисел на двузначные
Давайте изучим подход слева направо к умножению двузначного числа. Обратите внимание, что описанный здесь метод двузначного умножения также может быть рассчитан справа налево. Но мы рекомендуем делать это слева направо, так как идея изучения этих трюков состоит в том, чтобы помочь улучшить наши навыки счета в уме. Прежде всего, умственный расчет — это расчет слева направо.
Итак, ниже приведен метод умножения двух цифр, объясненный с помощью двух примеров. Подход, показанный в этих примерах, можно использовать для умножения любого двузначного числа.
Пример 1: Умножение 21 и 32
- Чтобы выполнить умножение на 2 цифры, разделим решение на 3 части. Количество частей здесь получается как 2x$n$-1, где $n$ представляет значение в n-разрядном умножении.
 В случае двузначного умножения n равно 2. Следовательно,
В случае двузначного умножения n равно 2. Следовательно,
21
x 32
————————
? | ? | ?- Самая левая часть получается путем умножения крайних левых цифр 2 из 21 и 3 из 32 => 2×3 = 6
21
x 32
————————
6 | ? | ?- Средняя часть получается путем перекрестного умножения первых двух цифр 2 и 2 и 1 и 3 с последующим сложением соответствующих произведений => 2×2 + 1×3 = 7
21
x 32
—— ——————
6 | 7 | ?- Правая часть получается путем умножения самых правых цифр в обоих числах => 1×2 = 2
21
x 32
————————
6 | 7 | 2- Таким образом, результат умножения двузначных чисел 21 и 32 равен 672.
Пример 2: Произведение 76 и 53 53, предварительно разделив раствор на три части.
- Левая часть получается путем умножения цифр десятков 7 в 76 и 5 в 53=>7×5=35
- Средняя часть получается путем перекрестного умножения 7 и 3, 6 и 5 и сложения соответствующих значений => 7×3+6×5=21+30=51
- Правая часть получается путем умножения самых правых цифр в обоих числах => 6×3 = 18
- Итак, мы вычислили результат умножения двузначных чисел 76 и 53 без использования калькулятора.
0 + 6 = 6
76
x 53
————————
? | ? | ?
76
x 53
————————
35 | ? | ?
76
x 53
——— —————
35 | 51 | ?
Примечание: За исключением левой части, все остальные части должны содержать только одну цифру, лишняя цифра, если таковая имеется, будет перенесена влево. Следовательно, избыток 1 из 51 будет перенесен в левую часть. Таким образом:
Следовательно, избыток 1 из 51 будет перенесен в левую часть. Таким образом:
76
x 53
————————
35 | 51 | ?
=> 40 | 1 | ?
76
x 53
————————
40 | 1 | 18
=> 40 | 2 | 8
Как умножать двузначные числа на однозначные числа
Теперь давайте изучим подход слева направо к умножению двузначного числа на однозначное число.
Если AB представляет собой двузначное число, которое нужно умножить на однозначное число, скажем, C. Затем подход слева направо к двузначному умножению на однозначное выполняется путем умножения A на C, а затем B на C.
A B
x C
————
=====>
Во время этого процесса умножения, если произведение B и C дает более 1 цифры, лишняя цифра будет перенесена влево.
Пример: Произведение 46 и 7
В 46 x 7 сначала умножьте крайнюю левую цифру 4 в 46 на 7 => 4×7 = 28
4 6
x 7
————–
28 | ?
Теперь умножьте цифру единиц 6 на 7: 6×7 = 42, а затем перенесите лишние 4 влево. Таким образом, 28 становится 32. Следовательно, мы имеем 46 x 7 = 322
4 6
x 7
————–
28 | 42
=> 32 | 2
Проверьте свое понимание
двузначное в предложении | Примеры предложений из Кембриджского словаря
Эти примеры взяты из корпусов и источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Кембриджского словаря, издательства Кембриджского университета или его лицензиаров.
Ранние оценки заявляли двойных — цифр показателей смертности; некоторые историки утверждают, что это было от 8 до 10 процентов.
Из Кембриджского корпуса английского языка
Возможно, большинство из нас может умножить два двойных — цифр чисел, но большинству будет трудно умножить два четырехзначных числа.
Из архива
Hansard
Пример из архива Hansard. Содержит парламентскую информацию под лицензией Open Parliament License v3.0
.Что еще хуже, в свете огромной нехватки финансирования, не существует ли опасность еще одного года двойной — цифра повышение муниципального налога?
Из архива
Hansard
Пример из архива Hansard. Содержит парламентскую информацию под лицензией Open Parliament License v3.0
.Советы должны устанавливать свои налоги, но нет абсолютно никаких причин для двойных — цифр повышения налогов в этом году.
С
Архив Hansard
Пример из архива Hansard. Содержит парламентскую информацию под лицензией Open Parliament License v3.0
Содержит парламентскую информацию под лицензией Open Parliament License v3.0
Сегодня это крупнейшая отрасль в мире, и она по-прежнему растет со скоростью двойных — цифр .
Из архива
Hansard
Пример из архива Hansard. Содержит парламентскую информацию под лицензией Open Parliament License v3.0
Они были предоставлены взаймы для стран, многие из которых имели темпы роста двойных — цифр .
Из архива
Hansard
Пример из архива Hansard. Содержит парламентскую информацию под лицензией Open Parliament License v3.0
. Первое — несправедливая оговорка «только вверх» — пережиток, давно пора отменить со дней двойной — цифра инфляция.
Из архива
Hansard
Пример из архива Hansard. Содержит парламентскую информацию под лицензией Open Parliament License v3.0
.Это относится к 11-му году группы двойных — цифр роста.
Из архива
Hansard
Пример из архива Hansard. Содержит парламентскую информацию под лицензией Open Parliament License v3.0
У нас была двойная — цифра инфляция в жилье в течение некоторого времени, и похоже, что она будет продолжаться.
От Europarl Parallel Corpus — английский
Существует полная занятость, рост реальной заработной платы, двухлетний двойной — цифра рост и мобильная рабочая сила.
С
Архив Hansard
Пример из архива Hansard. Содержит парламентскую информацию под лицензией Open Parliament License v3.0
.Мы не хотим возвращаться к временам, когда сбережения уничтожались каждые несколько лет взрывами двойных — цифр инфляции.
Из архива
Hansard
Пример из архива Hansard. Содержит парламентскую информацию под лицензией Open Parliament License v3.0
Менее затратным способом достижения аналогичного результата было бы разрешить только предварительно запрограммированный одиночный или двойной — короткий набор номера во время движения автомобиля.
Из архива
Hansard
Пример из архива Hansard. Содержит парламентскую информацию под лицензией Open Parliament License v3.0
Содержит парламентскую информацию под лицензией Open Parliament License v3.0
В прошлом году было зарегистрировано двойных — цифр роста.
Из архива
Hansard
Пример из архива Hansard. Содержит парламентскую информацию под лицензией Open Parliament License v3.0
.Годовой двойной — цифровой Рост был нормой в 80-х и 90-х годах, со значительным расширением производственных мощностей, крупных приобретений и предприятий в новых секторах рынка.
From
Wikipedia
Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.
В этот период также была двойная — цифра инфляция, пик которой составил более 20%.
From
Wikipedia
Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.
В 2007 году компания добилась 35% роста выручки, шестой год подряд компания достигла двойных — цифр роста выручки.
From
Wikipedia
Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.
Этот сектор вырос на двойных — цифр номеров за последние три года.
From
Wikipedia
Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.
У него также было четыре игры, в которых он показал двойных — цифр отборов мяча.
From
Wikipedia
Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.
У него было 30 двойных — цифр результативных попыток.
From
Wikipedia
Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.
В то время как услуги и промышленность выросли на двойных — цифр цифр, темпы роста сельского хозяйства снизились с 4,8% до 2%.
От
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Она также была у власти, когда безработица в приграничном городе начала значительно падать после двойных — цифр безработных.
From
Wikipedia
Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.
Например, плата за обучение увеличилась на двойных — цифр за каждый из последних четырех лет.
From
Wikipedia
Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.
Дабл-дабл — это сумма двойных — цифр в «двух из пяти» категорий в игре.
From
Wikipedia
Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.
Почти четверть этих школ сообщила об улучшении математики, выражающемся двузначным числом, и почти в 20 процентах школ наблюдалось двойное — цифровое улучшение чтения.
From
Wikipedia
Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.
Они не смогли улучшиться, опустившись до 610, их единственная двойная — цифра проигрышный сезон между 1964 и 1992 годами.
From
Wikipedia
Этот пример взят из Википедии и может быть повторно использован под лицензией CC BY-SA.
Эти примеры взяты из корпусов и из источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Кембриджского словаря, издательства Кембриджского университета или его лицензиаров.
Рабочие листы для сложения двух цифр
Наши рабочие листы для сложения двухзначных цифр, которые можно распечатать, содержат 2-значные и 1-значные числа, упражнения на сложение с 2-значными числами, сложение со словами или без них, сложение с перегруппировкой (переносом) или без перегруппировки, пропущенные цифры , и добавление 3, 4 и 5 слагаемых. Он также содержит 2-значные инновационные рабочие листы для сложения, основанные на десятичных блоках, балансировочных весах, сложении дартс, пирамиде сложения и соответствующих шариках для мороженого. Эти тщательно разработанные рабочие листы в формате PDF подходят для практики в 1-м и 2-м классах. Начните работать с нашими бесплатными рабочими листами!
Он также содержит 2-значные инновационные рабочие листы для сложения, основанные на десятичных блоках, балансировочных весах, сложении дартс, пирамиде сложения и соответствующих шариках для мороженого. Эти тщательно разработанные рабочие листы в формате PDF подходят для практики в 1-м и 2-м классах. Начните работать с нашими бесплатными рабочими листами!
Сумма до 20
В этих листах для 1 класса добавьте двузначные и однозначные числа, сумма которых не превышает 20.
Стандарт:
Лист 1 | Лист 2 | Лист 3 |
С задачами Word:
Лист 1 | Лист 2 | Лист 3 |
2-значный плюс однозначный
Добавьте двузначный плюс однозначный номер, расположенные по вертикали. Эти рабочие листы для сложения двузначных чисел для 2-го класса, которые можно распечатать, помогут вам развить навыки перегруппировки и отсутствия перегруппировки сложения.
Нет перегруппировки:
Лист 1 | Лист 2 | Лист 3 | Лист 4 | Лист 5
Нет перегруппировки с задачами Word:
Лист 1 | Лист 2 | Лист 3 | Лист 4 | Лист 5
Перегруппировка:
Лист 1 | Лист 2 | Лист 3 | Лист 4 | Лист 5
Перегруппировка с задачами Word:
Лист 1 | Лист 2 | Лист 3 | Лист 4 | Лист 5
Сложение двузначных чисел со словесными задачами
В каждом рабочем листе для 1-го и 2-го класса есть 12 стандартных двузначных чисел и две словесные задачи.
Нет перегруппировки:
Лист 1 | Лист 2 | Лист 3 | Лист 4 | Лист 5
Перегруппировка:
Лист 1 | Лист 2 | Лист 3 | Лист 4 | Лист 5
Упражнения на добавление двухзначных столбцов: без перегруппировки
В этом разделе содержатся упражнения на добавление столбцов без дополнений по перегруппировке.
15 на странице:
Лист 1 | Лист 2 | Лист 3 |
25 на странице:
Лист 1 | Лист 2 | Лист 3 |
50 на странице:
Лист 1 | Лист 2 | Лист 3 |
75 на странице:
Лист 1 | Лист 2 | Лист 3 |
100 на странице:
Лист 1 | Лист 2 | Лист 3 |
Двухзначное сложение в столбце Тренировка: перегруппировка
Найдите сумму двухзначных слагаемых. Требуется перегруппировка (перенос). У вас есть дополнительные упражнения на выбор от 15 до 100 на страницу.
15 на странице:
Лист 1 | Лист 2 | Лист 3 |
25 на странице:
Лист 1 | Лист 2 | Лист 3 |
50 на странице:
Лист 1 | Лист 2 | Лист 3 |
75 на странице:
Лист 1 | Лист 2 | Лист 3 |
100 на странице:
Лист 1 | Лист 2 | Лист 3 |
Горизонтальное двухзначное сложение: без перегруппировки
Улучшите свои математические навыки, решая эти задачи на горизонтальное сложение.
15 на странице:
Лист 1 | Лист 2 | Лист 3 |
25 на странице:
Лист 1 | Лист 2 | Лист 3 |
50 на странице:
Лист 1 | Лист 2 | Лист 3 |
75 на странице:
Лист 1 | Лист 2 | Лист 3 |
100 на странице:
Лист 1 | Лист 2 | Лист 3 |
Горизонтальное двухзначное сложение. Упражнения на сложение: перегруппировка
Двузначное сложение. Упражнения в этом разделе содержат рабочие листы сложения по перегруппировке с дополнениями, расположенными вдоль строки.
15 на странице:
Лист 1 | Лист 2 | Лист 3 |
25 на странице:
Лист 1 | Лист 2 | Лист 3 |
50 на странице:
Лист 1 | Лист 2 | Лист 3 |
75 на странице:
Лист 1 | Лист 2 | Лист 3 |
100 на странице:
Лист 1 | Лист 2 | Лист 3 |
Сложение с основанием десяти блоков
Подсчитайте длинные (десятки) и единицы (единицы). Запишите числа, представленные блоками с основанием десять. Сложите их, чтобы найти сумму.
Запишите числа, представленные блоками с основанием десять. Сложите их, чтобы найти сумму.
Лист 1 | Лист 2 | Лист 3
Балансировочные весы
Впишите пропущенные числа, уравновешивающие весы. Средний уровень имеет два пункта на каждой стороне балансировочной шкалы.
Easy:
Лист 1 | Лист 2 | Лист 3 |
Умеренный:
Лист 1 | Лист 2 | Лист 3 |
Пропущенные цифры
Найдите недостающую цифру, которая составляет сумму. В каждой задаче на легком уровне не хватает только одной цифры, а на среднем уровне — двух цифр.
Easy:
Лист 1 | Лист 2 | Лист 3 |
Умеренный:
Лист 1 | Лист 2 | Лист 3 |
Пирамида сложения
Сложите соседние числа, чтобы построить пирамиду. Рабочий пример показан на каждом листе.
Лист 1 | Лист 2 | Лист 3
Сопоставьте числа: Мороженое Тема
В каждой задаче у вас есть пара рожков мороженого с 4 шариками на каждом рожке.



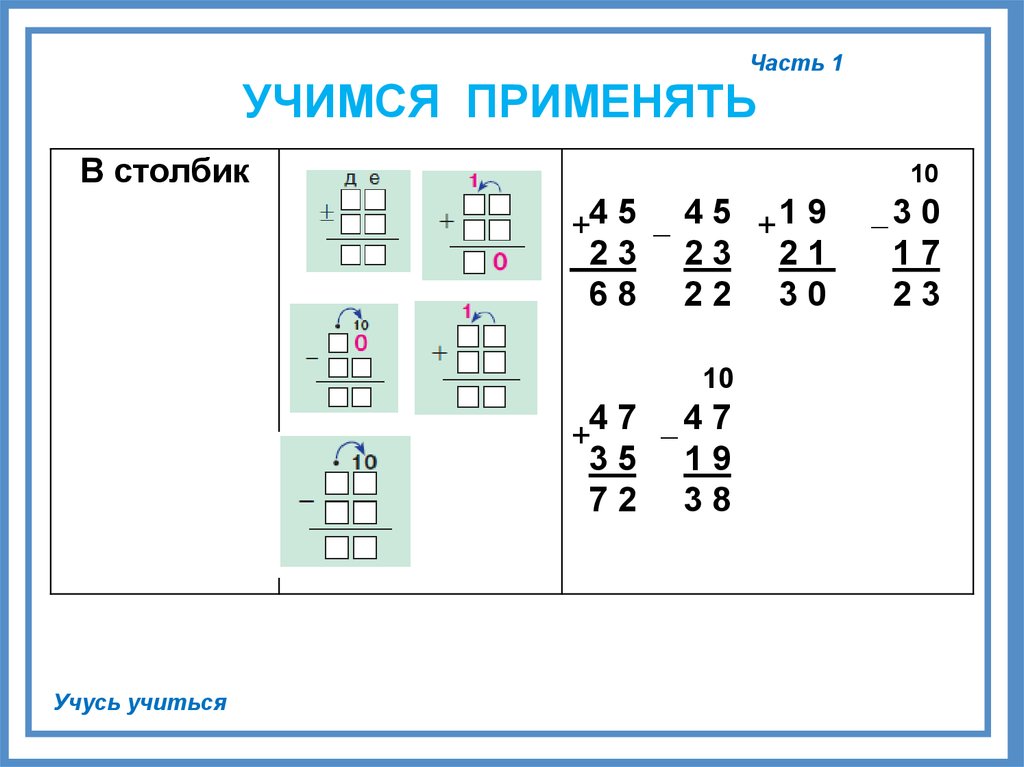


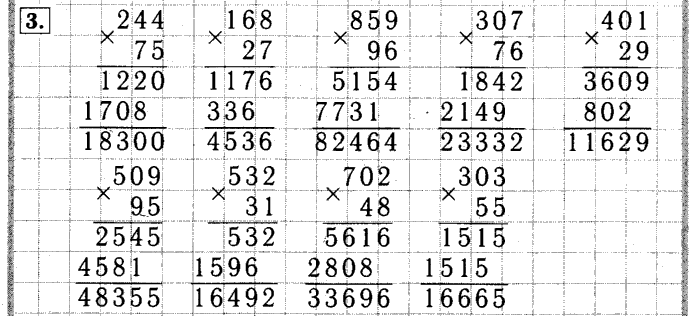 .. and a two — digit add — on to identify the caller, like here, 13.
.. and a two — digit add — on to identify the caller, like here, 13.


 Умножение
Умножение Потом складываются 2 произведения единиц на десятки. Затем прибавляется произведение единиц. Схематично это можно описать так:
Потом складываются 2 произведения единиц на десятки. Затем прибавляется произведение единиц. Схематично это можно описать так: Подгонять пример удобно, когда вам нужно быстро найти примерный или точный ответ. Желание подгонять примеры под определенные математические закономерности часто воспитывается на математических кафедрах в университетах или в школах в классах с математическим уклоном. Людей учат находить простые и удобные алгоритмы решения различных задач. Вот некоторые примеры подгонки:
Подгонять пример удобно, когда вам нужно быстро найти примерный или точный ответ. Желание подгонять примеры под определенные математические закономерности часто воспитывается на математических кафедрах в университетах или в школах в классах с математическим уклоном. Людей учат находить простые и удобные алгоритмы решения различных задач. Вот некоторые примеры подгонки:



 Ведь можно не тратить время и посчитать все в уме гораздо быстрее, а заодно размять мозги и произвести впечатление на окружающих (противоположного пола).
Ведь можно не тратить время и посчитать все в уме гораздо быстрее, а заодно размять мозги и произвести впечатление на окружающих (противоположного пола). До самой смерти большую часть вычислений Гаусс производил в уме.
До самой смерти большую часть вычислений Гаусс производил в уме.

 Получившееся в итоге трехзначное число — результат умножения исходного числа на 11 .
Получившееся в итоге трехзначное число — результат умножения исходного числа на 11 . По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно – ведь есть таблица умножения, которую вы знаете на зубок.
По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно – ведь есть таблица умножения, которую вы знаете на зубок.
 Согласно таблице умножения, нам подходят результаты 4 и 9 . Логично предположить, что результатом деления может быть либо число 74 , либо 79 . Проверяем:
Согласно таблице умножения, нам подходят результаты 4 и 9 . Логично предположить, что результатом деления может быть либо число 74 , либо 79 . Проверяем: А если вам понадобится помощь в решении более сложных и многоуровневых задач, обращайтесь к специалистам студенческого сервиса за быстрой и квалифицированной помощью!
А если вам понадобится помощь в решении более сложных и многоуровневых задач, обращайтесь к специалистам студенческого сервиса за быстрой и квалифицированной помощью!
 Теперь они только представляют этот прибор в уме и считают, мысленно передвигая косточки.
Теперь они только представляют этот прибор в уме и считают, мысленно передвигая косточки.



 Дети должны понимать, что, в отличие от букв, числа связаны друг с другом. 15 ровно на единицу больше, чем 14. Для этого можно использовать числовые линии и цветные счетчики, чтобы связать звук с количеством.
Дети должны понимать, что, в отличие от букв, числа связаны друг с другом. 15 ровно на единицу больше, чем 14. Для этого можно использовать числовые линии и цветные счетчики, чтобы связать звук с количеством.






 Затем мы добавим Digits At Tens Place:
Затем мы добавим Digits At Tens Place:
 Этот трюк поможет вам умножить любое двузначное число в уме. Это обобщенный подход, вы можете получить решение еще до того, как узнаете его. То есть, применяя метод умножения на двузначное число, описанный в этом посте, вы можете вычислить результат слева направо.
Этот трюк поможет вам умножить любое двузначное число в уме. Это обобщенный подход, вы можете получить решение еще до того, как узнаете его. То есть, применяя метод умножения на двузначное число, описанный в этом посте, вы можете вычислить результат слева направо. В первом примере основное внимание уделяется умножению двузначных чисел без переноса, а во втором — с переносом.
В первом примере основное внимание уделяется умножению двузначных чисел без переноса, а во втором — с переносом.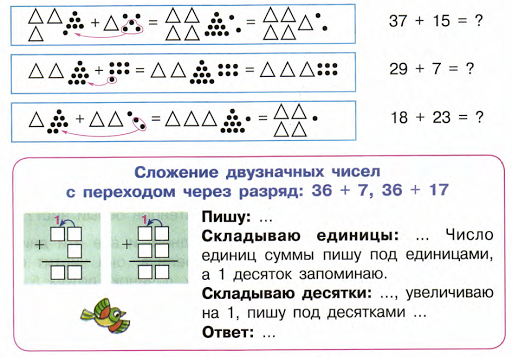 Мы рассмотрим этот трюк с умножением, разделив подход к умножению на двузначные числа на следующие разделы:
Мы рассмотрим этот трюк с умножением, разделив подход к умножению на двузначные числа на следующие разделы: В случае двузначного умножения n равно 2. Следовательно,
В случае двузначного умножения n равно 2. Следовательно,