Урок 3. Традиционное умножение в уме
Давайте рассмотрим, как можно умножать двузначные числа, используя традиционные методы, которым нас обучают в школе. Некоторые из этих методов, могут позволить вам быстро перемножать в уме двузначные числа при достаточной тренировке. Знать эти методы полезно. Однако важно понимать, что это лишь вершина айсберга.
В данном уроке рассмотрены наиболее популярные приемы умножения двузначных чисел.
Первый способ – раскладка на десятки и единицы
Самым простым для понимания способом умножения двузначных чисел является тот, которому нас научили в школе. Он заключается в разбиении обоих множителей на десятки и единицы с последующим перемножением получившихся четырех чисел. Этот метод достаточно прост, но требует умения удерживать в памяти одновременно до трех чисел и при этом параллельно производить арифметические действия.
Например: 63*85 = (60+3)*(80+5) = 60*80 + 60*5 +3*80 + 3*5=4800+300+240+15=5355
Проще такие примеры решаются в 3 действия. Сначала умножаются десятки друг на друга. Потом складываются 2 произведения единиц на десятки. Затем прибавляется произведение единиц. Схематично это можно описать так:
Сначала умножаются десятки друг на друга. Потом складываются 2 произведения единиц на десятки. Затем прибавляется произведение единиц. Схематично это можно описать так:
- Первое действие: 60*80 = 4800 — запоминаем
- Второе действие: 60*5+3*80 = 540 – запоминаем
- Третье действие: (4800+540)+3*5= 5355 – ответ
Вывод. Не трудно убедиться в том, что этот способ не является самым эффективным, то есть позволяющим при наименьших действиях получить правильный результат. Следует принять во внимание другие способы.
Второй способ – арифметические подгонки
Приведение примера к удобному виду является достаточно распространенным способом счета в уме. Подгонять пример удобно, когда вам нужно быстро найти примерный или точный ответ. Желание подгонять примеры под определенные математические закономерности часто воспитывается на математических кафедрах в университетах или в школах в классах с математическим уклоном. Людей учат находить простые и удобные алгоритмы решения различных задач.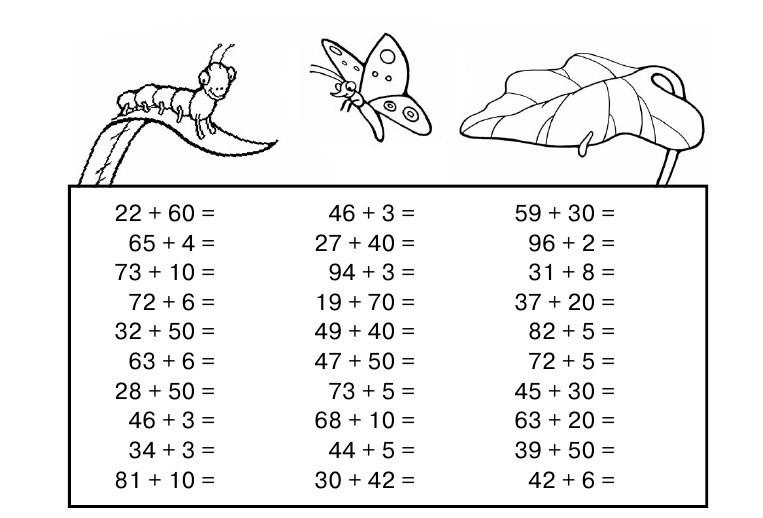 Вот некоторые примеры подгонки:
Вот некоторые примеры подгонки:
Пример 49*49 может решаться так: (49*100)/2-49. Сначала считается 49 на сто – 4900. Затем 4900 делится на 2, что равняется 2450, затем вычитается 49. Итого 2401.
Произведение 56*92 решается так: 56*100-56*2*2*2. Получается: 56*2= 112*2=224*2=448. Из 5600 вычитаем 448, получаем 5152.
Этот способ может оказаться эффективнее предыдущего только в случае, если вы владеете устным счетом на базе перемножения двузначных чисел на однозначные и можете держать в уме одновременно несколько результатов. К тому же приходится тратить время на поиск алгоритма решения, а также уходит много внимания за правильным соблюдением этого алгоритма.
Вывод. Способ, когда вы стараетесь умножить 2 числа, раскладывая их на более простые арифметические процедуры, отлично тренирует ваши мозги, но связан с большими мысленными затратами, а риск получить неправильный результат выше, чем при первом методе.
Третий способ — мысленная визуализация умножения в столбик
56*67 – посчитаем в столбик.
Наверное, счет столбиком содержит максимальное количество действий и требует постоянно держать в уме вспомогательные числа. Но его можно упростить. Во втором уроке рассказывалось, что важно уметь быстро умножать однозначные числа на двузначные. Если вы уже умеете это делать на автомате, то счет в столбик в уме для вас будет не таким уж и трудным. Алгоритм таков
Первое действие: 56*7 = 350+42=392 – запомните и не забывайте до третьего действия.
Второе действие: 56*6=300+36=336 (ну или 392-56)
Третье действие: 336*10+392=3360+392=3 752 – тут посложнее, но вы можете начинать называть первое число, в котором уверены – «три тысячи…», а пока говорите, складывайте 360 и 392.
Вывод: счет в столбик напрямую сложен, но вы можете, при наличии навыка быстрого умножения двузначных чисел на однозначные, его упросить. Добавьте в свой арсенал и этот метод. В упрощенном виде счет в столбик является некоторой модификацией первого метода. Что лучше – вопрос на любителя.
Как можно заметить, ни один из описанных выше способов не позволяет считать в уме достаточно быстро и точно все примеры умножения двузначных чисел. Нужно понимать, что использование традиционных способов умножения для счета в уме не всегда является рациональным, то есть позволяющим при наименьших усилиях достигать максимального результата.
Евгений Буянов
← 2 Простая арифметика4 Частные методики →
Как научить ребенка считать в уме: быстрый и проверенный способ
Несмотря на то, что в школе не требуют, чтобы к первому классу ребенок освоил навык устного счета, часть родителей стремится начать обучение как можно раньше. В каком возрасте ребенок должен считать в уме, с чего начинать обучение и какие методы обучения выбрать, «Газете.Ru» рассказали преподаватель математики и специалист по ментальной арифметике.
Умение хорошо и быстро считать не влияет напрямую ни на умственные способности, ни на способность к обучению школьным дисциплинам, объяснил преподаватель по математике и анализу данных Школы программистов МШП Дмитрий Коняев. Тем не менее, по мнению эксперта, такой навык крайне полезен и сильно облегчает жизнь, так что не будет лишним приобрести его уже в дошкольном возрасте.
Тем не менее, по мнению эксперта, такой навык крайне полезен и сильно облегчает жизнь, так что не будет лишним приобрести его уже в дошкольном возрасте.
«Устный счет можно сравнить с навыком скоростной печати на клавиатуре. Сам по себе этот навык почти ни на что не влияет, но облегчает жизнь каждый день, потому что в современном мире мы постоянно что-то печатаем. Также каждый день мы что-то считаем, и тянуться каждый раз за телефоном просто неудобно», – объяснил Коняев.
В каком возрасте ребенок должен считать в уме
«Оптимальный возраст для начала устного счета – от трех до пяти лет. Можно начать и раньше, если ребенок проявляет интерес к арифметике и довольно быстро осваивает навыки», – подчеркнул преподаватель математики и ментальной арифметики онлайн-школы «Коалиция» Арсений Кузнецов.
Преподаватель Коняев считает, что в среднем ребенок способен считать в уме уже с четырех лет. Однако, по его мнению, торопить события не стоит. «Если это произойдет позже — ничего страшного тут нет.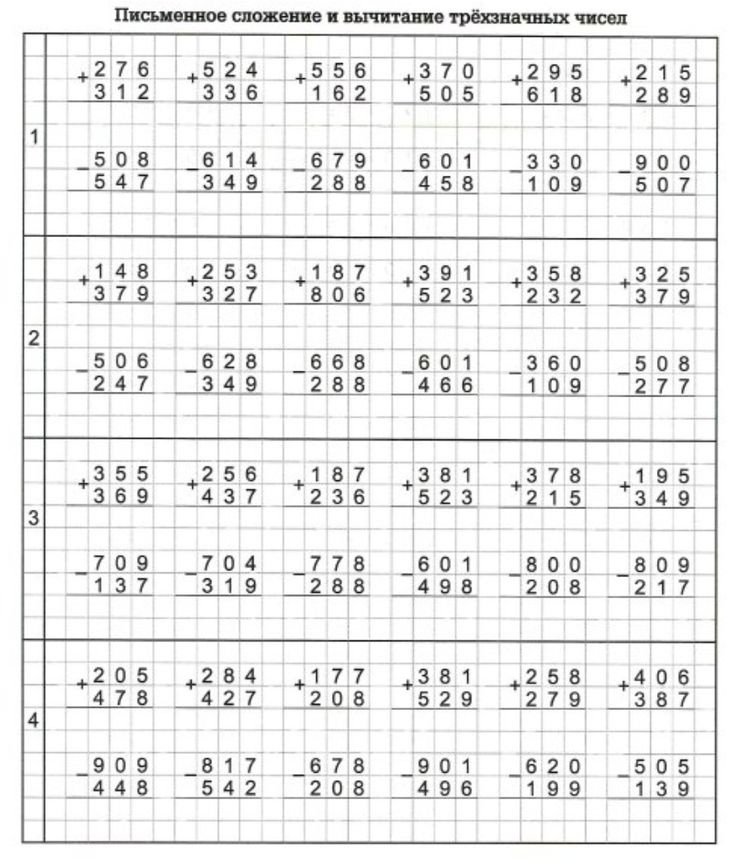 Давить на неразвитый мыслительный аппарат гораздо хуже», – предупредил специалист.
Давить на неразвитый мыслительный аппарат гораздо хуже», – предупредил специалист.
Как научить ребенка складывать и вычитать
Как быстро научить ребенка считать
Изучение цифр, понятий сложения и вычитания дети, как правило, осваивают в дошкольном возрасте…
31 мая 19:54
Сложение и вычитание – базовые арифметические действия, которые дошкольник вполне способен освоить. Арсений Кузнецов советует на первых стадиях производить счет на пальцах, в игровой форме с палочками и картинками.
Дмитрий Коняев поддерживает коллегу в том, что в освоении счета взрослым стоит опираться на игровую механику. «Гуляя по улице, предлагайте ребенку посчитать котов/окна/машины/деревья. Это прекрасный способ вовлечь в игру и развить навык», – объяснил Коняев.
Понятия «больше» и «меньше» также поможет освоить практикоориентированный подход, так как, по мнению специалистов, дети лучше воспринимают информацию, которая проецируется на реальную жизнь. «Первое время можно объяснять на примере конфет, кубиков, раскладывая большее количество в правую сторону, меньшее – в левую. Так у ребенка возникнут ассоциации, что меньшее число всегда находится левее», – рассказал Кузнецов. Он отметил, что ребенка важно обучить последовательности счета, и тогда с крепким фундаментом знаний дошкольнику будет проще переходить на более высокие уровни сложности.
Так у ребенка возникнут ассоциации, что меньшее число всегда находится левее», – рассказал Кузнецов. Он отметил, что ребенка важно обучить последовательности счета, и тогда с крепким фундаментом знаний дошкольнику будет проще переходить на более высокие уровни сложности.
close
100%
Как научить ребенка решать примеры с переходом через десяток
«Дети начинают чувствовать себя растерянно, когда помимо привычных примеров, где ответ получается не более 10, появляются вычисления, выходящие за рамки первого десятка», – поделился наблюдениями преподаватель Кузнецов.
Эксперт посоветовал обратиться к самому комфортному и действенному методу обучения – рисованию схем. Это поможет развеять страх и продемонстрирует, что новые цифры учить не придется, так как все базируется на значениях от 0 до 9.
«При сложении с переходом через десяток нужно дополнять первое слагаемое до 10, а затем прибавлять оставшиеся единицы, – рассказал математик. – Пример: 9 + 7 = ? 9 + 1 + 6 = 16».
Объяснить это ребенку эксперт посоветовал следующим образом: для округления цифры 9 до десятки не хватает 1. Значит, из 7 вычитаем 1 и прибавляем эту единицу к 9, чтобы получить круглое число. После вычитания 1 из 7 осталась шестерка. К 10 прибавляем 6 и находим ответ.
Как научить ребенка считать в уме двузначные числа
До перехода к устному счету необходимо отработать умение складывать и вычитать двузначные числа на бумаге. Эту задачу, по мнению преподавателя Коняева, стоит оставить школе.
Как научить ребенка читать: методики от опытного педагога
Ребенок, который научился читать в три года — гордость родителей. Но стоит ли торопить события и…
21 апреля 12:31
Если же родителям не терпится обучить ребенка этому навыку, то можно воспользоваться счетом в столбик. «Столбики дают наглядное представление о десятках и единицах, об операциях, производимых с ними. Когда ребенок начнет безошибочно проводить письменные вычисления, можно приступать к устным расчетам.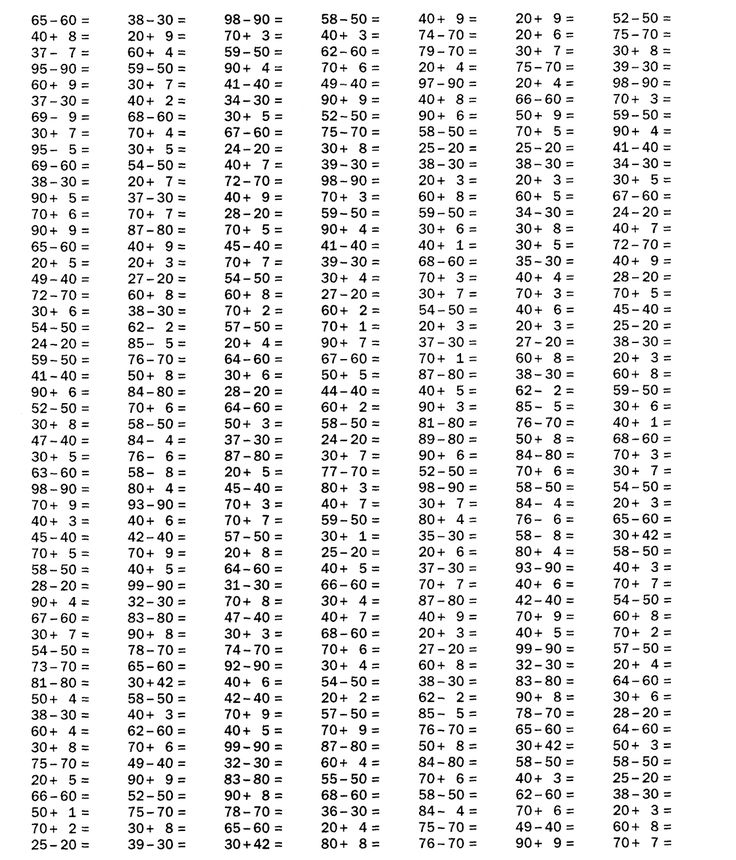 Стоит начинать с круглых чисел, вычитать из них десятки, затем пятерки, а после усложнять примеры, добавляя в них разнообразия», – рассказал Арсений Кузнецов.
Стоит начинать с круглых чисел, вычитать из них десятки, затем пятерки, а после усложнять примеры, добавляя в них разнообразия», – рассказал Арсений Кузнецов.
Специалист объяснил, что для освоения навыка дошкольнику может потребоваться больше времени, чтобы он научился представлять в уме ранее используемых столбцов, но занятия каждый день решат эту проблему.
close
100%
Подходит ли ментальная арифметика для обучения быстрому счету
Школы ментальной арифметики сейчас есть почти в любом российском городе, поэтому родителей не может не интересовать вопрос, поможет ли этот метод ребенку научиться быстро считать в уме.
Математик Кузнецов порекомендовал осваивать этот метод тем, кто готов к немалому вложению энергии и времени. Также обучение потребует от дошкольника терпения. Но наградой за труды станет способность к высокой концентрации внимания, гибкость мышления и памяти.
«Ментальная арифметика направлена на развитие умственных способностей ребенка и мелкой моторики рук. За данной методикой обучения скрываются усиленные тренировки и упорство, ее освоение займет около двух лет и первое время будет сопряжено с неверными расчетами. Сдвиги в лучшую сторону начнутся после пары месяцев занятий», – отметил эксперт.
За данной методикой обучения скрываются усиленные тренировки и упорство, ее освоение займет около двух лет и первое время будет сопряжено с неверными расчетами. Сдвиги в лучшую сторону начнутся после пары месяцев занятий», – отметил эксперт.
Он объяснил, что для освоения ментальной арифметики достаточно знать цифры от 0 до 9. Обучение протекает постепенно, и уровни сложности повышаются по мере прохождения предыдущих этапов.
Числа до 2 цифр — определение, разрядное значение
В двузначных числах есть только два разряда — разряд единиц и разряд десятков. Каждое число, состоящее более чем из 1 цифры, имеет разные цифры, описываемые их разрядными значениями. Двузначные числа начинаются с 10 и заканчиваются на 99. Другими словами, наименьшее двузначное число — 10, а наибольшее двузначное число — 99.
| 1. | Что такое двузначные числа? |
| 2. | Как записывать числа до 2 цифр? |
3. | Общие ошибки чисел до 2 цифр |
| 4. | Часто задаваемые вопросы о номерах до 2 цифр |
Что такое двузначные числа?
Двузначные числа — это числа, состоящие из двух цифр, которые начинаются с цифры 10 и заканчиваются цифрой 99. Они не могут начинаться с нуля, потому что в этом случае это будет считаться однозначной цифрой. Цифра в разряде десятков может быть любым числом от 1 до 9. Например, 45, 78, 12 — двузначные числа.
Разрядное значение в двузначных числах
Разрядное значение — это положение каждой цифры в числе. Когда мы говорим об однозначных числах, есть только одно разрядное значение, которое является разрядом единиц. Когда мы подходим к двузначным числам, есть два разряда — единицы и десятки. Обратите внимание на следующий рисунок, на котором показано двузначное число 23, написанное вместе с его разрядными значениями. Цифра 2 стоит на месте десятков и означает 20, а цифра 3 стоит на месте единиц и означает 3.
Присвоение разрядных значений
Мы знаем, что разрядное значение числа говорит о позиции цифры. В двузначных числах единственными разрядами являются десятки и единицы.
Давайте посмотрим на следующий набор чисел, чтобы понять сочетание единиц и десятков:
а.) 33 ⇒ 3 десятка + 3 единицы = (3 × 10) + (3 × 1) = 30 + 3 = 33
б.) 18 ⇒ 1 десяток + 8 единиц = (1 × 10) + (8 × 1) = 10 + 8 = 18
в.) 27 ⇒ 2 десятка + 7 единиц = (2 × 10) + ( 7 × 1) = 20 + 7 = 27
Как записывать числа до 2 цифр?
Двузначные числа можно записывать в виде цифр, прописью и в расширенной форме. Например, 45 — это двузначное число. Давайте посмотрим, как это можно записать тремя способами.
- В цифровой форме: 45
- Прописью: сорок пять
- В развернутом виде: 40+5
Двузначные числа в словах
Когда числа записываются словами с помощью разрядных значений, это помогает нам писать их по буквам. Самое маленькое двузначное число — 10, которое записывается как десять. После этого числа от 11 до 20 записываются как 11 – одиннадцать, 12 – двенадцать, 13 – тринадцать, 14 – четырнадцать, 15 – пятнадцать, 16 – шестнадцать, 17 – семнадцать, 18 – восемнадцать, 19.- девятнадцать, а 20 — двадцать. После этого они записываются как 21 — двадцать один, 22 — двадцать два, 23 — двадцать три и так далее, пока не дойдет до 30 — тридцать, и тот же образец следует после тридцати, сорока и так далее.
Самое маленькое двузначное число — 10, которое записывается как десять. После этого числа от 11 до 20 записываются как 11 – одиннадцать, 12 – двенадцать, 13 – тринадцать, 14 – четырнадцать, 15 – пятнадцать, 16 – шестнадцать, 17 – семнадцать, 18 – восемнадцать, 19.- девятнадцать, а 20 — двадцать. После этого они записываются как 21 — двадцать один, 22 — двадцать два, 23 — двадцать три и так далее, пока не дойдет до 30 — тридцать, и тот же образец следует после тридцати, сорока и так далее.
Двузначные числа в расширенной форме
Расширенная форма числа помогает узнать о его составляющих. Развернутую форму двузначного числа можно показать по-разному. Рассмотрим двузначное число 57.
- Число 57 можно записать в одной форме как 57 = (5 × десятков) + (7 × единиц)
- По-другому это можно записать как 57 = (5 × 10) + (7 × 1)
- Третий способ записать 57 в расширенной форме: 57 = 50 + 7.
Общие ошибки чисел до 2 цифр
- Дети часто могут назвать все числа до 99 (или 100), но могут ошибаться, когда их просят найти большее число между двумя числами.
 Они повторяют числа от 1 до 100 так, как будто выучили буквы алфавита. Если это произойдет, то найти большее число между 14 и 15 так же сложно, как найти большую букву между С и D. Дети должны понимать, что, в отличие от букв, числа связаны друг с другом. 15 ровно на единицу больше, чем 14. Для этого можно использовать числовые линии и цветные счетчики, чтобы связать звук с количеством.
Они повторяют числа от 1 до 100 так, как будто выучили буквы алфавита. Если это произойдет, то найти большее число между 14 и 15 так же сложно, как найти большую букву между С и D. Дети должны понимать, что, в отличие от букв, числа связаны друг с другом. 15 ровно на единицу больше, чем 14. Для этого можно использовать числовые линии и цветные счетчики, чтобы связать звук с количеством. - Дети склонны ошибаться при работе с числами при изменении разряда десятков. Например, при переходе от 19 к 20, от 29 к 30, от 39 к 40 и т. д. Часто двузначные числа вводятся без привязки к разрядным значениям. Хотя это облегчает запоминание чисел, это может быть не лучшей стратегией, поскольку дети не видят числа, составленные из общего набора цифр от 0 до 9. В этом случае можно использовать счеты для моделирования чисел и основания. -10 блоков могут быть использованы, чтобы помочь им визуализировать числа.
- Дети делают ошибки при написании или чтении чисел словами, особенно от одиннадцати до девятнадцати.
 Нет никакой замены практике. Дети должны практиковаться в написании названий чисел. Как правило, при небольшой преднамеренной и целенаправленной практике эту ошибку можно легко исправить.
Нет никакой замены практике. Дети должны практиковаться в написании названий чисел. Как правило, при небольшой преднамеренной и целенаправленной практике эту ошибку можно легко исправить.
Советы по числам до 2 цифр
Ниже приведены некоторые советы и рекомендации по числам до 2 цифр.
- При умножении любого однозначного числа (от 1 до 9) на 10 получается двузначное число. Например, 4 × 10 = 40
- Наименьшее двузначное число, состоящее только из одной цифры, равно 11.
- Наименьшее двузначное число, состоящее из двух разных цифр, равно 10. (10 также является наименьшим двузначным числом)
- Наибольшее двузначное число, использующее только одну цифру, равно 99. (99 также является наибольшим двузначным числом).
- Наибольшее двузначное число, использующее все разные цифры, равно 98.
- В двузначных числах есть только два разряда: десятки и единицы.
- Есть девяносто «двухзначных чисел», начиная с 10-99.

Вот список всех чисел до 2 цифр от 10 до 99.
Наименьшее двузначное число
Наименьшее двузначное число — 10, поскольку предыдущее число — 9, которое является однозначным числом.
Наибольшее двузначное число
Наибольшее двузначное число — 99, поскольку следующее число — 100, которое является трехзначным числом.
Важные примечания
Ниже приведены некоторые важные примечания, связанные с числами до 2 цифр, которые мы изучали в этой статье.
- Наименьшее двузначное число — 10, а наибольшее двузначное число — 99.
- Всего девяносто двузначных чисел.
- Двузначное число не может начинаться с 0, так как в этом случае оно будет считаться однозначным.
☛ Статьи по теме
- Номера до 3 цифр
- Номера до 4 цифр
- Номера до 5 цифр
- Номера до 6 цифр
- Номера до 7 цифр
- Номера до 8 цифр
- Номера до 9 цифр
- Номера до 10 цифр
Примеры двузначных чисел
Пример 1: В чем разница между самым большим двузначным числом и числом 20?
Решение: Наибольшее двузначное число = 99
.
Разница между 99 и 20 составляет 99 — 20 = 79
Пример 2: Создайте двузначное число, в котором 7 — это разряд десятков, а 5 — разряд единиц. Запишите номер в развернутой форме и напишите его номерное название.
Решение: Если 7 в разряде десятков и 5 в разряде единиц, число равно 75.
Расширенная форма 75 = 70 + 5. Это также можно записать как (7 десятков) + (5 единиц) или (7 × 10) + (5 × 1) 9.0185 Имя числа 75 — это семьдесят пять.Пример 3: Запишите первые четыре «двузначных числа» и последние четыре «двузначных числа».
Решение: Первые четыре двузначных числа: 10, 11, 12, 13.
Последние четыре двузначных числа: 96, 97, 98, 99.
перейти к слайдуперейти к слайдуперейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Записаться на бесплатный пробный урок
Практические вопросы по числам до 2 цифр
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о номерах до 2 цифр
Что такое двузначные числа в математике?
Число называется двузначным, если оно состоит из двух цифр, в которых разряд десятков должен стоять от 1 до 9, оно не может начинаться с нуля, потому что в этом случае оно станет однозначным числом. Например, 35, 45, 60, 11 и так далее — двузначные числа.
Сколько существует двузначных чисел?
Всего существует девяносто двузначных чисел, начиная с 10 и заканчивая 99. Это означает, что наименьшее двузначное число равно 10, а самое большое двузначное число равно 99.
Какое самое большое 2- Цифровой номер?
Самое большое двузначное число — 99, а следующее число — 100, которое является трехзначным числом.
Какое самое маленькое двузначное число?
Наименьшее двузначное число — 10, поскольку предыдущее число — 9, то есть однозначное число.
Какое наибольшее двузначное число делится на 10?
Самое большое двузначное число, которое делится на 10, — это 90. Хотя самое большое двузначное число — 99, оно не делится на 10.
Какое наибольшее двузначное число можно составить из 8 и 6?
Наибольшее двузначное число, которое можно составить из 8 и 6, равно 86. Поскольку 8 больше 6, поэтому мы оставляем 8 на разряде десятков и 6 на разряде единиц. Следовательно, 86 — это самое большое двузначное число, состоящее из цифр 8 и 6.
Напишите расширенную форму данного двузначного числа 65.
Расширенную форму числа 65 можно представить как 60 + 5. Это также можно записать как 6 десятков + 5 единиц или (6 × 10) + (5 × 1).
Сколько десятков в двузначном числе 20?
В данном числе 20 цифра 2 стоит на месте десятков. Следовательно, в числе 20 2 десятка. Это можно записать как 20 = 2 десятка + 0 единиц.
Могут ли двузначные числа начинаться с 0?
Нет, двузначные числа не могут начинаться с 0. Разряд десятков в двузначном числе не может быть нулем, это может быть любое число от 1 до 9, в противном случае оно будет считаться однозначным числом. Например, 05, 06, 07 — все однозначные числа, а 56, 78, 79 — двузначные числа.
Разряд десятков в двузначном числе не может быть нулем, это может быть любое число от 1 до 9, в противном случае оно будет считаться однозначным числом. Например, 05, 06, 07 — все однозначные числа, а 56, 78, 79 — двузначные числа.
Каковы разрядные значения в числах до 2 цифр?
Значение разряда помогает определить положение цифр. В двузначных числах всего два разряда — десятки и единицы. Например, в числе 98 9 стоит на месте десятков, а 8 — на месте единиц.
Какое самое большое двузначное простое число?
Самое большое двузначное простое число — 97, потому что 97 имеет только 2 делителя, 1 и 97.
Загрузить БЕСПЛАТНЫЕ учебные материалы
Загрузить бесплатные рабочие листы KG
Рабочий лист чисел
Умножение двузначных чисел | Как умножать, методы, примеры
Введение Умножение — это одна из четырех основных математических операций, а остальные три — это сложение, вычитание и деление. Прежде чем мы перейдем к изучению того, как умножать двузначные числа, давайте вспомним, что мы подразумеваем под умножением.
Умножение определяется как процесс нахождения произведения двух или более чисел. Полученный таким образом результат называется продуктом . Предположим, вы купили 6 ручек в один день и 6 ручек на следующий день. Всего ручек, которые вы купили, теперь 2 умножить на 6 или 6 + 6 = 12.
Это также можно записать как 2 x 6 = 12
Не тот символ, который используется для умножения. Символ (x) обычно используется для обозначения умножения. Другими распространенными символами, которые используются для умножения, являются звездочка (*) и точка (.)
Символ умноженияОбратите внимание на символ, используемый в приведенном выше примере для умножения. Символ (x) обычно используется для обозначения умножения. Другими распространенными символами, которые используются для умножения, являются звездочка (*) и точка (.)
Теперь давайте рассмотрим некоторые важные термины, которые используются при умножении двух чисел.
Некоторые важные термины, используемые при умножении –
Множимое . Число, которое нужно умножить, называется множимым.
Множитель — Число, на которое мы умножаем, называется множителем.
Произведение – Результат, полученный после умножения множителя на множимое, называется произведением.
Связь между множителем, множимым и произведением может быть выражена как –
Множитель × Множитель = Произведение
Давайте разберемся с этим на примере.
Предположим, у нас есть два числа 9 и 5. Мы хотим умножить 9 на 5.
Итак, мы выражаем это как 9 x 5, что дает нам 45.
Следовательно, 9 x 5 = 45
Здесь 9 равно множимое, 5 — множитель, 45 — произведение.
Теперь, когда мы поняли, что мы подразумеваем под умножением и терминами, связанными с ним, давайте перейдем к изучению умножения однозначных чисел.
Теперь давайте разберемся, как выполнять умножение, когда у нас есть многозначные числа.
Как умножать двузначные числа?Прежде чем мы приступим к пониманию умножения двузначных чисел, важно вспомнить, что подразумевается под двузначными числами?
Напомним, что каждая цифра числа имеет разрядное значение. Например, число 5 — это однозначное число, где 5 стоит на месте единицы. Точно так же в числе 27 цифра 2 стоит на месте десятков, а цифра 7 — на месте единиц. Итак, как мы определяем двузначные числа? Двузначные числа — это числа, состоящие из 2 цифр, т. е. числа, состоящие из цифр только на разрядах единиц и десятков. Например, числа 55 и 67 двузначные.
Теперь давайте перейдем к изучению умножения двузначных чисел. Когда дело доходит до умножения двузначных чисел, есть два метода умножения чисел. Этими методами являются метод расширенной записи и метод столбца. Давайте разберемся в обоих методах.
Метод расширенной записи В методе расширенной записи мы расширяем множимое согласно разрядным значениям, а затем умножаем каждое число на множитель. Затем мы суммируем все полученные результаты, чтобы получить окончательный ответ. Давайте разберемся на примере.
Затем мы суммируем все полученные результаты, чтобы получить окончательный ответ. Давайте разберемся на примере.
Например, умножить 35 на 40
Решение
Мы решим это шаг за шагом.
Шаг 1 – Запишите число (множимое) в развернутом виде. Получаем,
35 = 30 + 5
Шаг 2 – Умножаем каждое число на заданное число (множитель) по одному. Получаем,
30 х 40 + 5 х 40 = 1200 + 200
Шаг 3 — Складываем полученные результаты. Получаем,
1200 + 200 = 1400
Отсюда 35 х 40 = 1400
Хотя этот метод и прост, он может не подходить для больших чисел. Но он используется для понимания основных понятий умножения.
Метод столбцаВ этом методе мы разбиваем числа на столбцы и умножаем числа на множимое одно за другим. Есть два сценария использования этого метода.
Давайте разберемся с ними один за другим
Умножение без перегруппировки Этот метод вступает в силу, когда у нас есть меньшие числа, которые не требуют переноса каких-либо чисел на разряд следующего разряда. Давайте разберемся на примере.
Давайте разберемся на примере.
Например, умножьте 21 на 32
Решение
Чтобы получить результат, выполните следующие действия.
Шаг 1. Сначала мы записываем множимое и множитель в столбцах. Здесь у нас есть 21 как множимое и 32 как множитель.
Шаг 2. Теперь умножаем число, стоящее на месте множимого, т. е. 1, на число, стоящее на месте множителя, которое в данном случае равно 2. Получаем
. Шаг 3. Теперь умножаем число в десятом месте множимого на 2. Получаем
Шаг 4. Теперь нам нужно поставить 0 на место единиц в следующей строке в качестве заполнителя. Мы получим
Шаг 5. Поскольку мы завершили умножение множимого на первую цифру множителя, мы выполняем те же действия, что и выше для умножения множимого на следующее число множителя, а затем пишем результатом будет строка напротив 0, которую мы поместили в качестве заполнителя на предыдущем шаге. Получим –
Шаг 6 Теперь, когда мы перемножили все цифры множителя с множимым, сложим полученные цифры по вертикали. мы получим
мы получим
Полученный таким образом результат является нашим ответом. Следовательно, 21 x 32 = 672
Умножение с перегруппировкойВ приведенном выше случае у нас есть небольшие умножения, которые не требуют двузначных результатов ни на одном шаге. Но в случае больших чисел потребуется перенести число на число со следующим значением разряда. Это называется умножением с перегруппировкой. Давайте разберемся на примере.
Например, умножить 25 на 34
Решение
Мы будем использовать следующие шаги, чтобы получить наш результат.
Шаг 1. Сначала мы записываем множимое и множитель в столбцах.
Шаг 2. Умножьте цифру единицы множимого на 4. У нас есть 4 x 5 = 20. Запишите 0 в столбце единиц и перенесите 2 в столбец десятков.
Шаг 3 – Умножаем десятый разряд множимого на 4. Получаем 2 x 4 = 8. Прибавляем к нему 2, которые были перенесены, чтобы получить 8 + 2 = 10. Теперь запишем 0 в столбце десятков и перенесем 1 в сто столбик.
Теперь запишем 0 в столбце десятков и перенесем 1 в сто столбик.
Шаг 4 Теперь нам нужно поставить 0 на место единиц в следующей строке в качестве заполнителя. Мы получим
Шаг 5. Поскольку мы завершили умножение множимого на первую цифру множителя, мы выполняем те же действия, что и выше для умножения множимого на следующее число множителя, а затем пишем результатом будет строка напротив 0, которую мы поместили в качестве заполнителя на предыдущем шаге. Получим –
Шаг 6 Теперь, когда мы перемножили все цифры множителя с множимым, сложим полученные цифры по вертикали. мы получим
Полученный таким образом результат является нашим ответом. Следовательно, 25 x 34 = 850
Вышеуказанные шаги могут быть обобщены для определения умножения, которое обычно известно как длинное умножение. Определим эти шаги.
Длинное умножение Длинное умножение похоже на метод столбца, за исключением того факта, что здесь мы умножаем большие числа. Этот метод используется, когда множимое больше 9, т. е. множимое больше однозначного числа. Этот метод включает в себя следующие этапы –
Этот метод используется, когда множимое больше 9, т. е. множимое больше однозначного числа. Этот метод включает в себя следующие этапы –
- Сначала запишем множимое и множитель столбцами.
- Сначала умножьте число, стоящее на месте единицы множителя, на все числа множимого и запишите их горизонтально.
- Убедитесь, что вы записываете числа справа налево и каждое число находится под соответствующим разрядом множимого.
- Теперь перейдите к следующей строке.
- Поставьте 0 на месте единицы в этой строке.
- Теперь найдите цифру в разряде десятков множителя. Умножьте число, стоящее в десятом разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили 0,9.0070
- Снова перейти на следующую строку.
- Поставьте 0 на месте единиц и десятков в этой строке.
- Теперь найдите цифру в разряде сотен множителя. Умножьте число, стоящее в сотенном разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили два нуля.

- Продолжайте в том же духе, добавляя дополнительный ноль в каждой строке, пока не дойдете до конца множителя
- Сложите числа по вертикали в соответствии с их разрядностью.
- Полученное таким образом число и есть ваш результат.
Давайте разберем это на примере
Например, Умножьте 32 на 13
Решение
- Сначала мы запишем множимое и множитель в столбцах.
- Затем умножьте число, стоящее на месте множителя, на все числа множимого и запишите их горизонтально.
- Поместите 0 на место единиц следующей строки
- Теперь найдите цифру в разряде десятков множителя. Умножьте число, стоящее в десятом разряде множителя, на все числа множимого и запишите их горизонтально в строке, где вы отметили 0.
- В множимом больше нет числа. Теперь сложите числа по вертикали в соответствии с их разрядностью.
Окончательный ответ: 416. Следовательно, 32 x 13 = 416
Следовательно, 32 x 13 = 416
Давайте посмотрим на другой пример, где мы 3 цифры в множимом.
Например, Умножить 53 на 25
Решение
1. Сначала запишем множимое и множитель в столбцы
- Затем умножим число, стоящее на месте единицы, на все числа множителя множимое и запишем их горизонтально.
- Поставьте 0 на месте единицы следующей строки
- Теперь найдите цифру в разряде десятков множителя. Умножьте десятичное число множителя на все числа множимого и запишите их горизонтально в строке, где вы отметили 0.
- Теперь, когда мы умножили все цифры множителя на множимое, мы добавит полученные цифры по вертикали. Получим
Отсюда 53 х 25 = 1325
Решенные примеры Пример 1 В кинозале 58 рядов, в каждом ряду 25 мест. Сколько человек может разместиться в зале?
Сколько человек может разместиться в зале?
Решение Нам дано, что в кинозале 58 рядов и в каждом ряду 25 мест. Нам нужно найти количество человек, которое может разместиться в зале. Подытожим предоставленную нам информацию.
Количество рядов в кинозале = 58
Количество мест в каждом ряду = 25
Количество человек, которые могут разместиться в зале = ?
Количество человек, которые могут разместиться в зале, можно найти, умножив количество рядов на количество мест в каждом ряду. Это означает, что –
Количество человек, которые могут разместиться в зале = (Количество рядов в кинозале) x (Количество мест в каждом ряду) ……………………… ( 1 )
Подставляя данное значения в приведенном выше уравнении, мы будем иметь,
Количество человек, которые могут быть размещены в зале = 58 x 25
Теперь
Отсюда количество человек, которое может разместиться в зале = 1450
Пример 2 Ресторан приобрел 81 коробку пакетов с кетчупом. В каждой коробке было 49 пакетов кетчупа. Сколько всего пакетов с кетчупом купил ресторан?
В каждой коробке было 49 пакетов кетчупа. Сколько всего пакетов с кетчупом купил ресторан?
Решение Нам сообщили, что ресторан приобрел 81 коробку пакетов с кетчупом. В каждой коробке было 49 пакетов кетчупа. Нам нужно узнать, сколько всего пакетов кетчупа купил ресторан. Подытожим предоставленную нам информацию.
Количество коробок кетчупа, купленных рестораном = 81
Количество пачек кетчупа в каждой коробке = 49
Общее количество пачек кетчупа, купленных рестораном = ?
Чтобы найти значение количества упаковок кетчупа, купленных рестораном, нам нужно будет умножить количество упаковок кетчупа, купленных рестораном, на количество упаковок кетчупа в каждой коробке. Это означает, что
Общее количество упаковок кетчупа, купленных рестораном = (Количество упаковок кетчупа, купленных рестораном) x (Количество упаковок кетчупа в каждой коробке) ……………………………. ( 1 )
Подставив данные значения в приведенное выше уравнение, мы получим,
Общее количество пакетов кетчупа, купленных рестораном = 81 x 49
Теперь,
Следовательно, общее количество пакетов кетчупа, купленных рестораном ресторан = 3969.
Пример 3 Уильям купил 60 упаковок бумажных салфеток. В каждой упаковке было 56 салфеток. Сколько салфеток купил Уильям?
Решение Нам сообщили, что Уильям купил 60 упаковок бумажных салфеток. В каждой упаковке было 56 салфеток. Нам нужно найти количество салфеток, купленных Уильямом. Подытожим предоставленную нам информацию.
Количество упаковок бумажных салфеток, купленных Уильямом = 60
Количество салфеток в каждой упаковке = 56
Общее количество салфеток, купленных Уильямом = ?
Чтобы найти общее количество салфеток, купленных Вильямом, нам нужно будет умножить количество упаковок бумажных салфеток, купленных Вильямом, на количество салфеток в каждой упаковке. Это означает, что
Общее количество салфеток, купленных Вильямом = (Количество упаковок бумажных салфеток, купленных Вильямом) x (Количество салфеток в каждой упаковке) ………. ( 1 )
Подставив данные значения в приведенное выше уравнение, мы получим,
Общее количество тканей, купленных Уильямом = 60 x 56
Теперь,
Следовательно, общее количество тканей, купленных Уильямом = 3360
Основные факты и резюме- Умножение определяется как процесс нахождения произведения двух или более чисел.

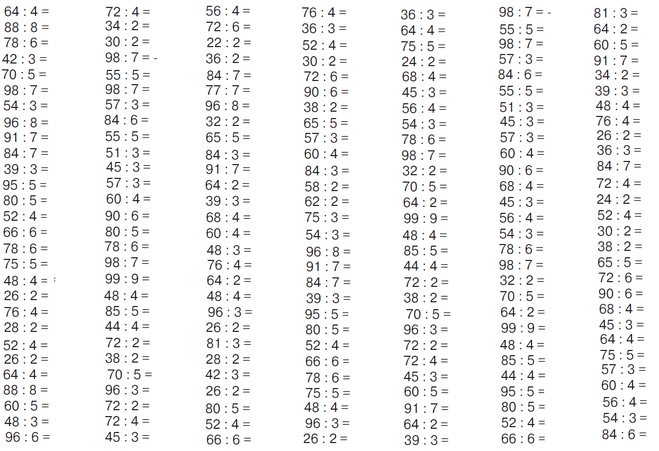 Они повторяют числа от 1 до 100 так, как будто выучили буквы алфавита. Если это произойдет, то найти большее число между 14 и 15 так же сложно, как найти большую букву между С и D. Дети должны понимать, что, в отличие от букв, числа связаны друг с другом. 15 ровно на единицу больше, чем 14. Для этого можно использовать числовые линии и цветные счетчики, чтобы связать звук с количеством.
Они повторяют числа от 1 до 100 так, как будто выучили буквы алфавита. Если это произойдет, то найти большее число между 14 и 15 так же сложно, как найти большую букву между С и D. Дети должны понимать, что, в отличие от букв, числа связаны друг с другом. 15 ровно на единицу больше, чем 14. Для этого можно использовать числовые линии и цветные счетчики, чтобы связать звук с количеством. Нет никакой замены практике. Дети должны практиковаться в написании названий чисел. Как правило, при небольшой преднамеренной и целенаправленной практике эту ошибку можно легко исправить.
Нет никакой замены практике. Дети должны практиковаться в написании названий чисел. Как правило, при небольшой преднамеренной и целенаправленной практике эту ошибку можно легко исправить.
