Как умножить дроби: 10 шагов (с иллюстрациями)
‘).insertAfter(«#intro»),$(‘
‘).insertBefore(«.youmightalsolike»),$(‘
‘).insertBefore(«#quiz_container»),$(‘
‘).insertBefore(«#newsletter_block_main»),ha(!0),b=document.getElementsByClassName(«scrolltomarker»),a=0;a
В этой статье:
Умножение до сокращения
Упрощение перед умножением
Дополнительные статьи
Умножение дробей – один из основных навыков при операциях с дробями. Чтобы умножить дроби, соответственно умножьте числители и знаменатели, а затем упростите полученную дробь (если возможно). Попрактиковавшись, вы сможете умножать дроби как профессиональный математик.
Шаги
1
Запишите задачу. Две дроби должны быть записаны так, чтобы их числители и знаменатели находились на одном уровне.

- Например: 2/4*2/4
2
Умножьте числители. 2*2=4.
3
Умножьте знаменатели. 4*4=16.
- Ответ: 4/16.
4
Упростите полученную дробь. Для этого разделите и числитель, и знаменатель на наибольший общий делитель (НОД — наибольшее число, на которое делится и числитель, и знаменатель). В нашем примере для дроби 4/16 НОД=4, поэтому разделите и числитель, и знаменатель на 4.
- 4/4 = 1
- 16/4 = 4
- Упрощенная дробь (и окончательный ответ): 1/4.
Реклама
1
Запишите задачу. Две дроби должны быть записаны так, чтобы их числители и знаменатели находились на одном уровне.
- Например: 2/4*2/4
2
Упростите первую дробь.
Для этого разделите и числитель, и знаменатель на наибольший общий делитель (НОД — наибольшее число, на которое делится и числитель, и знаменатель). В нашем примере для дроби 2/4 НОД=2, поэтому разделите и числитель, и знаменатель на 2.
В нашем примере для дроби 2/4 НОД=2, поэтому разделите и числитель, и знаменатель на 2.- 2/2 = 1
- 4/2 = 2
- Первая упрощенная дробь: 1/2. Она равна 2/4, то есть исходное значение дроби не изменилось.
- Для вычисления НОД запишите все делители отдельно для числителя, и отдельно для знаменателя. Затем выберите наибольший делитель, которое встречается как у числителя, так и у знаменателя:
- 2: 1, 2.
- 4: 1, 2, 4.
- 2 – наибольшее число, встречающееся как у числителя, так и у знаменателя, поэтому НОД=2.
3
Упростите вторую дробь. Процесс упрощения аналогичен упрощению первой дроби. Так как в нашем примере первая и вторая дробь равны, то и результат упрощения будет одинаковым.
- 2/4 = 1/2 – это вторая упрощенная дробь.
4
Умножьте числители упрощенных дробей.
- 1*1 = 1.
5
Умножьте знаменатели упрощенных дробей.

- 2*2 = 4.
6
Так как до умножения вы уже упростили дроби, то вы получили окончательный ответ.
- 1/2*1/2 = 1/4.
Реклама
Советы
- Для умножения целого числа на дробь представьте целое число в виде дроби, записав число в числитель, а в знаменатель – 1. Например, 36 представляется в виде дроби как 36/1.
- При умножении дробей порядок умножения числителей и знаменателей не имеет значения (если хотите, начните с умножения знаменателей).
Реклама
Об этой статье
На других языках
Как умножить дроби — Wiki How Русский
Умножение дробей – один из основных навыков при операциях с дробями. Чтобы умножить дроби, соответственно умножьте числители и знаменатели, а затем упростите полученную дробь (если возможно). Попрактиковавшись, вы сможете умножать дроби как профессиональный математик.
Эту страницу просматривали 15 552 раза.
Реклама
Как умножить дробь на отрицательное число?
Как умножить дробь на отрицательное число?
Чтобы найти произведение двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем перемножить дроби по правилу умножения дробей. Пример. При умножении отрицательной дроби на положительную результат будет отрицательным.
Как разделить и умножить дробь на дробь?
Как делить дробь на дробь? Выполняем следующую последовательность действий: числитель первой умножить на знаменатель второй, результат произведения записать в числитель новой дроби; знаменатель первой умножить на числитель второй, результат произведения записать в знаменатель новой дроби.
Как делить обыкновенные дроби?
Правило. Чтобы разделить обыкновенную дробь , надо числитель делимого умножить на знаменатель делителя, а знаменатель делимого умножить на числитель делителя. Первое произведение взять числителем, а второе — знаменателем. Чтобы разделить обыкновенные дроби, можно делимое умножить на дробь, обратную делителю.
Первое произведение взять числителем, а второе — знаменателем. Чтобы разделить обыкновенные дроби, можно делимое умножить на дробь, обратную делителю.
Как решить деление смешанных дробей?
Чтобы разделить одно смешанное число на другое, надо:
- преобразовать смешанные дроби в неправильные;
- умножить первую дробь на дробь, обратную второй;
- сократить полученную дробь;
- если получилась неправильная дробь преобразовать неправильную дробь в смешанную.
Как делить столбиком с запятыми?
Как разделить столбиком одну десятичную дробь на другую Переносим запятую в делимом и делителе вправо на то количество знаков, которое необходимо для превращения делителя в натуральное число. Если в делимом не хватит знаков, дописываем в него нули с правой стороны.
Как объяснить деление на двузначное число?
Алгоритм деления столбиком на двузначное число
- Находим первое неполное делимое.
 Это число, которое делится на делитель с получением числа больше или равного 1. …
Это число, которое делится на делитель с получением числа больше или равного 1. … - Определяем количество цифр в частном. …
- Находим цифры в каждом разряде частного. …
- Находим остаток (если есть). …
- Деление нужно непременно проверить умножением.
Как правильно делить двузначное число на однозначное?
Чтобы разделить двузначное число на однозначное, надо двузначное число представить в виде суммы разрядных слагаемых и разделить эту сумму на однозначное число.
Как правильно делить в столбик?
Начинаем делить «512» на «8» следующим образом:
- Определяем неполное частное. Для этого слева направо сравниваем цифры делимого и делитель. …
- «51» больше «8». Значит это неполное частное. …
- Приступаем к делению. Вспоминая таблицу умножения на «8», находим ближайшее к «51» произведение. …
- В остатке получилось «3».
Как решать примеры с остатком?
Порядок решения примеров на деление с остатком.
- Находим наибольшее число до «17», которое делится на «3» без остатка. Это «15». 15 : 3 = 5.
- Вычитаем из делимого найденное число из пункта «1». 17 − 15 = 2.
- Сравниваем остаток с делителем.
Как разделить 14 на 30 с остатком?
Ответ, проверенный экспертом Решение: 14:30=0 ( ост. 14) .
Как выполнить деление с остатком с проверкой?
Чтобы проверить деление с остатком, нужно делитель умножить на значение частного и прибавить остаток.
Как называют частное при делении с остатком?
Делимое, делитель, неполное частное, остаток от деления Натуральное число, на которое делят, называют делителем. В результате деления с остатком получаются два числа, одно из которых называют неполным частным, а другое – остатком.
Что такое неполное частное 4 класс?
«Неполное частное» – это число, показывающее какое максимальное количество раз, делитель содержится в делимом. 157. Выполни деление нацело и деление с остатком. Как получить делимое 60, используя значение частного и делитель?
157. Выполни деление нацело и деление с остатком. Как получить делимое 60, используя значение частного и делитель?
Как найти делитель если известно делимое и частное с остатком?
Решение Чтобы найти делитель, если известны делимое, неполное частное и остаток, нужно от делимого отнять остаток, и полученную разность разделить на неполное частное.
Умножение дробей – Математика для сделок: Том 1
Дроби
Следующее уравнение является примером умножения дробей. На первый взгляд это может показаться сложнее, чем сложение или вычитание дробей, но на самом деле это намного проще. Что может быть сложнее понять, так это ответ, который вы получаете, когда перемножаете дроби.
[латекс]\БОЛЬШОЙ\dfrac{1}{4}\times\dfrac{1}{2}=?[/latex]
Мы посмотрим на это визуально, используя для этого круг, разрезанный на части. Для начала разделим круг на 4 равные части. Одна из этих частей будет равна одной четверти круга.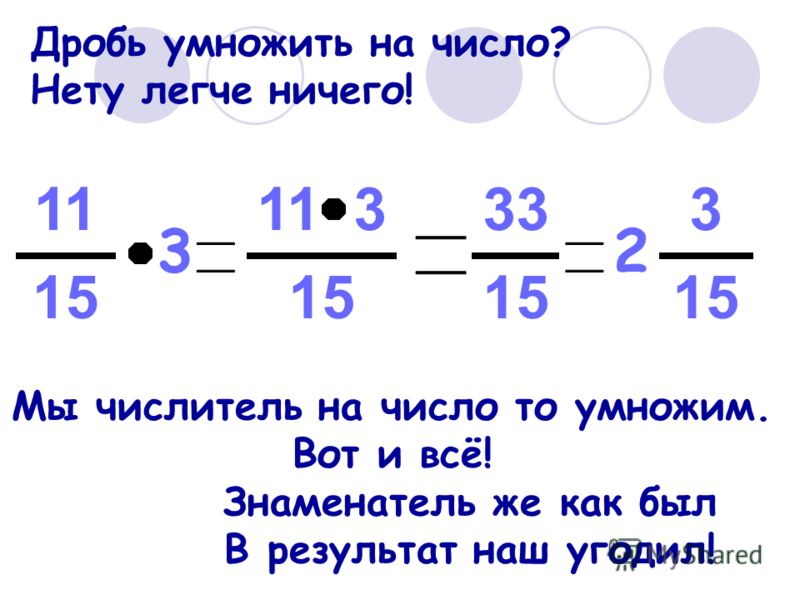
Если бы мы умножили эту ¼ на ½, то, что мы сделали бы математически, — это взяли бы ½ части ¼ или, по сути, разделили бы эту ¼ на две равные части. В конечном итоге это будет представлять ⅛ круга.
Математически это делается так:
Умножить числители вместе
[латекс]1\times1=1[/латекс]
И
Перемножить знаменатели вместе
[латекс]2\times4=8[/латекс]
В итоге получаем следующее:
[латекс]\БОЛЬШОЙ\dfrac{1}{2}\times\dfrac{1}{4}=\dfrac{1}{8}[/latex]
Вернемся к Эбигейл, Ханне и Наоми. Сейчас они прошли еще один уровень обучения и подходят к концу своего ученичества. Все трое работают над одним проектом — трехэтажным деревянным каркасным зданием, и каждый отвечает за черновую отделку 30 апартаментов. Каждую неделю они должны подключать ⅙ этих апартаментов. Однажды Ханне пришлось пропустить два дня. Таким образом, она работала только 3 из 5 дней, или ⅗ времени.
Начните с записи дробей, с которыми мы будем работать в этой ситуации.
[латекс]\dfrac{1}{6}\text{ Количество комплектов, которое необходимо выполнить в течение 5-дневной рабочей недели.}[/latex]
[latex]\dfrac{3}{5}\text{ Доля времени, отработанного в течение недели, 3 из 5 дней.}[/latex]
Затем умножьте две дроби вместе, придерживаясь нашей формулы умножение числителей вместе, а затем умножение знаменателей вместе.
[латекс]\НАИБОЛЬШИЙ\текст{числители }1\times3=3[/латекс]
[латекс]\НАИБОЛЬШИЙ\текст{знаменатели }6\times5=30[/латекс]
Таким образом, ответ:
[латекс]\БОЛЬШОЙ\dfrac{1}{6}\times\dfrac{3}{5}=\dfrac{3}{30}[/latex]
Который затем можно привести к наименьшим условиям:
[латекс]\БОЛЬШОЙ\dfrac{3}{30}\стрелка вправо\dfrac{1}{10}[/латекс]
Вот еще один пример. Давайте пройдемся по шагам в этом.
[латекс]\БОЛЬШОЙ\dfrac{5}{8}\times\dfrac{3}{4}=?[/latex]
Шаг 1 : Перемножьте числители.
[латекс]\НАИБОЛЬШИЙ5\times3=15[/латекс]
Шаг 2 : Перемножьте знаменатели.
[латекс]\НАИБОЛЬШИЙ8\times4=32[/латекс]
Шаг 3 : Поместите каждый из ответов в соответствующее место дроби.
[латекс]\БОЛЬШОЙ\dfrac{5}{8}\times\dfrac{3}{4}=\dfrac{15}{32}[/latex]
Шаг 4 : Поместите ответ в самый нижний термины, если необходимо, и изменить на смешанное число, если необходимо. В этом вопросе мы хороши с обеих сторон.
[латекс]\БОЛЬШОЙ\текст{Окончательный ответ}=\dfrac{15}{32}[/латекс]
До сих пор вы, возможно, думали, что получили это и это легко, но теперь давайте немного повысим уровень сложности.
[latex]\LARGE4\dfrac{2}{5}\times2\dfrac{1}{4}=?[/latex]
Прежде чем начать, вы видите проблему? Проблема в том, что вы сейчас пытаетесь перемножить два смешанных числа. Как это работает? Можете ли вы просто пойти дальше и попытаться умножить их такими, какие они есть? Ответ НЕТ, но решение проблемы не так сложно: вам просто нужно сделать один дополнительный шаг, прежде чем пройти через процесс.
Как это работает? Можете ли вы просто пойти дальше и попытаться умножить их такими, какие они есть? Ответ НЕТ, но решение проблемы не так сложно: вам просто нужно сделать один дополнительный шаг, прежде чем пройти через процесс.
Первое, что вам нужно сделать, это превратить каждое из смешанных чисел в неправильную дробь. С этого момента процесс такой же.
Шаг 1 : Превратите каждое из смешанных чисел в неправильную дробь. Это единственный способ ответить на этот вопрос. Вы не можете умножать числа в том состоянии, в котором они находятся.
[латекс]\НАИБОЛЬШИЙ4\dfrac{2}{5}=\dfrac{22}{5}[/latex]
(5 × 4 + 2 = 22 )
[латекс]\БОЛЬШОЙ2\dfrac{1}{4}=\dfrac{9}{4}[/латекс]
(4 × 2 + 1 = 9)
Шаг 2 : Перемножьте числители.
[латекс]\НАИБОЛЬШИЙ22\times9=198[/латекс]
Шаг 3 : Перемножьте знаменатели.
[латекс]\НАИБОЛЬШИЙ5\times4=20[/латекс]
Шаг 4 : Поместите каждый из ответов в соответствующее место дроби.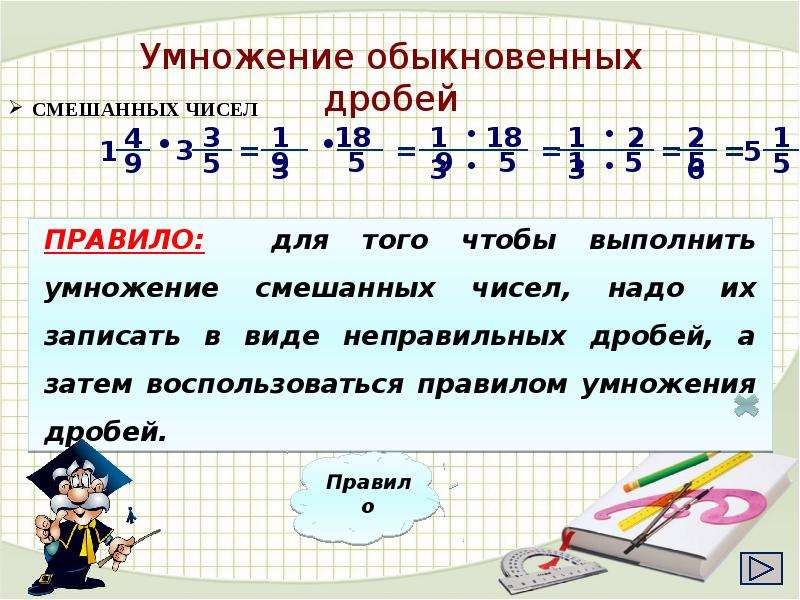
[латекс]\БОЛЬШОЙ\dfrac{22}{5}\times\dfrac{9}{4}=\dfrac{198}{20}[/latex]
Шаг 5 : Поместите ответ в самый нижний термины, если необходимо, и изменить на смешанное число, если необходимо. В этом случае мы должны сделать и то, и другое. Начнем с того, что представим дробь в наименьших условиях.
Тогда возьми это и составь смешанное число.
[латекс]\БОЛЬШОЙ\dfrac{99}{10}=9\dfrac{9}{10}\text{Смешанное число}[/latex]
Попробуйте сами задать пару вопросов. Убедитесь, что ваш ответ представлен в самом низком выражении, и, если необходимо, превратите его обратно в смешанное число. Когда закончите, посмотрите видеоответы, чтобы убедиться, что вы на правильном пути.
[латекс]\БОЛЬШОЙ\dfrac{4}{7}\times\dfrac{3}{8}=[/латекс]
[латекс]\БОЛЬШОЙ\dfrac{6}{11}\times\dfrac{5}{9}=[/latex]
[латекс]\БОЛЬШОЙ5\dfrac{1}{2}\times6\dfrac{3}{8}=[/латекс]
[латекс]\БОЛЬШОЙ7\dfrac{5}{9}\times8\dfrac{5}{7}=[/латекс]
2.
 2.1: Умножение дробей и смешанных чисел
2.1: Умножение дробей и смешанных чисел- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 61459
- Проект NROC
Цели обучения
- Умножение двух или более дробей.
- Умножить дробь на целое число.
- Умножить два или более смешанных числа.
- Решение прикладных задач, требующих умножения дробей или смешанных чисел.
Введение
Так же, как сложение, вычитание, умножение и деление при работе с целыми числами, вы также используете эти операции при работе с дробями. Есть много случаев, когда необходимо умножить дроби и смешанные числа . Например, по этому рецепту получится 4 коржа для пирога:
Например, по этому рецепту получится 4 коржа для пирога:
5 чашек крекеров
8 столовых ложек сахара
\(\ 1 \frac{1}{2}\) чашек растопленного сливочного масла
\(\ \frac{1 }{4}\) чайная ложка ванили
Предположим, вы хотите испечь только 2 коржа для пирога. Вы можете умножить все ингредиенты на \(\ \frac{1}{2}\), так как требуется только половина количества коржей. Научившись умножать дробь на другую дробь, целое число или смешанное число, вы сможете рассчитать ингредиенты, необходимые для 2 коржей для пирога.
Умножение дробей
Когда вы умножаете дробь на дробь, вы получаете «долю дроби». Предположим, у вас есть \(\ \frac{3}{4}\) шоколадного батончика, и вы хотите найти \(\ \frac{1}{2}\) из \(\ \frac{3}{4} }\):
Разделив каждую четверть пополам, вы можете разделить моноблок на восьмые части.
Затем выберите половину из них, чтобы получить \(\ \frac{3}{8}\).
В обоих вышеперечисленных случаях, чтобы найти ответ, вы можете перемножить числители вместе и знаменатели вместе.
Умножение двух дробей
\(\ \frac{a}{b} \cdot \frac{c}{d}=\frac{a \cdot c}{b \cdot d}=\frac{\text { произведение числителей }}{\text { произведение знаменателей }}\)
Пример:
\(\ \frac{3}{4} \cdot \frac{1}{2}=\frac{3 \cdot 1}{4 \cdot 2}=\frac{3}{8}\)
Умножение более двух дробей
\(\ \frac{a}{b} \cdot \frac{c}{d } \cdot \frac{e}{f}=\frac{a \cdot c \cdot e}{b \cdot d \cdot f}\)
Пример:
\(\ \frac{1}{3 } \cdot \frac{2}{4} \cdot \frac{3}{5}=\frac{1 \cdot 2 \cdot 3}{3 \cdot 4 \cdot 5}=\frac{6}{60 }\)
Пример
| \(\ \frac{2}{3} \cdot \frac{4}{5}\) | Умножение. |
Раствор
| \(\ \frac{2 \cdot 4}{3 \cdot 5}\) | Умножьте числители и умножьте знаменатели. |
| \(\ \frac{8}{15}\) | Упростите, если возможно. Эта фракция уже находится в наименьших условиях. Эта фракция уже находится в наименьших условиях. |
\(\ \frac{8}{15}\)
Если полученное произведение необходимо упростить до наименьших членов, разделите числитель и знаменатель на общие множители.
Пример
| \(\ \frac{2}{3} \cdot \frac{1}{4}\) | Умножение. Упростите ответ. |
Раствор
| \(\ \frac{2 \cdot 1}{3 \cdot 4}\) | Умножьте числители и умножьте знаменатели. |
| \(\ \frac{2}{12}\) | Упростите, если возможно. |
| \(\ \frac{2 \div 2}{12 \div 2}\) | Упростите, разделив числитель и знаменатель на общий множитель 2. |
\(\ \frac{2}{3} \cdot \frac{1}{4}=\frac{1}{6}\)
Вы также можете упростить задачу перед умножением, разделив общие факторы.
Пример
| \(\ \frac{2}{3} \cdot \frac{1}{4}\) | Умножение. Упростите ответ. |
Решение
| \(\ \frac{2 \cdot 1}{3 \cdot 4}=\frac{1 \cdot 2}{3 \cdot 4}\) | Переставьте числители так, чтобы вы увидели дробь с общим множителем. |
| \(\ \frac{1 \cdot 1}{3 \cdot 2}\) | Упростить. \(\ \frac{2}{4}=\frac{2 \div 2}{4 \div 2}=\frac{1}{2}\) |
\(\ \frac{2}{3} \cdot \frac{1}{4}=\frac{1}{6}\)
Вам не нужно использовать ярлык «сначала упростить» , но это может облегчить вашу работу, потому что числа в числителе и знаменателе будут меньше, пока вы работаете с ними.
Упражнение
\(\ \frac{3}{4} \cdot \frac{1}{3}\) Умножить. Упростите ответ.
Упростите ответ.
- \(\ \frac{3}{12}\)
- \(\ \фракция{4}{7}\)
- \(\ \фракция{1}{4}\)
- \(\ \фракция{36}{144}\)
- Ответить
- Неверно. \(\ \frac{3}{12}\) – это дробь, эквивалентная правильному ответу \(\ \frac{1}{4}\), но не в самом низком выражении. Вы должны разделить числитель и знаменатель на общий множитель 3. Правильный ответ: \(\ \frac{1}{4}\).
- Неверно. Возможно, вы добавили числители (3+1) и добавили знаменатели (4+3) вместо умножения. Правильный ответ: \(\ \frac{1}{4}\).
- Правильно. Один из способов найти этот ответ — перемножить числители и знаменатели, \(\ \frac{3 \cdot 1}{4 \cdot 3}=\frac{3}{12}\), а затем упростить: \(\ \frac {3 \div 3}{12 \div 3}=\frac{1}{4}\).
- Неверно. Вы наверное нашли общий знаменатель, правильно перемножили, но потом забыли упростить. Поиск общего знаменателя не обязателен и усложняет умножение, потому что вы работаете с большими, чем необходимо, числами.
 Правильный ответ: \(\ \frac{1}{4}\).
Правильный ответ: \(\ \frac{1}{4}\).
Умножение дроби на целое число
При работе как с дробями, так и с целыми числами полезно записывать целое число в виде неправильной дроби (дроби, в которой числитель больше или равен знаменателю). Все целые числа можно записать с «1» в знаменателе. Например: \(\ 2=\frac{2}{1}\), \(\ 5=\frac{5}{1}\) и \(\ 100=\frac{100}{1}\ ). Помните, что знаменатель говорит, сколько частей в одном целом, а числитель говорит, сколько частей у вас есть.
Умножение дроби на целое число
\(\ a \cdot \frac{b}{c}=\frac{a}{1} \cdot \frac{b}{c}\)
Пример:
\(\ 4 \cdot \frac{2}{3}=\frac{4}{1} \cdot \frac{2}{3}=\frac{8}{3}\)
Часто, когда умножив целое число на дробь, получится неправильная дробь. Часто желательно записать неправильные дроби в виде смешанного числа для окончательного ответа. Вы можете упростить дробь до или после переписывания ее в виде смешанного числа. См. примеры ниже.
См. примеры ниже.
Пример
| \(\ 7 \cdot \frac{3}{5}\) | Умножение. Упростите ответ и запишите в виде смешанного числа. |
Раствор
| \(\ \frac{7}{1} \cdot \frac{3}{5}\) | Перепишите число 7 в виде неправильной дроби \(\ \frac{7}{1}\). |
| \(\ \frac{7 \cdot 3}{1 \cdot 5}=\frac{21}{5}\) | Умножьте числители и умножьте знаменатели. |
| \(\ 4 \frac{1}{5}\) | Перепишите как смешанное число. \(\ 21 \div 5=4\) с остатком 1. |
\(\ 7 \cdot \frac{3}{5}=4 \frac{1}{5}\)
Пример
| \(\ 4 \cdot \frac{3} {4}\) | Умножение. Упростите ответ и запишите в виде смешанного числа. |
Решение
| \(\ \frac{4}{1} \cdot \frac{3}{4}\) | Перепишите число 4 в виде неправильной дроби \(\ \frac{4}{1}\). |
| \(\ \frac{4 \cdot 3}{1 \cdot 4}\) | Умножьте числители и умножьте знаменатели. |
| \(\ \frac{12}{4}=3\) | Упростить. |
\(\ 4 \cdot \frac{3}{4}=3\)
Упражнение
\(\ 3 \cdot \frac{5}{6}\) Умножить. Упростите ответ и запишите его в виде смешанного числа.
- \(\ 1 \frac{1}{7}\)
- \(\ 2 \frac{1}{2}\)
- \(\ \фракция{5}{2}\)
- \(\ \фракция{8}{6}\)
- Ответить
- Неверно. Возможно, вы добавили числители и добавили знаменатели, чтобы получить \(\ \frac{8}{7}\), которое является смешанным числом \(\ 1 \frac{1}{7}\).
 Убедитесь, что вы умножаете числители и умножаете знаменатели. Умножение двух чисел дает \(\ \frac{15}{6}\), а поскольку \(\ 15 \div 6=2 \mathrm{R} 3\), смешанное число равно \(\ 2 \frac {3}{6}\). Дробная часть упрощается до \(\ \frac{1}{2}\). Правильный ответ: \(\ 2 \frac{1}{2}\).
Убедитесь, что вы умножаете числители и умножаете знаменатели. Умножение двух чисел дает \(\ \frac{15}{6}\), а поскольку \(\ 15 \div 6=2 \mathrm{R} 3\), смешанное число равно \(\ 2 \frac {3}{6}\). Дробная часть упрощается до \(\ \frac{1}{2}\). Правильный ответ: \(\ 2 \frac{1}{2}\). - Правильно. Умножение двух чисел дает \(\ \frac{15}{6}\), а поскольку \(\ 15 \div 6=2 \mathrm{R} 3\), смешанное число равно \(\ 2 \frac{ 3}{6}\). Дробная часть упрощается до \(\ \frac{1}{2}\).
- Неверно. Умножение числителей и умножение знаменателей приводит к неправильной дроби \(\ \frac{5}{2}\), но вам нужно выразить это как смешанное число. Правильный ответ: \(\ 2 \frac{1}{2}\).
- Неверно. Возможно, вы добавили числители и поместили их над знаменателем числа 6. Убедитесь, что вы умножаете числители и умножаете знаменатели. Умножение двух чисел дает \(\ \frac{15}{6}\), а поскольку \(\ 15 \div 6=2 \mathrm{R} 3\), смешанное число равно \(\ 2 \frac{ 3}{6}\).
 Дробная часть упрощается до \(\ \frac{1}{2}\). Правильный ответ: \(\ 2 \frac{1}{2}\).
Дробная часть упрощается до \(\ \frac{1}{2}\). Правильный ответ: \(\ 2 \frac{1}{2}\).
- Неверно. Возможно, вы добавили числители и добавили знаменатели, чтобы получить \(\ \frac{8}{7}\), которое является смешанным числом \(\ 1 \frac{1}{7}\).
Умножение смешанных чисел
Если вы хотите умножить два смешанных числа или дробь и смешанное число, вы можете снова переписать любое смешанное число как неправильную дробь.
Итак, чтобы умножить два смешанных числа, запишите каждое из них как неправильную дробь, а затем умножьте, как обычно. Умножьте числители и умножьте знаменатели и упростите. И, как и раньше, при упрощении, если ответ выходит неправильной дробью, то переводить ответ в смешанное число.
Пример
| \(\ 2 \frac{1}{5} \cdot 4 \frac{1}{2}\) | Умножение. Упростите ответ и запишите в виде смешанного числа. |
Раствор
| \(\ 2 \frac{1}{5}=\frac{11}{5}\) | Замените 2 \(\ \frac{1}{5}\) на неправильную дробь. \(\ 5 \cdot 2+1=11\), а знаменатель равен 5. \(\ 5 \cdot 2+1=11\), а знаменатель равен 5. |
| \(\ 4 \frac{1}{2}=\frac{9{2}\) | Замените \(\ 4 \frac{1}{2}\) на неправильную дробь. \(\ 2 \cdot 4+1=9\), а знаменатель равен 2. |
| \(\ \frac{11}{5} \cdot \frac{9}{2}\) | Перепишите задачу на умножение, используя неправильные дроби. |
| \(\ \frac{11 \cdot 9}{5 \cdot 2}=\frac{99}{10}\) | Умножение числителей и умножение знаменателей. |
| \(\ \frac{99}{10}=9 \фракция{9}{10}\) | Запишите как смешанное число. \(\ 99 \div 10=9\) с остатком 9. |
\(\ 2 \frac{1}{5} \cdot 4 \frac{1}{2}=9 \frac{9}{10}\)
Пример
| \( \ \frac{1}{2} \cdot 3 \frac{1}{3}\) | Умножение. Упростите ответ и запишите в виде смешанного числа. |
Раствор
| \(\ 3 \frac{1}{3}=\frac{10}{3}\) | Замените \(\ 3 \frac{1}{3}\) на неправильную дробь. \(\ 3 \cdot 3+1=10\), а знаменатель равен 3. \(\ 3 \cdot 3+1=10\), а знаменатель равен 3. |
| \(\ \frac{1}{2} \cdot \frac{10}{3}\) | Перепишите задачу на умножение, используя неправильную дробь вместо смешанного числа. |
| \(\ \frac{1 \cdot 10}{2 \cdot 3}=\frac{10}{6}\) | Умножение числителей и умножение знаменателей. |
| \(\ \frac{10}{6}=1 \frac{4}{6}\) | Перепишите как смешанное число. \(\ 10 \div 6=1\) с остатком 4. |
| \(\ 1 \frac{2}{3}\) | Упростите дробную часть до меньших членов, разделив числитель и знаменатель на общий множитель 2. |
\(\ \frac{1}{2} \cdot 3 \frac{1}{3}=1 \frac{2}{3}\)
Как вы видели ранее, иногда полезно посмотреть для общих делителей в числителе и знаменателе, прежде чем упростить продукты.
Пример
| \(\ 1 \frac{3}{5} \cdot 2 \frac{1}{4}\) | Умножение. Упростите ответ и запишите в виде смешанного числа. Упростите ответ и запишите в виде смешанного числа. |
Раствор
| \(\ 1 \frac{3}{5}=\frac{8}{5}\) | Замените \(\ 1 \frac{3}{5}\) на неправильную дробь. \(\ 5 \cdot 1+3=8\), а знаменатель равен 5. |
| \(\ 2 \frac{1}{4}=\frac{9{4}\) | Замените \(\ 2 \frac{1}{4}\) на неправильную дробь. \(\ 4 \cdot 2+1=9\), а знаменатель равен 4. |
| \(\ \frac{8}{5} \cdot \frac{9}{4}\) | Перепишите задачу на умножение, используя неправильные дроби. |
| \(\ \frac{8 \cdot 9}{5 \cdot 4}=\frac{9 \cdot 8}{5 \cdot 4}\) | Переставьте числители так, чтобы вы увидели дробь с общим множителем. |
| \(\ \frac{9 \cdot 8}{5 \cdot 4}=\frac{9 \cdot 2}{5 \cdot 1}\) | Упростить. \(\ \frac{8}{4}=\frac{8 \div 4}{4 \div 4}=\frac{2}{1}\) |
| \(\ \frac{18}{5}\) | Умножить.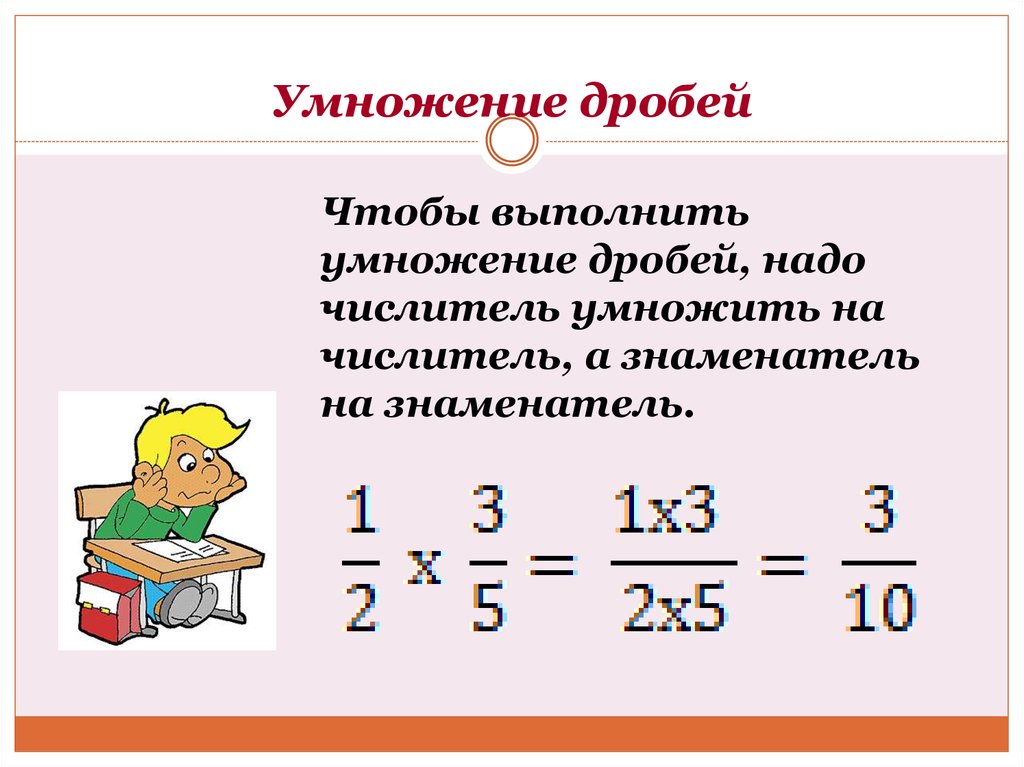 |
| \(\ \frac{18}{5}=3 \frac{3}{5}\) | Запишите в виде смешанной дроби. |
\(\ 1 \frac{3}{5} \cdot 2 \frac{1}{4}=3 \frac{3}{5}\)
В последнем примере тот же ответ будет можно найти, если перемножить числители и знаменатели, не удаляя общий множитель. Однако вы получите \(\ \frac{72}{20}\), а затем вам нужно будет еще упростить, чтобы получить окончательный ответ.
Упражнение
\(\ 1 \frac{3}{5} \cdot 3 \frac{1}{3}\)
- \(\ \frac{80}{15}\)
- \(\ 5 \фрак{5}{15}\)
- \(\ 4 \фрак{14}{15}\)
- \(\ 5 \фрак{1}{3}\)
- Ответить
- Неверно. Вероятно, вы правильно записали оба смешанных числа в виде неправильных дробей. Вы, вероятно, также правильно перемножили числители и знаменатели. Однако эту неправильную дробь еще нужно переписать как смешанное число и упростить.
 Деление \(\ 80 \div 15=5\) с остатком 5 или \(\ 5 \frac{5}{15}\), затем упрощение дробной части, правильный ответ \(\ 5 \frac{ 1}{3}\).
Деление \(\ 80 \div 15=5\) с остатком 5 или \(\ 5 \frac{5}{15}\), затем упрощение дробной части, правильный ответ \(\ 5 \frac{ 1}{3}\). - Неверно. Вероятно, вы правильно записали оба смешанных числа в виде неправильных дробей. Вы наверное тоже правильно перемножили числители и знаменатели, а ответ записали как смешанное число. Однако смешанное число не является самым низким. \(\ \frac{5}{15}\) можно упростить до \(\ \frac{1}{3}\) путем деления числителя и знаменателя на общий делитель 5. Правильный ответ: \(\ 5 \ дробь{1}{3}\).
- Неверно. Это результат сложения двух чисел. Чтобы умножить, запишите каждое смешанное число как неправильную дробь: \(\ 1 \frac{3}{5}=\frac{8}{5}\) и \(\ 3 \frac{1}{3}=\ гидроразрыв{10}{3}\). Затем умножьте числители и умножьте знаменатели: \(\ \frac{8}{5} \cdot \frac{10}{3}=\frac{80}{15}\). Затем запишите полученную неправильную дробь в виде смешанного числа: \(\ \frac{80}{15}=5 \frac{5}{15}\). Наконец, упростите дробную часть, разделив числитель и знаменатель на общий множитель 5.
 Правильный ответ: \(\ 5 \frac{1}{3}\).
Правильный ответ: \(\ 5 \frac{1}{3}\). - Правильно. Сначала перепишем каждое смешанное число в виде неправильной дроби: \(\ 1 \frac{3}{5}=\frac{8}{5}\) и \(\ 3 \frac{1}{3}=\frac {10}{3}\). Затем умножьте числители и умножьте знаменатели: \(\ \frac{8}{5} \cdot \frac{10}{3}=\frac{80}{15}\). Затем запишите в виде смешанной дроби \(\ \frac{80}{15}=5 \frac{5}{15}\). Наконец, упростите дробную часть, разделив и числитель, и знаменатель на общий множитель 5.
- Неверно. Вероятно, вы правильно записали оба смешанных числа в виде неправильных дробей. Вы, вероятно, также правильно перемножили числители и знаменатели. Однако эту неправильную дробь еще нужно переписать как смешанное число и упростить.
Решение задач на умножение дробей и смешанных чисел
Теперь, когда вы знаете, как умножать дробь на другую дробь, на целое число или на смешанное число, вы можете использовать эти знания для решения задач, связанных с умножением и дробными числами. Например, теперь вы можете рассчитать ингредиенты, необходимые для 2 крошек для пирога.
Пример
| 5 чашек крекеров 8 столовых ложек сахара \(\ 1 \frac{1}{2}\) чашек растопленного масла \(\ \frac{1}{4}\) чайная ложка ванили | Рецепт слева рассчитан на 4 коржа. Найдите ингредиенты, необходимые для приготовления только 2 коржей для пирога. Найдите ингредиенты, необходимые для приготовления только 2 коржей для пирога. |
Решение
| Поскольку рецепт рассчитан на 4 коржа, вы можете умножить каждый из ингредиентов на \(\ \frac{1}{2}\), чтобы найти размеры только для 2 коржей. | |
\(\ 5 \cdot \frac{1}{2}=\frac{5}{1} \cdot \frac{1}{2}=\frac{5}{2}\) Требуется\(\ 2 \frac{1}{2}\) стаканов крекеров. | 5 чашек крекеров Грэма: так как результатом является неправильная дробь, перепишите \(\ \frac{5}{2}\) как неправильную дробь \(\ 2 \frac{1}{2}\). |
\(\ 8 \cdot \frac{1}{2}=\frac{8}{1} \cdot \frac{1}{2}=\frac{8}{2}=4\) Необходимо 4 столовые ложки сахара. | 8 столовых ложек сахара: Это еще один пример умножения целого числа на дробь. |
\(\ \frac{3}{2} \cdot \frac{1}{2}=\frac{3}{4}\) Требуется\(\ \frac{3}{4}\) стакана топленого масла. | \(\ 1 \frac{1}{2}\) стаканов топленого масла: нужно умножить смешанное число на дробь. Итак, сначала перепишем \(\ 1 \frac{1}{2}\) как неправильную дробь \(\ \frac{3}{2}\): \(\ 2 \cdot 1+1\), а знаменатель равен 2. Затем перепишите задачу на умножение, используя неправильную дробь вместо смешанного числа. Умножить. |
\(\ \frac{1}{4} \cdot \frac{1}{2}=\frac{1}{8}\) Требуется\(\ \frac{1}{8}\) чайной ложки ванили. | \(\ \frac{1}{4}\) чайная ложка ванили: Здесь вы умножаете дробь на дробь. |
Ингредиенты, необходимые для 2 корок для пирога:
\(\ 2 \frac{1}{2}\) стаканов крекеров
4 столовые ложки сахара
\(\ \frac{3}{4} \) стакан топленого масла
\(\ \frac{1}{8}\) чайная ложка ванили
Часто задача указывает на необходимость умножения на дробь с использованием таких фраз, как «половина», «треть» или «\( \ \frac{3}{4}\) of. »
»
Пример
Стоимость отпуска составляет \(\ \$ 4500\), и вы должны заплатить \(\ \frac{1}{5}\) этой суммы при бронировании поездки. Сколько вам придется заплатить при бронировании поездки?
Раствор
| \(\ 4500 \cdot \frac{1}{5}\) | Вам нужно найти \(\ \frac{1}{5}\) из 4500. «Из» говорит вам умножать. |
| \(\ \frac{4,500}{1} \cdot \frac{1}{5}\) | Замените 4500 неправильной дробью, переписав ее с 1 в знаменателе. |
| \(\ \frac{4,500}{5}\) | Разделить. |
| \(\ 900\) | Упростить. |
Вам нужно будет заплатить \(\ \$ 900\) при бронировании поездки.
Пример
Круговая диаграмма слева представляет дробную часть ежедневной деятельности. Учитывая 24-часовой день, сколько часов тратится на сон? Посещение школы? Принимать пищу? Используйте круговую диаграмму, чтобы определить свои ответы. |
Решение
| \(\ \frac{1}{3} \cdot 24\) = количество часов сна | Сон — это \(\ \frac{1}{3}\) части пирога, поэтому количество часов, потраченных на сон, равно \(\ \frac{1}{3}\) из 24. |
| \(\ \frac{1}{3} \cdot \frac{24}{1}=8\) | Перепишите 24 в виде неправильной дроби со знаменателем 1. |
\(\ \frac{24}{3}=8\) 8 часов сна | Умножение числителей и умножение знаменателей. Упростить \(\ \frac{24}{3}\) до 8. |
| \(\ \frac{1}{6} \cdot 24\) = количество часов, проведенных в школе | Посещение школы — это \(\ \frac{1}{6}\) круга, поэтому количество часов, проведенных в школе, равно \(\ \frac{1}{6}\) из 24. |
| \(\ \frac{1}{6} \cdot \frac{24}{1}\) | Перепишите 24 в виде неправильной дроби со знаменателем 1. |
\(\ \frac{24}{6}=4\) 4 часов посещения школы | Умножение числителей и умножение знаменателей. Упростить \(\ \frac{24}{6}\) до 4. |
| \(\ \frac{1}{12} \cdot 24\) = количество часов, потраченных на еду | Еда равна \(\ \frac{1}{12}\) пирога, поэтому количество часов, проведенных за едой, равно \(\ \frac{1}{12}\) из 24. |
| \(\ \frac{1}{12} \cdot \frac{24}{1}\) | Перепишите 24 в виде неправильной дроби со знаменателем 1. |
\(\ \frac{24}{12}=2\) 2 часов, потраченных на еду | Умножение числителей и умножение знаменателей. Упростите \(\ \frac{24}{12}\) до 2. Упростите \(\ \frac{24}{12}\) до 2. |
Проведено часов:
сна: 8 часов
посещение школы: 4 часа
прием пищи: 2 часа
упражнения
Нейл купил дюжину (12) яиц. Он использовал \(\ \frac{1}{3}\) яиц на завтрак. Сколько яиц осталось?
- 8
- 4
- 9
- 3
- Ответить
- Правильно. \(\ \frac{1}{3}\) из 12 равно \(\ 4\left(\frac{1}{3} \cdot \frac{12}{1}=\frac{12}{3} =4\справа)\), поэтому он использовал 4 яйца. Поскольку \(\ 12-4=8\), осталось 8 яиц.
- Неверно. \(\ \frac{1}{3}\) от 12 равно 4, но это показывает, сколько яиц использовал Нейл, а не сколько у него осталось. Вам нужно вычесть 4 из 12, чтобы найти количество оставшихся яиц. Правильный ответ 8.
- Неверно. Возможно, вы ошибочно обнаружили, что \(\ \frac{1}{3}\) от 12 равно \(\ \text { 3. } \frac{1}{3}\) от 12 равно 4, а затем 12- 4 равно 8.

 В нашем примере для дроби 2/4 НОД=2, поэтому разделите и числитель, и знаменатель на 2.
В нашем примере для дроби 2/4 НОД=2, поэтому разделите и числитель, и знаменатель на 2.
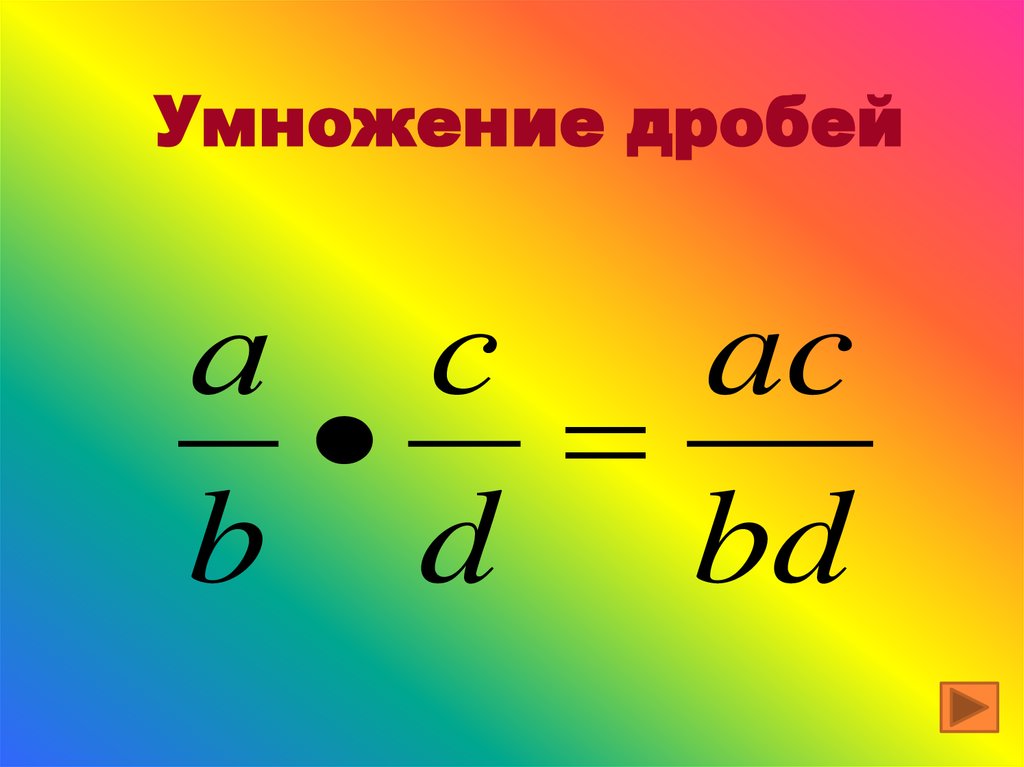 Это число, которое делится на делитель с получением числа больше или равного 1. …
Это число, которое делится на делитель с получением числа больше или равного 1. … Правильный ответ: \(\ \frac{1}{4}\).
Правильный ответ: \(\ \frac{1}{4}\). Убедитесь, что вы умножаете числители и умножаете знаменатели. Умножение двух чисел дает \(\ \frac{15}{6}\), а поскольку \(\ 15 \div 6=2 \mathrm{R} 3\), смешанное число равно \(\ 2 \frac {3}{6}\). Дробная часть упрощается до \(\ \frac{1}{2}\). Правильный ответ: \(\ 2 \frac{1}{2}\).
Убедитесь, что вы умножаете числители и умножаете знаменатели. Умножение двух чисел дает \(\ \frac{15}{6}\), а поскольку \(\ 15 \div 6=2 \mathrm{R} 3\), смешанное число равно \(\ 2 \frac {3}{6}\). Дробная часть упрощается до \(\ \frac{1}{2}\). Правильный ответ: \(\ 2 \frac{1}{2}\). Дробная часть упрощается до \(\ \frac{1}{2}\). Правильный ответ: \(\ 2 \frac{1}{2}\).
Дробная часть упрощается до \(\ \frac{1}{2}\). Правильный ответ: \(\ 2 \frac{1}{2}\). Деление \(\ 80 \div 15=5\) с остатком 5 или \(\ 5 \frac{5}{15}\), затем упрощение дробной части, правильный ответ \(\ 5 \frac{ 1}{3}\).
Деление \(\ 80 \div 15=5\) с остатком 5 или \(\ 5 \frac{5}{15}\), затем упрощение дробной части, правильный ответ \(\ 5 \frac{ 1}{3}\). Правильный ответ: \(\ 5 \frac{1}{3}\).
Правильный ответ: \(\ 5 \frac{1}{3}\).
