Деления столбиком пример: Онлайн калькулятор. Деление столбиком.

Содержание

Деление столбиком сокращенная запись калькулятор. Умножение и деление в столбик: примеры

Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком .

Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:

За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:

Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:

Под делимым будут записываться промежуточные вычисления:

Полностью форма записи деления столбиком выглядит следующим образом:

Как делить столбиком

Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:

Деление столбиком выполняется поэтапно.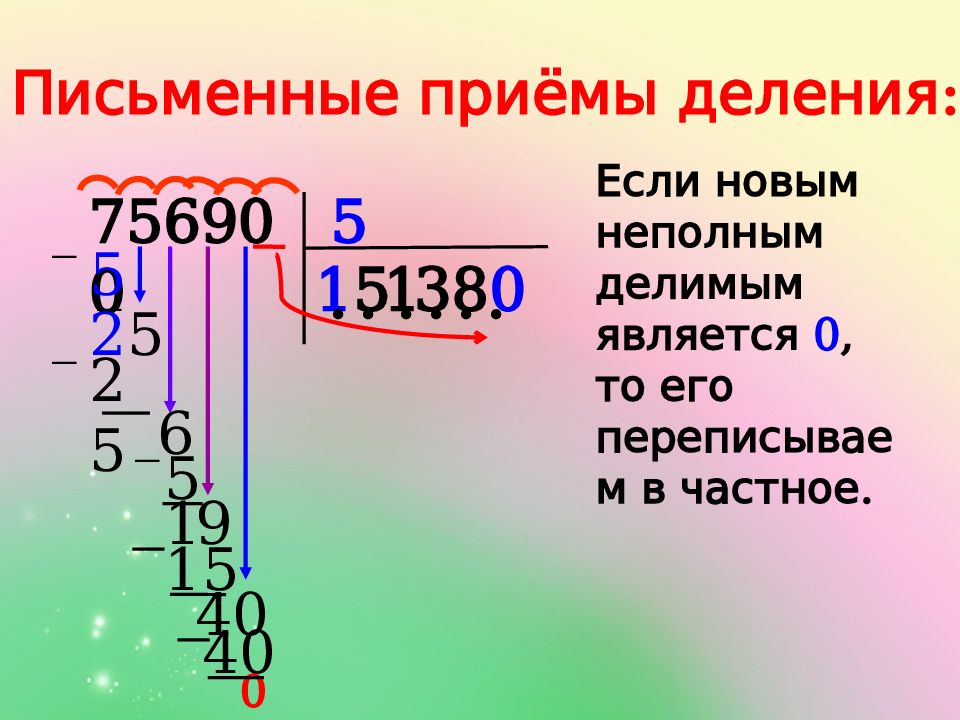

Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:

это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:

В нашем случае число 78 будет неполным делимым , неполным оно называется потому, что является всего лишь частью делимого.

Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.

Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:

Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78.

Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:

Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.

К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:

Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:

Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.

Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:

Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0: 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:

Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:

Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:

Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:

Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.

Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:

Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:

Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:

Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:

Деление столбиком с остатком

Пусть нам требуется разделить 1340 на 23.

Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:

Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:

Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:

1340: 23 = 58 (остаток 6)

Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:

3: 10 = 0 (остаток 3)

Калькулятор деления столбиком

Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.

Как делить десятичные дроби на натуральные числа? Рассмотрим правило и его применение на примерах.

Чтобы разделить десятичную дробь на натуральное число, надо:

1) разделить десятичную дробь на число, не обращая внимания на запятую;

2) когда закончится деление целой части, в частном поставить запятую.

Примеры.

Разделить десятичные дроби:

Чтобы разделить десятичную дробь на натуральное число, делим, не обращая внимания на запятую. 5 на 6 не делится, поэтому в частном ставим нуль. Деление целой части окончено, в частном ставим запятую. Сносим нуль. 50 делим на 6. Берем по 8. 6∙8=48. От 50 вычитаем 48, в остатке получаем 2. Сносим 4. 24 делим на 6. Получаем 4. В остатке — нуль, значит, деление окончено: 5,04: 6 = 0,84.

2) 19,26: 18

Делим десятичную дробь на натуральное число, не обращая внимания на запятую. Делим 19 на 18. Берем по 1. Деление целой части окончено, в частном ставим запятую. Вычитаем от 19 18. В остатке — 1. Сносим 2. 12 на 18 не делится, в частном пишем нуль. Сносим 6. 126 делим на 18, получаем 7. Деление окончено: 19,26: 18 = 1,07.

Делим 86 на 25. Берем по 3. 25∙3=75. От 86 вычитаем 75. В остатке — 11. Деление целой части окончено, в частном ставим запятую. Сносим 5. Берем по 4. 25∙4=100. От 115 вычитаем 100. Остаток — 15. Сносим нуль. 150 делим на 25. Получаем 6. Деление окончено: 86,5: 25 = 3,46.

4) 0,1547: 17

Нуль на 17 не делится, в частном пишем нуль. Деление целой части окончено, в частном ставим запятую. Сносим 1. 1 на 17 не делится, в частном пишем нуль. Сносим 5. 15 на 17 не делится, в частном пишем нуль. Сносим 4. Делим 154 на 17. Берем по 9. 17∙9=153. От 154 вычитаем 153. В остатке — 1. Сносим 7. Делим 17 на 17. Получаем 1. Деление окончено: 0,1547: 17 = 0,0091.

5) Десятичная дробь может получиться и при делении двух натуральных чисел.

При делении 17 на 4 берем по 4. Деление целой части окончено, в частном ставим запятую. 4∙4=16. От 17 вычитаем 16. Остаток — 1. Сносим нуль. 10 делим на 4. Берем по 2. 4∙2=8. От 10 вычитаем 8. В остатке — 2. Сносим нуль. 20 делим на 4.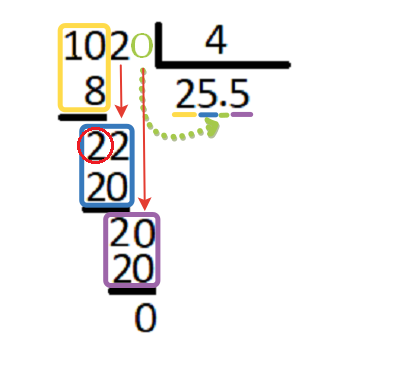

Берем по 5. Деление окончено: 17: 4 = 4,25.

И еще пара примеров на деление десятичных дробей на натуральные числа:

Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.

Деление – интересная операция, в чем мы и убедимся с вами в этой статье!

Деление чисел

Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.

Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.

Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».

Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.

Деление с остатком

Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.

Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).

Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).

Деление на 3 и 9

Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:

Найти сумму цифр делимого.

Поделить на 3 или 9 (в зависимости от того, что вам нужно).

Если ответ получается без остатка, то и число поделится без остатка.

Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.

Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.

Умножение и деление

Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.

Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.

Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.

Деление 3 класс

В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:

Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?

Задача 2 . На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?

Задача 3 .

Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?

Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?

Деление 4 класс

Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:

Деление в столбик

Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.

Рассмотрим пример, 512:8.

1 шаг . Запишем делимое и делитель следующим образом:

Частное будет записано в итоге под делителем, а расчеты под делимым.

2 шаг . Деление начинаем слева направо. Сначала берем цифру 5:

3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:

Теперь 51 больше 8. Это неполное частное.

4 шаг . Ставим точку под делителем.

5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:

6 шаг . Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:

7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»:

8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3.

* 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3:

10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.

Итак, ответ 64, без остатка.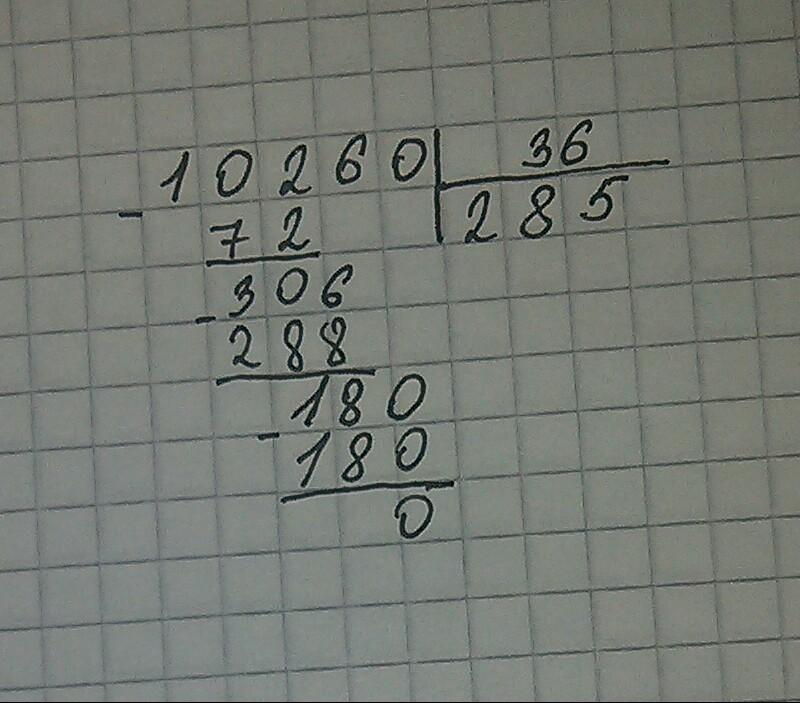 Если бы делили число 513, то в остатке была бы единица.

Деление трехзначных

Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.

Деление дробей

Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):

Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.

Деление числа на классы

Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.

Деление натуральных чисел

Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.

Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Деление презентация

Презентация – еще один способ наглядно показать тему деления.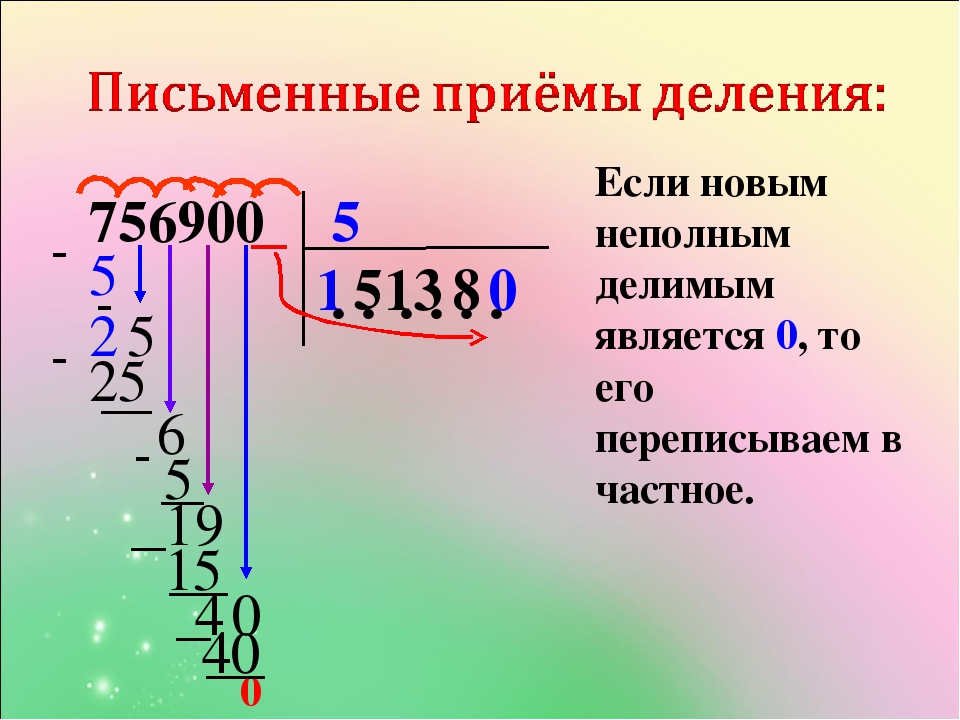 Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!

Примеры на деление

Легкий уровень

Средний уровень

Сложный уровень

Игры на развитие устного счета

Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.

Игра «Угадай операцию»

Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Упрощение»

Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Быстрое сложение»

Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Визуальная геометрия»

Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Копилка»

Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.

Игра «Быстрое сложение перезагрузка»

Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.

Развитие феноменального устного счета

Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.

Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

Скорочтение за 30 дней

Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.

Развитие памяти и внимания у ребенка 5-10 лет

В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера. Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.

Супер-память за 30 дней

Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.

Секреты фитнеса мозга, тренируем память, внимание, мышление, счет

Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.

Деньги и мышление миллионера

Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.

Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.

Один из важных этапов в обучении ребёнка математическим действиям – обучение операции деления простых чисел. Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?

Для того чтобы научить ребёнка делению, необходимо, чтобы он к моменту обучения уже освоил такие математические операции, как сложение, вычитание, а также имел чёткое представление о самой сущности действий умножения и деления. То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.

Я уже писала о том, Эта статья может стать для вас полезной.

Осваиваем операцию разделения (деления) на части в игровой форме

На этом этапе необходимо сформировать у ребёнка понимание того, что деление – это разделение чего-либо на равные части. Самый просто способ научить ребёнка этому – предложить ему разделить некоторое количество предметов между ним его друзьями или членами семьи.

Допустим, возьмите 8 одинаковых кубиков и предложите ребёнку разделить на две равные части – для него и другого человека. Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.

Важно: Следите, чтобы вначале ребёнок оперировал с чётным количеством предметов, для того, чтобы результатом деления было одинаковое количество частей. Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.

Умножаем и делим, используя таблицу умножения

Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.

Пример: 4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.

Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.

Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!

По сути, вам нужно научить ребёнка таблице умножения «наоборот», и запомнить её необходимо так же хорошо, как и саму таблицу умножения, ведь это будет необходимым, когда вы начнёте обучение делению в столбик.

Делим столбиком – приведем пример

Перед началом занятия вспомните вместе с ребёнком, как называются цифры в процессе операции деления. Что является «делителем», «делимым», «частным»? Научите безошибочно и быстро определять эти категории. Это будет очень полезным во время обучения ребёнка делению простых чисел.

Объясняем наглядно

Давайте разделим 938 на 7. В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить.

Шаг 1 . Записываем числа, разделив их «уголком».

Шаг 2. Покажите ученику числа делимого и предложите ему, выбрать из них то наименьшее число, которое окажется больше делителя. Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.

Шаг 3. Переходим к оформлению деления столбиком:

Умножаем делитель 7х1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.

Записываем результат.

Шаг 4. Число, которое мы видим, меньше делителя, поэтому необходимо его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.

Шаг 5. Далее действуем по уже известному алгоритму. Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7*3) записываем внизу под числом 23 в столбик.

Шаг.6 Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.

Из делимого у нас осталась неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.

Шаг.7 Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное= 134.

Как научить ребенка делению – закрепляем навык

Главное из-за чего у многих школьников возникает проблема с математикой — это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме — необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.

«Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
«Деление. Уровень 4. Рабочая тетрадь» от Kumon
«Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина — автора обучающих книг-бестселлеров

Самым главным, когда вы учите ребёнка делению в столбик, является усвоение алгоритма, который, в общем-то, достаточно прост.

Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей. Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.

Для того чтобы легко научить ребёнка операции деления нужно:

Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть». У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.

Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.

Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т.д.) во время конструирования, игр и наблюдений за природой.

Преподаватель, специалист детского развивающего центра
Дружинина Елена
специально для проекта сайт

Видео сюжет для родителей, как правильно объяснить ребенку деление в столбик:

Деление натуральных чисел, особенно многозначных, удобно проводить особым методом, который получил название деление столбиком (в столбик) . Также можно встретить название деление уголком . Сразу отметим, что столбиком можно проводить как деление натуральных чисел без остатка , так и деление натуральных чисел с остатком .

В этой статье мы разберемся, как выполняется деление столбиком. Здесь мы поговорим и о правилах записи, и о всех промежуточных вычислениях. Сначала остановимся на делении столбиком многозначного натурального числа на однозначное число. После этого остановимся на случаях, когда и делимое и делитель являются многозначным натуральными числами. Вся теория этой статьи снабжена характерными примерами деления столбиком натуральных чисел с подробными пояснениями хода решения и иллюстрациями.

Навигация по странице.

Правила записи при делении столбиком

Начнем с изучения правил записи делимого, делителя, всех промежуточных выкладок и результатов при делении натуральных чисел столбиком. Сразу скажем, что письменно выполнять деление столбиком удобнее всего на бумаге с клетчатой разлиновкой – так меньше шансов сбиться с нужной строки и столбца.

Сначала в одной строке слева направо записываются делимое и делитель, после чего между записанными числами изображается символ вида . Например, если делимым является число 6 105 , а делителем – 5 5, то их правильная запись при делении в столбик будет такой:

Посмотрите на следующую схему, иллюстрирующую места для записи делимого, делителя, частного, остатка и промежуточных вычислений при делении столбиком.

Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже делимого, и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше потребуется места. Например, при делении столбиком натурального числа 614 808 на 51 234 (614 808 – шестизначное число, 51 234 – пятизначное число, разница в количестве знаков в записях равна 6−5=1 ) для промежуточных вычислений потребуется меньше места, чем при делении чисел 8 058 и 4 (здесь разница в количестве знаков равна 4−1=3 ). Для подтверждения своих слов приводим законченные записи деления столбиком этих натуральных чисел:

Теперь можно переходить непосредственно к процессу деления натуральных чисел столбиком.

Деление столбиком натурального числа на однозначное натуральное число, алгоритм деления столбиком

Понятно, что разделить одно однозначное натуральное число на другое достаточно просто, и делить эти числа в столбик нет причин. Однако будет полезно отработать начальные навыки деления столбиком на этих простых примерах.

Пример.

Пусть нам нужно разделить столбиком 8 на 2 .

Решение.

Конечно, мы можем выполнить деление при помощи таблицы умножения , и сразу записать ответ 8:2=4 .

Но нас интересует, как выполнить деление этих чисел столбиком.

Сначала записываем делимое 8 и делитель 2 так, как того требует метод:

Теперь мы начинаем выяснять, сколько раз делитель содержится в делимом. Для этого мы последовательно умножаем делитель на числа 0 , 1 , 2 , 3 , … до того момента, пока в результате не получим число, равное делимому, (либо число большее, чем делимое, если имеет место деление с остатком). Если мы получаем число равное делимому, то сразу записываем его под делимым, а на место частного записываем число, на которое мы умножали делитель. Если же мы получаем число большее, чем делимое, то под делителем записываем число, вычисленное на предпоследнем шаге, а на место неполного частного записываем число, на которое умножался делитель на предпоследнем шаге.

Поехали: 2·0=0 ; 2·1=2 ; 2·2=4 ; 2·3=6 ; 2·4=8 . Мы получили число, равное делимому, поэтому записываем его под делимым, а на место частного записываем число 4 . При этом запись примет следующий вид:

Остался завершающий этап деления однозначных натуральных чисел столбиком. Под числом, записанным под делимым, нужно провести горизонтальную черту, и провести вычитание чисел над этой чертой так, как это делается при вычитании натуральных чисел столбиком . Число, получающееся после вычитания, будет остатком от деления. Если оно равно нулю, то исходные числа разделились без остатка.

В нашем примере получаем

Теперь перед нами законченная запись деления столбиком числа 8 на 2 . Мы видим, что частное 8:2 равно 4 (и остаток равен 0 ).

Ответ:

8:2=4 .

Теперь рассмотрим, как осуществляется деление столбиком однозначных натуральных чисел с остатком.

Пример.

Разделим столбиком 7 на 3 .

Решение.

На начальном этапе запись выглядит так:

Начинаем выяснять, сколько раз в делимом содержится делитель. Будем умножать 3 на 0 , 1 , 2 , 3 и т.д. до того момента, пока не получим число равное или большее, чем делимое 7 . Получаем 3·0=07 (при необходимости обращайтесь к статье сравнение натуральных чисел). Под делимым записываем число 6 (оно получено на предпоследнем шаге), а на место неполного частного записываем число 2 (на него проводилось умножение на предпоследнем шаге).

Осталось провести вычитание, и деление столбиком однозначных натуральных чисел 7 и 3 будет завершено.

Таким образом, неполное частное равно 2 , и остаток равен 1 .

Ответ:

7:3=2 (ост. 1) .

Теперь можно переходить к делению столбиком многозначных натуральных чисел на однозначные натуральные числа.

Сейчас мы разберем алгоритм деления столбиком . На каждом его этапе мы будем приводить результаты, получающиеся при делении многозначного натурального числа 140 288 на однозначное натуральное число 4 . Этот пример выбран не случайно, так как при его решении мы столкнемся со всеми возможными нюансами, сможем подробно разобрать их.

Сначала мы смотрим на первую слева цифру в записи делимого. Если число, определяемое этой цифрой, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого, и работать дальше с числом, определяемым двумя рассматриваемыми цифрами. Для удобства выделим в нашей записи число, с которым мы будем работать.

Первой слева цифрой в записи делимого 140 288 является цифра 1 . Число 1 меньше, чем делитель 4 , поэтому смотрим еще и на следующую слева цифру в записи делимого. При этом видим число 14 , с которым нам и предстоит работать дальше. Выделяем это число в записи делимого.

Следующие пункты со второго по четвертый повторяются циклически, пока деление натуральных чисел столбиком не будет завершено.

Сейчас нам нужно определить, сколько раз делитель содержится в числе, с которым мы работаем (для удобства обозначим это число как x ). Для этого последовательно умножаем делитель на 0 , 1 , 2 , 3 , … до того момента, пока не получим число x или число больше, чем x . Когда получается число x , то мы записываем его под выделенным числом по правилам записи, используемым при вычитании столбиком натуральных чисел. Число, на которое проводилось умножение, записывается на место частного при первом проходе алгоритма (при последующих проходах 2-4 пунктов алгоритма это число записывается правее уже находящихся там чисел). Когда получается число, которое больше числа x , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место частного (или правее уже находящихся там чисел) записываем число, на которое проводилось умножение на предпоследнем шаге. (Аналогичные действия мы проводили в двух примерах, разобранных выше).

Умножаем делитель 4 на числа 0 , 1 , 2 , …, пока не получим число, которое равно 14 или больше 14 . Имеем 4·0=014 . Так как на последнем шаге мы получили число 16 , которое больше, чем 14 , то под выделенным числом записываем число 12 , которое получилось на предпоследнем шаге, а на место частного записываем число 3 , так как в предпоследнем пункте умножение проводилось именно на него.

На этом этапе из выделенного числа вычитаем столбиком число, расположенное под ним. Под горизонтальной линией записывается результат вычитания. Однако, если результатом вычитания является нуль, то его не нужно записывать (если только вычитание в этом пункте не является самым последним действием, полностью завершающим процесс деления столбиком). Здесь же для своего контроля не лишним будет сравнить результат вычитания с делителем и убедиться, что он меньше делителя. В противном случае где-то была допущена ошибка.

Нам нужно вычесть столбиком из числа 14 число 12 (для корректности записи нужно не забыть поставить знак «минус» слева от вычитаемых чисел). После завершения этого действия под горизонтальной чертой оказалось число 2 . Теперь проверяем свои вычисления, сравнивая полученное число с делителем. Так как число 2 меньше делителя 4 , то можно спокойно переходить к следующему пункту.

Теперь под горизонтальной чертой справа от находящихся там цифр (или справа от места, где мы не стали записывать нуль) записываем цифру, расположенную в том же столбце в записи делимого. Если же в записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается. После этого выделяем число, образовавшееся под горизонтальной чертой, принимаем его в качестве рабочего числа, и повторяем с ним со 2 по 4 пункты алгоритма.

Под горизонтальной чертой справа от уже имеющейся там цифры 2 записываем цифру 0 , так как именно цифра 0 находится в записи делимого 140 288 в этом столбце. Таким образом, под горизонтальной чертой образуется число 20 .

Это число 20 мы выделяем, принимаем в качестве рабочего числа, и повторяем с ним действия второго, третьего и четвертого пунктов алгоритма.

Умножаем делитель 4 на 0 , 1 , 2 , …, пока не получим число 20 или число, которое больше, чем 20 . Имеем 4·0=0

Проводим вычитание столбиком. Так как мы вычитаем равные натуральные числа, то в силу свойства вычитания равных натуральных чисел в результате получаем нуль. Нуль мы не записываем (так как это еще не завершающий этап деления столбиком), но запоминаем место, на котором мы его могли записать (для удобства это место мы отметим черным прямоугольником).

Под горизонтальной линией справа от запомненного места записываем цифру 2 , так как именно она находится в записи делимого 140 288 в этом столбце. Таким образом, под горизонтальной чертой мы имеем число 2 .

Число 2 принимаем за рабочее число, отмечаем его, и нам еще раз придется выполнить действия из 2-4 пунктов алгоритма.

Умножаем делитель на 0 , 1 , 2 и так далее, и сравниваем получающиеся числа с отмеченным числом 2 . Имеем 4·0=02 . Следовательно, под отмеченным числом записываем число 0 (оно было получено на предпоследнем шаге), а на месте частного справа от уже имеющегося там числа записываем число 0 (на 0 мы проводили умножение на предпоследнем шаге).

Выполняем вычитание столбиком, получаем число 2 под горизонтальной чертой. Проверяем себя, сравнивая полученное число с делителем 4 . Так как 2

Под горизонтально чертой справа от числа 2 дописываем цифру 8 (так как она находится в этом столбце в записи делимого 140 288 ). Таким образом, под горизонтальной линией оказывается число 28 .

Принимаем это число в качестве рабочего, отмечаем его, и повторяем действия 2-4 пунктов.

Здесь никаких проблем возникнуть не должно, если Вы были внимательны до настоящего момента. Проделав все необходимые действия, получается следующий результат.

Осталось последний раз провести действия из пунктов 2 , 3 , 4 (предоставляем это Вам), после чего получится законченная картина деления натуральных чисел 140 288 и 4 в столбик:

Обратите внимание, что в самой нижней строчке записано число 0 . Если бы это был не последний шаг деления столбиком (то есть, если бы в записи делимого в столбцах справа оставались цифры), то этот нуль мы бы не записывали.

Таким образом, посмотрев на законченную запись деления многозначного натурального числа 140 288 на однозначное натуральное число 4 , мы видим, что частным является число 35 072 , (а остаток от деления равен нулю, он находится в самой нижней строке).

Конечно же, при делении натуральных чисел столбиком Вы не будете настолько подробно описывать все свои действия. Ваши решения будут выглядеть примерно так, как в следующих примерах.

Пример.

Выполните деление в столбик, если делимое равно 7 136 , а делителем является однозначное натуральное число 9 .

Решение.

На первом шаге алгоритма деления натуральных чисел столбиком мы получим запись вида

После выполнения действий из второго, третьего и четвертого пунктов алгоритма запись деления столбиком примет вид

Повторив цикл, будем иметь

Еще один проход дет нам законченную картину деления столбиком натуральных чисел 7 136 и 9

Таким образом, неполное частное равно 792 , а остаток от деления равен 8 .

Ответ:

7 136:9=792 (ост. 8) .

А этот пример демонстрирует, как должно выглядеть деление в столбик.

Пример.

Разделите натуральное число 7 042 035 на однозначное натуральное число 7 .

Решение.

Удобнее всего выполнить деление столбиком.

Ответ:

7 042 035:7=1 006 005 .

Деление столбиком многозначных натуральных чисел

Поспешим Вас обрадовать: если Вы хорошо усвоили алгоритм деления столбиком из предыдущего пункта этой статьи, то Вы уже почти умеете выполнять деление столбиком многозначных натуральных чисел . Это действительно так, так как со 2 по 4 этапы алгоритма остаются неизменными, а в первом пункте появляются лишь незначительные изменения.

На первом этапе деления в столбик многозначных натуральных чисел нужно смотреть не на первую слева цифру в записи делимого, а на такое их количество, сколько знаков содержится в записи делителя. Если число, определяемое этими цифрами, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого. После этого выполняются действия, указанные во 2 , 3 и 4 пункте алгоритма до получения конечного результата.

Осталось лишь посмотреть применение алгоритма деления столбиком многозначных натуральных чисел на практике при решении примеров.

Пример.

Выполним деление столбиком многозначных натуральных чисел 5 562 и 206 .

Решение.

Так как в записи делителя 206 участвуют 3 знака, то смотрим на первые 3 цифры слева в записи делимого 5 562 . Эти цифры соответствуют числу 556 . Так как 556 больше, чем делитель 206 , то число 556 принимаем в качестве рабочего, выделяем его, и переходим к следующему этапу алгоритма.

Теперь умножаем делитель 206 на числа 0 , 1 , 2 , 3 , … до того момента, пока не получим число, которое либо равно 556 , либо больше, чем 556 . Имеем (если умножение выполняется сложно, то лучше выполнять умножение натуральных чисел столбиком): 206·0=0556 . Так как мы получили число, которое больше числа 556 , то под выделенным числом записываем число 412 (оно было получено на предпоследнем шаге), а на место частного записываем число 2 (так как на него проводилось умножение на предпоследнем шаге). Запись деления столбиком принимает следующий вид:

Выполняем вычитание столбиком. Получаем разность 144 , это число меньше делителя, поэтому можно спокойно продолжать выполнение требуемых действий.

Под горизонтальной линией справа от имеющегося там числа записываем цифру 2 , так как она находится в записи делимого 5 562 в этом столбце:

Теперь мы работаем с числом 1 442 , выделяем его, и проходим пункты со второго по четвертый еще раз.

Умножаем делитель 206 на 0 , 1 , 2 , 3 , … до получения числа 1 442 или числа, которое больше, чем 1 442 . Поехали: 206·0=0

Проводим вычитание столбиком, получаем нуль, но сразу его не записываем, а лишь запоминаем его позицию, потому что не знаем, завершается ли на этом деление, или придется еще раз повторять шаги алгоритма:

Теперь мы видим, что под горизонтальную черту правее запомненной позиции мы не можем записать никакого числа, так как в записи делимого в этом столбце нет цифр. Следовательно, на этом деление столбиком закончено, и мы завершаем запись:

Математика. Любые учебники для 1, 2, 3, 4 классов общеобразовательных учреждений.
Математика. Любые учебники для 5 классов общеобразовательных учреждений.

Деление в столбик с запятыми калькулятор. Как научиться делить столбиком: примеры и решения

Деление столбиком неотъемлемая часть школьной программы и необходимое знание для ребенка. Чтобы избежать проблем на уроках и с их выполнением, следует давать ребенку основные знания еще с маленького возраста.

Гораздо легче объяснять ребенку определенные вещи и процессы в игровой форме, а не в формате стандартного урока (хотя на сегодняшний день существует достаточно разнообразных методик обучения в разных формах).

Из этой статьи вы узнаете

Принцип деления для малышей

Дети постоянно сталкиваются с разными математическими терминами, даже не подозревая, откуда они. Ведь многие мамочки, в форме игры, объясняют ребенку, что папы больше тарелка, в садик ходить дальше, чем в магазин и другие незамысловатые примеры. Всё это представляет ребенку первоначальное впечатление о математике, еще до похода ребёнка в первый класс.

Чтобы научить ребёнка делить без остатка, а позже с остатком, необходимо прямо предложить поиграть малышу в игры с делением. Разделите, например, конфеты между собой, а затем по очереди добавляйте следующих участников.

Сначала ребенок будет делить конфеты, отдавая каждому участнику по одной. А в конце вместе сделаете вывод. Следует пояснить, что «разделить» — значит всем одинаковое число конфет.

Если Вам необходимо растолковать этот процесс с помощью цифр, то можно привести пример в форме игры. Можно сказать, что цифра – это конфета. Следует объяснить, что число конфет, которые нужно делить между участниками – делимое. А количество человек, на которых делят эти конфеты – это делитель.

Потом следует показать это все наглядно, привести «живые» примеры, чтобы быстрее научить кроху делить. Играя, он намного быстрее все поймет и усвоит. Пока алгоритм объяснить будет сложно, и сейчас это не нужно.

Как обучить малыша делению в столбик

Объяснение крохе разных математических действий – это хорошая подготовка к походу в класс, особенно математический класс. Если Вы решили перейти к обучению ребенка делению столбиком, значит такие действия как сложение, вычитание, и что такое таблица умножения он уже усвоил.

Если же это у него все еще вызывает некоторые сложности, то нужно подтянуть все эти знания. Стоит напомнить алгоритм действий предыдущих процессов, научить свободно пользоваться своими знаниями. В противном случае малыш просто запутается во всех процессах, и перестанет что-либо понимать.

Для облегчения понимания этого, сейчас есть таблица деления для малышей. Принцип у нее такой же, как и у таблиц умножения. Но нужна ли уже такая таблица, если малыш знает таблицу умножения? Это зависит от школы и учителя.

При формировании понятия «деление» нужно обязательно делать все в игровой форме, приводить все примеры на знакомых ребенку вещах и предметах.

Очень важно, чтобы все предметы были четного числа, чтобы малышу было ясно, что итогом являются равные части. Это будет правильно, поскольку позволит крохе осознать, что деление — процесс обратный умножению. Если предметы будут нечетного количества, то итог выйдет с остатком и малыш запутается.

Умножаем и делим с помощью таблицы

При объяснении малышу взаимосвязи между умножением и делением, необходимо это все наглядно показывать на каком-либо примере. Например: 5 х 3 = 15. Вспомните, что итог умножения это произведение двух чисел.

И только после этого, объясняйте, что это обратный процесс к умножению и продемонстрируйте это наглядно с помощью таблицы.

Скажите, что нужно поделить результат «15» — на какой-то из множителей («5»/ «3»), и итогом будет постоянно иной, не принимавший участие в делении, множитель.

Также необходимо растолковать малышу, как правильно называются категории, которые выполняют деление: делимое, делитель, частное. И снова с помощью примера покажите, что из них является конкретной категорией.

Деление столбиком вещь не очень сложная, у нее есть свой легкий алгоритм, которому малыша нужно научить. После закрепления всех этих понятий и знаний, можно переходить к дальнейшему обучению.

В принципе, родителям стоит выучить с любимым чадом таблицу умножения в обратном порядке, и наизусть ее запомнить, так как это будет нужным при обучении делению столбиком.

Это делать необходимо до похода в первый класс, чтобы ребенку в школе было намного легче освоиться, и успевать за школьной программой, и чтобы класс из-за небольших неудач не начал дразнить ребенка. Таблица умножения есть и в школе, и в тетрадях, поэтому носить отдельную таблицу в школу не придется.

Делим с помощью столбика

Прежде чем приступить к занятию, нужно вспомнить названия цифр при делении. Что такое делитель, делимое и частное. Ребенок должен без ошибок делить эти цифры на правильные категории.

Самое главное при обучении деления столбиком, это усвоить алгоритм, который, в общем, довольно простой. Но сначала объясните ребенку значение слова «алгоритм», если он забыл его или до этого не изучал.

В том случае, если кроха прекрасно разбирается в таблице умножения и обратного деления, у него не будет никаких сложностей.

Однако на полученном результате долго задерживаться нельзя, необходимо регулярно тренировать приобретенные умения и навыки. Двигайтесь далее, как только станет ясно, что малыш понял принцип метода.

Необходимо научить малыша делить столбиком без остатка и с остатком, чтобы ребенок не пугался, что у него что-то не получилось разделить правильно.

Чтобы было проще обучить малыша процессу деления необходимо:

в 2-3 года понимание отношения целое-часть.
в 6-7 лет малыш должен свободно уметь выполнять сложение, вычитание и осознавать сущность умножения и деления.

Нужно побуждать интерес малыша к математическим процессам, чтобы этот урок в школе приносил ему удовольствие и желание учиться, и не мотивировать его на одних на уроках, но и в жизни.

Ребенок должен носить разные инструменты для уроков математики, учиться ими пользоваться. Однако если ребенку тяжело все носить, то не стоит его перегружать.

Научить ребенка делению столбиком просто. Необходимо объяснить алгоритм этого действия и закрепить пройденный материал.

Согласно школьной программе, деление столбиком детям начинают объяснять уже в третьем классе. Ученики, которые схватывают все «на лету», быстро понимают эту тему
Но, если ребенок заболел и пропустил уроки математики, или он не понял тему, тогда родители должны самостоятельно малышу объяснить материал. Нужно максимально доступно донести до него информацию
Мамы и папы во время учебного процесса ребенка должны быть терпеливыми, проявляя такт по отношению к своему чаду. Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям

Важно: Чтобы ребенок понял деление чисел, он должен досконально знать таблицу умножения. Если малыш плохо знает умножение, он не поймет деление.

Во время домашних дополнительных занятий можно пользоваться шпаргалками, но ребенок должен выучить таблицу умножения, прежде чем, приступать к теме «Деление».

Итак, как объяснить ребенку деление столбиком :

Постарайтесь сначала объяснить на маленьких цифрах. Возьмите счетные палочки, например, 8 штук
Спросите у ребенка, сколько пар в этом ряду палочек? Правильно — 4. Значит, если разделить 8 на 2, получится 4, а при делении 8 на 4 получится 2
Пусть ребенок сам разделит другое число, например, более сложное: 24:4
Когда малыш освоил деление простых чисел, тогда можно переходить к делению трехзначных чисел на однозначные

Деление всегда дается детям немного сложнее, чем умножение. Но усердные дополнительные занятия дома помогут малышу понять алгоритм этого действия и не отставать от сверстников в школе.

Начинайте с простого — деление на однозначное число:

Важно: Просчитайте в уме, чтобы деление получилось без остатка, иначе ребенок может запутаться.

Например, 256 разделить на 4:

Начертите на листе бумаги вертикальную линию и разделите ее с правой части пополам. Слева напишите первую цифру, а справа над чертой вторую
Спросите у малыша, сколько четверок помещается в двойке — нисколько
Тогда берем 25. Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа
Запишите под 25 цифру 24, и подчеркните, чтобы записать ответ — 1
Опять спрашивайте: в единице сколько помещается четверок — нисколько. Тогда сносим к единице цифру «6»
Получилось 16 — сколько четверок помещается в этом числе? Правильно — 4. Записываем «4» рядом с «6» в ответе
Под 16 записываем 16, подчеркиваем и получается «0», значит мы разделили правильно и ответ получился «64»

Письменное деление на двузначное число

Когда ребенок освоил деление на однозначное число, можно двигаться дальше. Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры.

Важно: Снова начинайте объяснять с простых действий. Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа.

Выполните вместе такое простое действие: 184:23 — как нужно объяснять:

Разделим сначала 184 на 20, получается примерно 8. Но мы не пишем цифру 8 в ответ, так как это пробная цифра
Проверяем, подходит 8 или нет. Умножаем 8 на 23, получается 184 — это именно то число, которое у нас стоит в делителе. Ответ будет 8

Важно: Чтобы ребенок понял, попробуйте вместо восьмерки взять 9, пусть он умножит 9 на 23, получается 207 — это больше, чем у нас в делителе. Цифра 9 нам не подходит.

Так постепенно малыш поймет деление, и ему будет легко делить более сложные числа:

Разделим 768 на 24. Определите первую цифру частного — делим 76 не на 24, а на 20, получается 3. Записываем 3 в ответ под чертой справа
Под 76 записываем 72 и проводим линию, записываем разность — получилось 4. Эта цифра делится на 24? Нет — сносим 8, получается 48
Цифра 48 делится на 24? Правильно — да. Получается 2, записываем эту цифру в ответ
Получилось 32. Теперь можно проверить — правильно ли мы выполнили действие деления. Сделайте умножение в столбик: 24х32, получается 768, значит все правильно

Если ребенок научился выполнять деление на двузначное число, тогда необходимо перейти к следующей теме. Алгоритм деления на трехзначное число такой же, как и алгоритм деления на двузначное число.

Например:

Разделим 146064 на 716. Берем сначала 146 — спросите у ребенка делится это число на 716 или нет. Правильно — нет, тогда берем 1460
Сколько раз число 716 поместится в числе 1460? Правильно — 2, значит пишем эту цифру в ответе
Умножаем 2 на 716, получается 1432. Записываем эту цифру под 1460. Получается разность 28, записываем под чертой
Сносим 6. Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4
Делим 2864 на 716. Берем по 3 — мало, по 5 — много, значит получается 4. Умножаем 4 на 716, получается 2864
Запишите 2864 под 2864, получается в разности 0. Ответ 204

Важно: Для проверки правильности выполнения деления, умножьте вместе с ребенком в столбик — 204х716=146064. Деление выполнено правильно.

Пришло время ребенку объяснить, что деление может быть не только нацело, но и с остатком. Остаток всегда меньше делителя или равен ему.

Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3):

Сколько восьмерок помещается в 35? Правильно — 4. Остается 3
Делится эта цифра на 8? Правильно — нет. Получается, остаток 3

После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3:

В ответе стоит цифра 4. После нее пишем запятую, так как добавление нуля говорит о том, что число будет с дробью
Получилось 30. Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
Сносим к цифре 6 цифру 0. Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
К цифре 4 дописываем 0 и делим на 8, получается 5 — записываем в ответ
Вычитаем 40 из 40, получается 0. Итак, ответ: 35:8=4,375

Совет: Если ребенок что-то не понял — не злитесь. Пусть пройдет пару дней и снова постарайтесь объяснить материал.

Уроки математики в школе также будут закреплять знания. Пройдет время и малыш будет быстро и легко решать любые примеры на деление.

Алгоритм деления чисел заключается в следующем:

Сделать прикидку числа, которое будет стоять в ответе
Найти первое неполное делимое
Определить число цифр в частном
Найти цифры в каждом разряде частного
Найти остаток (если он есть)

По такому алгоритму выполняется деление как на однозначные числа, так и на любое многозначное число (двузначное, трехзначное, четырехзначное и так далее).

Занимаясь с ребенком, чаще ему задавайте примеры на выполнение прикидки. Он должен быстро в уме подсчитать ответ. Например:

1428:42
2924:68
30296:56
136576:64
16514:718

Для закрепления результата можно использовать такие игры на деление:

«Головоломка». Напишите на листе бумаги пять примеров. Только один из них должен быть с правильным ответом.

Условие для ребенка: Среди нескольких примеров, только один решен правильно. Найди его за минуту.

Видео: Игра арифметика для детей сложение вычитание деление умножение

Видео: Развивающий мультфильм Математика Изучение наизусть таблицы умножения и деления на 2

За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:

Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:

Под делимым будут записываться промежуточные вычисления:

Полностью форма записи деления столбиком выглядит следующим образом:

Как делить столбиком

Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:

Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:

Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:

Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.

Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:

Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.

Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:

Деление столбиком с остатком

Пусть нам требуется разделить 1340 на 23.

Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:

1340: 23 = 58 (остаток 6)

3: 10 = 0 (остаток 3)

Калькулятор деления столбиком

Деление – интересная операция, в чем мы и убедимся с вами в этой статье!

Деление чисел

Деление с остатком

Деление на 3 и 9

Найти сумму цифр делимого.

Поделить на 3 или 9 (в зависимости от того, что вам нужно).

Если ответ получается без остатка, то и число поделится без остатка.

Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.

Умножение и деление

Деление 3 класс

В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:

Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?

Деление 4 класс

Деление в столбик

Рассмотрим пример, 512:8.

1 шаг . Запишем делимое и делитель следующим образом:

Частное будет записано в итоге под делителем, а расчеты под делимым.

2 шаг . Деление начинаем слева направо. Сначала берем цифру 5:

3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:

Теперь 51 больше 8. Это неполное частное.

4 шаг . Ставим точку под делителем.

7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»:

8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3.

* 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3:

10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.

Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.

Деление трехзначных

Деление дробей

Деление числа на классы

Деление натуральных чисел

Деление презентация

Примеры на деление

Легкий уровень

Средний уровень

Сложный уровень

Игры на развитие устного счета

Игра «Угадай операцию»

Игра «Упрощение»

Игра «Быстрое сложение»

Игра «Визуальная геометрия»

Игра «Копилка»

Игра «Быстрое сложение перезагрузка»

Развитие феноменального устного счета

Скорочтение за 30 дней

Развитие памяти и внимания у ребенка 5-10 лет

Супер-память за 30 дней

Секреты фитнеса мозга, тренируем память, внимание, мышление, счет

Деньги и мышление миллионера

Математический-Калькулятор-Онлайн v.1.0

Калькулятор выполняет следующие операции: сложение, вычитание, умножение, деление, работа с десятичными, извлечение корня, возведение в степень, вычисление процентов и др. операции.

Решение:

Как работать с математическим калькулятором

Клавиша	Обозначение	Пояснение
5	цифры 0-9	Арабские цифры. Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/-
.	точка (запятая)	Разделитель для обозначения десятичной дроби. При отсутствии цифры перед точкой (запятой) калькулятор автоматически подставит ноль перед точкой. Например: .5 — будет записано 0.5
+	знак плюс	Сложение чисел (целые, десятичные дроби)
—	знак минус	Вычитание чисел (целые, десятичные дроби)
÷	знак деления	Деление чисел (целые, десятичные дроби)
х	знак умножения	Умножение чисел (целые, десятичные дроби)
√	корень	Извлечение корня из числа. При повторном нажатие на кнопку «корня» производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2
x 2	возведение в квадрат	Возведение числа в квадрат. При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16
1 / x	дробь	Вывод в десятичные дроби. В числителе 1, в знаменателе вводимое число
%	процент	Получение процента от числа. Для работы необходимо ввести: число из которого будет высчитываться процент, знак (плюс, минус, делить, умножить), сколько процентов в численном виде, кнопка «%»
(	открытая скобка	Открытая скобка для задания приоритета вычисления. Обязательно наличие закрытой скобки. Пример: (2+3)*2=10
)	закрытая скобка	Закрытая скобка для задания приоритета вычисления. Обязательно наличие открытой скобки
±	плюс минус	Меняет знак на противоположный
=	равно	Выводит результат решения. Также над калькулятором в поле «Решение» выводится промежуточные вычисления и результат.
←	удаление символа	Удаляет последний символ
С	сброс	Кнопка сброса. Полностью сбрасывает калькулятор в положение «0»

Алгоритм работы онлайн-калькулятора на примерах

Сложение.

Сложение целых натуральных чисел { 5 + 7 = 12 }

Сложение целых натуральных и отрицательных чисел { 5 + (-2) = 3 }

Сложение десятичных дробных чисел { 0,3 + 5,2 = 5,5 }

Вычитание.

Вычитание целых натуральных чисел { 7 — 5 = 2 }

Вычитание целых натуральных и отрицательных чисел { 5 — (-2) = 7 }

Вычитание десятичных дробных чисел { 6,5 — 1,2 = 4,3 }

Умножение.

Произведение целых натуральных чисел { 3 * 7 = 21 }

Произведение целых натуральных и отрицательных чисел { 5 * (-3) = -15 }

Произведение десятичных дробных чисел { 0,5 * 0,6 = 0,3 }

Деление.

Деление целых натуральных чисел { 27 / 3 = 9 }

Деление целых натуральных и отрицательных чисел { 15 / (-3) = -5 }

Деление десятичных дробных чисел { 6,2 / 2 = 3,1 }

Извлечение корня из числа.

Извлечение корня из целого числа { корень(9) = 3 }

Извлечение корня из десятичных дробей { корень(2,5) = 1,58 }

Извлечение корня из суммы чисел { корень(56 + 25) = 9 }

Извлечение корня из разницы чисел { корень (32 – 7) = 5 }

Возведение числа в квадрат.

Возведение в квадрат целого числа { (3) 2 = 9 }

Возведение в квадрат десятичных дробей { (2,2) 2 = 4,84 }

Перевод в десятичные дроби.

Вычисление процентов от числа

Увеличить на 15% число 230 { 230 + 230 * 0,15 = 264,5 }

Уменьшить на 35% число 510 { 510 – 510 * 0,35 =331,5 }

18% от числа 140 это { 140 * 0,18 = 25,2 }

Презентация «Повторение по теме: «Деление «Столбиком»».

библиотека
материалов

Содержание слайдов

Номер слайда 1

Повторение по теме: «Деление столбиком»

Номер слайда 2

Номер слайда 3

Номер слайда 4

Номер слайда 5

Номер слайда 6

Номер слайда 7

Номер слайда 8

Номер слайда 9

Задания для закрепления

Презентация и конспект по математике на тему»Алгоритм деления столбиком»(4 класс)

Урок математики в 4 классе

УМК «Перспективная начальная школа»

Тема: Алгоритм деления столбиком

Цель:

Создание условий для усвоения учащимися математического понятия алгоритм деления столбиком и применения его для решения;

Задачи:

— учить анализировать запись деления четырехзначного числа на двузначное столбиком;

— формировать умение формулировать алгоритм деления столбиком, отвечая на вопросы;

— развивать математическую речь учащихся,

— Формировать соответствующие УУД

Личностные УУД:- способствовать самооценке на основе критерия успешности учебной деятельности.

Регулятивные УУД:- умение определить и формулировать цель на уроке с помощью учителя; планировать свое действие в соответствии с поставленной задачей; высказывать свое предположение; выбирать для выполнения посильные задания.

Коммуникативные УУД:- умение оформлять свои мысли в устной и письменной речи, слушать, понимать речь других; договариваться о правилах поведения и общения при работе в парах и следовать им.

Познавательные УУД:-выполнять действия по заданному алгоритму; строить логическую цепь рассуждений; отличать новое от уже известного с помощью учителя.

Прогнозируемые результаты:

Предметные:

Знание алгоритма письменного деления.

умение делить многозначные числа на двузначные письменным способом.

Метапредметные:

умение ставить учебные задачи и самостоятельно формулировать выводы.

умение слушать собеседника, излагать своё мнение и аргументировать свою точку зрения.

Личностные:

умение сотрудничать с учителем и сверстниками, умение определять успешность учебной деятельности

Усваиваемые математические термины: «алгоритм деления столбиком», «запись делимого», «первое промежуточное делимое», «остаток первого промежуточного деления», «число цифр в записи неполного частного».

Оборудование: проектор, презентация, учебник, пошаговый алгоритм в конверте.

ХОД УРОКА

1этап. Этап организации направленного внимания на начало учебного занятия

Цель этапа: организовать направленное внимание на начало урока.

— Для успешной работы на уроке нам необходимы следующее: учебник, рабочая тетрадь, ручка, карандаш, линейка. Если все необходимое на парте, садитесь.

Ученики проверяют необходимое на уроке оборудование, если все в наличии садятся, если нет достают все необходимое.

2этап. Мотивация (самоопределение) к учебной деятельности.(слайд1)

— Математику, друзья,

Не любить никак нельзя.

Очень строгая наука,

Очень точная наука,

Интересная наука-

Это математика!

2.1 Организационные записи в тетради. ( Слайд 2 )

— Открываем тетрадь. Записываем число, классная работа. Помним правила посадки при письме.

2.2 Минутка чистописания. ( Слайд 3-4 )

— Отгадайте, о каком числе идёт речь? Если из самого маленького четырехзначного числа вычесть самое большое трехзначное число, то получится….(1)

-Пропишите это число 1 строку.

3 этап. Актуализация знаний.

3.1. Устный счет

Задачи на смекалку: (Слайд 5)

Шесть картофелин варятся 30 минут. Сколькоминут варилась в кастрюле 1 картофелина?

Две лошади в упряжке пробежали расстояние за 4 часа. Сколько времени бежала каждая лошадь?

3.2 этап. Этап целеполагания

Цель этапа: Сформировать представления детей о том, что нового они узнают на уроке и чему научатся

Чтобы раскрыть название темы урока необходимо разгадать ребус. Он зашифрован в следующем задании: Карточка (работа в парах)

— Запишите остаток от деления данных чисел в таблицу:

18:7

82:9

45:6

37:8

88:9

35:9

— Цифре 6 — И, 2 – Л, 4 – О, 1 – А, 3 – Г, 5 – Р, 7 – Т, 8 – М.

— Расставьте числа в порядке возрастания. Какое слово получилось? (алгоритм)

— Что значит слово алгоритм?

— С какими алгоритмами мы уже знакомы? (письменного сложения, вычитания, умножения столбиком)

— С каким алгоритмом мы еще не знакомы? Назовите тему нашего урока.

( Алгоритм письменного деления) (Слайд 6)

Кто сформулирует цель нашего урока? Используйте для этого слова: составление, знакомство, применение, решение

(Слайд 7)

Итак, цель урока: составление алгоритма деления столбиком и применение его для решения.

3.3 этап. Цель этапа: повторить понятие, правило, алгоритм и способ использования алгоритма

Работа по учебнику

З а д а н и е 38. Не забудьте, что обозначает условное обозначение, (не торопись с ответом, подумай). Учащиеся выполняют деление столбиком.

– Как определить первое промежуточное делимое? (выделить дугой первые две цифры в записи делимого и рассмотреть соответствующее двузначное число)

– Как с его помощью определитьчисло цифр в записи неполного

частного? (По разряду первого промежуточного делимого.)

Как найти первую цифру в записи неполного частного?

(Выполнить деление первого промежуточного делимого на делитель.)

– Нужно ли записывать остаток, если он промежуточный и равен 0? (Нет.) Как получается следующее промежуточное делимое? Как найти следующую цифру в записи неполного частного? Какую цифру нужно писать в неполном частном, если промежуточное делимое меньше делителя? (Цифру 0.)

– Когда нужно заканчивать процесс деления? Какое число следует считать окончательным остатком деления?

4 этап. Этап объяснения

Цель этапа: сформировать понятие (алгоритм деления столбиком), обучение УУД (выполнять действия по заданному алгоритму; строить логическую цепь рассуждений;)

З а д а н и е 39 учащиеся переписывают запись деления столбиком в тетрадь.

4.1Этап физической разрядки

Цель этапа: смена вида деятельности

Физминутка (Слайд 7)

З а д а н и е 40. Учащиеся объясняют деление с остатком в столбик, отвечая на вопросы, система вопросов аналогична системе вопросов из №38, но только теперь речь пойдет о случае деления с остатком столбиком на двузначное число, при этом соответствующая запись деления уже перенесена детьми в готом виде в тетрадь, таким образом учащиеся самостоятельно составляют алгоритм деления столбиком, работа направлена на среднего ученика

— выделить дугой первые две цифры в записи делимого и рассмотреть соответствующее двузначное число

— Так как первое промежуточное делимое выражает число сотен 35 сотен, то запись неполного частного будет состоять из трех цифр;

— Нужно найти результат деления первого промежуточного делимого 35 на делитель 17 и записать соответствующую этому результату цифру 2 в старший разряд искомого неполного частного.

— Запись следующего промежуточного делимого получается с помощью приписывания к записи остатка цифры, следующей за первым промежуточным делимым, если остаток равен 0, то записывают только соответствующую цифру делимого

— Запись следующего промежуточного делимого получается с помощью приписывания к записи остатка цифры, следующей за первым промежуточным делимым

— Если промежуточное делимое меньше делителя, то в неполном частном на соответствующем месте нужно писать цифру 0.

— Деление нужно заканчивать тогда, когда будет выполнено деление последнего промежуточного делимого.

— Остаток, который получается при делении последнего промежуточного делимого на делитель, и будет окончательным остатком деления.

5 этап. Этап применения и первичного закрепления теоретических положений в условиях выполнения упражнений и задач.

Цель этапа: сформировать учебные действия по использованию алгоритма деления столбиком, продолжить формирование УУД по работе со словарем учебника.

З а д а н и е 41. Что обозначает это условное обозначение (проверь правильность выполнения задания), что обозначает звездочка (посмотри в словарь)

( Учащиеся формулируют алгоритм деления столбиком, используя не только дважды прозвучавшие ответы на эти же вопросы, но и пользоваться для ответов готовым алгоритмом приведенный в соответствующей статье словаря с.123)

Работаем в паре у одного открыто задание 41, у другого алгоритм. Один в паре читает вопрос, другой отвечает на него. В алгоритме записано как необходимо действовать, ваша задача ещё составить пошаговый план, что необходимо делать. Необходимые предложения вы найдете в конверте.

Правильно записать пример деления в столбик.

Найти первое промежуточное делимое и определить количество цифр в неполном частном.

Найти результат деления и правильно записать цифру в неполном частном и остаток (если остаток равен 0, то его не записывать).

Найти второе промежуточное делимое.

Действия из пунктов 4) и 5) повторить пока не будут использованы все цифры делимого.)

– Как нужно записать делимое и делитель? (Сначала записывают делимое, после этого справа от делимого ставят ├ (знак деления столбиком), в котором в верхней части записывают делитель, а нижнюю часть оставляют для записи искомого результата.)

– Как найти первое промежуточное делимое? (Отделяя последовательно цифры в записи делимого, находят первое промежуточное делимое и отмечают его в записи делимого с помощью дуги.)

– С помощью какого знака можно показать, какое число будет первым промежуточным делимым?

– Где записывается полученный результат первого промежуточного деления и как вычисляется остаток этого случая деления? (Находят результат деления с остатком первого промежуточного делимого на делитель и записывают полученное число в старший разряд искомого результата. После этого умножают полученный результат на делитель и записывают результат этого умножения под первым промежуточным делимым столбиком. Выполняют вычитание столбиком с целью получения остатка первого промежуточного деления.)

– Нужно ли записывать промежуточный остаток, если он равен 0? (Если остаток равен 0, то его не записывают.)

– Как получить второе промежуточное делимое и где оно записывается? (Запись второго промежуточного делимого получают с помощью приписывания к записи полученного ранее остатка цифры, которая в записи исходного делимого находится в старшем из неиспользуемых пока разрядов.)

– Где записывается полученный результат второго промежуточного деления и как вычисляется остаток этого случая деления?

– Если вычисленный остаток равен 0, то в каком случае его не нужно записывать? Можно ли утверждать, что все последующие случаи промежуточного деления повторяют процедуру второго случая промежуточного деления? Когда следует заканчивать процесс деления? (До тех пор пока в построении промежуточных делимых не будут использованы все цифры записи исходного делимого.)

– Где будет записано окончательное неполное делимое и окончательный остаток? Проверка на слайде алгоритма(Слайд 8)

6 этап. Этап формирование УУД

Цель этапа: закрепить, повторить, продолжить формирование УУД

Решение примеров № 42 (1,2,3 по алгоритму)

Для этого вы распределитесь в паре: один в паре консультирует, другой записывает решение.

У кого возникают вопросы просят помощи (поднятая рука), оказывает индивидуальную помощь, через 2-3 минуты выполнившие решение проверяет учитель и просит помочь одноклассникам, которые работают медленнее других.

7 этап. Этап контроля результатов деятельности учащихся или хода усвоения нового материала

Цель этапа: проконтролировать умение учеников использовать математические термины, алгоритм деления столбиком при решении примеров, ответах на вопросы

Учитель контролирует ответы детей, при решении примеров в течение всего урока.

8 этап. Этап рефлексии

Цель этапа: сформировать личную ответственность за результаты коллективной деятельности

-Какую цель мы поставили в начале нашего урока?

— Достигли мы цели урока? (познакомились с алгоритмом деления столбиком, учились его применять при решении примеров.)

— А теперь каждый оценит себя – достиг ли он цели урока — насколько хорошо вы усвоили алгоритм деления столбиком.

-Кто доволен своей работой на уроке, понял новую тему – в тетради на полях ставим зелёный квадратик.

— Кто не совсем доволен, допускал ошибки, еще нужно поработать над данной темой — жёлтый.

— Кто не понял материал, не доволен своей работой — красный.

— Если же какой-либо этап вы не усвоили, не надо переживать, потому что мы с вами на следующих уроках будем продолжать работу над закреплением алгоритма, но дома в качестве домашнего задания ученик должен еще раз изучить алгоритм письменного деления и галочками отметить не устранённые затруднения.

Дома. Р.Т. № 44; учеб. №37стр.14. + алгоритм

Спасибо за урок

Муниципальное автономное общеобразовательное учреждение

средняя общеобразовательная школа № 72 города Тюмени

Открытый урок по математике

4 «В» класс

«Перспективная начальная школа»

Тема: Алгоритм деления столбиком.

Подготовила:

учитель начальных классов

Заичкина Елена Петровна

Тюмень, 2017год

— Запишите остаток от деления данных чисел в таблицу:

Расставьте числа в порядке возрастания. Какое слово получилось?

47:5

18:7

82:9

45:6

37:8

88:9

35:9

— Цифре 6 — И, 2 – Л, 4 – О, 1 – А, 3 – Г, 5 – Р, 7 – Т, 8 – М.

————————————————————————————————————————————-

— Запишите остаток от деления данных чисел в таблицу:

Расставьте числа в порядке возрастания. Какое слово получилось?

47:5

18:7

82:9

45:6

37:8

88:9

35:9

— Цифре 6 — И, 2 – Л, 4 – О, 1 – А, 3 – Г, 5 – Р, 7 – Т, 8 – М.

————————————————————————————————————————————— Запишите остаток от деления данных чисел в таблицу:

Расставьте числа в порядке возрастания. Какое слово получилось?

47:5

18:7

82:9

45:6

37:8

88:9

35:9

— Цифре 6 — И, 2 – Л, 4 – О, 1 – А, 3 – Г, 5 – Р, 7 – Т, 8 – М.

Расставьте числа в порядке возрастания. Какое слово получилось?

47:5

18:7

82:9

45:6

37:8

88:9

35:9

— Цифре 6 — И, 2 – Л, 4 – О, 1 – А, 3 – Г, 5 – Р, 7 – Т, 8 – М.

Расставьте числа в порядке возрастания. Какое слово получилось?

47:5

18:7

82:9

45:6

37:8

88:9

35:9

— Цифре 6 — И, 2 – Л, 4 – О, 1 – А, 3 – Г, 5 – Р, 7 – Т, 8 – М.

Деление с остатком столбиком. Проверка деления с остатком

Привет, друзья! А вот и я.

Опять буду знакомить вас с новой темой. Я надеюсь, вы уже уверенно научились выполнять деление с остатком? Помните, как мы шестнадцать делили на пять?

Вспоминаем таблицу умножения и деления с числом пять. Находим число, которое делится на пять без остатка и на числовом луче находится ближе остальных к числу шестнадцать. Это пятнадцать. Пятнадцать делим на пять, получается три, а разницу между шестнадцатью и пятнадцатью – один, записываем в остаток.

Вы уже знаете, что знак умножения может записываться по-разному – иногда точкой, иногда косым крестиком, а на клавиатуре компьютера или мобильного телефона – звёздочкой. Но и знак деления тоже может выглядеть по-разному: в тетрадях вы обычно пишете двоеточие, иногда этот знак выглядит как горизонтальная черта, а над ней и под ней по точке. Но для письменного деления многозначных чисел используют знак деления, который похож на лежащую на боку букву Т. И сегодня мы воспользуемся таким знаком деления для того, чтобы выполнять деление с остатком столбиком.

Вот посмотрите, допустим, нам надо разделить число двадцать пять на четыре.

Как это записать, я покажу на разлиновке в клеточку. Ведь при таком способе решения, как и при сложении и вычитании столбиком, очень важна аккуратность записи. Итак, пишу делимое – число двадцать пять. Справа от него, отступив одну клеточку, пишу делитель – четыре. Между ними ставлю знак деления – вертикальная черта длиной в две клетки, а от неё – горизонтальная. Вот она, буква Т. Вот делимое, вот делитель. Под чертой место для частного.

Сначала выясним, сколько раз число четыре содержится в двадцати пяти. Четыре умножаем на нуль, равно нуль. Нуль меньше двадцати пяти. Так что нуль в качестве частного нам уж точно не подходит.

Четыре умножаю на один. Четыре. Это число тоже меньше двадцати пяти и тоже нас не устраивает. Четыре умножаю на два – шесть. Оно тоже меньше двадцати пяти. Четыре умножаю на три – двенадцать, четырежды четыре – шестнадцать, четырежды пять – двадцать. Четыре умножить на шесть – двадцать четыре. На семь – двадцать восемь. А двадцать восемь не меньше, а больше двадцати пяти.

Стоп! Теперь получилось число, которое больше нашего делимого. Но это недопустимо. Возвращаемся к шестёрке. Итак, четыре содержится в числе двадцать пять шесть раз. Записываю в частном число шесть. А под делимым – то число, которое получилось при умножении делителя и частного – двадцать четыре.

А теперь вычитаю из делимого это полученное число двадцать четыре. Видите, получилось вычитание столбиком. А результат вычитания – это остаток. Я надеюсь, вы не забыли, что остаток обязательно должен быть меньше делителя. В этом примере остаток один. Он меньше четырёх. Значит, деление выполнено верно.

Запомните, как расположены компоненты деления. Делимое и делитель находятся на одной строчке, между ними пропускается одна клеточка. Частное расположено под делителем, а под делимым – действие вычитания и остаток.

Конечно, у нас получилось очень длинное вычисление. Методом проб и ошибок, начиная с нуля, мы нашли нужное нам число. Но, если вы хорошо знаете таблицу умножения, подбор нужного числа не будет столь долгим и утомительным.

Вот, к примеру, надо сорок пять разделить на шесть. Вспомнив таблицу умножения числа шесть, мы можем сказать, что ближайшими числами к делимому, которые делятся на шесть, являются числа сорок два и сорок восемь. Сорок восемь получится в результате умножения шести на восемь. Но число сорок восемь больше сорока пяти, и оно нам не подойдёт.

Сорок два получится в результате умножения шести на семь. Сорок два меньше сорока пяти. Значит, шесть содержится в сорока пяти семь раз. А остаток три. Наш остаток меньше делителя, значит, деление выполнено верно.

Ну а если, к примеру, надо число семь разделить на девять. Сколько раз число девять содержится в семи? Ну конечно, нуль раз. В частном записываем нуль. Нуль умножили на девять, тоже получился нуль, вычитаем… Остаток семь.

Если делимое меньше делителя, то в ответе получится нуль, а остаток будет равен делимому.

Ребята, а вы знаете, несмотря на то, что вы вроде бы всё правильно делаете, при делении с остатком случаются и ошибки. Как же проверить, правильно ли было выполнено деление?

Ну конечно обратными действиями. Мы выполняли деление и, чтобы найти остаток, вычитание. Значит, для проверки нам понадобится умножение и сложение.

Давайте сейчас разделим число сорок три на одиннадцать. Запишем решение в строчку. Сколько раз одиннадцать содержится в числе сорок три? Ну понятно, что не нуль и не один раз. Если взять два, получится число двадцать два. Оно меньше сорока трёх. Если взять три раза – это тридцать три. Оно тоже меньше сорока трёх. Возьмём число четыре – получится сорок четыре. Оно больше сорока трёх. Стоп! Возвращаемся к числу три. Число одиннадцать содержится в сорока трёх три раза и остаток десять.

Вроде бы всё правильно. Но убедиться в этом мы сможем, только выполнив проверку. Сравниваем остаток с делителем. Десять меньше одиннадцати. Это правильно. Теперь деление и вычитание проверяем умножением и сложением.

Делитель, одиннадцать, умножаем на частное, три, и к результату прибавляем остаток, десять. Одиннадцать умножить на три – тридцать три, и плюс десять – сорок три.

Ну, вроде бы всё рассказал. Ну, а если что-то по рассеянности пропустил, вам обязательно расскажет это ваш мудрый учитель.

А теперь я предлагаю вам повторить то, о чём мы сегодня говорили.

* Деление с остатком можно записывать как в строчку, так и столбиком.

* При записи столбиком делимое и делитель находятся на одной строчке, между ними пропускается одна клеточка, в которой записывается знак деления, похожий на букву Т, лежащую на боку. Частное расположено под делителем, а под делимым – действие вычитания и остаток.

Если делимое меньше делителя, то в ответе получится нуль, а остаток будет равен делимому.

Деление с остатком можно проверить.

1. Для этого сначала сравниваются остаток с делителем.

Важно! Остаток должен быть меньше делителя!

После сравнения остатка с делителем выполняем второй этап проверки.

2. Умножить частное на делитель и к полученному произведению прибавить остаток.

Ну вот и пришло время нам сегодня попрощаться. Хороших вам отметок, ребята! До свидания!

Д

Деление столбиком.

Повторим деление столбиком, как ни странно, но многие к 9, а также к 11 классу, забывают как делить столбиком.

Поделим 3577 на 7 в столбик. В любой операции деления должно быть делимое, делитель и частное. В нашем случае 3577 – делимое, 7 – делитель, а результат деления, то есть ответ – частное.
Записываем делимое и делитель, разделяем их “уголком”

Смотрим на делимое – это у нас 3577 слева на право. Первое число идет 3, оно меньше делителя, то есть 7.

Поэтому нам нужно добавить следующее число, это 5, получим число 35.

35 больше 7, следовательно, мы можем поделить данные числа. Чтобы поделить 35 на 7 нужно взять по 5.

Умножаем 5 на 7 получаем 35, записываем и отнимаем, в результате 0. Если вы все сделали правильно, результат вычитания должен быть меньше делителя, 7. Если больше, значит вы неправильно определили, сколько раз 7 содержится в 35.

У нас осталось еще 2 числа — это две семерки. Сносим первую семерку 7.

Чтобы поделить 7 на 7 нужно взять по 1.

Умножаем 1 на 7 получаем в результате 7. Вычитаем эти 2 числа. Получили 0.

Сносим последнюю 7 и проделываем все тоже самое.
Чтобы поделить 7 на 7 нужно взять по одному. Умножаем 1 на 7 получаем в результате 7. Вычитаем эти 2 числа. Получили 0.

Остатка у нас не осталось, следовательно деление завершено. 3577:7=511

Что же делать если в результате остатка будет число большее нуля?

Рассмотрим следующий пример:

Поделим 1569 на 4 в столбик. 1569 – делимое, 4 – делитель, а результат деления, то есть ответ – частное.
Записываем делимое и делитель, разделяем их “уголком”

Смотрим на делимое – это у нас 1569 слева на право. Первое число идет 1 оно меньше делителя, 4.

Поэтому нам нужно добавить следующее число, это 5, получим число 15.

15 больше 4 следовательно мы можем поделить данные числа. Чтобы поделить 15 на 4 берем по 3.

Умножаем 3 на 4 получаем 12, записываем и отнимаем, в результате 3. Если вы все сделали правильно, результат вычитания должен быть меньше делителя, 3 меньше 4 – все правильно. Если больше, значит вы неправильно определили.
У нас осталось еще 2 числа это 6 и 9.Так как 3 на 4 не делиться на цело мы сносим 6 к 3 и получим число 36.

Чтобы поделить 36 на 4 нужно взять по 9. Умножаем 9 на 4 получаем в результате 36. Вычитаем эти 2 числа. Получаем 0.

Сносим последнюю 9 и проделываем все тоже самое.

Чтобы поделить 9 на 4 нужно взять по 2. Умножаем 2 на 4 получаем в результате 8. Вычитаем эти 2 числа. Получили 1.

Остался остаток равный 1, так как число 1569 у нас закончилось, мы к 1 сносим 0. Вспомним, что любое целое число можно представить как десятичную дробь, просто подписав запятую после числа и далее сколько нужно нулей, что мы и делаем. Раз закончились числа у целого числа и мы поставили запятую сделав его десятичной дробью, то и у частного то есть нашего ответа ставим запятую и только после этого записываем 0 к 1.

Чтобы поделить 10 на 4 нужно взять по 2. Умножаем 2 на 4 получаем в результате 8. Вычитаем эти 2 числа. Получили остаток равный двум 2.

Здесь тоже самое проделываем, сносим ноль к двойке,в результате получаем число 20. Чтобы поделить 20 на 4 нужно взять по 5. Умножаем 5 на 4 получаем в результате 20. Вычитаем эти 2 числа. Получили остаток равный 0.

Но в оформлении примеров мы ни когда у делимого не пишем запятую и нули. Я это сделала чтобы показать от куда берутся нуля, а запись должна выглядеть так:

Подписывайтесь на канал на YOUTUBE и смотри видео, готовься к экзаменам по математике и геометрии с нами.

Хочешь готовиться к экзаменам бесплатно? Репетитор онлайн бесплатно. Без шуток. ЗДЕСЬ

Используйте деление в столбик, чтобы разделить многочлены

Мы знакомы с алгоритмом деления в столбик для обычной арифметики. Мы начинаем с деления дивиденда на цифры, которые имеют наибольшее разрядное значение. Мы делим, умножаем, вычитаем, включаем цифру в позицию следующего разряда и повторяем. Например, разделим 178 на 3 в столбик.

Другой способ взглянуть на решение — как на сумму частей. Это должно показаться знакомым, поскольку это тот же метод, который используется для проверки деления в элементарной арифметике.

[латекс] \ begin {case} \ text {Divisor =} \ left (\ text {divisor} \ cdot \ text {quotient} \ right) \ text {+ elseder} \ hfill \\ 178 = \ left (3 \ cdot 59 \ right) +1 \ hfill \\ = 177 + 1 \ hfill \\ = 178 \ hfill \ end {case} [/ latex]

Мы называем это алгоритмом деления и обсудим его более формально после рассмотрения примера.

Деление многочленов, содержащих более одного члена, похоже на деление целых чисел в столбик. Мы можем записать полиномиальное делимое как произведение делителя и частного, добавленного к остатку.{2} -7x + 18 \ справа) -31 [/ латекс]

Мы можем идентифицировать дивиденд , делитель , частное и остаток .

Запись результата таким образом иллюстрирует алгоритм деления.

Общее примечание: алгоритм деления

Алгоритм деления утверждает, что, учитывая полиномиальное делимое [латекс] f \ left (x \ right) [/ latex] и ненулевой полиномиальный делитель [латекс] d \ left (x \ right) [/ latex] где степень [латекса] d \ left (x \ right) [/ latex] меньше или равна степени [latex] f \ left (x \ right), [/ latex] существуют уникальные многочлены [латекс ] q \ left (x \ right) [/ latex] и [latex] r \ left (x \ right) [/ latex] такие, что

[латекс] f \ left (x \ right) = d \ left (x \ right) q \ left (x \ right) + r \ left (x \ right) [/ латекс]

[латекс] q \ left (x \ right) [/ latex] — это частное, а [latex] r \ left (x \ right) [/ latex] — остаток.Остаток либо равен нулю, либо имеет степень строго меньше, чем [latex] d \ left (x \ right). [/ Latex]

Если [латекс] r \ left (x \ right) = 0, [/ latex], то [latex] d \ left (x \ right) [/ latex] равномерно делится на [латекс] f \ left (x \ right) . [/ latex] Это означает, что в данном случае оба [latex] d \ left (x \ right) [/ latex] и [latex] q \ left (x \ right) [/ latex] являются факторами [latex ] f \ left (x \ right). [/ латекс]

Как: даны полином и бином, используйте деление в столбик, чтобы разделить полином на бином.

Установить проблему разделения.
Определите первый член частного, разделив главный член дивиденда на главный член делителя.
Умножьте ответ на делитель и запишите его под аналогичными членами дивиденда.
Вычтите нижний бином из верхнего бинома.
Уменьшите следующий срок выплаты дивидендов.
Повторяйте шаги 2–5 до последнего члена дивиденда.

Если остаток не равен нулю, выразите дробью, используя делитель в качестве знаменателя.{2} + 20x — 3 [/ латекс] от [латекс] 4x + 5. [/ Латекс]

Решение

Что такое длинное деление? — Learning Street

Что такое длинное деление? Длинное деление — это метод деления больших чисел (3 или более цифр) на числа, состоящие из 2 или более цифр.

Вот как разложить столбик:

Во-первых, 15 не переходит в 8, поэтому посмотрите на следующую цифру.
15 переходит в 86 пять раз, поэтому напишите цифру 5 над 6.
(15 x 5 = 75)
Затем, чтобы вычислить остаток, уберите 75 от 86.
(86-75 = 11)

Затем перенесите 1, чтобы получить 111.
15 переходит в 111 семь раз, поэтому поставьте 7 над 1.
(15 x 7 = 105)
Теперь отнимите 105 от 111, чтобы получить остаток:
111 — 105 = 6

Наконец, перенесите 0 вниз, чтобы получилось 60.

15 переходит в 60 ровно 4 раза, поэтому поставьте 4 над 0.
(15 x 4 = 60)
Это дает вам ответ 574

(8610 ÷ 15).

Когда дети учатся делить в столбик?

В начале ключевого этапа 1 детей учат концепции разделения, учителя, вероятно, представят ее, заставляя детей делить между собой некоторые предметы. Например, некоторым детям можно дать 6 цветных кубиков, а затем попросить отдать половину из них однокласснику, сидящему рядом с ними.

На ключевой стадии 2, после изучения всех своих таблиц умножения и фактов деления, дети начнут использовать сокращенное деление (так называемый метод «автобусной остановки») в 5-м классе. Краткое деление используется для деления трех- или четырехзначных чисел на 1. цифровой номер. Затем учителя познакомят детей с методом деления в столбик, описанным выше, чтобы они могли использовать его для деления больших чисел на двузначные числа.

Как помочь детям с длинным делением?

Использование метода долгого деления потребует, чтобы дети были уверены в своих таблицах умножения и понимали, как умножение соотносится с делением, так как по мере их выполнения необходимо выполнять множество вычислений.Поэтому, если дети испытывают затруднения, было бы неплохо вернуться к своим таблицам умножения и убедиться, что они знают свои факты деления. Например,

если 6 x 4 = 24, то 24 ÷ 6 = 4.

Также важно, чтобы дети понимали различную терминологию, используемую в таких методах, как деление в столбик. Возможно, вам придется объяснить, что остаток — это число, оставшееся после вычисления. Например:

Число 27 не делится точно на 5, но мы можем разделить 25 точно на 5 (так как 5 x 5 = 25).Итак, если бы у Харриет было 27 сладостей, которые она могла бы разделить между ее 5 друзьями, каждая подруга получила бы 5 сладостей, а у Харриет осталось бы 2 конфеты.

Чтобы запомнить, в каком порядке выполнять вычисления в столбце, может быть полезно создать акроним, чтобы сделать его более запоминающимся. Например:

Как Learning Street помогает детям с длинным делением?

Подобно тому, что они будут делать в школе, Learning Street начнет с основ деления на более ранних курсах, поскольку, не зная основ, ребенок не может выучить столбик.Посредством расширения и повторения ребенок будет постепенно развивать свои знания о делении, прежде чем его познакомят с делением в столбик, за которым последуют расширение и повторение.

Тесты

могут включать в себя SAT, конкурсные тесты 11 Plus или выборочные независимые школьные экзамены.

Наши курсы

Нажмите, чтобы просмотреть доступные у нас курсы

длинное деление в предложении

Эти примеры взяты из корпусов и из источников в Интернете.Любые мнения в примерах не отражают мнение редакторов Cambridge Dictionary, Cambridge University Press или его лицензиаров.

Они были так удивлены, что дали ему повторный тест, с тем же длинным делением и умножением, но с изменением цифр.

Только мой учитель математики в начальной школе сказал, что мои длинные деления временами небезопасны.

Это было похоже на переход от длинных делений к биномиальной теореме.

Более того, у вас есть возраст , длинный , , раздел между двумя народами, которые веками были разделены вторжениями и конфликтами.

По сути, генетическая манипуляция похожа на длинное деление ; это метод достижения определенного результата.

Это не просто одна длинных делений сум.

Это действительно операция в длинном делении .

Я говорю о родовых качествах длинных деления .

При 17 млн фунтов стерлингов или около того в год, что займет двадцать шесть лет и три месяца, если мое подразделение long будет правильным, прежде чем будет выплачена общая сумма задолженности.

Популярная пресса обратила внимание на этот интересный вопрос о том, следует ли преподавать в школах длинное деление и длинное умножение без использования калькуляторов.

Длинный деление не используется для деления 1344 на 21.

Из

Википедия

Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Он повторяет использование полинома длинной деления или синтетического деления.
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Эта процедура работает путем вычисления цифр 1 / «p» в базе «b» по длинному делению .
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Одним из таких алгоритмов является long деление , которому учили многих школьников.
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
По сути, в базовом длинном делении есть только конечное число возможных остатков, и поэтому один раз должен быть повторяющийся образец.
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Если вы предпочитаете, мы также можем найти столько десятичных знаков, сколько нам нужно, продолжая цикл, как в стандартном long деление .
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Используя long деление , простое деление целых чисел, например, становится повторяющимся десятичным числом, 0.111 …, в котором цифры повторяются без конца.
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Длинная позиция Раздел из 23 480/37 теперь проходит как обычно, давая 634 с остатком 22.
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Зная таблицы умножения, два целых числа можно разделить на бумаге с помощью метода long деления .
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
По сути, этот метод представляет собой алгоритм длинных делений , адаптированный для мысленных вычислений.
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Длинный Деление стопы дает 1 остаток 29, который затем умножается на двенадцать, чтобы получить 348 дюймов.
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
При работе с модульной арифметикой каждый класс эквивалентности обычно представлен своим общим остатком, например, который можно найти с помощью long деления .
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Все возможные комбинации целочисленных множителей могут быть проверены на достоверность, и каждая действительная из них может быть исключена с использованием полинома длинного деления .
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Алгоритмы целочисленного деления вычисляют частное и остаток по двум целым числам, наиболее известным из таких алгоритмов является длинное деление .
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Это сокращенная форма длин деление .
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Хотя полином длинный деление сложнее, чем вычисление самой функции, синтетическое деление проще в вычислительном отношении.
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Видно, что эти процедуры являются просто механизированными версиями длинных деления и умножения.
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Этот тип повторяющейся десятичной дроби может быть получен с помощью long деления , если используется модифицированная форма обычного алгоритма деления.
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Краткое деление — это сокращенная форма длинного деления , подходящая для однозначных делителей.
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Кроме того, вычитания в длинном делении преобразуются в сложения путем переключения знаков в самом начале, предотвращая ошибки знаков.
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
По сравнению с традиционными методами краткого деления и длинного деления , разбиение на части может показаться странным, бессистемным и произвольным.
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Как и в случае полиномов от переменных, полином в операторе запаздывания можно разделить на другой, используя полином long деление .
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Метод гранки записывает меньше фигур, чем длинных делений , и приводит к получению интересных форм и изображений, поскольку он расширяется как над, так и под начальными линиями.
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Эти методы несколько различаются в зависимости от страны и времени, но обычно включают в себя обмен, перегруппировку, деление на и долгое умножение с использованием стандартных обозначений и стандартных формул для среднего, площади и объема.
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Сокращенная форма длинное деление называется коротким делением, которое почти всегда используется вместо длинного деления, когда делитель состоит только из одной цифры.
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Преимущества синтетического деления заключаются в том, что оно позволяет производить вычисления без записи переменных, использует мало вычислений и занимает значительно меньше места на бумаге, чем long деление .
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Умножение и деление выполняются цифра за цифрой на цифрах множителя или делителя, в процедуре, эквивалентной знакомой процедуре длинного умножения и длинных делений процедур, которым обучают в школе.
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Например, если ученику не хватало твердого понимания сложения, вычитания и умножения, он может не очень хорошо выполнить long деление .
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Его можно было использовать для сложения и вычитания, а с подвижной кареткой оператор также мог умножать и делить с помощью процесса длинного умножения и длинных деления .
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Казалось, что этот мальчик мог довольно эффективно складывать и вычитать, но не умел делать длинных делений и умножений.
Например, в первой статье показаны незначительные вариации обозначений алгоритмов, которые тривиально можно распознать как традиционные long деление .
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Первые два условия удовлетворяются простым определением «g», в то время как третье условие может быть доказано с использованием полинома long деления .
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Деннетт рассматривает эволюцию путем естественного отбора как алгоритмический процесс (хотя он разъясняет, что такие простые алгоритмы, как длинное деление , часто включают значительную степень случайности).
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Эти примеры взяты из корпусов и из источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Cambridge Dictionary, Cambridge University Press или его лицензиаров.
Длинный дивизион (Ключевой этап 2)
Что такое длинное деление? (Интерактивный виджет)
Используйте этот интерактивный виджет , чтобы увидеть пошаговое объяснение деления в столбик.
Вот случайно сгенерированная сумма в виде длинного деления.
Решить сейчас
Пройти пошагово
Сгенерировать новую сумму

Посмотрите похожие виджеты на длинное сложение, длинное вычитание и длинное умножение.
Что такое длинное деление?
Длинное деление — это метод деления чисел.
Длинное деление используется для деления чисел, состоящих из многих цифр.
Реальный пример того, как делать длинное деление
Делить в столбик очень просто. Разделите числа ниже.
Пошаговая инструкция:
Определите число , разделенное на (называемое делимым), и число, которое вы делите на (называемое делителем).
Запишите делимое внутри скобки в длинную делительную скобку и делителя снаружи слева от нее:
Разделите первую цифру делимого (1) на делитель (6).Не считайте остатки.
1 ÷ 6 = 0
6 переходит в 1 0 раза. Напишите ответ (0) над скобкой в столбик.
Умножьте ответ из Step 3 (0) на делитель (6).
0 × 6 = 0
Напишите ответ под цифрой, разделенной на:
Вычтите нижнее число (0) из верхнего числа (1).
1-0 = 1
Приведите следующую цифру делимого (3).
Разделим это число (13) на делитель (6). Не считайте остатки.
13 ÷ 6 = 2 ~~r 1~~
6 переходит в 13 2 раза. Напишите ответ (2) над скобкой в столбик.
Умножьте ответ из Step 8 (2) на делитель (6).
2 × 6 = 12
Напишите ответ под числом, разделенным на:
Вычтите нижнее число (12) из верхнего числа (13).
13–12 = 1
Приведите следующую цифру делимого (8).
Разделим это число (18) на делитель (6). Не считайте остатки.
18 ÷ 6 = 3
6 переходит в 18 3 раза. Напишите ответ (3) над скобкой в столбик.
Умножьте ответ из Step 13 (3) на делитель (6).
3 × 6 = 18
Напишите ответ под числом, разделенным на:
Вычтите нижнее число (18) из верхнего числа (18).
18–18 = 0
Нет больше цифр, которые нужно сбивать.
Ответ:
Решение 138 ÷ 6 равно 23.
Части дивизии
Число, на которое вы делитесь, — это дивидендов .
Число, которое вы разделите на , будет делителем .
Результатом деления является частное .
Short Cut для Long Division
Когда вы приобретете достаточно уверенности, вы заметите, что первые несколько шагов этого урока не нужны.В шаге 3 примера 1 делится на 6, поэтому не будет делиться хотя бы один раз. Поэтому выше было написано 0 . Вместо этого не делите на первую цифру делимого, а двигайтесь по цифрам слева направо, пока не найдете первое число больше делителя.
Только помните, что ответ должен быть написан над последней цифрой. 2 должно быть написано над 3 в 13, а не 1.
Помогите нам улучшить математику Монстр
Вы не согласны с чем-то на этой странице?
Заметили опечатку?
Сообщите нам, используя эту форму
См. Также
Как добавить числовую строку Основы сложения Длинное добавление Как вычесть на числовой прямой Основы вычитания Длинное вычитание Основы умножения Длинное умножение Длинное умножение с десятичными знаками Более пристальный взгляд на умножение Основы деления Деление в столбик с остатком Деление в столбик с десятичными знаками Что такое размещенная стоимость? Что такое числовая линия?
Как сделать длинное деление в Испании и видео тоже! Wagoners Abroad
Как сделать длинное деление в Испании и как делить в США.
Когда мы впервые переехали в Испанию, Ларс учился в 5 классе. Мы знали, что в его возрасте будет немного сложнее выучить испанский и подобрать другие предметы в классе. Мы были уверены, что он сразу же преуспеет в математике. Мы решили, что математика будет одинаковой, независимо от того, где вы находитесь в мире.
Вы берете числа и складываете, вычитаете, умножаете и делите. Как могло быть иначе? Что ж, нас ждал большой сюрприз, когда дело касалось математики, особенно How To Do Long Division в Испании !
Дивизион в Испании идет первым, затем в конце будет Дивизион в США.
Чем отличалось разделение от математики?
Дети не только изучали новый язык и слушали все свои уроки на испанском, но и математика бросила всех нас в тупик. Да математика! Мы думали, что математика — это просто числа, так как же мы могли ошибиться? Для Ани это было не так сложно, ведь раньше в США она занималась только сложением и вычитанием. Для Ларса это было не так.
Конечно, для Ларса сложение и вычитание не было проблемой, но его оценка была намного выше.Он уже выучил дроби и деление в США, поэтому предполагалось, что все будет продолжаться. Вы знаете, что они сделали! Это было именно там, где он должен быть, только вот в Испании числа делят по-другому! Да, вы правильно прочитали.
Длинное деление на испанском отличается от американского!
Я знаю, что вы думаете: «Математика есть математика, как вы можете по-другому делать деление?». Что ж, у нас были такие же мысли. Ларс обратился к нам за помощью с домашним заданием, и мы были в полном тупике.
Все было не в том месте, и мы не могли осмыслить это. Здесь мы как родители и должны быть в состоянии помочь нашим детям. Мы не знали, что делать. Алан быстро поработал в Интернете, чтобы попытаться найти примеры деления в столбик в Испании. Доступных примеров разделения было не так много, но мы собрали все воедино и, в конце концов, это выяснили.
Вы знаете, как вы посещаете страну, которая едет по «другой стороне дороги», и вашему мозгу требуется немного времени, чтобы привыкнуть? Вот вы в такси, сидите на пассажирском сиденье (место водителя в вашей стране), и все кажется неуместным.Вы испытаете тревогу и замешательство. Что ж, эта математика ничем не отличается. Такое чувство, что для нас, американцев, это дислексическое разделение. Ладно, держу пари, вам интересно, о чем я, черт возьми, говорю.
Скажем так, все наоборот!
Зная, что в Испании живет много новых семей с детьми от 10 лет, мы подумали, что было бы здорово предоставить им видео, показывающее, как выполнять деление в столбик в Испании. Иногда все обретает смысл, когда кто-то вам это объясняет.Это особенно сложно для людей этого возраста, поскольку они уже научились делению в столбик в своей стране, поэтому им нужно переучиваться, когда они приедут в Испанию. Что касается Ани, она впервые узнала об этом в Испании и не знает другого. Если мы когда-нибудь вернемся в США, ей будет трудно приспособиться к американскому способу деления на длинные позиции.
Угадайте, это не только в Испании!
Есть 11 стран, которые используют такое же деление в столбик. Иди разберись.Я не уверен, какой путь был первым, но если вы планируете переехать с детьми в любую из этих стран, деление в столбик будет для вас немного другим. С другой стороны, если вы живете в одной из этих стран и планируете переехать в другое место, для вас тоже все будет по-другому.
Испания
Италия
Франция
Португалия
Литва
Румыния
Турция
Греция
Бельгия
Россия
Иран
Как сделать длинное деление в Испании Примеры — Видео
Ларс был достаточно любезен, чтобы создать видео, которое поможет вам и покажет примеры того, как выполнять шаги длинного деления.

Пожалуйста, смотрите и оставляйте комментарии, если у вас есть какие-либо вопросы. Хотя это деление является тем, что мы испытали в Испании, оно также должно применяться, если вы пытаетесь сделать длинное деление в Италии, длинное деление во Франции и некоторых других европейских странах.
Приколите меня на потом!

Жизнь в Испании в качестве американского ребенка-эмигранта — испанская государственная школа образования
Как мы рассказывали вам во многих сообщениях, наши первые несколько месяцев в Испании были, мягко говоря, корректировкой.Вот несколько постов из прошлого, которые вы можете просмотреть на основе нашего опыта проживания в Испании в качестве американской семьи с детьми, посещающими испанские государственные школы.
Расскажите, что вы думаете о разделении на испанском языке. У вас есть чем поделиться? Вы американская семья, живущая в Испании? Неважно, откуда вы, скорее всего, у вас будут свои истории, которыми вы поделитесь с переездом в Испанию, так что не стесняйтесь делиться.
Как сделать длинный дивизион в США!
Многие люди спрашивали нас, чем это отличается от разделения в США.Поэтому вместо того, чтобы создавать новое видео, мы нашли идеальные видео о том, как делить для вас ниже!
Он объясняет все этапы длинного деления в ясной и легкой для обучения манере. Во-первых, это базовое деление одного числа на другое. Далее будет видео о делении в столбик, и вы сразу же узнаете, как делить!
Basic Division USA

Long Division USA

Калькулятор длинного деления | Как легко сделать длинное деление с остатками
Чтобы легко вычислить деление двух чисел, нужно очень хорошо знать процесс и правильно выполнять шаги.Итак, чтобы освоить деление чисел методом длинного деления, мы предоставили здесь подробный процесс вместе с решенным примером.
Деление в столбик с остатком еще никогда не было таким простым! Так что примите это как вызов и решите проблему самостоятельно, следуя приведенным ниже инструкциям.
Чтобы найти результат, который представляет собой отношение двух чисел, т. Е. Делимого и делителя, мы используем метод деления в столбик.
Сначала вам нужно определить дивиденд и делитель, а затем использовать эти значения в столбце.
В числителе данной дроби будет делимое, а в знаменателе — делитель. Обозначьте дивиденд и делитель в виде длинного деления.
Вероятно, вам придется добавить десятичную дробь и нули, если дивиденд меньше делителя. Продолжайте деление в столбик, пока не получите правильный результат для заданных чисел. Он выдаст остаток как в виде целого числа, так и в десятичном формате.
Результат может быть записан разными способами как частное и остаток, дробь и десятичная дробь, преобразованная из дроби.
Для лучшего понимания метода деления в столбик мы привели отработанный пример деления чисел методом деления в столбик. Обратитесь к приведенному ниже примеру и изучите пошаговый процесс решения деления в столбик.
Пример:
Рассчитать деление для 678/35 с помощью метода длинного деления?
Решение:
В данном входе 678/35 678 — числитель i.е. дивиденд, а 35 — знаменатель, т. е. делитель. Поскольку дивиденд больше делителя, вы можете продолжить процесс деления в длину и получить результат как таковой
Следовательно, коэффициент равен 19 , а остаток равен 13 .
Объяснение урока: полиномиальное деление в длину с остатком
В этом пояснительном механизме мы узнаем, как найти частное и остаток при делении многочленов, в том числе и в случае неприводимости дивизора.
Как и в случае с целыми числами, деление многочлена 𝑝 (𝑥) (делимого) на делитель 𝑑 (𝑥) дает частное 𝑞 (𝑥) и остаток 𝑟 (𝑥).
Напомним, что многочлен — это конечная сумма одночленов с неотрицательными показателями. Следовательно, выражения вида 2𝑥 + 2, 𝑥𝑦 − 10𝑥𝑦 + 𝑥 и 8 являются примерами многочленов, тогда как такие выражения, как √𝑥, 3𝑥 и 3𝑥 не являются полиномиальными выражениями. В этом объяснении мы сосредоточимся на делении многочленов от одной переменной.
Обычно при рассмотрении деления многочленов пишут 𝑝 (𝑥) 𝑑 (𝑥), а не 𝑝 (𝑥) ÷ 𝑑 (𝑥). Мы можем думать о делении в столбик как о найти многочлены 𝑞 и 𝑟 такие, что 𝑝 (𝑥) 𝑑 (𝑥) = 𝑞 (𝑥) + 𝑟 (𝑥) 𝑑 (𝑥) и мы говорим, что деление дает частное 𝑞 (𝑥) и остаток 𝑟 (𝑥).
Мы можем записать это эквивалентно как уравнение умножения следующим образом:
Однако не все уравнения в этой форме являются уравнениями с делением. Например, рассмотрим уравнение 2𝑥 + 7𝑥 − 4 = (𝑥 − 3) × (𝑥 − 1) + 𝑥 + 11𝑥 − 7.
Это можно записать как 2𝑥 + 7𝑥 − 4𝑥 − 3 = (𝑥 − 1) + 𝑥 + 11𝑥 − 7𝑥 − 3 но это не квалифицируется как деление на − 3, потому что, как и в случае с целочисленное деление, остаток всегда должен иметь меньшую степень, чем делитель.
Правильным уравнением деления в этом случае будет 2𝑥 + 7𝑥 − 4𝑥 − 3 = (2𝑥 + 13) + 35𝑥 − 3.
Остаток равен 35, который имеет степень 0, которая меньше степени от − 3, что равно 1.
Когда мы используем алгоритм деления, чтобы получить 𝑟 степени меньше, чем 𝑑, частное 𝑞 и остаток равны однозначно определен.Теперь мы опишем алгоритм деления, который мы можем использовать, чтобы найти 𝑞 и 𝑑.
Полное деление многочленов во многом аналогично полному делению целых чисел: на каждом шаге мы сравните старший коэффициент делителя с текущим остатком, который начинается с сам дивиденд. Цель на каждом этапе — удалить этот ведущий термин. Давайте посмотрим на примере того, как это сделать.
Воспользуемся примером деления 2𝑥 + 7𝑥 − 4 на 𝑥 − 3. чтобы продемонстрировать метод.
На первом этапе мы делим член высшей степени в дивиденде на член высшая степень в делителе. Следовательно, делим 2𝑥 на 𝑥 чтобы получить 2𝑥.
Результат этого деления пишем над чертой.
Теперь умножим этот член на делитель и запишем результат под делимым так, чтобы что члены равной степени выровнены.
Теперь вычтем полученное выражение из дивиденда.
В результате мы должны исключить термин с наивысшей степенью.Затем мы можем сбить члены дивиденда, чтобы получить выражение для нашего первого остатка. Если это из равной или более высокой степени, чем делитель, как здесь, мы повторяем этот процесс снова.
Отсюда делим члены высшей степени. То есть делим 13𝑥 на 𝑥, чтобы получить 13.
Мы пишем это над строкой рядом с нашим последним членом.
Теперь умножим этот член на делитель и запишем результат под делимым так, чтобы члены равной степени выравнивают.
Теперь вычтем полученное выражение из первого остатка.
В результате мы должны исключить термин с наивысшей степенью. На данный момент мы остаются с членом более низкой степени, чем делитель, поэтому мы останавливаемся. Частное 𝑞 (𝑥) — выражение над линией, а остаток это выражение внизу.
Обычно мы пишем это кратко следующим образом:
Условные обозначения, используемые при предварительном формировании длинного деления таким образом, относительно размещения члены многочленов меняются.Однако техника та же.
Пример 1: Полиномиальное деление в длину с делителем первой степени
Используйте полиномиальное деление для упрощения 2𝑥 + 5𝑥 + 7𝑥 + 4𝑥 + 1.
Ответ
В этом примере мы ожидаем нулевой остаток:
Таким образом, упрощение 2𝑥 + 5𝑥 + 7𝑥 + 4𝑥 + 1 = 2𝑥 + 3𝑥 + 4.
Следствием нулевого остатка является факторизация. В частном случае линейного дивизора получаем следующее.
Теорема о множителях
Многочлен 𝑝 (𝑥) делится на (𝑥 − 𝑎) (с нулевым остатком) тогда и только тогда, когда 𝑝 (𝑎) = 0.
Другими словами, когда 𝑎 является нулем полинома.
Так 𝑝 (𝑥) = (𝑥 − 𝑎) 𝑞 (𝑥) именно тогда, когда 𝑝 (𝑎) = 0.
Пример 2: Теорема о множителях и деление в столбик
Путем факторизации найдите все решения 𝑥 − 𝑥 − 14𝑥 + 24 = 0, учитывая, что (𝑥 + 4) множится в 𝑥 − 𝑥 − 14𝑥 + 24.
Ответ
Поскольку (𝑥 + 4) является множителем этого многочлена, мы можем использовать множитель теорема, чтобы заключить, что −4 является нулем многочлена. Мы можем использовать полиномиальное деление, чтобы найти другие факторы.
Так 𝑥 − 𝑥 − 14𝑥 + 24 = (𝑥 + 4) 𝑥 − 5𝑥 + 6 и мы можем факторизовать эту квадратичную, например, путем проверки: 𝑥 − 5𝑥 + 6 = (𝑥 − 2) (𝑥 − 3)  и поэтому 𝑥 − 𝑥 − 14𝑥 + 24 = (𝑥 + 4) (𝑥 − 2) (𝑥 − 3) .
Фактор (𝑥 − 2) соответствует нулю = 2, множитель (𝑥 − 3) дает нуль 𝑥 = 3. Итак, нули 𝑥 = 2, 𝑥 = 3, 𝑥 = −4.
Используя тот же метод, мы можем выполнить полиномиальное деление в столбик, когда делитель равен степени больше единицы. В следующем примере мы продемонстрируем это.
Пример 3: Полиномиальное деление в столбик с делителями более высокой степени
Используйте полиномиальное деление в столбик, чтобы найти частное 𝑞 (𝑥) а остаток 𝑟 (𝑥) при 𝑝 (𝑥) 𝑑 (𝑥), где 𝑝 (𝑥) = 𝑥 + 𝑥 + 𝑥 + 𝑥 + 𝑥 + 1 и 𝑑 (𝑥) = 𝑥 + 𝑥 + 1.
Ответ
Применяя алгоритм деления в столбик, получаем следующее деление:
Следовательно, частное 𝑞 (𝑥) = 𝑥 + 𝑥 − 𝑥 − 𝑥 и остаток 𝑟 (𝑥) = 3𝑥 + 2𝑥 + 1.
Конечно, не всегда следует ожидать, что в результате будут получены многочлены 𝑞 (𝑥) и 𝑟 (𝑥) иметь целые коэффициенты, даже если 𝑝 (𝑥) и 𝑑 (𝑥) делают.Следующий пример демонстрирует это.
Пример 4: Полиномиальное деление в длину
Выразите деление 𝑝 (𝑥) 𝑑 (𝑥) = 2𝑥 − 𝑥 + 52𝑥 − 5𝑥 + 8 в виде 𝑞 (𝑥) + 𝑟 (𝑥) 𝑑 (𝑥).
Ответ
Используя алгоритм деления в столбик, получаем следующее деление в столбик:
Следовательно, 2𝑥 − 𝑥 + 52𝑥 − 5𝑥 + 8 = 𝑥 + 52 + 𝑥 − 152𝑥 − 5𝑥 + 8.
Фактор-теорема является частным случаем теоремы об остатке.
Теорема об остатке
Когда многочлен 𝑝 (𝑥) делится на (𝑥 − 𝑎), остаток — постоянная 𝑝 (𝑎).
Пример 5: Теорема об остатке
Найдите остаток от деления 4𝑥 + 4𝑥 + 3 на 2𝑥 − 3.
Ответ
Хотя это можно сделать с помощью деления в столбик, мы также можем использовать теорему об остатке. Мы должны быть осторожны с приложением, потому что (2𝑥 − 3) не (𝑥 − 𝑎) для любого 𝑎. Однако предположим, что 𝑝 (𝑥) = 4𝑥 + 4𝑥 + 3 = (2𝑥 − 3) 𝑞 (𝑥) + 𝑟 с остатком — константа и фактор (𝑥). С 2𝑥 − 3 = 2𝑥 − 32, мы можем переписать вышеизложенное как 4𝑥 + 4𝑥 + 3 = 2𝑥 − 32𝑞 (𝑥) + 𝑟.
Это говорит о том, что остаток при 4𝑥 + 4𝑥 + 3 делится на 2𝑥 − 3 совпадает с остатком от деления на 𝑥 − 32. Поскольку это имеет правильный вид, применима теорема об остатке и 𝑟 = 𝑃32 = 432 + 432 + 3 = 44 (9) +42 (3) + 3 = 9 + 6 + 3 = 18.
Пример 6: Использование полиномиального деления в длину
Найдите значение, при котором выражение 30𝑥 + 57𝑥 − 48𝑥 − 20𝑥 + 𝑘 делится на 5𝑥 − 8.
Ответ
Это можно сделать полиномиальным делением.Мы должны ожидать остатка степени 1 или меньше, что будет включать константу 𝑘 и установить ее на ноль определит требуемый 𝑘.
Первый шаг — убедиться, что дивиденд правильно записан в порядке убывания. степени 𝑥: 𝑝 (𝑥) = 30𝑥 − 20𝑥 − 48𝑥 + 57𝑥 + 𝑘.
Используя алгоритм:
, мы находим, что остаток имеет степень 0 и равен 𝑘 + 40.
Поскольку 5𝑥 − 8 является множителем, только если деление дает нулевой остаток, условие на 𝑘 таково, что + 40 = 0; другими словами 𝑘 = −40.
Обратите внимание, что метод, использованный выше, всегда будет работать. Альтернатива (которая применима здесь) заключается в использовании теоремы об остатке. Обратите внимание, что 5𝑥 − 8 имеет нули ± 85. Если 𝑝 (𝑥) = 5𝑥 − 8𝑞 (𝑥)  с некоторым фактором 𝑞 (𝑥), затем вычисляя 𝑝 (𝑥), скажем, при 𝑎 = 85 должен дать ноль. Действительно, мы находим 𝑝85 = 𝑘 + 40.
Ключевые моменты
Используя аналогичный алгоритм для целочисленного деления в столбик, мы можем разделить многочлены.
Если мы разделим многочлен на множитель, мы не получим остатка.В противном случае мы будем слева с остатком степени меньше степени делителя.
Для простых линейных множителей вида 𝑥 − 𝑎 можно найти остаток применяя теорему об остатке, которая утверждает, что когда многочлен 𝑝 (𝑥) делится на (𝑥 − 𝑎), остаток — постоянная 𝑝 (𝑎).