Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

Справочник по математике

Алгебра

Деление многочленов. Корни многочленов

      Напомним, что разделить натуральное число   a   на натуральное число   b   – это значит представить число   a   в виде:

a = bc + r ,

где частное   c   и остаток   r   – целые неотрицательные числа, причем остаток   r   удовлетворяет неравенству:

      Если друг на друга делить многочлены, то возникает похожая ситуация.

      Действительно, при выполнении над многочленами операций сложения, вычитания и умножения результатом всегда будет многочлен. В частности, при перемножении двух многочленов, отличных от нуля, степень произведения будет равна сумме степеней сомножителей.

      Однако в результате деления многочленов многочлен получается далеко не всегда.

      Говорят, что один многочлен нацело (без остатка) делится на другой многочлен, если результатом деления является многочлен.

      Если же один многочлен не делится нацело на другой многочлен, то всегда можно выполнить деление многочленов с остатком, в результате которого и частное, и остаток будут многочленами.

      Определение. Разделить многочлен   a(x)   на многочлен   b(x)   с остатком – это значит представить многочлен   a(x)   в виде

a(x) = b(x) c(x) + r(x) ,

где многочлен   c(x)   – частное, а многочлен   r(x)   – остаток, причем, степень остатка удовлетворяет неравенству:

      Очень важно отметить, что формула

a(x) = b(x) c(x) + r(x)

является тождеством, т. е. равенством, справедливым при всех значениях переменной   x .

      При делении (с остатком или без остатка) многочлена на многочлен меньшей степени в частном получается многочлен, степень которого равна разности степеней делимого и делителя.

      Один из способов деления многочленов с остатком – это деление многочленов «уголком», что представляет собой полную аналогию с тем, как это происходит при делении целых чисел.

      К описанию этого способа деления многочленов мы сейчас и переходим.

      Пример. Заранее расположив многочлены по убывающим степеням переменной, разделим многочлен

2x⁴ – x³ + 5x² – 8x + 1

на многочлен

x² – x + 1 .

      Решение. Опишем алгоритм деления многочленов «уголком» по шагам:

1. Делим первый член делимого   2x⁴   на первый член делителя   x².   Получаем первый член частного   2x² .
2. Умножаем первый член частного   2x²   на делитель   x² – x + 1,   а результат умножения

2x⁴ – 2x³ + 2x²

пишем под делимым   2x⁴ – x³ + 5x² – 8x + 1 .

3. Вычитаем из делимого написанный под ним многочлен. Получаем первый остаток

x³ + 3x²– 8x .

Если бы этот остаток был равен нулю, или был многочленом, степень которого меньше, чем степень делителя ( в данном случае меньше   2),   то процесс деления был бы закончен. Однако это не так, и деление продолжается.

4. Делим первый член остатка   x³   на первый член делителя   x² .   Получаем второй член частного   x .
5. Умножаем второй член частного   x   на делитель    x² – x + 1 ,    а результат умножения

x³ – x² + x

пишем под первым остатком   x³ + 3x²– 8x .

6. Вычитаем из первого остатка написанный под ним многочлен. Получаем второй остаток

4x² – 9x + 1 .

Если бы этот остаток был бы равен нулю, или был многочленом, степень которого меньше, чем степень делителя, то процесс деления был бы закончен. Однако это не так, и деление продолжается.

7. Делим первый член второго остатка   4x²   на первый член делителя   x² .   Получаем третий член частного   4.
8. Умножаем третий член частного   4   на делитель   x² – x + 1 ,   а результат умножения

4x² – 4x + 4

пишем под вторым остатком.

9. Вычитаем из второго остатка написанный под ним многочлен. Получаем третий остаток

   – 5x – 3 .

   Степень этого остатка равна   1,   что меньше, чем степень делителя. Следовательно, процесс деления закончен.

10. Таким образом,

2x⁴ – x³ + 5x² – 8x + 1 =
= (x² – x + 1) (2x² + x +
+ 4) – 5x – 3 ,

где

      Запись изложенного процесса деления многочленов «уголком» имеет следующий вид:

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Деление | Математика

Определить, сколько раз нужно взять слагаемым меньшее число 2, чтобы получить большее число 6, значит определить, сколько раз число 2 содержится в 6, или сколько раз число 6 содержит 2.

Число 2 содержится в 6 три раза, ибо, чтобы получить 6, нужно взять сумму трех равных слагаемых:

6 = 2 + 2 + 2

Найти, сколько раз число 2 содержится в 6, значит разделить 6 на 2.

Определение. Деление есть такое действие, в котором по двум данным числам определяют, сколько раз одно число содержится в другом.

Данные числа в делении называются делимым и делителем, искомое называется частным.

Делимое есть то число, которое содержит другое.

Делитель есть то число, которое содержится в другом.

Частное показывает, сколько раз делитель содержится в делимом.

В данном примере делимое есть 6, делитель 2, частное 3.

Разделить 6 на 2 значит также разбить 6 на 2 равных слагаемых и отыскать их величину. Число 6 представится при помощи двух равных слагаемых в виде:

6 = 3 + 3

Каждое из равных слагаемых называется частью делимого.

Посредством деления целых чисел также узнается, как велико каждое слагаемое, если делимое разобьется на столько равных слагаемых, сколько в делителе единиц.

В этом случае делимое есть то число, которое делится или разбивается на равные части. Делитель показывает, на сколько равных частей делится делимое. Частное показывает, сколько приходится на каждую часть.

Способы деления

Имея два числа 12 и 4, мы можем разделить 12 на 4 различными способами.

1. С помощью сложения мы можем определить, сколько раз нужно взять 4 слагаемым для того, чтобы получить в сумме 12. Так, взяв 4 слагаемым 3 раза, находим в сумме:

   4 + 4 + 4 = 12,

   следовательно, 4 содержится в 12 три раза.

2. С помощью вычитания определяем, сколько раз можно из большего числа 12 вычесть меньшее 4. При этом мы вычитаем делитель до тех пор, пока это возможно. Так, вычитая последовательно из 12 по 4, имеем:

   12 — 4 = 8
   8 — 4 = 4
   4 — 4 = 0

   Отсюда находим, что можно вычесть 4 из 12 ровно три раза.

   Деление есть сокращенное вычитание равных вычитаемых.

3. Наконец, посредством умножения, мы можем определить, на какое число нужно помножить 4, чтобы получить 12. Умножая последовательно 4 на 1, 2, 3, находим, что для того, чтобы получить 12, нужно 4 помножить на 3.

Различные случаи при делении

При делении целых чисел бывают два случая:

1. Разделяя 12 на 4, мы находим в частном 3. Делитель 4 содержится ровно 3 раза в делимом 12. Вычитая последовательно из 12 по 4, мы могли вычесть число 4 ровно три раза и не получили никакого остатка. В этом случае говорят, что деление совершилось нацело или без остатка. Умножив частное 3 на делитель 4, получаем делимое 12.

2. Разделяя 26 на 8, мы при последовательном вычитании получаем:

26 — 8 = 18
18 — 8 = 10
10 — 8 = 2

Далее нельзя продолжать вычитания, потому что из 2 нельзя вычесть делитель 8. Число 2 называют остатком.

Остаток всегда меньше делителя. В этом случае говорят, что деление не совершается нацело

или деление совершается с остатком.

Разделяя 26 на 8, мы могли вычесть делитель 8 три раза, и у нас получился остаток 2. Число 3 мы будем называть целым частным. Целое частное есть не полное частное, ибо оно не выражает вполне, сколько раз меньшее число содержится в большем. Число 8 не содержится в 26 ровно 3 раза. В этом случае говорят: число 8 содержится в 26 три раза и еще получается остаток. Умножив делитель 8 на целое частное 3, мы не получим делимого 26, а число 24 — меньшее делимого. Чтобы получить делимое, нужно к этому произведению прибавить еще остаток 2.

Целое частное иногда называют просто частным.

Итак, при делении мы имеем два случая:

1. Деление нацело или без остатка. Когда делитель содержится в делимом ровное число раз, тогда деление совершается нацело или без остатка. Частное выражает, сколько раз делитель содержится в делимом.

   Делимое равно делителю, умноженному на частное. В этом случае деление есть действие в котором по данному произведению и одному из производителей находится другой производитель.

   Если дается произведение и множимое, отыскивают множитель, то есть число равных слагаемых; если дается произведение и множитель, отыскивают множимое, то есть величину равных слагаемых.

2. Деление с остатком. Когда делитель не содержится в делимом ровное число раз, тогда деление не совершается нацело, или деление совершается с остатком. Остаток всегда меньше делителя и делимое равно произведению делителя на целое частное, сложенное с остатком.

При делении целых чисел делимое всегда уменьшается во столько раз, сколько в делителе единиц, поэтому деление есть действие, обратное умножению.

Знак деления

1. Действие деления изображается знаком двоеточия ÷, который ставится между делимым и делителем.

   Деление числа 6 на 2 изображают письменно:

   6 ÷ 2 = 3 частное.

2. Действие деления обозначается также начертанием |–, где вертикальная черта отделяет делимое, а горизонтальная делитель от частного.

   В данном примере имеем:

В нашем примере деление изображается письменно:

Знак деления прешел к нам от древних математиков.

Основные приемы при делении

Делить значит последовательно вычитать делитель из делимого, пока это возможно. Этот способ деления можно считать общим. Прием этот, однако, приводит к длинным вычислениям, если делимое очень велико, поэтому существуют различные сокращенные приемы деления.

Чтобы определить частное в том случае, когда оно выражается одной цифрой, прибегают к таблице умножения.

Чтобы разделить 27 на 3 мы пишем

Для частного выбираем такое число, чтобы, умножив делитель на частное, получить делимое. Чтобы найти цифру частного, мы пробуем умножать делитель на разные числа или, как обыкновенно говорят, задаемся разными числами, и сравниваем произвдение делителя на частное с делимым.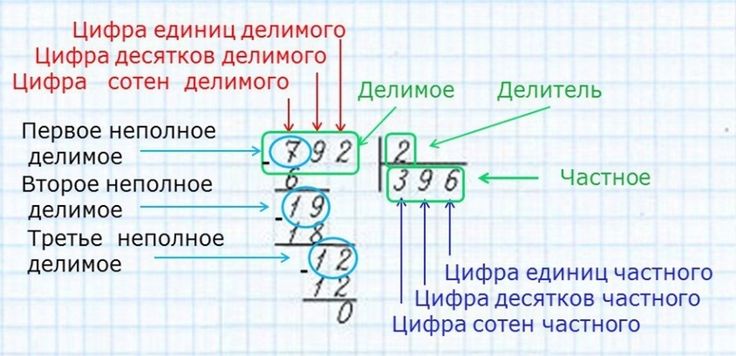

Разделяя 27 на 3 и перебирая в уме все произведения 3 на разные числа, содержащиеся в таблице умножения, находим, что произведение 3 × 9 составляет 27 и потому пишем в частном 9. Вычитая произведение делителя на частное из делимого, получаем в остатке нуль.

Само вычисление выражают письменно:

Деление совершилось нацело.

Иногда делитель не содержится в делимом ровное число раз; так, разделяя 27 на 4, мы не находим в таблице целого числа, которое, будучи помножено на 4, дало бы 27; тогда деление не совершается нацело.

Отыскивая целое частно, мы имеем при этом три случая:

1. Или мы задаемся очень малым числом; так, для данного примера, задавшись в частном 5 и умножив 4 на 5, имеем 20. Подписав произведение 20 под делимым и вычитая из 27, имеем:

   в остатке число 7 больше делителя 4. Это показывает, что частное 5 мало и его нужно увеличить.

2. Или, взяв для частного 7 и умножив его на делителя 4, получаем произведение 28 больше делимого, что показывает, что мы задались в частно очень большим числом. В таком случае нужно уменьшить цифру частного 7.

3. Взяв для частного 6, мы ход вычисления выражаем письменно:

   словесно: 4 в 27 содержится 6 раз, 4 * 6 = 24, подписываем 24 под делимым, вычитаем и получаем остаток 3. Остаток 3 меньше делителя, следовательно, цифра частного верна. Отсюда выводим следующее:

Правило определения частного:

1. Если при делении остаток более или равен делителю, цифра частного мала и ее нужно увеличить.

2. Если произведение делителя на частное больше делимого, цифра частно велика и ее нужно уменьшить.

3. Если остаток меньше делителя, цифра частного верна.

Это правило показывает, что при делении нужно для частного выбирать такое число, чтобы остаток был меньше делителя. Задаваться так, значит задаваться наибольшим целым числом.

В данном примере 27 не делится нацело на 4, а получается остаток 3; число 6 есть целое частное и

27 = 4 × 6 + 3 = 24 + 3

Делимое 27 равно произведению делителя 4 на целое частное 6, сложенному с остатком 3.

Деление многозначного числа на однозначное

Частное от деления многозначного числа на однозначное иногда выражается числом, состоящим также из нескольких цифр. В этом случае деление распадается на несколько отдельных действий.

Разделим 702 на 3. Частное содержит три цифры. Оно больше 100 и меньше 1000, ибо делимое больше 300 (3 × 100) и меньше 3000 (3 × 1000). Включая три цифры, частное содержит сотни, десятки и единицы. В данном случае разбиваем деление на три отдельных действия, то есть отыскиваем последовательно сотни, потом десятки и, наконец, единицы частного. Самое действие начинаем с сотен.

1. Отыскиваем сотни частного. Цифра сотен частного может происходить от деления сотен делимого на делитель 3. Десятки и единицы делимого не имеют никакого влияния на сотни частного, поэтому на них пока не обращаем внимания. Наибольшее число сотен в частном есть 2, ибо 3 содержится в 7 сотнях 2 сотни раз; пишем в частном 200. Умножая 200 на 3 и вычитая произведение 600 из делимого, получаем первый остаток 132.

2. Отыскиваем десятки частного. В остатке 132 находится 12 десятков. Единицы делимого не имеют влияния на десятки частного. Разделив 13 на 3, находим, что в частном могут быть только 4 десятка, — пишем 40 в частном. Умножая 40 на 3 и вычитая произведение 120, получаем в остатке 12.

3. Отыскиваем единицы частного. Разделив 12 на 3, находим для единиц частного 4. Умножая 4 на 3 и вычитая произведение 12, получаем в остатке 0.

Если не писать каждый раз лишних нулей и принимать в соображение только те цифры делимого, которые имеют влияние на частное, деление изобразится письменно:

словесно:

1. Отделяем 7 — одну цифру делимого; 3 в 7 содержится 2 раза, — пишем в частном 2; умножая на нее делителя 3 и вычитая произведение 6 из 7, получаем первый остаток 1.

2. Сносим 3 — следующую цифру делимого; 3 в 13 содержится 4 раза, 3-жды 4 составляет 12; вычитая 12 из 13, получаем в остатке 1.

3. Сносим 2 следующую цифру делимого; 3 в 12 содержится 4 раза, пишем в частном 4; 3-жды 4 составляет 12. Вычитая 12, получаем в остатке нуль и в частном 244.

Пример. Разделить 2417 на 3. Ход вычисления выразится письменно:

словесно:

1. Отделив одну цифру 2, мы видим, что 3 в 2 не содержится целое число раз, поэтому нужно отделить две цифры; 3 в 24 содержится 8 раз, — пишем 8 в частном. Умножив 8 на делителя 3 и вычитая произведение 24, получаем в остатке нуль.

2. Сносим следующую цифру 1; 3 в 1 не содержится, — пишем в частном нуль.

3. Сносим следующую цифру 7; 3 в 17 содержится 5 раз, — пишем в частном 5; 3-жды 5 составляет 15; вычитая 15 из 17, получим в остатке 2 и целое частное 805.

Деление многозначного числа на многозначное

При делении многозначного числа на многозначное поступаем точно так же, как поступали при делении многозначного числа на однозначное.

Разделяя число 37207 на 47, мы прежде всего определяем, из скольких цифр состоит частное. Частное меньше 1000 и больше 100, ибо 37207 меньше 47000 (47 × 1000) и больше 4700 (47 × 100), следовательно, частное состоит из сотен, десятков и единиц. Начиная с сотен, мы определяем каждую цифру частного отдельно:

1. Определяем сотни частного:

   Делимое 37207 имеет 372 сотни. Десятки и единицы делимого не имеют влияния на цифру сотен частного. В частном может быть только 7 сотен, ибо 47 содержится в 372 семь раз; пишем в частном 700.

   Умножая делитель на частное и вычитая из делимого, получаем первый остаток 4307.

2. Определяем десятки частного:

   Остаток 4307 содержит 430 десятков. Единицы не имеют влияния на цифру десятков частного. Делитель 47 содержится в 430 девять раз; пишем в частном 90.

   Умножая 90 на частное 47 и вычитая произведение 4330, получаем в остатке 77.

3. Определяем единицы частного:

   47 содержится в 77 один раз. Пишем в частном 1 и, вычитая из 77 произведение единицы на делитель, получаем в остатке 30.

Итак, после деления имеем в целом частном 791 и в остатке 30.

Если не писать каждый раз лишних нулей и принимать в соображение только те цифры делимого, которые имеют влияние на частное, ход вычисления изобразится письменно:

словесно:

1. Отделяем в делимом от левой руки к правой столько цифр, чтобы делитель мог содержаться в отделенной части делимого. В данном случае отделяем 3 цифры, 47 содержится в 372 семь раз; умножаем делитель 47 на 7, цифру частного, и, вычитая произведение 47 × 7 = 329 из 372, получаем в остатке 43.

2. К остатку 43 сносим 0, следующую цифру делимого; 47 содержится в 430 девять раз, пишем в частном 9. Умножая 47 на 9 и вычитая произведение 423 из 430, получаем остаток 7.

3. Сносим к остатку следующую цифру частного 7; 47 содержится в 77 один раз. Пишем единицу в частном.

Умножая ею делитель и вычитая 47 из 77, получаем в остатке 30 и в целом частно 791.

Пример. Разделить 671064 на 335. Деление изобразится письменно:

словесно:

1. Отделяем 671 в делимом; 335 содержится в 671 два раза, пишем в частном 2. Умножая 335 на 2 и вычитая произведение 670, получим в остатке 1.

2. Сносим 0, следующую цифру делимого; 335 не содержится в 10, — пишем для второй цифры частного 0.

3. Сносим 6, следующую цифру делимого; 335 не содержится в 106, — пишем для третьей цифры частного 0.

4. Сносим следующую цифру делимого 4; 335 содержится в 1064 три раза, — пишем в частном 3. Умножая делитель на 3 и вычитая произведение, получим в остатке 59 и в целом частном 2003.

Из предложенных примеров выводим следующее правило:

1. Чтобы разделить многозначное число на однозначное или многозначное, нужно отделить в делимом от левой руки к правой столько цифр, сколько их находится в делителе. Если делитель не содержится, отделяют в делимом одной цифрой больше. Разделив отделенное число на делитель, получают первую цифру частного, умножают ей делитель и полученное произведение вычитают из отделенной части делимого.

2. К остатку сносят следующую цифру делимого и снова задаются.

3. Если при этом получается число меньше делителя, пишут в частном нуль, сносят следующую цифру и снова задаются.

4. Получив новую цифру частного, поступают с нею так же, как и с первой цифрой.

5. Деление продолжают до тех пор, пока не снесут всех цифр делимого и не получат таким образом всех цифр частного.

Всякий раз, когда приходится делить, нужно задаваться в частном такою цифрой, чтобы остаток был меньше делителя. Чтобы легче найти такую цифру частного, при делении многозначного числа на многозначное обращают внимание на одну или две старшие цифры делителя и задаются только ими в соответствующей части делимого. При этом в делимом и в делителе отделяют от правой руки к левой одинаковое число цифр.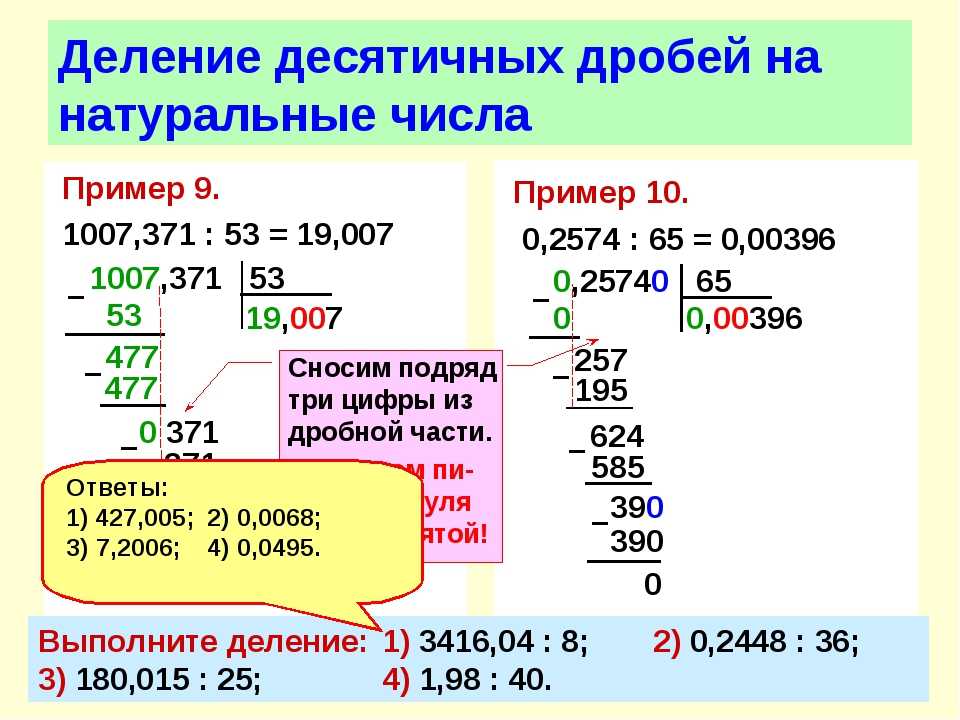 Так, определяя, сколько раз содержится 6373 в 27302, мы задаемся четырьмя, ибо 6 в 27 содержится 4 раза.

Полученная при этом цифра частного будет или равна или больше действительной. В последнем случае ее нужно уменьшить.

Иногда при делении не подписывают произведение цифры частного на делитель, а, подразумевая его в уме, подписывают один остаток. Сокращая таким образом деление, изображают его письменно:

словесно:

1. 8 в 43 содержится 5 раз; 5-ю 8 — сорок. Вычитая 40 из 43, получаем в остатке 3.

2. Сносим 2; 8 в 32 содержится 4 раза; 4-жды 8 составляет 32. Вычитая 32, получим в остатке нуль.

3. Сносим 8; 8 в 8-ми содержится 1 раз, 1-жды 8 составляет 8. Вычитая 8, получаем в остатке нуль и в частном 541.

Деление на 10, 100, 1000 и т. д.

Разделяя число на 10, мы десятки делимого обращаем в единицы, сотни в десятки, тысячи в сотни, вообще понижаем на единицу все порядки делимого. Этого мы достигаем, отделяя запятою цифру единиц. Число до запятой будет выражать частное, а после запятой — остаток.

Разделяя на 100, мы понижаем все порядки делимого на две единицы, для чего отделяем запятою от правой руки к левой две цифры и т. д. Отсюда правило:

Чтобы разделить какое-нибудь число на единицу с нулями, нужно от правой руки к левой отделить столько цифр, сколько нулей в делителе; тогда число до запятой выражает целое частное, а после запятой — остаток.

Пример. Разделяя 30207 на 100. Отделяя справа 2 цифры, находим 302,07. Целое частное будет 302, а остаток 7.

Деление на число, оканчивающееся нулями

Разделяя число 27057 на 400 и поступая при этом по общему правилу

мы замечаем, что две последние цифры делимого не оказывают никакого влияния на частное. Они являются в остатке без всякой перемены. Откуда правило:

Если делитель оканчивается нулями, отделяют в делимом запятою от правой руки к левой столько цифр, сколько зачеркнуто нулей в делителе, и делят часть делимого до запятой на значащие цифры делителя. Отделенные цифры делимого приписывают к остатку.

В данном примере деление представится в виде

f

Если делимое и делитель оканчиваются нулями, их зачеркивают поровну в делимом, делителе и производят деление; зачеркнутые нули делимого приписывают к остатку.

Чтобы разделить 27300 на 4100, делим 273 на 41:

Частное будет 6, а остаток 2700.

Число цифр частного. При делении отделяют в делимом от левой руки к правой столько цифр, сколько их находится во делителе, или одною больше. Каждой оставшейся цифре делимого соответствует особая цифра частного, следовательно, число цифр частного будет равно или разности числа цифр делимого и делителя или на единицу больше этой разности.

Зависимость между данными и искомыми деления

При делении целых чисел мы имеем два случая: а) деление нацело, или без остатка, и б) деление с остатком.

Каждому из этих случаев соответствует особая зависимость между данными и искомыми деления.

Деление нацело или без остатка

При делении нацело

1. Частное равно делимому, разделенному на делитель.

   Разделяя 42 на 7, имеем в частном 6; следовательно,

   42 ÷ 7 = 6, или 6 = 42 ÷ 7

2. Делимое равно делителю, умноженному на частное.

   42 = 6 × 7

3. Так как делитель и частное — два множителя, произведение которых равно делимому, то делитель равен делимому, разделенному на частное.

   7 = 42 ÷ 6

Деление с остатком

При делении с остатком

1. Делимое равно произведению делителя на целое частное, сложенное с остатком.

   При делении 47 на 6, имеем в целом частном 7, в остатке 5.

   Делимое 47 = 6 × 7 + 5.

2. Делимое без остатка делится нацело на делитель и на целое частное.

Разность делимого без остатка равна произведению делителя на целое частное, то есть эта разность при делении на делитель дает целое частное, при делении на целое частное дает делитель.

Объяснение урока: Полиномиальное деление в длинное без остатка

В этом объяснении мы узнаем, как выполнять деление многочленов в длинное.

Прежде чем мы начнем объяснять процесс деления многочленов в длину, давайте сначала вспомним, что значит делить целые числа и как мы применяем деление в длину к целым числам.

Если у нас есть два целых числа 𝑎 и 𝑏, где 𝑏 не равно нулю, то 𝑎𝑏 — это число что при умножении на 𝑏 дает 𝑎. Следовательно, 𝑎𝑏×𝑏=𝑎. Определим деление полиномы таким же образом.

Определение: Деление многочленов

Мы определяем частное двух многочленов, находя многочлен, произведение которого на делитель дает делимое.

Например, если мы хотим найти 𝑥+𝑥𝑥+1, мы можем отметить, что мы хотим найти многочлен, который при умножении на 𝑥+1 дает 𝑥+𝑥. Один из способов найти это значение — расширить произведение (𝑥+1)𝑥. У нас есть (𝑥+1)𝑥=𝑥+𝑥.

Таким образом, 𝑥+𝑥𝑥+1=𝑥.

Тогда мы можем спросить: «Как вообще найти выражение для частного полинома?»

Давайте сначала рассмотрим пример с целыми числами. Если мы хотим определить значение 175, мы сначала заметим, что 5 не имеет значения. перейти точно в 17. Вместо этого мы можем использовать длинное деление, чтобы вычислить это частное:

Сначала мы видим, что три пятерки составляют 15 и что у нас не может быть больше пятерок. Удалив это из 17, мы получим в остатке 2. Мы называем 17 делимым, поскольку оно делится на делитель 5, мы называем 3 частным, а 2 называем остатком.

Также стоит отметить, что мы говорим, что 𝑏 делит 𝑎, если его остаток равен 0 после деления на 𝑏. Если мы вызовем остаток после деления 𝑎 на 𝑏 𝑟, то мы можем гарантировать, что 𝑏>𝑟>0. Если это не так, то мы можем увеличить значение частного.

Причина этого в том, что процесс деления в большую сторону перезаписывает дробь. Допустим, что 𝑎𝑏 имеет частное 𝑞 и остаток 𝑟. Тогда 𝑏 переходит в 𝑎𝑞 раз и имеет остаток 𝑟. Это означает, что 𝑏×𝑞+𝑟=𝑎. Следовательно, 𝑎𝑏=𝑏×𝑞+𝑟𝑏𝑎𝑏=𝑏×𝑞𝑏+𝑟𝑏𝑎𝑏=𝑞+𝑟𝑏.

В нашем числовом примере это читается 175=3+25.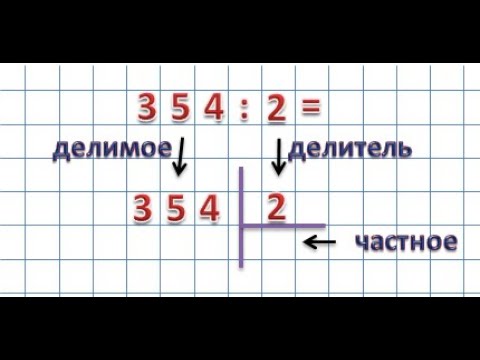

Мы почти готовы применить этот процесс к полиномам. Допустим, мы хотим разделить многочлен, называемый делимым, на другой многочлен, называемый делителем. Мы хотим сделать это, вычитая множители делителя из делимого до тех пор, пока мы больше не сможем этого делать. Чтобы понять, как это сделать, рассмотрим пример.

Предположим, мы хотим разделить 𝑥+5𝑥+6 на 𝑥+2. Нам нужно определить, сколько кратных 𝑥+2 мы можем удалить из 𝑥+5𝑥+6. Каждое кратное будет многочленом, поскольку произведения многочленов являются многочленами. Мы будем называть многочлен, который говорит нам число кратных 𝑥+2 мы удаляем частное. Это означает, что мы хотим найти многочлен, произведение которого на 𝑥+2 максимально близко к 𝑥+5𝑥+6, насколько это возможно.

Давайте запишем это деление, используя ту же запись деления, что и для целых чисел:

Заметим, что старший член делимого равен 𝑥, а старший член делителя равен 𝑥. Затем мы видим, что 𝑥𝑥=𝑥. Мы напишем это в нашем частном над 𝑥-членом:

Помните, что мы хотим вычесть произведение частного и делителя из делимого. Мы можем делать это термин за термином. Если мы умножим делитель на 𝑥, мы получаем 𝑥(𝑥+2)=𝑥+2𝑥.

Вычитая это из дивидендной доходности 𝑥+5𝑥+6−𝑥(𝑥+2)=𝑥−𝑥+5𝑥−2𝑥+6=3𝑥+6.

Запишем это в длинном делении следующим образом:

Прежде чем продолжить с делением может быть полезно рассмотреть то, что мы на самом деле показали. Мы показали, что 𝑥+5𝑥+6=𝑥(𝑥+2)+(3𝑥+6). Затем мы можем разделить на 𝑥+2, что дает 𝑥+5𝑥+6𝑥+2=𝑥(𝑥+2)+(3𝑥+6)𝑥+2=𝑥+3𝑥+6𝑥+2.

Таким образом, мы уменьшили степень делимого. Мы можем применить этот процесс снова, на этот раз с 3𝑥+6 в качестве дивиденда. Ведущий термин это новое делимое равно 3𝑥, а старший член делителя равен 𝑥. Итак, 3𝑥𝑥=3, и мы добавляем это в частное следующим образом:

Мы хотим убрать делитель из делимого 3 раза. Это дает нам (3𝑥+6)−3(𝑥+2)=3𝑥+6−3𝑥−6=0.

Мы можем представить это с помощью деления в длинном виде следующим образом:

В этом объяснении мы будем иметь дело только со случаями, когда остаток является нулевым полиномом. Однако стоит отметить, что каждый раз, когда мы выполняем этот процесс, мы понижаем степень делимого на степень делителя. Мы продолжаем этот процесс до тех пор, пока остаток не будет иметь меньшую степень, чем делитель. В этот момент, когда мы разделим их старшие члены, мы получим либо ноль, либо переменную, возведенную в отрицательную степень, которая не является мономом.

Используя полиномиальное длинное деление, мы показали, что 𝑥+5𝑥+6=𝑥(𝑥+2)+3(𝑥+2). Так, 𝑥+5𝑥+6𝑥+2=𝑥(𝑥+2)+3(𝑥+2)𝑥+2=𝑥+3.

Мы можем проверить это, умножив частное 𝑥+3 на делитель 𝑥+2. У нас есть (𝑥+2)(𝑥+3)=𝑥+2𝑥+3𝑥+6=𝑥+5𝑥+6.

Это работает как хорошая проверка, чтобы убедиться, что ответ правильный.

Мы можем обобщить работу в приведенном выше примере следующим образом:

Давайте теперь рассмотрим пример применения этого процесса для деления двух многочленов.

Пример 1. Деление многочленов с помощью длинного деления многочленов

Найдите частное деления 𝑥+2𝑥−3 на 𝑥−1.

Ответ

Мы можем найти выражение для 𝑥+2𝑥−3𝑥−1, используя деление в большую сторону. Первый шаг — найти частное старших членов делимое и делитель. Отметим, что 𝑥𝑥=𝑥. Итак, пишем 𝑥 в частном и вычитаем 𝑥(𝑥−1) от делимого. У нас есть 𝑥(𝑥−1)=𝑥−𝑥, поэтому мы видим, что

. Мы вычисляем, что 𝑥+2𝑥−3−𝑥−𝑥=𝑥+2𝑥−3−𝑥+𝑥=3𝑥−3.

Затем мы можем добавить это к нашему делению:

Мы хотим применить этот процесс снова, на этот раз с 3𝑥−3 в качестве делимого. Нам нужно посмотреть, сколько раз делитель 𝑥−1 переходит в делимое 3𝑥−3. Мы делаем это, сначала разделив их главные члены. Мы видим, что 3𝑥𝑥=3. Итак, мы добавляем 3 к частному, и затем нам нужно вычесть 3 (𝑥−1) из делимого. Мы находим, что 3(𝑥−1)=3𝑥−3. Вычитание этого дает нам следующее:

Мы находим, что (3𝑥−3)−(3𝑥−3)=0.

Следовательно, 𝑥+2𝑥−3𝑥−1=𝑥+3.

Мы можем проверить этот ответ, вычислив (𝑥+3)(𝑥−1)=𝑥+2𝑥−3.

В нашем следующем примере мы найдем частное двух многочленов, где оба многочлена немонические.

Пример 2. Деление многочлена на делитель первой степени для нахождения частного

Найдите частное, если 2𝑥+7𝑥−8𝑥−21 делится на 2𝑥+3.

Ответ

Мы можем разделить два многочлена, используя длинное полиномиальное деление. Во-первых, нам нужно разделить их ведущие члены. У нас есть 2𝑥2𝑥=𝑥. Мы добавляем это в наше частное, и это означает, что нам нужно вычесть 𝑥(2𝑥+3) из нашего дивиденда. Поскольку 𝑥(2𝑥+3)=2𝑥+3𝑥, мы можем сделать это следующим образом:

Вычислим, что 2𝑥+7𝑥−8𝑥−21−2𝑥+3𝑥=4𝑥−8𝑥−21. Мы показали, что 2𝑥+7𝑥−8𝑥−212𝑥+3=(2𝑥+3)𝑥+4𝑥−8𝑥−212𝑥+3=𝑥+4𝑥−8𝑥−212𝑥+3.



 можно применить этот процесс снова, чтобы разделить 4𝑥−8𝑥−21 на 2𝑥+3. Делим старшие члены, чтобы получить 4𝑥2𝑥=2𝑥. Таким образом, мы добавляем 2𝑥 к частному и вычитаем 2𝑥(2𝑥+3)=4𝑥+6𝑥 из делимого следующим образом:

Затем мы вычисляем, что 21.

Нам нужно применить этот процесс в последний раз, чтобы полностью разделить выражение.

На этот раз деление старших членов дает нам −14𝑥2𝑥=−7. Мы добавляем это к частному. Затем нам нужно вычесть −7(2𝑥+3)=−14𝑥−21 от этого нового делимого. Поскольку это равно делимому, мы получаем значение 0:

Следовательно, 2𝑥+7𝑥−8𝑥−212𝑥+3=𝑥+2𝑥−7.

В нашем следующем примере мы разделим немонический кубический многочлен на линейный многочлен.

Пример 3. Деление кубического многочлена на делитель первой степени для нахождения частного

Найдите частное деления −6𝑥+11𝑥+𝑥−6 на 𝑥−1.

Ответ

Мы можем разделить два многочлена, используя длинное полиномиальное деление. Во-первых, нам нужно разделить их ведущие члены. У нас есть −6𝑥𝑥=−6𝑥. Мы добавляем это к нашему частному, и это означает, что нам нужно вычесть −6𝑥(𝑥−1) из нашего делимого. Поскольку −6𝑥(𝑥−1)=−6𝑥+6𝑥, мы можем сделать это следующим образом:

Мы вычисляем, что −6𝑥+11𝑥+𝑥−6−−6𝑥+6𝑥=5𝑥+𝑥−6.

Так как степень 5𝑥+𝑥−6 больше или равна степени делитель, теперь нам нужно применить этот процесс снова, с 5𝑥+𝑥−6 в качестве нашего нового дивиденда.

Делим их старшие члены, чтобы получить 5𝑥𝑥=5𝑥, которое добавляем к частному. Затем нам нужно вычесть 5𝑥(𝑥−1)=5𝑥−5𝑥 от дивиденда. Мы можем сделать это следующим образом:

Мы вычисляем, что 5𝑥+𝑥−6−5𝑥−5𝑥=6𝑥−6.

Поскольку степень этого многочлена равна степени делителя, нам нужно применить этот процесс в последний раз, с 6𝑥−6 в качестве дивиденда.

Мы разделим их старшие члены, чтобы получить 6𝑥𝑥=6, которые затем прибавим к частному. Затем нам нужно вычесть 6(𝑥−1)=6𝑥−6 от дивиденда. Поскольку это равно делимому, мы получим остаток 0, как показано:

Таким образом, мы показали, что частное от деления −6𝑥+11𝑥+𝑥−6 на 𝑥−1 равно −6𝑥+5𝑥+6. Мы могли бы проверить этот ответ, вычислив (𝑥−1)×−6𝑥+5𝑥+6, чтобы убедиться, что мы получили исходное кубическое делимое.

В нашем следующем примере мы увидим, как применить полиномиальное деление в длину, чтобы найти недостающее измерение на заданной диаграмме.

Пример 4.

Определение размера с помощью полиномиального длинного деления

Учитывая, что площадь прямоугольника на диаграмме равна 2𝑥+𝑥−5𝑥−3, найдите выражение для ширины прямоугольника.

Ответ

Сначала вспомним, что площадь прямоугольника определяется произведением его длины на ширину. Это означает, что мы можем определить ширину этого прямоугольника путем деления его площади на длину. Это означает, что нам нужно разделить кубический многочлен на линейный многочлен. Мы можем сделать это, используя полиномиальное длинное деление.

Сначала разделим их старшие члены, чтобы получить 2𝑥2𝑥=𝑥. Мы добавляем это к частному, а затем вычитаем 𝑥(2𝑥+3) от дивиденда. Заметим, что 𝑥(2𝑥+3)=2𝑥+3𝑥 и что 2𝑥+𝑥−5𝑥−3−2𝑥+3𝑥=−2𝑥−5𝑥−3, как показано:

Поскольку степень −2𝑥−5𝑥−3 больше или равна степени делителя, нам нужно применить этот процесс снова, с −2𝑥−5𝑥−3 в качестве нового дивиденда.

Сначала мы разделим их старшие члены, чтобы получить −2𝑥2𝑥=−𝑥, а затем прибавим к частному. Теперь нам нужно вычесть −𝑥(2𝑥+3)=−2𝑥−3𝑥 из разделенного. Это дает нам следующее:

Мы вычисляем, что −2𝑥−5𝑥−3−−2𝑥−3𝑥=−2𝑥−3.

Поскольку степень этого многочлена равна степени делителя, нам нужно применить этот процесс в последний раз, с −2𝑥−3 в качестве делимого.

Мы разделим их старшие члены, чтобы получить −2𝑥2=−1, что мы прибавим к частному. Затем заметим, что −1(2𝑥+3)=−2𝑥−3. Это равно делимому, поэтому при вычитании мы получим 0. Это дает нам следующее:

Следовательно, 2𝑥+𝑥−5𝑥−32𝑥+3=𝑥−𝑥−1, а ширина прямоугольник задается как 𝑥−𝑥−1.

В нашем последнем примере мы будем использовать полиномиальное длинное деление и заданную делимость двух полиномов для определения значения неизвестного коэффициента.

Пример 5. Нахождение значения константы, делающей многочлен делимым

Найдите значение 𝑘, при котором выражение 30𝑥+57𝑥−48𝑥−20𝑥+𝑘 делится на 5𝑥−8.

Ответ

Сначала вспомним, что мы говорим, что многочлен делится на другой многочлен, если остаток от их деления равен 0. Это означает, что мы можем применить многочлен длинное деление на заданные многочлены, и мы знаем, что остаток должен быть нулевым многочленом.

Перед тем, как мы применим полиномиальное деление, стоит отметить, что полином пятой степени не дается в убывающих степенях 𝑥. Мы всегда должны переупорядочивать дивиденды, чтобы они имели убывающие степени 𝑥, поскольку мы всегда хотим удалить ведущие члены дивидендов. Итак, мы будем использовать 30 𝑥−20 𝑥−48 𝑥+57 𝑥+𝑘 в качестве дивиденда.

Чтобы применить полиномиальное деление в длину, нам сначала нужно разделить старшие члены. Получаем 30𝑥5𝑥=6𝑥. Мы добавляем это к частному а затем вычесть 6𝑥5𝑥−8 из делимого. Поскольку 6𝑥5𝑥−8=30𝑥−48𝑥, мы также включим терм 0𝑥, чтобы сохранить столбцы с одинаковыми степенями 𝑥. У нас есть

Мы подсчитали, что 30𝑥−20𝑥−48𝑥+57𝑥+𝑘−30𝑥−48𝑥=−20𝑥+57𝑥+𝑘.

Также стоит отметить, что мы добавляем деление, чтобы сохранить столбцы с одинаковыми степенями 𝑥.

Так как это не ноль, нам нужно применить этот процесс снова, с -20𝑥+57𝑥+𝑘 в качестве делимого.

Сначала мы разделим главные члены, чтобы получить −20𝑥5𝑥=−4𝑥, и добавим это к частному. Далее нам нужно вычесть −4𝑥5𝑥−8 из делимого. Заметим, что −4𝑥5𝑥−8=−20𝑥+32𝑥. Затем мы можем вычесть это из дивиденда следующим образом:

Мы можем вычислить, что −20𝑥+57𝑥+𝑘−−20𝑥+32𝑥=25𝑥+𝑘.

Поскольку это не ноль, нам нужно применить этот процесс снова, с 25𝑥+𝑘 в качестве дивиденда.

Делим их старшие члены, чтобы получить 25𝑥5𝑥=5, и прибавляем это к нашему частному. Затем мы вычитаем 55𝑥−8 из дивиденда следующим образом:

Мы подсчитали, что 25𝑥+𝑘−55𝑥−8=25𝑥+𝑘−25𝑥+40=𝑘+40.

Поскольку нам говорят, что деление точное, мы знаем, что остаток должен быть нуль. Следовательно, 𝑘+40=0.

Мы можем решить это, чтобы увидеть, что 𝑘=−40.

Давайте закончим повторением некоторых важных моментов из этого объяснения.

Ключевые моменты

• Мы определяем частное двух многочленов, находя многочлен, произведение которого на делитель дает делимое.
• Мы можем делить многочлены в длинное деление.
• Мы можем проверить наш ответ, умножив делитель на частное.
• Если многочлен остатка от деления двух многочленов является нулевым многочленом, то говорят, что делимое делит делитель.
• Мы всегда должны переупорядочивать дивиденды, чтобы они имели убывающие степени 𝑥, поскольку мы всегда хотим удалить ведущие члены дивидендов.

Как делить большие числа с помощью длинного деления

Рабочая тетрадь по базовой математике и предварительной алгебре для чайников с онлайн-практикой

Книга для изучения Купить на Amazon

Чтобы разделить большие числа, используйте длинное деление . В отличие от других операций «Большой четверки», деление в полные числа движется слева направо. Для каждой цифры в делимое (число, которое вы делите), вы завершаете цикл деления, умножения и вычитания.

В некоторых задачах число в самом низу задачи не равно 0. В этих случаях ответ имеет остаток , , который является остатком, который необходимо учитывать. В этих случаях вы пишете r , а затем любое оставшееся число.

Примеры вопросов

1. Разделить 956/4.

   239. Начните с написания проблемы следующим образом:

   Для начала спросите, сколько раз 4 входит в 9, то есть что такое 9/4? Ответ: 2 (с небольшим остатком), поэтому напишите 2 прямо над 9. Теперь умножьте 2 x 4, чтобы получить 8, поместите произведение прямо под 9 и нарисуйте линию под ним:

   Вычтите 9–8, чтобы получить 1. ( Примечание: После вычитания результат должен быть меньше делителя (в этой задаче делитель равен 4). Затем опустите следующее число (5), чтобы получилось новый номер 15.

   Эти шаги составляют один полный цикл. Чтобы выполнить задачу, нужно просто повторить их. Теперь спросите, сколько раз 4 входит в 15, то есть что такое 15/4? Ответ 3 (с небольшим остатком). Итак, напишите 3 над 5, а затем умножьте 3 x 4, чтобы получить 12. Запишите произведение под 15.

   Вычтите 15 – 12, чтобы получить 3. Затем уменьшите следующее число (6), чтобы получить новое число 36.

   Еще один цикл завершен, так что начните следующий цикл, спросив, сколько раз 4 входит в 36, то есть сколько будет 36/4? На этот раз ответ 9. Запишите 9 над 6, умножьте 9 на 4 и поместите это под 36.

   Теперь вычтите 36 – 36 = 0. Поскольку у вас больше нет чисел, которые нужно записывать, вы закончили, и ответ (то есть частное ) является самым верхним числом задачи:

2. Разделить 3042 / 5.

   608 r 2. Начните с написания задачи следующим образом:

   Для начала спросите, сколько раз 5 входит в 3. Ответ 0, потому что 5 не входит в 3, поэтому напишите 0 над 3. Теперь вам нужно задать тот же вопрос, используя первые две цифры делителя: Сколько раз 5 входит в 30 — то есть чему равно 30/5? Ответ 6, поэтому поместите 6 над 0.