Деление натуральных чисел в столбик: правила, примеры
В данной публикации мы рассмотрим правила и практические примеры того, каким образом натуральные числа (двузначные, трехзначные и многозначные) можно делить столбиком – с остатком и без него.
- Правила деления в столбик
- Без остатка
- С остатком
- Примеры деления в столбик
Правила деления в столбик
Без остатка
Чтобы найти частное от деления одного числа на другое (с любым количеством разрядов) можно выполнить это арифметическое действие в столбик.
Рассмотрим правила деления на практическом примере для лучшего понимания. Допустим, нам нужно трехзначное число разделить на однозначное, к примеру 256 на 8. Вот, что мы делаем:
1. Пишем делимое (256), затем немного отступаем от него и в этой же строке дописываем делитель (8). Затем между этими числами дорисовываем уголок.
Результат будем записывать под делителем.
2. В делимом слева направо отсчитываем минимально необходимое количество разрядов таким образом, чтобы полученное из содержащихся в них цифр новое число было больше, чем делитель. В нашем случае числа 2 недостаточно, поэтому к нему добавляем 5 и в итоге получаем 25.
Примечание: Если крайняя левая цифра делимого больше делителя, добавлять к нему цифру следующего разряда не нужно, и мы сразу приступаем к следующему шагу.
3. Определяем, сколько целых раз наш делитель содержится в полученном из цифр делимого числе (25). В нашем случае – три раза. Пишем цифру 3 в отведенном для этого месте, затем умножаем ее на делитель (3 ⋅ 8). Получившееся число (24) отнимаем из 25 и остается единица. Важно, чтобы результат вычитания (остаток) обязательно был меньше делителя, иначе мы неправильно выполнили вычисления.
Примечание: Правила и примеры вычитания чисел столбиком приведены в отдельной публикации.
4. К остатку (1) добавляем следующую цифру делимого (6), чтобы получить новое число, которое снова больше, чем делитель.
Примечание: Если при добавлении следующей цифры образовавшееся новое число все еще меньше делителя, берем еще одну цифру справа (если есть такая возможность), при этом в частном пишем ноль. В противном случае, получается деление с остатком, которое мы рассмотрим далее.
5. В числе 16 содержится ровно два раза по восемь (2 ⋅ 8), следовательно, пишем 2 в частном, затем выполняем вычитание (16 – 16) и получаем остаток, равный нулю.
На этом деление столбиком числа 256 на 8 успешно выполнено, и частное равно 32.
С остатком
В целом, алгоритм действий аналогичен вышеописанному. Разница лишь в том, что при последнем вычитании остается неделимой остаток, к которому больше нечего дописывать из делимого, т.к. все его разряды уже были использованы. Остаток обычно записывается справа от результата в скобках.
Например, остаток от деления 112 на 5 равняется двум.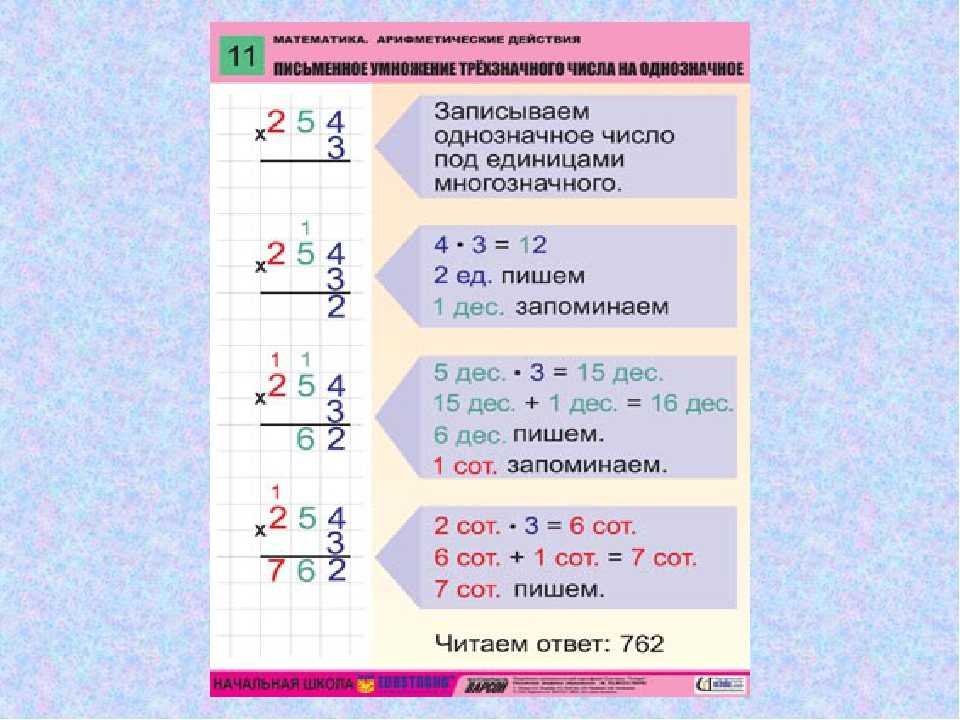
То есть 112 : 5 = 22 (2).
Пояснение: в результате вычитания 10 из 12 получается 2, но к нему больше нечего дописать из делимого.
Примеры деления в столбик
Пример 1
Разделим трехзначное число на двузначное, например 378 на 21.
Ответ: 378 : 21 = 18.
Пример 2
Найдем частное от деления чисел 1537 и 35.
Пояснение: в данном случае в делимом нужно сразу отсчитать слева не две, а три цифры, т.к. числа 1 и 15 меньше 35.
Ответ: 1537 : 35 = 43 (32)
Все правила деления в столбик: Деление натуральных чисел столбиком
Содержание
Деление натуральных чисел столбиком | Математически правила деления
Определение
Деление столбиком — это стандартный математический метод для деления простых или сложных многозначных чисел изучаемый в 4 классе начальной школы. При делении столбиком, как и при обычном делении, первое число — это делимое, второе — делитель, а результат — частное.
В столбик можно выполнять как деление натуральных чисел без остатка, так и деление натуральных чисел с остатком.
Правила записи чисел при делении столбиком
Сначала делимое и делитель записываются в одну строку слева направо, после чего следует символ вида:
Например, если делимое равно 7439, а делитель 43, то правильная запись в столбце будет следующей:
Рассмотрим следующую схему, которая иллюстрирует, где записывать делимое, делитель, частное, остаток и промежуточные вычисления при делении по столбцу:
Рассмотрим общую схему, которая иллюстрирует, где записывать делимое, делитель, частное, остаток и промежуточные вычисления при делении по столбцу:
Из схемы выше видно, что частное будет написано под делителем, т. е. ниже горизонтальной линии, а промежуточные расчеты пишутся под делимым.
Деление столбиком на однозначное число
Практические навыки лучше всего отрабатываются на простых примерах. Поэтому делим числа 9 и 3 в столбик. Конечно, эту операцию легко проделать в уме или по таблице умножения, однако подробный разбор для наглядности будет полезен, хотя мы уже знаем, что 9 ÷ 3= 3.
Итак, сначала запишем делимое и делитель по методу деления в столбик:
Далее определяем число делителей, имеющихся в делимом. Как определить? Поэтапно умножать делитель на 0, 1, 2, 3…, до тех пор, пока в итоге не получится число, равное или большее, чем делимое. Если в итоге сразу окажется число, равное делимому, под делителем запишем число, на которое делитель умножался.
Иными словами, когда получается число, большее делимого, под делителем записываем число, высчитанное на предпоследнем этапе. Вместо неполного частного записываем число, на которое делитель умножался на предпоследнем этапе.
\[3 \times 0=0 ; 3 \times 1=3 ; 3 \times 2=6 ; 3 \times 3=9\]
Итак, мы имеем число, равное делимому. Запишем его под делимыми, а вместо частного стоит число 3, на которое мы умножили делитель:
Теперь осталось вычесть числа под делителем (тоже методом столбца). В нашем случае 9 — 9 = 0.
Этот пример деления числа без остатка. Число после вычитания имеетс остаток от деления.
Если он равен нулю, числа полностью делятся. Теперь рассмотрим пример деления числа с остатком.
Разделим натуральное число 7 на натуральное число 5.
При этом 5 последовательно умножается на 0, 1, 2, 3. ..получаем в результате:
\[5 \times 0=0<9 ; 5 \times 1=5<9 ; 5 \times 2=10>9\]
Под делимым запишем число, полученное на предпоследнем этапе. Под делителем пишем число 1 — неполное частное, полученное на предпоследнем этапе. Именно на 1 мы помножили делитель, когда получили 5.
В завершение операции вычитаем 5 из 7 и получаем:
Это пример деления числа с остатком. Неполное частное равно 1, а остаток равен 2. Теперь, после изучения простейших примеров, поделим многозначные натуральные числа на однозначные значения.
Изучим механизм деления столбиком на примере деления числа 140288 на число 4.
Понять суть принципа намного легче на практических примерах, и этот пример был избран неслучайно, так как описывает все вероятные аспекты деления натуральных чисел столбиком.
Алгоритм деления столбиком
Рассмотрим подробне алгоритм деления натуральных чисел в столбик. Для этого запишем числа совместно со знаком деления столбиком. Далее смотрим на первую цифру слева в записи делимого. Вероятны два случая: число, вычисляемое этой цифрой, больше делителя и наоборот. В первом моменте работаем с этим числом, во втором добавочно берем последующую цифру в записи делимого и работаем с подобающим двузначным числом. В соответствии с этим пунктом выберем в примере число, с которым будем работать первоначально. Это число 14, так как первая цифра делимого 1 меньше делителя 4.
Определите, сколько раз числитель входит в полученное число. Обозначим это число как x = 14 Последовательно умножаем делитель 4 на каждый элемент ряда натуральных чисел N, включая ноль: 0, 1, 2, 3 0, 1, 2, 3 и так далее. Мы делаем это до тех пор, пока результат не будет х или число больше, чем х. Когда результат умножения равен 14, мы записываем его под выбранным числом в соответствии с правилами вычитания столбца.
Под делителем пишут множитель, на который умножался делитель. Если результатом умножения является число больше х, то под выбранным числом вписываем число, полученное на предпоследнем шаге, а вместо неполного частного (под делителем) вписываем множитель, на который производилось умножение на предпоследний шаг.
В соответствии с алгоритмом имеем:
\[4 \times 0=0<14;\\4 \times 1=4<14;\\4 \times 2=8<14;\\4 \times 3=12<14;\\14 \times 4=16>14.\]
Под отмеченным числом пишем полученное на предпоследнем шаге число 12. Вместо частного пишем множитель 3.
Вычтите 12 из 14 и запишите результат под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем.
Число 2 меньше числа 4, поэтому запишем под горизонтальной чертой после двойки число, находящееся в следующем числе делимого. Если в делимом больше нет цифр, то деление окончено. В нашем примере после числа 2, полученного в предыдущем пункте, пишем следующую цифру делимого — 0.
Соответственно, помечаем новое рабочее число — 20.
Важно
Пункты 2 − 4 циклически повторяются до окончания деления натуральных чисел.
Снова вычисляем, сколько содержится делителей в числе 20. Умножая 4 на 0, 1, 2, 3. . получаем: \[4 \times 5=20\]. Так как в результате мы получили число равное 20 , пишем под отмеченным числом, а вместо частного в следующем бите пишем 5 — множитель, на который производилось умножение.
Проведем вычитание: 20 − 20 = 0
Цифру ноль писать не будем, потому что этот шаг не является концом деления. Давайте просто запомним место, где мы могли его написать и рядом напишем число из следующего разряда делимого — в нашем случае это число 2.
Умножьте делитель на 0, 1, 2, 3.. и сравните результат с отмеченным числом:
\[4 \times 0=0<2;\\4 \times 1=4>2\]
Следовательно, под отмеченным числом пишем число 0, а под делителем в следующем разряде частного тоже пишем 0.
Выполняем операцию вычитания и записываем результат под чертой.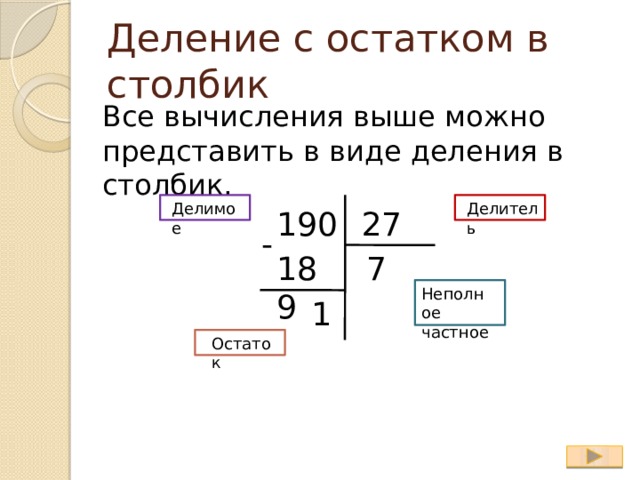
Справа, под чертой, прибавьте число 8, так как это следующая цифра делимого числа.
Следовательно, получаем новое рабочее число – 28, и снова повторяем пункты алгоритма.
Вычислив все по правилам, получаем результат:
Переносим последнюю цифру делимого 8 под черту. В последний раз повторяем шаги алгоритма 2 − 4 и получаем:
В нижней строке пишем число 0. Это число пишется только в последней фазе деления, когда операция завершена.
Рассмотрев алгоритм деления можно выделить общее правило деления натуральных чисел в столбиком:
- Делим тысячи;
- Делим сотни:
- Делим десятки;
- Делим единицы.
Рассмотрим другие примеры:
Пример №1
Выполним деление 7485 на 3:
Следовательно, 7485 : 3 = 2495
Проверка:
2495*3=7485
Пример № 2:
Разделим 318624 на 6:
Проверка: \[54104 \times 6=318624\]
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Деление на многозначные натуральные числа столбиком
Алгоритм деления на многозначные числа столбиком весьма схож с ранее изученным механизмом деления многозначного числа на единичное число.
Точнее, преобразования касаются только первого абзаца, а пункты 2-4 остаются без изменений. Если при делении на однозначное число мы смотрели только на первую цифру делимого, то сейчас будем смотреть на столько цифр, сколько их в делителе.Когда число, вычисляемое этими цифрами, больше делителя, мы берём это как рабочую цифру, иначе прибавляем лишнюю цифру из следующей цифры делимого. Далее следуем пунктам, изложенным в прошлом алгоритме. Изучим применение алгоритма многозначного деления на примере.
Пример №3
Разделим 5562 на 206.
В делителе три числа, поэтому в делимом сразу выбираем 556. Умножьте 206 на 0, 1, 2, 3.. и получаем:
\[206 \times 0=0<556;\\206 \times 1=206<556\\206 \times 2=412<556; \text { деление}\\206 \times 3=618>556\]
Следовательно, под делителем записываем результат предпоследнего действия, а под делимым — множитель 2.
Продолжаем вычисления:
В результате получаем число 144.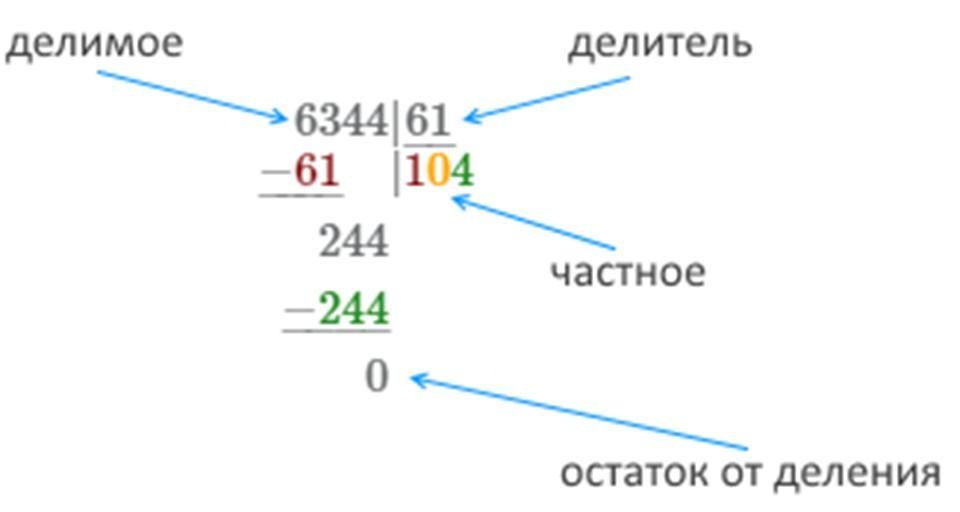
Справа от результата под чертой пишем число из соответствующей цифры делимого и получаем новое рабочее число – 1442.
Повторяем пункты 2 − 4. Получаем:
\[\begin{gathered} 206 \times 5=1030<1442; \\ 206 \times 6=1236<1442; \\ 206 \times 7=1442,1442=1442 \end{gathered}\]
Под выделенным числом записываем 1442, а в следующий разряд частного записываем цифру 7- множитель.
Выполним вычитание в столбик, и поймем, что операция деления окончена: в делителе больше нет цифр, чтобы писать их справа от результата вычитания.
Ответ: 27
Пример № 4
Разделим 36261 на 153
Проверка: \[237 \times 153=36261\].
Ответ: 237
Пример № 5
Разделим 25725000 на 70
Проверка: \[367500 \times 70=25725000\].
Ответ: 367500
Примеры деления на многозначное число с остатком
Пример №6:
Разделим 14507 на 186
Проверка: \[186 \times 77=14507\].
Пример №7:
Разделим 300428 на 505
Проверка: \[505 \times 594=300428\].
Деление десятичной дроби на натуральное число
Деление десятичной дроби в столбик производится по правилам деления натуральных чисел.
Рассмотрим детальней на примере: \[1505,86 \div 43=35,02\].
Пример №8:
Разделим 5612,8 на 350,8
Проверка: \[350,8 \times 16=5612,8\]
Деление «в столбик» — теперь по-русски 🙂 – Вадим Стеркин
Математика в 3 классе невозможна без поисковых технологий 🙂 Просматривая статистику посещений своего блога осенью 2008 г, я обратил внимание, что с начала сентября в него ежедневно приходят из Google несколько человек по запросу деление в столбик. Действительно, я когда-то писал о том, как делят в столбик американцы. Как ни странно, именно эта запись стояла первой в списке результатов поисковика, но она ничем не помогала бедным школьникам и их родителям.
Беглый просмотр других результатов поисковика не выявил алгоритма деления в первой десятке, и даже в русской Википедии статья еще ждала своего автора.
Я решил восполнить пробел, не претендуя на полноту изложения материала или профессиональный педагогический подход.
Итак, дорогие школьники, сегодня мы будем делить 861 на 7 в столбик. Если вы еще не знаете, в любой операции деления должно быть делимое, делитель и частное. В нашем случае 861 – делимое, 7 – делитель, а результат деления – частное. Его и будем искать.
Для начала записываем рядом делимое и делитель, затем разделяем их «уголком».
Теперь нужно внимательно посмотреть на цифры делимого и, двигаясь слева направо, найти в нем наименьшее число, которое больше делителя. Чисел тут три: 8, 86 и 861. Из них наименьшим является 8. Теперь нужно ответить на главный вопрос! Сколько раз наш делитель (7) содержится в числе 8? Один раз. Поэтому смело пишем 1 под чертой – это первая цифра частного, которое мы пытаемся найти.
А где же столбик? Сейчас будет 🙂 Теперь умножаем 7 на 1 и получаем 7. Записывем полученный результат под первым числом делимого и вычитаем в столбик, то есть из 8 вычитаем 7.
Получаем 1.
Если вы все сделали правильно, результат вычитания должен быть меньше делителя. Если больше, значит вы неправильно определили, сколько раз 7 содержится в 8. Поскольку результат вычитания меньше делителя, нам нужно его увеличить для продолжения нашего нелегкого труда. И делать это мы будем за счет следующей цифры делимого. Поскольку 8 мы уже использовали, берем 6 и приписываем к единице.
Теперь отвечаем на уже знакомый вопрос. Сколько раз 7 содержится в 16? Два раза. Приписываем двойку к единице под чертой — это вторая цифра частного. Умножаем 7 на 2, получаем 14 и записываем результат под 16.
Дальше идем по уже знакомому пути. Вычитаем 14 из 16, получаем 2 (2 меньше 7, значит все сделано правильно). Используем третью и последнюю цифру делимого – 1, сносим ее вниз и приписываем к двойке, получая 21.
Снова отвечаем на знакомый вопрос. Сколько раз 7 содержится в 21? Три раза. Пишем тройку под чертой. Умножаем 7 на 3, получаем 21 и записываем в столбик под 21.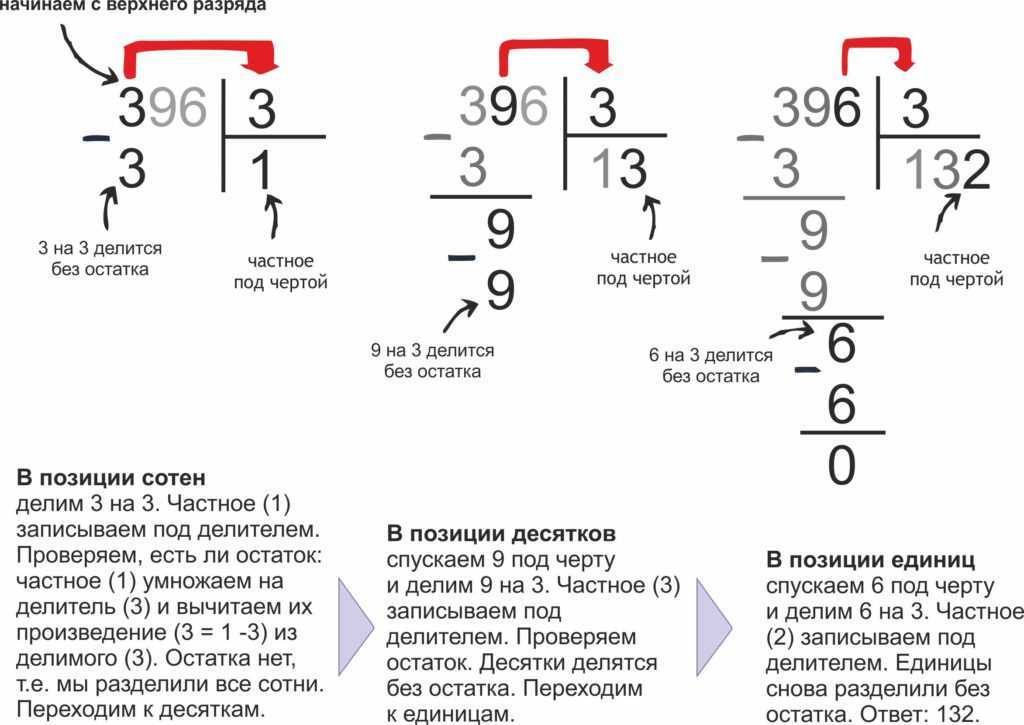
Вычитаем 21 из 21, получаем 0. Ура, деление выполнено без остатка! Ответ – 123.
Если вы использовали все цифры делимого, а ноль так и не получился, значит либо деление без остатка невозможно, либо вы ошиблись в арифметике. Выполните проверку… при помощи калькулятора – Пуск – Выполнить – calc.
Конец урока 🙂
Распределить содержимое ячейки по соседним столбцам
Excel для Microsoft 365 Excel для Интернета Excel 2021 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Дополнительно… Меньше
Вы можете разделить содержимое ячейки и распределить составные части по нескольким соседним ячейкам. Например, если ваш рабочий лист содержит столбец Полное имя
Советы:
Выполните следующие действия:
Примечание. Диапазон, содержащий столбец, который вы хотите разделить, может включать любое количество строк, но не более одного столбца.
Важно оставить достаточное количество пустых столбцов справа от выбранного столбца, что предотвратит перезапись данных в любых соседних столбцах распространяемыми данными. При необходимости вставьте количество пустых столбцов, которых будет достаточно, чтобы содержать каждую из составных частей распределенных данных.
- Выберите ячейку, диапазон или весь столбец, содержащий текстовые значения, которые вы хотите разделить.
На вкладке Данные в группе Работа с данными щелкните Текст в столбцы .
Следуйте инструкциям Мастера преобразования текста в столбцы , чтобы указать, как вы хотите разделить текст на отдельные столбцы.
Примечание. Для получения справки по выполнению всех шагов мастера см. раздел Разделение текста на разные столбцы с помощью мастера преобразования текста в столбцы или нажмите
Справка в мастере преобразования текста в столбцы.
Эта функция недоступна в Excel в Интернете.
Если у вас есть настольное приложение Excel, вы можете использовать кнопку Открыть в Excel
Нужна дополнительная помощь?
Вы всегда можете обратиться к эксперту в техническом сообществе Excel или получить поддержку в сообществе ответов.
См. также
Обзор формул в Excel
Как избежать неработающих формул
Найдите и исправьте ошибки в формулах
Сочетания клавиш и функциональные клавиши Excel
Функции ТЕКСТ (справочник)
Функции Excel (по алфавиту)
Функции Excel (по категориям)
Деление на 100 — Математика с мамой
Опубликовано Математика с мамой
Деление на 100
- В этом примере мы делим 400 на 100.
- Чтобы разделить число на 100, переместите все цифры на два разряда вправо.
- Цифра «4» перемещает из столбца сотен в столбец единиц (единиц).
- «0» в столбце десятков перемещается в столбец десятков.
- «0» в столбце единиц перемещается в столбец сотых.
- 400 ÷ 100 = 4,00
- Если после запятой только нули, то их не следует записывать.
- Следовательно, мы можем написать: 400 ÷ 100 = 4.
- Деление на 100 имеет тот же эффект удаления двух цифр «0» только , если исходное число заканчивалось двумя цифрами «0» в столбцах десятков и единиц соответственно .
Чтобы разделить на 100, переместите каждую цифру на два разряда вправо.
Если число заканчивается двумя цифрами «0» в столбцах десятков и единиц, деление на 100 имеет тот же эффект, что и удаление этих цифр.
- Чтобы разделить на 100, переместите все цифры на два разряда вправо.
- В этом примере цифра «5» перемещается из столбца сотен в столбец единиц.
- Цифра «2» перемещается из столбца десятков в столбец десятков.
- Цифра «7» перемещается из столбца единиц в столбец сотых.
- 527 ÷ 100 = 5,27
- Цифры «5», 2’ и 7’ остаются в том же порядке в ответе.
Чтобы разделить число на 100, переместите каждую цифру этого числа на два столбца разряда вправо .
Если число заканчивается двумя нулевыми цифрами в столбце десятков и единиц, то деление на 100 имеет тот же эффект, что и удаление этих двух нулевых цифр.
Этот трюк работает только с целыми числами , которые находятся в таблице умножения на 100 (оканчивающиеся двумя нулями).
В приведенном выше примере у нас есть 400 ÷ 100 = 4.
Чтобы разделить число на 100, переместите все его цифры на две колонки разряда вправо.
Цифра «4» перемещается из столбца сотен в столбец единиц.
Цифра «0» в столбце десятков перемещается в столбец десятков сразу после запятой.
Цифра «0» в столбце единиц перемещается в столбец сотых.
400 ÷ 100 равно 4,00.
Если число имеет только нули после запятой, то это целое число и нет необходимости записывать эти нули.
Лучше писать: 400 ÷ 100 = 4.
Видно, что мы просто «убрали два нуля».
Этот трюк работает только для целых чисел , у которых на самом деле есть два нуля в столбцах десятков и единиц, которые нужно удалить.
Важно понимать, как работает деление любого числа на 100, потому что не все числа, которые мы делим на 100, оканчиваются двумя нулями.
Например:
Чтобы разделить 527 на 100, мы переместим каждую цифру в 527 на две позиции вправо .
Начнем с переноса «5» из столбца сотен на две позиции в столбец единиц .
Затем «2» и «7» будут следовать за «5».
2 перемещается из столбца
Каждая цифра сдвинулась на две позиции вправо, поэтому 527 ÷ 100 = 5,27.
Если самая большая цифра числа находится в столбце сотен, то эта цифра переместится в столбец единиц при делении на 100.
Остальные цифры справа будут отображаться в том же порядке справа от десятичной точки.
Таким образом, в этом примере «5» — это цифра слева от десятичной точки, а затем «2» и «7» будут в том же порядке, сразу после десятичной точки.
В следующем примере нам дано число меньше 100 и состоит только из двух цифр. Мы по-прежнему следуем тем же правилам деления на 100 и перемещаем каждую цифру на два разряда вправо .
Начнем с перемещения «1» на две позиции вправо из столбца десятков
в столбец десятых . Затем следует цифра «9». Мы перемещаем его из столбца единиц в столбец сотых .Всякий раз, когда слева от десятичной точки не осталось цифр, в столбец
из единиц записывается одна цифра «0».
Следовательно, 19 ÷ 100 = 0,19.
Нас могут попросить разделить однозначное число на 100.
Например:
Хотя 6 имеет только одну цифру, мы по-прежнему следуем тому же правилу деления на 100. Мы перемещаем 6 на два разряда вправо . Он перемещается из столбца единиц в столбец 9.0005 столбец десятых .
Поскольку в столбце из единиц больше нет цифры, а в столбце из десятых есть пробел, мы записываем ноль в оба столбца, чтобы показать, что их значения равны нулю.
Следовательно, 6 ÷ 100 = 0,06.
Мы должны быть осторожны, имея дело с числами, где между двумя другими ненулевыми цифрами стоит ноль.
Например:
Чтобы разделить на 100, мы должны убедиться, что мы переместили каждая цифра в 30.2 два знака вправо, включая ноль . Мы перемещаем 3 из столбца десятков в столбец десятых , мы перемещаем ноль из столбца единиц в столбец сотых и мы перемещаем 2 из столбца десятых в столбец тысячных .
Правила делимости на 2, 3, 4, 5, 6, 9 и 10
Число a делится на число b, если a \div b имеет остаток от нуля (0). Например, 15 разделить на 3 равно 5, а это означает, что его остаток равен нулю. Затем мы говорим, что 15 делится на 3.
В другом нашем уроке мы обсуждали правила делимости для 7, 11 и 12. На этот раз мы рассмотрим правила или тесты делимости для 2 , 3 , 4 , 5 , 6 , 9 и 10 . Поверьте мне, вы сможете выучить их очень быстро, потому что вы можете не знать, что у вас уже есть базовое и интуитивное понимание этого. Например, очевидно, что все четные числа делятся на 2. Это в значительной степени правило делимости для 2 . Цель этого урока правил делимости — формализовать то, что вы уже знаете.
Правила делимости помогают нам определить, делится ли одно число на другое, не прибегая к фактическому процессу деления, такому как метод деления в длинное число.
Если рассматриваемые числа численно достаточно малы, нам может не понадобиться использовать правила для проверки делимости. Однако для чисел, значения которых достаточно велики, мы хотим иметь некоторые правила, которые служили бы «ярлыками», чтобы помочь нам выяснить, действительно ли они делятся друг на друга.
Число делится на 2, если его последняя цифра 0, 2, 4, 6 или 8.
Пример 1. Делится ли число 246 на 2?
Решение: Поскольку последняя цифра числа 246 оканчивается на 6, это означает, что оно делится на 2.
Пример 2. Какие из чисел 100, 514, 309 и 768 делятся на 2?
Решение: Если мы рассмотрим все четыре числа, то только число 309 не оканчивается на 0, 2, 4, 6 или 8. Мы можем сделать вывод, что все числа выше, кроме 309делятся на 2.
Число делится на 3, если сумма цифр этого числа делится на 3.
Пример 1. Делится ли число 111 на 3?
Решение: Сложим цифры числа 111.
Получим 1 + 1 + 1 = 3. Так как сумма цифр делится на 3, значит, число 111 также делится на 3.
Пример 2: Какое из двух чисел 522 и 713 делится на 3?
Решение: сумма цифр числа 522 (5+2+2=9) равно 9, которое делится на 3. Это делает 522 делящимся на 3. Однако число 713 имеет 11 в виде суммы его цифр, что явно не делится на 3, поэтому 713 не делится на 3. Следовательно, только 522 делится на 3.
Число делится на 4, если две последние цифры числа делятся на 4.
Пример 1. Какое единственное число в приведенном ниже наборе делится на 4?
{945, 736, 118, 429}
Решение: Обратите внимание на две последние цифры четырех чисел в наборе. Обратите внимание, что 736 — единственное число, в котором две последние цифры (36) делятся на 4. Мы можем заключить, что 736 — единственное число в наборе, которое делится на 4.
Пример 2: верно или неверно. Число 5 554 делится на 4.
Решение: Последние две цифры числа 5 554 равны 54, что не делится на 4.
Это означает, что данное число НЕ делится на 4, поэтому ответ ложно .
Число делится на 5, если последняя цифра числа 0 или 5.
Пример 1. Множественный выбор. Какое число делится на 5?
А) 68
B) 71
C) 20
D) 44
Решение. Чтобы число делилось на 5, его последняя цифра должна быть либо 0, либо 5. вариантов, только число 20 делится на 5, поэтому ответом является выбор C .
Пример 2. Выберите все числа, которые делятся на 5.0085 343
E) 600
Решение. И 105, и 600 делятся на 5, потому что они оканчиваются либо на 0, либо на 5. Таким образом, варианты B и E являются правильными ответами.
Число делится на 6, если оно делится и на 2, и на 3.
Пример 1. Делится ли число 255 на 6?
Решение. Чтобы число 255 делилось на 6, оно должно делиться на 2 и 3.
Давайте сначала проверим, делится ли оно на 2. Обратите внимание, что 255 не является четным числом (любое число, оканчивающееся на 0, 2, 4). , 6 или 8), что делает его неделимым 2. Дальше проверять не нужно. Теперь мы можем сделать вывод, что это число не делится на 6. Ответ: 9.0005 НЕТ .
Пример 2. Делится ли число 4608 на 6?
Решение. Число является четным, поэтому оно делится на 2. Теперь проверьте, делится ли оно на 3. Сделаем это, сложив все цифры числа 4 608, что равно 4 + 6+ 0 + 8 = 18. Очевидно, сумма цифр делится на 3, потому что 18 ÷ 3 = 6. Поскольку число 4608 делится и на 2, и на 3, то оно также должно делиться на 6. Ответ: ДА .
Число делится на 9если сумма цифр делится на 9.
Пример 1. Делится ли число 1764 на 9?
Решение: Чтобы число делилось на 9, сумма его цифр также должна делиться на 9. Для числа 1764 мы получаем 1 + 7 + 6 + 4 = 18. Поскольку сумма цифр равна 18 и делится на 9, поэтому 1764 должно делиться на 9.
Пример 2. Выберите все числа, которые делятся на 9.0085 3 512
C) 8 874
D) 22,778
E) 48,069
Решение: ДЛЯ ДЛЯ ДАВЛЕНИЯ КАЖДЫЙ КАЖДЫ 7,065, 7 + 0 + 6 + 5 = 18, которое делится на 9.
Число делится на 10, если его последняя цифра равна 0.
Числа 20, 40, 50, 170 и 990 делятся на 10, потому что их последняя цифра равна нулю, 0 С другой стороны, 21, 34, 127 и 468 не делятся на 10, так как они не оканчиваются нулем.
Вас также могут заинтересовать:
Правила делимости на 7, 11 и 12
Правила делимости — Математическая лаборатория
w3.org/1999/xhtml» cellspacing=»0″> Вам нужно быть 3 для этой группы. Один член
директор, один регистратор и один координатор по материалам. Эта деятельность должна занимать 3 — 4 занятия. Все ваши классные работы должны быть размещены в вашем дуотанге по математике.
Часть 1. Станьте экспертом по делимости
1. Возьмите четыре каталожные карточки и напишите разные цифры от 0 до 9.
на каждой карточке.
2. Из четырех вариантов цифр составьте
список всех возможных комбинаций четырехзначных чисел с использованием каждой цифры
один раз. Для этого используйте прикрепленный файл Тест на делимость и введите каждое число, которое вы создаете, в первый столбец. Обратите внимание, что существует 24 возможных комбинации чисел (подсказка: систематизированный список может помочь вам получить все 24).
3. Разделите каждое из 24 чисел на 2, 3, 5, 6, 9., и 10 решить
если числа делятся без остатка. Если
число делится без остатка, напишите «да» в графе
графический органайзер.
Если число делится неравномерно, напишите «нет» в графическом органайзере.
4. Составьте диаграмму, показывающую «правило» делимости для каждого из
номера 2, 3, 5, 9 и 10.
Таблица образцов
| Номер | Divisibility Rule |
Part 2: Play Divisibility Rocks:
1. Take a deck of cards ( распечатайте приложение с изображением делимых камней и вырежьте карточки), ключ делимости (распечатайте приложение) и мешок с камнями (принесите в школу застежку с небольшими камнями, которые собирает ваша группа).
2. Раздайте карты лицевой стороной вниз поровну между игроками. Откажитесь от любых дополнений.
3. Поместите кучу камней в центр игрового круга.
4. Решите, кто первый. Человек справа от него отвечает за ключ делимости.
5. Первый игрок переворачивает свою верхнюю карту и решает, делится ли число на карте на 2, 3, 5, 9 и 10. Он берет по одному камню из центральной стопки за каждый ответ «да».
6. Если игрок слева не согласен, он или она может «бросить вызов», сказав «Вызов!» Затем оба игрока обращаются к тому, кто держит ключ, чтобы узнать, кто прав. Если претендент прав, этот человек получает камни. Если претендент неверен, первоначальный игрок получает камни, а претендент теряет свой ход.
7. Игра продолжается по часовой стрелке, каждый игрок делает свой ход, меняя игрока, который держит ключ, и человека, который бросает вызов.
8. Когда каждый игрок сделал ход, подсчитываются камни. Тот, у кого больше камней, получает все карты с этого хода. Камни возвращаются в центральную кучу.
9. Если ничья, оба игрока, участвующие в ничьей, переворачивают свою следующую карту и собирают камни для этой карты.