как делить в столбик без остатка, примеры, упражнения, правила в 2022 году
Как выглядит запись деления в столбик
Деление в столбик записывается в следующем виде:
Процесс вычисления выполняется в области под делимым.
Деление в столбик на однозначное число
1432 : 4
Деление числа 1432 на 4 в столбик записываем следующим образом:
Алгоритм решения следующий: деление начинаем со старших разрядов, чтобы составленное из них число было больше делителя. В нашем примере начинаем с числа 14 соток, образовавшихся из 1 разряда тысячных и 4 сотых. Ведь 1<4, поэтому привлекаем следующий разряд, соответственно 14>4, выполним деление и ищем наибольшее целое число, в частном получим 3 (в доле записываем результаты деления слева направо), частное будет из 3 цифр. Умножим 3 на 4, получим 12 и найдем разницу 14-12 = 2 сотых. Следующий этап – ищем частное от десятых, для этого необходимо раздробить остаток 2 сотых на десятки, это будет 20 десятков и добавляем число десятков, которые есть в делимом, получим 20+3=23 десятка.
Говорят, что к 20 десяткам мы «сносим» 3 десятка и продолжаем делить. 23:4= 5 десятков и вычитаем из 23 десятков произведение 4 на 5 десятков: 23 – 20 = 3 десятка (остаток). Чтобы найти единицы частного, сносим до остатка 2 единицы, получим 34 единицы. Делим 34 на 4, получаем целое число 9 без остатка. Таким образом, 1432: 4 = 358.
Деление в столбик на двухзначное число
19824 : 56
Алгоритм деления такой же, как и при делении на однозначное число. Начинаем делить с высших разрядов, поскольку 19 не делится на 56 и меньше делителя, берем 198 сотен и делим на 56, частное будет из 3 цифр. Получаем в доле 3 сотни (записываем цифру 3 первой в результате деления). Далее вычитаем из 198 сотен произведение чисел 3 и 56 (198 – 3⋅56 = 30). Раздробим остаток на десятки, получим 300 десятков и «сносим» еще 2 десятка из деленного, записываем число 302 и делим его на 56. В частном записываем 5, как результат деления 302 на 56. Умножаем 5 на 56 и записываем 280 под числом 3 .
Деление в столбик трехзначное на двухзначное число
304 : 19
Поскольку 3<19, делимым будет 30, частное будет содержать 2 цифры. Делим 30 на 19, в частное записываем 1. Из 30 вычитаем произведение 1 на 19, получим 11 десятков и сносим 4. После этого делим 114 единиц на 19, в частное записываем результат деления 6. Проверяем умножением: 6 на 19 = 114. 114 вычесть 114 = 0, деление выполнено правильно и без остатка.
Деление в столбик на трехзначное число
4500 : 125
Начинаем деление из 450 десятков, частное будет содержать 2 цифры. 450 : 125 = 3. Умножаем 3 на 125 и от 450 вычитаем полученное произведение.
Получившуюся разницу 75 десятков раздробим в единицы и снесем 0 единиц из делимого. 750 единиц делим на 125, в частное записываем 6. Из 750 вычитаем произведение 6 на 125, получим 0. Соотношение (частное) от деления 4500 на 125 равно 36.
Деление в столбик двухзначное на двухзначное число
Рассмотрим на примере деления 84 на 14
При делении двухзначного числа на двухзначное частное будет однозначным числом.
Поскольку 8 < 14, то делимым будет число 84. Далее будем подбирать число, которое при умножении на 14 даст 84. Методом проб: 5 ⋅ 14 = 70, число 5 не является частным, перемножим большее число 6 ⋅ 14 = 84. Следовательно, записываем число 6, которое является частным от деления 84 на 14.
72 : 12
Запись в столбик будет выглядеть так:
Попробуем подобрать однозначное число, при умножении которого на 2, получим 2 на месте единиц. Это может быть либо число 1, либо число 6. Очевидно, что число 1 нам не подходит, потому что 12 умножить на 1 не будет равно 72.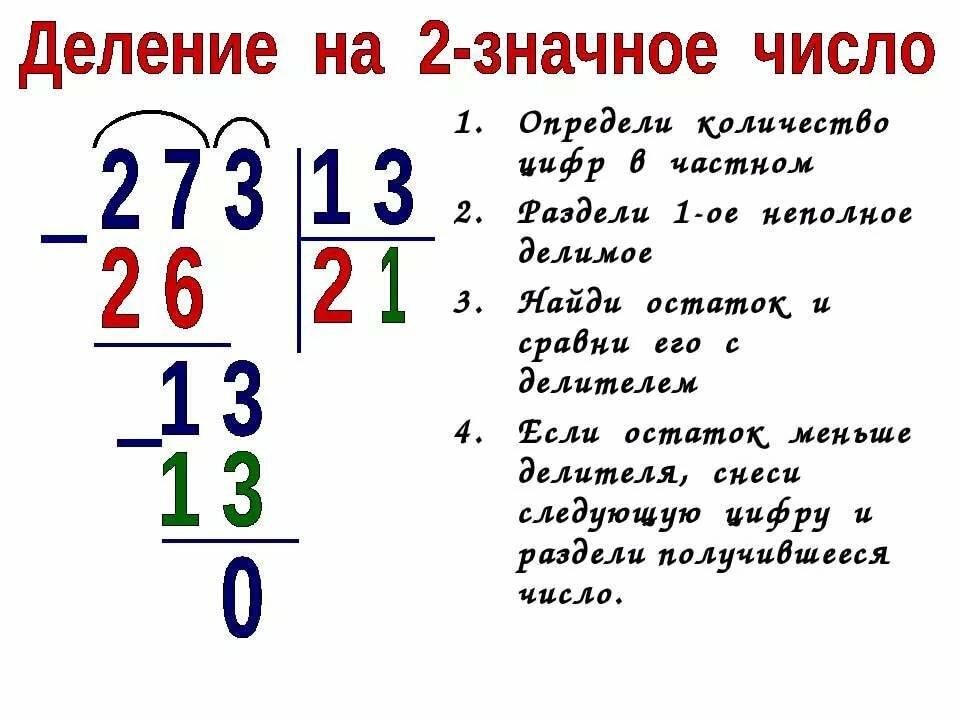
Проверим число 6, 6 умножить на 12 равно 72. Следовательно, число 6 является частным от деления 72 на 12.
Деление в столбец чисел с нулями
Рассмотрим пример, когда делимое заканчивается нулями.
10800 : 25
1 < 25, 10 < 25, 108 > 25 поэтому начинаем деление со 108 соток. 108 : 25 = 4 записываем в остаток. Из 108 вычитаем произведение 25 на 4, получим 8. Сносим 0 из делимого, получим 80 десятков и делим их на 25. В частное записываем 3. Вычитаем из 80 произведение 3 на 25, получим 5. Сносим 0 из делимого, и 50 делим на 25, в частное записываем 2. Результат деления – число 432.
296000 : 4
Деление начинаем с 29 : 4 = 7 записываем в частное, 28 – (7 ⋅ 4) = 1. Следующий этап: 16 : 4 = 4. Находим разность 4 – 1 ⋅ 4 = 0. Остаток нулей (2 нули) из делимого переносим в частное. Результат деления — число 74000
Пошаговый алгоритм деления столбиком
Рассмотрим пример 938 : 7
Шаг 1
Записываем числа, разделив их «уголком».
Шаг 2
Сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Шаг 3
Умножаем делитель 7 ∙ 1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2. Записываем результат.
Шаг 4
Число, которое мы видим, меньше делителя, поэтому его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.
Шаг 5
Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7 ∙ 3) записываем внизу под числом 23 в столбик.
Шаг 6
Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике.
Путём вычитания в столбике (23 — 21) получаем разницу. Она равняется 2.
Из делимого у нас осталось неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.
Шаг 7
Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное = 134.
Рассмотрим ещё деление в столбик на примере 512 : 8.
1 шаг. Запишем делимое и делитель следующим образом:
Частное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг. Деление начинаем слева направо. Сначала берем цифру 5
3 шаг. Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:
Теперь 51 больше 8. Это неполное частное.
4 шаг. Ставим точку под делителем.
5 шаг. После 51 стоит еще цифра 2, а значит, в ответе будет ещё одно число, то есть, частное – двузначное число.
Ставим вторую точку:
6 шаг. Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
7 шаг. Затем записываем число ровно под числом 51 и ставим знак «-»:
8 шаг. Затем из 51 вычитаем 48 и получаем ответ 3.
9 шаг. Сносим цифру 2 и записываем рядом с цифрой 3:
10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
Ответ: 64
Как и в остальных случаях выполнения письменных приёмов вычислений, при делении очень важно не отступать от алгоритма.
Запомните:
Когда число цифр разряда меньше делителя, надо добавить к нему число цифр следующего разряда.
Если при делении неполного делимого остался остаток, спускаем его под черту и к нему приписываем цифру следующего разряда.
Остаток не может быть больше делителя!
Если цифра неполного делимого меньше делителя, то в частном пишем 0.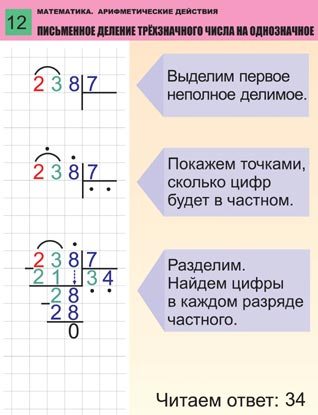
Вы сегодня получили ключ к успеху в математике. Смело открывайте им замки любой сложности.
Разделение столбцов — edshelf
Платформы
- iPad
- Айфон
- Рабочий стол Windows
Субъекты
- Математика
Возраст учащихся
- 8
- 9
- 10
- 11
- 12
Категории
- Калькуляторы
- Упражнения и тренировки
- Учебные пособия
Это математическое приложение можно использовать для обучения и изучения метода деления на столбики. Приложение простое в использовании и имеет интуитивно понятный интерактивный интерфейс с настраиваемыми цветами и другими настройками. Пользователь может решать задачи случайного деления.
Метод деления по столбцам
Метод деления по столбцам представляет собой простую вариацию традиционного метода деления по столбцам. Линии рисуются для разделения цифр делителя.
Каждый столбец разрядных значений решается слева направо.
В программе «Повседневная математика» метод деления столбцами является одним из алгоритмов деления.
Одобрено учителями
Рита Зени, Начальная школа Ecole Sandy Hill, Абботсфорд, Британская Колумбия, Канада:
«Математические приложения от Esa Helttula позволяют учащимся практиковать и закреплять конкретные вычислительные стратегии, преподаваемые в классе, с одинаковыми или минимальными затратами. подмости по мере необходимости.
Они также обеспечивают индивидуальную обратную связь с каждым учащимся с оперативностью, которая не всегда возможна при использовании карандаша и бумаги. Возможность регулировать уровень сложности в соответствии со своими потребностями также очень мотивирует учащихся. Я так рада, что наткнулась на этот замечательный образовательный инструмент!»
Простое в использовании приложение
Числа выравниваются автоматически, чтобы пользователь мог сосредоточиться на выполнении операций для каждого столбца.
После того, как вы решите операцию для каждого частичного произведения, правильный ответ прилетит в нужное место. Если вы нажмете не ту кнопку, ответ появится над клавиатурой, но не будет двигаться.
Сложность можно установить с помощью настроек
– Делимое может иметь от 2 до 5 цифр
– Делитель может иметь 1 или 2 цифры
– Пользовательские и случайные задачи
– Текущая операция может быть скрыта
– Операнды текущая операция может быть выделена
— скорость анимации может быть установлена .com, Учителя с приложениями и другие уважаемые сайты и организации.
Некоторые из других 24 математических приложений iDevBooks: сложение столбцов, длинное умножение, длинное деление, вычитание столбцов, умножение решеток, визуальная таблица умножения, вычитание частичных разностей, деление частичных частных, сложение частичных сумм, десятичное округление и т. д.
Обратная связь и запросы на новые функции
Приветствуются новые идеи по улучшению этого приложения.
Пожалуйста, посетите idevbooks.com, чтобы оставить отзыв.
Конфиденциальность
В этом приложении нет рекламы или встроенных покупок, и оно не передает никаких данных во время работы приложения. Это приложение также не содержит ссылок на другие приложения или в Интернете.
| План | Цена | Детали |
|---|---|---|
| Разделение столбцов | 3,99 $ | Платное приложение для iOS и программа для Windows. |
Войдите или создайте учетную запись, чтобы поделиться своим опытом работы с этим инструментом.
Реализации евклидова деления
Примечание: Эта статья была переведена с помощью автоматического переводчика и одного проход был сделан, чтобы удалить самые большие ошибки.Если вы хотите сделать эту статью читабельной, вы можете сообщать мне об ошибках перевода (слово, предложение, абзац) по связавшись со мной по адресу электронной почты внизу страницы.
СпасибоПринцип
В этой статье обсуждается евклидово деление, фундаментальный предмет, представляющий
отправной точкой для всех вопросов, связанных с простыми числами и факторизацией целых чисел.
Например, пакет с 12 шариками, которые можно раздать трем людям, или бабушкин торт. разрезать на 8 порций, пока нас 6 за столом.
Мы считаем, что в этой статье мы работаем с положительными целыми числами (набор N натуральных чисел), таким образом, это справедливое распределение иногда невозможно без появления «половинок», «четвертей», «третье лицо» или другое… Например, 3 мяча, которые нужно распределить между 2 людьми, дают каждому по 1 мячу. и мы не пытаемся отрезать последнее… Этот остаток нераспределенный откладывается, это остаток.
Обратите внимание, что на рациональных числах (установите Q) и так далее на действительных числах (очень грубо плавающие числа) распространение возможно, но может дать что-то с трудом представимое в реальной жизни, например 10/3 = 3,3333… это означает от 3 до бесконечности, в них сложно разрезать торт условия…
С математической точки зрения определение евклидова деления натуральных чисел
выглядит следующим образом:
Пусть a и b — целые числа и b отлично от 0, существует единственная пара (q, r) целых чисел
такие как:
- а = бк + р
- р < б
Примечание 1 : Мы находим это понятие справедливого распределения с помощью термина «bq» и
остаток с термином «r».
Примечание 2 : Для целых чисел (набор Z целых чисел, положительных и отрицательных) мы имеем почти
такое же определение. Только второе условие меняется и становится |r| < |б|.
Об имени на условиях евклидова деления «a = bq + r» имеем:
- а дивиденд
- b это делитель
- q это частное
- р остаток
Проведение испытаний
В этой статье мы представим некоторые известные реализации евклидова деления и
сравните их, чтобы увидеть, какие из них наиболее эффективны и быстрее.
Но оценить время и
столкнуться с результатами, у нас должна быть небольшая тестовая программа, которая будет измерять время
различные реализации деления, а также проверьте три следующих критерия, чтобы избежать
предвзятость в тестировании:
- Тестовые наборы должны быть согласованными: одно деление составляет миллисекунду, если мы тестируем только одно подразделение, мы не можем извлечь соответствующую информацию, потому что времени слишком мало. Мы будем поэтому делайте прогоны в 20 миллионов делений.
- Наборы тестов должны быть одинаковыми для каждой реализации: для сравнения двух реализаций евклидова деления, он обязательно будет использовать тот же набор тестов, потому что деление с разные методы на разные номера не интересны.
- Создайте несколько тестовых наборов с разными свойствами: идея состоит в том, чтобы протестировать реализации разделение на наборы, имеющие разные свойства, с целью выдвижения сильных и слабых сторон реализации.
Java-класс EuclideTestCaseGenerator отвечает за создание наборов тестов.
Этот
будет создавать наборы в соответствии с 3 методами: один с именем «случайный» будет брать случайным образом числа a (
дивиденд) и b (делитель) между 1 и 1000 миллиардов, другой называется «A > B» idem для
«случайный», за исключением того, что a обязательно больше, чем b, и последний назван «custom», такой же, как случайный
с а > 4*b.
Наконец, класс Java EuclideBench является оркестратором для запуска реализаций
Евклидово деление. Реализации должны реализовывать (как java) интерфейс IEuclide.
источник
Первая реализация
Самый простой способ вычислить евклидово деление опирается на его определение: «сколько раз я могу поставить b в ?». Это приводит к простому и относительно короткому алгоритму. состоящий из вычитания столько раз, сколько это может быть b (делитель) a (делимое), пока не получите остаток меньше b.
общедоступный длинный [] евклид( длинный а, длинный b) {
длинный r = а;
длинный q = 0;
в то время как (r >= b) {
r = r — b;
q = q + 1;
}
long [] евклид = { q, r };
возврат евклид;
}
На данный момент у нас нет никаких элементов сравнения с другими реализациями, но
поверьте метод наивен :).
Все, что мы видим в этом алгоритме, — это риск не результата, когда a слишком велико по сравнению с b.
потому что переменная r в инструкции «r = r — b» не уменьшается достаточно быстро. Сложность
алгоритма равен O(a).
источник
Вторая реализация
Чтобы улучшить первую реализацию, может быть интересно закодировать десятичное деление, которое мы
учиться в школе. А для тех, кто не помнит, как это работает, по простой схеме
это намного лучше, чем длинная речь, чтобы запомнить метод… позаботьтесь о том, чтобы схема показала
как выучить молодой французский. По тому уголку света, где вы изучали положение
цифры и визуальные изменения, но общие принципы остаются прежними:
т.е. 87 = 7 * 12 + 3
На уровне реализации метод состоит в умножении b (делитель) на 10 несколько
раз меньше, чем a (делимое), то делаем деление идентично первому
реализации и, наконец, снова с дивидендом остатка от деления
предыдущий шаг.
общедоступный длинный [] евклид( длинный a, длинный b) {
длинный r = а;
длинный q = 0;
длинный n = 1;
длинный вспомогательный = 0;
в то время как (r >= b) {
в то время как (b * n <= a) {
n *= 10;
}
n /= 10;
дополнительно = b * n;
в то время как (r >= вспомогательный) {
r = r — вспомогательный;
q = q + n;
}
a = r;
n = 1;
}
long [] евклид = { q, r };
возврат евклид;
}
В этой статье мы будем приводить результаты в виде трех таблиц, представляющих прогон
на каждом из трех тестовых наборов (случайный, A > B и A > 4 * B).
Важно видеть, что
направление чтения сверху вниз и алгоритмы должны сравниваться только в
контекст пробега. Здесь мы случайно взяли 40 миллионов чисел (2 умножить на 20 миллионов) и
рассчитал время, необходимое наивному и десятичному алгоритму для выполнения 20 миллионов евклидовых
дивизии (это пробег 1). Затем мы взяли другие числа, такие как A > B, и повторили 20
миллион делений (прогон 2), затем то же самое для A > 4 * B (прогон 3).
Все это говорит о том, что мало интереса сравнивать 2 отдельных прогона, потому что наборы данных
отличается, хотя верно то, что мы видим, что время увеличивается между 3 прогонами, этот рост
трудно поддается количественной оценке.
Посмотрим, что получится.
| Случайный выбор | А > В | А > 4 * В | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Работа/проверка | n1 / 150660990 | н2 / 294686702 | n3 / 1221575580 | ||||||
| Наивный | 1. 437 | 2.281 | 5.375 | ||||||
| Десятичный | 2,0 | +0,563 | 2,984 | +0,703 | 4.032 | -1,343 | |||
Эта вторая реализация показывает, что наивный метод работает быстрее, когда мы берем случайные значения.
или когда a (делимое) больше, чем b (делитель), потому что алгоритм очень прост
и иди быстро. К минусам, когда b в 4 раза меньше, чем a, производительность меняется на обратную и десятичная дробь
метод становится намного быстрее.
В тестовом случае A > B мы можем задаться вопросом, почему нет усиления, просто потому, что тестовый набор
неадекватный! Проблема возникает из-за распределения чисел при случайной стрельбе. За
например, если мы выберем число от 0 до 1000, у нас будет 890,99% шанс попасть в 4-значный
число (результаты можно экстраполировать на n цифр), на 4-значных числах мы имеем отношения a / b
очень низкий, поэтому результат A > B неубедителен.
Добавляя условие A > 4 * B, мы
искусственно увеличить соотношение, и мы ясно видим выигрыш.
Второй алгоритм меньше зависит от отношения a/b, потому что мы начинаем с умножения на 10 б столько раз, сколько необходимо, чтобы оказаться ближе к а. источник
Третья реализация
Чтобы оптимизировать время вычисления евклидова деления, мы изменим стратегию на
реализация алгоритма, основанного на дихотомии. Этот метод позволяет очень быстро найти
значение, используя старую добрую пословицу «разделяй и властвуй».
Здесь дихотомический поиск будет сосредоточен на значении q (частное). Подход состоит
первый шаг к ограничению q, затем многократно разрезая этот интервал на две равные части и выбирая
интервал содержит q.
Следует отметить, что эти операции по границе и резке будут выполняться со степенью 2
или, другими словами, мы используем бинарные операции, облегчающие работу компьютера. 9n
Критерии дихотомии следующие:
- Если b * ((альфа + бета) / 2) <= a, то альфа = (альфа + бета) / 2
- Если b * ((альфа + бета)/2) > а, то бета = (альфа + бета)/2
И это работает! Шаг за шагом мы приближаемся (и находим) частное q.
Для большего
подробности, включая математическую демонстрацию метода, см. во французской Википедии.
статья о Евклидовом
деление (раздел бинарного метода). К сожалению, не нашел на английском языке.
0;
long aux = b;
if (a < b) {
long [] euclide = { 0, a };
возврат евклид;
}
в то время как (aux <= a) {
aux = (aux << 1);
n++;
}
long alpha = (1 << (n - 1));
длинный бета = (1 << n);
в то время как (n— > 0) {
aux = (альфа + бета) >> 1;
если ((aux * b) <= a) {
alpha = aux;
} else {
beta = aux;
}
}
long [] евклид = { альфа, а — (b * альфа) };
возврат евклид;
}
И мы улучшаем производительность…
С подходом дихотомии мы чувствуем, что «пробел» преодолен.
Поскольку десятичный метод позволяет
большой выигрыш при условии, что a (дивиденд) очень велик по сравнению с b
(делитель), здесь создается впечатление обобщённого выигрыша на всех наборах тестов. А это
нормально, потому что мы прошли log2(a).
источник
| Случайный выбор | А > В | А > 4 * В | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Работа/проверка | n4 / 198332981 | n5 / 394652967 | n6 / 13 | 002||||||
| Наивный | 1,578 | 2,75 | 5.921 | ||||||
| Десятичный | 2,0 | +0,422 | 3,0 | +0,25 | 4,032 | -1,889 | |||
| Бинарная дихотомия | 1,375 | -0,625 | 2,015 | -0,985 | 3,297 | -0,735 | |||
Четвертая реализация
Всегда стремясь к производительности, мы делаем большой скачок назад в истории цивилизации.
так как собираемся вдохновить из технического подразделения в Древнем Египте на реализацию четвертого
алгоритма Евклидова деления.
Вопрос: Были ли все египтяне во времена фараонов потенциальными учеными-компьютерщиками?
Никто не знает, кроме их методов умножения
и деление
полагался в основном на числа разложения в степени 2, чтобы выполнить эти 2 операции.
В основном они рассуждали в двоичном формате, чтобы иметь возможность умножать и делить.
- Насчет умножения, целью было преобразовать в бинарный первый оператор (см.
Википедия для этого преобразования), а затем построить таблицу степеней 2, умноженных на
второй оператор (легко, просто умножьте на 2 второй оператор столько раз, сколько хотите), и
наконец, суммируя значения в таблице как «где установлен бит».
Пример с 18 * 9 = ? 18 (двоичный) 9 * 2 (n раз) 0 9 1 18 there is 1, we pick 0 36 0 72 1 144 there is 1, мы выбираем Значит 18+144=162=18*9. 
- Что касается деления, то египтяне использовали тот же принцип, но в обратном порядке.
Они начали с построения таблицы степеней числа 2, умноженного на делитель (всегда с умножение на 2) до тех пор, пока не получится число больше а (делимое). Затем они восстанавливают «результат в двоичном виде» путем выбора числа, такие как их сложения не превышают a. Этот выбор, начиная с наибольшего числа (самый старший бит).Пример 218 / 6 = ? n 6 * 2 (n times) Addition 5 192 192 we pick because 192 < 218 4 96 X we don’t pick Потому что 192 + 96 = 288 ET 288> 218 3 48 x Мы не выбираем, потому что 192 + 48> 218 2 24 216.2 = 36, остаток r равен 2 (218 — 116). Большинство сайтов в Интернете говорят о разделении Египта как об историческом подходе, а не как о Информатика.
Таким образом, мы находим принцип работы и много информации, описывающей предмет.
в текстовом виде. К минусам мы не видели примера реализации алгоритма, но это не мешает
неважно, просто сделай это!общедоступный длинный [] евклид( длинный а, длинный б) {
длинный n = 0;
длинное p = b;
if (a < b) {
long [] euclide = { 0, a };
возврат евклид;
}
в то время как (p <= a) {
p = (p << 1);
n++;
}
p = (p >> 1);
н—;
long q = (1 << n);
long aux = p; 9n, но и цикл «пока (n > 0)» в центре программы. По сути, эти два алгоритма эквивалентны, один можно переписать в другой. sourceЧто касается производительности, мы снова получаем большую скорость. Конечно, не так сильно, как изменение от от десятичного до дихотомического, но выигрыш в 0,2 с (кроме случайного) в среднем является почетным.
Направление чтения по пробегу (и сверху вниз).
Не сравнивайте два отдельных запуска.Случайный А > В А > 4 * В Работа/проверка n7 / 162438146 n8 / 313167294 n9 / 1211389641 Наивный 1.406 2,781 5,5 Десятичный 2,016 +0,61 3,0 +0,219 3,828 -1,672 Бинарная дихотомия 1,39 -0,626 2,0 -1,0 3,015 -0,813 Бинарный египетский 1,36 -0,03 1,781 -0,219 2,719 -0,296 Пятая реализация
А вот последняя реализация евклидова деления, это метод бинарной дихотомии, дополненной методом Горнера.
По сути, это просто более изящная переписка египетской дивизии (четвертой реализации), который сам по себе эквивалентен третьему (если следовать…).общедоступный длинный [] евклид( длинный a, длинный b) {
long r = a;
длинный q = 0;
длинный n = 0;
long aux = b;
в то время как (вспомогательный <= a) {
вспомогательный = (вспомогательный << 1);
n++;
}
в то время как (n > 0) {
aux = (aux >> 1);
н—;
q = (q << 1);
if (r >= aux) {
r = r — aux;
q++;
}
}
long [] евклид = { q, r };
возврат евклид;
}По производительности на нашем старом тестовом компьютере AMD 3200 2 Ghz хуже, чем реализации египетской дивизии, посмотреть, нет ли на других машинах (или др.
Таким образом, мы находим принцип работы и много информации, описывающей предмет.
в текстовом виде. К минусам мы не видели примера реализации алгоритма, но это не мешает
неважно, просто сделай это!
