Урок математики по теме «Деление дробей в уравнениях»
Форма урока: объяснение нового материала.
Цели урока:
- Обучающая: выработать навыки учащихся умножать и делить обыкновенные дроби, решать и оформлять задачи на уравнения.
- Воспитательная: воспитывать самостоятельность, аккуратность
- Развивающая: развивать внимание, математическую речь, вычислительные навыки учащихся, интерес к математике.
Ожидаемые результаты: дети научаться решать задачи и уравнения на дроби.
Этапы урока |
Время (мин) | Слайды |
Организационный момент. |
2 | Слайд 1 |
| Устная работа и повторение ранее изученного | 8 | Слайды 2, 3, 4, 5,6 |
| Формирование новых знаний и умений | 10 | Слайды 7, 8 |
| Физкультминутка | 2 | Слайды 9, 10 |
| Закрепление нового материала | 5 | Слайд 11 |
| Проверка знаний (с/р) | 10 | Слайд 12 |
| Постановка домашнего задания | 1 | Слайд 13 |
| Подведение итогов урока | 2 |
ХОД УРОКА
I. Организационный этап
– Здравствуйте, мы проведем сегодня урок по
теме «Деление дробей в уравнених».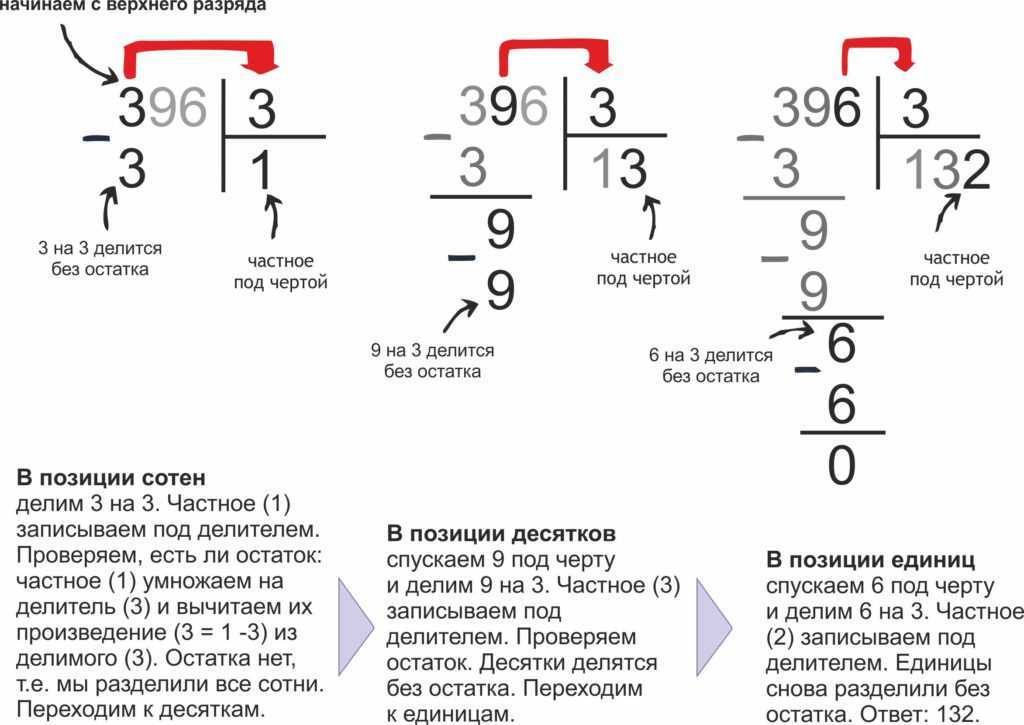
Откройте
тетради, запишите число, классная работа и тему
урока.
Целью нашего урока является закрепление и
проверка умений умножать и делить обыкновенные
дроби, а также повторить навыки решения задач и
уравнений.
II. Устный опрос учащихся
Чтобы умным в жизни стать
Надо дроби изучать
1) Переведите смешанную дробь в неправильную (Приложение 1, слайд 3)
2) Выделите целую часть (Приложение 1, слайд 4)
3) Умножьте дроби (Приложение 1, слайд 5)
– Повторим правило умножения двух дробей: Чтобы умножить дробь на дробь нужно перемножить их числители и знаменатели и первое произведение записать числителем, а второе знаменателем.
4) Выполните деление (в тетрадях с последующей взаимопроверкой, сосед у соседа) (Приложение 1, слайд 6)
– Повторим правило деления двух дробей: Чтобы
разделить одну дробь на другую, нужно первую
дробь умножить на дробь, обратную второй.
III. Формирование новых знаний и умений
– При изучении темы деление большое значение имеет умение решать уравнения. Рассмотрим пример и запишем его в тетрадь. (Приложение 1, слайд 7)
– Чтобы решить уравнение необходимо
определить какой компонент в уравнении является
неизвестным.
– Какой?
– 1 множитель
– Правильно! Чтобы найти неизвестный множитель,
что нужно сделать?
– Находим корень уравнения, выполняя деление. Выполним проверку и запишем ответ.
– А теперь давайте проверим ваше умение решать задачи.
№ 597 (Приложение 1, слайд 7)
– Сколько всего прошел лыжник ? (26 км)
– Сколько километров прошел в первый день?
(неизвестно)
– Сколько километров прошел во второй день?
(неизвестно)
– Какую величину, с какой сравнивают?
– Что возьмем за х?
– Как найти дробь от числа?
– Сколько километров прошел за два дня?
– Как найти?
– Составим уравнение.
– 14 км лыжник прошел во второй день
26 – 14 = 12 км лыжник прошел в первый день.
№ 598 (Приложение 1, слайд 8)
– Вспомним что такое 1% (одна сотая)
– Какой дробью запишем 75% (75/100 = 3/4)
– Сколько грибов собрала белка? (неизвестно)
– Сколько грибов собрал бельчонок? (неизвестно)
– Какую величину, с какой сравнивают?
– Что обозначим за икс?
– Как найти дробь от числа?
– Сколько собрали вместе белка и бельчонок?
– Составим уравнение.
200 грибов собрала белка
350 – 200 = 150 грибов собрал бельчонок
IV. Физкультминутка
– Встаем и выполняем несколько упражнений.
А теперь, ребята, встали,
Быстро руки вверх подняли,
В стороны, вперёд, назад
Повернулись вправо, влево,
Тихо сели, вновь за дело.
V. Закрепление нового материала
№ 594
– Сколько собрал Митя?
– Сколько собрал Коля?
– Какую величину, с какой сравнивают?
– Что обозначим за икс?
– Как найти дробь от числа?
– Сколько собрали вместе мальчики?
28 грибов собрал Митя
64 – 28 = 36 грибов собрал Коля
VI. «Математический выбор»
Уравнения, оцениваемые в 3 балла: Уравнения, оцениваемые в 5 баллов:
1) 1)
2) 2)
3) 3)
4) 4)
Уравнения, оцениваемые в 6 баллов:
1)
2)
3)
4)
Оценки: 5 – 12 баллов; 4 – 9 баллов; 3 – 6 баллов.
Каждый выбирает себе уравнения по «плечу».
Учитель во время работы оценивает учеников.
VII. Итог урока
– С каким настроением вы сегодня работали на
уроке?
– Какая задача для вас была самой интересной?
– Ребята чему мы научились на сегодняшнем уроке?
– Как найти часть от числа?
– Как найти неизвестный множитель?
Оценки за урок.
VIII. Домашнее задание
– С листов решить любые три уравнения, из тех которые не решали в классе.
Как объяснить ребенку деление?
Конечно же, прежде чем ваш ребенок отправится в первый класс ему необходимо освоить азы арифметики.
Первоначально ему необходимо научиться правильно, понимать задание, а так же решать его в необходимой последовательности. Лучше всего изначально научить ребенка складывать, вычитать и умножать, а уж только потом делить. Самое главное вы должны понимать, что для того чтобы ребенок понимал как выполнить то или иное действие ему необходимо все демонстрировать наглядно.
В данной статье мы подробно поговорим о том, как объяснить ребенку деление.
На самом деле, делить ребенок начинает еще в самом маленьком возрасте. Просто он еще до конца не осознает, что он участвует в данном процессе. Вы должны изначально объяснить ребенку, что такое целое, больше, меньше и т.д., он должен начать понимать каких игрушек больше, а каких меньше.
1. Поиграйте с малышом в делениеДля этого возьмите, к примеру, конфеты и попросите его поделиться с вами поровну. Изначально конечно ребенок будет действовать самым простым способом, он будет перекладывать конфетки по одной. В этом нет ничего страшного ведь малыш еще совсем маленький. После того как ребенок закончит делить конфеты помогите ему сосчитать сколько всего изначально их было.
Вы можете предложить малышу взять яблоки и угостить каждого члена семьи. Так же необходимо пояснить своему чаду, что не всегда, получается, разделить предметы поровну.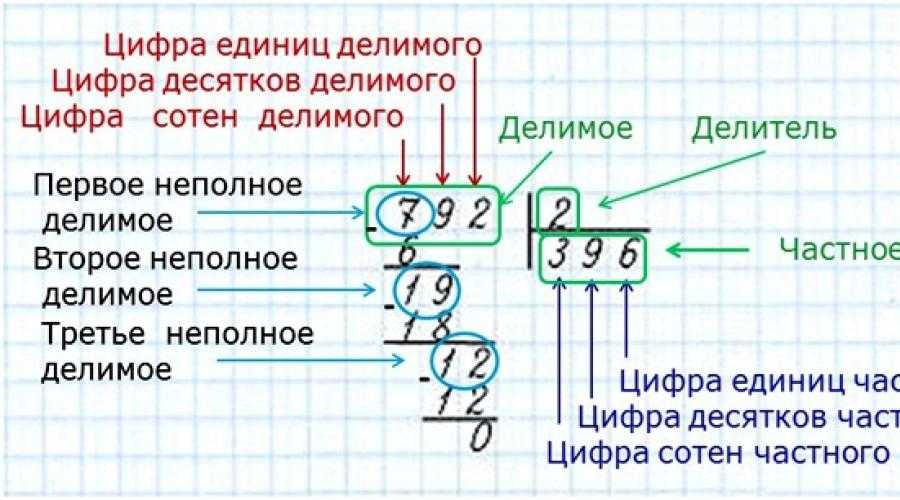
Приведите ему пример, что у вас есть пять подушек и вам необходимо поделить их между двумя людьми поровну. Такое попросту не возможно, потому что кому-то достанется три подушки, а кому-то две.
Объясните ребенку, что первое число это и есть те самые конфеты, а вот второе это вы и он (или еще больше участников). И главное скажите ему, что абсолютно неважно, какие именно предметы он будет делить, самое главное узнать, сколько предметов в итоге окажется у каждого из участников.
Из всего вышесказанного можно сделать вывод о том, что для того чтобы ребенок как можно быстрее понял как делить предметы, ему нужно все наглядно демонстрировать. Приводите ему как можно больше примеров, рисуйте с ним, берите какие-либо предметы и делите их. Если вы будете следовать всем перечисленным рекомендациям, то будьте уверены, ваш ребенок очень скоро сможет без труда делить числа.
Процесс деления можно представить, например, так: если 10 монет раздать 2 людям, то каждый получит по 5 монет.
Или так: 10 монет, разложенных в стопки по 2 монеты, дадут 5 стопок.
Как выполняется деление?
Деление одного числа (делимого) на другое (делитель) показывает, сколько делителей содержится в делимом. Например, при делении 4 на 2 мы находим, сколько чисел 2 содержится в числе 4. Результат деления называется частным.
Как деление связано с умножением?
Деление — это операция, обратная умножению. Если вы знаете результат деления, то можете записать соответствующее произведение, и наоборот.
Возврат к исходному значению
Если 10 (делимое) поделить на 2 (делитель), то получится 5 (частное). Умножая частное (5) на делитель (2), мы получаем значение исходного
делимого (10).
Другой подход к делению
Деление также показывает, сколько раз в делимом встречаются группы, равные делителю. Ответом будет то же самое частное.
В этом примере 30 футбольных мячей делятся на группы по 3 мяча.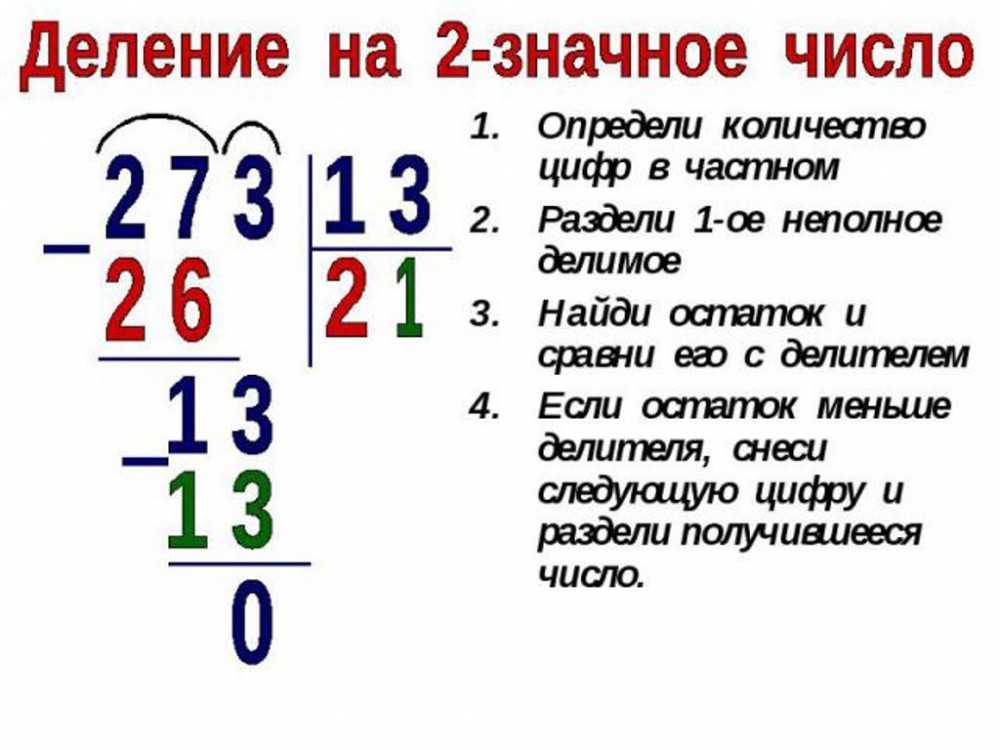
Получилось ровно 10 групп по 3 мяча (без остатка), поэтому 30 : 3 = 10.
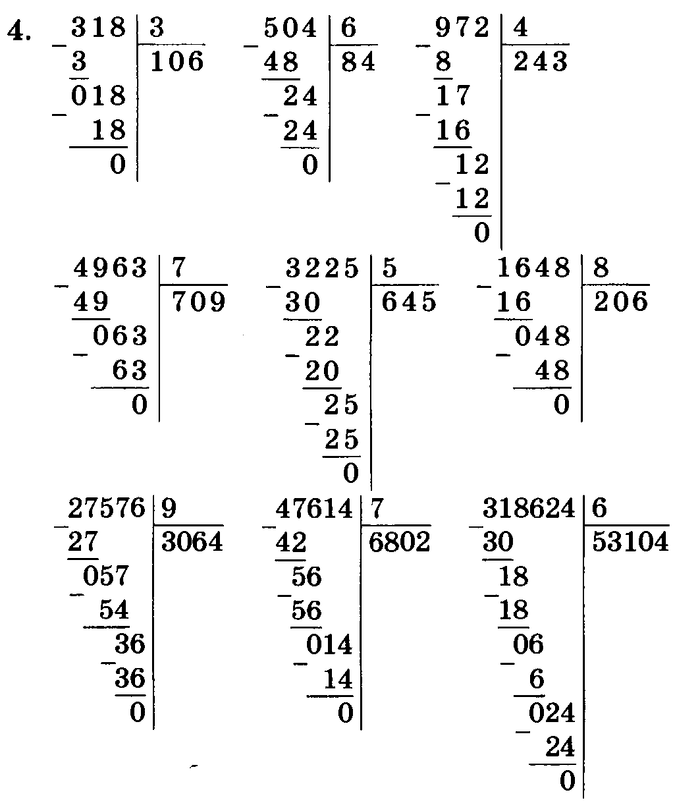
Схема деления деления на однозначное число
Деление с остатком
Если одно число не делится на другое нацело, возникает остаток. Его можно преобразовать в десятичную дробь, как показано ниже.
Упрощение деления
Иногда делитель можно представить как произведение нескольких сомножителей. Тогда процедура деления сводится к нескольким более простым делениям.
Этим методом можно пользоваться и в более сложных задачах.
Используйте синтетическое деление, чтобы определить, является ли данное значение k нулем этого многочлена. Если нет, определите p(k).
Предварительное вычисление алгебры Предварительное исчисление Предварительное исчисление
МакКинли К.
спросил 13/11/20 Используйте синтетическое деление, чтобы определить, является ли данное значение для нулем этого многочлена.
Если нет, определите .
p(x)=2x 3 −3x 2 −11x−20; k=4
является ли k нулем этого многочлена?
Подписаться І 1
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Рейнальдо Г. ответил 13.11.20
Репетитор
Опыт работы учителем предварительного исчисления
См. таких репетиторов
Смотрите таких репетиторов
Если остаток от деления равен нулю, это доказывает, что делитель является множителем делимого.
Учитывая p(x) = 2x 3 — 3x 2 — 11x — 20 и k = 4:
4 | 2 -3 -11 -20 дано
4 | 2 -3 -11 -20 ниже 2
2
4 | 2-3-11-20 умножить 4*2=8; -3 + 8 = 5
8
2 5
4 | 2-3-11-20 умножить 4*5=20; -11 + 20 = 9
8 20
2 5 9
4 | 2-3-11-20 умножить 4*9=36; -20 + 36 = 16
8 20 36
2 5 9 16
p(k) = p(4) = 16, согласно теореме об остатках
Поскольку остаток не равен нулю, то k = 4 является , а не нулем многочлена.
Голосовать за 0 голос против
Подробнее
Отчет
Патрик Л. ответил 13.11.20
Репетитор
4,8 (58)
Использование математики в технике и естественных науках
См. таких репетиторов
Смотрите таких репетиторов
4 | 2 -3 -11 -20
8 20 36
2 5 9 16
P(4) = 16. По теореме об остатках 4 не равно нулю, поскольку остаток не равен нулю.
Если вы используете Desmos и введете полиномиальную функцию, то пересечение по оси x будет около (3,709, 0). В этом случае k = 4 не является одним из нулей.
Голосовать за
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
