Урок 29. деление многозначного числа на однозначное — Математика — 4 класс
Математика, 4 класс
Урок № 29. Деление многозначного числа на однозначное
Перечень вопросов, рассматриваемых в теме:
— как письменно делить многозначное число на однозначное?
— какой алгоритм письменного деления многозначного числа на однозначное?
Глоссарий по теме:
Алгоритм – последовательность действия (шагов).
Многозначными считают числа больше тысячи.
Многозначные числа – это числа класса тысяч и класса миллионов. Многозначные числа образуются, называются, записываются с опорой не только на понятие разряда, но и понятие класса.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 4 класс. Учебник для общеобразовательных организаций. Ч.1 — М.; Просвещение, 2017. – С.82.
2. Моро М. И., Волкова С. И. Математика. Рабочая тетрадь 4 класс. Часть 1. М.; Просвещение, 2016. – С.54-55.
И. Математика. Рабочая тетрадь 4 класс. Часть 1. М.; Просвещение, 2016. – С.54-55.
3. Волкова С. И. Математика. Проверочные работы 4 класс. М.; Просвещение, 2017. – С. 46-47.
4. Волкова С. И. Математика. Тесты 4 класс. М.; Просвещение, 2017. – С.36 -37.
5. Кочергина А.В. Учим математику с увлечением (Методическая библиотека). М.: 5 за знания, 2007. – с. 33.
Теоретический материал для самостоятельного изучения:
Посмотрите на выражения. Что их объединяет? Это числовые выражения на действие деление, делитель – однозначное число. Как вы думаете, какое лишнее? Да, вы правы: второе выражение лишнее, потому что делимое – многозначное число. Мы еще не умеем решать такие выражения. Этому и предстоит нам научиться.
852 : 3, 7854 : 7, 768 : 8, 915 : 3
Давайте вспомним, как делить трехзначное число на однозначное. Разделим 852 на 3 столбиком. Начинаем деление с сотен – это первое неполное делимое: в частном будет три цифры. Делим 8 на 3, в частном будет 2 сотни. Умножаем 2 на 3, чтобы узнать сколько сотен разделили. Получается 6 сотен разделили. Вычитаем 6 из восьми, получаем 2. Столько сотен осталось. Сравниваем остаток 2 с делителем : 2 меньше трех, значит цифра в частном побрана верно. Сносим 5 десятков. Две сотни и пять десятков – это 25 десятков. Делим десятки на 3. В частном пишем цифру 8. Умножаем 8 на 3, получаем 24. Столько десятков разделили. Вычитаем 24 из двадцати пяти, остаток 1. Один меньше трех. Сносим единицы. Один десяток и две единицы – это 12 единиц. Делим на 3, берем по 4. Четыре умножаем на 3, получаем 12. Двенадцать вычитаем из двенадцати. Остаток 0. Деление завершили. Читаем результат: 284.
Умножаем 2 на 3, чтобы узнать сколько сотен разделили. Получается 6 сотен разделили. Вычитаем 6 из восьми, получаем 2. Столько сотен осталось. Сравниваем остаток 2 с делителем : 2 меньше трех, значит цифра в частном побрана верно. Сносим 5 десятков. Две сотни и пять десятков – это 25 десятков. Делим десятки на 3. В частном пишем цифру 8. Умножаем 8 на 3, получаем 24. Столько десятков разделили. Вычитаем 24 из двадцати пяти, остаток 1. Один меньше трех. Сносим единицы. Один десяток и две единицы – это 12 единиц. Делим на 3, берем по 4. Четыре умножаем на 3, получаем 12. Двенадцать вычитаем из двенадцати. Остаток 0. Деление завершили. Читаем результат: 284.
Рассмотрим деление числа пяти тысяч пятьсот сорока четырех на 6. Деление начинать надо с высшего разряда тысяч. Но 5000 нельзя разделить на 6, чтобы в частном были тысячи. Поэтому будем делить сотни.
55 сотен мы сможем разделить на 6 так, чтобы в частном получились сотни. В этом случае говорят 55 – это первое неполное делимое числа 5544. Посмотри, как можно его выделить. Теперь определим количество цифр в частном. Так как деление мы начали с сотен, в частном получим три цифры. Обозначим тремя точками места, где будем записывать цифры частного. Теперь находим первую цифру частного: для этого 55 делим на 6, получаем 9. Пишем 9 на месте сотен в частном. Умножаем 9 на 6, получаем 54. Столько сотен разделили. Записываем 54 под неполным делителем 55. Находим остаток, для этого вычитаем 54 из пятидесяти пяти. Получим 1. Столько сотен разделили. Теперь надо сравнить остаток с делителем: 1 меньше 6, значит цифра 9 в частном подобрана верно. Деление еще не закончено, так как можно образовать следующее неполное делимое из десятков. При делении сотен осталась 1 сотня, добавим еще 4 десятка. Всего 14 десятков. И повторяем все действия пункта по плану. Первые два пункта повторять не надо.
Посмотри, как можно его выделить. Теперь определим количество цифр в частном. Так как деление мы начали с сотен, в частном получим три цифры. Обозначим тремя точками места, где будем записывать цифры частного. Теперь находим первую цифру частного: для этого 55 делим на 6, получаем 9. Пишем 9 на месте сотен в частном. Умножаем 9 на 6, получаем 54. Столько сотен разделили. Записываем 54 под неполным делителем 55. Находим остаток, для этого вычитаем 54 из пятидесяти пяти. Получим 1. Столько сотен разделили. Теперь надо сравнить остаток с делителем: 1 меньше 6, значит цифра 9 в частном подобрана верно. Деление еще не закончено, так как можно образовать следующее неполное делимое из десятков. При делении сотен осталась 1 сотня, добавим еще 4 десятка. Всего 14 десятков. И повторяем все действия пункта по плану. Первые два пункта повторять не надо.
Делим 14 на 6, получаем 2. Столько десятков будет в частном. Умножим 2 на 6. Получаем 12. Столько десятков разделили. Вычитаем 12 из четырнадцати, получаем 2. Столько десятков осталось разделить. Сравниваем остаток с делителем: 2 меньше шести, значит цифра 2 в частном побрана верно.
Столько десятков осталось разделить. Сравниваем остаток с делителем: 2 меньше шести, значит цифра 2 в частном побрана верно.
Деление еще не закончено. Образуем следующее неполное делимое из единиц. При делении десятков осталось 2 десятка. Добавим 4 единицы, получаем 24 единицы. Делим 24 на 6, получаем 4 – столько единиц мы разделили. Запишем цифру 4 на месте единиц в частном. Умножаем 4на 6 , получаем 24. Столько единиц разделили. Вычитаем 24 из двадцати четырех. Осталось 0, он меньше делителя. Значит число единиц подобрано верно. Больше неполных делимых образовать нельзя. Значит деление завершено. Получили 924.
Задания тренировочного модуля:
1.Найдите значения выражения, считая устно или письменно:
6524 : 7
Варианты ответов:
1.842
2.934
3.932
Правильный вариант:
932
2. Выполните вычисления:
(17437 – 10297) : 7
Правильный вариант:
1020
3. Допишите предложения:
- Чтобы найти неизвестный множитель, нужно…
- Чтобы найти неизвестный делитель, нужно.
 ..
..
Правильные варианты:
1) произведение разделить на другой множитель
2) делимое разделить на частное
Карточка по математике «Деление многозначного числа на трехзначное» | Тренажёр по математике (4 класс) на тему:
Опубликовано 20.06.2017 — 20:54 — Шахова Ольга Сергеевна
Карточка по математике «Деление многозначного числа на трехзначное»
Скачать:
Предварительный просмотр:
27434 : 638 36271 : 83 16728 : 204 32128 : 502 18411 : 323 27434: 638 | 36271 : 437 40338 : 747 22275:297 56144 : 638 52731 : 567 42583 : 439 | 50917:863 52839:927 46464 : 726 24444 : 388 12648 : 527 14674 : 638 | 27232 : 296 63984 : 688 15762 : 426 41325 : 475 385284 : 582 326214 : 378 |
131052 : 326 613718 : 743 436656 : 528 309342 : 654 437544 : 927 385451 : 737 | 487432 : 764 164346 : 258 427614 : 589 615042 : 846 411162 : 834 491016 : 998 | 577252 : 653 416776 : 472 169372 : 526 319124 : 988 61610 : 305 286567 : 563 | 698088:348 826281:909 542944:893 40803 : 201 4912768 : 896 1243984 : 464 |
4859535 : 867 845018 : 449 2461908 : 579 574866 : 654 2441152 : 448 864063 : 589 | 6640491: 759 861651: 987 6244730 : 874 868175 : 451 693852 : 201 4968058 : 794 | 7297208 : 974 6088434 : 638 236275 : 727 24056 : 388 12121 : 527 21536 : 628 | 27528 : 296 64672 : 688 15336 : 426 41800 : 475 107724 : 876 65484 : 963 |
168144 :372 331540 : 605 35984 : 173 25724 : 236 122720 : 472 260400 : 744 | 84513 : 429 160440 : 573 132192 : 324 272640 : 284 448574 : 712 87396 : 215 | 30075 : 401 73278 : 354 24786 : 306 12443 : 541 13806 : 531 16443 : 307 | 23206 : 283 214082 : 526 409236 : 804 11352 : 132 226688 : 736 78192 : 724 |
25544 : 124 48664 : 316 197209 : 199 130935 : 215 122720 : 472 160440 : 573 | 897744 : 472 130935 : 215 347300 : 575 544428 : 213 213 816 : 472 35984 : 173 | 298298 : 149 86415 : 105 181298 : 734 298298 : 149 429 260 : 845 396 390 : 905 | 132840 : 328 61610 : 305 181298 : 734 61610 : 305 47008 : 904 447 950 : 527 |
По теме: методические разработки, презентации и конспекты
Конспект урока «Умножение многозначного числа на трехзначное»
Конспект урока по математике, УМК «Школа XXI века», 4 класс. ..
..
Умножение многозначного числа на трехзначное (презентация)
Презентация к уроку, УМК «Начальная школа XXI века», 4 класс, математика…
Письменное деление многозначного числа на трехзначное.
Садриева Гульнара Ренатовна МБОУ «Школа № 127»4 класс МатематикаТема «Письменное деление многозначного числа на трехзначное»Урок проведен в технологии деятельностного методаТип урока: ОНЗ…
Умножение многозначного числа на трехзначное Математика 4 класс
Тип урока: урок рефлексии. Цель урока: сформировать знания учащихся по теме: умножение многозначного числа на трёхзначное. Задачи урока:1.Сформиров…
Конспект урока по математике 4 класс тема «Умножение многозначного числа на трехзначное число»
Тип урока: урок формирования и совершенствования умений и навыков.Цель урока: повторить, закрепить знаний по умножению многозначного числа на трехзначное число, применять знания на практике….
Технологическая карта урока математика «Деление многозначного числа на трехзначное число с остатком» (УМК «Школа России», 4 класс)
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА МАТЕМАТИКИ Дата: 10. 05.2022Школа: №74Класс: 4 «М»Урок: 1Время: 8.00-8.45Кабинет: 203Студент: Закирова Эльвира РахимовнаУчитель: Новикова Анна Александровна…
05.2022Школа: №74Класс: 4 «М»Урок: 1Время: 8.00-8.45Кабинет: 203Студент: Закирова Эльвира РахимовнаУчитель: Новикова Анна Александровна…
Технологическая карта урока математики «Письменное деление многозначного числа на трехзначное число» (УМК «Школа России», 4 класс)
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА МАТЕМАТИКИ Дата: 03.05.2022Школа: №74Класс: 4 «М»Урок: 1Время: 8.00-8.45Кабинет: 203Студент: Закирова Эльвира РахимовнаУчитель: Новикова Анна Александровна…
Поделиться:
Урок математики «Деление многозначных чисел на двухзначное число в коррекционной школе VIII-го вида
Урок по математике в 7 классе по теме: “Деление многозначных чисел на двузначное число в коррекционной школе VIII вида” с использованием ЭОРов (Приложение 1).
3 четверть, январь, 2012.
Место в системе уроков: (Приложение
2) четвёртый урок по теме: “Деление на
двузначное число”.
(Приложение 2 для ученика.
Тип урока: комбинированный урок. Комбинированный урок сочетает в себе различные виды работ — объяснение, закрепление, проверку и др.
Цель: продолжать учить алгоритму деления многозначного числа на двузначное число.
Ожидаемый результат: решают примеры на деление способом подбора.
Задачи урока:
Образовательная:
продолжать учить делить многозначное число на двузначное методом подбора;
повторить приёмы устного вычитания;
продолжать отрабатывать навыки счета письменных случаев деления на однозначное число и умножения на двузначное число в процессе решения задач на движение.
Развивающая:
развивать вычислительные навыки, познавательный интерес, умение рассуждать;
творческие способности посредством составления задачи;
Воспитательная:
воспитывать эстетический вкус, аккуратность
при работе в тетради, толерантность.
Коррекционная:
стимулировать познавательную деятельность учащихся;
коррекция внимания, мышления, зрительной памяти.
Оборудование: Учебный комплекс для учащихся: Учебник “Математика” для 7 класса/Под ред. Т.В.Алышева/ М. Пр. 2010 г., персональный компьютер с программой PowerPoint, медиа-проектор, текст задачи, таблица-алгоритм, пособия и ЭОРы по теме (Приложение 4), листок рефлексии.
Ход урока
Презентация. Слайд №1
I. Организация начала урока. Концентрация внимания.
— Здравствуйте, ребята! Рада вас видеть.
Рапорт дежурного: сегодня 19 января 2012 года, четверг, урок по счёту 5-й – математика. В классе все. Класс к уроку готов.
Психологическая минутка.
А теперь проверь, дружок,
Ты готов начать урок?
Все ль на месте, всё ль в порядке,
Книжка, ручка и тетрадка?
Все ли правильно сидят?
Все ль внимательно глядят?
Знаю, каждый хочет получать
На уроке только “5”.
— Хорошо. Начинаем работать. Проверим осанку.
II. Сообщение темы и цели урока.
— А теперь вспомним, чем занимались на последних уроках?
Прекрасные результаты на прошлом уроке показали такие учащиеся:………..
А ……………….. учащимся пожелаю успеха сегодня на уроке.
Я вам предлагаю продолжить учиться делить многозначные числа на 2 значное число.
Итак, тема урока: “Деление многозначных чисел на двузначное число”.
III. Подготовка к активной деятельности на основном этапе.
Запишем число, классная работа, тему урока в тетрадях. Слайд №2.
Для того, чтобы хорошо выполнять письменное
деление нужно уметь выполнять и другие
арифметические действия. Какие? И знать хорошо
таблицу умножения. Знать алгоритм письменного
деления на 1-зн. число, алгоритм умножения на 2-зн.
число, чтобы сделать проверку.
Давайте, ребята, учиться считать,
Делить, умножать, прибавлять, вычитать.
Запомните все, что без точного счета
Не сдвинется с места любая работа.Без счета не будет на улице света,
Без счета не может подняться ракета,
Без счета письмо не найдет адресата,
И в прятки сыграть не сумеют ребята.Считайте, ребята, точнее считайте,
Хорошее дело смелей прибавляйте,
Плохие дела поскорей вычитайте.Учебник научит вас точному счёту.
Скорей за работу, скорей за работу.
Устные упражнения – компоненты и результат действия вычитания:
А) Математический тренажёр. Слайд №3.
Повторим приёмы устного вычитания: 1 приём №1: 86-23=63 (Приложение)
3 приём №2. 75-43=
2 приём №3 61-29=
Вычислим и выберем ответ: 78-39 = №4
Счет цепочкой: 77:11 x 4-28= …(0). Слайд №4.
Какое число нужно вставить в рамку: ? + 850 = 1 000. Слайд №5
Слайд №5
А) Проверяю знание таблицы умножения (Презентация) на 7 (ЭОР №5). Приложение
Делим.
-
Умножаем.
Вычитаем.
Сносим
| Памятка _________ |
Слайд №6
B) Алгоритм письменного деления в столбик.
На доску вывешиваются памятка:
Что означает черта в алгоритме деления? Остаток
должен быть меньше делителя, а в противном случаи
– ошибка. Если остаток больше или равен делителю,
то сразу можно сделать вывод о том, что допущена
ошибка, результат выполнен неверно.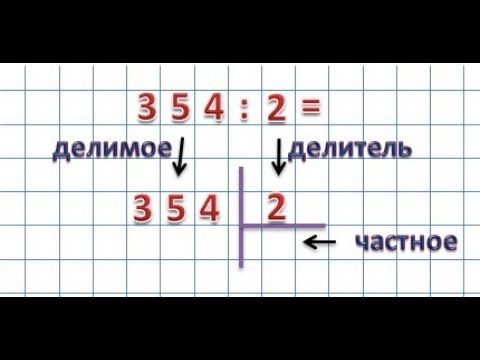
Деление на однозначное число:
Правильно, ли выполнено действие?
Назовите компоненты и результат действия деления.
Как получили число 4?
Как получили число 24?
Что при этом узнали?
Что показывает число 3?
Как его получили?
Назовите все остатки, которые могут быть получены при делении на 6.
Может ли в остатке быть получено число 6? Почему?
C) Повторение алгоритма умножения двузначных чисел.
Те, кто ещё плохо его запомнил, могут воспользоваться таблицей-памяткой, которая лежит у вас на партах.
Памятка — Умножу первый множитель на число единиц. — Получу первое неполное произведение. — Умножу первый множитель на число десятков. — Получу второе неполное произведение. — Сложу неполные произведения. — Читаю ответ. |
На доску вывешиваются опорные слова: “неполное произведение” и памятка.
Компоненты и результат действия умножения.
Устный комментарий: 248×75= Пособие на доске
Назовите первый множитель. (248)
Как обозначаем знак “умножить”? (х)
Назовите второй множитель. (75)
Как его записать? (Единицы под единицами, десятки под десятками).
Что сначала умножаем? (Первый множитель на число единиц).
Потом? (Первый множитель на число десятков).
Каковы ваши дальнейшие действия? (Складываем неполные произведения).
Запомните этот алгоритм, т.к. он нам пригодится в дальнейшем. (Когда будем проверять действие деление).
Итоги данной работы.
III. Изучение нового материала
Прочитайте примеры. Выберите те, которые
относятся к теме урока.
Работа по учебнику с.166 №550.
Внимательно рассмотрите образцы решения примеров. Определим количество цифр в частном.
Образец решения примера дает учитель:
- 60 384:24 =
- 11 040:32 =
- 154 125:45=
Ищем частное способом подбора, используем памятку:
Алгоритм решения:
Объяснение:
- Отделяем знаки первого неполного делимого, определяем количество цифр в частном.
- Подбираем первую цифру частного, умножаем делитель на эту цифру, вычисляем остаток.
- Сносим следующий знак делимого, получаем второе неполное делимое.
- Подбираем вторую цифру частного, умножаем делитель на эту цифру, вычисляем остаток; …
- Остаток отсутствует, значит деление закончено.

На доску вывешиваются опорные слова: “ неполное делимое”.
Учитель объясняет и решает на доске 1-ый пример (ученики записывают его в тетради).
1-ая физкультминутка, осанка.
Поднимает руки класс – это раз,
Повернулась голова – это два,
Руки вниз и впереди – это три,
Руки в стороны пошире развернули на четыре,
А потом к плечам прижать – это пять,
Всем ребятам тихо сесть – это шесть
Проверим осанку.
Внимание: Посмотрите на примеры на доске, что вы видите? (Записаны проверки действий деления). Выполним проверку 1-ого примера (вызывается к доске ученик).
V. Первичная проверка понимания нового материала.
Учащийся решает у доски пример с опорой на алгоритм: Слайд №8.
№550 (2). – а). Назовите первое неполное делимое в
каждом случае. Выполните деление с объяснением
Выполните деление с объяснением
(у каждого ученика алгоритм деления с объяснением). I группа учащихся работает с опорой на доску.
II группа учащихся работает в тетради самостоятельно следующие примеры.
Дополнительный вопрос для отвечающего: Определи количество цифр в частном, если известно, что первые две цифры в делимом больше первых двух цифр в делителе. — ЭОР №6 (Деление на 2-зн. число). Приложение
Гимнастика для глаз. Слайд №9. Приложение
VI. Закрепление знаний.
Дифференцированная работа: Слайд №10.
Творческое задание — задача: стр.163 № 535. Составьте задачи. Найдите недостающие числа (Приложение 2).
| Транспорт | Скорость V (км/ч) |
Время t (ч) |
Расстояние S (км) |
| Мотоцикл | ? | 3 | 135 |
| Автобус | 53 | ? | 265 |
| Поезд | 57 | 8 | ? |
| Автомобиль | 64 | ? | 384 |
Что объединяет эти задачи? (Эти задачи на
движение). Какие величины здесь используются.
Какие величины здесь используются.
Как найти скорость? (Расстояние разделить на время). Что означает скорость в задачах на движение? (Скорость – это расстояние за единицу времени)
Как найти время пути? (Расстояние разделить на скорость)
Как найти расстояние? (Скорость умножить на время). ЭОР №9 — (9 км x 45=405 км). Приложение
Самостоятельная работа учащихся в тетради по решению задачи (учитель оказывает помощь ученикам 1 группы):
1. 135 км : 3 =45 км
Ответ: Скорость мотоциклиста 45 км в час.
Дополнительный вопрос для отвечающего: Зная первое неполное делимое определи количество цифр в частном. Выбери правильный ответ — ЭОР №7 (Деление. Определение количества цифр в частном). Приложение
Вторая группа учащихся записывает решении задачи самостоятельно.
(Тот, кто решил первым, записывает ответы на
доске. Неправильно решенные примеры
объясняются).
Неправильно решенные примеры
объясняются).
2. 265 км : 53 км=5 (ч)
Ответ: 5 часов был в пути автобус.
3. 57 км x 8=456 км
Ответ: 456 км проехал поезд за 8 часов.
Дополнительный вопрос для сильного: Определи количество цифр в частном. Выбери верный вариант. — ЭОР №8 (Деление на 3-зн. число). Приложение
VII. Информация по домашнему заданию, инструктаж по его выполнению.
Повторить таблицу умножения и деления на 6, стр.166 №550(3)(а) – 1 стр. Сильным доделать задачу №535. Слайд №11.
VIII. Итоги урока, оценка знаний, рефлексия.
Наш урок подходит к концу. Был ли он интересен?
Полезен? Узнали ли вы что-либо нового? Каким
способом выполняется письменное деление на 2-зн.
число? (Способом подбора). Что повторили?
Расскажите алгоритм письменного умножения на
двузначное число. Расскажите алгоритм
письменного деления на двузначное число.
Релаксация. Слайд №12.
Учащийся ставит “+” в какой-то отдел листка рефлексии. (Приложение 2)
Листок рефлексии:
| Понял! Уроком доволен. |
Не совсем понял, Хочу понять. |
Ни чего не понял. | И не хочу понимать! |
Благодарю детей за хорошую работу, ставлю оценки в журнал.
Надеюсь, что полученные на уроке знания и навыки пригодятся в дальнейшем обучении и в жизни. А урок я хотела бы закончить отрывком из стихотворения А.С. Пушкина:
О, сколько нам открытий чудных
Готовит просвещенья дух
И опыт – сын ошибок трудных
И гений – парадокса друг.
Урок окончен. Молодцы дети – плодотворно поработали.
В оставшееся время. Разгадайте ребус, он вам скажет куда вы пойдёте после этого урока. Слайд №13.
(Учитель контролирует выполняемость работы, проставляет количество верных ответов на уроке заносит результаты в карту анализа)
Карта анализа результатов работы учащихся.
| № | Список учащихся | Устная работа | Работа по теме | Дополнительно | Оценка |
| 1 | Арутюнова | ||||
| 2 | Васильева | ||||
| 3 | Лаиджев | ||||
4. |
Маслюков | ||||
| 5 | Паньков | ||||
| 6 | Хован | ||||
| 7 | Шевченко | ||||
| 8 | Фаррухзаде |
Заключение.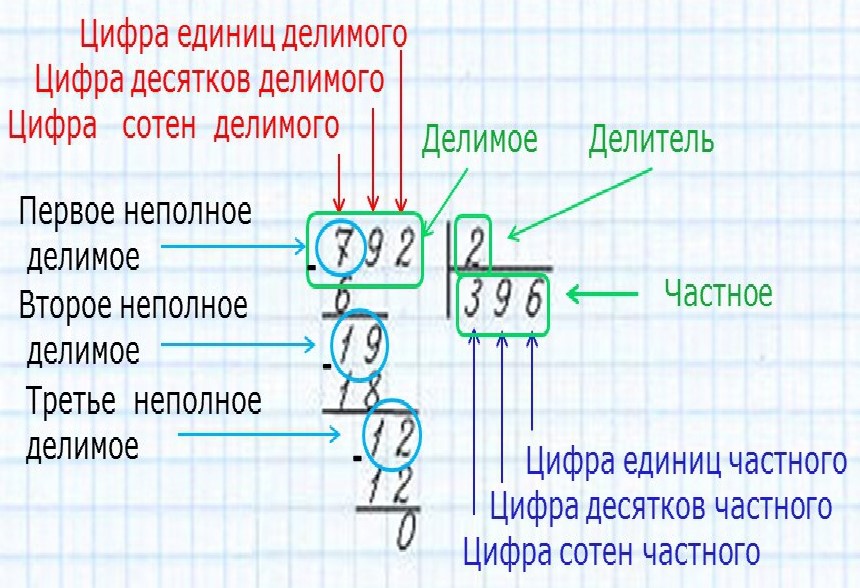
Данный тип урока – комбинированный. Комбинированный урок сочетает в себе различные виды работ – повторение, объяснение, закрепление, проверку, самостоятельную работу и др..
В ходе закрепления использовалось сочетание разнообразных методов обучения: объяснительно-иллюстративный, наглядный методы обучения, беседа, упражнения. Методы обучения были выбраны в соответствии с психологическими, возрастными особенностями детей.
Урок способствовал коррекции внимания,
мышления, зрительной памяти, стимулировал
мыслительную деятельность учащихся. Учащиеся с
ограниченными умственными возможностями не
способны к долговременному восприятию учебного
материала. Поэтому на уроке
использовалось чередование видов
деятельности: устная работа, работа у доски, по
карточкам, коррекционно-развивающие игры, работа
с учебником, самостоятельная работа. Во время
урока использовалась наглядность, которая
способствовала повышению познавательной
активности учащихся, ЭОРы (информационные,
практические, контрольные), которые скачиваются
с Интернета с образовательных сайтов. Обучающиеся проявляли активность, высокую
работоспособность, самостоятельность.
Обучающиеся проявляли активность, высокую
работоспособность, самостоятельность.
Результат рефлексии показал, что 98% учащихся уроком довольны, материал поняли. Каждый учитель, будь то педагог-наставник, или молодой специалист, обязательно вносит в свои уроки частичку нестандартного, нетрадиционного, оригинального, стремясь сделать их интересными, доступными для понимания, и, на мой взгляд самой лучшей оценкой нашей работы является искренние и такие простые фразы, которые слышишь после урока: “Мне было интересно на этом уроке”, “Как много нового я узнал!”, “Спасибо за урок”.
Я считаю, что мне удалось реализовать замысел урока, достичь поставленные цели. Проведённый урок был направлен на формирование положительной “Я – концепции” личности учеников. На уроке был создан благоприятный психологический климат.
Методика изучения деления многозначных чисел — Мегаобучалка
А) Деление многозначного числа на однозначное
Умение делить многозначное число на однозначное фактически начинает формироваться при рассмотрении деления трехзначных чисел в разделе «Числа от 1 до 1000».
Изучение деления трехзначных чисел на однозначное число начинается с устных приемов. Вначале целесообразно вспомнить знакомые детям случаи деления двузначных чисел на однозначное. При этом следует вспомнить рассуждения для разных случаев:
48 : 4; 48 : 3. Обобщая, повторяем вывод: при делении двузначного числа на однозначное делим десятки, а затем делим единицы.
Приступая к делению трехзначных чисел, следует провести аналогии с рассмотренными ранее случаями:
48 : 4, 848 : 4= (800+40+8): 4; 48 : 3, 480 : 3 = (300 + 180) : 3.
Установив сходство и различия, подводим детей к основному выводу: делим, начиная с единиц высшего разряда, сначала делим сотни, затем десятки, затем единицы, то есть делим поразрядно.
Уже при устных вычислениях можно ввести некоторые новые для детей термины, которые будут употребляться в дальнейшем.
Например, в случае 480 : 3 = (300 +180): 3 = 300 : 3 +180 : 3, числа 300 и 180 называют неполными делимыми.
Переход к письменным приемам деления трехзначных чисел следует проводить с постепенным нарастанием сложности.
После решения нескольких примеров на деление устно целесообразно предложить детям случай, где выполнить вычисления устно будет трудно. Например, 968: 4. Представляя делимое в виде суммы удобных слагаемых, то есть, выделяя неполные делимые, дети, естественно, будут испытывать трудности. Здесь следует напомнить детям, что, если трудно вычислять, можно записать столбиком. Однако запись в столбик при делении отличается от столбика при умножении. Поэтому вначале следует показать эту запись на знакомом детям материале, объясняя, где что записываем и как при этом рассуждаем:
8:2=4; 15:3=5; 13:4=3 (ост. 1).
_ 8 ∟2 _15 ∟3 _13 ∟4
8 4 15 5 12 3
0 0 1
Затем следует рассмотреть случай, записав его в столбик, когда каждый разряд делимого делится на делитель. Например, решая пример 846 : 2 = (800 + 40 + 6): 2 = 800 : 2 + 40 : 2 + 6 : 2 и повторив ход устных рассуждений, предлагается записать решение в столбик.
_ 846∟ 2При решении показывается и ход рассуждений:
8 423 1. Начинаем делить с сотен. Смотрим, сколько сотен в делимом (8). 8
_4 на 2 делится. Значит первое неполное делимое 8 сотен. Определяем,
4 сколько всего цифр будет в частном (3). Ставим 3 точки.
_6 Находим эти цифры частного. 8 сотен делимна 2 получим 4. В частном
6 пишем 4 на месте сотен. Узнаем, сколько сотен разделилось. 4 умножа
0 ем на 2, получим 8, записываем под сотнями. Из 8 вычесть 8 будет 0, его писать не будем. Сотни разделились все.
2. Делим десятки. 4 десятка — второе неполное делимое. 4 разделить на 2 будет 2. Пишем в частном цифру 2 на месте десятков. Узнаем, сколько десятков разделилось. 2 умножим на 2, получим 4. Из 4 вычесть 4 получим 0. Десятки разделились все.
3. Делим единицы. 6 единиц — третье неполное делимое. 6 разделить на 2 будет 3. Пишем в частном 3. Узнаем, сколько единиц разделилось. 3 умножим на 2, получим 6. Из 6 вычесть 6 будет 0. Все число разделилось. Читаем ответ: 423.
6 разделить на 2 будет 3. Пишем в частном 3. Узнаем, сколько единиц разделилось. 3 умножим на 2, получим 6. Из 6 вычесть 6 будет 0. Все число разделилось. Читаем ответ: 423.
Теперь следует вернуться к решению примера 984 : 4 в столбик и на нем повторить ход рассуждений, обращая внимание на некоторые новые моменты.
_948 ∟4 1. Делим сотни. 9 сотен делится на 4 с остатком. Значит
8 237 9 сотен — первое неполное делимое. В частном будет 3
_14 цифры, ставим три точки.
12 2. 9 делим на 4, возьмем по 2.
_28 3. Узнаем, сколько сотен разделилось. 2 умножим на 4,
28 получаем 8.
0 4. Из 9 вычесть 8, получаем 1. Остаток 1 меньше делителя. Можно делить дальше.
5. Делим десятки. 1 сотня да 4 десятка в делимом получаем 14 десятков — это второе неполное делимое и т.д.
Следующий элемент усложнения состоит в том, что первая цифра делимого может быть меньше делителя.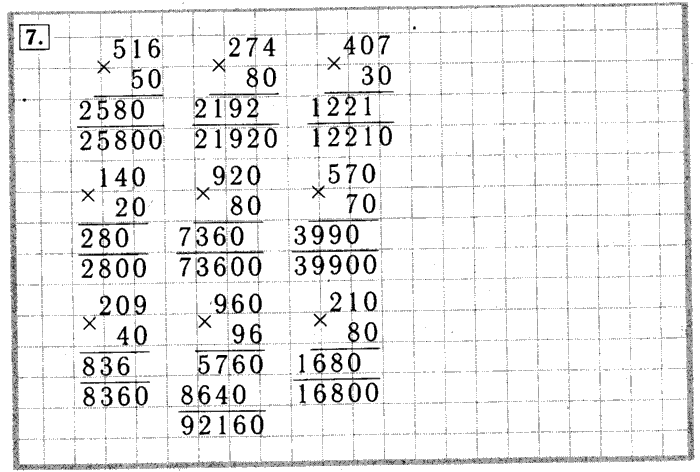 Это значит, что первое неполное делимое будет образовано двумя первыми цифрами делимого. В частном получится цифр на 1 меньше, чем в делимом.
Это значит, что первое неполное делимое будет образовано двумя первыми цифрами делимого. В частном получится цифр на 1 меньше, чем в делимом.
Пример. 348 : 4
Здесь следует обратить внимание детей на образование первого неполного делимого.
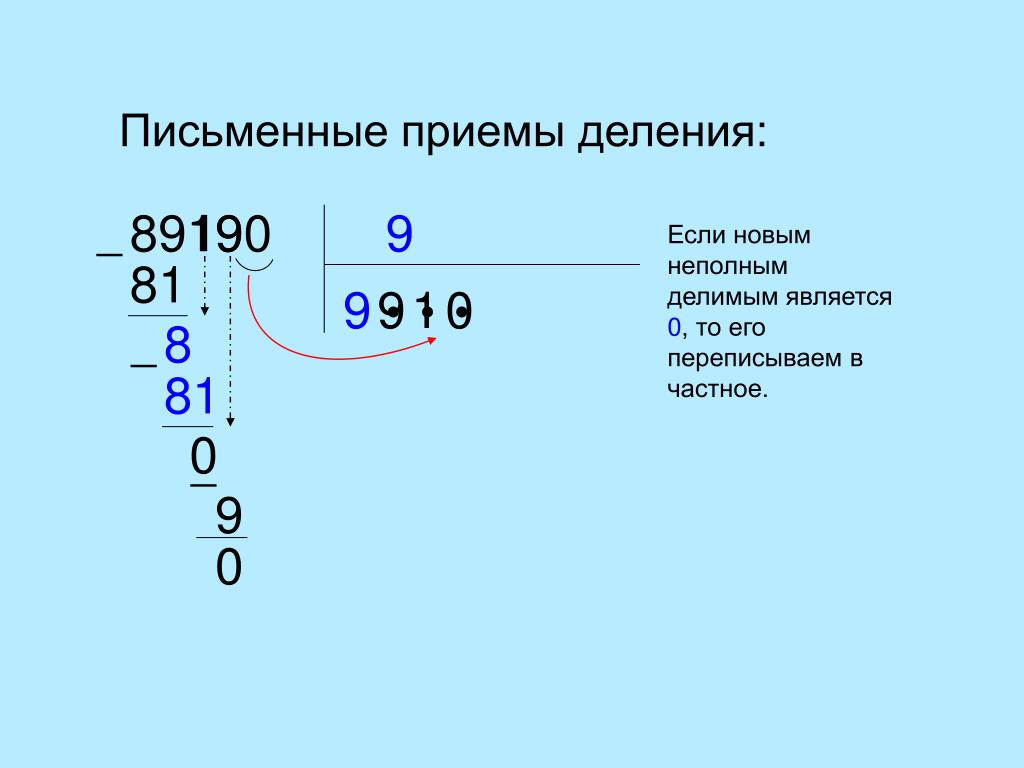
Наиболее коварными для детей являются случаи деления, когда в середине или на конце частного получаются нули. В таких случаях дети часто допускают ошибки, теряя нули.
При решении первого такого примера запись следует выполнять подробно, затем показать ее в сокращенном виде.
_915 ∟3 _915 ∟3
9 305 9 305
_1 … _15 …
0 15
_ 15 0
15
В качестве подготовительных упражнений, наряду с другими, с детьми обязательно следует вспомнить решение примеров, которые должны решаться при изучении деления с остатком
1:3=0 (ост. 1) 2:6=0 (ост. 2)
Чтобы облегчить детям усвоение алгоритма деления, рекомендуется использовать памятку вида:
1. Прочитай и запиши пример;
Прочитай и запиши пример;
2. Установи высший разряд и число цифр в частном;
3. Раздели, чтобы найти цифру высшего разряда частного;
4. Умножь, чтобы узнать, сколько единиц этого разряда разделили;
5. Вычти, чтобы узнать, сколько единиц этого разряда осталось разделить;
6. Сравни остаток с делителем;
7. Если получился остаток, то вырази его в единицах следующего за ним низшего разряда и прибавь к ним единицы такого же разряда делимого;
8. Продолжай деление так же, пока не решишь пример до конца;
9. Проверь результат.
Вначале этой памяткой пользуется только учитель. При этом важно, чтобы объяснения давались им в той же последовательности. Затем с памяткой знакомятся учащиеся. В классе она вывешивается в виде таблицы, а для себя каждый ученик записывает на отдельном листке.
Начинают работать учащиеся с памяткой под руководством учителя, проговаривая каждое задание и ответ на него. Затем начинают пользоваться сами, проговаривая рассуждения про себя. И, наконец, выполняют операции самостоятельно в соответствии с заданиями.
И, наконец, выполняют операции самостоятельно в соответствии с заданиями.
Эта работа получает свое естественное продолжение в разделе «Числа, которые больше 1000». Здесь продолжается работа по формированию у детей умения выполнять деление чисел в пределах миллиона.
Все случаи деления многозначных чисел изучаются в такой последовательности:
— деление многозначного числа на однозначное;
— деление многозначного числа на числа, оканчивающиеся нулями;
— деление многозначного числа на двузначное и трехзначное число. Приступая к рассмотрению первого случая деления, следует провести работу по восстановлению в памяти детей необходимых сведений:
— смысл действия деления; названия компонентов и результата действия деления;
— связь умножения и деления;
— таблица умножения и деления;
— внетабличные случаи деления двузначного числа на однозначное;
— деление с остатком;
— деление трехзначных чисел на однозначное число (устные приемы
и письменные).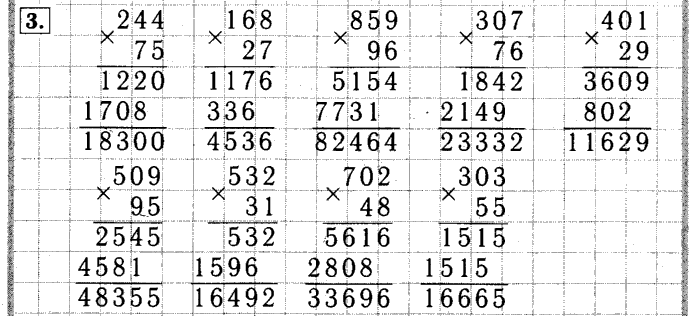
В результате этого, деление многозначного числа на однозначное будет являться логическим продолжением начатой ранее работы.
Начинать следует с устных приемов. После решения примероввида:
84 : 2 и 484 : 2;
И 840 : 3,
следуетпредложить примеры:
6484:2= (6000+400+80+4): 2 ==6000:2+400:2+80:2+4:2 =3242;
8400 : 3 = (6000 + 2400) : 3 = 2800.
Проведя сравнение, установив сходство и различие, подводим детей к выводу:
— делим, начиная с единиц высшего разряда;
— делим поразрядно.
Приступая к рассмотрению письменных приемов деления многозначных чисел, естественно, повторить деление трехзначных чисел в столбик.
Случаи деления трехзначных чисел следует взять разные, начиная с легких, то есть таких, когда количество цифр в частном такое же, как и в делимом, а затем усложнить.
Пример.
_9648 ∟4
8 2412
_16
16
_4
4
_8
8
1964 ∟4 3624∟4 36240∟4
… … ….
При решении этих примеров надо обратить внимание детей на ход рассуждений, вспомнить памятку, а затем показать, как применить ее и при решении новых примеров.
Деление на двузначное число — способы и примеры решений » Kupuk.net
Главная » Уроки » Математика
Автор Беликова Ирина На чтение 3 мин Просмотров 316
Деление на двузначное число похоже на тот же процесс с однозначным числом, но занимает больше времени. Однако есть немало методов, которые упрощают процесс. Научиться выполнять деление быстро помогут основные правила и серьезная практика.
Деление на двузначное число устно
Осуществляется такое деление методом подбора. Например, нужно разделить число 90 на двузначное число 15 без остатка.
Чтобы это сделать устно, нужно подобрать такое число, которое при умножении его на 5 (15 оканчивается на 5) даст число, оканчивающееся на 0 (так как 90 оканчивается на ноль).
90 : 15 = 6
Какое число при умножении на 5 даст в результате число с цифрой 0 на конце? Их несколько.
Подбираем:
5 * 2 = 10;
5 * 4 = 20;
5 * 6 = 30.
Теперь проверяем. Если цифра нам подходит, то, умножив ее на 15, получим 90:
2 * 15 = 30;
4 * 15 = 60;
6 * 15 = 90.
Последняя цифра 6 подходит. Мы выполнили деление: 90 : 15 = 6.
Деление в столбик на двузначное число
Деление в столбик школьники проходят еще в младших классах на уроках математики. В дальнейшем его применяют как вспомогательное средство при решении задач. Но если не пройти в нормальном виде деление уголков, то могут возникнуть затруднения и с трехзначными числами.
Рис. 1
На рисунке 1 показан принцип деления и названия основных элементов процесса. Как и при делении на однозначные числа, работает алгоритм перехода от крупных к мелким единицам.
Порядок действий опишем, взяв для примера вычисление, представленное на рисунке 1:
Выделить самое маленькое двузначное число 63, которое можно поделить на делитель 61. Оно всегда больше того, которое является делителем.
Оно всегда больше того, которое является делителем.
Делим 63 на 61. Сколько раз 61 поместится в 63? Один. Записываем под уголком единицу. Это первая цифра частного.
Умножаем делитель на эту первую цифру: 61 * 1 = 61, вычитаем из 63 число 61, проводим черту и пишем разность — 2.
Сносим следующую цифру делимого — 4. Получаем число 24. Оно не делится на 61, потому записываем ноль на место второй цифры частного (это место рядом с цифрой 1 в нашем примере).
Сносим следующую (последнюю в нашем примере) цифру, это 4. Получаем число 244. Делим его на 61. Применим правило устного деления, описанное выше. Нужно подобрать такую цифру, которая при умножении на последнюю цифру (у 61 последняя цифра 1) даст ответ, оканчивающийся на последнюю цифру делимого (у 244 последняя цифра 4, она нам и нужна). Т. е. 4 * 1 = 4. Проверка: 61 * 4 = 244. Мы подобрали цифру 4 и она нам подошла.
Вписываем 4 третьей цифрой частного в уголок, получаем 104. Умножаем 61 на 4 и вычитаем результат из 244. Получаем 0. Деление выполнено.
Умножаем 61 на 4 и вычитаем результат из 244. Получаем 0. Деление выполнено.
В данном примере делимое — трёхзначное число. В общем случае процесс сноса цифр делимого и деления их на делитель продолжается до тех пор, пока не закончатся все цифры делимого. Этот принцип подходит для трехзначных, четырехзначных и других многозначных чисел.
Примеры деления в столбик на двузначное число
Рассмотрим некоторые примеры. Они довольно простые и помогут понять основные моменты данного способа.
Пример 1
Найдём значение частного чисел 265 и 53:
Пример 2
Найдем результат деления чисел 624 и 52:
Пример 3
Рассмотрим более сложные случаи деления в столбик. Найдем значение частного чисел 1610 и 35:
Найдем значение частного чисел 1610 и 35:
Пример 4
Деление пятизначного числа на двузначное. Узнаем значение частного чисел 10150 и 35:
Пример 5
Деление многозначного числа на двузначное с остатком. Вычислим, чему будет равно частное чисел 1978 и 38:
Деление на двузначное число можно выполнять в столбик и устно, но многозначные числа устно считать намного сложнее. Немногие школьники могут похвастаться подобными умениями.
Освоение процесса деления поможет школьникам в дальнейшем обучении. Так же существует немало тренажеров и онлайн-калькуляторов, которые можно использовать в свою пользу.
Оцените автора
Деление многозначного числа на однозначное
Урок 24.
 Математика 4 класс ФГОС
Математика 4 класс ФГОСКак можно многозначное число разделить на однозначное? Существует несколько способов: выполнить деление, раскладывая числа на разрядные слагаемые или на удобные для деления слагаемые. Но, конечно, гораздо легче выполнять деление столбиком. Решалочка объяснит способ записи простых случаев письменного деления многозначного числа на однозначное. В этих примерах каждый разряд делится на делитель. А ещё она напомнит, какой результат получается при делении на 1, и почему нельзя делить на 0.
Конспект урока «Деление многозначного числа на однозначное»
Привет, ребята!
Сегодня нам с вами предстоит вспомнить приёмы деления многозначного числа на однозначное. А ещё я напомню вам, как выполняется деление с числами нуль и один.
И начнём мы вот с такого примера.
624 : 2 =
Знаете ли вы, как устно
разделить число шестьсот двадцать четыре на два? Да всё очень просто! В этом
числе каждый разряд делится на два. Мы просто разложим делимое на сумму
разрядных слагаемых, потом каждое из них разделим на делитель. И
полученные результаты сложим.
Мы просто разложим делимое на сумму
разрядных слагаемых, потом каждое из них разделим на делитель. И
полученные результаты сложим.
624 : 2 = (600 + 20 + 4): 2 = 600 : 2 + 20 : 2 + 4 : 2 = 312
Ну а если надо пятьсот семьдесят четыре разделить на семь?
574 : 7 = (560 + 14) : 7 = 560 : 7 + 14 : 7 = 82
Тут уж не получится делить каждый разряд. Поэтому мы будем раскладывать не на сумму разрядных слагаемых, а на сумму удобных для деления слагаемых.
Пять меньше семи, и разделить на семь мы его не сможем. Возьмём пятьдесят семь. Пятьдесят семь на семь не делится, зато делится пятьдесят шесть. Поэтому в качестве первого слагаемого мы берём пятьдесят шесть десятков – это число пятьсот шестьдесят. Остаётся один десяток и четыре единицы – это число четырнадцать. Оно будет вторым слагаемым. Делим каждое из них на семь, складываем результаты. Ответ: восемьдесят два.
Попробуйте-ка вы сами, ребята,
выполнить деление, раскладывая числа на разрядные или удобные для деления
слагаемые.
Вот, например, найдите значения вот этих числовых выражений.
693 : 3 =
486 : 6 =
Ну, проверьте, так ли вы выполнили решение?
693 : 3 = (600 + 90 + 3) : 3 = 600 : 3 + 90 : 3 + 3 : 3 = 231
486 : 6 = (480 + 6) : 6 = 480 : 6 + 6 : 6 = 81
А теперь давайте вспомним, как трёхзначные числа делятся столбиком. Запишите решение этих же примеров столбиком.
Проверьте свои решения.
Я уверена, что и решение столбиком вы записали верно. А как вы думаете, друзья, всегда ли числа можно разделить нацело? Конечно, нет! Представьте себе такую ситуацию.
В школу привезли сорок три новые парты. Их надо разделить поровну между четырьмя классами. Сколько парт поставят в каждый класс?
Тааак. Парт 43. классов 4. 43 на
4 нацело не делится… ммм… А вот сорок – делится. Получается, что каждому
классу достанется по десять парт. Да ещё три парты останутся. В резерве )).
43 на
4 нацело не делится… ммм… А вот сорок – делится. Получается, что каждому
классу достанется по десять парт. Да ещё три парты останутся. В резерве )).
43 : 4 =10 (ост. 3)
Ответ: каждому классу достанется по 10 парт, и ещё 3 парты останется.
А помните ли вы, как проверять деление с остатком? Надо частное умножить на делитель, и прибавить остаток. Вот как у меня:
Проверка:
10 ∙ 4 + 3 = 43
В результате получилось делимое, значит, деление с остатком было выполнено верно.
Ну и осталось нам вспомнить деление с числами нуль и один.
Я думаю, вы помните, что, если нуль делить на любое число, в ответе получится нуль.
Ведь, как говорится, на сколько бы частей дырку от бублика ни поделили, бублика отведать не получится.
А можно ли делить на нуль? Ну
конечно же нет. Кто забыл, почему нельзя? Попробуйте
выполнить обратное действие, умножение. Какое бы число ни получилось в ответе,
а может быть только нулём и никаким другим числом. Ведь при умножении
любого числа на нуль в ответе будет нуль. Но если а равно нулю, то и в
ответе может быть только нуль. Других вариантов нет. Так что, мы просто должны
помнить: на нуль делить не будем.
Какое бы число ни получилось в ответе,
а может быть только нулём и никаким другим числом. Ведь при умножении
любого числа на нуль в ответе будет нуль. Но если а равно нулю, то и в
ответе может быть только нуль. Других вариантов нет. Так что, мы просто должны
помнить: на нуль делить не будем.
А вот с единицей всё гораздо проще. Если число делим на один, то частное будет равно делимому. А если делимое и делитель равны, то частное будет равно числу один.
Ну и напоследок, я предлагаю вам решить несколько примеров, а потом мы их проверим.
58 : 26 =
0 : 514 =
317 : 1 =
568 : 568 =
Ребята, проверьте вашу работу.
58 : 26 = 2 (ост. 6)
0 : 514 = 0
317 : 1 = 317
568 : 568 = 1
Если вы всё сделали правильно, значит урок не прошёл мимо вас, и вы готовы к новым свершениям в нашей замечательной стране Математике.
Ну что же, сегодня нам пора прощаться. До встречи, друзья!
До встречи, друзья!
Предыдущий урок 23 Нахождение неизвестных множителя, делимого или делителя
Следующий урок 25 Приём письменного деления на однозначное число
Получите полный комплект видеоуроков, тестов и презентаций Математика 4 класс ФГОС
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Деление многозначных чисел на многозначные числа
Здесь вам придется напрячь свой мозг и выжать из него максимум, ведь делить многозначное число на многозначное число не так просто.
Принцип деления тот же, что и раньше. Здесь также нужно найти первый неполный делитель. Здесь вы также можете найти остаток от деления.
Во-первых, мы вводим новое понятие — круглое число . Круглое число — это число, оканчивающееся на ноль. Например, следующие числа круглые:
10, 20, 30, 500, 600, 1000, 13000
Любое число можно превратить в круглое. Для этого первые цифры, образующие наибольшую цифру, оставляют без изменений, а остальные цифры заменяют нулями.
Например, превратим число 19 в круглое число. Первая цифра числа 1 образует старшую значащую цифру (цифру десятков) — цифру оставляют как есть, а оставшиеся 9 заменяют нулем. Результат равен 10.
Другой пример. Превратим число 125 в круглое число. Первая цифра 1 образует самый большой разряд (место сотен) — цифру оставляем без изменений, а остальные 25 цифр заменяем нулями. Результат 100.
Другой пример. Превратите число 2431 в круглое число. Первая цифра 2 — это самая большая цифра (цифра тысячи), оставьте ее без изменений, а остальные цифры 431 замените нулями. Конечным результатом будет 2000.
Другой пример.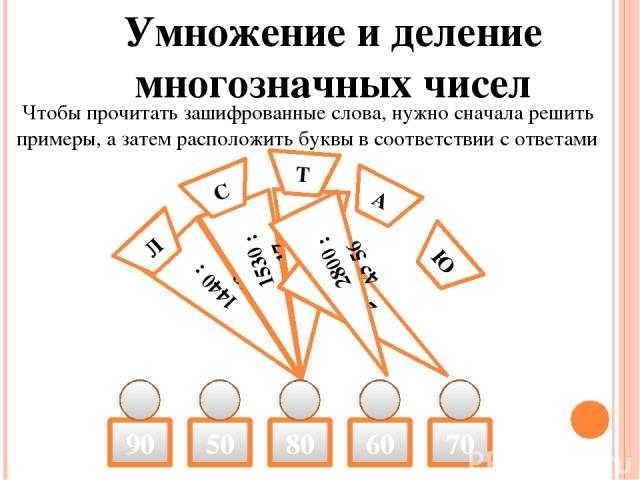 Превратим число 13735 в круглое число. Первые две цифры 13 образуют большую цифру (десятки тысяч) — эти две цифры оставляем без изменений, остальные цифры 735 заменяем нулями. Результат 13000.
Превратим число 13735 в круглое число. Первые две цифры 13 образуют большую цифру (десятки тысяч) — эти две цифры оставляем без изменений, остальные цифры 735 заменяем нулями. Результат 13000.
Предупреждение. Далее будут обобщены понятия круглых чисел и перевода любого числа в круглое число.
Назад к делению многозначных чисел на многозначные числа. Сложность деления таких чисел заключается в том, что дробь приходится находить путем сопоставления. Для этого прибегают к различным приемам, например к превращению делителя и делителя в круглые числа.
Пример 1. Найти значение выражения 88 : 12
Запишите это выражение с углом:
Задайте вопрос, сколько цифр 12 в числе 88? Трудно ответить с первого раза. Вы должны рассуждать.
Мы помним со школы, что частное угадывали, говоря «возьми два» или «возьми три».
Попробуем угадать частное. К сожалению, вы не можете просто взять это с неба. Частное должно быть таким, чтобы при умножении его на делитель получилось число, меньшее делителя, но очень близкое к нему или равное ему.
Предположим, что частное равно 2. Умножаем это частное на делитель 12
Что это дает? Получившееся число меньше делителя, но близко к нему? Нет. Это конечно меньше делителя 88, но очень далеко от него. Так что два как частное не подходит. Давайте угадаем следующее число. Допустим, частное равно 5.
Что это нам дает? Получившееся число, конечно, меньше, но оно не близко к делимому 88. Так что пять как частное тоже не подходит. Попробуем взять 8 сразу.
На этот раз полученное число больше кратного числа. И оно должно быть меньше делимого, но очень близко к нему или равно ему. Так что восемь как частное тоже не подходит.
Наконец-то мы нашли правильное частное! Умножив частное 7 на делитель 12, получим 84, что меньше делителя, но близко к нему. Теперь находим остаток от деления. Для этого из 88 вычтем 84 и получим 4.
88 : 12 = 7 (4 осталось)
Чек: (12 х 7) + 4 = 84 + 4 = 88
Как видно из примера, на подбор привата уходит драгоценное время. Если мы сидим за зачетом или экзаменом, где важна каждая минута, этот метод нам явно не поможет.
Если мы сидим за зачетом или экзаменом, где важна каждая минута, этот метод нам явно не поможет.
Чтобы сэкономить время, вы можете превратить делитель и делитель в круглые числа, а затем разделить эти круглые числа. Делить круглые числа намного проще и удобнее.
Например, чтобы разделить 90 на 10, просто отнимите нули от обоих чисел и разделите 9 на 1. В результате получится 90 : 10 = 9.
Количество отбрасываемых нулей должно быть строго одинаковым. Например, если мы разделим 900 на 90, то из каждого числа выпадем ноль, потому что в 900 два нуля, а в 90 только один. Отбросив ноль от каждого числа, получим выражение 90 : 9 = 10. В итоге получим 900 : 90 = 10.
В делении круглых чисел тоже нет ничего сложного. Попытайтесь понять это. Если не понимаете, изучите несколько раз. Это очень важно.
Вот несколько примеров того, как делить круглые числа. Отбрасываемые нули заштрихованы серым цветом:
800 : 10 = 80 (отбросьте все нули и разделите 80 на 1, получите 80)
800 : 80 = 10 (усекаем на ноль и делим 80 на 8, поэтому мы 10)
900 : 10 = 90 (усекается на ноль и делится на 90, делится на 1, получается 90)
400 : 50 = 8 (усекается на ноль и делится 40 на 5, получается 8)
320 : 80 = 4 (ноль был усечен и 32 поделен на 8, что дало 4)
Если вы заметили, в конце концов все сводится к таблице умножения.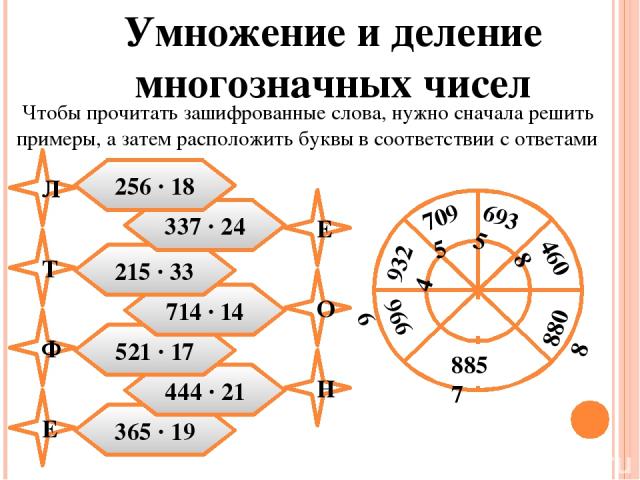 Вот почему школы требуют, чтобы вы знали его наизусть. Мы тоже этого требуем, хотя и не принуждаем.
Вот почему школы требуют, чтобы вы знали его наизусть. Мы тоже этого требуем, хотя и не принуждаем.
Теперь давайте решим предыдущий пример 88 : 12, где мы пытались найти частное путем угадывания. Сначала превращаем делитель и делитель в круглые числа.
Круглое число для 88 равно 80.
А круглое число для 12 равно 10.
Теперь разделим полученные круглые числа:
Теперь проверим правильность частного. Для этого умножаем частное на делитель (8 на 12). Мы уже проверяли восьмерку как частное, когда решали этот пример угадыванием. Не подошло, потому что после умножения на делитель мы получили число 96, которое больше делителя. Но частное 7, которое меньше восьми только на единицу, подходит.
Отсюда можно сделать вывод, что в выражении 88 : 12 частное, полученное при превращении делителя и делителя в круглые числа, больше всего на единицу. Наша задача — уменьшить это частное на единицу.
Уменьшим 8 на единицу: 8 — 1 = 7. Семь — это частное. Запишите его в правом углу нашего примера:
Семь — это частное. Запишите его в правом углу нашего примера:
Как видите, таким образом мы решили этот пример намного быстрее.
Пример 2. Найдите значение выражения 1296 : 144
Запишите это выражение в углу. Сразу находим первый неполный делитель. Он образован всеми четырьмя цифрами делителя:
Это деление многозначного числа на многозначное число. Давайте применим метод, который мы только что изучили. Превратим делитель и делитель в круглые числа, а затем разделим их.
Для делителя 1296 круглое число равно 1000. А для делителя 144 круглое число равно 100.
Делим 1000 на 100, получаем 10. Полученное 10 проверяем умножением на делитель 144
Десятки не подходят, потому что умножение дает число больше делителя.
Попробуем получить 9, уменьшив десятки на единицу.
Проверяем девятку. Для этого умножаем его на делитель:
Красиво! Полученное число было не только ближе к делимому, но и равно ему. Это означает, что деление было сделано без остатка. Заполните этот пример, вычитая полученное число 1296 с 1296
Это означает, что деление было сделано без остатка. Заполните этот пример, вычитая полученное число 1296 с 1296
1296: 144 = 9
Проверка: 144 x 9 = 1296
Пример 3. Попробуем решить большой и осложненный пример 227,492: 331
Напишите это выражение в углу. Сразу определите первый неполный делитель. Оно образовано первыми четырьмя цифрами делимого 2274. Итак, сначала разделим 2274 на 331. Превратим их в круглые числа.
Для 2274 круглое число равно 2000. А для 331 круглое число равно 300.
делитель, а это недопустимо.
Продолжаем решать наш пример. Вычтем из 2274 1986, получим 288:
288 — это остаток от деления 2274 на 331. Далее, чтобы продолжить деление, нужно снести девятку:
Теперь надо разделить 2889на 331. Превратите их в круглые числа и разделите. Сразу проверяем полученное таким образом частное:
Мы проверили семерку. Опять получили число, далекое от делителя 2889. Так что и семерка не подходит. Проверим восьмерку:
Опять получили число, далекое от делителя 2889. Так что и семерка не подходит. Проверим восьмерку:
Восьмерка подходит. Он отвечает на вопрос, сколько чисел 331 в числе 2889. Если бы мы взяли по девять, то умножив на делитель, мы бы получили число 2979, которое уже больше делителя 2889..
Теперь выносим остаток от деления 2889 на 331. Для этого из 2889 вычитаем 2648 и получаем 241.
241 это остаток от деления 2889 на 331. главный делитель:
Теперь делим 2412 на 331. Возьмем 7
Теперь находим последний остаток. Для этого из 2412 вычтем 2317 и получим 95. На этом пример завершается:
227492 : 331 = 687 (95 в балансе)
Проверить: (331 x 687) + 95= 227 397 + 95 = 227 492
Это конец этого урока. Не расстраивайтесь, если сразу не научитесь делить числа на угол. Этот навык нарабатывается со временем в сочетании с интенсивными тренировками. Ошибки не страшны. Самое главное понять.
Самое главное понять.
Обратите внимание, что в этом уроке мы рассмотрим только деление с остатком. На следующих уроках мы рассмотрим деление без остатка. Это сделано для того, чтобы не усложнять обучение. Как говорится, всему свое время.
УПРАЖНЕНИЯ
Задача 1. Выполнение Отделение:
Решение:
Показать решение
Задача 2. Выполнение Дивизии:
Решение:
Показать решение
Задача 3. Выполните:
Показать решение
.
Решение:
Показать решение
Задача 4. Выполнить деление:
Решение:
Показать решение
Задача 5. 9003 выполнить деление:
Solution:
Показать решение
Видеоурок
Деление многозначных десятичных знаков — Common Core: Математика для 6-го класса
All Common Core: Математические ресурсы для 6-го класса
6 диагностических тестов 186 практических тестов Вопрос дня Карточки Learn by Concept
Common Core: помощь по математике для 6-го класса »
Система счисления »
Свободное сложение, вычитание, умножение и деление многозначных десятичных чисел: CCSS. Math.Content.6.NS.B.3 »
Деление многозначных десятичных дробей
Math.Content.6.NS.B.3 »
Деление многозначных десятичных дробей
Решите:
Возможные ответы:
Правильный ответ:
Объяснение:
Первое, что мы хотим сделать при делении десятичных дробей, — это превратить делитель в целое число. Мы делаем это, перемещая запятую вправо:
Если мы переместим десятичную запятую на одну позицию в делителе, мы также должны переместить десятичную запятую на одну позицию в делимом:
Новая задача на деление должна выглядеть следующим образом:
*Обратите внимание, что мы уже поставили десятичную дробь в нашем ответе. Когда мы делим десятичные дроби, мы помещаем десятичную дробь прямо над десятичной дробью в делимом, но только после того, как мы выполнили первые два шага по перемещению десятичной точки в делителе и делимом.
Теперь мы можем разделить как обычно:
Подумайте: сколько раз 76 может войти в 197
76 может войти в 197 два раза, поэтому мы пишем 2 над 7 в делимом:
Затем мы умножаем 2 на 76 и записываем это произведение под 197 и вычитаем:
Теперь мы уменьшаем 6 из делимого, чтобы получить 45 в 456.
Подумайте: сколько раз можно 76 перейти в 456?
76 может войти в число 465 шесть раз, поэтому мы пишем 6 над 6 в делимом:
Затем мы умножаем 6 на 76 и записываем это произведение под 456 и вычитаем:
У нас остается без остатка и конечное частное 2,6
Сообщить об ошибке
Возможные ответы:
Правильный ответ:
Объяснение:
Первое, что мы хотим сделать при делении десятичных дробей, — это превратить делитель в целое число. В этом случае делитель уже является целым числом, поэтому никаких изменений не требуется.
В этом случае делитель уже является целым числом, поэтому никаких изменений не требуется.
Задача на деление должна выглядеть следующим образом:
*Обратите внимание, что мы уже поставили десятичную дробь в нашем ответе. Когда мы делим десятичные дроби, мы помещаем десятичную дробь прямо над десятичной дробью в делимом, но только после того, как мы выполнили первые два шага по перемещению десятичной точки в делителе и делимом.
Теперь мы можем разделить как обычно:
Подумайте: сколько раз 12 может войти в 8
12 не может войти в 8, поэтому мы пишем 0 над 8 в делимом:
Так как 12 не может входим в число 8, объединяем разряд единиц и разряд десятых и думаем, сколько раз 12 может войти в число 85. Число разделено на десятичную дробь, но ради умножения мы думаем о нем как о 85.
Подумайте: сколько раз может 12 войти в 85
12 может войти в 85 семь раз, поэтому мы пишем 7 над 5 в делимом:
Затем мы умножаем 12 на 7 и записываем это произведение под 85 и вычитаем:
Теперь мы уменьшаем 8 из делимого, чтобы превратить 1 в 18.
Подумайте: сколько раз можно 12 перейти в 18?
12 может войти в 18 один раз, поэтому мы пишем 1 над 8 в делимом:
Затем мы умножаем 12 на 1 и записываем это произведение под 18 и вычитаем:
Теперь у нас осталось с 6 в нашем делимом, и мы не можем умножить 12 на что-либо, чтобы получить 6. Мы присоединяем или добавляем ноль к нашему делимому, который мы можем перенести рядом с 6, и теперь это будет 60. Мы не изменили значение нашего делимое, мы добавили ноль, чтобы число делилось на 12.
Подумайте: сколько раз 12 может перейти в 60?
12 может войти в 60 пять раз, поэтому мы пишем 5 над 0 в делимом:
Затем мы умножаем 12 и 5 и записываем это произведение под 60 и вычитаем:
У нас остается
Возможные ответы:
Правильный ответ:
Объяснение:
Первое, что мы хотим сделать при делении десятичных дробей, — это превратить делитель в целое число. В этом случае делитель уже является целым числом, поэтому никаких изменений не требуется.
В этом случае делитель уже является целым числом, поэтому никаких изменений не требуется.
Задача на деление должна выглядеть следующим образом:
*Обратите внимание, что мы уже поставили десятичную дробь в нашем ответе. Когда мы делим десятичные дроби, мы помещаем десятичную дробь прямо над десятичной дробью в делимом, но только после того, как мы выполнили первые два шага по перемещению десятичной точки в делителе и делимом.
Теперь мы можем делить как обычно:
Подумайте: сколько раз 9 может войти в 8
9 не может войти в 8 поэтому мы пишем 0 над 8 в делимом:
Так как 9 не может входим в число 8, объединяем разряд единиц и разряд десятых и думаем, сколько раз 9 может входить в число 87. Число разделено на десятичную дробь, но ради умножения мы думаем о нем как о 87.
Подумайте: сколько число 9 может входить в число 87
9 может входить в число 87 девять раз, поэтому мы пишем 9над 7 в делимом:
Затем мы умножаем 9 на 9 и записываем это произведение под 87 и вычитаем:
Теперь мы уменьшаем 3 из делимого, чтобы превратить 6 в 63.
Подумайте: сколько раз 9 может быть 63?
9 может войти в 63 семь раз, поэтому мы пишем 7 над 3 в делимом:
Затем мы умножаем 9 и 7 и записываем это произведение под 63 и вычитаем:
У нас не осталось остатка и окончательное частное 0,97
Сообщить об ошибке
Возможные ответы:
Правильный ответ: 903
3 Объяснение:
Первое, что мы хотим сделать при делении десятичных дробей, — это превратить делитель в целое число. Мы делаем это, перемещая запятую вправо:
Если мы переместим десятичную запятую на один разряд в делителе, мы также должны переместить десятичный разряд на один разряд в делимом:
Новая задача на деление должна выглядеть следующим образом:
*Обратите внимание, что мы уже поставили десятичную дробь в нашем ответе. Когда мы делим десятичные дроби, мы помещаем десятичную дробь прямо над десятичной дробью в делимом, но только после того, как мы выполнили первые два шага по перемещению десятичной точки в делителе и делимом.
Теперь мы можем разделить как обычно:
Подумайте: сколько раз 18 может войти в 45
18 может войти в 45 два раза, поэтому мы пишем 2 вместо 5 в делимом:
Затем мы умножаем 2 на 18 и записываем это произведение под 45 и вычитаем:
Теперь 18 нельзя умножить на целое число, чтобы получить 9, поэтому приложите или добавьте ноль к делимому, чтобы получить число, которое делится на 18. Мы не меняем значение делимого, добавляя ноль. Перенесите этот 0 рядом с 9, чтобы получить 90.
Подумайте: сколько раз 18 может превратиться в 90?
18 может войти в 90 пять раз, поэтому мы пишем 5 над 0 в делимом:
Затем мы умножаем 5 и 18 и записываем это произведение под 90 и вычитаем:
У нас не осталось остатка и окончательное частное равно 2,5
Сообщить об ошибке
7Решить:
3
Возможные ответы:Правильный ответ:
Объяснение:
Первое, что мы хотим сделать при делении десятичных дробей, — это превратить делитель в целое число. Мы делаем это, перемещая десятичный разряд вправо:
Мы делаем это, перемещая десятичный разряд вправо:
Если мы переместим десятичную дробь на один разряд в делителе, мы также должны переместить десятичную дробь на один разряд в делимом:
Новая задача на деление должна выглядеть следующим образом: уже поставили запятую в наш ответ. Когда мы делим десятичные дроби, мы помещаем десятичную дробь прямо над десятичной дробью в делимом, но только после того, как мы выполнили первые два шага по перемещению десятичной точки в делителе и делимом.
Теперь мы можем делить как обычно:
Подумайте: сколько раз 52 может войти в 1
52 не может войти в 1, поэтому мы пишем 0 над 1 в делимом:
Мы не использовали 1 в разряде сотен, так что теперь мы подставляем 0 в разряд десятков и пытаемся разделить его на 52
Подумайте: сколько раз 52 может входить в 10
52 не может входить в 10, поэтому мы пишем 0 над 0 в делимом:
Мы не использовали 10, поэтому теперь мы подставляем 1 из разряда единиц и пытаемся разделить его на 52
Подумайте: сколько раз 52 может войти в 101
52 может войти в 101 один раз, поэтому мы пишем 1 над 1 в делимом:
Затем мы умножаем 52 на 1 и записываем это произведение под 101 и вычтите:
Теперь мы уменьшим 4 из делимого, чтобы превратить 49 в 494. напишите 9 над 4 в делимом:
напишите 9 над 4 в делимом:
Затем мы умножаем 52 на 9 и пишем это произведение под 494 и вычитаем:
Теперь 52 нельзя умножить на целое число, чтобы получить 26, поэтому приложение или добавьте ноль к делимому, чтобы получить число делится на 52. Мы не меняем значение делимого, добавляя ноль. Сократите этот 0 рядом с 26, чтобы получить 260.
Подумайте: сколько раз 52 может перейти в 260?
52 может войти в 260 пять раз, поэтому мы пишем 5 над 0 в делимом:
Затем мы умножаем 52 на 5 и записываем это произведение под 260 и вычитаем:
У нас не осталось остатка, и окончательное частное равно 1,95
Сообщить об ошибке
3Решить:
Возможные ответы:
Правильный ответ:
Объяснение:
Первое, что мы хотим сделать при делении десятичных дробей, — это превратить делитель в целое число.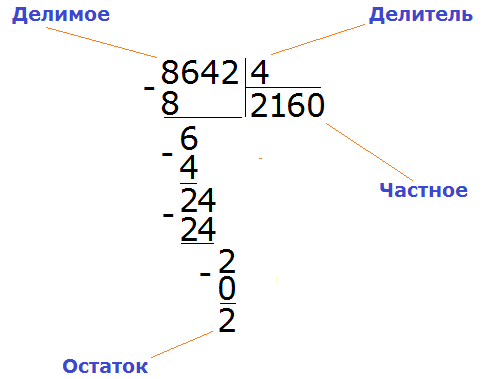 Мы делаем это, перемещая десятичный разряд вправо:
Мы делаем это, перемещая десятичный разряд вправо:
Если мы переместим десятичную дробь на один разряд в делителе, мы также должны переместить десятичную дробь на один разряд в делимом:
Новая задача на деление должна выглядеть следующим образом: уже поставили запятую в наш ответ. Когда мы делим десятичные дроби, мы помещаем десятичную дробь прямо над десятичной дробью в делимом, но только после того, как мы выполнили первые два шага по перемещению десятичной точки в делителе и делимом.
Теперь мы можем разделить как обычно:
Подумайте: сколько раз 2 может войти в 4
2 может войти в 4 два раза, поэтому мы пишем 2 над 4 в делимом:
Далее, мы умножаем 2 на 2 и пишем это произведение под 4 и вычитаем:
Теперь мы уменьшаем 0 из делимого, чтобы превратить 0 в 00.
Подумайте: сколько раз 2 может войти в 0
2 может перейти в 0 ноль раз, поэтому мы пишем 0 вместо 0 в делимом:
Затем мы умножаем 2 на 0 и пишем это произведение под 0 и вычитаем:
Теперь мы уменьшаем 9 из делимого, чтобы сделать 0 в 9.
2 может превратиться в 9 четыре раза, поэтому мы пишем 4 вместо 9 в делимом:
Затем мы умножаем 2 и 4 и пишем это произведение под 9 и вычитаем:
Теперь 2 нельзя умножить на целое число, чтобы получить a 1, поэтому добавьте ноль к делимому, чтобы получить число, делящееся на 2. Мы не меняем значение делимого, добавляя ноль. Поместите этот 0 рядом с 1, чтобы получить 10.
Подумайте: сколько раз 2 может быть 10?
2 может войти в 10 пять раз, поэтому мы пишем 5 над 0 в делимом:
Затем мы умножаем 2 и 5 и записываем это произведение под 10 и вычитаем:
У нас остается без остатка и конечное частное 204,5
Сообщить об ошибке
Какое число в задаче является делимым?
Возможные ответы:
Ни один из вариантов ответа не является правильным.
Правильный ответ:
Объяснение:
Делимое — это то, что вы делите или делите в задаче на деление. Это сумма, которую вы хотите разделить. В этой задаче дивиденд. В задаче на деление первым указывается делимое.
Это сумма, которую вы хотите разделить. В этой задаче дивиденд. В задаче на деление первым указывается делимое.
Сообщить об ошибке
Какая модель правильно представляет блок сотен?
Возможные ответы:
Правильный ответ:
Объяснение:
Модели часто используются, чтобы помочь представить деление десятичных дробей и помочь связать связанное уравнение с визуальным представлением.
Вам нужно заштриховать прямоугольник площадью 0,24. Итак, заштрихуйте 24 квадратика, в десятичной модели.
Существует множество прямоугольников площадью 0,24. Вам нужно заштриховать тот, который имеет длину 0,6.
Отсутствует коэффициент 0,4, который, как мы видим, представлен на оси Y блока сотен.
Площадь прямоугольника 0,4 на 0,6 равна 0,24. Следовательно, 0,24 ÷ 0,6 = 0,4
Сообщить об ошибке
Решите задачу, используя предоставленную модель области.
Возможные ответы:
Правильный ответ:
Объяснение:
Модели часто используются, чтобы помочь представить деление десятичных дробей и помочь связать связанное уравнение с визуальным представлением.
Вам нужно заштриховать прямоугольник площадью 0,12. Итак, заштрихуйте 12 маленьких квадратов в десятичной модели.
Существует множество прямоугольников площадью 0,12. Вам нужно заштриховать тот, который имеет длину 0,3.
Отсутствует коэффициент 0,4, который, как мы видим, представлен на оси Y блока сотен.
Площадь прямоугольника 0,4 на 0,3 равна 0,12. Следовательно, 0,12 ÷ 0,3 = 0,4
Сообщить об ошибке
Какая модель правильно представляет блок сотен?
Возможные ответы:
Правильный ответ:
Объяснение:
Модели часто используются, чтобы помочь представить деление десятичных дробей и помочь связать связанное уравнение с визуальным представлением.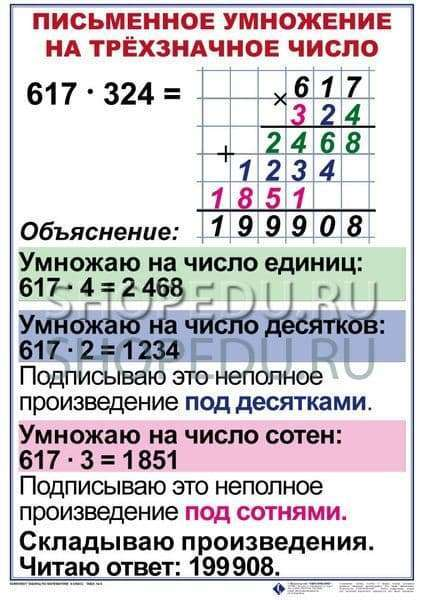
Вам нужно заштриховать прямоугольник площадью 0,25. Итак, заштрихуйте 25 квадратиков, в десятичной модели.
Существует множество прямоугольников площадью 0,25. Вам нужно заштриховать тот, который имеет длину 0,5.
Отсутствует коэффициент 0,5, который, как мы видим, представлен на оси Y блока сотен.
Площадь прямоугольника 0,5 на 0,5 равна 0,25. Следовательно, 0,25 ÷ 0,5 = 0,5
Сообщить об ошибке
Уведомление об авторских правах
All Common Core: Математические ресурсы для 6-го класса
6 диагностических тестов 186 практических тестов Вопрос дня Карточки Учитесь по концепции
Деление многозначных чисел на однозначные числа (определение, типы и примеры)
Пример 1. Найти 8420 ÷ 5. результат.
_______
5 ) 8420
Начнем с цифры в разряде «тысяч», 8. 8 «тысячи» ÷ 5 дадут 1 тысячу, а остаток 3 «тысячи».
1
_______
5) 8420
-5
———
3
Теперь мы снизим 4 сотен »справа от 3« тысячи ».
1
_______
5) 8420
-5
——— —
34
, перегруппируя 3 «тысячи» и 4 «Сотни», мы получим 34 «сотни». Мы разделим 34 «сотни» на 5, чтобы получить 6 «сотни» с оставшимися 4 «сотнями».
16
_______
5) 8420
-5
———
34
-30
‘ справа от 4 «сотни». Методом перегруппировки 4 «сотни» и 2 «десятка» дадут нам 42 «десятка».
16
_______
5 ) 8420
-5
—
34
-30
———-42
Теперь 42 ‘десятка’ ÷ 5 дадут нам 8 ‘десятков’ как 2 ‘der’.
168
_______
5) 8420
-5
——— —
34
-30
—— —
42
-409
———
42
-409
———
-40
———
-40
———
— 2
Теперь опустим 0 из разряда единиц справа от 2 десятков. Если соединить 2 «десятка» и 0 «единиц», то получится 20 «единиц». 20 «единиц», разделенных на 5, дадут нам 4 «единицы».
Если соединить 2 «десятка» и 0 «единиц», то получится 20 «единиц». 20 «единиц», разделенных на 5, дадут нам 4 «единицы».
1684
_______
5) 8420
-5
———-
34
-30
—— —
42
-409
———-
42
-409
———-
42
-409
———- 20
-20
————
0
Таким образом, 8420 ÷ 5 дает нам 1684 в качестве ответа.
Пример 2 . Найдите 6874 ÷ 7 методом частичного частного.
Решение : давайте сначала рассмотрим выражение как:
_______
7) 6874
Метод частичного коэффициента включает в себя вычищенное множественное дивизор, который меньше, чем дивиденд. Здесь мы начнем с вычитания кратных 7, пока не получим 0 в качестве остатка. Множители, которые умножаются на делитель, называются частичными частными.
Итак, 7 раз 900 даст нам 6300, что меньше дивидендов, 6874. Мы вычнем 6300 из 6874, и это даст нам 574.
Мы вычнем 6300 из 6874, и это даст нам 574.
900
_______
7) 6874
— 6300
——— —
— 6300
———– 574
У нас осталось 574, и мы снова вычтем еще одно кратное 7. Мы можем использовать кратное 80, поскольку 7 умножить на 80 дает нам 560.
0003
900
_______
7) 6874
— 6300
———–
574
— 560
— —
14
. Теперь мы остаемся с 14 и 703
140003
. Теперь мы остаемся с 14 и 703
140003
. 2 дает нам 14. Мы вычтем это из последней части делимого.
2
80
900
_______
7 ) 6874
– 6300
———–
574
– 560
————
14
– 14
————-
0
Теперь, когда мы достигли 0 в остатке, давайте теперь посмотрим, как мы разбили 6874 на 6300, 560 и 14. Соответствующие частичные частные равны 900, 80, и 2.
Соответствующие частичные частные равны 900, 80, и 2.
Следовательно, окончательный коэффициент:
900 + 80 + 2 = 982
Таким образом, 6874 ÷ 7 = 982.
Пример 3. Joseph имеет 4750 поздравительных открыток. Он положит в каждый конверт по 5 карточек для каждой семьи в своем районе. Сколько конвертов нужно для открыток?
Решение : В каждом конверте может поместиться 5 карт, поэтому нам нужно вычислить 4750 ÷ 5.
Воспользуемся методом деления в большую сторону с перегруппировкой.
_______
5 ) 4750
4 «тысячи» не могут быть разделены между 5 группами. Итак, перегруппируем 4 тысячи в 47 «сот».
9
_______
5) 4750 47 «Сотни» ÷ 5
— 45
——-
2
Приведем 5 к правой части 2, а затем снова разделим.
950
_______
5) 4750 47 ‘Сотни. 00 0 «единиц» ÷ 5
00 0 «единиц» ÷ 5
– 00
———––
0
5 0
Остаток 5 0
Частное равно 950. Это означает, что всего требуется 950 конвертов.
Пример 4. У Натана 240 шоколадок, и он решает раздать по 5 шоколадок каждому ученику в своем классе. Сколько учеников в классе Натана? Используйте модель области и метод частичного частного, чтобы найти ответ.
Решение : Нам нужно найти 240 ÷ 5.
Итак, в классе Натана 48 учеников.
Математические видео и ресурсы / Деление многозначных чисел
- Главная
- Кризис COVID-19
- Кризис Covid-19
- О нас
- Около 79-й улицы
- Расписание дня
- символов
- Информация DASA
- Связаться со школой 79th Street
- План улучшения школы
- Академики
- »
- ЛАБОРАТОРИЯ СТЕМА
- Список поставок на 2022-2023 гг.

- План школьного консультирования на 79-й улице
- Математические видео и ресурсы
- NF FCEP Оценка потребностей учителей и опросы непедагогического персонала
- План всестороннего школьного образования
- СИМБАЛОО
- Студенческая жизнь
- Инструментальная музыка
- Клубы продленного дня на 79-й улице
- Это НФХС
- Родитель опекун
- Информационные бюллетени на 79-й улице — Звездный экспресс
- Интернет-безопасность для родителей, учителей и детей
- Информация о родительском портале
- Группа обучения родителей (PEG)
- Школьная медсестра
- Центр обслуживания школьников
- Официальные уведомления, касающиеся школы на 79-й улице
- eFlyers
- Проблемы с посещаемостью — будь крутым будь в школе
- Веб-страницы учителей
- »
- Аверса, А-Класс 6
- Чейз, C — Pre K
- Чилле, S — Pre K4
- Костанцо, К.
 — Музыка
— Музыка - Костанцо, Р. — физкультура
- ДалПорто, Эстония — TA Руководитель PEP
- DiCanio P — Класс 2
- Динин, S — 5 класс
- Домингес, E — класс 1
- Данлэп, R — 4-й класс
- Карабедян, П — 4 класс
- Джокой, А — Арт
- ЛаРок, К — 2 класс
- Макри, J-класс pre-k
- Майшак, С — Специальное образование
- Мараццо, S — Детский сад
- Мелсон, C
- Мильвиль, А. — Консультант
- Орфано, J – 3 и 5 классы
- Пасек, L — 3 класс
- Педулла, M — 3 класс
- Пресутти, J — 1 класс
- Ричардс, B-Класс 2
- Ротелла, А — класс 5
- Орфано, Г — Директор
- Йост, J — Детский сад
- Захер, J — 6 класс
- Образец домашней страницы Elementary
- Математические видео и практика
- Видео и практика для 3 класса
- Округление чисел до 10 и 100
- Представление дробей разными способами
- Решите проблемы со словами о прошедшем времени
- Решить задачи на деление слов
- Решить задачи на умножение слов
- Умножение однозначных целых чисел на кратные десяти
- Понимание деления как проблем с неизвестными факторами
- Рисование гистограмм
- Пиктограммы
- Видео и практика для 4 класса
- Сравнение дробей
- Умножение многозначных целых чисел на однозначное число
- Применить формулу площади
- Применить формулу для периметра
- Рисование точек, линий, сегментов линий, лучей и углов
- Вычитание дробей
- Добавление дробей
- Понимание цифр и их позиционного значения
- Видео и практика для 5 класса
- Добавление дробей в словесные задачи
- Вычитание дробей в текстовых задачах
- Округление десятичных дробей до любого места
- Умножение и деление на десятичные дроби
- Умножение многозначных чисел с использованием стандартного алгоритма
- Нахождение площади прямоугольника
- Чтение и запись десятичных дробей до тысячных
- Умножение смешанных чисел и дробей
- Видео и практика для 6 класса
- Наибольший общий делитель
- Нахождение точки на координатной плоскости
- Разделить многозначные числа
- Создание таблиц соотношений и построение на координатной плоскости
- Понимание расценок за единицу и языка расценок
- Видео и практика для 3 класса
- Дополнительные ресурсы
Разделить многозначные числа
Щелкните здесь, чтобы попрактиковаться в делении многозначных чисел.
Щелкните здесь, чтобы попрактиковаться в делении больших многозначных чисел.
Модуль 4. Умножение и деление многозначных чисел. Руководство по курсу
Обзор модуля:
цифра и решение задач на умножение. Учащиеся узнают о делении на однозначные числа и делении на двузначные числа. Учащиеся узнают, как использовать частичные частные для решения задач на деление в большую сторону, как использовать частичные частные для степеней, отличных от 10, и как использовать традиционное деление в полные и как его можно применить к задачам.
- Материалы
- цели
- Ключевые слова
- Задания
- Карандаши
- Мелки или цветные карандаши 9Ноутбук 1220
- Ножницы
- Клей
- Хайлайтер
- Маркеры
- Чистая бумага
Цели модуля:
| Урок № | Название урока | Объектив(ы) |
|---|---|---|
| 1 | Умножение однозначных чисел |
|
| 2 | Умножение многозначных чисел |
|
| 3 | Умножение словесных задач |
|
| 4 | Разделение однозначных чисел |
|
| 5 | Разделение двузначного числа |
|
| 6 | Частичные коэффициенты |
|
| 7 | Частные частные с остатками |
|
| 8 | Подробнее о частных частных |
|
| 9 | Частичные коэффициенты против длинного деления |
|
Ключевые слова модуля:
| Ключевые слова |
|---|
| умножение продукт многозначный задача со словами дивиденд делитель частное остаток частичное частное |
Задания к модулям:
| Урок № | Название урока | Страница № | Название задания |
|---|---|---|---|
| 2 | Умножение многозначных чисел | 6 | Назначение |
| 5 | Разделение двузначного числа | 6 | Назначение |
| 7 | Частные частные с остатками | 7 | Назначение |
| 9 | Частичные коэффициенты против длинного деления | 6 | Назначение |
Примечания для обучающего тренера:
| Урок № | Название урока | Примечания |
|---|---|---|
| 1 | Умножение однозначных чисел | В своей тетради по математике попросите вашего ученика описать умножение частичного произведения и стандартный алгоритм умножения. |
| 2 | Умножение многозначных чисел | В своей тетради по математике пусть ваш ученик запишет шаги, используемые для умножения многозначных чисел. |
| 3 | Умножение словесных задач | В своей тетради по математике попросите вашего ученика описать способы решения текстовых задач с помощью умножения. |
| 4 | Разделение однозначных чисел | В своей тетради по математике пусть ваш ученик напишет задачу на деление и обозначит делимое, делитель и частное. Затем попросите их описать, что такое остаток. Наконец, попросите их написать шаги для деления на однозначные делители и как вы можете проверить задачу деления. |
| 5 | Разделение двузначного числа | В своей тетради по математике пусть ваш ученик запишет шаги по делению на двузначные делители. |
| 6 | Частичные коэффициенты | В своей тетради по математике попросите вашего ученика описать, как использовать частичные частные для решения задач на деление. |
| 7 | Частные частные с остатками | В своей тетради по математике попросите вашего ученика объяснить, как применять частичные частные к задачам с остатками. |
| 8 | Подробнее о частных частных | В своей тетради по математике попросите вашего ученика объяснить, что они узнали на этом уроке. |
| 9 | Частичные коэффициенты против длинного деления | В своей тетради по математике попросите вашего ученика написать шаги для решения задач на деление с использованием длинного деления. |
- Наводящие вопросы
- Видео Вопросы
Наводящие вопросы по модулю:
Когда учащийся начинает урок, задайте ему вопросы, чтобы проверить предварительное знание и понимание, а также обзор концепций, учил. В конце урока еще раз задайте вопросы посмотрите, изменится ли их ответ.
| Название урока | Вопрос |
|---|---|
| Умножение однозначного числа |
|
| Умножение многозначных чисел |
|
| Умножение словесных задач |
|
| Отдел однозначных номеров |
|
| Двузначный номер Раздел |
|
| Неполные частные |
|
| Неполные частные с остатком |
|
| Подробнее о неполных частных |
|
| Неполные частные и длинное деление |
|
Вопросы по видеомодулю:
Когда ученик смотрит видео, найдите время, чтобы задать ему вопросы
о том, что они смотрели. Предлагаемые вопросы к видео в
этот модуль перечислены здесь. Предложение: пусть учащийся посмотрит
все видео сначала до конца. Тогда пусть смотрят
видео во второй раз, когда они смотрят его, останавливают видео и
задавать вопросы.
Предлагаемые вопросы к видео в
этот модуль перечислены здесь. Предложение: пусть учащийся посмотрит
все видео сначала до конца. Тогда пусть смотрят
видео во второй раз, когда они смотрят его, останавливают видео и
задавать вопросы.
| Название урока | Видео | Вопрос |
|---|---|---|
| Умножение однозначного числа | Умножение однозначных чисел |
|
| Умножение многозначных чисел | Умножение многозначных чисел |
|
| Умножение словесных задач | Умножение словесных задач |
|
| Отдел однозначных номеров | Раздел однозначных чисел |
|
| Двузначный номер Раздел | Двузначный цифровой раздел |
|
| Неполные частные | Неполные частные |
|
| Неполные частные с остатком | Неполные частные с остатками |
|
| Подробнее о неполных частных | Подробнее о неполных частных |
|
| Частичные частные против длинного деления | Неполные частные и длинное деление |
|
Модуль Рекомендуемые книги для чтения вслух:
Найдите время, чтобы прочитать ученику или попросить его прочитать вам вслух. Читайте разные книги каждый день. Во время чтения книжной точки
из преподаваемых концепций. Вы можете приобрести эти книги или
найти их в вашей местной библиотеке.
Предлагаемые темы для обсуждения во время чтения книги:
Читайте разные книги каждый день. Во время чтения книжной точки
из преподаваемых концепций. Вы можете приобрести эти книги или
найти их в вашей местной библиотеке.
Предлагаемые темы для обсуждения во время чтения книги:
- В чем основная идея?
- Какие три вещи вы узнали нового?
- Какое отношение эта книга имеет к тому, что вы изучаете?
| # | Книга | Автор | Лексил Уровень |
|---|
Внешний модуль:
Потратьте некоторое время, чтобы применить то, чему учит ваш ученик, на практике. Мир. Предлагаемые экскурсии ниже.
Мир. Предлагаемые экскурсии ниже.
| # | Прогулка |
|---|
Игры для детей в Multi-Digit Division Online
Игры для детей на Multi-Digit Division Online — SplashLearnФильтр
МАРКА
ТИП СОДЕРЖИМОГО
- Чувство числа (387)
- Дополнение (341)
- Вычитание (238)
- Умножение (199)
- Дивизия (109)
- Передовая дивизия (8)
- Факты о дивизионе (43)
- Знакомство с дивизией (18)
- Многозначный дивизион (40)
- Длинный дивизион (29)
- Разделить числа, кратные 10 или 100 (8)
- Стратегии дивизиона (3)
- Фракции (173)
- Десятичные дроби (150)
- Геометрия (128)
- Измерение (175)
- Время (35)
- Деньги (57)
- Алгебра (35)
- Словесные задачи (57)
- Чтение (2209)
- Письмо (184)
Длинные игры для детей (29)
Просмотреть все 29 игрРазделение двухзначных чисел на однозначные
Нахождение частного
Окунитесь в безумие математической мультивселенной, научившись находить частное.
4 4.НБТ.6
ПОДРОБНЕЕ
Разделить 3-значное число на 1-значное число
Найдите частное путем деления трехзначных чисел на однозначные числа
Найдите частное путем деления трехзначных чисел на однозначные числа.
4 4.НБТ.6
ПОДРОБНЕЕ
Разделить 4-значное число на 1-значное число
Выбрать 4-значное число, которое делится
Помогите детям попрактиковаться в делении с помощью этой игры «Выбери 4-значное число, которое делится».
4 4.НБТ.6
ПОДРОБНЕЕ
Деление двухзначных чисел на однозначные числа
Разделите каждое выражение и сопоставьте частное
Дети должны разделить каждое выражение и сопоставить частное, чтобы попрактиковаться в делении.
4
4. НБТ.6
НБТ.6
ПОДРОБНЕЕ
Игры для детей на деление кратных 10 или 100 (8)
Просмотреть все 8 игрДеление на числа, кратные 10 или 100
Деление с использованием шаблонов нулей
Наслаждайтесь чудом математики, изучая, как делить с использованием шаблонов нулей.
4 4.НБТ.6
ПОСМОТРЕТЬ ПОДРОБНОСТИ
Деление кратных 10 или 100
Деление кратных 10 и 100
Научитесь решать задачи путем деления кратных 10 и 100.
4 4.НБТ.6
ПОДРОБНЕЕ
Разделите число, кратное 10 или 100
Заполните частное
Дети должны ввести частное, чтобы попрактиковаться в делении.
4 4.НБТ.6
ПОДРОБНЕЕ
Деление кратных 10 или 100
Определение шаблонов нулей и деление
Научитесь решать математические задачи, определяя закономерности нулей и деления.
4 4.НБТ.6
ПОСМОТРЕТЬ ПОДРОБНОСТИ
Division Strategies Games for Kids (3)
Посмотреть все 3 игрыDivision Strategies
Выберите выражение для оценки
Погрузитесь в мир математики, выбрав выражение для правильной оценки.
5 5.НБТ.6
ПОДРОБНЕЕ
Стратегии отдела
Определите первую цифру частного
Дети должны определить первую цифру частного, чтобы попрактиковаться в делении.
5 5.НБТ.6
ПОДРОБНЕЕ
Стратегии дивизии
Оцените частное
Используйте свои навыки дивизиона, чтобы оценить частное.
5 5.НБТ.6
ПОСМОТРЕТЬ ПОДРОБНОСТИ
Все игры для детей в многозначном разделе
Деление двузначных чисел на однозначные числа
Выбор числа, которое делится на заданное число
Дети должны выбрать число, которое делится на заданное число, чтобы попрактиковаться в делении.
4 4.НБТ.6
ПОДРОБНЕЕ
Разделение трехзначных чисел на однозначные числа
Выбор числа, которое делится на
Практикуйте суперсилу деления, научившись правильно выбирать число, которое делится.
4 4.НБТ.6
ПОДРОБНЕЕ
Разделить 4-значное число на 1-значное число
Завершить уравнение деления
Практикуйте суперсилу деления, научившись составлять уравнение деления.
4 4.НБТ.6
ПОДРОБНЕЕ
Разделение двузначных чисел на однозначные числа
Правильный выбор недостающей части уравнения деления
Используйте свои навыки деления, чтобы выбрать правильную недостающую часть уравнения деления.
4 4.НБТ.6
ПОДРОБНЕЕ
Разделить 3-значное число на 1-значное число
Завершить уравнение деления, заполнив частное или делитель
Дети должны завершить уравнение деления, заполнив частное или делитель.
4 4.НБТ.6
ПОДРОБНЕЕ
Разделить 4-значное число на 1-значное число
Выбрать правильный остаток
Проявите себя в математическом мире, научившись выбирать правильный остаток.
4 4.НБТ.6
ПОДРОБНЕЕ
Разделение двухзначных чисел на однозначные
Разделение на числа от 2 до 5
Дети должны делить на числа от 2 до 5, чтобы практиковаться в делении.
4 4.НБТ.6
ПОДРОБНЕЕ
Деление 3-значного числа на 1-значное число
Использование метода длинного деления для деления на делимое от 2 до 5
Дети должны использовать метод длинного деления для деления на делимое от 2 до 5.
4 4.НБТ.6
ПОДРОБНЕЕ
Разделение 4-значных чисел на однозначные числа
Ввод правильного частного и остатка после деления двузначного числа на однозначное число
Ввод правильного частного и остатка после деления двузначного числа на однозначное число .
4 4.НБТ.6
ПОДРОБНЕЕ
Деление двузначных чисел на однозначные
Деление на числа от 6 до 9
Потренируйтесь делить числа от 6 до 9 в этой игре.
4 4.НБТ.6
ПОДРОБНЕЕ
Разделение 3-значных чисел на 1-значные
Заполните пропущенные числа в решении
Попрактикуйтесь в концепции деления, заполнив пропущенные числа в решении.
4 4.НБТ.6
ПОДРОБНЕЕ
Деление 4-значных чисел на однозначные числа
Деление 4-значных чисел на однозначные числа
Наслаждайтесь чудом математической мультивселенной, изучая, как делить 4-значные числа на однозначные числа.
4 4.НБТ.6
ПОДРОБНЕЕ
Разделение двухзначных чисел на однозначные
Нахождение остатка
Погрузитесь в мир деления, найдя остаток.
4 4.НБТ.6
ПОСМОТРЕТЬ ДЕТАЛИ
Разделение трехзначного числа на однозначное число
Нахождение остатка при делении трехзначного числа на однозначное число
Дети должны найти остаток при делении трехзначного числа на однозначное число.
4 4.НБТ.6
ПОДРОБНЕЕ
Разделение двузначных чисел на однозначные
Нахождение частного и остатка
Используйте свои навыки деления, чтобы найти частное и остаток.
4 4.НБТ.6
ПОСМОТРЕТЬ ПОДРОБНОСТИ
Разделите 3-значное число на 1-значное число
Разделите и заполните частное и остаток
Разделите и заполните частное и остаток для практики деления.
4 4.НБТ.6
ПОДРОБНЕЕ
Разделить 2-значное число на 1-значное число
Найти количество групп
Найти количество групп для практики деления.
4 4.НБТ.6
ПОДРОБНЕЕ
Разделить 3-значное число на 1-значное число
Завершите решение о делении
Примените свои знания о делении, чтобы завершить решение о делении.
4 4.НБТ.6
ПОДРОБНЕЕ
Деление двузначных чисел на однозначные числа
Деление, когда делимое находится в диапазоне от 2 до 5
Используйте свои навыки деления, чтобы разделить, когда делимое составляет от 2 до 5.
4 4.НБТ.6
ПОДРОБНЕЕ
Деление 3-значного числа на 1-значное
Завершение решения длинного деления
Используйте свои навыки деления, чтобы завершить решение деления в длину.
4 4.НБТ.6
ПОДРОБНЕЕ
Деление двухзначных чисел на однозначные числа
Заполните решение деления, если делимое находится в диапазоне от 6 до 9
Дети должны решить деление, если делимое находится между 6 и 9.
4 4.НБТ.6
ПОДРОБНЕЕ
Деление на числа, кратные 10 или 100
Деление с использованием шаблонов нулей
Наслаждайтесь чудом математики, изучая, как делить с использованием шаблонов нулей.
4 4.НБТ.6
ПОДРОБНЕЕ
Деление кратных 10 или 100
Деление кратных 10 и 100
Научитесь решать задачи путем деления кратных 10 и 100.
4 4.НБТ.6
ПОДРОБНЕЕ
Разделите число, кратное 10 или 100
Заполните частное
Дети должны ввести частное, чтобы попрактиковаться в делении.
4 4.НБТ.6
ПОДРОБНЕЕ
Разделение кратных 10 или 100
Определение закономерностей нулей и деления
Научитесь решать математические задачи, определяя закономерности нулей и деления.
4 4.НБТ.6
ПОДРОБНЕЕ
Деление кратных 10 или 100
Деление кратных 100 и нахождение частного
Разделение кратного 100 и нахождение частного.
4 4.НБТ.6
ПОДРОБНЕЕ
Разделение кратных 10 или 100
Выбор правильного делителя
Погрузитесь в мир математики с помощью нашей игры «Выбери правильный делитель».
4 4.НБТ.6
ПОДРОБНЕЕ
Деление кратных 10 или 100
Деление 3-значных кратных 10 и 100
Деление 3-значных кратных 10 и 100 для тренировки деления.
4 4.НБТ.6
ПОДРОБНЕЕ
Разделить кратное 10 или 100
Разделить 4-значное число, кратное 100
Помогите ребенку взлететь, помогая ему разделить 4-значное число, кратное 100.
4 4.НБТ.6
ПОДРОБНЕЕ
Division Strategies
Выберите выражение для оценки
Погрузитесь в мир математики, выбрав выражение для правильной оценки.
5 5.НБТ.6
ПОДРОБНЕЕ
Стратегии деления
Определите первую цифру частного
Дети должны определить первую цифру частного, чтобы попрактиковаться в делении.
5 5.НБТ.6
ПОДРОБНЕЕ
Стратегии дивизии
Оцените частное
Используйте свои навыки дивизиона, чтобы оценить частное.
5 5.НБТ.6
ПОДРОБНЕЕ
Обучение многозначному делению с помощью игр Деление — это метод разделения группы вещей на одинаковые части. Как одна из четырех основных математических операций, таких как сложение, вычитание, умножение и деление. Деление дает справедливый результат деления, деление есть операция, обратная умножению. Если 3 группы по 4 дают при умножении 12, то 12, разделенные на 3 равные группы, дают по 4 в каждой группе при делении.
Как одна из четырех основных математических операций, таких как сложение, вычитание, умножение и деление. Деление дает справедливый результат деления, деление есть операция, обратная умножению. Если 3 группы по 4 дают при умножении 12, то 12, разделенные на 3 равные группы, дают по 4 в каждой группе при делении.
SplashLearn позволяет вашим детям практиковаться в основах с помощью игр на многозначное деление:
- Введи частное: В этой игре есть поле, в котором ваш ребенок должен заполнить правильное частное в своем поле для ответа. Им будет доступно несколько вариантов, и ваш ребенок должен выбрать правильный вариант среди всех.
- Деление на числа, кратные 10 и 100: Этот набор задач поможет вашему ребенку лучше понять деление. Эта игра позволит вашему ребенку практиковать все больше и больше задач, что поможет им усвоить основные понятия деления. Эта игра включает в себя деление с использованием чисел, кратных 10 и 100.

 ..
..



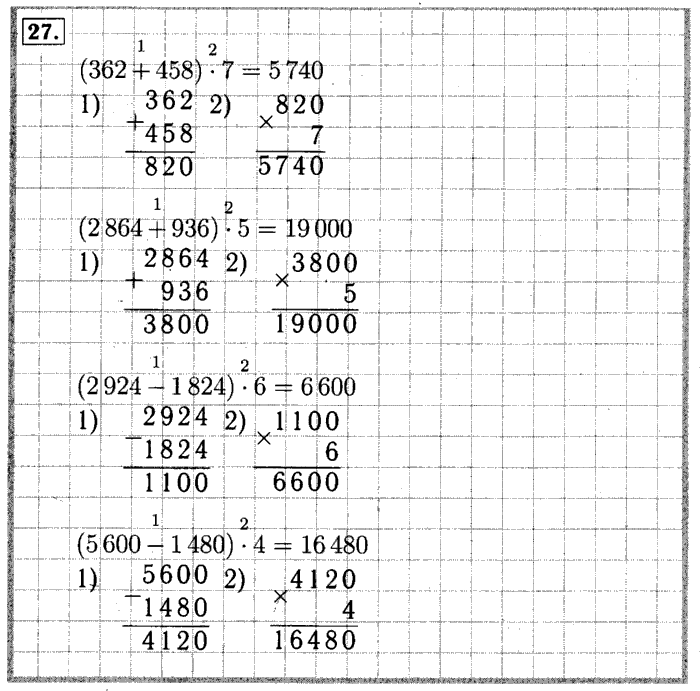
 — Музыка
— Музыка