Порядок выполнения действий в примерах

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Презентация
учителя
Здравствуй, четвероклассник.
Приглашаю тебя на урок по теме «Порядок
выполнения действий ».
Сегодня тебе предстоит повторить порядок
выполнения действий в выражениях со
скобками и без скобок; совершенствовать
навык решения задач и примеров.
Надеюсь, что тебе понравится мое задание.

Буду рада прочитать твой ответ в строке
«комментарий».
Твой учитель.
Познакомься с содержанием
урока. Узнай, что ты сможешь
сделать на этом уроке.

3. Порядок выполнения действий.

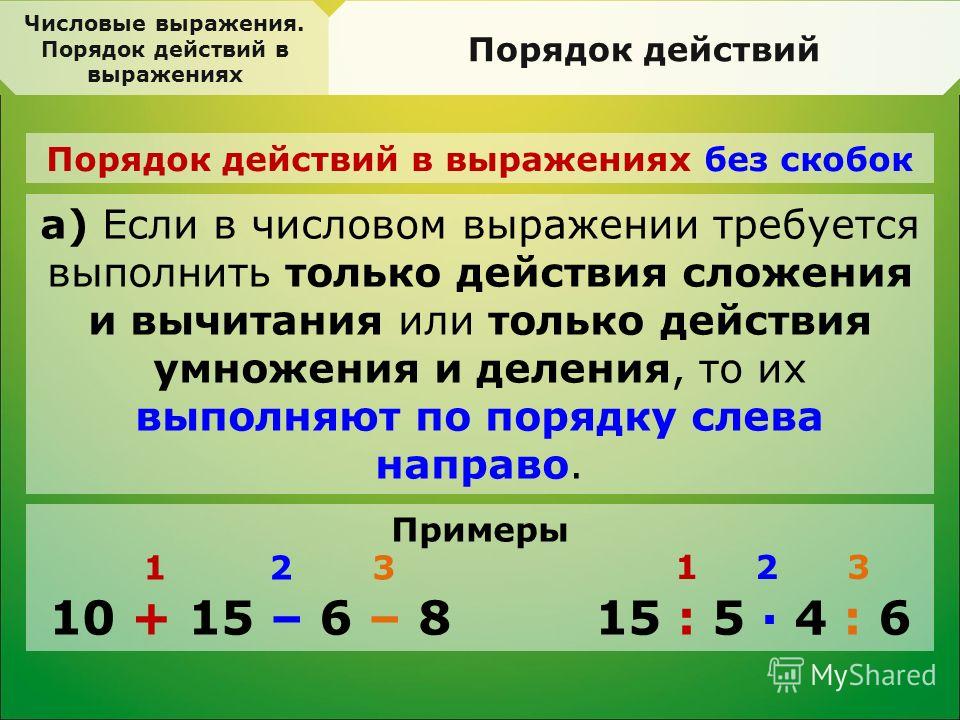
Если тебе нужно выполнить несколько арифметических
действий (сложение, вычитание, умножение и деление), то
сначала выполняют умножение и деление по порядку слева
направо, а затем сложение и вычитание по порядку слева
направо.
Например,
В числовом выражении 4 арифметических действия:
вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над
арифметическими знаками: сначала производим деление,
потом умножение, затем вычитание и сложение.
1)15 : 3 = 5
2) 6 • 8 = 48
3) 10 — 5 = 5
4) 5 + 48 = 53
Вспомни
правило.

4. Порядок выполнения действий.

Если в выражении есть скобки, то сначала выполняют
действия в скобках, но обязательно учитывать первое и
второе правила.
Например,
Вспомни правило.
В числовом выражении 4 арифметических действия:
вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над
арифметическими знаками: сначала производим вычитание в
скобках, затем деление, потом умножение и сложение.
1) 25 — 10 = 15
2) 15 : 3 = 5
3) 6 • 8 = 48
4) 5 + 48 = 53

5. Порядок выполнения действий.

Например,
В числовом выражении 4 арифметических действия: сложение,
деление, сложение и деление.
Определим порядок действий и запишем их над
арифметическими знаками: сначала производим действия в
скобках (деление, затем сложение), затем деление, потом
сложение.
1) 12 : 4 = 3
2) 6 + 3 = 9
3) 18 : 9 = 2
4) 42 + 2 = 44
Посмотри фильм.
По ходу просмотра фильма постарайся
вспомнить материал 3 класса.
Если ты что-то не помнишь,
останавливай просмотр фильма в
непонятных местах и просматривай их
еще раз.
После просмотра фильма выполни
задания на Рабочем листе (его надо
скачать и распечатать, чтобы тебе было
удобно).
Будет здорово, если в комментариях ты
напишешь, все ли у тебя получилось.

English     Русский Правила

Онлайн тест по Математике по теме Порядок действий

Математический тест «Порядок действий» составлен таким образом, чтобы учащиеся 4-го класса, изучающие тему сложения, вычитания, умножения и деления, могли проверить и закрепить полученные знания на практике. Как правило, решение простых примеров с двумя числами не вызывает у детей никаких сложностей, но, когда в одном выражении сочетается несколько видов математических действий, встает вопрос о том, в какой последовательности их необходимо выполнять.

В зависимости от того, как это сделать, результат ответа может получиться разным, но правильный вариант всего один. Поэтому важно четко представлять себе алгоритм вычислений в таких сложных выражениях. Чтобы хорошо пройти тест, нужно повторить, как выполняются действия в выражениях, где есть скобки (сначала то, что в скобках, потом последовательно все остальное) и без скобок (сначала умножение и деление, потом сложение и вычитание по порядку).

Задания в тесте подобраны по принципу постепенного усложнения. Правильно выполнив все задания, можно с уверенностью сказать о хорошем уровне подготовки ученика.

---

---

Пройти тест онлайн

1. Какое действие в выражении сделаешь первым 110 – ( 60 +40) :10 х 8 ?

сложение


деление


вычитание

2. Какое действие в выражении 110 – ( 60 +40) :10 х 8 сделаешь вторым?

вычитание


деление


умножение

3. Выбери правильный вариант ответа выражения 110 – ( 60 +40) :10 х 8:

800


8


30

4. Ответом на выражение 150 : ( 80 – 60 :2) х 3 будет:

9


45


1

5. В каком из выражений последнее действие умножение?

1001 :13 х (318 +466) :22


391 х 37 : 17 х (2248:8 – 162)


10000 – (5 х 9+56 х 7) х 2

6. В каком из выражений первое действие вычитание?

2025 :5 – (524 – 24 :6) х45


5870 + (90-50 +30) х8 -90


5400 :60 х (3600:90 -90)х5

7. Выбери верное высказывание: «В выражении без скобок действия выполняются:»

по порядку


сначала в скобках


сначала деление и умножение, затем по порядку

8. Выбери верное высказывание: «В выражении со скобками действия выполняются:»

сначала в скобках


по порядку записи


сначала деление и умножение, затем по порядку

9. Выбери верный ответ 90 – (50- 40:5)+ 30 :

78


92


36

10. Выбери верный ответ 100-(18:3+45)

100


49


55

---

---

Ещё никто не оставил комментария, вы будете первым.

Написать комментарий

Другие тесты

арифметика — Порядок старшинства, умножение против деления

спросил 6 лет, 7 месяцев назад

Изменено 6 лет, 7 месяцев назад

Просмотрено 3к раз

$\begingroup$

Недавно у меня возникло сомнение по поводу порядка старшинства математических операций умножения и деления. Учитывая, что у нас есть такой простой вопрос, как этот

 80/10*5
 

без скобок, какой должен быть ответ?

Должно ли это быть 40 , учитывая, что и умножение, и деление имеют одинаковый приоритет, и в этой ситуации они должны выполняться слева направо?

Или

Должно ли быть

8/5 , учитывая, что умножение имеет приоритет перед делением?

• арифметика

$\endgroup$

$\begingroup$

Думайте об этом как $$ 80 \дел 10 \cdot 5 $$ Так как $\div$ и $\cdot$ имеют одинаковый приоритет. Однако, в зависимости от контекста, это также может означать $\frac{80}{10 \cdot 5}$., но это почти никогда не бывает, если у вас нет квадратных скобок вокруг $10 \cdot 5$.

$\endgroup$

1

$\begingroup$

Если у вас есть несколько бинарных операций, записанных в «горизонтальной форме», например, в $80\div 10\times 5$, имеющих одинаковый приоритет, вы выполняете их в порядке слева направо. Итак, в этом случае 80$\дел 10\умножить на 5=8\умножить на 5=40$ (и да, порядок

имеет значение в данном случае и тому подобное).

Альтернативный способ думать об этом — «относиться к знаку деления так же, как к отрицательному знаку (он идет с числом справа)». Таким образом, мы можем думать о $80\div 10\times 5$ как $80\ раз \frac{1}{10}\times 5$, и у нас есть ассоциативность и коммутативность, так как это все умножение.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Как ввести умножение и деление на начальных уровнях

Умножение и деление — это следующий шаг после сложения и вычитания, и его следует преподавать по ступенчатой ​​спирали в течение всех лет начальной школы. Оба понятия можно и нужно вводить вместе, уже во втором классе.

Прежде чем овладеть таблицей умножения, учащиеся должны сначала понять понятия умножения и деления. С этой целью мы требуем, чтобы учащиеся усвоили четыре концепции, выраженные в следующих утверждениях «Я могу»:

• Я могу использовать сложение, чтобы найти общее количество объектов, расположенных в прямоугольных массивах до 5 строк и до 5 столбцов. ; напишите уравнение, выражающее сумму в виде суммы равных слагаемых.
• Я могу разделить заданное количество конкретных предметов, объяснить, можно ли это сделать одинаково, и найти количество в каждой группе. Например. Найдите количество яблок в каждой группе, если 12 яблок разделить на 3 группы.
• Я могу найти количество групп, зная количество конкретных объектов и число в каждой группе. Например. Найдите количество групп, если 12 яблок разделить на группы по 3.
• Я могу определить, состоит ли группа объектов (до 20) из четного или нечетного числа, например, путем объединения объектов в пары или подсчета их по 2; Напишите уравнение, выражающее четное число в виде суммы двух равных слагаемых.

Давайте рассмотрим эти задачи более подробно:

Во-первых, мы хотим, чтобы учащиеся привыкли к графическим обозначениям того, что мы пытаемся выполнить, т. е. распределять предметы по группам для облегчения подсчета. Будьте последовательны в соглашении, например. «3 группы по 4» выражается как 3×4, а 3×4 изображается как 3 ряда по 4.

Как только мы сможем «интерпретировать», что означает произведение 3 и 4, мы введем простейшую стратегию для нахождения общего числа, то есть общее число для 3 групп по 4 равно 4 + 4 + 4 (равные слагаемые) .

Для учащихся не критично знать окончательный ответ (т. е. 12), получение концепции — это то, чего мы хотим достичь.

После того, как учащиеся поймут, как группировать предметы для их подсчета, следующим логическим шагом будет изучение дополнительной задачи деления – здесь у нас есть сумма, и мы хотим разбить ее на группы. Одно и то же уравнение деления может иметь две разные интерпретации.

1 – Количество элементов в каждой группе

2 – Количество групп

Мы видим, что одно и то же уравнение 12 ÷3 означает две разные вещи. На этом этапе важно понимать разницу между этими двумя сценариями, так как это повторится позже, когда они будут изучать дроби.

Как и в случае с умножением, более важно увидеть, как работает расположение объектов для обоих сценариев, чем получить правильный ответ «4» в данный момент.

Здесь мы хотим ввести родственную концепцию — видя, что группа объектов является четной, если объекты могут быть организованы в две равные группы.

Старайтесь избегать таких правил, как «Числа, оканчивающиеся на четное число или нуль, четны». Вместо этого сосредоточьтесь на понимании того, что если в группе четное количество элементов, ее можно поровну разделить на две группы.

После того, как объекты разделены на две группы, мы можем легко увидеть, что сумма состоит из суммы двух равных чисел, в данном случае 12 = 6 + 6,

Видео объяснение и план урока (ресурс участника)

• https://teachablemath.com/lesson-plans/grade-2-lesson-plans/grade-2-semester-1-week-10-11/

Common Core Standards

• C3 Определить, имеет ли группа объектов (до 20) нечетное или четное число элементов, например, путем объединения объектов в пары или подсчета их по 2; Напишите уравнение, выражающее четное число в виде суммы двух равных слагаемых.
• C4 Используйте сложение, чтобы найти общее количество объектов, расположенных в прямоугольных массивах до 5 строк и до 5 столбцов; напишите уравнение, выражающее сумму в виде суммы равных слагаемых.