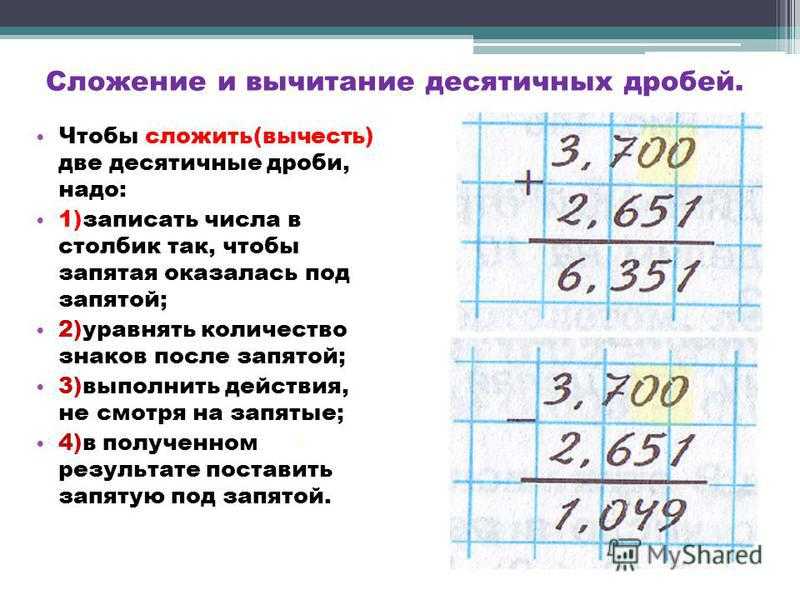
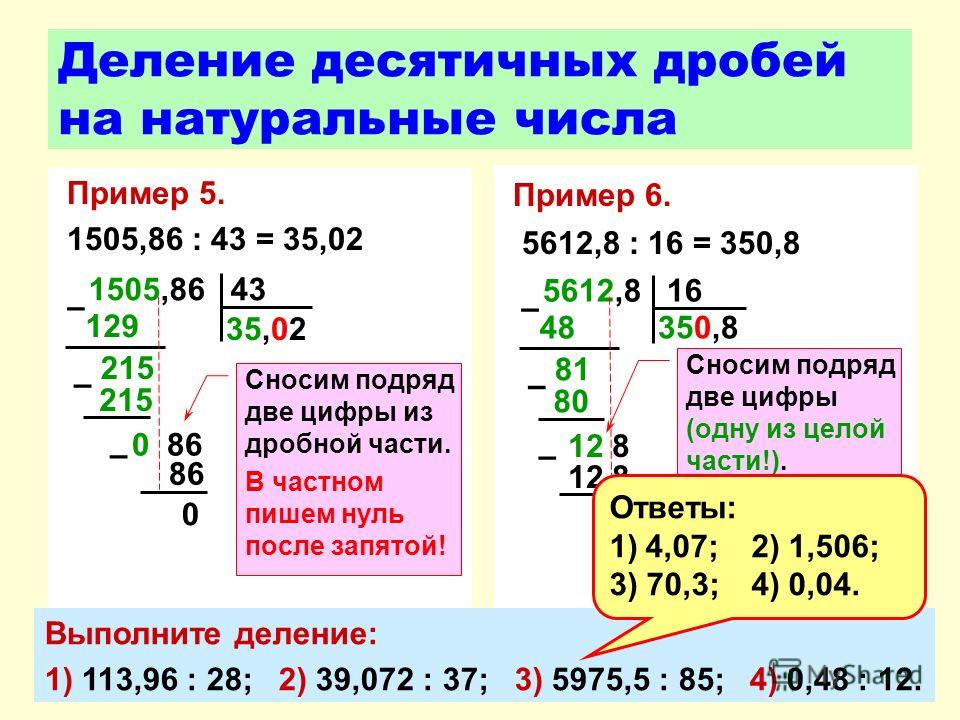
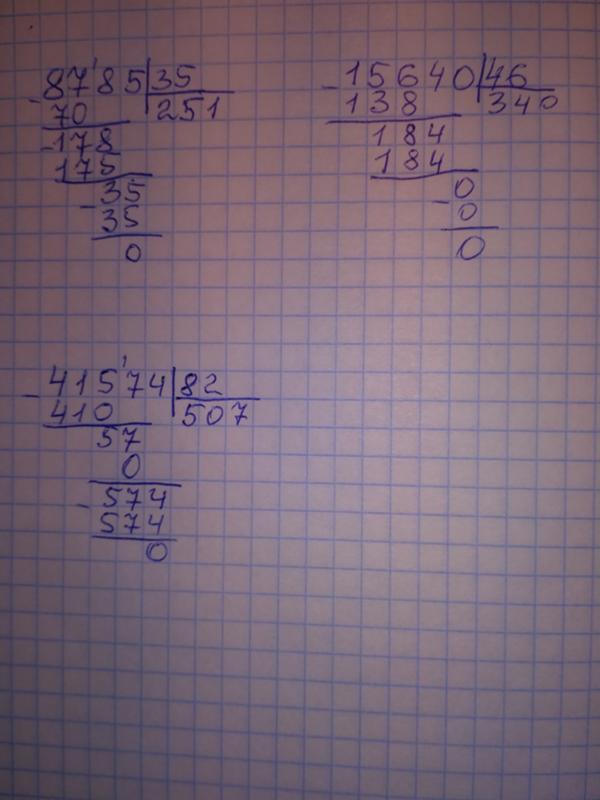Деление десятичных дробей в столбик (5 класс) – правило и примеры к теме

4

Средняя оценка: 4

Всего получено оценок: 194.

4

Средняя оценка: 4

Всего получено оценок: 194.

Деление десятичных дробей открывает огромные просторы в плане вычислений. Только приобретя навыки деления десятичных дробей в рамках математики 5 класса, ученик может осознать, что практически любое число можно разделить без остатка. Разберемся в теме подробнее.

Деление с целыми числами

Делить можно как целое число на десятичную дробь, так и наоборот.

При делении обязательно нужно учитывать, в каком виде необходимо получить результат: в дробном или десятичном. Иначе говоря, можно получить результат, который записывается в строчку, а можно получить дробь.

Рассмотрим оба варианта для начала с целыми числами.

Чтобы получить дробь в качестве результата деления нужно делитель и делимое представить в виде дроби. Разделим 18 на 1,9

Что такое 18? Это дробь ${18\over{1}}$. Соответственно $1,9={19\over{10}}$

При делении дробей дробь-делитель переворачивается, и получившиеся дроби перемножаются.

$${18\over{1}}:{19\over{10}}={18\over{1}}:{10\over{19}}={180\over{19}}$$ – при желании получившуюся дробь можно привести в десятичный вид.

В дробях черта означает знак деления. Это важно знать, так как это свойство очень часто используется при преобразованиях и вычислениях

Для деления в столбик нужно учесть, что как только останется неделимый остаток, нужно поставить запятую и дописать столько нулей, сколько необходимо для продолжения процедуры деления. Конкретно данное число получится бесконечным, но об этом речь пойдет немного позже.

Что делать, если необходимо поделить целое число на десятичное, с получением конечного итога в виде правильной или неправильной десятичной дроби? Нужно помножить делимое и делить на 10 в такой степени, чтобы получились целые числа, и произвести деление. Эта процедура в математике называется перенесением запятой.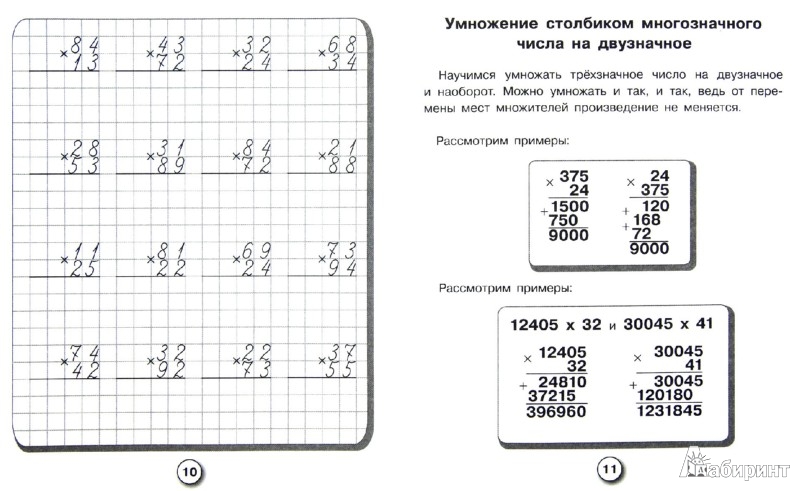

72:3,6=720:36=20 – если бы было 0,36, то домножить нужно было бы на 100 и так далее.

Для деления действует правило знаков умножения. Отрицательное число при делении на отрицательное дает положительный результат. Положительное на положительное – также положительное. А вот если разделить положительное на отрицательное или наоборот, то получится значение со знаком минус.

Не нужно пугаться больших результатов. Это нормально и даже более того – это правильно. При делении целого числа на дробное, при условии, что дробь была правильной, результат должен получится больше делимого. Под правильной дробью подразумевается дробь, которая меньше 1.

Деление с дробными числами

С дробными числами все обстоит примерно также. Главная проблема – это страх перед дробями. Если поделить целое число на дробное не кажется большой проблемой, то вот при делении дроби на дробь почему-то на учеников нападает иррациональный страх.

Чтобы его не было просто перенесите запятую.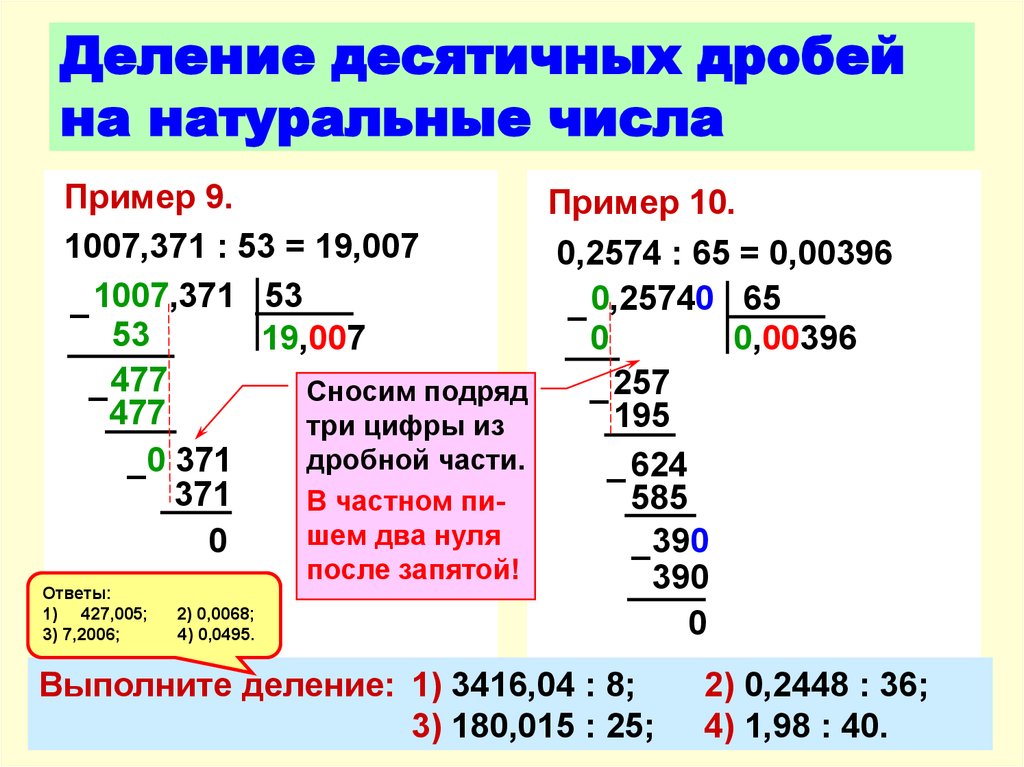

$3,8:0,5=38:5$ – а дальше в действие вступают правила деления без остатка.

$$3,8:0,5=38:5=7,6$$

Если вдруг необходимый результат нужно записать в виде дроби, то процесс упрощается еще больше. В результате преобразований делимое переместится в числитель, а делитель в знаменатель. Смотрите внимательно за преобразованиями и не теряйте запятых:

$$3,5:1,8={35\over{10}}:{18\over{10}}={{35*10}\over{18*10}}={35\over{18}}$$ – вот и весь расчет. Иногда приходится применять деление десятичных дробей в столбик. В этом случае, проще всего также воспользоваться этим методом.

Бесконечные числа

Иногда случаются неприятные ситуации, когда в результате расчетов получаются бесконечные числа. Таким называют число, количество знаков после запятой у которого бесконечно. Вспомним уже приведенный пример:

$18 : 1,9=180:19=9,473684…$- и так можно продолжать до бесконечности. К слову, иногда такие числа попадаются даже при точных вычислениях. Например, число пи, которое часто принимают за значение 3,14 на самом деле бесконечно. До конца его вычислить до сих пор не удалось. Более того, цифры после запятой у этого числа повторяются без определенных параметров, что является одной из загадок математики.

Что делать в этом случае? Записать дробью или, если это позволяет условие задачи, просто округлить

Если цифра перед округляемым значением меньше 5, то значение не меняется. Иначе – увеличивается на 1.

$18 : 1,9=180:19=9,473684…=9,47$ – чаще всего значения округляются до сотых.

Что мы узнали?

Мы узнали, как можно делить целые числа на десятичные дроби и дроби на дроби. Привели правило деления десятичных дробей. Вычислили несколько примеров и поговорили о примерах с бесконечным результатом.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Светлана Телегина

  10/10

• Оксана Шкилева

  10/10

• Максим Точилин

  10/10

• Никита Яшин

  9/10

• Вова Коваленко

  6/10

• Veronica Soldatova

  8/10

Оценка статьи

4

Средняя оценка: 4

Всего получено оценок: 194.

---

А какая ваша оценка?

Урок математики 5 класс «Деление натуральных чисел» (ФГОС) | Презентация к уроку (5 класс) по теме:

Деление натуральных чисел

 Урок комплексного применения знаний и способов действий 

на основе системно — деятельностного метода обучения

5 класс

                                                Ф. И. О. Жукова Надежда Николаевна

Место работы: МАОУ СОШ №6 г.Пестово

    Должность: учитель математики

Тема Деление натуральных чисел  

(учебное занятие комплексного применения знаний и способов действий) 

Цель: создание условий для совершенствования знаний , умений    и навыков деления натуральных чисел  и способов действий в измененных условиях  и нестандартных ситуациях

УДД :          

                                                      Предметные

Моделируют ситуацию, иллюстрирующие арифметическое действие и ход его выполнения, выбирают алгоритм решения нестандартной задачи, решают уравнения на основе зависимости между компонентами и результатом арифметического действия.

Метапредметные

Регулятивные: определяют цель учебной деятельности, осуществляют средства ее достижения.

Познавательные : передают содержание в сжатом или развернутом виде.

Коммуникативные: умеют высказать свою точку зрения, пытаясь ее обосновать, приводя аргументы.

                                                   Личностные:

 Объясняют самому себе свои отдельные ближайшие цели саморазвития, дают позитивную самооценку результата учебной деятельности, понимают причины успеха учебной деятельности, проявляют познавательный интерес к изучению предмета.

Ход урока

1.Организационный момент.

В труде применяем сложение,

Сложению честь и почет!

К умениям прибавим терпение,

И сумма успех принесет.

Нельзя забывать вычитание.

Чтоб зря не потратился день,

Из суммы стараний и знаний

Мы вычтем безделье и лень!

В труде умножение поможет,

Чтобы полезной работа была,

Стократ трудолюбие умножим-

Умножатся наши дела.

Деление служит на деле,

Оно нам поможет всегда.

Кто трудности поровну делит-

Разделит успехи труда!

Поможет любое из действий-

Они нам удачу несут.

И в жизни поэтому вместе

Шагают наука и труд.

II. Формулирование темы и задач урока

-Вам понравилось стихотворение? Чем оно вам понравилось?

(ответы учащихся)

-Очень хорошо вы сказали. Прочитанные строки очень хорошо подходят к нашему сегодняшнему уроку. Вспомните услышанное вами стихотворение и попробуйте определить тему урока.

( Деление натуральных чисел) (слайд 1) . Запишите число и тему урока в тетради.

-Сегодня первый урок по теме «Деление чисел»? Что у вас не получается еще и чему бы вы хотели научиться? (ответы учащихся)

— Итак, сегодня мы будем совершенствовать  навыки деления, будем учиться обосновывать свои решения ,находить ошибки и исправлять их, оценивать свою работу и работу своих одноклассников.

 III .Подготовка к активной учебно-познавательной деятельности

1. Мотивация учения школьников

Делению человечество обучалось дольше всего. До сих пор в Италии сохранилась поговорка «Трудная вещь — деление». Это трудно и с точки зрения математики, и технически, и нравственно. Не каждому человеку дано умение делить и делиться.

 

  В средние века человек, усвоивший деление, получал звание «доктор абака »

 Абак-это счеты.

      Сначала знака для действия деления не было. Это действие писали словом.

 А математики Индии записывали деление первой буквой названия действия.

 Знак двоеточия для обозначения деления вошел в употребление в 1684г благодаря немецкому математику Готфриду Вильгельму Лейбницу.

    Деление еще обозначают косой или горизонтальной чертой. Этот знак впервые стал использовать итальянский ученый Фибоначчи.

 -Как выполняем деление многозначных чисел? (Уголком)

А вы помните как называются компоненты при делении? ( слайд 2 )

  — А вы знаете, что компоненты деления : делимое, делитель ,частное впервые в России  ввел Магницкий .Кто это и как этого ученого звали по-настоящему? Подготовьте ответы на эти вопросы к следующему уроку.

      2)  Актуализация опорных знаний учащихся

1. Графический  диктант

     1.Деление — это действие , с помощью которого по произведению и одному из множителей находят другой множитель.

      2.Деление обладает переместительным свойством.

      3.Чтобы найти делимое, надо частное умножить на делитель.

      4. Делить можно на любое число.

      5.Чтобы найти делитель, надо делимое разделить на частное.

      6.Равенство с буквой значение которой надо найти, называют уравнением

              (Обозначения :  да;      —  нет)   (слайд 3)

        КЛЮЧ:                           (слайд 4)

   

             б) Индивидуальная работа  учащихся  по карточкам.

           (одновременно с диктантом)

1. Докажите, что число 4 — корень уравнения 44: х + 9 =20.
2. Решение. Если х=4.то 44:4+9=20

                                                      11+9=20

                                                        20=20,верно.

            2.Вычисли: а) 16224 : 52 =           (312)         г) 13725 :45 =         (305)

                                 б)  4230 :18 =             (235)         д)  54756 : 39 =       (1404)

                                 в) 9800 : 28=             (350)

             3.Решите уравнение:     124 : (у – 5) = 31

                                         Ответ: у=9

             4. Двое учащихся работают по карточкам: решают по 3 задания и задают друг другу вопросы по теории

             в) Коллективная проверка индивидуальной работы  (слайд 5)

             (Учащиеся задают отвечающим вопросы по теории)

4. Применение знаний и способов действий

            а) Самостоятельная работа с самопроверкой   (Слайды 6 -7)

     Выберите и решите только те примеры, в которых в частном три цифры:

          Вариант 1                                                 Вариант 2

    а)2888: 76  =         (38)                                 а)2491 :93=              (47)

    б)6539:13  =          (503)                               б)5698: 14=              (407)

   в) 5712 : 28 =         (204)                                в)9792: 32=              (306)

        б)Физкультминутка.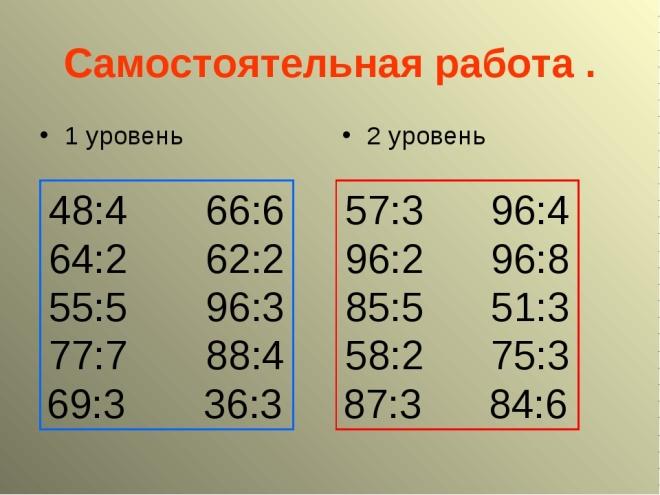

Дружно встали, потянулись.

Руки на пояс, повернулись.

Вправо, влево, раз, другой,

Повертели головой.

На носочках постояли,

Спинку стрункой подержали

А теперь, тихонько сели,

Мы с вами еще не все успели.

         в)Работа в парах      (слайд 8)

 (во время работы в парах при необходимости учитель дает консультации)

       № 484 (учебник, стр76)

     х см-длина одной из сторон восьмиугольника

         4х+4·4 =24

         4х+16=24

          4х=24-16

           4х=8

            х=2

      2 см-длина одной из сторон восьмиугольника

Решить уравнения:

а) 96 : х = 8         б) х : 60 = 14      в) 19 * х = 76

           г)Работа в группах

   Прежде чем приступить к выполнению заданий, прочитайте правила работы в группах  

                                      

Группа I ( 1ряд)

                         Правила работы в группах

• Активно участвуй в совместной работе.
• Внимательно выслушивай собеседника.
• Не перебивай товарища, пока он не закончит свой рассказ.
• Выскажи свою точку зрения по данному вопросу, будь при этом вежлив.
• Не смейся над чужими недостатками и ошибками, но тактично укажи на них.

     Исправь ошибки:

      а)9100:10=91;                                          а) 9100 :10 = 910      

      б)5427: 27=21;                                         б) 5427 : 27 = 201                                                

      в)474747: 47=101;                                   в) 474 747 : 47 = 10101

      г)42·11=442.                                             г) 42 · 11 = 462

Группа II ( 2ряд )

                         Правила работы в группах

• Активно участвуй в совместной работе.
• Внимательно выслушивай собеседника.
• Не перебивай товарища, пока он не закончит свой рассказ.
• Выскажи свою точку зрения по данному вопросу, будь при этом вежлив.
• Не смейся над чужими недостатками и ошибками, но тактично укажи на них.

               

    Проверьте, верно ли выполнено задание. Предложите свое решение

             Найдите значение выражения х:19 +95, если  х =1995.

            Решение.

      Если х=1995, то   х:19 +95 =   1995 :19 +95=15+95=110

                                                       (1995: 19 + 95 = 200)

Группа III (3 ряд )

                                      Правила работы в группах

• Активно участвуй в совместной работе.
• Внимательно выслушивай собеседника.
• Не перебивай товарища, пока он не закончит свой рассказ.
• Выскажи свою точку зрения по данному вопросу, будь при этом вежлив.
• Не смейся над чужими недостатками и ошибками, но тактично укажи на них.

               

                   Докажите , что при решении уравнения допущена ошибка.

                   Решите уравнение.

                  124: (у-5) =31

                    у-5 = 124·31                                                   у – 5 =124 : 31

                    у-5 = 3844                                                       у – 5 = 4

                    у = 3844+ 5                                                     у = 4+ 5

                    у = 3849                                                           у = 9

                  Ответ:3849                                                      Ответ: 9

            д) Взаимопроверка работы в парах

         Учащиеся обмениваются тетрадями и проверяют работы друг друга, подчеркивают ошибки  простым карандашом и выставляют отметку

            е) Отчет групп о проделанной работе

                            (Слайды 5-7)

       На слайде демонстрируется задание для каждой группы. Руководитель группы объясняет допущенную ошибку и записывает на доске решение, предложенное группой.

           V. Контроль знаний учащихся

             Индивидуальное тестирование  «Момент истины»

                             Тест по по теме «Деление»

               Фамилия, имя___________________________________________

                                     

 Вариант1

                     Подчеркните правильный ответ или запишите свой ответ

                    1.Найдите частное чисел  2876 и 1.

     а)    1  ;      б) 2876;            в) 2875;        г) свой ответ_______________

                   2.Найдите корень уравнения 96 : х =8

   а)    88  ;      б) 12;            в) 768;       г) свой ответ ________________

                  3.Найдите частное чисел 3900 и  13.

   а)   300  ;      б) 3913;        в) 30;       г) свой ответ_______________

                 4.В одной коробке 48 карандашей, а в другой в 4 раза меньше. Сколько    карандашей в двух коробках ?                    

                    а)   192;      б) 60;        в) 240;       г) свой ответ________________

             5.Найдите два числа, если одно из них в 3 раза больше другого, а их

               их сумма равна  32.      

   а)   20 и  12 ;      б) 18 и  14;        в)26  и 6;       г) свой  ответ_________

                                   Тест по по теме «Деление»

               Фамилия, имя___________________________________________

                                      Вариант 2

                     Подчеркните правильный ответ или запишите свой ответ

                 1.Найдите частное чисел  2563 и 1.

     а)    1  ;      б) 2563  ;        в) 2564;        г) свой ответ_______________

                 2.Найдите корень уравнения  105 : х = 3

   а)    104 ;      б) 35 ;            в) 315 ;       г) свой ответ ________________

                 3.Найдите частное чисел 7800 и  13.

   а)600  ;      б) 7813 ;        в) 60;       г) свой ответ_______________

               4. В одной кадке пасечник имел 24 кг. меда, а в другой в 2 раза больше. Сколько килограммов меда было у пасечника в двух кадках?

   а)   12 ;      б) 72 ;   в) 48 ;   г) свой ответ_______________

              5.Найдите два числа, если одно из них в 4 раза меньше другого, а

               их разность равна  27

 а)   39  и 12  ;      б) 32 и 8;        в) 2 и 29;       г) свой ответ_____________

              Ключ для проверки теста

             Вариант 1

     

Номер задания	1	2	3	4	5
Ответ	б	б	а	б	8;  24

               Вариант 2

     

Номер задания	1	2	3	4	5
Ответ	б	б	а	б	9; 36

   

                VI.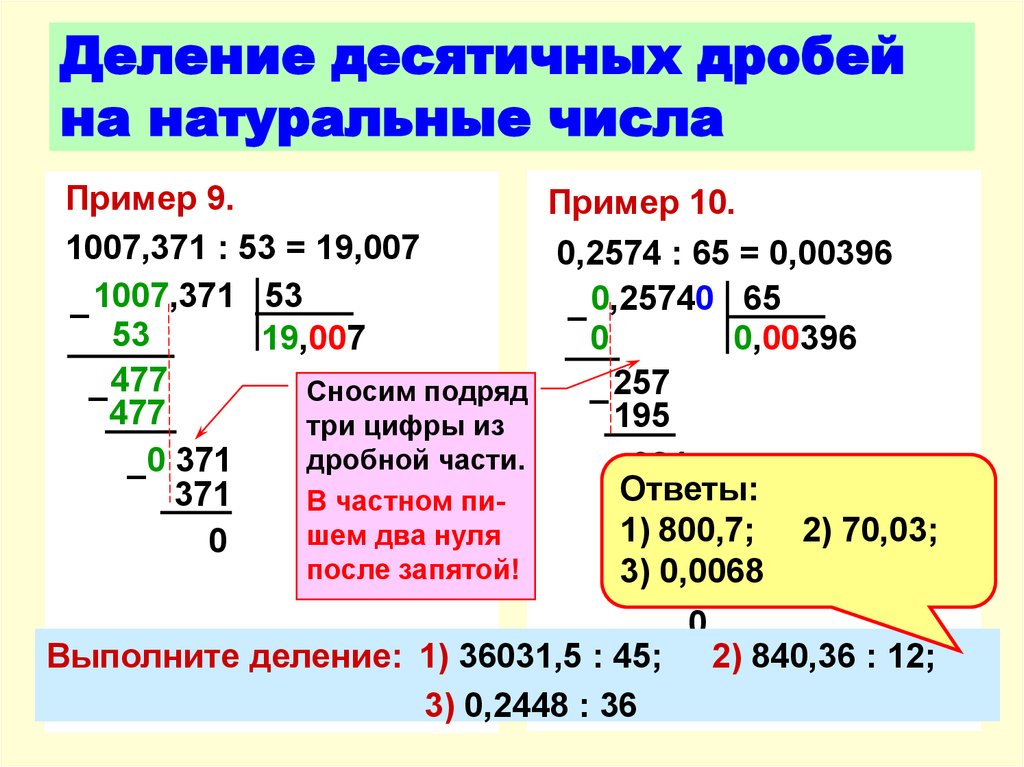  Итог урока. Домашнее задание.

    Дом. Задание. П.12, №520,523,528 (сочинение).

        Итак, наш урок подошел к концу. Я хотела бы взять у вас интервью об итогах вашей работы.

    Продолжите предложения:

         Своей работой на уроке я…             доволен\ не доволен  

         У меня получилось …

          Было трудно  …

         Материал урока мне был …         полезен/ бесполезен

         Чему учит математика?

Расчет оценок

О расчетах в журнале оценок

Вы можете легко добавлять расчеты в журнал оценок по курсу. Расчет — это формула, которая дает числовой результат, используемый для просмотра или присвоения оценок, обычно на основе других оцененных элементов.

Вы можете создавать свои собственные формулы и использовать общие арифметические операции, включая сложение, вычитание, умножение и деление, а также использовать групповые операторы (круглые скобки).

Вы можете добавлять расчеты на основе среднего, общего, максимального или минимального значения переменных, которые вы включаете, таких как категории, оцененные элементы и другие расчеты. Например, добавьте вычисление, отображающее среднее значение всех заданий, чтобы учащиеся имели общее представление о своей успеваемости. Вы можете добавить столько вычислений, сколько вам нужно.

В представлении курса Ultra каждый курс имеет одну схему оценивания по умолчанию, используемую для оценок и вычислений. В настоящее время вы не можете создавать новые схемы, но можете внести изменения в схему по умолчанию.

Подробнее о схеме оценивания по умолчанию

---

Создание встроенных расчетов

В списке оцениваемых элементов или представлении сетки учащихся щелкните значок плюса в том месте, где вы хотите добавить вычисление, и выберите Добавить вычисление.

Подробнее о двух просмотрах журнала оценок

Интерфейс расчета

Введите осмысленный заголовок для расчета. Если вы не добавите заголовок, в журнале оценок появится Новый расчет и дата. Вы можете использовать замещающий текст в качестве заголовка, если формула на странице действительна и сохранена. При желании добавьте описание и сделайте столбец вычислений видимым для учащихся. Учащиеся видят рассчитанные оценки на своих страницах оценок, но не видят ваших описаний или формул.

Определите, как будет выглядеть результат вычисления. В меню «Выберите схему оценок» выберите «Баллы», «Процент» или «Буквы».

Создайте свою формулу. На левой панели выберите функцию, переменную или оператор, чтобы добавить их на правую панель.

Функции и переменные

• Среднее: генерирует среднее значение для выбранного количества оцененных элементов, категорий и других вычислений. Например, можно найти средний балл по всем тестам.
• Итого: генерирует итог на основе совокупного количества баллов, относящихся к разрешенным баллам. Вы можете выбрать, какие оцениваемые элементы, категории и другие расчеты будут включены в расчет.
• Минимум: генерирует минимальную оценку для набора оцененных элементов, категорий и других вычислений. Например, можно найти минимальный балл по всем заданиям.
• Максимум: генерирует максимальную оценку для выбранных оцениваемых элементов, категорий и других расчетов. Например, вы можете найти максимальный балл по всем обсуждениям.
• Переменная: выберите в меню отдельный оцениваемый элемент или расчет. Вы можете добавлять только одну переменную за раз. Продолжайте добавлять переменные с левой панели, чтобы добавить столько переменных, сколько вам нужно.

Операторы

• Добавить (+)
• Вычесть (-)
• Разделить ( / )
• Умножить ( * )
• Открытая скобка (
• Закрыть скобки )
• Значение: после того как в формуле появится текстовое поле, щелкните его, чтобы добавить числовое значение. Вы можете включить семь цифр до десятичной точки и четыре цифры после нее. Когда вычисление генерируется и появляется в таблицах оценок учащихся, после запятой появляются только две цифры.

Создайте формулу

Например, выберите Итого на левой панели, чтобы добавить эту функцию на правую панель. Разверните список и установите флажки для элементов, которые вы хотите добавить в формулу. При выборе категории включаются все элементы в этой категории. Вы должны выбрать оцениваемые элементы и другие расчеты индивидуально. Прокрутите список, чтобы просмотреть все элементы. В меню «Переменная» выберите элемент, чтобы выбрать его.

Сделав выбор в меню, щелкните в любом месте за пределами меню, чтобы выйти и сохранить выбор на правой панели. Каждый элемент, который вы добавляете в формулу, отображается в конце. Вы можете нажать и перетащить любой добавленный элемент, чтобы изменить порядок формулы. Чтобы удалить элемент, выделите его и нажмите X. Вы можете повторно использовать любую функцию, переменную или оператор.

Когда вы выбираете Сохранить или Подтвердить, система проверяет точность вашей формулы. Validate проверяет формулу, пока вы остаетесь на странице. Вы не можете сохранить расчет, пока он не будет математически обоснован.

Выберите Очистить, чтобы удалить все элементы с правой панели и начать заново.

Пример формулы для итоговой суммы за первый квартал:

Создайте итоговый расчет, который включает категории «Задание» и «Тест» и оценку «Посещаемость», но не включает оценку «Всплывающий тест».

Категории «Задание» и «Тест» находятся в меню «Итого». Посещаемость и Pop Quiz — это отдельные оцениваемые элементы в меню Variable.

Формула: Итого по категории «Задание» + Категория теста + Посещаемость — Вспл. викторина

Если формула недействительна, рядом с кнопкой «Подтвердить» появляется встроенное сообщение об ошибке. Проблемы в вашей формуле выделены красным на правой панели.

Примеры сообщений об ошибках:

• Несовпадающий оператор: такие символы, как (+) или (-), не совпадают с другой частью формулы. Пример: Оцененный элемент + (ничего).
• Несовпадающая функция, переменная или значение. Обычно появляется, когда оператор отсутствует между двумя переменными, например, между двумя оцениваемыми элементами или категориями.
• Некоторые сообщения об ошибках являются специфическими, например, Несопоставленная открывающая скобка, чтобы предупредить вас о том, чего именно не хватает.

Вновь созданный вычисляемый элемент появится в вашем журнале оценок. В представлении списка элементов нажмите значок «Переместить» в строке вычисления, чтобы перетащить его в новое место и отпустить. Выбранный вами порядок также отображается в представлении сетки и на страницах оценок учащихся.

Напоминание: учащиеся не увидят расчет, пока за него не будет выставлена ​​оценка и вы не сделаете элемент видимым для них.

Удаление оцененных элементов в расчете

Если вы удалите оцененный элемент, используемый в расчете, вы получите предупреждение при открытии расчета:

Элемент был удален из журнала оценок, который использовался в этом расчете. Мы обновили расчет, где это возможно, но вам может потребоваться ваше внимание.

Возможно, вам потребуется обновить расчет. Учащиеся увидят обновленный расчет на своих страницах оценок, если вы сделали его видимым для них.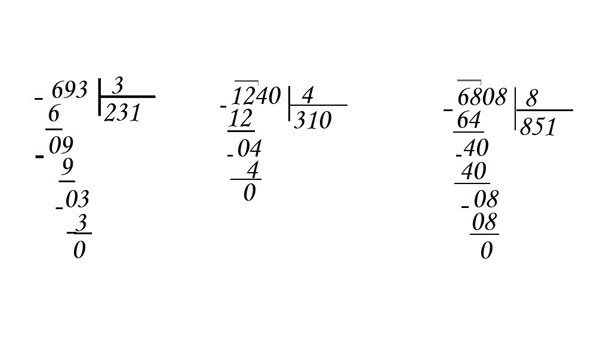

---

Создание взвешенных расчетов

Взвешенный расчет создает оценку на основе результатов выбранных оцениваемых элементов, категорий, других расчетов и их соответствующих процентов. Вы можете использовать обычные арифметические операции для создания нужного веса.

Например, если у вас есть четыре теста и один итоговый тест, вы можете взвесить каждый из них для расчета «Взвешенных тестов».

Выберите тесты по отдельности в меню «Переменная» и выберите «Значение», чтобы добавить процент для каждого теста, например 0,15. Добавьте необходимые операторы, такие как Multiply и Add.

Базовая формула:

Тест 1 x 0,15 + Тест 2 x 0,15 + Тест 3 x 0,15 + Тест 4 x 0,15 + Заключительный экзамен x 0,40

(Тест 1 x 0,15) + (Тест 2 x 0,15) + (Тест 3 x 0,15) + (Тест 4 x 0,15) + (Выпускной экзамен x 0,40)

Расчет действителен в любом случае и дает тот же результат.

В представлении списка элементов выберите вычисление, чтобы просмотреть рассчитанную оценку каждого учащегося, или откройте представление сетки учащихся и перейдите к столбцу.

Подробнее о взвешивании и общей оценке

 

---

Клавиатурные команды

Если вы используете навигацию с помощью клавиатуры, вы можете переходить между панелями для создания формулы.

Добавьте в формулу функции и операторы. На панелях «Функция» и «Оператор» с помощью клавиш со стрелками вверх и вниз выберите элемент из списка и нажмите клавишу ВВОД, чтобы добавить его в формулу.

Переупорядочить формулу. Выделите элемент формулы и нажмите клавишу ВВОД. Используйте клавиши со стрелками, чтобы переместить элемент, и снова нажмите Enter, чтобы поместить его.

Выберите элементы для включения в функции. Выделите функцию или переменную в формуле и нажмите пробел. В меню выберите элементы журнала оценок, которые необходимо включить. Нажмите Esc, чтобы закрыть меню.

Учебник по алгебре для колледжа 37

Алгебра для колледжа
Учебник 37: Синтетический отдел и
теоремы об остатках и факторах

---

WTAMU > Virtual Math Lab > College Algebra

 

Цели обучения

---

После завершения этого руководства вы сможете:

1. Чтобы разделить многочлен на двучлен вида x — c , используя синтетическое деление.
2. Используйте теорему об остатках в сочетании с синтетическим делением, чтобы найти функциональная ценность.
3. Используйте теорему о множителях в сочетании с синтетическим делением, чтобы найти множители. и нули полиномиальной функции.

Введение

---

В этом уроке мы рассмотрим синтетическое деление. Вы можете использовать синтетическое деление всякий раз, когда вам нужно разделить многочлен функцией бинома вида x — c . Мы можем использовать это, чтобы найти несколько вещей. Один — фактическое частное и остаток вы получите, когда вы разделите полиномиальную функцию на x — c . Кроме того, теорема об остатках утверждает, что остаток, который мы получаем, когда на самом деле применяется синтетическое деление дает нам функциональное значение. Другое использование — поиск факторов и нули. Факторная теорема утверждает, что если функциональное значение равно 0 при некотором значении c , тогда x — c это множитель и c это ноль. Вы можете не только найти эту функциональную ценность, используя синтетические деление, но и найденное частное может помочь в процессе факторинга. Похоже, синтетическое деление может помочь нам в нескольких разных типах проблем. Я думаю, вы готовы открыть для себя чудесный мир синтетического деления.

 

 

Учебник

---

Синтетический отдел

Синтетическое деление — это еще один способ деления многочлена на двучлен x — c , где c равно константа.

Шаг 1: Настройка синтетического разделение.

Простой способ сделать это — сначала настроить его так, как если бы вы делали длинные подразделение, а затем настроить синтетическое подразделение.

Если вам нужен обзор по постановке задачи на деление в длину, не стесняйтесь перейти к Урок 36: Длинный Разделение.

Делитель (то, на что вы делите) находится снаружи коробки. Делимое (то, на что вы делите) находится внутри коробки.

Когда вы записываете делимое, убедитесь, что вы записываете его по убыванию степени, и вы вставляете 0 для любых недостающих терминов. Например, если у вас возникла проблема, многочлен, начинается со степени 4, затем следующая наивысшая степень равна 1. Он отсутствует степени 3 и 2. Поэтому, если бы мы поместили его в разделительную рамку, мы бы написал бы так:

.

Это позволит вам выстроить одинаковые термины при решении задачи.

Когда вы устанавливаете это с помощью синтетического деления, напишите c для делителя x — c . Затем запишите коэффициенты делимого справа, сверху. Включите любые 0, которые были вставлены для отсутствующих терминов.

Шаг 2. Сбросьте ведущий коэффициент в нижнюю строку.

Шаг 3. Умножьте c на значение, только что написанное в нижней строке.

Поместите это значение прямо под следующим коэффициентом в делимом:

Шаг 4. Добавьте столбец, созданный на шаге 3.

Запишите сумму в нижней строке:

Шаг 5. Повторите пока не сделано.

Шаг 6: Запишите отвечать.

Числа в последней строке составляют ваши коэффициенты частного а также остаток. Последнее значение справа — это остаток. Работая справа налево, следующее число — ваша константа, следующее — коэффициент для x , следующий коэффициент на х в квадрате и т.д…

Степень частного на единицу меньше степени делимого. Например, если степень делимого равна 4, то степень частное 3.

Пример 1 : Деление с использованием синтетического деления: .

Шаг 1: Настройте синтетический разделение.

Полное деление выглядело бы вот так:

Синтетическое деление будет выглядеть так:

Шаг 2. Принесите вниз по ведущему коэффициенту в нижнюю строку.

*Сбить 2

Шаг 3. Умножьте c на значение, только что написанное в нижней строке.

*(-1)(2) = -2
*Поместите -2 в следующую колонку

Шаг 4. Добавьте столбец, созданный на шаге 3.

*-3 + (-2) = -5

Шаг 5. Повторите пока не сделано.

Шаг 6: Напишите вне ответ.

Числа в последней строке составляют ваши коэффициенты частного а также остаток. Последнее значение справа — это остаток. Работая справа налево, следующее число — ваша константа, следующее — коэффициент для x , следующий коэффициент для x в квадрате и т.д…

Пример 2 : Разделить с помощью синтетического деления: 

Шаг 1: Настройка синтетического разделение.

Полное деление выглядело бы вот так:

Синтетическое деление будет выглядеть так:

Шаг 2. Принесите вниз по ведущему коэффициенту в нижнюю строку.

*Наберите 1

Шаг 3. Умножьте c на значение, только что написанное в нижней строке.

*(1)(1) =1
*Поместите 1 в следующую колонку

Шаг 4. Добавьте столбец, созданный на шаге 3.

*0 + 1 = 1

Шаг 5. Повторите пока не сделано.

Шаг 6: Запись вне ответ.

Числа в последней строке составляют ваши коэффициенты частного а также остаток. Последнее значение справа — это остаток. Работая справа налево, следующее число — ваша константа, следующее — коэффициент для x , следующий коэффициент для x в квадрате и т.д…

Теорема об остатках

Если многочлен f ( x ) делится на x — c , затем
напоминание равно f ( c ).

Это означает, что мы можем применить синтетическое деление и последнее число справа, который является остатком, расскажет нам, что такое функционал значение с есть.

Пример 3 : Дано , используйте теорему об остатках, чтобы найти f (-2).

Шаги к синтетическому подразделению так же, как описано выше.   Отличается то, что является окончательным ответ будет. На этот раз мы ищем функционал значение, поэтому наш ответ будет не частным, а только напоминанием.

Используя синтетическое деление, чтобы найти остаток, мы получаем:

Опять же, наш ответ на этот раз не частное, а остаток.

Окончательный ответ: f (-2) = -27


Факторная теорема

Если f ( x ) является многочленом И

1) f ( c ) = 0, тогда x — c является коэффициентом f ( x ).

2) x — c является коэффициентом f ( x ), тогда f ( c ) = 0,

Имейте в виду, что алгоритм деления

делимое = делитель (частное) + напоминание

Таким образом, если напоминание равно нулю, вы можете использовать это, чтобы помочь вам разложить полином на множители. Если x — c — множитель, вы можете переписать исходный многочлен как ( x — c ) (частное).

Вы можете использовать синтетическое деление, чтобы помочь вам с этим типом проблемы. Теорема об остатках утверждает, что ф ( с ) = остаток. Итак, если остаток равен 0, когда вы применяете синтетическое деление, тогда x — c является коэффициентом f ( x ).

Пример 4 : Используйте синтетическое деление, чтобы разделить на x — 2. Используйте результат, чтобы найти все нули ф .

Шаги к синтетическому подразделению так же, как описано выше.   Отличается то, что является окончательным ответ будет. На этот раз мы ищем все нули из ф . Мы начнем с деления с помощью синтетическое деление, а затем переписать f ( x ) как ( x — 2)(частное).

Используя синтетическое деление, чтобы найти частное, мы получаем:

Обратите внимание, что остаток равен 0. Это означает, что ( x — 2) является коэффициентом .

Перезапись f ( x ) как ( x — 2)(частное) получаем:

Нам нужно закончить эту задачу, приравняв this к нулю и решить это:

*Множитель трехчлена

* Установите 1-й коэффициент = 0

* Установите 2-й коэффициент = 0

*Установить 3-й коэффициент = 0

Нули этой функции x = 2, -3 и -1.

Пример 5 : Решите уравнение учитывая, что 3/2 является нулем (или корнем) числа .

Шаги к синтетическому подразделению так же, как описано выше.   Отличается то, что является окончательным ответ будет. На этот раз мы ищем все нули выключенный. Мы начнем с деления, используя синтетическое деление, а затем перепишите f ( x ) как ( x — 3/2)(частное).

Используя синтетическое деление, чтобы найти частное, мы получаем:

Обратите внимание, что остаток равен 0. Это означает, что ( x — 3/2) является коэффициентом .

Перезапись f ( x ) как ( х — 3/2) (частное) мы получаем:

Нам нужно закончить эту задачу, установив это равным нулю и решить это:

 

*Учитывайте разницу квадратов

*Обратите внимание, что 1-й множитель равен 2, что является константой, 
, что никогда не может = 0

* Установите 2-й коэффициент = 0

* Установите 3-й фактор = 0
 
 

* Установите 4-й коэффициент = 0

Решение или нули этой функции: x = 3/2, -1 и 1.

Практические задачи

---

Это тренировочные задачи, которые помогут вам перейти на следующий уровень. Это позволит вам проверить и понять, понимаете ли вы эти виды проблем. Математика работает так же, как и все в противном случае, если вы хотите добиться в этом успеха, вам нужно практиковаться. Даже лучшие спортсмены и музыканты получали помощь на этом пути и много практиковаться, практиковаться, практиковаться, чтобы преуспеть в своем виде спорта или игре на инструменте. На самом деле практики много не бывает.

Чтобы получить максимальную отдачу от этих, вы должны решить проблему на свой собственный, а затем проверьте свой ответ, нажав на ссылку для ответа/обсуждения для этой проблемы . По ссылке вы найдете ответ а также любые шаги, которые привели к поиску этого ответа.

 

Практика Задача 1а: Деление с помощью синтетического деления.

 

1а.
(ответ/обсуждение к 1а)

 

Практика Задача 2а: Учитывая функцию f ( x ), используйте остаток Теорема для нахождения f (-1).

 

2а.
(ответ/обсуждение к 2а)

 

Практика Задача 3a: Решите данное уравнение, учитывая, что 1/2 равно нулю (или корень) из .

 

3а.
(ответ/обсуждение к 3а)

 

 

 

Нужна дополнительная помощь по этим темам?

---

Следующие веб-страницы могут помочь вы в темах, которые были освещены на этой странице:

http://www. purplemath.com/modules/synthdiv.htm
Эта веб-страница поможет вам с синтетическим делением.

http://www.purplemath.com/modules/remaindr.htm
Эта веб-страница поможет вам с теоремой об остатках.

http://www.purplemath.com/modules/factrthm.htm
Эта веб-страница поможет вам с теоремой о факторах.

Обратитесь за помощью за пределами Класс, найденный в Учебнике 1: Как преуспеть в математическом классе для некоторых больше предложений.

---

WTAMU > Виртуальная математическая лаборатория > Алгебра колледжа

Последняя редакция Ким Сьюард от 15 марта 2012 г.
Авторское право на все содержимое (C) 2002–2012 гг.