Приоритет | Python

Представим, что нужно вычислить такое выражение: 2 + 2 * 2. Именно так и запишем:

print(2 + 2 * 2)  # => 6

В школьной математике есть понятие «приоритет операции». Приоритет определяет, в какой последовательности должны выполняться операции. Умножение и деление имеют больший приоритет, чем сложение и вычитание, а приоритет возведения в степень выше всех остальных арифметических операций. Например: 2 ** 3 * 2 вычислится в 16.

Но нередко вычисления должны происходить в порядке, отличном от стандартного приоритета. Тогда приоритет нужно задавать круглыми скобками. Так было и в школе, например: (2 + 2) * 2. Скобки можно ставить вокруг любой операции. Они могут вкладываться друг в друга сколько угодно раз. Вот примеры:

print(3 ** (4 - 2))  # => 9
print(7 * 3 + (4 / 2) - (8 + (2 - 1)))  # => 14

Главное при этом соблюдать парность — закрывать скобки в правильном порядке.

Это часто становится причиной ошибок не только у новичков, но и у опытных программистов. Для удобства ставьте сразу открывающую и закрывающую скобку, а потом пишите внутреннюю часть. Редактор на нашем сайте (и большинство других редакторов кода) делают это автоматически: вы пишете (, а редактор сразу добавляет ). Это касается и других парных символов, например, кавычек. О них поговорим в будущих уроках.

Иногда выражение сложно воспринимать визуально. Тогда можно расставить скобки, не повлияв на приоритет:

# Было
print(8 / 2 + 5 - -3 / 2)  # => 10.5
# Стало
print(((8 / 2) + 5) - (-3 / 2))  # => 10.5

Важно запомнить: код пишется для людей. Код будут читать люди, а машины будут только исполнять его. Для машин код — корректный или некорректный. Для них нет «более» понятного или «менее» понятного кода.

Дано вычисление 70 * 3 + 4 / 8 + 2.

Расставьте скобки так, чтобы оба сложения (3 + 4

) и (8 + 2) высчитывались в первую очередь. Выведите на экран результат.

Упражнение не проходит проверку — что делать? 😶

Если вы зашли в тупик, то самое время задать вопрос в «Обсуждениях». Как правильно задать вопрос:

• Обязательно приложите вывод тестов, без него практически невозможно понять что не так, даже если вы покажете свой код. Программисты плохо исполняют код в голове, но по полученной ошибке почти всегда понятно, куда смотреть.

В моей среде код работает, а здесь нет 🤨

Тесты устроены таким образом, что они проверяют решение разными способами и на разных данных. Часто решение работает с одними входными данными, но не работает с другими. Чтобы разобраться с этим моментом, изучите вкладку «Тесты» и внимательно посмотрите на вывод ошибок, в котором есть подсказки.

Мой код отличается от решения учителя 🤔

Это нормально 🙆, в программировании одну задачу можно выполнить множеством способов. Если ваш код прошел проверку, то он соответствует условиям задачи.

В редких случаях бывает, что решение подогнано под тесты, но это видно сразу.

Прочитал урок — ничего не понятно 🙄

Создавать обучающие материалы, понятные для всех без исключения, довольно сложно. Мы очень стараемся, но всегда есть что улучшать. Если вы встретили материал, который вам непонятен, опишите проблему в «Обсуждениях». Идеально, если вы сформулируете непонятные моменты в виде вопросов. Обычно нам нужно несколько дней для внесения правок.

Кстати, вы тоже можете участвовать в улучшении курсов: внизу есть ссылка на исходный код уроков, который можно править прямо из браузера.

Нашли ошибку? Есть что добавить? Пулреквесты приветствуются https://github.com/hexlet-basics

«Чему равно 6÷2(1+2)?» — Яндекс Кью

Сообщества

МатематикаНаукаЗашкваршн

Александр Кульков

25 января 2016  ·

404,0 K

Ответить7Уточнить

Достоверно

Степан Лисовский

Философия

1,1 K

Физтех, М Ф Т И   · 22 июн 2017

Если считать, что знак умножения допустимо опускать в любом случае, то выражение очевидно преобразуется в 6/2*(2+1) = 9 (в соответствии с классическим порядком действий, где умножение и деление обладают равным приоритетом).

Однако так считают не все. Достаточно интуитивным является, что знак умножения допустимо опускать не во всех случаях, а только непосредственно между двумя сомножителями. Соответственно, ориентируясь на то, что знак умножения по факту опущен, считаем произведение

2(1+2) неразрывным и равным 6 и уже на него делим 6/6 = 1 (т.е. приоритет скрытого умножения признаётся более высоким по отношению к делению).

В качестве примера, где скрытое умножение обладает повышенным приоритетом по отношению к обычным умножению и делению можно считать «Курс теоретической физики» Ландау-Лифшица и другую физическую литературу.

2 эксперта согласны

62,9 K

Степан Лисовский

9 июня 2018

В физике есть не только mg, но и k(T1+T2) и т.п. Скобки никогда не были помехой для восприятия записи слитно… Читать дальше

Комментировать ответ…Комментировать…

Andrei Novikov

Математика

2,2 K

кандидат физико-математических наук, математик, исследователь, data scientist, предпринима. ..  · 13 апр 2021

Вот поэтому математики не пишут дроби в строчку, потому что найдется умник который скажет, что это не так считается. Математик запишет это выражение как 6 —— 2(1+2) И все сразу же станет ясно. Или запишет как 6 — (1+2) 2 И все станет еще яснее. На пишущем лежит бремя того, что выражение читалось максимально однозначно, а тот кто пишет 6÷2(1+2) — скорее… Читать далее

11,2 K

Николай Глаголев

16 августа 2021

Согласен с мыслью, что запись могла быть проще для понимания. Однако, если стоит задача прочитать этот пример, то… Читать дальше

Комментировать ответ…Комментировать…

Дмитрий Ушаков

Математика

69

Студент ВМК Московского Государственного Университета. Немного программирую, люблю…  · 21 мар 2021

Не думайте об этом слишком много. Данный пример был придуман кем-то нехорошим, просто чтобы позлить комментаторов. Ответ зависит от того, в каком порядке выполнять действия. Лично я уверен в том, что данное выражение — именно в таком виде, в котором оно записано — равно 1. Посмотрите два видео Бориса Трушина об этом вопросе: https://www.youtube.com/watch?v=ypSF_bRbFbY… Читать далее

11,1 K

Askar Imanakunov

21 марта 2021

Шесть делим на два, умножаем на три

Комментировать ответ…Комментировать…

Достоверно

Вадим Румянцев

Программирование

3,7 K

Специалист в области разработки систем управления. Трансгуманист. Интересуюсь…  · 9 нояб 2019

Это вопрос правил синтаксиса той нотации, в которой записано это математическое выражение. Не зная, в контексте какого формального языка употреблено это выражение, ответить невозможно. Как мне помнится, в школьной математике учат опускать знак умножения при вынесении общего множителя за скобку (факторизации). В данном случае этим множителем является только двойка, так… Читать далее

3 эксперта согласны

39,8 K

Надежда Д.

11 июля

Даже страшно становится , сколько людей, пытаясь показать свой ум, скатываются к банальному абсурду. Это пример из… Читать дальше

Комментировать ответ…Комментировать…

Риэлтор в Москве Рощина Елена, Агентство недвижимости

96

Частный риэлтор в Москве, специалист по купле-продаже жилой недвижимости, +7-926-2241150…  · 31 мая 2021

Отвечает

Рощина Елена

Здесь может быть два ответа и зависит от соглашений ( нотации/правил) заложенных при написании. В математике написание направленно на упрощение ( записать сложные вещи простым языком ). В обычной школе принято опускать знак умножения вынося за скобку ( например 6/2х означает 6/(2*х)). Поэтому в данном примере школьник бы дал ответ 6/(2*(1+2))=1 Но можно Просто заменить… Читать далее

Николай Глаголев

13 сентября 2021

Не соглашусь вот с этим предложением: «Но можно Просто заменить пропуск умножением то получится 6/2*(1+2)=9» 6/2… Читать дальше

Комментировать ответ…Комментировать…

Макс Евтишкин

Программирование

21

Математик и программист Python.  · 15 июл

Знак умножения между 2 и 1+2 опускается. 6/2*(1+2). Дальше по действиям: 1) 1+2=3 2) 6/2=3 3) 3*3=9. Ответ 1 получается из неверных соображений, что опущенный знак умножения выполняется первым и получается 6/6 (это мое мнение) Поэтому ответ 9. Читать далее

Николай Глаголев

3 ноября

После первого действия вы поменяете произведение 2(2+1) умножением 2 на (2+1). Согласно правилу «деление числа на. .. Читать дальше

Комментировать ответ…Комментировать…

Первый

10 сент 2020

Отвечает

Леха В

раз пошла такая математика, то мне больше нравится ответ 18! и я сейчас объясню как его получить. упрощаем выражение выносим 3 за скобки 3(2:1)(1+2) теперь делаем действия в скобках 3(2)(3) раскрываем скобки 3*2*3 все, мы упростили и никаких вопросов! умножаем ответ 18!!! Читать далее

Максим Балакирев

29 июня 2021

Ну, настроение подняли, спасибо!))
6/2≠3(2/1)
6/2=3(2/2)=3×1=3

Комментировать ответ…Комментировать…

Достоверно

Инесса Спиркина

3

инженер, увлекаюсь комментариями в соцсетях  · 9 окт 2021

Сначала нужно выполнить действие в скобках: 1+2=3.
Затем действия выполняются по порядку слева направо.
Второе действие 6:2=3 .
Нам остаëтся 3 умножить на то, что получилось в скобках : 3*3=9
Ответ: 9.

2 эксперта согласны

Сергей Чабовский

подтверждает

15 декабря 2021

Арифметика

Комментировать ответ…Комментировать…

Николай Глаголев

43

Просят написать какую нибудь хрень. Вот пожалуйста  · 28 мар 2021

Знак умножения пропускать можно в определенных случаях, поэтому запись верная, но в первую очередь важно определить порядок действий. Рассуждаем так: для решения этой задачи в первую очередь нужно раскрыть скобочки, однако ТК знак умножения пропущен между скобочкой и числом, а не буквой или другой скобочкой, то проводить первым действием вычисления в скобочках нельзя… Читать далее

Комментировать ответ…Комментировать…

Денис Кутушев

3

Интересуюсь иногда чем-то .   · 21 сент 2020

Запись 6:2(1+2)=1 Запись 6:2*(1+2)=9 Именно такие записи с такими ответами не нарушают ни одно правило Так было, так есть и так будет. Хоть в математике, хоть в алгебре, Про порядок действий. 6:2(1+2)= ? Заменим a=6, b=2, c=(1+2), тогда a:bc=6:2(1+2)=6:2*(1+2)= 9, но тогда при a:cb =a:bc тоже должно быть верно . подставим значения в a:cb =6:(1+2)2=6:(1+2)*2=6:3*2=4. и… Читать далее

виктор чеботарев

23 сентября 2020

Денис. Запись 6:2(1+2)=1 – нарушает правила: 1- порядок действий со скобками: — сначала выполняются действия в… Читать дальше

Комментировать ответ…Комментировать…

Math 1010 онлайн

Отсутствие оператора означает умножение

По соглашению, когда оператор опущен, это означает умножение. Например, 3a означает 3*a , а 3(4+2) равно 18. xy означает x*y .

(На самом деле есть исключение из этого правила в виде смешанные числа которые для наших целей в основном бесполезны, и их следует избегать. )

По соглашению , формулы оцениваются в следующей последовательности:

1. Возведение в степень.
2. Умножение и деление.
3. Сложение и вычитание
4. В случае операций одного уровня приоритета, оценка продолжается слева направо .

На самом деле, в приведенном выше списке должен быть пункт 0, предшествующий всем остальные: стандартные функции, такие как логарифмы, тригонометрические функции и т. д. Однако мы будем не используйте такие функции в Math 1010. (Но вы будете изучать их в очень подробно в Math 1030, 1050 и 1060, а также в исчислении.)

Если бы эти условности были абсолютными, нас бы сильно задушили, Чтобы предотвратить это бедствие, соглашения могут быть изменены с помощью круглых скобок:

• Сначала оцениваются выражения в скобках.

Проиллюстрируем эти правила несколькими примерами:

• 2+3*4 = 2+12 = 14.    Обратите внимание, что умножение выполняется перед сложением.
• (2+3)*4 = 5*4 = 20.    Скобки используются для укажите, что добавление должно выполняться первым. 92р

  Скобки могут быть вложенными , т.е. пары совпадающих скобок могут содержаться внутри других пар скобки. Например,

  12-(6-(4-2)) = 12 — (6-2) = 12 — 4 = 8.

  Для вычисления формул, содержащих вложенные пары скобок, начните с самых внутренних пар и двигайтесь дальше.

  Почему учащиеся неправильно понимают порядок операций — Future Set Tech Camp

  Многие из моих учеников средней и старшей школы помнят PEMDAS, аббревиатуру, предназначенную для представления порядка операций для вычисления математических выражений, из предыдущего класса. «Пожалуйста, извините, моя дорогая тетя Салли», — говорят они (или «Пожалуйста, съешьте мои чипсы с сальсой», — сказал мне один умный студент). «Скобки, экспоненты, умножение, деление, сложение, вычитание», — говорят они. Это здорово, правда? Эти студенты помнят порядок действий, верно? Разве PEMDAS не прекрасен?

  Нет, PEMDAS , а не потрясающий. ПЕМДАС ошибается. Или, скорее, неправильное понимание многими студентами порядка выполнения операций и виной всему PEMDAS.

  Давайте рассмотрим простой пример: 4 — 3 + 10 ÷ 5 × 2.

  Поскольку скобки и показатели степени отсутствуют, PEMDAS заставляет многих студентов думать, что мы должны начать с оценки умножения. Таким образом:

  4 — 3 + 10 ÷ 5 × 2 =

  4 — 3 + 10 ÷ 10

  Затем эти ученики перейдут к делению:

  4 — 3 + 10 ÷ 10 =

  4 — 3 + 1

  Затем сложение:

  4 — 3 + 1 =

  4 — 4

  И, наконец, вычитание: 4 —

  5 0

  Элегантное решение! И все с помощью PEMDAS! Какое чудесное изобретение!

  Или это то, что сказал бы , если бы это решение было правильным.

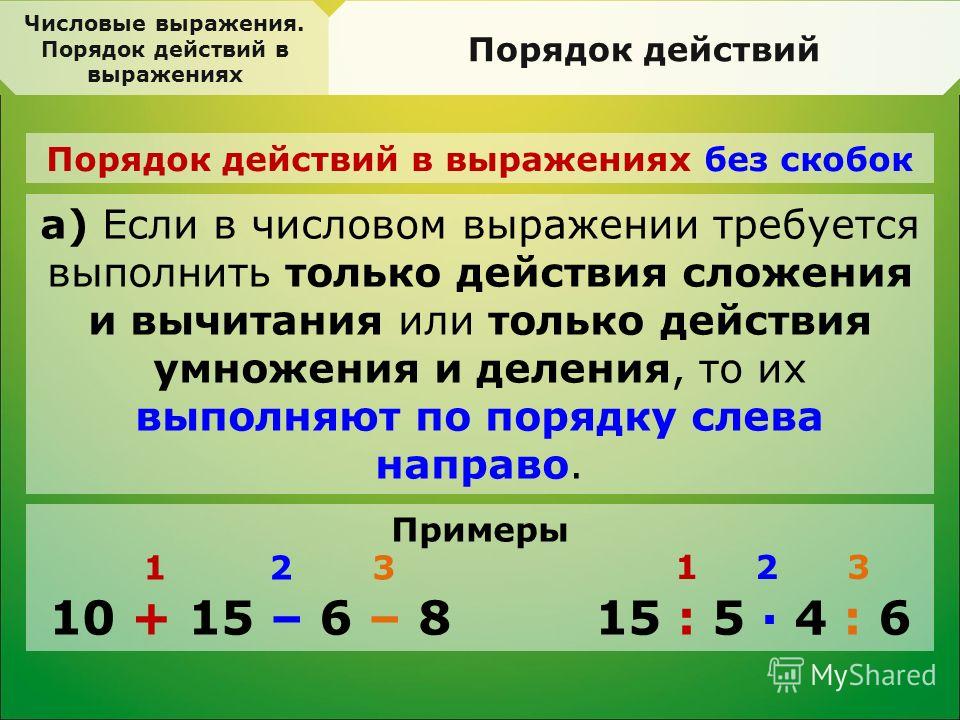
  Для многих студентов PEMDAS подразумевает, что порядок операций состоит из шести шагов, по одному на каждую букву аббревиатуры. Фактически порядок операций состоит из четырех шагов:

  1. Оценка операций в скобках

  2. Оценить экспоненты

  3. Оценка умножения и деления слева направо

  4. Оценка и выявленные.