Сочетательное свойство сложения

План-конспект открытого урока по математике

(УМК «Начальная школа XXI века)

Класс: 3.

Тема урока: «Сочетательное свойство сложения».

Тип урока: урок сообщение новых знаний.

Форма урока: урок

Методы: словесный, наглядный, анализа, стимулирования мотивации.

Цель: знакомство с сочетательным свойством сложения.

Задачи урока:

1. Учить применять сочетательное свойство сложения при нахождении значения выражения.

2. Развивать логическое мышление, речь, память; вычислительные навыки сложения и вычитания столбиком.

3. Воспитывать взаимопонимание и взаимоуважение к одноклассникам и учителю, интерес к математике.

Оборудование:

Ход урока.

I.Организационный момент.

Учитель: Здравствуйте, ребята! Сегодня у нас на уроке присутствуют гости. Поприветствуйте гостей.

Учащиеся: (приветствуют).

Учитель: Ребята, давайте поиграем в игру «Здравствуй, друг!». «Здравствуй, солнце, я твой лучик. Здравствуй, я – от сердца ключик». После этих слов «первые» номера поворачиваются налево ко «вторым», глядя в глаза своему партнёру, проговаривают: «Здравствуй, друг, здравствуй, друг. Ты прекрасней всех вокруг!».

Учитель: Ребята, давайте протянем правую руку и достанем удачу, протянем левую руку и достанем успех. Они нам пригодятся сегодня на уроке. А успех и удача приходят только к тем, кто любит трудиться.

II. Актуализация знаний

Учащиеся нашей гимназии трудятся круглый год. Помимо учебы в школе они еще трудятся на пришкольном участке. Начиная с ранней весны до поздней осени, ребята выращивают овощи для нашей столовой. Как вы понимаете слово «пришкольный»?

На пришкольном участке ребята выращивают различные овощи: морковь, картофель, лук и так далее. Давайте прочитаем задачу и узнаем, какой урожай собрали ребята в этом году.

Петя собрал сведения об урожае, выращенном на пришкольном участке нашей гимназии. Он выяснил, что шестые классы собрали 54 кг моркови, 34 кг лука, 1 кг помидоров и 23 кг картофеля. Седьмые классы собрали 55 кг моркови, 4 кг помидоров и 59 кг картофеля. А восьмые классы собрали 46 кг моркови, 15 кг лука, 2 кг помидоров и 17 кг картофеля. Заполни таблицу данными, которые собрал Петя.

Классы	Собранный урожай, кг
	морковь	лук	помидоры	картофель
6 — е	54 кг	34 кг	1 кг	23 кг
7 – е	55 кг		4 кг	59 кг
8 — е	46 кг	15 кг	2 кг	17 кг

Используя данные таблицы, ответьте на вопросы.

Какие классы собрали больше всего картофеля; помидоров?

На сколько килограмм моркови больше собрали седьмые классы, чем восьмые?

Во сколько раз меньше килограмм помидоров собрали восьмые классы, чем седьмые?

На сколько килограмм больше картофеля собрали седьмые классы, чем шестые?

Сколько килограмм лука собрали всего? Помидоров? Картофеля?

III. Постановка учебной задачи

— Массу, каких овощей мы вычисляли дольше? (картофеля) Почему?

— Мы с вами решали задачи по действиям. Запишем нахождение массы картофеля выражением.

+ (23+59)+17

— Посмотрим на это выражение внимательно. Можем ли мы этот пример вычислить быстрее? Как?

— Какое свойство сложения чисел мы уже с вами знаем? (переместительное свойство: от перестановки слагаемых сумма не меняется).

Это свойство мы применяем при сложении двух слагаемых, а в нашем примере три слагаемых.

— Подумайте, чему же будем учиться на уроке?

— Цель нашего урока (познакомиться с Сочетательным Свойством Сложения и научиться его применять)

IV. Открытие нового знания, способа действия.

— Как вы понимаете слово «сочетательное»?

В толковом словаре Ожегова дается такое определение:

Сочетание – соединение, расположение чего-нибудь, образующее единство, целое.

— Давайте поиграем в игру «Сочетаемое – не сочетаемое». Найдите сочетаемые предметы.

— Что значит, сочетаются? (подходят, соответствуют) Складываем мы числа, значит и сочетать будем их.

— Какие числа у нас сочетаются в выражении (23+59)+17? Какие числа можно сложить до круглого числа?

+ 23+17+ 59 = 99

— В выражении (23+59)+17 мы также получили 99, значит

(23+59)+17 = (23+17)+59

— Прочитайте выражения: (к сумме чисел 23 и 59 прибавить 17; к сумме чисел 23 и 17 прибавить 59).

— Почему мы вместо одного слагаемого взяли в скобки другое слагаемое?

+ Потому что так числа сочетаются и легче решить пример.

— Давайте еще раз скажем, как называется это свойство сложения.

+ Сочетательное свойство сложения.

— Прочитаем определение в учебнике на странице 79.

— Прочитайте правило глазками.

Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего. Это свойство сложения называют сочетательным свойством сложения.

— Прочитаем хором.

— Как вы понимаете это правило?

V. Включение нового в активное использование

— Давайте вернемся к нашей таблице. Используя сочетательное свойство сложения, найдем массу моркови.

(54+55)+46 = (54+46)+55= 155 (кг)

— Молодцы. Поработаем в учебнике. Откройте учебник на странице 80, № 4. Вычислим значения выражений, используя сочетательное свойство сложения.

(624+158)+42= (158+42)+ 624 = 200+ 624= 824

(396+121)+439= (121+439)+ 396= 560+ 396 = 956

— А сейчас поработаем самостоятельно. Посмотрите на №3. Прочитайте задание. Что надо сделать?

— А вам я даю задание на карточках (для детей ОВЗ)

(21+37)+19=

24 + (48+26)=

— Предлагаю вам решить задачи:

1 ряд «В одном ящике лежат 36 красных и 25 жёлтых яблок, в другом – 75 зелёных яблок. Сколько яблок в двух ящиках?»

(36 +25) + 75 =36+(25+75) = =136 (яб)

2 ряд «В одной клетке 13 белых и 8 серых кроликов, а в другой – 22 чёрных кролика. Сколько кроликов в двух клетках?»

(13 + 8) + 22 = 13 + ( 8 + 22) = 43 (к)

3 ряд « На праздник взяли 50 красных шаров и 25 синих шаров, а жёлтых взяли всего5 шаров. Сколько всего шаров купили на праздник?»

(25 + 5) + 50 = 80 (ш)

VI. Итог урока. Рефлексия

— Какая была цель нашего урока?

+ Познакомиться с Сочетательным Свойством Сложения и научиться его применять.

— Смогли ли мы ее достичь?

— В чем заключается сочетательное свойство сложения?

— Все ли научились применять это свойство?

— У вас на столах лежит «дерево успеха». Оцените свои достижения на уроке. Кто доволен своей работой, кому сегодня сопутствовал успех, нарисуйте себя на вершине дерева, если некоторые вопросы вызвали затруднения – нарисуйте себя посередине дерева, а если урок показался вам скучным и вам не сопутствовал успех – внизу. Покажите мне свои деревья.

VII. Домашнее задание:

1. Рабочая тетрадь с.35 № 116. Вычисли удобным способом.

2. Рабочая тетрадь с.35 № 116 – вычисли удобным способом;

№ 117 – сравни выражения не выполняя вычислений.

1. Составить три выражения, при решении которых использовалось бы сочетательное свойство сложения.

— Молодцы. На этом урок окончен. Спасибо за работу.

Сочетательное свойство умножения — Кафедра учителей начального образования — Школьные методические объединения — Каталог материалов

Тема: «Сочетательное свойство умножения».

Тип урока: урок введения нового знания.

Цель: познакомить с сочетательным свойством умножения и формировать представления о возможности использования изученного свойства для рационализации вычислений.

Задачи:

Личностные: формировать мотивацию к обучению и целенаправленной познавательной деятельности,

Метапрепредметные:

-Познавательные: делать выводы на основе обобщения умозаключений, делать выводы на основе обобщения умозаключений, преобразовывать информацию из одной формы в другую: представлять информацию в виде текста, таблицы, схемы.

-Регулятивные: совместно с учителем обнаруживать и формулировать учебную проблему; совместно с учителем обнаруживать и формулировать учебную проблему; составлять план решения отдельной учебной задачи совместно с классом; в диалоге с учителем и другими учащимися учиться вырабатывать критерии оценки и определять степень успешности выполнения своей работы и работы всех, исходя из имеющихся критериев.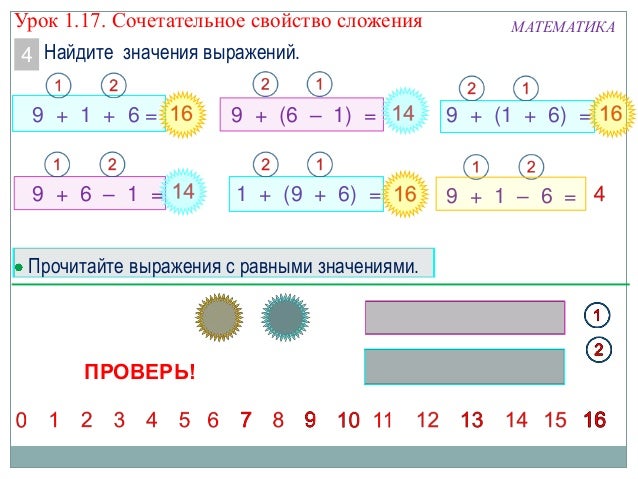

-Коммуникативные: слушать других, пытаться принимать другую точку зрения, быть готовым изменить

свою точку зрения; доносить свою позицию до других: высказывать свою точку зрения и пытаться её обосновать, приводя аргументы; доносить свою позицию до других.

3. Предметные: познакомить с сочетательным и переместительным свойством умножения.

Оборудование: карточки с заданием, наглядный материал (таблицы), презентация.

ХОД УРОКА

I. Организационный момент

Тут затеи, и задачи,
Игры, шутки, всё для вас!
Пожелаю всем удачи —
За работу, в добрый час!

II. Актуализация знаний.

 

— Устной счёт:

345+250= 4*9=

8*5= 430+60=

7*3= 502+38=

678+230= 6*6=

-На какие две группы можно распределить выражения?

1гр. -арифметическое действие сложение

2гр- умножение

— Игра «Найди лишнее»

385 53 865 957 680 534 (классификация на группы ЛИШНЕЕ 35 – двузначное, 680 – в записи числа нет цифры 5).

45 72 36 54 9 81 27 23 18 (9 – однозначное, 23 не делится на 9)

-Математический диктант

1) Увеличьте 9 в 2 раза

2) Уменьшите 40 в 8 раз

3)

4) Найди сумму чисел 37 и 7

5)Уменьшаемое 20, вычитаемое 8. Найди разность

Напишите самое большое трёхзначное число

III. Постановка проблемы.

Найди значения выражений, используя сочетательное свойство сложения.

(366+107)+203=

(504+158)+32=

(8*3)*2=

-что заметили?

-как выполнить вычисления?

IV. Изучение нового материала

1) Если мы будем выполнять умножение в том порядке, в каком записаны выражения, то возникнут трудности. Что же поможет нам снять эти трудности?

(8*3)*2=8*(3*2)=

2) Работа по учебнику

с. 89, № 1 (Выскажи своё предположение о результатах, которые получат Волк и Заяц. Проверь себя, выполнив вычисления).

(3*2)*4= 3*(2*4)=

3) № 2. Проверь, равны ли значения выражений. Устно.

Запись на доске:

(5 • 2) • 3 и 5 • (2 • 3)
(3 • 2) • 4 и 3 • (2 • 4)

4) Сделай вывод. Правило.

Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего.
– Расскажите сочетательное свойство умножения.
– Объясните сочетательное свойство умножения на примерах

5) Коллективная работа

уч. стр 90 №3

Найди значения выражений, используя сочетательное свойство умножения.

(8*2)*2 (6*2)*3 (19*1)*0

(7*3)*3 (9*2)*4 (12*9)*0

2) Работа в парах (по карточкам):

Найди выражения, в которых нужно использовать сочетательное свойство умножения. Вычисли.

(9*2)*2=

(253+19)+31=

(8*4)*2=

(9*3)*3=

(167+204)+6=

(49+307)+3=

V. Физминутка

Игра «Тучки». Повторяем таблицу умножения

VI. Закрепление изученного

Работа по учебнику.

Решение задачи.

(с. 90, № 4) Прочитайте текст. Докажите, что это задача.
– Выделите условие, вопрос.
– Назовите числовые данные.
– Что они обозначают?
– Какая это задача по структуре?
– Решите задачу без краткой записи составлением выражения. Для этого используйте следующую карточку:

Карточка-помощница

 

 

( • ) •

– В тетради решение задачи можно оформить следующим образом: (3 • 6) • 3

– Можем ли мы решить задачу в таком порядке?

Решение.

(3 • 6) • 3 = (3 • 3) • 6 = 9 • 6 = 54 (л)-сока во всех ящиках

Ответ: 54 литра

VII Самостоятельная работа (карточка)

1вариант

Найди значения выражений, используя сочетательное свойство умножения. Запиши результаты в порядке увеличения.

(6*2)*2=___________________________________________________________

(8*2)*4=___________________________________________________________

(5*3)*3=___________________________________________________________

__________________________________________________________

Найди значения выражений, используя сочетательное свойство сложения. Запиши результаты в порядке уменьшения.

(25+307)+3=________________________________________________________

(36+208)+12=_______________________________________________________

(243+86)+14=_______________________________________________________

___________________________________________________________________

2 вариант

1. Найди значения выражений, используя сочетательное свойство умножения. Запиши результаты в порядке увеличения.

(7*2)*2=___________________________________________________________

(6*2)*3=___________________________________________________________

(9*2)*4=___________________________________________________________

__________________________________________________________

2.Найди значения выражений, используя сочетательное свойство сложения. Запиши результаты в порядке уменьшения.

(35+308)+2=________________________________________________________

(26+207)+13=_______________________________________________________

(143+86)+14=_______________________________________________________

____________________________________________________________________

VIII. Повторение пройденного материала.

Уч. стр. 90№7

1)900-(627-58)=331

2)250+250+250=750

3)(6*9)+(158+168)=380

IХ. Итог урока

– Чему учились сегодня на уроке?
– В чём же заключается смысл сочетательного свойства умножения?

Х. Рефлексия

– Кто считает, что понял смысл сочетательного свойства умножения?

–Кто доволен своей работой на уроке? Почему?
– Кто знает, над чем ему еще надо поработать?
– Ребята, если вам урок понравился, если вы довольны своей работой, то поставьте руки на локти и покажите мне ладошки. А если вы были чем-то расстроены, то покажите мне обратную сторону ладошки.

XI. Информация о домашнем задании

1.Р.т. стр.41№143,144
2. Придумать и записать 3 выражения на новую тему с решением ( по желанию)

Оценки за урок.

 

 

комбинированное свойство Определение | Law Insider

означает любую и всю недвижимую и личную собственность, сервитуты и другие интересы в ней, вместе с расположенными на ней сооружениями и улучшениями, которые в настоящее время или в будущем принадлежат Ассоциации для общего пользования и удовольствия Владельцев.

означает все участки налогооблагаемого имущества оценщика, для которых разрешения на строительство были выданы 1 мая предыдущего финансового года или ранее, при условии, что такие участки оценщика были созданы 1 января предыдущего финансового года или ранее, и что каждый такой участок оценщика Посылка связана с Лотом, как разумно определено Советом.

означает все участки налогооблагаемого имущества оценщика, которые не являются застроенной недвижимостью.

означает имущество, которое соответствует любому из следующих критериев:

означает (i) оценочную стоимость после окончательной

или практически все свои активы другому Лицу, где «Лицо» означает любое физическое лицо, корпорацию, товарищество, совместное предприятие, компанию с ограниченной ответственностью, ассоциацию, акционерное общество, траст, некорпоративную организацию, правительство или любое агентство или их политическое подразделение или любое другое юридическое лицо; (ii) В случае (x) Объединения, когда вознаграждение держателям Обыкновенных акций в обмен на их акции выплачивается исключительно денежными средствами, или (y) роспуска, ликвидации или ликвидации Компании, Держатели должны имеют право на получение после сдачи своего варранта выплат наравне с держателями обыкновенных акций или других ценных бумаг, выпущенных при исполнении варранта, как если бы варрант был исполнен непосредственно перед таким событием, за вычетом цены исполнения. В случае любого Объединения, описанного в настоящем Разделе 4, выжившее или приобретающее Лицо и, в случае любого роспуска, ликвидации или ликвидации Компании, Компания должны незамедлительно внести депозит агенту или доверенному лицу в пользу Владельцы средств, если таковые имеются, должны выплатить Держателям суммы, на которые они имеют право, как описано выше. После того, как такие средства и сданный ордер будут получены, Компания обязана доставить чек на соответствующую сумму (или, в случае или вознаграждении, отличном от денежных средств, такое другое вознаграждение, которое уместно) такому Лицу или Лицам, как она могут быть направлены в письменной форме Владельцами, сдающими такой ордер.

имеет значение, указанное в пункте 2.6 настоящего Соглашения.

имеет значение, указанное в Разделе 14.07(а).

означает любой продукт, содержащий как фармацевтически активный агент или ингредиент, который составляет Лицензионный продукт, так и один или несколько других фармацевтически активных агентов или ингредиентов, которые не являются Лицензированным продуктом.

означает любое имущество в пределах муниципалитета, на котором есть строение, предназначенное для постоянного или периодического проживания, проживания или использования людьми или животными, и из которого должны или могут сбрасываться сточные воды.

означает и относится к тем участкам земли, которые указаны на любом зарегистрированном подразделении Объектов и предназначены для общего пользования и удовольствия владельцев Объектов.

имеет значение, указанное в Разделе 5.11(c)(i)(A) ​​настоящего документа.

Имущество, в котором Компания имеет долю участия, которое не было приобретено с целью получения арендного или другого операционного дохода, в отношении которого не ведется разработка или строительство и в отношении которого добросовестно не планируется разработка или строительство , начать в течение одного (1) года.

означает грузовой автомобиль или седельный тягач, а

имеет значение, указанное в Разделе 313. 021(2) НАЛОГОВОГО КОДЕКСА ТЕХАСА и в соответствии с толкованием Правил контролера и Генерального прокурора Техаса, поскольку эти положения существовали на Дата начала рассмотрения заявки.

означает любое имущество, находящееся в собственности, сданное в аренду или управляемое соответствующей Стороной или любой из ее Дочерних компаний, или в отношении которой такая Сторона или Дочерняя компания имеет обеспечительный интерес или иной интерес (включая доверительный интерес), и, если этого требует контекст, включает владельца или оператора такого имущества, но только в отношении такого имущества.

означает затопленный самолет; подводное судно, включая корабль, лодку, каноэ, ялик, плот или баржу; такелаж, снаряжение, фитинги, атрибуты и оборудование подводного самолета или плавсредства; личное имущество офицеров, членов экипажа и пассажиров затопленного самолета или плавсредства; груз затонувшего самолета или плавсредства, который был покинут, брошен, брошен или оставлен, и в отношении которого владельцы и страховщики отказались от попыток возврата; и затопленные материалы, образовавшиеся в результате деятельности доисторических и исторических коренных американцев.

означает комбинацию двух (2) или более несвязанных сетевых элементов, которые были или не были ранее объединены или подключены к сети CenturyLink, как того требует FCC, Комиссия или настоящее Соглашение.

означает правомочную недвижимость, которая включает в себя три или более жилых единиц и может также содержать компонент коммерческой недвижимости в том же здании.

имеет значение, указанное в разделе 7.01(o).

DocID» \* MERGEFORMAT 22527540.2 238213-10001 MAIA BIOTECHNOLOGY, INC. ПЛАН ПООЩРЕНИЯ АКЦИЙ НА 2021 г. «), между Maia Biotechnology, Inc. («Компания») и ____________________ («Опцион»).

означает судно, предназначенное для перевозки нефти или твердых грузов навалом.

означает каждое имущество или другой актив в такой форме, которая может быть разрешена Законом штата Делавэр, но за исключением денежных средств, внесенных в Партнерство. После корректировки балансовой стоимости внесенного имущества в соответствии с разделом 5. 5 (d) такое имущество больше не должно представляют собой Вносимую собственность, но должны считаться Скорректированной собственностью.0004

означает права и интересы CenterPoint Houston в соответствии с Распоряжением о финансировании после того, как эти права впервые переданы Компании или переданы в залог в связи с выпуском Облигаций на переход, включая право налагать, взимать и получать через Плату за переход подлежащая уплате розничными потребителями электроэнергии в пределах сертифицированной зоны обслуживания CenterPoint Houston, существовавшей на 1 мая 1999 г., сумма, достаточная для покрытия Обусловленных расходов CenterPoint Houston, разрешенных в Приказе о финансировании, право на получение Платы за переход в суммах и в сроки, достаточные для выплачивать основную сумму долга и проценты и вносить другие вклады в связи с Облигациями на переходный период, а также всеми доходами и сборами, полученными в результате Сборов на переходный период.

означает в отношении Материнской компании и ее Дочерних компаний, находящихся в 100 Заемщик или такая дочерняя компания, находящаяся в полной собственности (или такая дочерняя компания, не находящаяся в полной собственности, или неконсолидированное аффилированное лицо), которая в настоящее время находится в стадии разработки, коэффициент занятости которой не достиг 80% или более, и в отношении которого произведены улучшения (кроме улучшений арендатора на незанятых космос), связанные с развитием, не были завершены. Термин «Недвижимость под застройку» включает недвижимое имущество типа, описанного в непосредственно предшествующем предложении, которое удовлетворяет обоим из следующих условий: (i) оно должно быть (но еще не приобретено) Заемщиком или любой из его Полностью Дочерние компании, находящиеся в собственности (или, в случае любого расчета, подлежащего Корректировке доли собственности, применимая Дочерняя компания, не находящаяся в полной собственности, или Неконсолидированное аффилированное лицо) после завершения строительства в соответствии с договором, в соответствии с которым продавец такого недвижимого имущества должен разработать или провести ремонт до и в качестве предварительного условия для такого приобретения, и (ii) третья сторона развивает такое имущество, используя средства кредита, который Гарантирован Заемщиком или любой из его Дочерних компаний, находящихся в полной собственности, или иным образом прибегает к ним (или, в случае любого расчета, зависящего от Корректировки доли собственности, применимой дочерней компании, не находящейся в полной собственности, или неконсолидируемой аффилированной компании). Недвижимость в застройке, в отношении которой все улучшения (кроме улучшений незанятых помещений арендатором), связанные с развитием такой собственности, были завершены в течение как минимум 12 месяцев, и в остальном она не отвечает требованиям, предъявляемым к приемлемой собственности, на момент или до конца такого 12-месячного периода, перестает быть Объектом Застройки, несмотря на тот факт, что такой Объект не достиг коэффициента заполнения не менее 80%.

означает имущество, потенциально опасное для общественной безопасности в случае кражи, утери или потери, или которое подлежит исключительной физической охране, защите, контролю и ответственности. Примеры включают оружие, боеприпасы, взрывчатые вещества, контролируемые вещества, радиоактивные материалы, опасные материалы или отходы или драгоценные металлы.

Объяснение урока: Свойства комбинаций

В этом объяснении мы узнаем, как использовать свойства комбинаций для упрощения выражений и решения уравнений.

Комбинация — это набор 𝑟 элементов, выбранных без повторение из сборника 𝑛 предметы, в которых порядок не имеет значения. Ключевое различие между комбинацией и перестановкой заключается в том, что порядок не имеет значения. Для перестановки, порядок имеет значение. Попробуйте подсчитать количество способов, которыми мы можем назначить роль президента и вице-президента в группа из 5 человек: Мона, Амер, Самар, Бассем, и Далия. Если мы выберем Мона, потом Далия, это будет не то же самое, что Далия, то мона так как первый выбор будет президентом, а второй — вице-президентом. Однако, если бы мы просто хотели комитет из двух человек, не важно, выберем ли мы Мону, затем Далию или Далию, затем Мона. Следовательно, считая с перестановками приводит к тому, что мы пересчитываем количество возможных вариантов, если порядок не имеет значения. Фактически, мы пересчитываем ровно в 𝑟 раз. Таким образом, мы можем определить число 𝑟 комбинаций из 𝑛 как число из 𝑟 перестановки 𝑛 разделить на 𝑟.

Определение: Количество комбинаций заданного размера

Количество комбинаций размера 𝑟, взятых из коллекция предметов 𝑛 предоставлена 𝐶=𝑃𝑟=𝑛𝑟𝑛−𝑟.

Обозначение 𝐶 можно прочитать как 𝑛-𝐶-𝑟 или как 𝑛 выберите 𝑟 и также называется биномиальным коэффициент. Еще одно чрезвычайно распространенное обозначение 𝐶: 𝑛𝑟; однако существуют также различные другие формы обозначений обычно используется, например, 𝐶, 𝐶, 𝐶, и 𝐶(𝑛,𝑟).

Этот объяснитель сосредоточится на ключевых свойствах 𝐶 и как мы можем применить их для упрощения выражений и решения уравнений. Мы начинаем с рассмотрим пример, в котором мы используем формулу для вычисления выражения, включающего комбинации.

Пример 1. Оценка комбинаций

Определите значение 𝐶𝐶 без использования калькулятора.

Ответить

Напомним, что 𝐶=𝑛𝑟𝑛−𝑟.

Подставляя 𝑛=23 и 𝑟=8, получаем 𝐶=23823−8=238×15.

Аналогично, подставляя 𝑛=23 и 𝑟=6, получаем 𝐶=236×17.

Подставляя их в данное выражение, получаем ××𝐶𝐶=2381523617.

Используя правила дробей, мы можем переписать это как 𝐶𝐶=238×156×1723.

Отменив общий множитель 23, мы получим 𝐶𝐶=6×178×15.

Поскольку 𝑛=𝑛(𝑛−1)×⋯×2×1, мы можем упростить это, чтобы получить 17×168×7=347.

Чтобы решить предыдущий пример, мы могли бы просто использовать комбинации на нашем калькуляторе, чтобы вычислить выражение. Тем не менее, рост умение оперировать формулами перестановок и комбинаций даст нам необходимые навыки, необходимые для решения более сложных задач.

Давайте рассмотрим пример, где мы находим неизвестное из уравнения, которое включает перестановку и комбинацию.

Пример 2: Равенство комбинаций и перестановок

Если 𝐶=𝑃, найдите значение (я) числа 𝑟.

Ответ

Напомним, что из определения комбинаций мы имеем 𝐶=𝑃𝑟.

Подставив это в данное уравнение, получим 𝑃=𝐶=𝑃𝑟.

Перекрестное умножение на 𝑟 и деление на 𝑃, мы можем переписать это как 𝑟=1.

У нас может возникнуть соблазн сразу же сделать вывод, что 𝑟=1. Однако это будет лишь частичным ответом, поскольку, вспоминая определение факториала, мы также имеем, что 0=1.

Обратите внимание, что когда 𝑟=0, мы имеем 𝐶=𝑃=1 и когда 𝑟=1, мы имеем 𝐶=𝑃=𝑛.

Следовательно, два возможных значения 𝑟 равны 1 и 0.

В следующем примере мы найдем выражение, включающее перестановки, которое равно заданному выражению, включающему комбинации.

Пример 3: Связь между комбинациями и перестановками

Что из следующего равно 𝐶×𝐶𝐶?

1. 𝑃𝑃
2. 𝑃𝑃
3. 𝑃𝑃
4. 𝑃𝑃

Ответ

Начнем с того, что заметим, что 𝐶=𝑛. Следовательно, мы можем переписать выражение: 𝐶×𝐶𝐶=𝑛𝐶𝐶.

Поскольку все, что мы пытаемся найти, это выражение, включающее перестановки, мы должны попытаться выразить комбинации в терминах перестановок. Для этого можно использовать определение, что 𝐶=𝑃𝑟 переписать наше выражение как 𝐶×𝐶𝐶=𝑛67.

Отмена 6, имеем 𝐶×𝐶𝐶=7𝑛𝑃𝑃, который мы также можем записать как 𝐶×𝐶𝐶=𝑃.

Вспоминая свойство перестановок, что 𝑛𝑃=𝑃, мы можем переписать 𝑃7𝑛=𝑃.

Следовательно, 𝐶×𝐶𝐶=𝑃𝑃.

Следовательно, правильный ответ C.

До сих пор мы просто использовали определение и формулу для 𝐶 для решения проблем. Много проблем с участием комбинаций можно решить таким образом. Однако часто мы можем решать проблемы более простым и понятным способом, будучи знакомым со свойствами комбинаций. Одно из таких свойств связано с симметрией комбинаций.

Уведомление из определения 𝐶=𝑛𝑟𝑛−𝑟 что существует симметрия относительно знаменателя. Если мы заменим 𝑛−𝑟 вместо 𝑟 в формуле мы находим, что мы получаем одно и то же выражение: 𝐶=𝑛𝑛−𝑟𝑛−(𝑛−𝑟)=𝑛𝑟𝑛−𝑟.

Это приводит к общей идентичности комбинаций.

Тождество: симметрия комбинаций

Для заданных натуральных чисел 𝑟 и 𝑛, удовлетворяющих 𝑟𝑛, имеем 𝐶=𝐶.

Это имеет некоторые интересные последствия для решения уравнений, включающих 𝐶 с неизвестными в 𝑟. Следующий пример продемонстрирует одно из таких следствий.

Пример 4: Симметрия комбинаций

Найдите возможные значения 𝑟, которые удовлетворяют уравнению 𝐶=𝐶.

Ответ

Используя правило 𝐶=𝐶, мы получаем это 𝐶=𝐶=𝐶.

Таким образом, 𝑟=15 или 𝑟=6.

Последний пример показал, что если 𝐶=𝐶 тогда 𝑎=𝑏 или 𝑎=𝑛−𝑏.

Рассмотрим еще один пример, требующий симметрии комбинаций.

Пример 5: Использование симметрии комбинаций

Если 𝐶+𝐶=2𝐶, найти 𝑛.

Ответ

Используя свойство 𝐶=𝐶, мы можем переписать 𝐶=𝐶. Замена это в данное уравнение, мы находим 2𝐶=2𝐶.

Отсюда следует, что 𝑛−42=43 или 𝑛−42=𝑛−43. Поскольку последний из них несовместим, мы имеем, что единственный решение 𝑛=85.

В следующем примере мы определим неизвестную константу в комбинациях, когда нам известно, что выражения, включающие комбинации, образуют арифметическую последовательность.

Пример 6. Решение задач на комбинации

Учитывая, что 3×𝐶,4×𝐶,6×𝐶, — арифметическая прогрессия, найдите все возможные значения 𝑛.

Ответ

В арифметической прогрессии существует постоянная разница между последовательными условия. Следовательно, разница между двумя первыми и двумя последними членами будет равны, и мы можем написать 6×𝐶−4×𝐶=4×𝐶−3×𝐶. 

Переставляя, получаем 8×𝐶=6×𝐶+3×𝐶.

Использование определения 𝐶=𝑛𝑟𝑛−𝑟, мы можем переписать это как 8𝑛11𝑛−11=6𝑛12𝑛−12+3𝑛10𝑛−10.

Разделив на общий делитель числа 𝑛, получим 811𝑛−11=612𝑛−12+310𝑛−10.

Теперь мы можем умножить на 12𝑛−10, чтобы получить 8×12𝑛−1011𝑛−11=6×12𝑛−1012𝑛−12+3×12𝑛−1010𝑛−10.

Используя свойство факториала, которое 𝑛=𝑛𝑛−1, мы можем переписать это как 8×12×1111×(𝑛−10)𝑛−11𝑛−11=6×1212×(𝑛−10)(𝑛−11)𝑛−12𝑛−12+3×12×11×1010×𝑛−10𝑛−10 .

Сокращая общие множители в числителях и знаменателях, имеем 8×12(𝑛−10)=6(𝑛−10)(𝑛−11)+3×12×11.

Теперь мы можем разделить на 6, чтобы получить 8×2(𝑛−10)=(𝑛−10)(𝑛−11)+3×2×11.

Раскрывая скобки, получаем 16𝑛−160=𝑛−21𝑛+110+66.

Собирая подобные члены, мы приходим к квадратичному 0=𝑛−37𝑛+336.

Решая это с помощью факторизации или квадратичной формулы, получаем 𝑛=21 и 𝑛=16.

Одним из других ключевых свойств комбинаций является рекурсивная связь:

Формула: Рекурсивная связь в комбинациях

𝐶+𝐶=𝐶, где 0𝑟𝑛.

Чтобы вывести эту формулу, мы можем использовать определение 𝐶 писать левую часть как 𝐶+𝐶=𝑛−1𝑟𝑛−𝑟−1+𝑛−1𝑟−1𝑛−𝑟.

Мы хотели бы выразить это как одну дробь над общим знаменателем 𝑟𝑛−𝑟. Мы можем сделать это, умножив первый член на 𝑛−𝑟𝑛−𝑟 а второй член через 𝑟𝑟 следующим образом: 𝐶+𝐶=(𝑛−𝑟)𝑛−1𝑟(𝑛−𝑟)𝑛−𝑟−1+𝑟𝑛−1𝑟𝑟−1𝑛−𝑟.

Используя свойства факториалов, которые 𝑛=𝑛𝑛−1, мы можем переписать это как 𝐶+𝐶=(𝑛−𝑟)𝑛−1𝑟𝑛−𝑟+𝑟𝑛−1𝑟𝑛−𝑟.

Выразив это в виде одной дроби и раскрыв скобки, мы имеем 𝐶+𝐶=𝑛𝑛−1−𝑟𝑛−1+𝑟𝑛−1𝑟𝑛−𝑟.

Упрощая и используя то же правило факториалов, мы имеем 𝐶+𝐶=𝑛𝑟𝑛−𝑟=𝐶 как требуется.

Сейчас мы обратим внимание на один пример, где мы применяем это свойство упростить уравнение.

Пример 7: Попарные суммы комбинаций

Определите значение 𝐶+𝐶.

Ответ

Похоже, это выражение будет чрезвычайно трудоемко вычислить или вычислить. трудно упростить. Тем не менее, первое понимание, которое мы получаем, замечая что когда 𝑟=15 в сумме, мы имеем член 𝐶=𝐶. Убрав это слагаемое из суммирования, имеем

В этот момент мы можем применить рекурсивное отношение, 𝐶+𝐶=𝐶, и упростить это до 𝐶+𝐶=𝐶+𝐶.

Теперь мы видим, что если мы проделаем то же самое еще раз и возьмем последний член из суммирования, мы имеем

Следовательно, 𝐶+𝐶=𝐶+𝐶.

Продолжая тем же методом, мы в конце концов придем к последнему члену в сумме, 𝐶, и имеют выражение

Таким образом, все выражение упрощается до 𝐶+𝐶=𝐶.

Для последней пары примеров мы будем рассматривать суммы всех комбинаций 𝐶 для данного 𝑛.

Пример 8: суммы комбинаций

Найдите значение 𝐶+𝐶+𝐶+⋯+𝐶.

Ответ

Использование определения 𝐶=𝑛𝑟𝑛−𝑟, мы можем переписать это выражение как 𝐶+𝐶+𝐶+⋯+𝐶=50×5+51×4+52×3+⋯+55×0.

Оценивая каждое слагаемое, имеем 𝐶+𝐶+𝐶+⋯+𝐶=1+5+10+10+5+1=32.

В последнем примере мы обнаружили, что сумма всех комбинаций 𝐶 для 𝑛=5 есть 32; не случайно это равно 2. На самом деле общее правило состоит в том, что сумма всех 𝐶 для любого заданного 𝑛 равно 2. Мы можем записать это как 𝐶+𝐶+𝐶+⋯+𝐶+𝐶=2, или более кратко, мы имеем следующее тождество.

Идентичность: сумма комбинаций

Для любого положительного целого числа 𝑛 имеем 𝐶=2.

Возможно, это правило не так уж удивительно, если учесть рекурсивное отношение для каждого термина: 𝐶+𝐶=𝐶.

Поскольку это не относится к 𝑟=0 или 𝑟=𝑛, мы можем переписать сумму как 𝐶 = 𝐶+ 𝐶+𝐶+𝐶+𝐶+𝐶+𝐶+⋯+𝐶+𝐶+𝐶.

Поскольку 𝐶=1=𝐶 и 𝐶=1=𝐶, мы можем переписать это выражение как  𝐶=𝐶+𝐶+𝐶+𝐶+𝐶+𝐶+𝐶+⋯+𝐶+𝐶+𝐶.

Перегруппировав термины, мы имеем  𝐶=𝐶+𝐶+𝐶+𝐶+𝐶+𝐶+⋯+𝐶+𝐶=2𝐶+𝐶 𝐶.

Следовательно, сумма 𝐶 вдвое больше суммы 𝐶. Более того, поскольку 𝐶=1, мы видим, что сумма 𝐶 для данного 𝑛 будет сила двух; в частности, это будет 2.

Наконец, рассмотрим переменную сумму комбинаций.

Пример 9: Переменные суммы комбинаций

Найдите значение 𝐶−𝐶+𝐶−𝐶+𝐶.

Ответ

Напомним, что 𝐶=𝑛𝑟𝑛−𝑟. Используя это, мы видим, что 𝐶−𝐶+𝐶−𝐶+𝐶=40×4−41×3+42×2−43×1+44×0.

Оценка каждого термина дает нам 𝐶−𝐶+𝐶−𝐶+𝐶=1−4+6−4+1=0.

Опять же, общее правило состоит в том, что чередующиеся суммы 𝐶 равны нулю: 𝐶−𝐶+𝐶−⋯+(−1)𝐶+(−1)𝐶=0 или, более кратко,

Идентичность: чередующаяся сумма комбинаций

Для любого натурального числа 𝑛 имеем (−1)𝐶=0.

Альтернативный способ представить это состоит в том, что суммы нечетных и четных членов равны. Это неудивительно, когда 𝑛 нечетно из-за отражающая симметрия: 𝐶=𝐶. Однако, как показал предыдущий пример, это справедливо и для четных 𝑛.

Давайте повторим несколько важных понятий из объяснения.

Ключевые точки

• Количество комбинаций размера 𝑟, взятых из набор размера 𝑛 задается 𝐶=𝑃𝑟=𝑛𝑟𝑛−𝑟.
• Комбинации обладают следующими ключевыми свойствами: заданы положительные целые числа 𝑟 и 𝑛, удовлетворяющие 𝑟𝑛,
  • Свойство симметрии: 𝐶=𝐶,
  • Рекурсивное свойство: 𝐶+𝐶=𝐶,
  • Сумма: 𝐶=2,
  • Переменная сумма: (−1)𝐶=0.