Правила умножения числа на ноль

Всем нам в школе учителя прочно вбили в голову простейшее правило: «Любое число, умноженное на ноль, равняется нулю!». И все мы хорошо его запомнили и применяем в жизни, не задаваясь вопросом: «Почему?». Но вот мы выросли, у нас появились дети, и пришло время объяснять им те самые простейшие правила так, чтобы было понятно и запомнилось навсегда. Как это сделать? Какие слова подобрать? Будем разбираться.

Содержание:

Правила умножения любого числа на ноль

Что такое ноль

Из истории

Какие действия в математике можно выполнять с нулём

Умножение на ноль, правило математики

Деление на ноль, правило математики

Подведём итоги

Всем нам в школе учителя прочно вбили в голову простейшее правило: «Любое число, умноженное на ноль, равняется нулю!». И все мы хорошо его запомнили и применяем в жизни, не задаваясь вопросом: «Почему?». Но вот мы выросли, у нас появились дети, и пришло время объяснять им те самые простейшие правила так, чтобы было понятно и запомнилось навсегда.

Как это сделать? Какие слова подобрать? Будем разбираться.

Что такое ноль

Вокруг этой цифры всегда велось много споров. Число 0 занимает особое место в математике, даже несмотря на то, что оно буквально означает «ничто», «пустота». Ноль — это целое число, одна из цифр в десятичной системе счисления. Цифра ноль, поставленная справа от другой цифры, увеличивает числовое значение всех цифр, стоящих левее, на разряд — десяток, сотню и так далее. Например, если рядом с 5 ставим 0, получаем 50, если рядом с 50 ставим 0, получаем 500. А ещё ноль — это число, отделяющее положительные цифры от отрицательных на числовой прямой. Сам ноль при этом знака + / — не имеет.  

Какие действия в математике можно выполнять с нулём

С нулём выполняются все арифметические действия: сложение, вычитание, умножение, деление, возведение в степень. При выполнении сложения и вычитания с нулём обычно проблем и сложностей не возникает. Здесь всё просто. 

Если к любому числу добавить 0, это означает, что к нему не прибавилось ничего. Слагаемое каким было, таким и осталось, сколько раз ноль ни прибавляй.

‍

 

‍

То же самое будет, если отнять ноль. 

Если ноль разделить на любое ненулевое число, то в результате тоже получится ноль. 

А вот операция умножения гораздо менее очевидна. Не все понимают, почему при умножении на 0 получается 0. Именно умножение на ноль мы сейчас рассмотрим подробнее, так как в нём содержатся некоторые нюансы. А заодно поговорим немного и о делении на ноль.

Умножение на ноль, правило математики

Чтобы разобраться, чем отличается умножение числа на ноль от умножения других чисел друг на друга, нужно для начала понять определение умножения в целом. Умножение — одно из основных действий в математике. Умножение — это арифметическое действие, когда сложение одинаковых чисел происходит искомое количество раз. В этом действии участвуют два составляющих компонента — множимое и множитель. Результат их умножения называют произведением. То есть для натуральных чисел умножением, по сути, является многократное сложение. Таким образом, чтобы умножить число a на число b, необходимо b раз сложить a.        

                            a ⋅ b = a + a + … + a} b

Так, пример 4 х 3 = 12 можно заменить следующим выражением: 4 + 4 + 4 = 12. То есть число 4 было взято 3 раза. 

А можно ли умножать на ноль? Можно, только это бессмысленно и бесполезно. Ведь ноль — это ничто, пустота. А какой смысл умножать на пустоту? Тут, как ни крути, всё равно будет получаться ноль. 

Как на примере объяснить это правило детям? Попробуем вот так:

‍

• если съесть пять раз по два яблока, получится 2 * 5 = 2 + 2 + 2 + 2 + 2 = 10, то есть в итоге будет съедено 10 яблок;
• если съесть по два яблока трижды, получится 2 * 3 = 2 + 2 + 2 = 6, в итоге будет съедено 6 яблок;
• если съесть по два яблока ноль раз, то 2 * 0 = 0 * 2 = 0 + 0 = 0, в итоге не съедено ни одного яблока.

Ведь съесть ноль раз — это означает не съесть ни одного. Ноль — это ничего, а когда у вас нет ничего, то на сколько его ни умножай, всё равно будет ноль.

Правда, иногда выдвигаются следующие возражения: предположим, у человека в руке 2 яблока. Если он не съел их, то яблоки не пропадут, они так и останутся у него в руке. Почему же тогда результат равен нулю? Да, яблоки действительно из руки никуда не денутся. Но ведь в примере мы считаем именно съеденные яблоки, то есть те из них, которые были съедены, проще говоря, оказались в желудке человека. А в последнем случае они туда не попали. Поэтому человек съел ноль яблок. 

Итак, основное правило гласит: при умножении числа на ноль и при умножении нуля на число в ответе всегда будет получаться ноль.

a ⋅ 0 = 0

0 ⋅ a = 0

Это правило умножения на ноль в математике действительно для любых чисел: положительных, отрицательных, целых, дробей, разрядных, рациональных, иррациональных. В любом случае произведение будет нулевым.

Для лучшего запоминания правила приведём примеры умножения на ноль:

0 ⋅ 3 = 0 + 0 + 0 = 0

0 ⋅ 4 = 0 + 0 + 0 + 0 = 0

756 ⋅ 0 = 0

293 ⋅ 0 = 0

Деление на ноль, правило математики

А что же с делением на 0? Мы со школы помним правило: на ноль делить нельзя. Все это заучивают, не требуя лишних доказательств. Нельзя так нельзя. Большинство людей действительно не делит на ноль только исходя из этого правила, не пытаясь найти ответ, по которому станет понятен этот запрет. А почему, собственно, нельзя? 

Деление в математике — действие, обратное умножению, также состоящее из двух компонентов — делимого и делителя. Результат деления называют частным. Также иногда результат деления называют отношением. Если умножение для натуральных чисел заменяет многократное сложение, то, соответственно, деление будет заменять многократное вычитание.

Чтобы было понятнее, рассмотрим на примерах.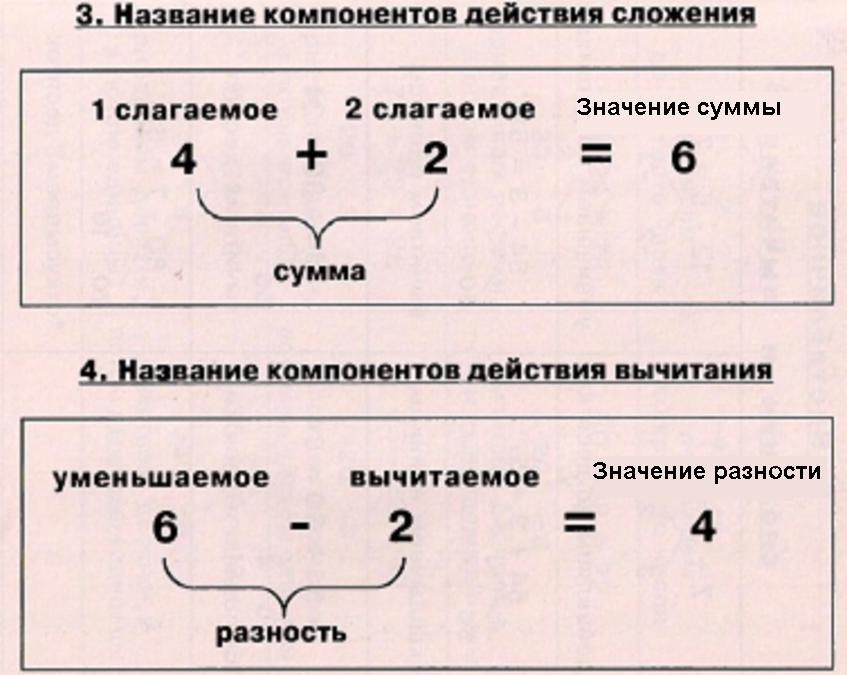

• Разделим число 8 на число 2 (8 : 2). Из действия вычитания мы находим, что число 2 содержится в 8 четыре раза. В данном случае 8 — делимое, 2 — делитель, 4 — частное.
• Теперь разделим 0 на 2 (0 : 2). Чтобы 0 разделить на 2, надо найти число, при умножении которого на 2 получится 0. Это ноль, так как 0 ⋅ 2 = 0. Значит, 0 ⋅ 2 = 0. При делении нуля на любое число, не равное нулю, частное равно нулю. 
• А теперь попробуем разделить 4 на 0 (4 : 0). Данное выражение можно представить и в виде уравнения: 0 ⋅ x = 4. Следовательно, чтобы разделить 4 на ноль, необходимо найти такое число, при умножении на которое получится 4, а это невозможно исходя из того, что мы выяснили ранее.

Следовательно, делить на 0 нельзя, так как такого числа, при умножении которого на ноль получится 4, не существует. И всё-таки лучше всего это правило просто запомнить и никогда не нарушать. Для лучшего запоминания предложите своему ребёнку выучить небольшое стихотворение:

Расскажу тебе, позволь, 

Чтобы не делил на 0! 

Режь 1, как хочешь, вдоль, 

Только не дели на 0!

Таким образом, с нулём возможно совершать любые арифметические действия: прибавлять и вычитать любые числа, умножать на значения, не равные нулю, возводить в степень, не равную нулю. Единственное ограничение — ноль не может быть делителем для любого действительного числа. В арифметике подобные действия считаются невозможными и бессмысленными.

Подведём итоги

Итак, сегодня мы выяснили, что за цифра такая — ноль. Мы узнали историю её возникновения. А также разобрались, чем отличается умножение числа на 0 от умножения других чисел друг на друга, а также почему на ноль нельзя делить. Чтобы закрепить полученные новые знания, важно отработать их на практике. Поэтому для закрепления и лучшего запоминания предложите своему ребёнку решить примеры:

7 * 0 

15 * 0

0 * 9

0 * 346

72 : 9 * 0

Конечно же, во всех этих примерах ответ будет 0:

7 * 0 = 0

15 * 0 = 0

0 * 9 = 0

0 * 346 = 0

72 : 9 * 0 = 0

Закрепляем тему «Умножение на ноль»

Закрепить эту и многие другие изученные темы по математике можно на образовательной платформе iSmart. С помощью онлайн-тренажёров дети в  увлекательной форме наработают вычислительную беглость в решении примеров с умножением на ноль.  

Вот так, например, выглядят задания для второго класса:

А так выглядит сам каталог заданий по математике образовательной платформы iSmart: 

Образовательная платформа iSmart разработана учителями и специалистами в области детской психологии в соответствии с требованиями ФГОС. Она предлагает программы подготовки по всем изучаемым в школе предметам, пакеты заданий для подготовки к контрольным работам, тестам, ВПР, олимпиадам, а также изучение дополнительных предметов, не вошедших в школьную программу.

Регистрируйте своего ребёнка и начинайте заниматься прямо сейчас!

‍

Электронный справочник по математике для школьников арифметика арифметические действия

Справочник по математике

Арифметика

Арифметика целых чисел

Содержание

Арифметика. Арифметические действия

Обратные арифметические действия

Свойства арифметических действий

Порядок выполнения арифметических действий

Умножение натуральных чисел на 10, 100, 1000; и т.д.

Арифметика. Арифметические действия

Арифметическим действием называют операцию, удовлетворяющую ряду свойств и позволяющую по нескольким данным числам найти новое число.

Арифметикой называют науку, изучающую простейшие свойства чисел и арифметических действий.

Существуют шесть арифметических действий: сложение, вычитание, умножение, деление, возведение в степень, извлечение корня.

Обратные арифметические действия

Вычитание – это арифметическое действие, обратное к сложению, деление – действие, обратное к умножению, извлечение корня – действие, обратное к возведению в степень.

Например,

Свойства арифметических действий

	a + b = b + a ,
	(a + b) + c = a + (b + c)
	a + 0 = 0 + a = a
	a + ( – a ) = 0
	На 0 делить нельзя.

Порядок выполнения арифметических действий

Сложение и вычитание называют действиями первой ступени, умножение и деление – действиями второй ступени, возведение в степень и извлечение корня – действиями третьей ступени.

Действия одной ступени выполняются в том же порядке, в каком они записаны в формуле.

Если в формуле содержатся действия разных ступеней, то сначала выполняют действия высших ступеней, а затем низших ступеней.

Если формула содержит скобки, то сначала выполняют действия в скобках. Скобки бывают круглыми, квадратными и фигурными, причем между ними нет никакой разницы.

Если скобки содержат другие скобки, то сначала выполняют действия во «внутренних» скобках.

Умножение натуральных чисел на 10, 100, 1000 и т.д.

Для того, чтобы умножить натуральное число на 10 ,  100 ,  1000 &nbsp и т.д., нужно справа приписать к нему столько нулей, сколько содержится в числе 10 ,  100 ,  1000 &nbsp и т.д. соответственно.

Действительно, например, число 3610 состоит из трёх тысяч, шести сотен и одного десятка, поэтому

что и требовалось показать.

интуиция — Понимание определения группового действия.

Задавать вопрос

спросил 4 года 11 месяцев назад

Изменено 6 месяцев назад

Просмотрено 736 раз

$\begingroup$

Цитата из определения группового действия Вольфрама —

В общем, групповое действие — это когда группа действует на множество, переставляя его элементы, так что отображение группы в группу перестановок множества является гомоморфизмом.

Всегда ли группа, действуя на множество, всегда переставляет элементы? Когда появляется слово перестановки, я могу думать о группе перестановок $S_{n}$, но что происходит, когда какая-то другая группа действует на множество?

Кроме того, отображение из группы в группу перестановок множества является гомоморфизмом, это все равно, что сказать, что существует гомоморфизм между группой и множеством элементов, хм, интуитивно понятно?

Также есть ли потрясающие приложения для групповых действий или визуализации?

• групповая теория
• интуиция
• групповые действия
• мотивация

$\endgroup$

1

$\begingroup$

Если группа $G$ действует на любом множестве $X$, то причина того, что действие элемента группы $g \in G$ является перестановкой — т. {-1}$. По определению группового действия действие $g \in G$, за которым следует действие $h \in G$, равно действию $hg$; поэтому мы говорим, что действие является гомоморфизмом. 92$. В геометрии есть много-много других интересных действий, подобных этому.

$\endgroup$

$\begingroup$

Всегда есть тривиальное действие от любой группы к любому множеству, которое не переставляет все транзитивно. В общем, групповое действие группы $G$ на множестве $X$ можно рассматривать как отображение $\phi:G\to S_X$, симметричную группу на элементах $X$. Таким образом, групповое действие содержит все перестановки $X$, когда отображение $\phi$ сюръективно. Мы не хотим сказать, что это групповое действие является гомоморфизмом между $G$ и $X$, потому что $X$ не имеет собственной структуры. Именно $S_X$, группа перестановок, имеет структуру, с которой мы хотим иметь дело, и у нас уже есть слово для групповых гомоморфизмов.

9к$. Фактически, одно из доказательств теоремы Коши также использует групповые действия и теорему о стабилизаторе орбиты.

$\endgroup$

$\begingroup$

«Перестановка» — не очень хорошее слово, если только вы не занимаетесь конкретно действиями над конечными множествами. Групповое действие группы $G$ на множестве $X$ эквивалентно групповому гомоморфизму $G\to\mathsf{Bij}(X)$, где $\mathsf{Bij}(X)$ — группа биекции, т. е. обратимые функции, на $X$. Когда $X$ — конечное множество, то это будет группа перестановок элементов $X$. Гомоморфизм $G\to\mathsf{Bij}(X)$ не похож на гомоморфизм из $G$ в $X$, поскольку он даже не имеет смысла: для $X$ не определена и не требуется групповая структура. Гомоморфизм отображает $g\in G$ в обратимую

функция $X\to X$, где структура группы определяется композицией функций.

Исторически математики обычно интересовались групповыми действиями. Лишь позднее идея группы стала самостоятельным понятием. Теорема Нётер полностью изменила то, как мы концептуализируем физику, и речь идет о групповых действиях (Ли). Это дает такие результаты, как сохранение энергии из-за симметрии при переносе времени. Стандартная модель — это калибровочная теория, а упомянутые калибровочные симметрии относятся к групповым действиям (Ли). Это тесно связано с теоремой Нётер.

$\endgroup$

1

действие в nLab

Пропустить навигационные ссылки | Домашняя страница | Все страницы | Последние версии | Обсудить эту страницу |

Действия

эта запись о понятии действия в алгебре (одного алгебраического объекта на другой объект). О понятии функционала действия в физике см. там.

---

Контекст

Алгебра

высшая алгебра

универсальная алгебра

Алгебраические теории

• алгебраическая теория / 2-алгебраическая теория / (∞,1)-алгебраическая теория

• монада / (∞,1)-монада

• операда / (∞,1)-операда

Алгебры и модули

• алгебра над монадой

  ∞-алгебра над (∞,1)-монадой

• алгебра над алгебраической теорией

  ∞-алгебра над (∞,1)-алгебраической теорией

• алгебра над операдой

  ∞-алгебра над (∞,1)-операдой

• действие

  , действие ∞

• представление, ∞-представление

• модуль

  , ∞-модуль

• ассоциированный пучок, ассоциированный ∞-пучок

Высшие алгебры

• моноидальная (∞,1)-категория

  • симметричная моноидальная (∞,1)-категория

  • моноид в (∞,1)-категории

  • коммутативный моноид в (∞,1)-категории

• симметричная моноидальная (∞,1)-категория спектров

  • разбить произведение спектров

  • симметричное моноидальное произведение спектров

  • кольцевой спектр, модульный спектр, алгебраический спектр

• A-∞ алгебра

  • Кольцо A-∞, пространство A-∞

• C-∞ алгебра

• кольцо E-∞, алгебра E-∞

  • ∞-модуль, (∞,1)-расслоение модулей

  • теория мультипликативных когомологий

• L-∞ алгебра

  • теория деформации

Презентации категории моделей

• Структура модели

  на симплициальных Т-алгебрах / гомотопическая Т-алгебра

• структура модели на операдах

  структура модели на алгебрах над операдой

Геометрия на формальных дуальных алгебрах

• Двойственность Исбелла

• производная геометрия

Теоремы

• Гипотеза Делиня

• гипотеза раскрытия петли

• моноидальный корреспонденция Долд-Кан

Изменить эту боковую панель

Теория представлений

Теория представлений

Геометрическая теория представлений

Ингредиенты

• линейная алгебра, алгебра, высшая алгебра

Определения

представление, 2-представление, ∞-представление

• группа, ∞-группа

• групповая алгебра, алгебраическая группа, алгебра Ли

• векторное пространство, n-векторное пространство

• аффинное пространство, симплектическое векторное пространство

• действие

  , действие ∞

• модуль

  , эквивариантный объект

• бимодуль, эквивалент Морита

• индуцированное представление, взаимность Фробениуса

• гильбертово пространство, банахово пространство, преобразование Фурье, функциональный анализ

• Орбита

  , коприсоединенная орбита, форма Киллинга

• унитарное представительство

• геометрическое квантование, когерентное состояние

• цоколь, колчан

• модульная алгебра, комодульная алгебра, действие Хопфа, измерение

Геометрическая теория представлений

• D-модуль, извращенная связка,

• Группа Гротендика, лямбда-кольцо, симметрическая функция, формальная группа

• главное расслоение, торсор, векторное расслоение, алгеброид Атьи Ли

• геометрическая теория функций, группоидификация

• Категория Эйленберга-Мура, алгебра над операдой, категория, скрещенный модуль

• теоремы реконструкции

Теоремы

• Теорема Бореля-Вейля-Ботта

• Be?linson-Bernstein локализация?

• Теория Каждана-Люстига

• Теорема разложения BBDG

Изменить эту боковую панель

Теория моноидов

Теория моноидов по алгебре:

• моноид, бесконечность-моноид

• моноидный объект, моноидный объект в категории (бесконечность, 1)

  • полукольцо, установка, кольцо, ассоциативная унитальная алгебра

• Пн, CПн

• гомоморфизм моноидов

• субмоноид, частный моноид?

• делитель, кратный?, частное?

• обратный элемент, блок, неприводимый элемент

• идеально в моноиде

• главный идеал в моноиде

• коммутативный моноид

  • тензорное произведение коммутативных моноидов

• сокращаемый моноид

• НОД моноид

• уникальный моноид факторизации

• моноид Безу

• главный идеальный моноид

• группа

  , абелева группа

• абсорбирующий моноид

  • делитель нуля

  • цельный моноид

• свободный моноид, свободный коммутативный моноид

• графический моноид

• моноидная затворная группа

• Модуль

  поверх моноида

• локализация моноида

• завершение группы

• моноид эндоморфизма

• суперкоммутативный моноид

Изменить эту боковую панель

• Идея
• Определения
• Действия группы
• Действия моноида
• Действия категории
• Действия группового объекта
• Действия моноидного объекта
• Действия набора
• Примеры
• Связанные концепции
• Каталожные номера
• Групповые действия

Идея

Существуют различные варианты понятия чего-то действующего на что-то другое. Все они тесно связаны.

Простейшая концепция действия предполагает, что один набор XX действует на другой набор YY, и такое действие задается функцией от произведения XX на YY на YY

act:X×Y→Y. действие\двоеточие X \times Y \to Y \,. 9Y, чтобы иметь структуру кольца/алгебры, YY должен быть своего рода абелевой группой или векторным пространством с действием линейными функциями; тогда действие также вызывается модулем или представлением .

В терминах некарриванного действия X×Y→YX\times Y\to Y условие «сохранения», грубо говоря, говорит о том, что последовательное действие с двумя элементами в XX равносильно сначала их умножению, а затем действию с результатом:

(1) действие (x2, действие (x1, y)) = действие (x2 ⋅ x1, y). действие (x_2, действие (x_1, y)) = действие (x_2 \ cdot x_1, y) \,.

Точнее, это условие для левого действия ; правильное действие определяется двойственно в терминах отображения Y×X→YY\times X\to Y.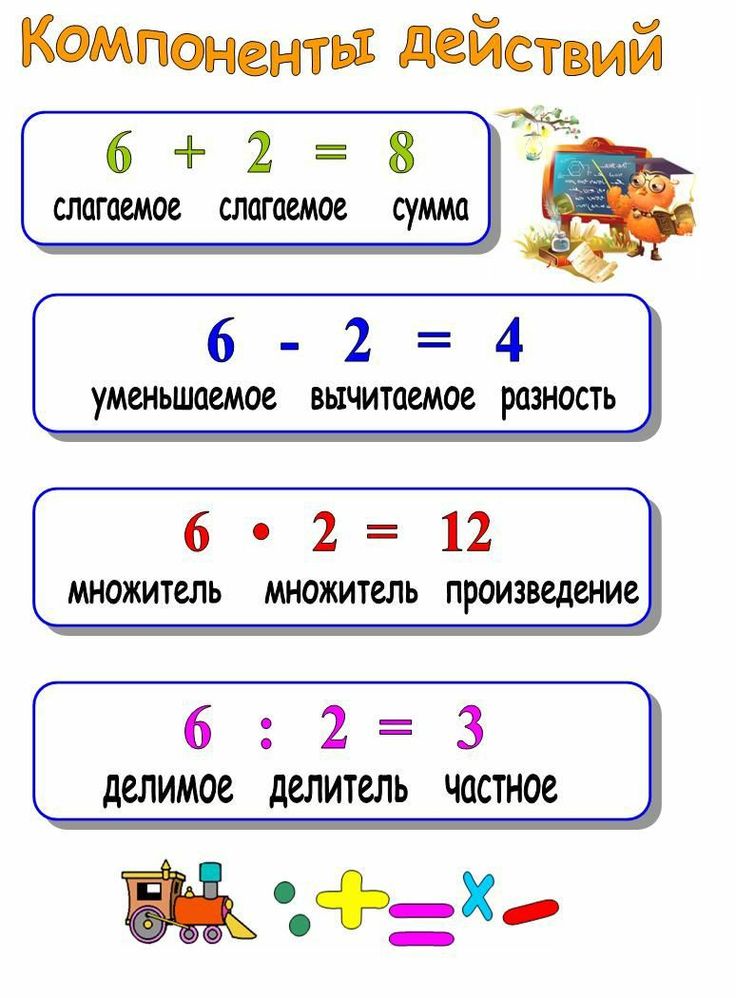 Если XX не имеет алгебраической структуры или если его релевантная структура коммутативна, то между ними нет существенной разницы; но в целом они могут быть совершенно разными.

Это свойство действия также часто можно отождествить со свойством функтора: оно характеризует функтор от развертывания цикла BX\mathbf{B}X моноида XX до категории (такой как Set), объектом которой является YY. Различие между левыми и правыми действиями отражается в дисперсии; действие слева дает ковариантный функтор, тогда как действие справа выражается через контравариантность.

Таким образом, практически каждый вид функтора, n-функтор и обогащенный функтор можно рассматривать как определяющий обобщенный вид действия. Этот взгляд на действия особенно распространен в теории обогащенных категорий, где, например, коэнды можно рассматривать как производящие тензорные произведения действий в этом общем функторном смысле.

При построении Гротендика (или одном из его вариантов) эта перспектива превращается в перспективу, где действием XX является некоторое расслоение Y/XY/X над BX\mathbf{B}X, слоем которого является YY:

Y⟶Y/X↓BX. \множество{ Y &\longrightarrow& Y/X \\ && \Кнопка «Стрелка вниз \\ && \mathbf{B}X } \,.

Здесь тотальное пространство Y/XY/X этого расслоения обычно является «слабым» фактором (например, гомотопическим фактором) действия, откуда и обозначение. Если рассматривать BX\mathbf{B}X как классификационное пространство для XX-универсального главного расслоения, то это расслоение Y/X→BXY/X \to \mathbf{B}X является YY-расслоением, которое ассоциировано через действие к этому универсальному набору. Подробнее об этом взгляде на действия см. в разделе 9.0059 ∞-действие .

Определения

Действия группы

Действие группы GG на объект SS в категории 𝒞\mathcal{C} является представлением GG на SS, то есть гомоморфизмом групп ρ:G→Aut (S)\rho \colon G \to Aut(S), где Aut(S)Aut(S) — группа автоморфизмов SS в 𝒞\mathcal{C}.

Групповые действия, особенно непрерывные действия на топологических пространствах, также известны как группы преобразований (начиная с Klein 1872, Sec. 1, см. также Koszul 65 Bredon 72, tom Dieck 79, Том Дик 87). В качестве альтернативы, если действующая группа GG понята, можно назвать (Бредон 72, гл. II) пространство XX, снабженное действием GG, топологическим G-пространством (или G-множеством , G-многообразием ). и др., в зависимости от обстоятельств).

Как указано выше, более абстрактное, но эквивалентное определение рассматривает группу GG как категорию (группоид), обозначаемую BG\mathbf{B} G, с единственным объектом *\ast. Тогда действие GG в категории CC эквивалентно функтору вида

ρ:БГ→𝒞 \rho \colon \mathbf{B} G \to \mathcal{C}

Здесь объект SS предыдущего определения есть ρ(*)\rho(\ast) этого единственного объекта.

Конкретно, если 𝒞\mathcal{C} является категорией, подобной Set, то действие эквивалентно функции

G×S⟶S(g,s)↦ρ(g)(s) \множество{ G \times S &\longrightarrow& S \\ (g,s) &\mapsto& \rho(g)(s) }

, удовлетворяющее свойству действия

(2)∀g1,g2,sρ(g1⋅g2)(s)=ρ(g1)(ρ(g2)(s)) \занижено{ г_1, г_2, с }{\для всех} \;\;\; \rho(g_1 \cdot g_2)(s) «=» \ро(g_1) \большой( \ро(г_2)(ы) \большой) 9{\mathbf{B} М}. Когда CC является SetSet, это называется MSet.

Рассмотрение этого в расширенной теории категорий дает внутреннее понятие объектов действия .

Действия категории

Можно также ¹ определить действие категории DD на категорию CC как функтор от DD до CC, но обычно его называют просто функтором.

Другая точка зрения на ту же ситуацию: (малая) категория — это монада в категории интервалов в Set. Действие категории является алгеброй для этой монады. См. действие категории в наборе.

С другой стороны, действие моноидальной категории (а не в моноидальной категории, как указано выше) называется модульной категорией (также «категорией»). Это понятие можно, конечно, расширить до действий в моноидальной бикатегории, где в случае CatCat как моноидальной бикатегории оно специализируется на понятии модульной категории.

Действия группового объекта

Предположим, у нас есть категория CC с бинарными произведениями и конечным объектом **. Существует альтернативный способ просмотра групповых действий в Set, так что мы можем говорить о действии группового объекта GG в CC на объект XX из CC. 9A, в Set гомоморфизм групп

α:G→Aut(X)\alpha: G\to Aut(X)

соответствует функции

act:G×X→Xact: G\times X\to X

, который будет иметь различные свойства, кодирующие, что α\alpha был гомоморфизмом групп:

act(g1g2,x)=act(g1,act(g2,x))act(g_1g_2,x) = act(g_1, act(g_2,x))

act(1,x)=xact(1,x) = x

и их можно закодировать схематически.

Благодаря этому мы можем определить действие группового объекта GG в CC на объект XX из CC как морфизм

act:G×X→Xact: G\times X\to X

удовлетворяющие условиям, что некоторые диаграммы (предоставленные читателю), кодирующие эти два правила, коммутируют.

Преимущество этого состоит в том, что не требуется, чтобы категория CC имела внутренние групповые объекты автоморфизмов для всех рассматриваемых объектов.

Например, только локально компактные топологические пространства имеют группы топологических автоморфизмов с хорошим поведением, и поэтому действия топологических пространств на топологических пространствах должны быть либо ограничены действиями на локально компактных пространствах, либо определены как выше.

В качестве другого примера, в категории проконечных групп, рассматриваемых как топологические группы, не все объекты имеют группы автоморфизмов, для которых естественная топология является проконечной. Таким образом, проконечные групповые действия на (основном топологическом пространстве) проконечной группы должны быть либо заданы в этой форме, либо ограничены действиями на проконечных группах, для которых группа автоморфизмов естественно проконечна.

Действия моноидного объекта

Предположим, у нас есть категория CC с бинарными произведениями и конечным объектом **. Существует альтернативный способ просмотра действий моноида в Set, так что мы можем говорить о действии объекта моноида MM в CC на объект XX из CC. 9A, в Set моноидному гомоморфизму

α:M→End(X)\alpha: M\to End(X)

соответствует функция

act:M×X→Xact: M\times X\to X

, который будет иметь различные свойства, кодирующие, что α\alpha был гомоморфизмом моноидов:

act(m1m2,x)=act(m1,act(m2,x))act(m_1m_2,x) = act(m_1, act(m_2,x))

act(1,x)=xact(1,x) = x

и их можно закодировать схематически.

Из-за этого мы можем определить действие моноидного объекта MM в CC на объект XX из CC как морфизм

act:M×X→Xact:M\times X\to X

удовлетворяющие условиям, что некоторые диаграммы (предоставленные читателю), кодирующие эти два правила, коммутируют.

Преимущество этого в том, что он не требует, чтобы категория CC имела внутренние моноидные объекты эндоморфизма для всех рассматриваемых объектов.

Действия множества

Действие множества на множество было определено выше; он состоит из функции act:X×Y→Yact: X\times Y\to Y. Это может быть эквивалентно представлено колчаном с YY в качестве вершины, с ребрами, помеченными элементами XX, и такой, что каждая вершина имеет с каждой меткой выходит ровно одна стрелка. (Это своего рода «конструкция Гротендика».) Это также то же самое, что и простой (непрерывный) детерминированный автомат, где YY — множество состояний, а XX — множество входов.

То, что действие является типом колчана, помеченного ребром, можно увидеть, явно задав функции проекции произведения, p1p_1 и p2p_2, X×YX\×Y. \quad}{\leftarrow}X\times Y\underoverset{\quad act \quad}{p_2}{\rightrightarrows}Y

Форма этой диаграммы соответствует форме ребра, помеченного колчаном:

Labels←labelEdges⇉ targetsourceVerticesLabels\overset{\quad label \quad}{\leftarrow}Edges\underoverset{\quad target \quad}{source}{\rightrightarrows}Вершины 9{*}_1, у)

Действие множества XX само по себе также называется бинарной операцией , а множество XX называется магмой .

Примеры

• Представление — это «линейное действие».

• В симплектической геометрии рассматриваются гамильтоновы действия.

• В топологии: топологическое G-пространство

  • действие круга

  • групповое действие на н-сфере

(…)

• объект действия

• действие , ∞-действие,

  • сопряженное действие, сопряженное действие

  • диагональное действие

  • переходное действие, свободное действие, обычное действие

  • правильное действие, правильное прерывистое действие

• сотрудничество

• представление, ∞-представление

• модуль

  , ∞-модуль

• монада действия

• ассоциированный пучок, ассоциированный ∞-пучок

• частное, частное стек, частное тип

• теория представлений, теория инвариантов

• эквивариантная гомотопическая теория

  • Структура модели Бореля

• биактион

Ссылки

Групповые действия

О групповых действиях, в основном в топологических пространствах, следовательно, в виде топологических G-пространств:

Историческое происхождение:

• Felix Klein, Vergleichende Betrachtungen über neuere geometrische Forschungen (1872) Mathematische Annalen, том 43, страницы 63–100 1893 (doi: 10.