Математика и гармония: Математические алгоритмы

            Изобилие математических алгоритмов особенно бросается в глаза: алгоритмы вычитания десятичных положительных дробей, умножение десятичных дробей (столбиком), деление десятичных дробей и т.д. и т.п.

Ещё раннее каждый школьник изучает алгоритмы сложения натуральных чисел, вычитания натуральных чисел, таблицу умножения.

Знание алгоритмов поможет избежать многих вычислительных ошибок. Остановимся на алгоритмах, изучаемых в пятом и шестом классах. Итак,

5 класс

Алгоритмы арифметических действий:

Алгоритм умножения числа на произведение (сочетательное свойство умножения)
Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.
Алгоритм вычитания суммы
Для того чтобы вычесть сумму из числа, можно вначале вычесть из этого числа первое слагаемое, а потом из полученной разности – второе слагаемое;
Алгоритм вычитания числа из суммы
Чтобы из суммы вычесть число, можно вычесть его из одного слагаемого, а к полученной разности прибавить второе слагаемое.
Алгоритм умножения числа на произведение (сочетательное свойство умножения)
Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.
Алгоритм умножения суммы на число (распределительное тельное свойство умножения относительно сложения)
Для того чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить получившиеся произведения.
Алгоритм умножения разности на число (распределительное тельное свойство умножения относительно вычитания)
Для того, чтобы умножить разность на число, можно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе.

Алгоритмы при решении уравнений:

Алгоритм нахождения неизвестного слагаемого
Чтобы найти неизвестное слагаемое, надо их суммы вычесть известное слагаемое.
Алгоритм нахождения неизвестного уменьшаемого
Чтобы найти неизвестное уменьшаемое, надо сложить вычитаемое и разность.
Алгоритм нахождения неизвестного вычитаемого
Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть и разность.
Алгоритм нахождения неизвестного множителя
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
Алгоритм нахождения неизвестного делимого
Чтобы найти неизвестное делимое, надо частное умножить на делитель.
Алгоритм нахождения неизвестного делителя
Чтобы найти неизвестный делитель, надо делимое разделить на частное.

Алгоритм решения задач с помощью уравнения
1. Прочитать внимательно условие задачи;
2. Записать кратко условие задачи, записав все величины (единицы их измерения) , названные в задаче, установив связи и зависимости между ними;
3.Выбрать неизвестное задачи;
4. Выразить остальные величины задачи, установить связи их с неизвестным задачи;
5. Составить уравнение задачи, обосновав его условием задачи;
6. Решить уравнение;
7. Сделать проверку;
8. Выписать ответ.
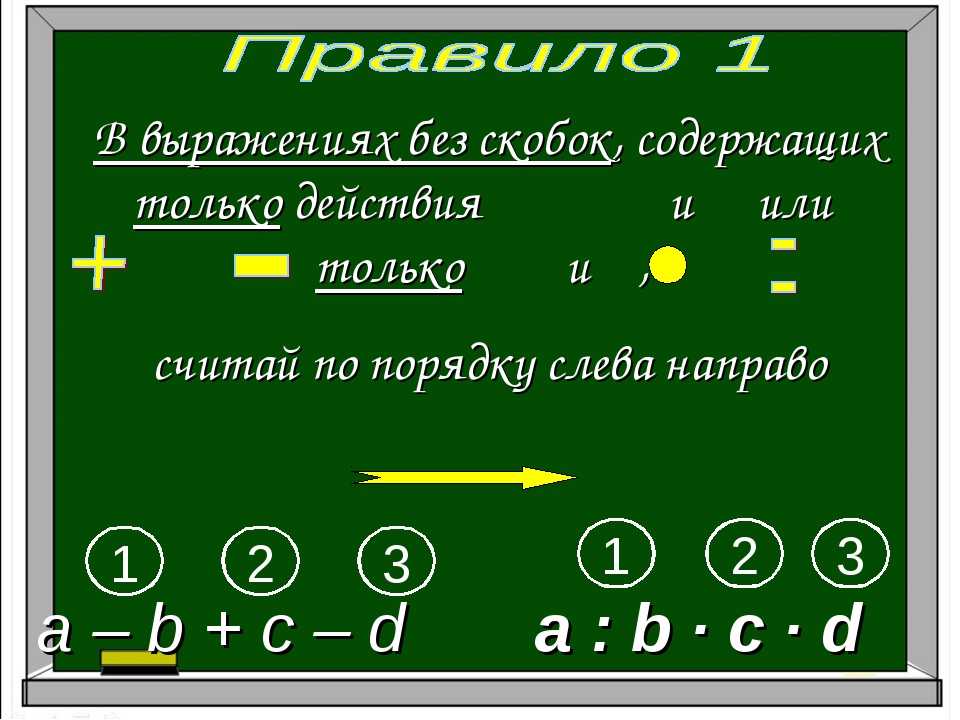
Алгоритм выполнения порядка действий
1. Если в выражении нет скобок, и оно содержит действия только одной ступени, то их выполняют по порядку слева направо.
2. Если выражение содержит действия первой (сложение и вычитание) и второй (умножение и деление) ступени и в нем нет скобок, то сначала выполняют действия второй ступени, а потом – действия первой ступени.
3. Если в выражении есть скобки, то сначала выполняют действия в скобках (учитывая при этом правила 1 и 2).

Алгоритмы для обыкновенных дробей
Алгоритм сравнения дробей с одинаковыми знаменателями
а) Выбрать наибольшую дробь с одинаковыми знаменателями ту, у которой больше числитель;
б) Выбрать наименьшую дробь с одинаковыми знаменателями ту, у которой меньше числитель.
Алгоритмы сложения и вычитания дробей с одинаковыми знаменателями
а) При сложении дробей с одинаковыми знаменателями числители складывают, а знаменатели оставляют тот же;
б) При вычитании дробей с одинаковыми знаменателями из числителя уменьшаемого вычитают числитель вычитаемого, а знаменатели оставляют тот же.
Алгоритмы представления смешанного числа в виде неправильной дроби
1. Умножить его целую часть на знаменатель дробной части;
2. К полученному произведению прибавить числитель дробной части;
3. Записать полученную сумму числителем дроби, а знаменатель дробной части оставить без изменения.

Алгоритмы для десятичных дробей
Алгоритм сложения (вычитания) десятичных дробей
Чтобы сложить (вычесть) десятичные дроби, нужно:
1. уравнять в этих дробях количество знаков после запятой;
2. записать их друг под другом так, чтобы запятая была записана под запятой;
3. выполнить сложение (вычитание), не обращая внимания на запятую;
4. поставить в ответе запятую под запятой в данных дробях.

Алгоритм округления десятичных дробей
а) Если первая отброшенная или замененная нулём цифра равна 5, 6,7, 8, 9, то стоящую перед ней цифру увеличивают на 1.
а) Если первая отброшенная или замененная нулём цифра равна 0, 1, 2, 3, 4, то стоящую перед ней цифру оставляют без изменения.
Алгоритм умножения десятичной дроби на натуральное число
Чтобы умножить десятичную дробь на натуральное число, надо:
1. умножить её на это число, не обращая внимания на запятую;
2. в полученном произведении отделить запятой столько цифр справа , сколько их отделено запятой в десятичной дроби.
Алгоритм умножения десятичной дроби на 10, 100, 1000, ….
Чтобы умножить десятичную дробь на 10, 100, 1000, … надо в этой дроби перенести запятую на столько цифр вправо, сколько нулей стоят в множителе после единицы.
Алгоритм деления десятичных дробей на натуральные числа
Чтобы разделить десятичную дробь на натуральное число, надо:
1. разделить дробь на это число, не обращая внимания на запятую;
2. поставить в частном запятую, когда кончится деление целой части.
Алгоритм деления десятичной дроби на 10, 100, 1000, ….
Чтобы разделить десятичную дробь на 10, 100, 1000, …надо перенести запятую в этой дроби на столько цифр влево, сколько нулей стоит после единицы в делителе.
Алгоритм умножения десятичных дробей
Чтобы перемножить две десятичные дроби, надо:
1. выполнить умножение, не обращая внимания на запятые;
2. отделить запятой столько цифр справа, сколько их стоит после запятой в обоих множителях вместе;
3. если в произведении получается меньше цифр, чем надо отделить запятой, то впереди пишут нуль или несколько нулей.
Алгоритм умножения числа на 0,1; 0,01, 0,001 …
Для того чтобы умножить число на 0,1; 0,01, 0,001 надо:
1. разделить его на 10,100, 1000;
2. перенести запятую на столько цифр, сколько нулей стоит перед единицей в множителе.
Алгоритм деления числа на десятичную дробь
Для того чтобы разделить число на десятичную дробь, надо:
1. В делимом и в делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе;
2. после этого выполнить деление на натуральное число.
Алгоритм деления числа на 0,1; 0,01, 0,001
Для того чтобы разделить десятичную дробь на 0,1; 0,01, 0,001…, надо:
перенести в ней запятую вправо на столько цифр, сколько в делителе стоит нулей перед единицей ( то есть умножить её на 10, 100, 1000.
Алгоритм нахождения среднего арифметического
Для нахождения среднего арифметического нескольких чисел надо:
1.найти сумму этих чисел;
2. разделить полученную сумму на число слагаемых;
3. выписать частное в ответ.
Алгоритм обращения десятичной дроби в проценты:
Чтобы обратить десятичную дробь в проценты надо умножить дробь на 100.
Алгоритм перевода процентов в десятичную дробь
Чтобы перевести проценты в десятичную дробь, надо разделить число процентов на 100.

6 класс

Признаки делимости

Признак делимости на 10
Если запись натурального числа оканчивается цифрой 0, то это число делится без остатка на 10.
Например:
100; 1000; 100000 и т.п.
Признак делимости на 5
Если запись натурального числа оканчивается цифрами 0 и 5, то это число делится без остатка на 5.
Например:
45; 55; 15; 10; 10000 и т.п.
Признак делимости на 2
Если запись натурального числа оканчивается четной цифрой, то это число четно и делится без остатка на 2.
Например:
32; 12; 224; 2098 и т. п.
Признак делимости на 3
Если сумма цифр числа делится на 3, то и число делится на 3.
Например:
15; 273; 474; 765; и т.п.
Признак делимости на 9
Если сумма цифр числа делится на 9, то и число делится на 9.
783; 549; 1233; 27954; и т.п.

Разложение на простые множители
Алгоритм нахождения НОД (наибольшего общего делителя)
Чтобы найти наибольший общий делитель нескольких натуральных чисел, надо:
1. разложить их на простые множители;
2. из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел;
3. найти произведение оставшихся множителей.
Например:
48 = 2*2*2*2*3; 36 = 2*2*3*3; НОД(48;36)= 2*2*3 = 12.

Алгоритм нахождения НОК (наименьшего общего кратного)
Чтобы найти наименьшее общее кратное нескольких натуральных чисел, надо:
1. разложить их на простые множители;
2. выписать множители, входящие в разложение одного из чисел;
3. добавить к ним недостающие множители из разложений остальных чисел;
4. найти произведение оставшихся множителей.
Например:
48 = 2*2*2*2*3; 36 = 2*2*3*3; НОК(48;36)= 2*2*2*2*3*3 = 144.

Алгоритмы для обыкновенных дробей
Алгоритм сокращения дробей
Для того чтобы сократить дробь необходимо и числитель и знаменатель дроби разделить на их общий делитель, отличный от 1.

Алгоритм приведения дробей к общему знаменателю
Чтобы привести дроби к наименьшему общему знаменателю надо:
1. Найти наименьшее общее кратное знаменателей этих дробей, оно и будет их наименьшим общим знаменателем;
2. разделить наименьший общий множитель на знаменатели данных дробей, т.е. найти для каждой дроби дополнительный множитель;
3. умножить числитель и знаменатель каждой дроби на её дополнительный множитель;

Алгоритм сравнения, сложения, вычитания
дробей с разными знаменателями
Чтобы сравнить (сложить, вычесть) дроби с разными знаменателями надо:
1. привести данные дроби к наименьшему общему знаменателю;
2. сравнить, сложить, вычесть полученные дроби.

Алгоритм сложения смешанных чисел
Чтобы сложить смешанные числа надо:
1. привести дробные части этих чисел к наименьшему общему знаменателю;
2. отдельно выполнить сложение целых частей и отдельно дробных частей. Если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить её к полученной целой части.

Алгоритм вычитания смешанных чисел
Чтобы вычесть смешанные числа надо:
1. привести дробные части этих чисел к наименьшему общему знаменателю; если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить её в неправильную дробь, уменьшив на единицу целую часть;
2. отдельно выполнить вычитание целых частей и отдельно дробных частей.

Алгоритм умножения дроби на натуральное число
Чтобы умножить дробь на натуральное число , надо её числитель умножить на это число, а знаменатель оставить без изменения.

Алгоритм умножения дроби на дробь
Чтобы умножить дробь на дробь надо:
1. найти произведение числителей и произведение знаменателей этих дробей;
2. первое произведение записать числителем, а второе – знаменателем.

Алгоритм умножения смешанных чисел
Чтобы умножить смешанные числа надо:
1.их записать в виде неправильных дробей;
2.воспользоваться правилом умножения дробей.

Алгоритм нахождения дроби от числа
Чтобы найти дробь от числа, надо умножить число на эту дробь.

Алгоритм умножения смешанного числа на натуральное число
(применение распределительного свойства умножения)
Чтобы умножить смешанное число на натуральное число надо:
1. умножить целую часть на натуральное число;
2. умножить дробную часть на это натуральное число;
3. сложить полученные результаты.

Алгоритм деления обыкновенных дробей
Чтобы разделить одну дробь на другую надо:
1. делитель представить в виде обратной дроби;
2. провести умножение делимого и преобразованного делителя.

Алгоритм нахождения числа по его дроби
Чтобы найти число по данному значению его дроби, надо это значение разделить на дробь.
Арифметические действия с положительными и отрицательными числами
Алгоритм сложения отрицательных чисел
Чтобы сложить два отрицательных числа, надо:
1. сложить их модули;
2. поставить перед полученным числом знак « — ».
Например: — 8,7 + (- 3.5) = — (8,7 +3.5) = — 12,2.

Алгоритм сложения чисел с разными знаками
Чтобы сложить два числа с разными знаками, надо:
1. из большего модуля слагаемых вычесть меньший;
2. поставить перед полученным числом знак того слагаемого , модуль которого больше.
Например: 6,1 + (- 4,2) = + (6,1 — 4,2) = 1,9.

Алгоритм нахождения длины отрезка на координатной прямой
Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату его левого конца.

Алгоритм умножения чисел с разными знаками
Чтобы перемножить два числа с разными знаками, надо:
1.перемножить модули этих чисел;
2. поставить перед полученным числом знак « — ».
Например: (-1,2) * 0,3 = — (1,2 * 0,3) = — 0,36.

Алгоритм умножения отрицательных чисел
Чтобы перемножить два числа с отрицательными знаками, надо перемножить их модули.
Например: (-3,2) * (-9) =  3,2 * 9 = 28,8.

Алгоритм деления отрицательного числа на отрицательное
Чтобы разделить отрицательное число на отрицательное, надо разделить модуль делимого на модуль делителя.
Например: — 4,5 : (-1,5) = 4,5 : 1,5 = 3.

Алгоритм деления чисел с разными знаками
При делении чисел с разными знаками, надо:
1. разделить модуль делимого на модуль делителя;
2. поставить перед полученным числом знак « — ».
Например: 3,6 : (-3) = — (3,6 : 3) = — 1,2.

Алгоритмы раскрытия скобок
а) Если перед скобками стоит знак «+», то можно опустить скобки и этот знак «+», сохранив знаки слагаемых, стоящих в скобках. Если первое слагаемое в скобках записано без знака, то его надо записать со знаком «+».
Например: — 2,87 + (2,87 – 7,639) = — 2,87 + 2,87 – 7,639 = 0 -7,639 = -7,639.
б). Если перед скобками стоит знак « — », то надо заменить этот знак на « + »,
поменяв знаки всех слагаемых в скобках на противоположные, а потом раскрыть скобки.
Например: 16 – (10 – 18 + 12) = 16 + ( — 10 + 18 – 12) = 16 — 10 + 18 — 12 = 12.

Электронный справочник по математике для школьников арифметика арифметические действия

Справочник по математике

Арифметика

Арифметика целых чисел

Содержание

Арифметика. Арифметические действия

Обратные арифметические действия

Свойства арифметических действий

Порядок выполнения арифметических действий

Умножение натуральных чисел на 10, 100, 1000; и т. д.

Арифметика. Арифметические действия

Арифметическим действием называют операцию, удовлетворяющую ряду свойств и позволяющую по нескольким данным числам найти новое число.

Арифметикой называют науку, изучающую простейшие свойства чисел и арифметических действий.

Существуют шесть арифметических действий: сложение, вычитание, умножение, деление, возведение в степень, извлечение корня.

Обратные арифметические действия

Вычитание – это арифметическое действие, обратное к сложению, деление – действие, обратное к умножению, извлечение корня – действие, обратное к возведению в степень.

Например,

Свойства арифметических действий

	a + b = b + a ,
	(a + b) + c = a + (b + c)
	a + 0 = 0 + a = a
	a + ( – a ) = 0
	На 0 делить нельзя.

Порядок выполнения арифметических действий

Сложение и вычитание называют действиями первой ступени, умножение и деление – действиями второй ступени, возведение в степень и извлечение корня – действиями третьей ступени.

Действия одной ступени выполняются в том же порядке, в каком они записаны в формуле.

Если в формуле содержатся действия разных ступеней, то сначала выполняют действия высших ступеней, а затем низших ступеней.

Если формула содержит скобки, то сначала выполняют действия в скобках. Скобки бывают круглыми, квадратными и фигурными, причем между ними нет никакой разницы.

Если скобки содержат другие скобки, то сначала выполняют действия во «внутренних» скобках.

Умножение натуральных чисел на 10, 100, 1000 и т.д.

Для того, чтобы умножить натуральное число на 10 ,  100 ,  1000 &nbsp и т.д., нужно справа приписать к нему столько нулей, сколько содержится в числе 10 ,  100 ,  1000 &nbsp и т.д. соответственно.

Действительно, например, число 3610 состоит из трёх тысяч, шести сотен и одного десятка, поэтому

что и требовалось показать.

Порядок операций

Порядок операций

(6+4) 7 3 знак равно

 

Порядок выполнения работ

Когда дети сначала изучают сложение, вычитание, умножение и деление, они начинают с выполнения операций над двумя числами. Но что происходит, когда выражение требует нескольких операций? Со временем математики разработал набор правил, называемый порядком операций, чтобы определить, какую операцию выполнять первой. Правила таковы:

1. Умножать и делить слева направо.
2. Сложение и вычитание слева направо.

При упрощении выражения, такого как
12 4 + 5 3 6, вы должны сначала вычислить 12 4 так как порядок действий требует от вас начинать с левой стороны выражения и выполнять умножение или деление (в зависимости от того, что наступит раньше) перед сложением или вычитанием. После 12 4 вычисляется, вы продолжаете двигаться слева направо при поиске для умножения или деления.

Таким образом, чистый шаг состоит в том, чтобы вычислить 5 3. Теперь, когда все умножение и деление завершены, вы должны продолжить сложение или вычитание (в зависимости от того, что наступит раньше) слева направо. Шаги показаны ниже.

12 4 + 5 3 6
3 + 5 3 6 (с 12 4 = 3)
3 + 15 6 (начиная с 5 3 = 15)
18 6 (поскольку 3 + 15 = 18)
12 (поскольку 18 6 = 12)

Символы группировки, такие как круглые скобки ( ), квадратные скобки [ ] или фигурные скобки { }, позволяют определить порядок выполнения определенных операций. Посмотрите на это выражение:

6 + 4 7 3
6 + 28 3 (так как 4 7 = 28)
34 3 (поскольку 6 + 28 = 34)
31 (поскольку 34 3 = 31)

Что произойдет, если вставить в выражение круглые скобки? Скобки позволяют определить, какая операция выполняется первой. Порядок операций гласит, что операции внутри круглых скобок выполняются до операций вне скобок. скобки. Что произойдет, если мы поместим круглые скобки вокруг 6 + 4?

(6 + 4) 7 3
10 7 3 (6 + 4 = 10, что делается первым, потому что оно заключено в скобки)
70 3 (возобновляется нормальный порядок работы, и 10 7 = 70)
67 (поскольку 70 3 = 67)

Обратите внимание, что ответ значительно отличается от предыдущего. Что, если мы поместим скобки вокруг 7 3?
6 + 4 (7 3)
6 + 4 4 (На этот раз 7 3 в скобках, так что мы делаем это в первую очередь.)
6 + 16 (Поскольку круглых скобок не осталось, мы выполняем умножение перед сложением.)
22 (поскольку 6 + 16 = 22)

Этот набор скобок дает еще один ответ. Итак, когда задействованы круглые скобки, правила порядка операций таковы:

1. Действия в скобках.
2. Умножать и делить слева направо.
3. Сложение и вычитание слева направо.

 

1.3 Порядок действий (обзор) — Алгебра среднего уровня

Глава 1: Обзор алгебры

При упрощении выражений важно делать это в правильном порядке. Рассмотрим задачу 2 + 5 ⋅ 3, решенную двумя разными способами:

.

Метод 1: добавить первый	Метод 2: сначала умножить
Добавить: 2 + 5 ⋅ 3	Умножить: 2 + 5 ⋅ 3
Умножить: 7 ⋅ 3	Добавить: 2 + 15
Решение: 21	Решение: 17

Предыдущий пример показывает, что если одну и ту же задачу решить двумя разными способами, она приведет к двум разным решениям. Однако только один метод может быть правильным. Получается, что второй способ правильный. Порядок операций заканчивается самой простой операцией — сложением (или вычитанием). Прежде чем сложение будет завершено, выполните все повторные сложения, также известные как умножение (или деление). Прежде чем умножение будет завершено, выполните все повторные умножения, также известные как показатели степени. Когда что-то должно быть сделано не по порядку, чтобы это было на первом месте, заключайте это в скобки (или объединяйте символы). Таким образом, этот список представляет собой порядок операций, используемых для упрощения выражений.

1-й Скобки (группировка)

2-й Экспоненты

3-й Умножение и деление (слева направо)

4-й Сложение и вычитание (слева направо)

Умножение и деление находятся на одном уровне, потому что это одна и та же операция (деление — это просто умножение на обратное). Это означает, что умножение и деление должны выполняться слева направо.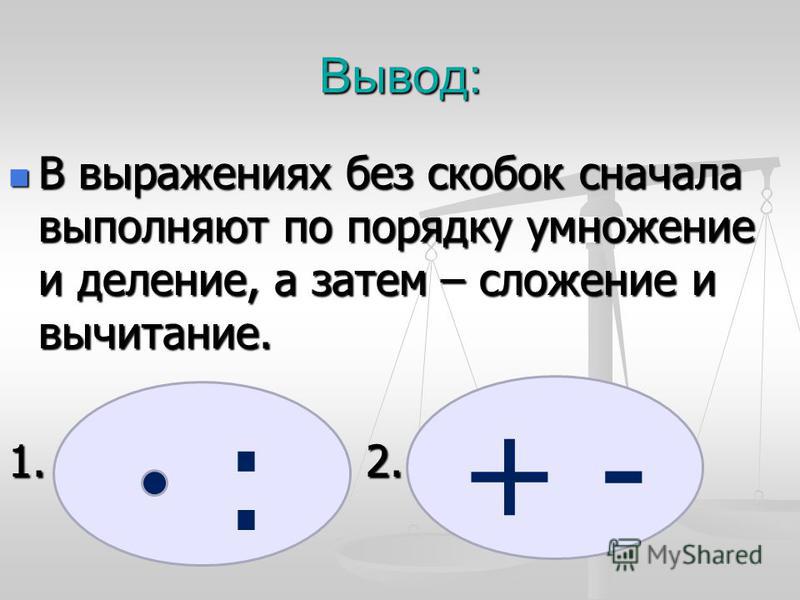 Поэтому в одних задачах на первом месте стоит деление, а в других — умножение. То же самое верно для сложения и вычитания (вычитание — это просто сложение противоположного).

Часто учащиеся используют слово BEMDAS, чтобы запомнить порядок операций, поскольку первая буква каждой операции образует слово (записывается как B E MD AS). Помните BEMDAS, чтобы гарантировать, что умножение и деление выполняются слева направо (то же самое со сложением и вычитанием).

Оцените, используя порядок операций.

   

Очень важно не забывать умножать и делить слева направо!

Оцените, используя порядок операций.

   

Если в задаче несколько наборов скобок, начните с самого внутреннего набора и двигайтесь наружу. Внутри каждого набора скобок упростите порядок операций. Чтобы было легче узнать, какая левая скобка соответствует какой правой скобке, будут использоваться различные типы символов группировки, такие как фигурные скобки { }, квадратные скобки [ ] и круглые скобки ( ).

Все они делают одно и то же: они группируют символы и должны быть оценены в первую очередь.

Оцените, используя порядок операций.

Как показано в примере 1.3.3, для решения проблемы может потребоваться несколько шагов. Ключ к успешному решению проблем с порядком операций — найти время, чтобы показать свою работу и выполнять по одному шагу за раз. Это снизит вероятность ошибиться в пути.

Существует несколько типов символов группировки, которые можно использовать помимо круглых и фигурных скобок. Одним из таких символов является полоса дроби. Весь числитель и весь знаменатель дроби должны быть вычислены перед сокращением. Сократив дробь, можно одновременно упростить числитель и знаменатель.

Оцените, используя порядок операций.

Другим типом группирующего символа является абсолютное значение. Все, что находится внутри набора скобок абсолютного значения, должно оцениваться, как если бы это был обычный набор скобок. Затем, как только внутренняя часть завершена, возьмите абсолютное значение — или расстояние от нуля — чтобы сделать число положительным.