Что сначала делается умножение или деление: Порядок выполнения действий в математике: правила, примеры

Содержание

Порядок выполнения действий в математике: правила, примеры

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Арифметика Порядок действий в математике

В данной публикации мы рассмотрим правила в математике касательно порядка выполнения арифметических действий (в том числе в выражениях со скобками, возведением в степень или извлечением корня), сопроводив их примерами для лучшего понимания материала.

Порядок выполнения действий
- Общее правило
- Примеры со скобками
- Возведение в степень/извлечение корня

Отметим сразу, что действия рассматриваются от начала примера к его концу, т.е. слева направо.

Общее правило

сначала выполняются умножение и деление, а затем сложение и вычитание полученных промежуточных значений.

Давайте подробно рассмотрим пример: 2 ⋅ 4 + 12 : 3.

Над каждым действием мы написали число, которое соответствует порядку его выполнения, т. е. решение примера состоит из трех промежуточных действий:

2 ⋅ 4 = 8
12 : 3 = 4
8 + 4 = 12

Немного потренировавшись в дальнейшем можно все действия выполнять цепочкой (в одну/несколько строк), продолжая исходное выражение. В нашем случае получается:

2 ⋅ 4 + 12 : 3 = 8 + 4 = 12.

Если подряд идут несколько действий умножения и деления, то они также выполняются подряд, и их можно объединить при желании.

Решение:

5 ⋅ 6 : 3 = 10 (совместное выполнение действий 1 и 2)
18 : 9 = 2
7 + 10 = 17
17 – 2 = 15

Цепочка примера:

7 + 5 ⋅ 6 : 3 – 18 : 9 = 7 + 10 – 2 = 15.

Примеры со скобками

Действия в скобках (если они есть) выполняются в первую очередь. А внутри них действует все тот же принятый порядок, описанный выше.

Решение можно разбить на действия ниже:

7 ⋅ 4 = 28
28 – 16 = 12
15 : 3 = 5
9 : 3 = 3
5 + 12 = 17
17 – 3 = 14

При расстановке действий выражение в скобках можно условно воспринимать как одно целое/число.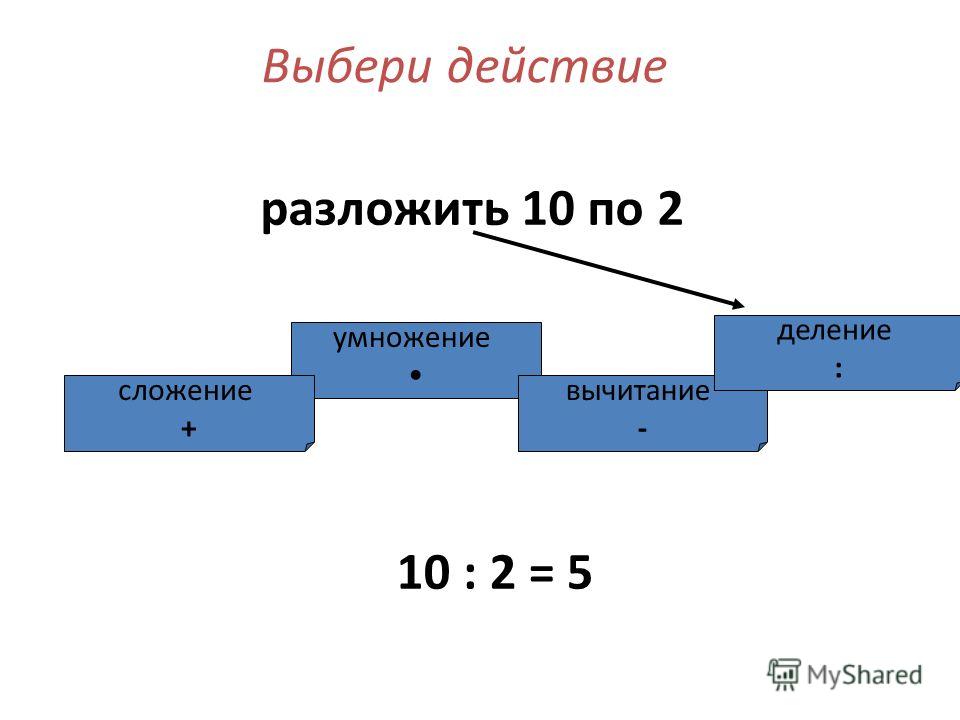 Для удобства мы выделили его в цепочке ниже зеленым цветом:

15 : 3 + (7 ⋅ 4 – 16) – 9 : 3 = 5 + (28 – 16) – 3 = 5 + 12 – 3 = 14.

Скобки в скобках

Иногда в скобках могут быть еще одни скобки (называются вложенными). В таких случаях сперва выполняются действия во внутренних скобках.

Раскладка примера в цепочку выглядит так:

11 ⋅ 4 + (10 : 5 + (16 : 2 – 12 : 4)) = 44 + (2 + (8 – 3)) = 44 + (2 + 5) = 51.

Возведение в степень/извлечение корня

Данные действия выполняется в самую первую очередь, т.е. даже до умножения и деления. При этом если они касаются выражения в скобках, то сначала производятся вычисления внутри них. Рассмотрим пример:

Порядок действий:

19 – 12 = 7
7² = 49
6² = 36
4 ⋅ 5 = 20
36 + 49 = 85
85 + 20 = 105

Цепочка примера:

6² + (19 – 12)² + 4 ⋅ 5 = 36 + 49 + 20 = 105.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

§ Порядок действий в решении примеров по математике

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

Скрыть меню

На главную страницу

Войти при помощи

Темы уроков

Начальная школа

Геометрия: начальная школа
Действия в столбик
Деление с остатком
Законы арифметики
Периметр
Порядок действий
Разряды и классы. Разрядные слагаемые
Счет в пределах 10 и 20

Математика 5 класс

Взаимно обратные числа и дроби
Десятичные дроби
Натуральные числа
Нахождение НОД и НОК
Обыкновенные дроби
Округление чисел
Перевод обыкновенной дроби в десятичную
Площадь
Проценты
Свойства сложения, вычитания, умножения и деления
Среднее арифметическое
Упрощение выражений
Уравнения 5 класс
Числовые и буквенные выражения

Математика 6 класс

Масштаб
Модуль числа
Окружность. Площадь круга
Отношение чисел
Отрицательные и положительные числа
Периодическая дробь
Признаки делимости
Пропорции
Рациональные числа
Система координат
Целые числа

Алгебра 7 класс

Алгебраические дроби
Как применять формулы сокращённого умножения
Многочлены
Одночлены
Системы уравнений
Степени
Уравнения
Формулы сокращённого умножения
Функция в математике

Геометрия 7 класс

Точка, прямая и отрезок
Что такое аксиома и теорема

Алгебра 8 класс

Квадратичная функция. Парабола
Квадратные неравенства
Квадратные уравнения
Квадратный корень
Неравенства
Системы неравенств
Стандартный вид числа
Теорема Виета

Алгебра 9 класс

Возрастание и убывание функции
Нули функции
Область определения функции
Отрицательная степень
Среднее
геометрическое

Алгебра 10 класс

Иррациональные числа

Алгебра 11 класс

Факториал

Это место оставлено для самой лучшей фразы. Администратор

на главную

Введите тему

Русский язык Поддержать сайт

При расчётах примеров нужно соблюдать определённый порядок действий. С помощью правил ниже, мы разберёмся в каком порядке выполняются действия и для чего нужны скобки.

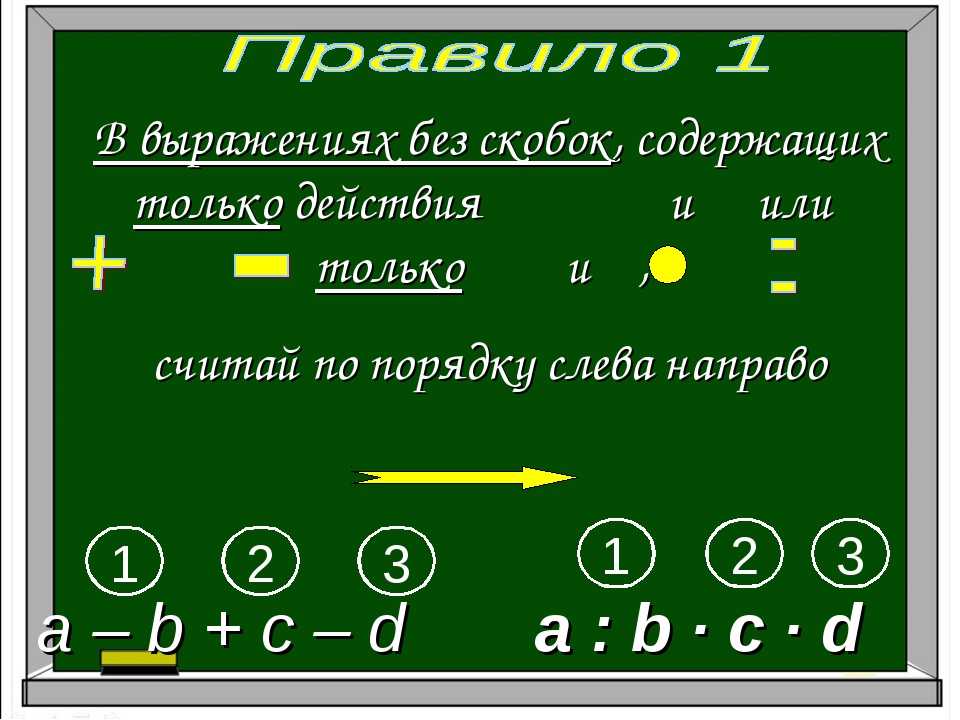
Если в выражении скобок нет, то:

сначала выполняем слева направо все действия умножения и деления;

а потом слева направо все действия сложения и вычитания.

Рассмотрим порядок действий в следующем примере.

Напоминаем вам, что порядок действий в математике расставляется слева направо (от начала к концу примера).

При вычислении значения выражения можно вести запись двумя способами.

Первый способ

Каждое действие записывается отдельно со своим номером под примером.
После выполнения последнего действия ответ обязательно записывается в исходный пример.

Запомните!

При расчёте результатов действий с двузначными и/или трёхзначными числами обязательно приводите свои расчёты в столбик.

Второй способ

Второй способ называется запись «цепочкой». Все вычисления проводятся в точно таком же порядке действий, но результаты записываются сразу после знака равно.

Запомните!

Если выражение содержит скобки, то сначала выполняют действия в скобках.

Внутри самих скобок действует правило порядка действий как в выражениях без скобок.

Если внутри скобок находятся ещё одни скобки, то сначала выполняются действия внутри вложенных (внутренних) скобок.

Порядок действий и возведение в степень

Если в примере содержится числовое или буквенное выражение в скобках, которое надо возвести в степень, то:

Сначала выполняем все действия внутри скобок
Затем возводим в степень все скобки и числа, стоящие в степени, слева направо (от начала к концу примера).
Выполняем оставшиеся действия в обычном порядке

ПОРЯДОК ДЕЙСТВИЙ

Как посчитать 2 + 3 х 7? Ответ 35 или ответ 23? Чтобы знать правильный ответ, нужно знать правильный порядок действий в отношении сложения, вычитания, умножения, деления и т. д.

Правило 20:: Умножение и деление должны быть завершены до сложение и вычитание.
2 + 3 х 7 = 2 + 21 = 23 — правильный ответ на поставленный выше вопрос.

Как вычислить (2 + 3) x (7 — 3)? ответ 32, 20 или ответ 14? Чтобы знать правильный ответ, нужно знать правильный порядок операций сложения, вычитания, умножения, деления и скобок.

Правило 21:: Выражения в скобках рассматриваются как одно число и должен быть рассчитан в первую очередь.
(2 + 3) х (7 — 3) = 5 х 4 = 20 — правильный ответ на вопрос выше. проблема

Как бы вы вычислили [3 + 7 — (2 + 3 x 6) +2 x 5 -7 +1]?

Правило 22:

Если скобки заключены в другие скобки, работайте изнутри наружу.

В выражении выражение (2 + 3 x 6) является самой внутренней скобкой и должно быть вычислено первым. 2 + 3 х 6 = 2 + 18 = 20.

Теперь выражение изменено на . Следующая скобка, которую нужно вычислить, это 7 — 20 + 2 x 5 = 7 – 20 + 10 = — 13 + 10 = — 3.

Теперь выражение сокращается до [3 + {-3} — 7 + 1] = 0 — 7 + 1 = — 6.

Как бы вы рассчитали.

Правило 23:: В скобках указано упростить выражение в круглых скобках, прежде чем продолжить. Отдел символ играет ту же роль, что и скобка. Он предписывает вам рассматривать количество над числителем, как если бы оно было заключено в скобки, и рассматривать количество под числителем, как если бы оно были заключены в еще одну скобку.
Когда вы закончите это задача, у вас есть то, что кажется двумя дробями, которые вы добавляете. Не так! может быть написано и умножение должно быть завершено перед сложением в каждом скобка..
= Оба скобки были упрощены. Теперь выполните умножение на урожай . Последнее, что нужно делать это дополнение.

Если вы хотите больше примеров и задач для работы, нажмите на соответствующее слово.

: Правило 20
: Правило 21
: Правило 22
: Правило 23

Меню Назад к простым дробям [Удостоверение личности] [Факторизация целых чисел] [Сокращение дробей] [Умножение] [Разделение] [Строительные фракции] [Добавление] [Вычитание] [Порядок работы] Домашняя страница S.O.

S MATHematics

Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard.

Автор: Нэнси Маркус

Порядок действий — Бесплатная помощь по математике

Введение

Порядок операций — очень простая концепция, необходимая для правильного понимания математики. В отличие от чтения, где мы всегда работаем слева направо, иногда с математикой нам нужно решить одну часть задачи перед другой, иначе окончательный ответ может быть неверным! Мы используем термин «порядок операций», чтобы описать, над какой частью проблемы нужно работать в первую очередь. Возьмем это уравнение в качестве примера:

$$ 4+6 \дел 2 * 11 = ? $$

Если бы вы просто решали слева направо, ответ был бы неверным. Давайте сделаем это сейчас: 4 + 6 = 10. Разделите это на 2, чтобы получить 5. Умножьте 5 на 11, чтобы получить 55. К сожалению, хотя это казалось правильным, этот ответ неверен.

Правильный порядок действий

Порядок действий позволит вам правильно решить эту задачу. Порядок такой: Скобки , Экспоненты , Умножение и Деление и, наконец, Сложение и вычитание . Всегда сначала выполняйте операции внутри круглых скобок, а затем выполняйте операции с показателями степени. После этого выполните все умножение и деление слева направо, и, наконец, выполните все сложение и вычитание слева направо.

Популярным способом запоминания заказа является аббревиатура PEMDAS. Скобки, экспоненты, умножение и деление, сложение и вычитание. Вы также можете создать небольшую фразу, например «

P аренда ».E xcuse M y D ear A unt S ally.» Что бы вы ни выбрали, убедитесь, что вы очень хорошо знаете все шесть шагов порядка операций.

РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7