Умножение и деление на 10, 100, 1000
В концентре 1000 были рассмотрены случаи умножения на 10 и 100. Это же правило распространяется и на умножение, и на деление многозначных чисел на 10 и 100.
Однако первоначально следует повторить с учащимися те случаи умножения 1000 на однозначное число, которые они рассматривали еще при изучении нумерации:
1000×2=1000+1000=2000
или
1 тыс.х2=2 тыс.=2000 1000×5=1 тыс. х 5=5 тыс.=5000
Рассматривается еще несколько случаев умножения 1000 на числа. После этого учащиеся, сравнивая произведение, множители, смогут самостоятельно сделать вывод:
Если один множитель — число 1000, то в произведении ко второму множителю надо приписать три нуля. 234
Используя знание переместительного закона умножения, учащиеся смогут решить примеры вида 3×1000.
Деление на 1000, так же как и
деление на 10, 100, как пока-м.шает
опыт, лучше усваивается как деление по
содержанию.
Рассматривается еще несколько аналогичных примеров. В ре-‘ультате учащиеся делают вывод по аналогии с делением на 10 и
100.
Если делитель равен тысяче, то в делимом надо отбросить три нуля и полученное число записать в частное.
Примеры на деление на 10, 100, 1000 записывается в строчку (42 000:1000=42) и решаются устно. Решаются примеры на деление как без остатка, так и с остатком: 80: 10=8 800: 100=8 8000: 1000=8
85: 10=8 (ост. 5)
807: 100=8 (ост. 7)
8507: 1000=8 (ост. 507)
870: 100=8 (ост. 70)
Учитель
постоянно должен напоминать учащимся,
что остаток должен
быть меньше делителя.
Действие деления
как без остатка, так
и с остатком учащиеся должны учиться
проверять. Например:
3800:100=38.
Проверка. 38х 100=3800. 7518:1000=7 (ост. 518). Проверка. 7×1000+518=7518.
Познакомившись с умножением и делением на единицу с нулями, учащиеся с трудом дифференцируют правила умножения и деления на 10, 100, 1000, смешивают эти правила, не могут вспомнить, когда нужно нули приписывать, а когда их отбрасывать. Это происходит особенно часто при умножении в случае, когда в первом множителе есть нули. Например: 3800×10. В произведении ученик может написать число 380. При делении
235
3856:10 в частное ученик переписывает делимое и нуль сщ т. е. получает 38 560.
Такие ошибки возникают, как правило, при самостоятельно»! выполнении действий, когда некому наводящим вопросом актуали» зировать вовремя имеющиеся знания, направить внимание учени« ка на анализ выполняемой операции с числами.
Предупреждению
возможных ошибок и лучшей дифференциации
действий умножения и деления на 10, 100,
1000 служит чередование
примеров на умножение и деление, их
сопоставление,
сравнение ответов (при умножении число
увеличивается, при делении
уменьшается), способов выполнения
действий, а также решение
сложных примеров, в которых имеются оба
действия: 4700:100×1000.
Умножение и деление на разрядные числа (десятки, сотни, тысячи)
Умножение на разрядные числа. Подготовительным упражнением к умножению на разрядные числа является повторение табличного умножения, умножения на однозначное число, а также на 10, 100, 1000. Следует вспомнить, как круглое число представить в виде произведения двух чисел (например, 20=2-10, 500=5-100, 6000=6-1000), повторить уже известные учащимся случаи умножения на круглые числа (например, 24 12-20= 12-(2-10)=(12-2)-10=24-10=240), вспомнить 30 правило: чтобы умножить число на круглые десятки, 720 нужно умножить это число на число десятков и к полученному произведению приписать нуль, т. е. умножить его на 10.
Это
правило учащиеся применяют и при
умножении больших чисел
в пределах 10 000, 100 000 и 1 000 000. Аналогично
учащиеся знакомятся
с умножением двузначных, трех- и
четырехзначных чисел
на круглые сотни: 25 — 300=25 — 3 • 100=75 •
100=7500.
На умножение на круглые тысячи распространяется уже известное учащимся правило умножения числа на круглые десятки и сотни.
Сначала рассматривается устно решение примеров вида: 7×5000. Можно 5000 записать как произведение 5-1000. 7 — (5 — 1000Ы7 • 5) -1000=35 -1000=35 000.
Деление на разрядные числа. Учащиеся уже знакомы с делением на круглые десятки и сотни. При изучении действий в 236
пределах 1000 они опираются на этот знакомый материал. Поэтому необходимо повторить табличное деление, деление на 10, 100, 1000 и, так же как в умножении, вспомнить, как представить круглые числа в виде произведения двух чисел (30=3-10, 100=3-100, 3000=3-1000), повторить устные и письменные случаи деления.
400:20=400:10:2=40:2=20
Деление на круглые сотни, а затем и тысячи можно показать ма устных случаях деления, основываясь на приеме последовательного деления:
2500:500=2500:100:5=25:5=5;
250 000:5000=250 000:1000:5=250:5=50.
Затем вводится деление на круглые десятки, сотни и тысячи с остатком. Например: 670:40. В частном будет двузначное число. В частном берем по 1, умножаем 1 на 40. Вычитаем 67—40=27. 270 делим на 40. Сначала делим 270 и 40 на 10. Затем делим неполное делимое и делитель: 27:4. Берем по 6. Умножаем 6 на 40, получаем 240. Вычитаем. Остаток 30 (меньше 40), частное 16.
9210
670
3(57″
Т6~
Наряду с общими случаями учащиеся разбирают решение особых случаев, когда в частном получаются нули:
825000 «6000 | 3000 •275″ |
22500 «21000 | |
15000 «15000 |
Найдите значение выражения (действия с дробями) – как решать
Формулировка задачи: Найдите значение выражения (действия с дробями).
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 1 (Действия с дробями).
Рассмотрим, как решаются подобные задачи на примерах.
Пример задачи 1:
Найдите значение выражения 5/4 + 7/6 : 2/3.
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. И выполним необходимые действия в нужном порядке:
Ответ: 3
Пример задачи 2:
Найдите значение выражения (3,9 – 2,4) ∙ 8,2
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. При этом действия в скобках выполняются раньше, чем действия за скобками. И выполним необходимые действия в нужном порядке:
Ответ: 12,3
Пример задачи 3:
Найдите значение выражения 27 ∙ (1/3 – 4/9 – 5/27).
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. При этом действия в скобках выполняются раньше, чем действия за скобками. И выполним необходимые действия в нужном порядке:
Ответ: –8
Пример задачи 4:
Найдите значение выражения 2,7 / (1,4 + 0,1)
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. При этом действия в скобках выполняются раньше, чем действия за скобками. И выполним необходимые действия в нужном порядке:
Ответ: 1,8
Пример задачи 5:
Найдите значение выражения 1 / (1/9 – 1/12).
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. При этом действия в скобках выполняются раньше, чем действия за скобками.
2) : 754.
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. При этом действия в скобках выполняются раньше, чем действия за скобками. И выполним необходимые действия в нужном порядке. Также в данном случае нужно применить формулу разности квадратов:
Ответ: 702
Проблемы с PEMDAS (и решение)
Если вы находитесь на Facebook, вы, вероятно, видели один из множества графиков, подобных приведенному выше.
Идея состоит в том, чтобы решить проблему, а затем опубликовать свой ответ. Из того, что я наблюдал, около половины респондентов дают правильный ответ, а другая половина приходит к неправильному ответу. Корень этой проблемы? Порядок операций.
В отличие от чтения на английском, арифметические действия не выполняются слева направо. Существует определенный порядок, в котором должны выполняться сложение, вычитание, умножение и деление (не говоря уже о скобках и показателях степени).
И для большинства из нас, старожилов, этот порядок представлен аббревиатурой PEMDAS (или ее вариациями).
P – круглые скобки
E – степени
M – умножение
D – деление
A – сложение
S – вычитание
Я выучил мнемонику «Пожалуйста, извините, моя дорогая тетя Салли», чтобы помочь мне запомнить порядок операций.
Идея проста: чтобы решить арифметическую задачу (или упростить алгебраическое выражение), вы сначала обращаетесь к любым операциям внутри скобок (или квадратных скобок). Затем показатели степени, затем умножение и/или деление и, наконец, сложение и/или вычитание.
Но с этим процессом действительно много проблем. Во-первых, поскольку умножение и деление обратны (они уничтожают друг друга), совершенно законно делить перед умножением. То же самое касается сложения и вычитания. Это означает, что PEMDAS, PEDMSA и PEMDSA также являются приемлемыми аббревиатурами. (Теперь уже не так черно-бело, а?)
Во-вторых, бывают случаи, когда круглые скобки подразумеваются.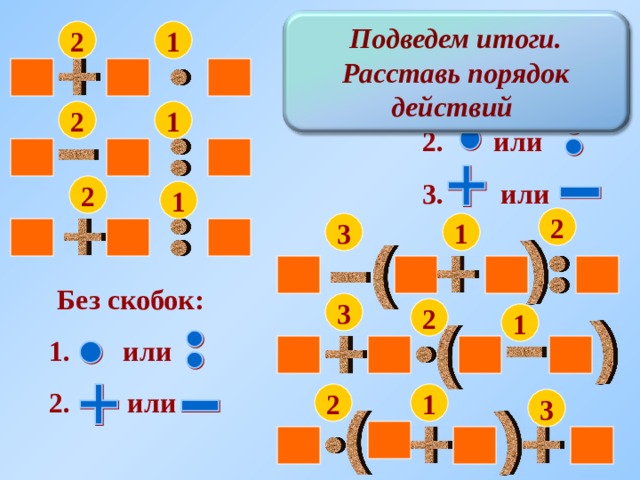
Взгляните:
Если вы воспринимаете PEMDAS буквально, у вас может возникнуть соблазн разделить 6 на 3, а затем 2 на 1 перед сложением.
Проблема в том, что скобки подразумеваются, просто потому, что задача включает сложение в числителе (вверху) и знаменателе (внизу) дроби. Правильный способ решения этой проблемы таков:
Таким образом, в конце концов, PEMDAS может вызвать еще большую путаницу. Конечно, как должны знать давние читатели «Математики для взрослых», существует несколько способов решить математическую задачу. Хорошо хорошо. Это не означает, что существует более одного порядка операций. НО действительно умные преподаватели математики придумали новый способ0026 обучение порядку действий. Это называется треугольник босса или треугольник иерархии операций. ( Треугольник с выступом намного привлекательнее!)
Идея проста: показатели степени (степени) являются основой умножения, деления, сложения и вычитания. Умножение и деление — это боссы сложения и вычитания.
Начальник всегда идет первым. Но поскольку умножение и деление сгруппированы (как сложение и вычитание), эти операции имеют равную силу. Таким образом, любой из пары может ходить первым.
А как насчет круглых скобок (или квадратных скобок)? Внимательно посмотрите на то, что изображено в треугольнике. Если вы заметили, что это всего операций , поставьте себе золотую звезду. Скобки не являются операциями, но они являются контейнерами для операций. Взгляните на следующее:
Вам действительно нужно сначала сделать то, что в скобках? Или вы получите тот же ответ, если сначала найдете 3 x 2? Скобки на самом деле не относятся к порядку. Они о группировке. В данном случае вам не нужно находить 4 + 3, потому что 4 является частью группировки (7 — 1 x 4). (Не верите? Попробуйте выполнить действия в этой задаче в другом порядке. Из-за того, где расставлены скобки, вы обязательно получите правильный ответ более одного раза.)
Вот и все — Треугольник Босса и новый взгляд на порядок операций.
Есть много разных причин, по которым этот новый процесс может быть проще для некоторых детей. Вот лишь некоторые из них:
1. У учащихся со склонностью к зрению есть инструмент, соответствующий их стилю обучения.
2. Учащиеся начинают связывать то, что я называю «парными операциями», и то, что настоящие учителя математики называют «обратными операциями»: умножение и деление и сложение и вычитание. Это значительно помогает, когда учащиеся начинают складывать и вычитать целые числа (положительные и отрицательные числа) позже.
3. Указание на то, что парные операции (x и ÷, + и -) имеют равную мощность, дает учащимся большую гибкость при выполнении сложных вычислений и упрощении алгебраических выражений.
Более того, знание Треугольника Босса может помочь родителям лучше понять математические задания своего ребенка, особенно если они не зависят от PEMDAS.
Так что вы думаете? Имеет ли для вас смысл Треугольник Босса? Или вы предпочитаете PEMDAS? Чему научиться решать эти и другие задачи, купите книгу, которая поможет таким взрослым, как вы, с этими и другими задачами по математике здесь.
Как использовать PEMDAS и решать с порядком операций (примеры)
Обновлено 21 декабря 2020 г.
Ли Джонсон вы не понимаете PEMDAS. Простая аббревиатура определяет порядок операций в математике, и вы должны запомнить ее, если вам нужно регулярно выполнять вычисления. PEMDAS означает круглые скобки, показатели степени, умножение, деление, сложение и вычитание, сообщая вам порядок, в котором вы выполняете различные части длинного выражения. Узнайте, как это использовать, и вас никогда не смутят такие задачи, как 3 + 4 × 5 – 10, с которыми вы можете столкнуться.
Совет: PEMDAS описывает порядок операций:
P – Скобки
E – Показатель степени
M и D – Умножение и деление
A и S – Сложение и вычитание.
Решайте любые задачи с различными типами операций в соответствии с этим правилом, работая сверху (круглые скобки) вниз (сложение и вычитание), отмечая, что операции в одной и той же строке можно выполнять слева направо по мере их появления.
в вопросе.
Каков порядок операций?
Порядок операций говорит вам, какие части длинного выражения нужно вычислить в первую очередь, чтобы получить правильный ответ. Если вы, например, будете подходить к вопросам слева направо, в большинстве случаев вы получите совсем другой результат. PEMDAS описывает порядок операций следующим образом:
P – Скобки
E – Показатель степени
M и D – Умножение и деление
A и S – Сложение и вычитание.
Когда вы решаете длинную математическую задачу с многочисленными операциями, сначала посчитайте что-нибудь в скобках, а затем перейдите к показателям степени (т. работать слева направо). Наконец, вы можете работать над сложением и вычитанием (опять же, просто работайте слева направо).
Как запомнить PEMDAS
Запоминание аббревиатуры PEMDAS, вероятно, является самой сложной частью ее использования, но есть мнемонические приемы, которые можно использовать для облегчения этой задачи.
Наиболее распространенным является «Пожалуйста, извините мою дорогую тетю Салли», но есть и другие альтернативы: «Люди повсюду принимают решения о суммах» и «Толстые эльфы могут потребовать перекусить».
Как решать проблемы с порядком операций
Ответы на задачи, связанные с порядком операций, просто означают запоминание правила PEMDAS и его применение. Вот несколько примеров порядка операций, чтобы прояснить, что вам нужно делать.
4 + 6 × 2 — 6 ÷ 2
Выполните операции по порядку и проверьте каждую. Здесь нет круглых скобок или показателей степени, поэтому перейдите к умножению и делению. Во-первых, 6 × 2 = 12 и 6 ÷ 2 = 3, и их можно вставить, чтобы решить простую задачу: 92 + 2)
Здесь вы сначала решаете раздел в скобках: 5 × 6 2 + 2. Однако эта задача также требует применения PEMDAS. Сначала идет показатель степени, поэтому 6 2 = 6 × 6 = 36. Остается 5 × 36 + 2.