Порядок выполнения действий, 5-й класс
Тип урока: урок повторения и закрепления материала.
Цели урока.
Образовательные:
- повторить и закрепить правила, определяющие порядок выполнения действий первой и второй ступени, схему и программу выполнения действий;
- распределительный закон умножения.
Развивающие:
- развитие умений записывать выражения по программе вычислений, выполнять действия по схеме.
- развитие самостоятельности мышления: выражать своё мнение, выделять главное, делать выводы.
- развитие личностного саморазвития учащихся.
- развитие умений и навыков вычислительного характера.
Воспитательные:
- воспитание культуры общения, усидчивости,
внимания и трудолюбия.

- формирование самостоятельности и активности, гуманных отношений на уроке.
Оборудование:
МКТ, карточки с заданиями для самостоятельной работы.
Структура урока.
- Организационный момент. (2 мин.)
- Актуализация знаний. (12 мин.)
- Использование знаний в стандартной ситуации. (10 мин.)
- Математический диктант. (5 мин.)
- Самостоятельная работа с последующей проверкой. (12 мин.)
- Постановка домашнего задания. (1 мин.)
- Подведение итогов. (3 мин.)
Ход урока
1. Организационный момент.
Проверяется готовность класса, учащихся к уроку. Учитель отмечает отсутствующих и объявляет цели урока.
2. Актуализация знаний.
Учитель проверяет домашнее задание учащихся. Одного из учеников приглашает к доске для решения № 646 из домашнего задания.
Предполагаемая запись ученика на доске:
Решение:
(1215 + 1387) – 64 • 29 = 746.
- Сложить числа 1215 и 1387.
- Перемножить числа 64 и 29.
- Вычесть из результата команды 1 результат команды 2.
Остальные учащиеся в это время выполняют устные упражнения. (На экране появляются задания с помощью МКТ).
- Вместо квадратиков подставьте такие числа, кроме 1, чтобы равенства оказались верными.
| 6 | |
| б) __ • 4 • ? в = 60в | 3; 5 |
- Вычислите:
| а) 63 • 49 + 49 • 137 | 9800 |
| б) 348 • 25 – 148 • 25 | 5000 |
Учитель предлагает прокомментировать решения.
Предполагаемые ответы учащихся:
- Выполним умножение чисел 63 и 49.
- Умножим число 49 на 137.
- Результат команды 1 сложим с результатом команды 2.
Учитель.
Все ли согласны с решением?Ученик.
Я не согласен с ней. Можно решить этот пример удобным способом. Для этого применим распределительный закон умножения относительно сложения. Находим сумму чисел 63 и 137, в результате которой, получим круглое число 200 и умножим это число на 49.Получим ответ: 9800. Учитель. Правильно.Аналогично решается задание б).
Учитель дает несколько минут времени для повторения опорных знаний. Учащиеся работают в парах. Затем учитель вызывает к доске двух учеников.
Ученик 1. Какие действия относятся к действиям первой ступени?
Ученик 2. Сложение и вычитание чисел
называют действиями первой ступени.
Сложение и вычитание чисел
называют действиями первой ступени.
Ученик 1. Какие действия относятся к действиям второй ступени?
Ученик 2. Умножение и деление чисел называют действиями второй ступени.
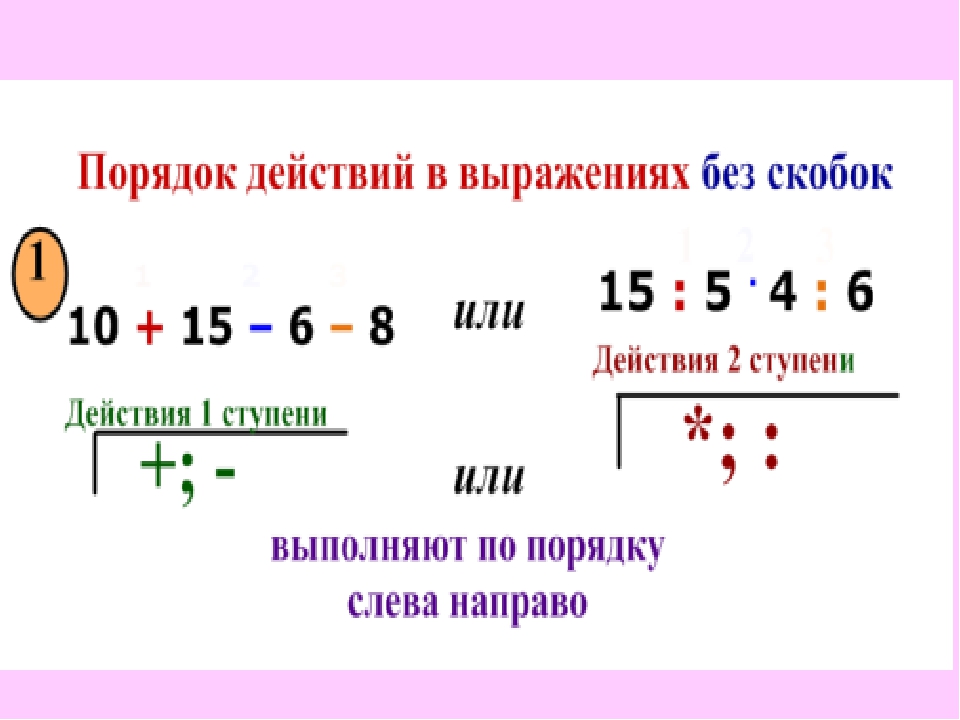
Ученик 1. В каком порядке выполняют действия , если выражение содержит действия первой и второй ступени и в нем нет скобок?
Ученик 2. Если выражение содержит действия первой и второй ступени, и в нём нет скобок, то сначала выполняют действия второй ступени, а затем – действия первой ступени.
Ученик 1. В каком порядке выполняют действия в выражениях без скобок, если в него входят действия одной и той же ступени?
Ученик 2. Если в выражении нет скобок, и оно содержит действия только одной ступени, то их выполняют слева направо.
Ученик 1. В каком порядке выполняют действия в выражениях, где содержатся скобки?
Ученик 2. Если в выражении есть скобки,
то сначала выполняют действия в скобках
(учитывая при этом правила 1 и 2 ).
Если в выражении есть скобки,
то сначала выполняют действия в скобках
(учитывая при этом правила 1 и 2 ).
Учитель вызывает к доске другую пару.
Как задать программу вычислений выражения: (814 + 36 • 27) : ( 101 – 2052 : 38)?
Запишем следующие команды:
- Перемножим числа 36 и 27.
- Сложим 814 с результатом команды 1.
- Разделим 2052 на 38.
- Вычитаем из 101 результат команды 3.
- Разделим результат команды 2 на результат команды 4.
Учитель предлагает рецензировать ответы учащихся, а затем дает задание одному из учеников для составления схемы вычисления и нахождения значения выражения.
Предполагаемая запись ученика на доске:
Учитель. Какие выводы можно сделать из ответов учащихся?
Ученик.
Каждое выражение задает программу своего вычисления и эту программу можно изобразить в виде схемы.
3. Использование знаний в стандартной ситуации.
Учитель предлагает сначала задания для устного решения по цепочке №№ 634 (в, г), 635, 637, 638 (б, г), а затем дает задание всему классу решить письменно №№ 632(а), 631.
№ 631.
По заданной схеме запишите выражение и выполните действия.
№ 632 (а).
Составьте схему вычисления и найдите значение выражения.
а) 86 • 12 : 8 + 1414 : 14 = 230.
Одновременно у доски двое учащихся выполняют №№ 629, 630.
Физкультминутка.
(Учащиеся с помощью специальных упражнений снимают усталость, набирают силы для дальнейшей работы).Математический диктант.
Запишите числовое выражение и найдите его значение:
- Разность семидесяти и двадцати девяти,
увеличенная на одиннадцать.

- Частное шестидесяти и пяти, увеличенное вдвое.
- Из пятидесяти вычесть сумму двадцати четырех и девяти.
- Какое действие выполняется последним при нахождении значения выражения 79 – 27 + 13 – 9 + 11?
- Какое действие выполняется первым при нахождении значения выражения 85 + (42 – 18) – 15?
Верно ли высказывание:
- Сложение и вычитание называют действиями второй ступени.
- В выражении (78 + 94) – 137 скобки можно не писать, так как при этом порядок действий не изменится.
- В выражении (175 – 100) : 25 скобки можно не писать, так как при этом порядок действий не изменится.
IV. Самостоятельная работа с последующей проверкой.
Вариант 1.
Найдите значение выражения, применяя распределительный закон умножения:
| а) 143 • 24 + 24 • 157 | 7200 |
| б) 36 • 248 – 148 • 36 | 3600 |
Решите уравнение:
а) 37у = 444;
б) 300 – 6к = 48;
в) (с – 8) • 12 = 132;
г) 30в – 2в = 532.
Запишите программу вычислений выражения (6944 : 32 – 183) • (79 + 47), составьте схему вычисления и найдите его значение.
Вариант 2.
Найдите значение выражения, применяя распределительный закон умножения:
| а) 746 • 58 – 58 • 546 | 11600 |
| б) 43 • 27 + 35 • 27 – 58 • 27 | 540 |
Решите уравнение:
а) у : 17 = 34;
б) 7с + с – 12 = 28;
в) 243 – (к + 83) = 112;
г) 232: в + 21 = 50.
Запишите программу вычислений выражения (1833: 47 + 467)• 57 — 47• 307, составьте схему вычисления и найдите его значение.
Вариант 3
Найдите значение выражения, применяя распределительный закон умножения:
| а) 367 • 287 + 287 • 133 | 143500 |
| б) 56 • 49 + 227 • 49 – 283 • 49; | 0 |
Решите уравнение:
а) 416 : к + 24 = 50;
б) 42у – 28у + 180 = 600.
Угадайте корень уравнения у + у – 35 = у + 20.
Запишите программу вычислений выражения 378 • 305 – 8208 : (44 • 506 – 22188), составьте схему вычисления и найдите его значение.
Учитель с помощью МКТ высвечивает на экране ответы каждого задания. Учащиеся карандашом исправляют свои ошибки и ставят себе оценку.
V. Постановка домашнего задания.
Учитель. Повторить п.15, решить №№ 644, 647 ( в, г, е ), 649.
Составить кроссворд по теме: “Умножение и деление натуральных чисел” (это задание выполняют только желающие).
Подведение итогов.
Учитель предлагает учащимся оценить ответы тех учеников, которые были самыми активными на уроке. Затем вместе с учащимися подводит итог урока.
Найдите значение выражения (действия с дробями) – как решать
Формулировка задачи: Найдите значение выражения (действия с дробями).
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 1 (Действия с дробями).
Рассмотрим, как решаются подобные задачи на примерах.
Пример задачи 1:
Найдите значение выражения 5/4 + 7/6 : 2/3.
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. И выполним необходимые действия в нужном порядке:
Ответ: 3
Пример задачи 2:
Найдите значение выражения (3,9 – 2,4) ∙ 8,2
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. При этом действия в скобках выполняются раньше, чем действия за скобками. И выполним необходимые действия в нужном порядке:
Ответ: 12,3
Пример задачи 3:
Найдите значение выражения 27 ∙ (1/3 – 4/9 – 5/27).
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. При этом действия в скобках выполняются раньше, чем действия за скобками. И выполним необходимые действия в нужном порядке:
Ответ: –8
Пример задачи 4:
Найдите значение выражения 2,7 / (1,4 + 0,1)
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. При этом действия в скобках выполняются раньше, чем действия за скобками. И выполним необходимые действия в нужном порядке:
Ответ: 1,8
Пример задачи 5:
Найдите значение выражения 1 / (1/9 – 1/12).
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. При этом действия в скобках выполняются раньше, чем действия за скобками. 2) : 754.
2) : 754.
Решение:
Вычислим значение выражения. Для этого определим порядок действий: сначала умножение и деление, затем сложение и вычитание. При этом действия в скобках выполняются раньше, чем действия за скобками. И выполним необходимые действия в нужном порядке. Также в данном случае нужно применить формулу разности квадратов:
Ответ: 702
Действия с логарифмами. Набиваем руку!
В данном уроке мы будем учиться работать с логарифмом на уже весьма и весьма приличном уровне. Поэтому для успешного решения примеров этого урока рекомендую погулять по ссылкам:
Что такое логарифм?
Действия с логарифмами. Постигаем азы!
Почитайте, пока не поздно.) Почитали? Всё понятно! Отлично! Тогда движемся дальше.)
Теперь настал черёд завязывания более крепкой дружбы с логарифмами и, соответственно, решения серьёзных (в том числе сложных и нестандартных) примеров.
Чтобы не скакать из темы в тему, прежде всего я ещё разочек выпишу все основные свойства и формулы логарифмов. Вот они:
Это основной набор формул, необходимых для успешной работы с логарифмами практически на любом уровне сложности. Иногда в школе (и в некоторых продвинутых учебниках) дают больше формул, но в целом приведённого перечня для решения большей части примеров оказывается вполне достаточно. Эти формулы надо помнить! Но, ещё раз повторяю, не просто помнить, а уметь применять! Причём в обоих направлениях — как слева направо, так и справа налево. Вроде бы это всё и так понятно и очевидно, но… дальше всё поймёте.) Как надо помнить формулы, я вам вряд ли смогу подсказать, а вот как уметь применять — подробно расскажу и покажу в этом уроке.
Итак, продолжаем наши игры!
Все формулы. Все степени. Много дробей! Двоюродные и троюродные братья.
Ну что ж, теперь приступаем к работе со всеми формулами (кроме последней формулы перехода к новому основанию). Используем все свойства степеней и активно включаем в работу степени с отрицательными и дробными показателями. Поди сообрази, что, например,
Используем все свойства степеней и активно включаем в работу степени с отрицательными и дробными показателями. Поди сообрази, что, например,
0,04 = 5-2.
Или
Это уже не родные, а двоюродные и троюродные братья по степени получаются…)
Посему, если есть пробелы в степенях, то для начала милости прошу сюда:
Что такое степень. Свойства степеней.
Ну, а для тех, кто со степенями давно на «ты» — продолжаем.)
Пример 1
За что зацепиться? Хорошо, если сразу догадались, а если нет? Если нет, значит, перечитываем первый практический совет прошлого урока — переходим к обыкновенным дробям!
У нас в одну кучу намешаны десятичная дробь и смешанное число. Вот и перейдём к единообразию — к обычным дробям. А там, глядишь, и забрезжит свет в конце тоннеля…
Пишем:
Так, уже кое-чего проясняется: 49 с семёркой родня, а 100 — с десяткой:
49 = 72
100 = 102
Стало быть, по свойствам степеней можно записать:
Ну, вот и спасительный лучик света! Выносим двойку за логарифм и получаем:
Уже всё стало выглядеть гораздо симпатичнее. Всё бы ничего, только основание 7/10 и аргумент 10/7 у нас записаны кверху ногами. Что делать? Да свойства степеней вспомнить! На этот раз — с отрицательным показателем:
Всё бы ничего, только основание 7/10 и аргумент 10/7 у нас записаны кверху ногами. Что делать? Да свойства степеней вспомнить! На этот раз — с отрицательным показателем:
И снова выносим показатель степени (минус единицу) за знак логарифма, переворачиваем аргумент и получаем:
Ответ: -2
Готово дело.) Теперь пробуем самостоятельно:
Ответ: -1
А теперь вовлекаем в наш увлекательный процесс корни. То есть, не что иное, как… степени с дробными показателями. Да-да!
Пример 2
Надеюсь, вы не забыли, что lg — это просто логарифм по основанию 10? Или десятичный логарифм? Пример достаточно простой, без заморочек. Надо всего лишь вспомнить, что корень кубический из 7000 — это 70001/3. С семёркой — аналогично. А дальше по формуле разности логарифмов да по формуле деления степеней. Получим:
Получим:
Ответ: 1
Вот так вот. Здесь мы снова перешли к обычным дробям. Но не от десятичных дробей или смешанных чисел, а от корней. В этом безобидном примере вполне можно было бы и без дробей обойтись, работать напрямую с корнями, но в более сложных примерах корни могут вконец запутать. Как, например, вот в таком примерчике:
Пример 3
С чего начать? И тройка есть, и девятка. Правда, три в квадрате — это и будет девятка… Но в примере ещё и корни разных степеней смешались в кучу — квадратный и кубический! Ужас… Но паниковать и сдаваться рано. Перейдём-ка от корней к степеням с дробными показателями! Распишем девятку как 32. А там, того гляди, всё и наладится.)
Верные мысли! Итак, по свойствам степеней для основания и для аргумента мы можем записать:
Вот всё и прояснилось.) Оба числа — и основание, и аргумент — оказались… родственниками! По тройке. ) Только совсем уж дальними. Даже не троюродными, а десятиюродными братьями: основание — это три в степени 3/2, а аргумент — та же тройка, но в степени 7/3… Тем не менее факт остаётся фактом — родство по степени (хоть и очень дальнее) установлено. Вот и все формулы и свойства заработали! Выносим наши дробные показатели из за знак логарифма и аккуратно считаем:
) Только совсем уж дальними. Даже не троюродными, а десятиюродными братьями: основание — это три в степени 3/2, а аргумент — та же тройка, но в степени 7/3… Тем не менее факт остаётся фактом — родство по степени (хоть и очень дальнее) установлено. Вот и все формулы и свойства заработали! Выносим наши дробные показатели из за знак логарифма и аккуратно считаем:
Вот так. Здесь уже, конечно, немножко повозиться со степенями пришлось. А что делать… Так что не стесняемся переходить от корней к дробям! И всё получится. Обязательно.)
Вот вам и очередные практические советы:
При наличии дробей в примере, переходим от дробей к степеням с отрицательными показателями.
При наличии корней переходим от корней к степеням с дробными показателями.
Что ж, пришла пора разгрызть и какой-нибудь особо крепкий орешек. Как, например, вот такой примерчик:
Пример 4
Вычислить:
Опять же, с чего начинать? Если имеете хоть малейшее представление — флаг вам в руки. Вперёд и с песнями, как говорится.) Если понятия не имеете — подключаем зелёные практические советы и размышляем синим цветом. Примерно так:
Вперёд и с песнями, как говорится.) Если понятия не имеете — подключаем зелёные практические советы и размышляем синим цветом. Примерно так:
«Ух, наворотили… Кошмар! Напролом явно не решается, надо сначала как-то преобразовывать пример. Но — как? Будем вспоминать практические советы.
1. Если в одном примере смешались в кучу разные типы дробей, то переходим к обыкновенным дробям.
Где здесь дроби? Дробей не видно. Ладно, этот пункт пока пропустим. Что там у нас ещё есть? Вот это:
2. Степени популярных чисел надо знать. В лицо! При наличии в примере разных чисел пытаемся найти «братьев по степени».
Так, кое-какая зацепочка уже появилась… 121 — это 11 в квадрате. Ещё можно расписать 125 как 5 в кубе и 9 как 3 в квадрате, но 5 и 3 — никакие не братья и не сёстры по степени. Пригодится или нет — пока непонятно, но к сведению примем. Поехали дальше.)
3. Любую степень можно записать множителем перед логарифмом. И наоборот — любой числовой коэффициент можно спрятать внутрь логарифма. Если он мешает, конечно.
И наоборот — любой числовой коэффициент можно спрятать внутрь логарифма. Если он мешает, конечно.
Коэффициентов в нашем примере нет, логарифмы и так чистые. Отметаем этот совет. Что у нас там ещё припасено?
4. Всегда прикидываем, нельзя исходное выражение преобразовать под какую-нибудь готовую формулу?
Вот и прикидываем: на что похож внешний вид нашего примера? Ну же? Ну, конечно! На самую первую формулу — основное логарифмическое тождество! Единственная формула, где логарифм тусуется в показателе степени.
С ним мы пока что ни разу не работали. Что ж, поработаем! Попробуем преобразовать наш пример под эту формулу: других вариантов как-то выкрутиться у нас просто нет!
Но в формуле в показателе стоит один логарифм! А у нас — сумма. Что нам мешает сложить логарифмы по соответствующей формуле суммы? Основания мешают! Они… они — разные! Ну-ка, может, ещё не все практические советы у нас использованы? Вспоминаем:
5. При наличии дробей в примере, переходим от дробей к степеням с отрицательными показателями. При наличии корней переходим от корней к степеням с дробными показателями.
При наличии дробей в примере, переходим от дробей к степеням с отрицательными показателями. При наличии корней переходим от корней к степеням с дробными показателями.
Так, ну дробей в нашем примере нету, это видно. А вот корень в основании — преобразуем. Вот так:
А во втором логарифме в основании тоже стоит 11, только в квадрате… Уже кое-какие проблески! Выпишу-ка я показатель отдельно, дабы не запутаться… С учётом наших размышлений.)
Уже лучше. Теперь выносим показатели степеней из оснований перед логарифмами (не забыть бы перевернуть…):
Великолепно! Основания логарифмов выровнялись! Только вот новая беда… Коэффициенты появились… Хотелось бы сложить логарифмы, ан нет, не канает… Так стоп! Чего же я туплю-то! Можно же их по другой формуле спрятать вовнутрь!
Ну вот. Уже идеально для формулы сложения! Только внутри логарифмов что-то несусветное стало твориться. Не беда, перейдём к маленьким числам: зря, что ли, мы 125 и 9 в виде степеней пятёрки и тройки расписывали?
Не беда, перейдём к маленьким числам: зря, что ли, мы 125 и 9 в виде степеней пятёрки и тройки расписывали?
Пока всё чин-чинарём. Теперь, по правилам действий со степенями, можно записать:
Вот, практически, и всё. Досчитываем наш показатель по формуле сложения логарифмов:
Пример становится всё лучше и лучше! Возвращаемся к нашему исходному примеру, вставляем в него наш преобразованный показатель и получаем ответ!
Йес!!! Ничего себе, примерчик, однако ж…»
Ответ: 75
Вот такой пример. Запутанный, да, я не спорю. И зачем я так детально его разобрал? С практическими советами, мыслями… Мог бы и в пару строк уложиться… Дело в том, что разбор одного конкретного примера — занятие бесполезное. Не попадётся он. А вот разъяснить на конкретном примере, как именно надо выкручиваться в любом (да-да, любом!) задании — совсем другое дело!
Главное в этом разборе — подход. Мы применяем весь наш арсенал инструментов к конкретному примеру. Пробуем поочерёдно все инструменты, как ключики к замку. Что-то срабатывает, а что-то нет. Это не страшно и не смертельно. Не подошло — пробуем что-то другое! Что-то обязательно подойдёт! Сложные и запутанные задания именно так и решаются. И никак иначе.)
Мы применяем весь наш арсенал инструментов к конкретному примеру. Пробуем поочерёдно все инструменты, как ключики к замку. Что-то срабатывает, а что-то нет. Это не страшно и не смертельно. Не подошло — пробуем что-то другое! Что-то обязательно подойдёт! Сложные и запутанные задания именно так и решаются. И никак иначе.)
Конечно, с опытом всё будет делаться гораздо короче и какие-то шаги будут в уме делаться и вообще пропускаться. За ненадобностью. Тут практика рулит. Тренироваться и решать надо. Используя изложенный здесь подход. И тогда всё получится. Обязательно!
Формула перехода к новому основанию. Немного приколов… И немного формул сокращённого умножения.
Поднимаемся ещё на ступень повыше. Запускаем теперь в дело самую последнюю формулу из нашего списка — это формула перехода к новому основанию. Вот она:
В чём суть этой формулы, когда она применяется и как именно она работает? Объясняю по пунктам.
Формула эта применяется, когда основания логарифмов — разные. Но не просто разные, а ещё и не родственные по степени! Которые друг в друга через простую степень не превращаются. Скажем, 2 и 3. Или 5 и 7. Заметьте, что нам уже встречались разные основания у логарифмов в одном и том же примере, но там или всё и так славненько срасталось, или переход был через степени. Например, если основания логарифмов 1/125 и 25, то можно догадаться, что это родня! По пятёрке. Ибо 1/125 = 5-3, а 25 = 52. Не так очевидно, конечно, но и мы уже всё-таки на серьёзном уровне с вами. А дальше дело техники: выносим показатели за логарифмы и — вперёд.
Но если основания не родственные, а без выравнивания оснований в примере никак, то выход только один — работать по этой формуле.
Запомнить её очень легко. По шагам:
1) Слева пишем логарифм, основание которого нам не нравится. Справа рисуем черту дроби.
2) В числитель пишем логарифм числа b, но уже по новому основанию k. Какому именно основанию? А какому угодно! В том-то весь и фокус! Естественно, тому, которое нам удобнее. Кроме единицы, разумеется.)
Какому именно основанию? А какому угодно! В том-то весь и фокус! Естественно, тому, которое нам удобнее. Кроме единицы, разумеется.)
3) В знаменатель пишем логарифм старого основания a по тому же новому основанию k.
Обратите внимание на саму структуру формулы: слева в основании буквы k вообще нет! В этом-то и вся фишка! Это означает, что новому логарифму мы можем выбрать какое угодно основание. Обычно выбирают то, которое нам удобно в конкретном примере. Если, скажем, в примере куча логарифмов по основанию 3 и затесался один по основанию 7, то его и менять будем. На тройку.
А в знаменатель пишем логарифм старого основания. Так уже математика требует. В результате логарифм со старым основанием исчезает из примера. Вот и всё. Вот и вся суть формулы перехода. Ну что, посмотрим на формулу перехода в действии?
Пример 5
Вычислить:
Что тут можно увидеть? Ну, во-первых, разные основания. Причём не родственные: из четвёрки пятёрку простым возведением в степень никак не получить. Во-вторых, наблюдаем произведение логарифмов. Такой формулы в наших свойствах нету. Не путаем с логарифмом произведения! Или с суммой логарифмов… Что же делать? Первым делом перейдём к одному основанию. Что-то же делать всё равно надо! К какому основанию пойдём? Ну, ясное дело, что не к 30 или 1,234. У нас на выбор два варианта — либо к четвёрке, либо к пятёрке. В данном примере абсолютно без разницы, к чему переходить. Давайте к четвёрке пойдём: всё-таки число поменьше.) Итак, первый логарифм не трогаем (у него и так основание четыре), а вот второй логарифм превращаем по формуле перехода в дробь:
Причём не родственные: из четвёрки пятёрку простым возведением в степень никак не получить. Во-вторых, наблюдаем произведение логарифмов. Такой формулы в наших свойствах нету. Не путаем с логарифмом произведения! Или с суммой логарифмов… Что же делать? Первым делом перейдём к одному основанию. Что-то же делать всё равно надо! К какому основанию пойдём? Ну, ясное дело, что не к 30 или 1,234. У нас на выбор два варианта — либо к четвёрке, либо к пятёрке. В данном примере абсолютно без разницы, к чему переходить. Давайте к четвёрке пойдём: всё-таки число поменьше.) Итак, первый логарифм не трогаем (у него и так основание четыре), а вот второй логарифм превращаем по формуле перехода в дробь:
Всё. Логарифм по основанию 5 из примера благополучно исчез, и в основаниях остались только четвёрки. Вставляем полученную дробь в наш пример, упрощаем и считаем:
Ответ: 2
Вот так. Откуда же я узнал, что надо переходить к другому основанию? Ведь я мог и что-то ещё замутить. Скажем, log516 расписать как
Скажем, log516 расписать как
log516 = log524 = 4log52
и дальше как-то ещё выкручиваться. Да. Можно. Но с богатым опытом приходит уже так называемое математическое чутьё на формулы и преобразования.) Когда в уме наперёд уже умеешь просчитывать, к чему может привести тот или иной манёвр и не идёшь по заведомо негодному пути.
Вот вам очередной практический совет на данную тему.
Если перед вами сложное логарифмическое выражение, в котором основания логарифмов разные, то первым делом пробуем сделать их одинаковыми. Или через степени или по формуле перехода. Очень часто этот манёвр срабатывает проясняет дальнейшую ситуацию.
А теперь рассмотрим один фокус на формулу перехода, который частенько любят проделывать составители примеров. По-другому эту фишку даже и не назовёшь. Настолько элементарна, а в тупик может поставить даже отличника!
Настолько элементарна, а в тупик может поставить даже отличника!
Пример 6
Вычислить:
Основания уже одинаковые, но формулы деления логарифмов не существует, да… Можно, конечно, сообразить, что 125 = 53 и старым добрым способом, но что делать, если внутри логарифмов сидит что-нибудь более навороченное? Вот и впадают в ступор…
Здесь же достаточно всего лишь разглядеть формулу перехода к новому основанию. Вернее, не просто формулу, а её правую часть! И, если запустить эту формулу справа налево, то сразу получим:
И все дела! Да-да! Это ответ.)
Ответ: 3
Частенько эту фишку применяют с какими-нибудь совершенно дикими основаниями. На испуг берут, типа.) Как, например, вот такое задание:
Пример 7
Вычислить:
В основании число «пи», как тут не испугаться… Однако, если догадаться, что наша ужасная дробь — всего лишь правая часть формулы перехода к новому основанию и сработать справа налево, то получим всего-навсего:
Вот и всё. И нету больше никакого «пи».) А уж сложить парочку логарифмов с одинаковыми основаниями — пустяшное дело. Не пример, а одно удовольствие:
И нету больше никакого «пи».) А уж сложить парочку логарифмов с одинаковыми основаниями — пустяшное дело. Не пример, а одно удовольствие:
log1236 + log124 = log12144 = 2
Ответ: 2
Вот такой вот приёмчик. Теперь, надеюсь, не растеряетесь, в случае чего.)
Рассмотрим ещё одну распространённую фишку с формулой перехода. Вернее, её частный случай.
Что произойдёт, если за новое основание мы возьмём аргумент логарифма? Давайте посмотрим!
Во как! Оказывается, если поменять местами a и b, то наш новый логарифм станет всего лишь обратным к старому! Весьма и весьма полезная формулка. Имеет смысл запомнить.) Решим примерчик и на эту тему:
Пример 8
Вычислить:
Что делать будем? Скобки раскрывать? Можно, конечно, но пример явно намекает на более элегантное преобразование. Перейдём в логарифме по основанию 40 к основанию 2. Двойка чем-то привлекательнее, чем сорок, не находите?) Поскольку в аргументе логарифма стоит также двойка, то при переходе к основанию 2 достаточно просто перевернуть этот логарифм. И все дела.)
Перейдём в логарифме по основанию 40 к основанию 2. Двойка чем-то привлекательнее, чем сорок, не находите?) Поскольку в аргументе логарифма стоит также двойка, то при переходе к основанию 2 достаточно просто перевернуть этот логарифм. И все дела.)
Получим:
И что дальше? Куда пристегнуть тройку? А дальше новый фокус! Дело всё в том, что мы не можем напрямую сложить логарифм и число. Но зато логарифмы между собой — запросто! Как выкрутимся? А сделаем-ка из тройки… логарифм! Да-да! Для этого сначала выберем ему основание. Вариантов выбора много, но я предлагаю выбрать 2. Думаю, возражений не будет?)
А дальше пишем вот такое простое равенство:
3 = log223
Всё легко и просто: тройка уходит показателем в степень нашего выбранного основания. Сама цепочка превращений выглядит вот так:
По этапам:
1) Вместо тройки пишем степень с выбранным основанием 2 и показателем, равным этой самой тройке.
2) Берём логарифм от этой степени по тому же самому основанию 2.
3) Всё!
Конечно, можно было бы и сразу тройку на логарифм заменить, благо здесь числа совсем простые, но лучше запомнить эту простую цепочку. А то придётся где-нибудь, к примеру, превращать в логарифм по основанию 11 число 1/7… А по цепочке всё совсем элементарно:
Просекли фишку? Тогда возвращаемся к нашим баранам и дорешиваем:
Ответ: 1
Да… Кто бы мог подумать.)
Конечно, в числовых выражениях этот приёмчик с превращением числа в логарифм достаточно экзотичен. Но вот в логарифмических уравнениях и неравенствах он применяется на полную катушку! Имейте его в виду.)
Заметьте, что обычно мы стараемся поступать наоборот — упрощать всякие ужасы типа дробей, корней, синусов да логарифмов. Доводить их, по возможности, до конечного числа. А тут — наоборот, из числа делаем логарифм. Что хотим, то и творим! Так что математика — на самом деле весьма и весьма творческая наука! Во многом даже искусство.)
Что хотим, то и творим! Так что математика — на самом деле весьма и весьма творческая наука! Во многом даже искусство.)
Запоминаем:
При необходимости любое число можно превратить в логарифм по любому основанию (кроме единицы, конечно).
Осталось разобраться с совсем уж хардкорными примерами. Где и так пробуешь и сяк, но не упрощается он никак! На такие примеры есть своё особое секретное оружие.) Срабатывает безотказно. Если уметь грамотно им пользоваться, конечно. Как вам такой примерчик!
Пример 9
Вычислить:
За что зацепиться? Все основания уже одинаковые (семёрка), но это особо не спасает. Кстати, обращаю ваше внимание на весьма и весьма частый косяк. В числителе стоят квадраты логарифмов. Именно самих логарифмов, а не их аргументов! Это означает, что вынести двойки из логарифмов наружу мы не имеем права! Не там двойки стоят… Стало быть, уже привычных нам логарифмических формул, готовых к употреблению, нету. Что же делать?
Что же делать?
Спокойно! Без паники! Никто и никогда не может гарантировать, что сразу влёт всё решится.) К сожалению…
Чтобы расправиться с этим злым примером, забудем на минутку про логарифмы и плавненько переместимся в седьмой класс. Формулы сокращённого умножения не забыли, надеюсь? А теперь внимательно присматриваемся к нашему примеру. Что ещё, кроме логарифмов, в нём можно увидеть? Разность… Разность ква… Ну, конечно! Разность квадратов! Такая родная и до боли знакомая формула:
a2–b2 = (a—b)(a+b)
Правда, в применении к логарифмам. Ну и что из этого? Ведь в формуле под буковками a и b может скрываться всё что угодно — и логарифмы, и синусы, и степени — любые выражения! Формула всё равно сработает!
Итак, заменяем наш числитель на произведение скобок по формуле разности квадратов:
Вот и всё встало на свои места! И все формулы заработали! Решать пример стало одно удовольствие. )
)
В первых скобках (разность) получается:
Во вторых скобках (сумма) будет:
Вставляем в пример наши промежуточные результаты, сокращаем и получаем:
Ответ: 1
Простенько и со вкусом.) Здесь-то всё ясно. Но в тревожной боевой обстановке ЕГЭ подобный пример может и в ступор вогнать. Дело всё в том, что большинство учеников подсознательно пытаются решить пример в том формате, в котором он задан. Например, если задан пример на логарифмы, то мы с головой погружены в логарифмы и варимся только в них, а вынырнуть на поверхность да оглядеться вокруг — не можем. С тригонометрией аналогично — решаем пример только в рамках тригонометрии. И, в случае чего, не можем напрячься и выскочить из этих жёстких рамок… А надо уметь! Хотя бы иногда.)
Посему очередной по счёту практический совет:
Замороченные примеры проверяем на алгебру седьмого класса — разложение на множители, формулы сокращённого умножения и т. п.
п.
Ещё из той же оперы для самостоятельного решения:
lg24 + lg16·lg25 + lg225 =
Ответ: 4
Ну что, поздравляю! Вот мы и набрались достаточного количества знаний для уверенной работы с логарифмами практически на любом уровне сложности! Дальше путь только один — решать примеры! Как можно больше.) И особо рекомендую не пренебрегать зелёными советами. Они не зря даются в материале.) Их надо помнить и им надо следовать.) И тогда не логарифмы будут командовать вами, а вы — логарифмами.)
До встречи!
Что такое PEMDAS? — Определение, правила и примеры — Видео и стенограмма урока
Почему важен PEMDAS?
Без PEMDAS нет указаний для получения только одного правильного ответа. В качестве очень простого примера, чтобы вычислить 2 * 4 + 7, я мог бы сначала умножить, а затем сложить, чтобы получить 15. У меня также есть возможность сначала сложить, а затем умножить и получить 22. Какой ответ правильный? Используя PEMDAS, единственный правильный ответ — 15, потому что порядок букв в PEMDAS говорит мне, что умножение M должно выполняться перед сложением A.
У меня также есть возможность сначала сложить, а затем умножить и получить 22. Какой ответ правильный? Используя PEMDAS, единственный правильный ответ — 15, потому что порядок букв в PEMDAS говорит мне, что умножение M должно выполняться перед сложением A.
Вот объяснение правил, приведенных в PEMDAS:
- P, поскольку первая буква означает, что вы сначала выполняете любые вычисления в группировке символов.
- Затем найдите показатели степени, E. Игнорируйте любые другие операции и возьмите любые числа с показателями степени в соответствующие степени.
- Несмотря на то, что M для умножения в PEMDAS предшествует D для деления, эти две операции фактически имеют одинаковый приоритет. Выполняйте только эти две операции в том порядке, в котором они происходят слева направо.2) + 10
- 36 — 2 (20 + 12/4 * 3-4) + 10
- 36 — 2 (20 + 3 * 3-4) + 10
- 36 — 2 (20 + 12/4 * 3-4) + 10
- Осознайте важность PEMDAS и произнесите фразу, которая поможет вам запомнить порядок действий
- Использование PEMDAS в математических выражениях
- Понять, как PEMDAS применяется к выражениям дробей и абсолютных значений
- Преобразуйте делитель в обратный
- Измените знак деления на символ умножения и умножьте
- Упростите ответ, если возможно
- Умножьте числители, чтобы получить новый числитель
- Умножьте знаменатели, чтобы получить новый знаменатель
- Упростите окончательную дробь, если возможно
- Преобразовать делитель в обратный
- Измените знак деления на знак умножения и умножьте
- Упростите , если возможно
Игнорируя сложение и вычитание, я завершаю следующую операцию умножения. 2} + 12/4.3 |, шаги будут следующими:
2} + 12/4.3 |, шаги будут следующими:
Краткое содержание урока
PEMDAS — это аббревиатура слов скобка, экспоненты, умножение, деление, сложение, вычитание. Для любого выражения сначала следует упростить все показатели, затем умножить и разделить слева направо и, наконец, сложить и вычесть слева направо. Слово «круглые скобки» стоит первым в этом аббревиатуре, чтобы указать, что любое выражение в символе группировки, такое как круглые скобки, должно быть сначала упрощено.Этот приказ также можно запомнить, используя фразу «, пожалуйста, извините, дорогая тетя Салли».
Результаты обучения
Изучив этот урок на PEMDAS, откройте для себя свою способность:
Умножение и деление уравнений и неравенств
Пример задачи
Решите уравнение 8 x = 5 x + 24.
Первое, что мы делаем, это вычитаем 5 x с каждой стороны и получаем 3 x = 24.
Мы еще не обсуждали, что делать с такого рода уравнениями, но вы можете это выяснить. думая о шкале баланса. Если три копии x весят в сумме 24, то каждая x должна весить одну треть от 24. То есть x = 24 ÷ 3 = 8. Надеюсь, мы все еще не говорим о хакерских мешках, потому что наши лодыжки, вероятно, не выдержат такого веса.
Другими словами, мы делим обе части 3 x = 24 на 3, чтобы получить x отдельно.
3 x = 24
3 x ÷ 3 = 24 ÷ 3
x = 8
Вот еще один способ подумать об этом: чтобы получить только x , мы умножили обе части уравнения на . Это не совпадение, что это мультипликативная инверсия числа 3. Было ли у вас «ага!» момент? Потому что мы это сделали.
В общем, всякий раз, когда мы сталкиваемся с уравнением вида ( коэффициент ) x = ( некоторое значение ), мы умножаем обе части уравнения на обратную величину коэффициента. Поскольку любое число, умноженное на его обратную величину, равно 1 (просто попробуйте найти число, в котором это не сработает — мы вас осмеливаем), это оставляет нам уравнение, которое имеет x на одной стороне, а решение к уравнению с другой стороны.
Поскольку любое число, умноженное на его обратную величину, равно 1 (просто попробуйте найти число, в котором это не сработает — мы вас осмеливаем), это оставляет нам уравнение, которое имеет x на одной стороне, а решение к уравнению с другой стороны.
Как и в случае сложения и вычитания, умножение или деление обеих частей уравнения на одну и ту же величину допустимо, если мы не делим на ноль. Помните: все дело в том, чтобы делать с одной стороной то, что вы делаете с другой. Если вы угощаете левую сторону, вам лучше принести достаточно, чтобы поделиться со всем классом.
Будьте осторожны: При решении уравнения, какую бы операцию вы ни выполняли с одной стороной, вы должны также выполнить и с другой стороны. Мы знаем, что уже сказали это, но надеемся, что в 47-й раз будет очарование. Если вы добавляете 5 в левую часть уравнения, вы должны добавить 5 в правую часть уравнения. Если вы разделите правую часть уравнения на 3, вам также необходимо разделить левую часть уравнения на 3.
Пример задачи
Какое решение для 5 x — 10 = 3 x + 8?
Сначала получите все x на одной стороне уравнения, вычтя 3 x с каждой стороны:
2 x — 10 = 8
Затем прибавьте 10 к обеим сторонам:
2 x = 18
Наконец, разделите каждую часть уравнения на 2:
x = 9
Напомним, что деление на 2 аналогично умножению на половину.Если вы хотите, чтобы кто-то бросил на вас «рыбий глаз», попробуйте заказать футлинга в метро и затем спросите, могут ли они умножить его вдвое.
Мы можем представить себе деление обеих частей уравнения на 2 или умножение обеих частей уравнения на. Пока мы делаем арифметику правильно, в любом случае мы найдем тот же ответ в конце. Однако, когда речь идет о дробях, обычно лучше подумать об умножении на обратное умножение, чем о делении на дробь.
Пример задачи
Решите уравнение
Нам нужно, чтобы y было само по себе, поэтому умножьте обе части уравнения на мультипликативную обратную величину, которая равна. Это сократит дробь в левой части уравнения:
Это сократит дробь в левой части уравнения:
y = 10
. Если вы предпочитаете разделить обе части уравнения на, во что бы то ни стало, сделайте это. Остерегайтесь любых змей, которые могут попытаться укусить вас за лодыжки. Предупреждение: эти змеи могут быть замаскированы под числа.
Одна вещь, которая может сбить нас с толку, если мы не будем осторожны, — это запись с отрицательными знаками. Когда — x отображается в уравнении, x умножается на -1. Если вам полезно переписать — x как (-1) x , сделайте это. Если кто-то посмеется над вами из-за этого, сообщите нам его имя, и о ситуации позаботятся. Мы не говорим, что сделаем им что-то , мы просто говорим … позаботятся о .
Как делить дроби: 3 простых шага для решения сложных задач
Научить своих учеников делить дроби может быть так же просто, как обучение умножению…. когда вы знаете все маленькие уловки, чтобы получить правильный ответ. Но — как и в случае с любой другой математической концепцией — когда вы преподаете деление, вы не хотите, чтобы ваши ученики всего решали задачу. Вы хотите, чтобы они понимали, что происходит в каждом вопросе. Но в том-то и дело. Трудно заставить их понять деление дробей, если вы сами этого не понимаете. Мы тоже немного запутались в этом. Вот почему мы рассмотрели лучшие инструменты и самые простые способы убедиться, что ваш класс понимает ключевые концепции деления дробей .Обратите пристальное внимание, и к концу этой статьи вы станете полностью экипированным и очень уверенным мастером деления дробей.
Но — как и в случае с любой другой математической концепцией — когда вы преподаете деление, вы не хотите, чтобы ваши ученики всего решали задачу. Вы хотите, чтобы они понимали, что происходит в каждом вопросе. Но в том-то и дело. Трудно заставить их понять деление дробей, если вы сами этого не понимаете. Мы тоже немного запутались в этом. Вот почему мы рассмотрели лучшие инструменты и самые простые способы убедиться, что ваш класс понимает ключевые концепции деления дробей .Обратите пристальное внимание, и к концу этой статьи вы станете полностью экипированным и очень уверенным мастером деления дробей.Оглавление
Как работает деление дробей
Обучение студентов тому, как делить дроби, является частью Общих государственных стандартов математической практики. Одна из самых ценных вещей, которую нужно научить ваших студентов при делении дробей, — это то, что означает ответ. Взгляните на пример ниже:½ ÷ ⅙ = 3
Почему в решении больше числа, чем участвующие дроби? Когда вы делите дробь, вы спрашиваете , сколько групп делителя (второе число) может быть найденным в дивиденде (первое число). Для приведенного выше уравнения мы спрашиваем, сколько ⅙ появляется в ½. Представьте приведенное в качестве примера уравнение в виде торта. У тебя осталась половина торта. Если каждая порция торта составляет от всего, сколько порций у вас осталось? Как видите, у вас осталось три порции торта!
Для приведенного выше уравнения мы спрашиваем, сколько ⅙ появляется в ½. Представьте приведенное в качестве примера уравнение в виде торта. У тебя осталась половина торта. Если каждая порция торта составляет от всего, сколько порций у вас осталось? Как видите, у вас осталось три порции торта!Как разделить дроби
Если вы просто разделите дроби, как при делении обычной математической задачи, вы, скорее всего, создадите несколько сложных дробей и получите что-то похожее на это:
Шаг 1: Преобразуйте делитель в обратную величину
Обратную величину вы умножаете на число, чтобы получить значение единицы.Если вы хотите превратить два в один посредством умножения, вам нужно умножить его на 0,5. В дробной форме это выглядит так:²⁄₁ × ½ = 1
Чтобы найти обратную дробь, вы просто переворачиваете числа. Знаменатель становится числителем и наоборот. Еще раз взгляните на пример уравнения:½ ÷ ⅙ =?
Первый шаг к решению проблемы — превратить наш делитель,, в обратную величину.⅙ → ⁶⁄₁
Шаг 2: Измените знак деления на символ умножения и умножьте
Деление и умножение — это противоположности друг другу.Когда вы создаете обратное число, вы также создаете его противоположность. В задаче деления, когда вы превращаете делитель в обратную величину, вам также необходимо изменить уравнение с деления на умножение. Теперь, когда вы нашли обратную величину вашего делителя, вы можете изменить уравнение с деления на умножение.
½ ÷ ⅙ =? → ½ × ⁶⁄₁ =?
У нас есть подробное руководство по умножению дробей, но вот краткое руководство:1 × 6 = 6 2 × 1 = 2 ½ × ⁶⁄₁ = ⁶⁄₂
Теперь вы готовы к упрощению, чтобы получить окончательный ответ!Шаг 3. Если возможно, упростите свой ответ
Дроби символизируют часть целого. Это означает, что многие дроби представляют одно и то же значение, так почему бы не сделать дробь как можно более простой? Например, вы почти никогда не говорите пять десятых или ⁄₁₀.То же / другое? Умножение / деление дроби на 2/2.Полное видео на https://t.co/aYmHjxOMdB #mtbos #iteachmath #samediffmath pic.twitter.com/RunWrKLQ3J
— Беркли Эверетт (@BerkeleyEverett) 16 декабря 2018 г.
 Вместо этого вы упрощаете это до половины или ½. Чтобы уменьшить дробь до ее простейшего вида, вы делите числитель и знаменатель на их наибольший общий множитель .Наибольший общий делитель в ⁄ — пять. Разделив оба числа на пять, вы получите ½. В примере вопроса наибольший общий делитель ⁄₂ равен двум. Это превратит ваше решение из ⁶⁄₂ в ³⁄₁, что равносильно слову три. Следовательно:
Вместо этого вы упрощаете это до половины или ½. Чтобы уменьшить дробь до ее простейшего вида, вы делите числитель и знаменатель на их наибольший общий множитель .Наибольший общий делитель в ⁄ — пять. Разделив оба числа на пять, вы получите ½. В примере вопроса наибольший общий делитель ⁄₂ равен двум. Это превратит ваше решение из ⁶⁄₂ в ³⁄₁, что равносильно слову три. Следовательно:½ ÷ ⅙ =? → ½ × ⁶⁄₁ = ⁶⁄₂ → ³⁄₁ → 3
Создание обратной величины и умножение уравнения вместо деления позволяет пропустить несколько шагов в уравнении. Это ярлык, который значительно упростит жизнь вашим ученикам!Примеры деления на дроби
Трехэтапная стратегия отлично подходит для простых задач с дробями, но что происходит, когда вы сталкиваетесь с целыми числами, смешанными дробями, неправильными дробями и задачами, основанными на словах? Процесс остается по большей части тем же, но в зависимости от типа проблемы может быть еще пара шагов.Давайте рассмотрим несколько примеров различных типов задач:Как разделить неправильные дроби
 Вид этих дробей может вызвать недоумение, но порядок действий не меняется. Пример 1 :
Вид этих дробей может вызвать недоумение, но порядок действий не меняется. Пример 1 :⅓ ÷ ⁶⁄₅ =? → ⅓ × ⅚ = ⁵⁄₁₈
Пример 2 :⁷⁄₆ ÷ ¾ =? → ⁷⁄₆ × ⁴⁄₃ = ²⁸⁄₁₈ → ¹⁴⁄₉ → 1 ⁵⁄₉
Независимо от того, где находится неправильная дробь, вы все равно переворачиваете делитель на обратную, а затем умножаете две дроби.Как разделить смешанные дроби
3 ⅓ ÷ ⅖ =? → ¹⁰⁄₃ ÷ ⅖ =? → ¹⁰⁄₃ × ⁵⁄₂ = ⁵⁰⁄₆ → ²⁵⁄₃ → 8 ⅓
Пример 2:¼ ÷ 2 ⅙ =? → ¼ ÷ ¹³⁄₆ =? → ¼ × ⁶⁄₁₃ = ⁶⁄₅₂ → ³⁄₂₆
Пример 3:2 ½ ÷ 1 ⅓ =? → ⁵⁄₂ ÷ ⁴⁄₃ =? → ⁵⁄₂ × ¾ = ¹⁵⁄₈ → 1 ⅞
Как разделить дроби на целые числа
 Прежде чем приступить к делению, вам нужно превратить целое число в дробь. Чтобы превратить целое число в дробь, сделайте в числителе целое число, а знаменатель — единицу.
Прежде чем приступить к делению, вам нужно превратить целое число в дробь. Чтобы превратить целое число в дробь, сделайте в числителе целое число, а знаменатель — единицу.3 → ³⁄₁
После того, как целое число превратится в дробь, вы можете продолжить решение задачи с помощью трехэтапной стратегии. Пример:⅓ ÷ 3 =? → ⅓ ÷ ³⁄₁ =? → ⅓ × ⅓ = ⅑
Как разделить дроби с одинаковым знаменателем
Когда у вас одинаковый знаменатель, нет необходимости находить обратную или умножать.Вы можете просто разделить дроби, чтобы получить ответ. Знаменатели уравняют друг друга и дадут вам единицу. Любую дробь со знаминателем, равным единице, можно упростить до числителя. Пример 1:⅘ ÷ ⅖ = ²⁄₁ → 2
Пример 2:⅓ ÷ ⅔ = ½ / 1 → ½
Проблемы со словами деления дробей
Проблемы со словами могут быть сложными, потому что вы Мы должны научить ваших студентов понимать, какая ценность становится дивидендом, а какая — делителем. Как и во всех задачах деления, в задаче со словом вы пытаетесь выяснить, сколько групп одного числа можно найти в другом. Лучший способ понять, какое это число, на примере. Есть 25 ½ километровый участок шоссе, который необходимо отремонтировать. Строительная бригада может ремонтировать 4 ¼ километра дорог в неделю. Сколько недель потребуется на ремонт трассы? В этом уравнении вы ищите количество недель, необходимое для ремонта шоссе.Чтобы получить этот ответ, вам нужно увидеть, сколько групп по 4 (количество шоссе, которое можно отремонтировать в неделю) могут уместиться в 25 ½ (общая длина шоссе, которое необходимо отремонтировать). Таким образом, 25 ½ будет вашим дивидендом, а 4 ¼ — вашим делителем! После вставки чисел в правильные места вы обнаружите, что на ремонт шоссе уйдет шесть недель. Чтобы убедиться, что ваши ученики следуют за вами, вы можете работать вместе решить проблемы со словами, а затем попросите их поднять руку, если они думают, что одно число — это делимое.
Как и во всех задачах деления, в задаче со словом вы пытаетесь выяснить, сколько групп одного числа можно найти в другом. Лучший способ понять, какое это число, на примере. Есть 25 ½ километровый участок шоссе, который необходимо отремонтировать. Строительная бригада может ремонтировать 4 ¼ километра дорог в неделю. Сколько недель потребуется на ремонт трассы? В этом уравнении вы ищите количество недель, необходимое для ремонта шоссе.Чтобы получить этот ответ, вам нужно увидеть, сколько групп по 4 (количество шоссе, которое можно отремонтировать в неделю) могут уместиться в 25 ½ (общая длина шоссе, которое необходимо отремонтировать). Таким образом, 25 ½ будет вашим дивидендом, а 4 ¼ — вашим делителем! После вставки чисел в правильные места вы обнаружите, что на ремонт шоссе уйдет шесть недель. Чтобы убедиться, что ваши ученики следуют за вами, вы можете работать вместе решить проблемы со словами, а затем попросите их поднять руку, если они думают, что одно число — это делимое. Затем снова спросите, считают ли они, что другое число является делимым. Затем выберите учащегося, чтобы он объяснил, почему одно число является делимым, а другое — делителем. Это не только привлечет внимание студентов, но и даст вам возможность увидеть, как студенты обрабатывают материал, который вы преподаете!
Затем снова спросите, считают ли они, что другое число является делимым. Затем выберите учащегося, чтобы он объяснил, почему одно число является делимым, а другое — делителем. Это не только привлечет внимание студентов, но и даст вам возможность увидеть, как студенты обрабатывают материал, который вы преподаете!Как Prodigy может помочь вам научить делить дроби
Prodigy Game поможет вам научить делить дроби, отслеживать, как идут дела у ваших учеников, и задавать конкретные вопросы для подготовки вашего класса к стандартизированному тестированию — все бесплатно .Математическая игра вдохновляет ваших учеников учиться — и большую часть времени они даже не подозревают, что проходят тестирование. У вас есть несколько вариантов, в том числе возможность сосредоточить внутриигровые вопросы по темам, которые вы преподаете, актуальную статистику и отчеты о прогрессе. Вот как вы можете использовать Prodigy в своем классе, чтобы: Prodigy работает быстрее, чем рабочие листы, как и все «Маркировка» выполняется за вас — и в режиме реального времени. Вы можете просматривать отчеты по всему классу и видеть, с какими темами сталкиваются разные ученики! Вы также можете создавать задания для каждого ученика в зависимости от его конкретных потребностей и стилей обучения.Всем вашим ученикам будет предоставлена возможность попрактиковаться в вопросах, с которыми у них возникнут проблемы, и улучшить свои общие математические навыки. Когда время тестирования не за горами, вы можете создать практический тест в игре, чтобы узнать, нужно ли охватывать какие-либо темы. Класс с большей глубиной. Игра Prodigy всегда бесплатна для учителей.
Вы можете просматривать отчеты по всему классу и видеть, с какими темами сталкиваются разные ученики! Вы также можете создавать задания для каждого ученика в зависимости от его конкретных потребностей и стилей обучения.Всем вашим ученикам будет предоставлена возможность попрактиковаться в вопросах, с которыми у них возникнут проблемы, и улучшить свои общие математические навыки. Когда время тестирования не за горами, вы можете создать практический тест в игре, чтобы узнать, нужно ли охватывать какие-либо темы. Класс с большей глубиной. Игра Prodigy всегда бесплатна для учителей.Рабочие листы деления на дроби
Чтобы убедиться, что ключевые концепции передаются при обучении делению дробей, вы также можете использовать рабочие листы для своего класса. Вы можете поместить в рабочий лист набор различных вопросов, чтобы увидеть, что учащиеся понимают и с чем они борются.Единственный недостаток рабочих листов в том, что их разметка может занять много времени. Чем больше времени уйдет на отметку, тем больше времени потребуется, чтобы увидеть, с чем вашим ученикам нужна помощь. Вот несколько веб-сайтов, на которых можно получить рабочие листы, которые вы можете попробовать в своем классе:
Вот несколько веб-сайтов, на которых можно получить рабочие листы, которые вы можете попробовать в своем классе:1. DadsWorksheets.com
DadsWorksheets.com предлагает широкий выбор рабочих листов на выбор в зависимости от темы, над которой вы работаете. Все рабочие листы снабжены ключом ответа, чтобы упростить задачу. Все, что они предлагают, можно загрузить и распечатать прямо с веб-сайта.2. Common Core Sheets
Common Core Sheets выводит ваши рабочие листы на новый уровень, позволяя настраивать ваши уроки. Вы можете выбрать типы вопросов, которые хотите отображать на своих листах. Вы также можете выбрать, хотите ли вы, чтобы дроби были упрощены или преобразованы в смешанные числа для ответов. Конечный продукт дает вам два рабочих листа. В первом есть только вопросы, а во втором — все ответы, включая процесс получения решения.3. K5 Learning
K5 Learning предоставляет рабочие листы для классов от детского сада до пятого класса.Они охватывают множество тем, представленных в учебной программе, и для каждого предмета есть несколько рабочих листов. PDF-файл, который вы можете скачать с их веб-сайта, включает в себя рабочие листы и ключ ответа.
PDF-файл, который вы можете скачать с их веб-сайта, включает в себя рабочие листы и ключ ответа.Калькулятор деления дробей
Когда ваши ученики учатся делить дроби, вы можете показать им калькулятор дробей. Это онлайн-инструменты для быстрого решения задач дроби. Они отлично подходят для проверки ваших ответов, но будьте осторожны, показывая эти инструменты вашему классу. Калькуляторы дробей можно использовать, когда учащиеся выполняют домашнее задание, но вы не хотите, чтобы они полагались на них при решении вопросов, иначе они выиграли бы ». я ничему не учусь.Если вы используете Calculator.net, они покажут вам все различных шагов, которые необходимо предпринять для решения проблемы!Заключительные мысли о том, как делить дроби
При обучении делить дроби скажите своим ученикам, что они пытаются найти, сколько делителей можно найти в дивиденде. Самый простой способ разделить дроби — выполнить три простых шага: