Дорофеев Г.В. Решение задач на умножение и деление | Учебно-методический материал по математике (2 класс) на тему:

Дорофеев Г.В. Уроки математики во 2 классе

МЕТОДИЧЕСКИЙ КОММЕНТАРИЙ К ОСНОВНЫМ РАЗДЕЛАМ УЧЕБНИКА

Раздел 1

ЧИСЛА ОТ 1 ДО 20. ЧИСЛО 0

Изучение двух новых арифметических действий — умножения и деления — является основой курса математики 2 класса. Главный залог успешного усвоения этого материала — глубокое и осмысленное понимание детьми конкретного смысла этих действий, раскрытие связи умножения с уже изученным действием — сложением.

Подготовительная работа к введению новых действий начинается в конце первого года обучения, при изучении сложения и вычитания чисел первого и второго десятков. Она сводится к решению соответствующих примеров и задач с опорой на действия с предметными множествами. В процессе такой работы учащиеся осознают роль группового счета (двойками, тройками и т. д.), усваивают его способы, решают примеры на нахождение суммы одинаковых слагаемых.

Желательно предлагать второклассникам задания практического содержания, близкие им из жизненного опыта. Например, нужно сосчитать, сколько новогодних шаров в коробке с ячейками. В коробке 2 ряда ячеек, по 4 ячейки в каждом ряду. Дети рассматривают несколько вариантов (шары можно считать по одному, по два или по четыре), записывают решение и выясняют, что группами, т. е. в данном случае парами или четверками, считать удобнее. Учащиеся приводят примеры из жизни, когда ведется счет по группам: по два (или парами), по три (или тройками) и т. д.

Особое внимание в этот период должно быть уделено и абстрактному счету по группам (например, «Считайте по 2 до 20»), а также выполнению практических заданий на нахождение суммы одинаковых слагаемых или деление по содержанию и на равные части.

1. Нарисуйте по 2 кружка 3 раза. Сколько всего кружков вы нарисовали?

Число всех кружков дети находят действием сложения, записывая под рисунком соответствующее выражение.

2.  Возьмите 8 кружков и разложите их по 2 кружка. Сколько раз по 2 кружка получилось?

3. Возьмите 6 карандашей и разложите их поровну в 3 коробки. Сколько карандашей в каждой коробке?

Аналогично можно предлагать и сюжетные задачи.

1. Катя купила 5 одинаковых марок, по 2 р. каждая. Сколько денег заплатила Катя за все марки?

2. Мама принесла из сада 9 тюльпанов и разделила их в букеты, по 3 тюльпана в каждом. Сколько получилось букетов?

Ключевым этапом подготовительной работы к изучению действия умножения является выполнение учащимися заданий на нахождение суммы нескольких одинаковых слагаемых. Отличие предлагаемой методики состоит в том, что наряду с традиционными заданиями на выявление суммы одинаковых слагаемых и нахождение ее значения в учебник включен ряд новых упражнений с опорой на числовой луч, например, таких:

1. Кузнечик прыгает по числовому лучу от точки 0. В каждом его прыжке по 2 деления.

1) В каких точках числового луча кузнечик может оказаться? не может оказаться?

2) В какой точке луча будет кузнечик через 3 прыжка? через 4 прыжка? через 7 прыжков?

3) Сколько прыжков нужно сделать кузнечику, чтобы оказаться в точке 4? 8? 10? 16? 20?

2.  Реши примеры с помощью числового луча.

3+3+3  4 + 4 + 4 + 4 + 4  6 + 6 + 6

      3. Запиши примеры цифрами и реши их.

1)  по 3 взять 2 раза;

2)  по 2 взять 4 раза;

3)  по 1 взять 7 раз;

4)  по 4 взять 4 раза;

5)  по 5 взять 3 раза;

6)  по 8 взять 2 раза.

4. Используя числовой луч, ответь на вопросы

1)  Сколько раз по 2 содержится в числе 6?

2)  Сколько раз по 7 содержится в числе 14?

3)  Сколько раз по 6 содержится в числе 18?

4)  Сколько раз по 10 содержится в числе 20?

5. Замени каждое число суммой одинаковых слагаемых.

4= +  16=  +   8=  +  +  +   12=  +  +  +  3=  +  +  9 =  +  +

Умножение рассматривается как нахождение суммы одинаковых слагаемых. Для ознакомления с этим действием желательно предложить задачу, которую легко можно проиллюстрировать, например, такую:

«На каждой тарелке по 5 яблок. Сколько яблок на 3 тарелках?»

Под руководством учителя учащиеся записывают решение: 5 + 5 + 5 = 15 (яб.).

— Чем интересна эта сумма? (Слагаемые одинаковые.)

— Сколько раз взяли по 5 яблок? (3 раза.)

Учитель сообщает, что сумму одинаковых слагаемых можно записать так: 5 · 3, — и знакомит учащихся с вариантами прочтения примера 5 · 3 = 15: «5 умножить на 3, получится 15» или «По 5 взять 3 раза, получится 15». Затем на закрепление выполняются задания на замену суммы одинаковых слагаемых произведением двух чисел, одно из которых — слагаемое, которое повторяется, а другое — количество таких слагаемых, и наоборот.

Здесь важно обратить внимание учащихся на то, что на первом месте записано число 5, которое берется слагаемым, а на втором месте — число 3, которое показывает, сколько одинаковых слагаемых надо взять.

При объяснении смысла нового действия — умножения — необходимо делать акцент на целесообразности замены суммы нескольких одинаковых чисел произведением двух чисел, одно из которых — слагаемое, которое повторяется, а другое — количество таких слагаемых. Например, рассуждения учащихся при вычислении суммы 3 + 3 + 3 + 3 + 3 + 3 могут быть такими: «Слагаемые в сумме одинаковые: слагаемое 3 берем 6 раз. Заменю сумму произведением. Пишу 3, затем знак умножения и 6. По 3 взять 6 раз, получится 18».

При решении задач на нахождение произведения учащиеся должны усвоить, что если получается сумма одинаковых слагаемых, то задачу можно решить умножением. Важно при этом понимать, что означает каждое число в такой записи.

Например, предлагается задача: «Три девочки вырезали по 2 снежинки каждая. Сколько всего снежинок вырезали девочки?»

При анализе текста задачи следует разъяснить учащимся, что значит в данном условии слово каждая (т. е. первая девочка вырезала 2 снежинки, вторая — 2 снежинки и третья — 2 снежинки). После инсценировки этой задачи с помощью учениц класса дети подводятся к выбору действия для решения задачи. Для этого учитель говорит: «Было 3 девочки (называет их имена), каждая вырезала по 2 снежинки (учитель дает каждой девочке по 2 снежинки). Как узнать, сколько всего снежинок вырезали девочки?»
Сначала задача решается сложением: 2 + 2 + 2 = 6 (с.). Затем, опираясь на знания учащихся о том, что умножение — это сложение одинаковых слагаемых, учитель выясняет, каким еще действием можно записать решение задачи. Для этого учитель проводит такую беседу:

— Чем интересна сумма 2 + 2 + 2? Что вы заметили? (Слагаемые одинаковые.)

— Сколько одинаковых слагаемых в сумме? (Три.)

— Каким одним действием можно записать решение этой задачи? (Умножением.)

— Запишите решение задачи умножением. (2 · 3 = 6 (с.).)

После решения задач с опорой на предметную деятельность следует перейти к решению задач такого же вида с опорой на иллюстрацию (или символические изображения предметов). Например: «В каждом ряду по 6 парт. Сколько всего парт в 3 таких рядах?»

Задачу можно проиллюстрировать с помощью квадратов, что поможет учащимся быстро найти решение: 6 · 3 = 18 (п.). Заметим, что на начальном этапе выполнение рисунка к задаче на нахождение произведения очень полезно хотя бы потому, что помогает учащимся не только лучше уяснить условие задачи, но и разобраться, какое данное обозначает количество стульев в каждом ряду, а какое — количество рядов. В этой связи весьма полезными являются упражнения на подбор к условию задачи рисунка из ряда предложенных. Например, учащимся предлагается задача: «В одной коробке 4 мяча. Сколько мячей в 3 таких коробках?» — и несколько иллюстраций к ней. Учащимся необходимо найти среди них подходящую.

Заметный обучающий эффект дают также и упражнения на иллюстрацию с помощью предметных множеств или рисунка заданного произведения. Например: «Нарисуйте снежинки и расположите их так, чтобы количество снежинок можно было вычислить с помощью произведения 5 · 4». В дальнейшем, когда учащиеся познакомятся с переместительным свойством умножения, эти задания снова можно использовать для проверки понимания смысла выполняемых действий и предупреждения формализма в знаниях учащихся.

Конкретный смысл действия деления раскрывается при решении задач на деление по содержанию и на равные части. Сначала вводятся задачи на деление по содержанию, а затем задачи на деление на равные части. Это обусловлено тем, что практически легче выполнить операции над множествами при решении задач на деление по содержанию, чем при делении на равные части. Кроме того, операции, выполняемые при делении на равные части, включают в себя действия, выполняемые при решении задач на деление по содержанию.

Ознакомление учащихся с задачами на деление желательно провести с опорой на предметную деятельность. На специально отведенном уроке пропедевтического характера учитель создает в классе определенные жизненные ситуации и ставит перед учащимися задачи, для решения которых необходимо произвести операцию деления по содержанию или на равные части. На этом уроке все действия выполняются только на предметном уровне или с опорой на весьма конкретную наглядность в виде рисунков и схем. В дальнейшем так называемый подход обучения «от рук к голове» будет использоваться достаточно часто, с тем чтобы сформировать у учащихся необходимые ассоциативные связи и облегчить им понимание смысла действия деления. На этом этапе решение задач на деление ограничивается лишь наглядной иллюстрацией и устными ответами. Когда же учащиеся познакомятся со знаком деления и научатся читать и записывать примеры на деление, решение оформляется письменно.

У детей может сложиться представление о двух видах деления (по содержанию и на равные части). Чтобы предупредить это ошибочное представление, учитель на специально отведенном уроке должен провести следующую работу: предложить учащимся решить две задачи — задачи на деление по содержанию и на равные части и сравнить их. С этой целью лучше предлагать задачи с одинаковыми числовыми данными.

Например:

1) 12 апельсинов разложили в пакеты, по 3 апельсина в каждый. Сколько пакетов понадобилось?

2) 12 апельсинов разложили поровну в 3 пакета. Сколько апельсинов в одном пакете?

Учащиеся должны обратить внимание на сходство и различие записей решения этих задач (действия одинаковые, а наименования в ответе разные).
Взаимосвязь между компонентами и результатами действий умножения и деления раскрывается на основе составления и решения задач по рисунку. Например, по данному рисунку можно составить одну задачу на умножение, которая решается так: 3 · 4 = 12 (п.), — и две задачи на деление, которые решаются так: 12 : 3 = 4 (т. ) и 12 : 4 = 3 (п.).

— Чем похожи эти задачи? (Одинаковые числовые данные.)

— Чем эти задачи различаются? (Одна задача решается умножением, две другие — делением).

— Прочитайте решение первой задачи, называя компоненты и результат действия. (Первый множитель 3, второй множитель 4, произведение равно 12.)

Вывод: Если произведение двух чисел разделить на один из множителей, то получится другой множитель.

Для закрепления материала можно предложить задания вида «К примеру 8 · 2 = 16 составьте два примера на деление».

Аналогичные задания на закрепление знания смысла действий умножения и деления и их взаимосвязи желательно как можно чаще включать в содержание урока, особенно на этапе устного счета.

К концу 2 класса учащиеся должны научиться бегло решать простые задачи на деление и умножение всех рассмотренных видов.

Как ребенку быстро и легко выучить таблицу умножения?

Таблицу умножения обычно начинают проходить уже во втором классе, когда дети уверенно освоили сложение. Педагоги обычно говорят, что таблицу нужно учить наизусть, чтобы «отлетала от зубов». Казалось бы, это не так уж и необходимо. Например, умножить 7 на 6 — это то же самое, что просто взять 6 раз по 7 и сложить, не запоминая лишних цифр… Но мало того, что эти сложные операции затянут выполнение контрольных работ, — в обычной жизни, за пределами школы, знание таблицы умножения требуется постоянно. В магазине, дома, а в будущем — и на работе… Так что же, каждый раз строить длинные цепочки вычислений или доставать калькулятор? Нет, выучить таблицу все же придется — зато раз и навсегда.

Как помочь ребенку выучить таблицу умножения?

Помочь ребенку выучить таблицу умножения не так уж сложно, если правильно подойти к обучению. Вот несколько рекомендаций.

Заинтересуйте

У ребенка должна появиться мотивация. Не конфета и прогулка, хотя на усмотрение родителей можно использовать и эти методы, а что-то более значимое и долгосрочное. Сначала продемонстрируйте, в каких случаях, кроме урока в школе, таблица умножения необходима. Например, он хочет угостить пятерых друзей любимыми конфетами — каждому раздать по три, — и сколько же всего конфет принести? Или на день рождения к ребенку собираются три семьи, в каждой по три человека — сколько пар столовых приборов надо приготовить?

Нарисуйте школьнику печальную перспективу: вот в магазине его, доверчивого неуча, обманывает продавец. А вот он на работе не может умножить две цифры и достает калькулятор, а коллеги поднимают его на смех. Вот, в конце концов, он спустя годы решает в классе куда более длинные и сложные примеры, чем предлагают ему пока, и «плавает», потому что не знает основ. Без таблицы умножения в математике дальше не продвинуться! А без математики — не окончить школу и не пойти учиться на того, кем ребенок сейчас мечтает быть…

А чтобы избежать всех этих проблем, надо-то всего лишь взять и выучить эту таблицу! И уж с каким восхищением будут смотреть учителя и одноклассники, которым умножение пока не дается

Объясните суть таблицы умножения

В умножении второе число обозначает, сколько раз нужно сложить первое с самим собой. Это базовый момент, который должен усвоить ребенок, и заодно подстраховка, если он все-таки в ответственный момент забыл какой-то один результат в таблице умножения. Но, как мы уже заметили, постоянно на метод последовательного сложения вместо умножения полагаться не стоит.

Чтобы школьник лучше понял смысл, продемонстрируйте ему, что, например, 4 х 3 — это три ряда по 4 клеточки в каждом. Пусть сосчитает число клеточек — это и будет произведение цифр.

Успокойте и упростите

Наверняка ребенок ужаснется, увидев столбцы примеров на умножение сзади на обложке своей тетради: «И это все я должен знать назубок?!» Объясните, что все не так ужасно, как выглядит, ведь от перемены мест множителей произведение не меняется. То есть достаточно запомнить, сколько будет 3 х 4, чтобы понять, сколько — 4 х 3. А значит, учить придется не столь и много.

Используйте таблицу Пифагора

Вместо длинных рядов чисел продемонстрируйте таблицу Пифагора. В ее строках и столбцах — множители, а на пересечении — произведение. Покажите ребенку, как с ней работать, лучше всего — с карандашом: ищешь первое число по вертикали, второе — по горизонтали, а там, где они «встречаются», и есть значение произведения. Какую цифру искать в столбце, а какую — в строке, совершенно неважно, ведь перемена мест множителей роли не играет.

Эта таблица наглядна, и учиться по ней гораздо приятнее, особенно если у школьника хорошо развита визуальная память. Да и знания по ней можно проверить за пару секунд.

Чтобы заинтересовать ребенка, можно рассказать, что таблице умножения почти 4 тыс. лет, и нашли ее в Древнем Вавилоне. Только та таблица была гораздо более сложной и громоздкой — 60-ричной, а не десятичной, какую используют в России. Между прочим, в Великобритании таблица заканчивается не на 10 х 10, как у нас, а на 12 х 12, потому что там другие система мер длины и денежное обращение (фут равен 12 дюймам, шиллинг — 12 пенсам). И в английском образовании на изучение таблицы умножения ребенку дают время аж до 11 лет.

Не перегружайте

Дети хорошо усваивают информацию, в том числе для долговременной памяти. Но переутомлять ребенка не стоит. Выделите по одному-два дня на каждый кусок таблицы умножения — например, сегодня мы выучим таблицу на 2, завтра закрепим, послезавтра начнем — на 3, и так далее.

Важно начинать с простого. Разделавшись с таблицей на 3 и 4, младшеклассник уже усвоит основные принципы таблицы умножения, и дальше будет легче.

Повторяйте

Чем чаще, тем лучше: если учить таблицу умножения с разбросом в пять дней, толку не будет. Для создания нейронных связей в мозгу нужны регулярность и привычка. Пусть ребенок не только отвечает на ваши вопросы, но и регулярно натыкается на таблицу. Например, можно повесить красочный плакат в его комнате.

Проверяя знания ребенка, также двигайтесь от простого к более сложному: вначале, задавая ему вопрос «Сколько будет 3 х 2?», давайте ему больше времени на размышление. На первых порах следом за «3 х 2» спрашивайте «3 х 3», а со временем, когда школьник усвоит таблицу умножения лучше, предлагайте примеры вразнобой.

Укажите на закономерности

Некоторые принципы умножения помогут сократить время на лишние вычислительные операции:

1. Умножив на 0, мы получим 0, на 1 — то же число, а на 10 — то же число, но с ноликом на конце.
2. Умножить на 2 — это сложить число с самим собой.
3. Умножить на 4 — это умножить на 2 и еще раз на 2. Поскольку ребенок пока не научился умножать двузначные числа, но уже хорошо умеет складывать, ему будет проще умножить на 2 и прибавить к получившемуся числу такое же. Например, 6 х 4 = 6 х 2 + 6 х 2 = 12 + 12 = 24.
4. При умножении на 5 произведение (результат умножения) заканчивается на 5 или 0, причем поочередно — например, 1 х 5 = 5, 2 х 5 = 10, 3 х 5 = 15.
5. При умножении на 9 проще умножить на 10 (то есть приставить к исходному числу 0), а потом вычесть это исходное число: 9 х 9 = 9 х 10 — 9 = 81.
6. Кстати, когда ребенок чуть освоится с умножением и начнет решать примеры подлиннее, объясните: там, где есть умножение, сложение и вычитание, по умолчанию сначала выполняется умножение. Если только нет скобок — действие в них как раз должно быть совершено первым. Так, в примере 9 х (10 — 9) результат будет уже другой: сначала решается то, что в скобках, а потом уже выполняется умножение: 9 х 1 = 9.
7. При умножении на 11 (такие операции пригодятся ребенку чуть позже) изначальная цифра удваивается: 6 х 11 = 66, 8 х 11 = 88. Если речь о двухзначных числах, тоже можно обойтись без калькулятора: возьмите умножаемое число и между двумя его цифрами вставьте их сумму. Например: 12 х 11 = 132 (между 1 и 2 — 3).

Запоминание закономерностей таблицы умножения — еще один способ успокоить ребенка. Если он что-то и забудет, результат можно будет «вывести».

5 эффективных способов выучить таблицу умножения

Не ограничивайтесь одним методом объяснения и запоминания. Научить можно разными способами:

1. На пальцах и палочках

С этого стоит начинать знакомство с таблицей умножения. Легче всего показать «два раза по два» на пальцах или каких-то предметах. Правда, с более сложными вычислениями — например, с таблицей на 8 — будет труднее. муторнее.

Но при этом по пальцам легко освоить умножение на 9. Расположите руки вниз ладонями и мысленно пронумеруйте пальцы слева направо от 1 до 10. Загните палец, которому соответствует число, на которое нужно умножить 9. Например, если пример звучит как «9 х 5», это будет большой палец левой руки. Теперь считайте, что все пальцы слева (4) — десятки, а справа (5) — единицы. Таким образом, ответ — 45.

2. Через приложения на телефоне

Современным школьникам, возможно, больше понравится изучать таблицу умножения на экране любимого гаджета. Упражняться можно не только в учебное время, но и на каникулах или в транспорте по дороге в школу — скорее всего, такую тренировку ученик будет воспринимать скорее как игру, чем как домашнее задание, и ему самому будет интереснее.

Приложений немало: в некоторых ребенку одновременно предлагается решить пример, уложиться в предложенное время и накопить баллы/призы. Азарт, как известно, — отличный стимул.

3. По карточкам

Это более «древний», но тоже близкий к игровому способ запоминания. Распечатайте примеры из таблицы умножения на карточках: на одной стороне — пример, на другой — ответ (только проследите, чтобы цифры в ответе не просвечивали, лучше взять плотный картон). Разложите карточки в ряд и предложите ребенку выбрать пример. Если он отвечает верно, убирайте карточку с поля, если нет — перекладывайте ее в конец ряда. Игра заканчивается, когда карточек на столе не остается. Эту игру можно проводить и на время — пусть ребенок соревнуется сам с собой или с другими детьми.

4. По стихам

Стишки про таблицу умножения есть в интернете — в такой форме любая теория запоминается лучше. Например: «Осьминоги шли купаться: дважды восемь ног — шестнадцать», «Два атлета взяли гири, это — дважды два — четыре». Этот способ лучше использовать как вспомогательный, в дополнение к остальным — не будешь же придумывать стишок на каждый пример. Впрочем, были бы желание и фантазия.

5. По играм и мультикам

Одна из популярных игр — «Математическое лото». В нее стоит играть группой детей, находящихся примерно на одном уровне знаний таблицы умножения. Механика примерно та же, что с карточками, только на одних карточках пишутся примеры, на других — ответ. Раздайте детям те, что с ответами, — например, по 4 числа-ответа на каждой карточке, — а те, что с примерами, оставьте себе и поочередно показывайте группе. Пусть тот, кто найдет в карточке ответ, зачеркнет это число и назовет вслух. Например, ведущий говорит: «9 х 9». Тот, у кого в карточке есть число 81, зачеркивает его и называет вслух. Выигрывает тот, кто первым зачеркнул все числа в своей карточке и при этом решил примеры верно.

Еще больше ребенка может заинтересовать игра «Золотоискатели». У нее интересная «легенда»: искатели сокровищ нашли остров, где спрятан клад, но должны тщательно просчитывать ходы, чтобы первыми находить лучшие тайники. Для игры требуются поле — незаполненная таблица Пифагора (можно нарисовать квадрат с ячейками самостоятельно, десяток произвольно выбранных клеток раскрасьте желтым цветом), игровой кубик и ручка.

Первый игрок бросает кубик — сколько ему выпало, столько шагов от старта в любую сторону (но в одном направлении) он может сделать. В клетку, на которой остановился, игрок вписывает произведение чисел, на пересечении которых находится. Это будет количество монет, которые он нашел. Если удалось остановиться на желтой клетке — игрок нашел сундучок, и сумма удваивается. Причем если на этой клетке остановится потом другой игрок (а по правилам он имеет на это право), монет из сундучка он уже не получит.

Следующий игрок, бросая кубик, отсчитывает шаги уже от той клетки, где остановился соперник. Игра заканчивается, когда остается пять пустых клеток. Естественно, выигрывает тот, кто собрал больше монет.

Увлекательна и «Борьба прямоугольников». Это игра на двоих. Нужны только лист бумаги в клеточку, два фломастера, два кубика и по одному цветному карандашу для обоих участников. Каждый игрок по очереди бросает по два кубика. Выпавшие цифры — множители. Игрок рисует на листке со своей стороны прямоугольник или квадрат, стороны которого по количеству клеток равны числам на кубиках. В середине фигуры записывается ее площадь, то есть произведение чисел. Когда на листе не остается места для новых фигур, игру можно завершить. Выиграл тот, кому повезло заполнить фигурами больше клеточек на бумаге.

Другая, менее творческая игра, предлагает участникам из написанных на плакате чисел от 1 до 90 назвать те, что встречаются в таблице умножения на то или иное число. Можно устроить соревнование на время — раздать плакаты нескольким детям и предложить каждому вычеркивать или подчеркивать числа.

Можно заказать в интернете или найти в магазине уже готовые настольные игры на тему умножения — «Много-много» или «Цветариум».

Онлайн-игры для запоминания таблицы умножения, которые можно свободно отыскать в Сети, ничего не скачивая, схожи механикой с играми в мобильных приложениях. Ребенку даются все те же примеры на умножение, но в картинках (вместо 3 х 2 на «доске» рисуется три звездочки, а потом «х 2»), или тренажер на время с результатами: игрок решает сгенерированные компьютером примеры и видит в табличке, сколько дал правильных и неправильных ответов.

По тому же принципу построены развивающие «арифметические» мультфильмы: на экране появляется то или иное, меняющееся количество птичек/зверюшек/конфет, фоном идет веселая тематическая песенка. Но это, опять же, скорее для закрепления уже усвоенного материала, чем для его изучения.

Итак, ничего сложного и ужасного — чередуя разные методы освоения материала, вы постепенно достигнете успеха. Не настраивайтесь на быстрый результат — вероятно, до того, как школьник сможет уверенно отвечать на любой вопрос по таблице, пройдет не меньше месяца. Зато результат будет приносить плоды всю жизнь.

Математика и логика для детей 7-13 лет

Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате

узнать подробнее

Сложение, вычитание, умножение и деление: правила

Может быть полезно понять, как использовать различных математических операции , поскольку их можно использовать каждый день во многих различных ситуациях, точно так же, как вычисление того, как можно разделить поровну пакет со сладостями.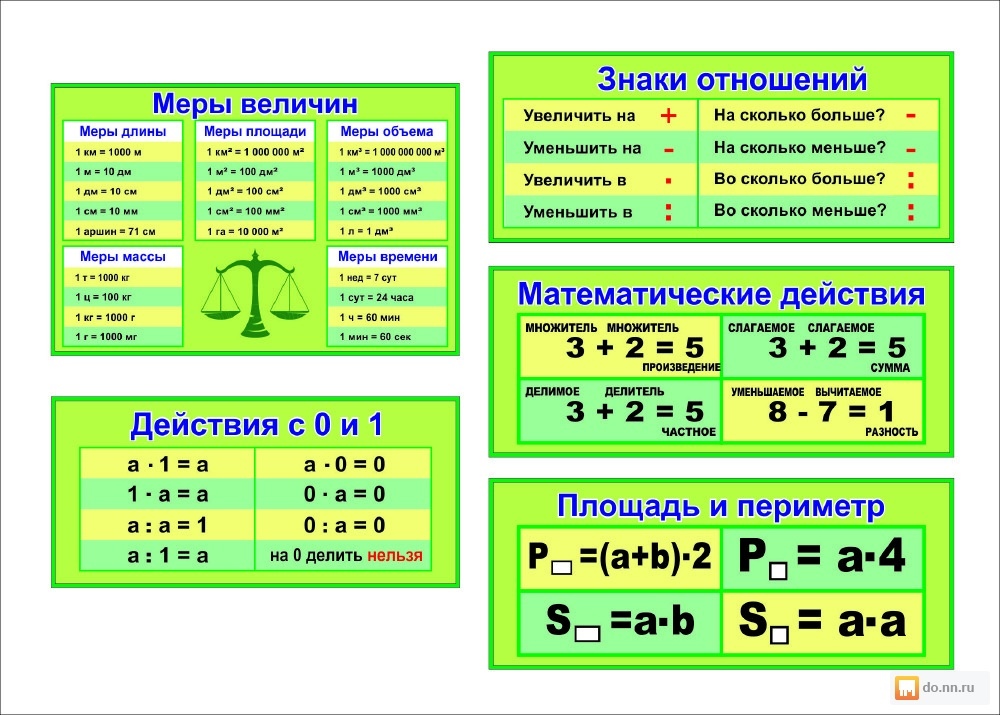 между группой людей.

Определение сложения, вычитания, умножения и деления

Сложение, вычитание, умножение и деление — все типы операций, используемых в математике.

Сложение

Сложение — это тип операции, результатом которой является сумма двух или более чисел. Существует знак, обозначающий операцию сложения, называемый знаком плюс, то есть +.

Вычитание

Вычитание — это тип операции, результатом которой является нахождение разницы между двумя числами. Знак, обозначающий операцию вычитания, называется знаком минус и выглядит он так: -.

Умножение

Умножение — это операция, требующая сложения равными группами, в результате умножения получается произведение. Знак, обозначающий операцию умножения, можно назвать знаком умножения, и он выглядит так: ×.

Деление

Деление — операция, обратная умножению, заключается в разбиении числа на равные части. Знак, обозначающий операцию деления, называется просто знаком деления и выглядит так: ÷.

Правила сложения, вычитания, умножения и деления

Существуют различные правила и методы, которые могут быть полезны при использовании каждой из этих операций.

Сложение

При сложении двух или более чисел можно использовать метод сложения столбцов. Это включает в себя размещение чисел одно над другим в столбце, затем вы работаете справа налево, добавляя числа, которые находятся в одном столбце.

Вычислить 122+552

Решение:

Для начала вы можете расположить числа друг над другом: с 2 и 2:

122+5524

Теперь переходим к 2 и 5:

122+55274

И, наконец, 5 и 1:

122+552672

9 0002 Следовательно, 122+552=672

Если два числа, которые вы добавляете, больше 10, вы можете перенести это число.

Вычитание

При вычитании двух чисел можно также использовать метод столбца; метод вычитания столбцов. Это работает так же, как метод сложения столбцов, однако вы вычитаете числа, а не добавляете их.

Вычислить 538-214

Решение:

Для начала вы можете расположить числа друг над другом, поместив число, от которого вы вычитаете, сверху:

538-214

Теперь работает справа влево отнять одно число от другого, начиная с 8 и 4:

538-2144

Теперь переходим к 3 и 1:

538-21424

И, наконец, 5 и 2:

538-214324

Следовательно, 5 38-214=324

Если вычитаемое число выше числа, из которого вычитается, нужно будет взять цифру из столбца слева.

Умножение

При умножении двух чисел можно использовать различные методы, включая метод сетки. Это включает в себя разбиение двух чисел и размещение их в сетке. Затем вы выполняете отдельные умножения, а затем складываете их все вместе.

Вычислить 23×42

Решение:

Для начала нарисуйте сетку, разбейте свои числа и поместите их в сетку следующим образом:

	20	3
40
2

Заполнить в сетке вы просто умножаете каждое число в столбцах:

	20	3
40	800	120
2	40	6

Теперь вы можете сложить все значения вместе, чтобы найти ответ на вопрос, может быть проще сделать это пошагово:

800+120=920

40+6=46

920+46=966

Следовательно, 23×42=966

Деление

9 0002 При делении числа на другой вы можете использовать метод, называемый коротким делением, этот метод лучше всего работает, когда вы делите число на 10 или меньше. Короткое деление предполагает мысленное деление числа на более мелкие этапы.

Вычислить 306÷9

Решение:

Для начала вы можете нарисовать свой расчет, записав число, на которое вы делите, слева, а число, которое вы делите, запишите справа, как показано ниже:

9306

Теперь вам нужно проработать число, которое вы делите по одной единице за раз, начните с выяснения, сколько раз 9 может перейти в 3. Поскольку это невозможно, вам нужно перенести 3 к следующему блоку:

93306

Теперь вы можете подумать о том, сколько раз 9 может перейти в 30. 9 входит в 30 три раза с остатком три:

9×3=27

Затем это можно записать в ваше деление, как показано ниже, с помощью делимое число записывается над вычислением, а остаток 3 переносится на 6:

9333036

Наконец, вы можете вычислить, сколько раз 9 входит в число 36:

9×4=36

93433036

900 02 Следовательно, 306÷9=34

Взаимосвязи сложения, вычитания, умножения и деления

Операции могут иметь взаимосвязи друг с другом. Существует связь между сложением и вычитанием, а также связь между умножением и делением.

Сложение и вычитание

Сложение и вычитание можно считать обратными друг другу. Это просто означает, что операции противоположны, вы можете отменить сложение, вычитая то же число, и наоборот!

Умножение и деление

Умножение и деление также считаются обратными друг другу, если вы хотите отменить умножение, вы можете просто разделить число.

Примеры сложения, вычитания, умножения и деления

Вычислить 647+278

Решение:

Для начала вы можете расположить числа друг над другом:

647+278 90 005

Теперь работает справа слева, сложите два горизонтальных числа вместе. Начиная с 7 и 8, так как они равны 15, вам нужно перенести 1 на:

647+27815

Теперь вам нужно сложить вместе 4, 7 и 1, опять же, поскольку это больше 10, вам нужно перенести единицу:

647+2781125

Наконец, вы можете сложить вместе 6, 2 и 1:

647+27811925

Вычислить 732-426

Решение:

Для начала вы можете расположить числа друг над другом, поместив число, из которого вы вычитаете, сверху: 9000 5

732 -426

Теперь, работая справа налево, вычтите одно число из другого, начиная с 2 и 6. Поскольку 6 больше двух, вам нужно позаимствовать цифру из столбца слева:

72312-4266

Теперь из 2 можно вычесть 2:

72312-42606

Наконец, из 7 можно вычесть 4:

72312-426306 90 005

Вычислить 53×35

Решение:

Для начала нарисуйте сетку, разбейте свои числа и поместите их в сетку следующим образом: 5

Чтобы заполнить таблицу, просто умножьте каждое число в столбцах:

9 0104

	50	3
30	1500	90
5	250	15

Теперь вы можете сложить все значения вместе, чтобы найти ответ на вопрос, может быть проще сделать это пошагово:

1500+90=1590

250+15=265

1590+265=1855

Вычислить 434÷7

Решение:

Начнем с того, что выпишем сумму, используя краткую метод деления:

7434

Теперь начнем с подсчитав, сколько раз 7 входит в 4, это невозможно, поэтому вы можете перенести 4 в 3:

74434

Затем вы можете посмотреть, сколько раз 7 может войти в 43:

7×6= 42

Это оставляет нам остаток от 1, который можно перенести на 4:

7644314

Наконец, подсчитайте, сколько раз 7 может составить 14:

7×2=14

76244314

Следовательно, 434÷7=62

Применение s сложения, вычитания, умножения и деления

Эти операции часто используются в повседневной жизни, давайте рассмотрим несколько примеров:

У Эми 326 наклеек в коллекции наклеек, у Клэр 213 наклеек. Сколько наклеек у них было бы, если бы они объединили свои коллекции?

Решение:

Запуск с размещения двух чисел друг друга:

326+213

Теперь вы можете добавить их вместе, работая слева, начиная с 6 и 3:

326+2139

Проработайте числа:

326+213539

Таким образом, если Эми и Клэр объединит свои коллекции, в их коллекции будет 539 наклеек .

У Сэма 142 конфеты, он отдает своему другу 54, сколько конфет осталось у Сэма?

Решение:

Чтобы узнать, сколько конфет у Сэма, мы можем вычесть 54 из 142. Начните с размещения двух чисел друг над другом:

142-54

Теперь действуем справа налево, вычесть одно число из другого. Не забывайте, так как 2 меньше 4, вам нужно взять единицу из столбца слева:

13412-548

Теперь вы можете двигаться дальше, опять же, поскольку 3 меньше 5, вам нужно будет взять единица из столбца слева:

113412-5488

Следовательно, у Сэма осталось 88 конфет .

Дейв готовит на 12 человек, но по его рецепту он рассчитан только на 4. Если по рецепту требуется 72 грамма пасты, сколько пасты понадобится Дейву?

Решение:

Чтобы узнать, сколько пасты понадобится Дейву для его рецепта, мы можем использовать операцию умножения. Поскольку 4 входит в 12, 3 раза, Дейву понадобится в три раза больше, чем указано в рецепте. Для этого мы можем использовать метод сетки:

9 0127

	70	2
3	210	6

Теперь вы можете сложить два числа вместе:

210+6=216

Следовательно, Дейву понадобится . 216 грамм пасты на 12 персон.

Барбара обедает с тремя друзьями, счет составляет 188 фунтов стерлингов, и они решают разделить его поровну. Сколько платит каждый человек?

Решение:

Для начала запишите задачу, используя метод короткого деления. Счет составил 188 фунтов стерлингов, и его делят между 4 людьми, поэтому его можно записать следующим образом:

4188

Теперь сделайте первый шаг и посмотрите, сколько раз 4 может войти в первое число слева. Поскольку 4 не может превратиться в 1, 1 можно перенести:

41188

Теперь подсчитайте, сколько раз 4 может превратиться в 18:

4×4=16

Это оставляет нам остаток 2:

4411828

Наконец, сколько раз 4 можно ввести в число 28:

4×7=28

44711828

Это означает, что каждому человеку нужно будет заплатить 47 фунтов стерлингов .

Сложение, вычитание, умножение и деление – основные выводы

• Существует множество различных типов математических операций, в том числе:
  • Сложение – операция, результатом которой является сумма двух или более чисел.
  • Вычитание — операция, результатом которой является нахождение разницы между двумя числами.
  • Умножение, которое представляет собой операцию, требующую сложения в равных группах, в результате умножения получается произведение.
  • Деление — операция, обратная умножению, включает в себя разбиение числа на равные части.

каков порядок действий в математике – Домашнее напряжение

• 1 каков порядок действий в математике
  • 1.1 Каков порядок действий? Определение Правила Примеры Факты
  • 1.2 Порядок действий – Википедия
  • 1.3 Рабочий пример Порядок действий (PEMDAS) – Академия Хана
  • 1.4 Порядок действий – Basic-mathematics.com
  • 1.5 Введение в порядок действий (видео) | Khan Academy
  • 1.6 Порядок действий – PEMDAS – Mathematics is Fun
  • 1.7 Порядок действий Что это такое и зачем это нужно | Purplemath
  • 1.8 Порядок действий по темам алгебры – GCFGlobal.org
  • 1.9 Каков порядок действий в математике? – Определение…

Каков порядок работы? Правила определения Примеры Факты

Порядок операций — это правило, которое сообщает нам последовательность, в которой мы должны решать выражение с помощью нескольких операций. Один из способов запомнить этот порядок — это PEMDAS. Каждая буква в PEMDAS представляет собой математическую операцию. Порядок операций Шаги в скобках Первый шаг — решить операцию в скобках или скобках.

Порядок действий – Википедия

В математике и компьютерном программировании порядок операций (или приоритет операторов) представляет собой набор правил, отражающих соглашения о том, какие процедуры следует выполнять в первую очередь для вычисления определенного математического выражения.

Рабочий пример Порядок действий (PEMDAS) – Академия Хана

Порядок действий (PEMDAS) необходим для решения сложных математических задач. PEMDAS расшифровывается как умножение и деление экспонентных скобок (тот же уровень) и сложение и вычитание (тот же уровень). Следуя этим шагам, вы сможете упростить и точно решить математические выражения и обеспечить правильный окончательный ответ.

Порядок операций — Basic-mathematics.com

Порядок операций — это определенный порядок или набор правил, согласованных математиками, которым необходимо следовать при выполнении арифметических операций для упрощения выражений. Правила порядка операций Вот порядок выполнения операций, которым вы должны следовать в указанном ниже порядке, чтобы избежать разных ответов при упрощении выражений.

Ознакомление с порядком операций (видео) | Академия Хана

Этот пример показывает шаги и поясняет цель порядка операций, так что существует ОДИН способ интерпретировать математическое утверждение. Создано Салом Ханом. Вопросы Советы и благодарности

Порядок действий — PEMDAS — Математика — это весело

Операции PEMDAS Операции означают такие вещи, как сложение, вычитание, умножение, деление, квадрат и т. д. Если это не число, то, вероятно, это операция. Но когда вы видите что-то вроде … 7 + (6 × 5 2 + 3) … какую часть вы должны вычислить в первую очередь? Начать слева и идти направо? Или я иду справа налево?

Оперативный порядок Что это такое и зачем он нужен | Purplemath

Операции сложения, вычитания, умножения, деления, возведения в степень и группировки; порядок этих операций указывает, какие операции имеют приоритет над другими операциями (т.