Урок 2. Простые арифметические закономерности
Чтобы уметь решать сложные арифметические задачи, нужно для начала хорошенько усвоить некоторые базовые закономерности. Скорее всего, они у вас не вызовут трудностей.
Однако уделите этим задачам должное внимание, поскольку от того, как быстро вы сможете считать простейшие примеры, напрямую зависит ваше умение быстро выполнять более сложные математические операции.
Счет на автомате
Существует определенный набор простейших арифметических правил и закономерностей, которые не только нужно знать для устного счета, но и постоянно держать в голове, чтобы в нужный момент оперативно применить самый эффективный алгоритм. Для этого необходимо довести их использование до автоматизма, закрепить в машинальной памяти, чтобы от решения самых простых примеров успешно перейти к более сложным арифметическим действиям.
Вот основные алгоритмы, которые нужно знать, помнить и применять мгновенно, автоматически:
Вычитание 7, 8, 9. Чтобы вычесть 9 из любого числа, нужно вычесть из него 10 и прибавить 1. Чтобы вычесть 8 из любого числа, нужно вычесть из него 10 и прибавить 2. Чтобы вычесть 7 из любого числа, нужно вычесть из него 10 и прибавить 3. Если обычно вы считаете по-другому, то для лучшего результата вам нужно привыкнуть к этому новому способу.
Чтобы вычесть 9 из любого числа, нужно вычесть из него 10 и прибавить 1. Чтобы вычесть 8 из любого числа, нужно вычесть из него 10 и прибавить 2. Чтобы вычесть 7 из любого числа, нужно вычесть из него 10 и прибавить 3. Если обычно вы считаете по-другому, то для лучшего результата вам нужно привыкнуть к этому новому способу.
Умножение на 9. Быстро умножить любое число на 9 можно следующим образом: сначала умножьте это число на 10 (просто добавьте ноль в конце), а затем вычтите из результата само число. Например: 89*9=890-89=801. Эту операцию необходимо довести до автоматизма.
Умножение на 2. Для устного счета очень важно уметь быстро умножать любое число на 2. Для умножения на 2 некруглых чисел пробуйте округлять их до ближайших более удобных. Так 139*2 проще считать, если сначала умножить 140 на 2 (140*2=280), а потом вычесть 1*2=2 (именно 1 нужно прибавить к 139, чтобы получить 140). Итого: 140*2-1*2=280-2=278.
Деление на 2. Для устного счета также важно уметь быстро делить любое число на 2. Несмотря на то, что многим умножение и деление на 2 дается достаточно просто, в сложных случаях так же пытайтесь округлять числа. Например, чтобы разделить 198 на 2, нужно сначала разделить 200 (это 198+2) на 2 и отнять 1 (1 мы получили, разделив прибавленные 2 на 2). Итого: 198/2=200/2-2/2=100-1=99.
Для устного счета также важно уметь быстро делить любое число на 2. Несмотря на то, что многим умножение и деление на 2 дается достаточно просто, в сложных случаях так же пытайтесь округлять числа. Например, чтобы разделить 198 на 2, нужно сначала разделить 200 (это 198+2) на 2 и отнять 1 (1 мы получили, разделив прибавленные 2 на 2). Итого: 198/2=200/2-2/2=100-1=99.
Деление и умножение на 4 и 8.
Умножение на 5. Умножать на 5 очень просто. Умножение на 5, и деление на 2 – это практически одно и то же. Так 88*5=440, а 88/2=44, поэтому всегда умножайте на 5, поделив число на 2 и умножив его на 10.
Умножение на 25. Умножение на 25 соответствует делению на 4 (с последующим умножением на 100). Так 120*25 = 120/4*100=30*100=3000.
Умножение на однозначные числа. Чтобы быстро считать в уме, полезно уметь умножать двузначные и трехзначные числа на однозначные. Для этого нужно умножать двух- или трехзначное число поразрядно. Например, умножим 83*7. Для этого сначала умножим 8 на 7 (и допишем ноль, так как 8 — разряд десятков), и прибавим к этому числу произведение 3 и 7. Таким образом, 83*7=80*7 +3*7= 560+21=581. Возьмем более сложный пример: 236*3. Итак, умножаем сложное число на 3 по разрядно: 200*3+30*3+6*3=600+90+18=708.
Например, умножим 83*7. Для этого сначала умножим 8 на 7 (и допишем ноль, так как 8 — разряд десятков), и прибавим к этому числу произведение 3 и 7. Таким образом, 83*7=80*7 +3*7= 560+21=581. Возьмем более сложный пример: 236*3. Итак, умножаем сложное число на 3 по разрядно: 200*3+30*3+6*3=600+90+18=708.
Определение диапазонов. Чтобы не запутаться в алгоритмах и по ошибке не выдать совсем неверный ответ, важно уметь строить примерный диапазон ответов. Так умножение однозначных чисел друг на друга может дать результат не более 90 (9*9=81), двузначных — не более 10 000 (99*99=9801), трехзначных не более — 1 000 000 (999*999=998001).
Деление 1000 на 2, 4, 8, 16. И наконец, полезно знать деление чисел, кратных 10 на числа, кратные двум: 1000=2*500=4*250=8*125=16*62,5.
Примечание. Эти закономерности являются ключевыми для счета в уме. Если какая-то из них вызывает у вас трудность – потренируйтесь, так как дальнейшие алгоритмы потребуют быстрого совершения описанных выше арифметических операций.
Тренировка
Если вы хотите прокачать свои умения по теме данного урока, можете использовать следующую игру. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что числа каждый раз разные.
Перед тем как начать игру, рекомендуем зарегистрироваться, чтобы результат был сохранен в вашей истории, и вы смогли бы видеть собственный прогресс.
Cтатистика На весь экран
Евгений Буянов
← 1 Внимание и концентрация3 Традиционное умножение →
Тест-тренажёр «Умножение и деление на 2» онлайн для 2 класса от ЛогикЛайк!
Математика / 2 класс / Тесты
Онлайн-тест на умножение и деление для 2 класса отличная подготовка к математическому диктанту в школе. Тест может быть использован как для изучения, так и для повторения темы.
В тесте используются именно те формулировки заданий, которые учителя применяют на уроках. Задания раскрывают понимание ребенком взаимосвязи умножения и деления, знание компонентов этих действий, а также умения решать задачи.
Задания раскрывают понимание ребенком взаимосвязи умножения и деления, знание компонентов этих действий, а также умения решать задачи.
Результат теста:
Более 2500 заданий для развития математических способностей и логического мышления — в онлайн‑курсе ЛогикЛайк.
Тест составлен на основе программного материала по математике для учеников 2 класса и соответствует требованиям ФГОС.
Найди произведение чисел 4 и 2.
Варианты ответов:
а) 6
б) 8
в) 7
г) 9
Узнать ответ
Ответ: б) 8.
Первый множитель 7, второй множитель 2.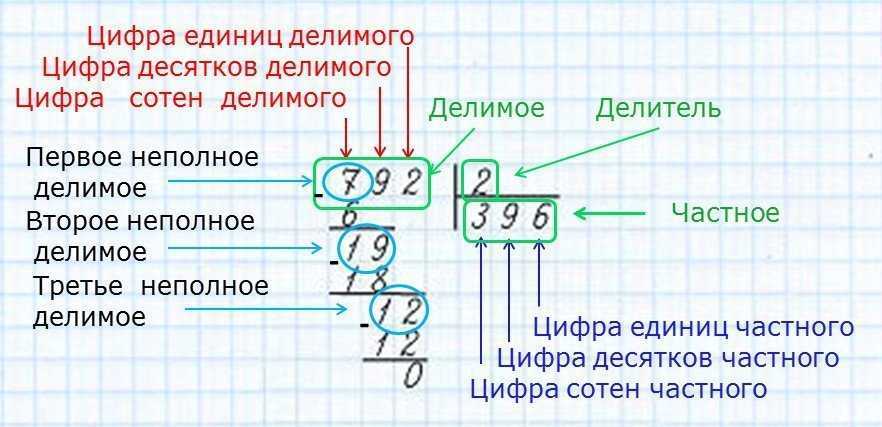 Чему равно произведение?
Чему равно произведение?
Варианты ответов:
а) 15
б) 12
в) 14
Узнать ответ
Ответ: в) 14.
На сколько нужно умножить 2, чтобы получить 18?
Варианты ответов:
а) 9
б) 7
в) 8
г) 6
Узнать ответ
Ответ: а) 9.
Какое число умножили на 2 и получили 16?
Варианты ответов:
а) 6
б) 7
в) 9
г) 8
Узнать ответ
Ответ: г) 8.
Выбери множители, произведение которых равно 12.
Варианты ответов:
а) 6 и 4
б) 6 и 2
в) 2 и 10
Узнать ответ
Ответ: б) 6 и 2.
Какое число надо вставить в «окошко», чтобы равенство было верным?
14 : ☐ = 7
Варианты ответов:
а) 3
б) 2
в) 4
Узнать ответ
Ответ: б) 2.
Найди частное чисел 10 и 2.
Варианты ответов:
а) 5
б) 6
в) 8
г) 7
Узнать ответ
Ответ: а) 5.
В каком примере ошибка?
Варианты ответов:
а) 18 : 2 = 7
б) 9 × 2 = 18
в) 16 : 2 = 8
Узнать ответ
Ответ: а) 18 : 2 = 7.
Близнецам Ване и Вове подарили 14 подарков. Каждому досталось поровну. Сколько подарков получил каждый мальчик?
Каждому досталось поровну. Сколько подарков получил каждый мальчик?
Варианты ответов:
а) 8
б) 6
в) 7
Узнать ответ
Ответ: в) 7.
В бидоне было 16 литров кваса. Сколько литров кваса выпил дедушка, если осталась половина?
Варианты ответов:
б) 7 литров
в) 8 литров
Узнать ответ
Ответ: в) 8 литров.
Ещё больше онлайн-тестов смотрите в разделе «Тесты по математике для 2 класса».
Порядок операций — Триггерные идентификаторы
Порядок операций: Порядок операций — это правила, которым мы следуем при выполнении операций над математической формулой. Когда в любом выражении есть более одной операции, мы используем порядок операций.
Когда в уравнении есть несколько арифметических операций, мы используем правило DOMAS .
В правиле BODMAS
- Всегда сначала решать скобки
- Затем решить Порядок действий
- Подразделение
- Умножение
- Дополнение
- Вычитание
- Скобки
- Экспоненты
- Умножение
- Подразделение
- Дополнение
- Вычитание
Если кто-то попросит вас упростить уравнение типа «3 – 2 × 4», то возникает общий вопрос, что я могу сделать в первую очередь. Должен ли я сначала вычесть, а затем умножить «(3-2) × 4 = 1 × 4 = 4»?
Или сначала умножить, а затем вычесть «3 -2 × 4=3 – 8 = -5»?
Какой ответ правильный? Кажется, что ответ зависит от того, под каким углом вы смотрите на проблему. В математике один вопрос имеет один точный ответ и не может дать несколько ответов одной задачи, поэтому для решения этой задачи мы используем « порядок операции ». Порядок работы: круглые скобки, показатели степени (корень, степень), деление, умножение, сложение и вычитание. В уравнениях, где присутствуют все операции, правильный порядок решения уравнений сначала раскройте круглые скобки, затем решите показатели степени, затем вы должны решить деление, затем вы должны решить умножение, а затем вы должны решить сложение, а затем вычитание.
В математике один вопрос имеет один точный ответ и не может дать несколько ответов одной задачи, поэтому для решения этой задачи мы используем « порядок операции ». Порядок работы: круглые скобки, показатели степени (корень, степень), деление, умножение, сложение и вычитание. В уравнениях, где присутствуют все операции, правильный порядок решения уравнений сначала раскройте круглые скобки, затем решите показатели степени, затем вы должны решить деление, затем вы должны решить умножение, а затем вы должны решить сложение, а затем вычитание.
Примечание: для умножения или деления ( всегда решать вопросы слева направо).
Сложение и вычитание ( всегда решать уравнения слева направо ).
Как запомнить порядок действий Обычный метод запоминания порядка действий PEMDAS — использование сокращений (« ПОЖАЛУЙСТА, ИЗВИНИТЕ МОЮ ДОРОГУЮ ТЕТУ САЛЛИ »).
- Сначала решить скобки.
Всегда обращайте внимание на круглые скобки в уравнении. Если в уравнении есть круглые скобки, сначала решите их, потому что они имеют более высокий приоритет, чем операции другого порядка.
- Правильный путь:
Правильный способ решения уравнений — сначала решить скобки, затем показатели степени, умножение, деление, сложение и вычитание. Вы всегда будете использовать правило DOMAS для решения алгебраических уравнений.
5 × (8 + 4) (сначала раскройте скобки)
5 × 12 = 60 (затем умножьте уравнение)
- Неправильно:
Если вы не следуете правилу DOMAS, ваш ответ неверен.
5× (8 + 4) = 40 + 4 = 44
- Решение показателей степени (степень, корень) перед сложением, вычитанием, умножением и делением.

- Правильный путь
Правильный способ решения уравнений — сначала решить скобки, затем показатели степени, умножение, деление, сложение и вычитание. Вы всегда будете использовать правило
4 × 3 2 (сначала решить показатели степени)
4 × 9 = 36 (затем умножить выражение)
- Неверный путь
6
Если сначала решить умножение, а затем решить показатель степени, то ответ будет неверным. Если вы не следуете правилу DOMAS, ваш ответ неверен.
4 × 3 2 = 12 2 = 144
Умножение и деление Теперь посмотрите на любой оператор деления и умножения в уравнении. Необязательно, чтобы деление всегда предшествовало умножению, эти операторы решаются слева направо. Посмотрите слева направо, если какой-либо оператор (умножение или деление) идет первым, решите их. Они имеют более низкий приоритет, чем экспонента и круглые скобки.
Они имеют более низкий приоритет, чем экспонента и круглые скобки.
- Правильный путь
Правильный способ решения уравнений — сначала решить скобки, затем показатели степени, умножение, деление, сложение и вычитание. Вы всегда будете использовать правило DOMAS для решения алгебраических уравнений.
20 ÷ 5× 2 (смотрим слева направо, какой оператор идет первым)
4 × 2 = 8
20 × 2÷ 5 (смотрим слева направо, какой оператор идет первым )
40 ÷ 5 =8 ( Ответ всегда один и тот же )
Сложение и вычитание
То же самое в случае сложения и вычитания, мы всегда будем идти слева направо. Просто посмотрите на ниже:
10 + 4 – 6
Посмотрите слева направо, сначала решите 10 + 4, затем вычтите из 6.
Узнайте больше об идентификаторах Trig.
Правило BODMAS (скобка, выключение, деление, умножение, сложение, вычитание)
В математике при решении арифметических уравнений, т.
BODMAS — это аббревиатура, имеющая значение скобок, порядков или степеней, деления или умножения, сложения или вычитания. Он дает порядок операций, которые мы должны выполнять при решении задач.
Следовательно, сначала мы должны решить скобки, затем мы должны решить порядки, т.е. степень или корень, затем мы должны решить деление или умножение, которое идет первым из левой части уравнения, и, наконец, мы должны выполнить сложение или вычитание.
Класс периметра, площади и объема 5 …
Пожалуйста, включите JavaScript + (7 + 8) =?
Теперь по БОДМАСу сначала решаем скобку.
= 26 ⸓ 2 x 6 — 4 2 + 15 B Рэкет решается (7 + 8) = 15
= 26 ⸓ 2 x 6 — 16 + 15 O RDE 2 = 16
= 13 x 6 — 16 + 15 D IVISIS0005
= 93 — 16 A DDITION Решается 78 + 15 = 93
= 77 S UBTraction слева — первое 93 — 16 = 77
Таким образом, 26 x 6 — 4 2
.
