😃 Изучаем арифметику онлайн, математические игры и упрощенные приемы
Что такое арифметика? Арифметика – раздел математики, работающий с числами и вычислениями (действиями с числами).
Арифметику начинают изучать в начальной школе, потому что это основа математики, там изучаются основные операции с числами: сложение, вычитание, умножение, деление.
Арифметика – самый основной, базовый раздел математики. Возникновению она обязана потребностям людей в счете.
- Ментальная арифметика
- Математика и арифметика
- Обучение арифметике
- Уроки арифметики
- Игры на развитие счета
- Развитие феноменального устного счета
Ментальная арифметика
Что называется ментальной арифметикой? Ментальная арифметика – это метод обучения быстрому счету, пришедший из древности.
В настоящее время, в отличии от предыдущего, преподаватели стараются не только обучить детей скорости счета, но и стараются развить мышление.
Сам процесс обучения строится на использовании и развитии обоих полушарий мозга. Главное – уметь их использовать вместе, потому что они дополняют друг друга.
Главное – уметь их использовать вместе, потому что они дополняют друг друга.
Действительно, левое полушарие отвечает за логику, речь и рациональность, а правое – за воображение.
В программу обучения входит обучение работы и использование такого инструмента, как абакус.
Абакус – главный инструмент в изучении ментальной арифметики, потому что ученики учатся работать с ними, перебирать костяшки и осознавать суть счета. Со временем абакус стает вашим воображением, а обучаемые представляют их, опираются на эти знания и решают примеры.
Отзывы о данных методах обучения весьма положительные. Есть один минус – обучение платное, а его позволить могут не все. Поэтому путь гения зависит от материального положения.
Ускоряем устный счет, НЕ ментальная арифметика
Математика и арифметика
Математика и арифметика тесно связанные понятия, а вернее арифметика – раздел математики, работающий с числами и вычислениями (действиями с числами).
Арифметика – основной раздел, а значит и основа математики. Основа математики – важнейшие понятия и операции, составляющие базу, на которой строятся все последующие знания. В число главных операций входят: сложение, вычитание, умножение, деление.
Арифметика, как правило, изучается в школе с самого начала обучения, то есть. с первого класса. Дети осваивают базу математики.
Сложение – это арифметическое действие, в процессе которого складываются два числа, а их результатом будет новое – третье.
Формула сложения выражается так: a + b = c.
Вычитание – это арифметическое действие, в процессе которого из первого числа вычитается второе число, а итогом будет третье.
Формула сложения выражается так: a — b = c.
Умножение – это действие, в итоге которого находится сумма одинаковых слагаемых.
Формула такого действия имеет вид: a1+a2+…+an=n*a.
Деление– это разбивание на равные части какого-либо числа или переменной.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Записаться на курсПодробнее
Обучение арифметике
Обучение арифметике производится в стенах школы. С первого класса дети начинают изучение базового и главного раздела математики – арифметики.
Сложение чисел
Сложение – это сумма двух или нескольких чисел. Например, 2 + 3 = 5, и графически это можно представить так:
Большие число делиться на части, возьмем число 1234, а в нем: 4-единицы, 3-десятки, 2-сотни, 1-тысячи. Итак, если мы прибавляем 4 к 7, то 4+7=10+1, то есть 1 десяток и 1 единица. Если складывая числа в одном разряде (единицах, например) у вас число больше 10, но меньше 20, то в десяток вы добавляете единицу, а остальное оставляете на месте единиц.
Еще один пример: 8+9, получаем 10+7, значит в десятки мы добавляем 1, а на место единиц записываем 7, получаем 17.
Вычитание чисел
Вычитание – обратная операция сложению. Например, из 6 нужно вычесть 5. 6-5=1, 6 больше числа 5 на единицу, значит, и ответ будет единицей. Можно для проверки произвести сложение 1+5=6.
Большое число делится на части, возьмем число 1234, а в нем: 4-единицы, 3-десятки, 2-сотни, 1-тысячи. Если вычитать единицы, то все легко и просто. Но допустим пример: 14 — 7. В числе 14: 1 – десяток, а 4 – единицы. Один десяток – 10 единиц. Тогда получаем 10 + 4 — 7, сделаем так: 10 — 7 + 4, 10 — 7 = 3, а 3 + 4 = 7. Ответ найден верно!
Рассмотрим пример 23 — 16. Первое число 2 десятка и 3 единицы, а второе 1 десяток и 6 единиц. Представим число 23 как 10 + 10 + 3, а 16 как 10 + 6, тогда представим 23 — 16 как 10 + 10 + 3 — 10 — 6. Тогда 10 — 10 = 0, останется 10 + 3 — 6, 10 — 6 = 4, тогда 4 + 3 = 7. Ответ найден!
Аналогично делается с сотнями и тысячами/
Умножение чисел
Умножение чисел осваивается детьми во втором классе, и ничего в этом сложного нет. Сейчас мы рассмотрим умножение на примерах.
Сейчас мы рассмотрим умножение на примерах.
Пример 2*5. Это значит либо 2+2+2+2+2, либо 5+5. Берем 5 два раза или 2 пять раз. Ответ, соответственно, 10.
Пример 4*3. Аналогично, 4+4+4 или 3+3+3+3. Три раза по 4 или четыре раза по 3. Ответ 12.
Пример 5*3. Делаем так же как и предыдущие примеры. 5+5+5 или 3+3+3+3+3. Ответ 15.
Деление чисел
Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.
Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение. 3*3=9. Верно? Абсолютно.
Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.
Ускоряем устный счет, НЕ ментальная арифметика
Научитесь быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Записаться на курсПодробнее
Правила арифметики
Порядок выполнения операций в выражении – очень важен!
Если пример имеет вид 2+3-4, то порядок в нем может быть каким угодно. Потому что операции сложения и вычитания имеют одинаковый приоритет. Если выполним сначала сложение, то получим: 5-4=1, а если сначала вычитание, то: 2-1=1. Как видите результат одинаковый.
Аналогично с выражением умножения и деления. Операции умножения и деления имеют одинаковый приоритет. Например, 28:4. Выполним сначала умножение: 16:4=4, а если деление: 22=4.
Порядок имеет смысл, когда в выражении смешиваются операции сложения или вычитания, с операциями умножения или деления. Например:
Например:
2+22. Первым действием выполняются ВСЕ операции умножения и деления, а только потом сложения и вычитания. То есть выражение 2+22 = 2+4=6.
Но в выражениях присутствуют скобки. Скобки имеют свойство менять порядок операций. Рассмотрим предыдущий пример, только со скобками: (2+2)*2. В таком случае сначала выполняются операции в скобках, а затем вне скобок в порядке: 1. Умножение и деление 2. Сложение и вычитание.
Так, (2+2)2=42=8.
Как вы могли убедиться на примерах, скобки имеют роль. И порядок операций так же.
Уроки арифметики
Уроки арифметики – школьные уроки, вплоть до шестого класса. Дальше математика открывает свои разделы: геометрия и алгебра, а позже и тригонометрия.
Подробно об операциях вы можете прочитать в наших статьях:
сложение
вычитание
умножение
деление
Арифметика 5 класс
В пятом классе школьник начинают изучение таких тем как: дробные числа, смешанные числа. Информацию про операции с этими числами вы можете найти в наших статьях по соответствующим операциям.
Информацию про операции с этими числами вы можете найти в наших статьях по соответствующим операциям.
Дробное число – это отношение двух чисел друг к другу или же числителя к знаменателю. Дробное число можно заменить операцией деления. Например, ¼ = 1:4.
Смешанное число – это дробное число, только с выделенной целой частью. Целая часть выделяется при условии, что числитель больше знаменателя. Например, была дробь: 5/4, ее можно преобразовать, путем выделения целой части: 1целая и ¼.
Примеры для тренировки:
Задание №1:
Задание №2:
Арифметика 6 класс
В 6ом классе появляется тема преобразования дробей в строчную запись. Что это значит? Например, дана дробь ½, она будет равна 0,5. ¼ = 0.25.
Примеры могут составляться в таком стиле: 0.25+0.73+12/31.
Примеры для тренировки:
Задание №1:
Задание №2:
Игры для развития устного счета и скорости счета
Существуют прекрасные игры, способствующие развитию счета, помогающие развивать математические способности и математическое мышление, устный счет и скорость счета! Можно играть и развиваться! Вам интересно? Прочтите краткие статьи об играх и обязательно попробуйте себя.
Игра «Быстрый счет»
Игра «быстрый счет» поможет вам ускорить устный счет. Суть игры в том, что на представленной вам картинке, потребуется выбрать ответ да или нет на вопрос «есть ли 5 одинаковых фруктов?». Идите за своей целью, а поможет вам в этом данная игра.
Играть сейчас
Игра «Математические сравнения»
Игра «Математические сравнения» потребует от вас сравнения двух чисел на время. То есть вам предстоит выбрать как можно быстрее одно из двух чисел. Помните, что время ограничено, а чем больше вы ответите верно, тем лучше будут развиваться ваши математические способности! Попробуем?
Играть сейчас
Игра «Быстрое сложение»
Игра «Быстрое сложение» — отличный тренажер быстрого счета. Суть игры: дано поле 4×4, то есть. 16 чисел, а над полем семнадцатое число. Ваша цель: при помощи шестнадцати чисел составить 17, пользуясь операцией сложения. Например, над полем у вас написано число 28, то в поле вам надо найти 2 таких числа, которые в сумме дадут число 28. Вы готовы попробовать свои силы? Тогда вперед, тренироваться!
Вы готовы попробовать свои силы? Тогда вперед, тренироваться!
Играть сейчас
Развитие феноменального устного счета
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Записаться на курсПодробнее
Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Подходит детям и взрослым, читающим до 5000 слов в минуту.
Записаться на курсБесплатный урок
Развитие памяти и внимания у ребенка 5-10 лет
Цель курса: развить память и внимание у ребенка так, чтобы ему было легче учиться в школе, чтобы он мог лучше запоминать.
После прохождения курса ребенок сможет:
- В 2-5 раз лучше запоминать тексты, лица, цифры, слова
- Научится запоминать на более длительный срок
- Увеличится скорость воспоминания нужной информации
Записаться на курсПодробнее
Супер-память за 30 дней
Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Записаться на курсПодробнее
Как улучшить память и развить внимание
Бесплатное практическое занятие от advance.
Записаться бесплатноПодробнее
Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.
Записаться на курсПодробнее
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Записаться на курсПодробнее
Умножение и деление трёхзначных чисел на однозначное в случаях 242?4, 968?4
Тема: Умножение и деление
трёхзначных чисел на однозначное
в случаях 2424, 9684
Задачи: 1.Формировать умение умножать и делить трёхзначные числа на однозначные, находить неизвестный компонент в уравнении путём нахождения частного, отработать умение решать задачи на приведение к единице.
2. Развивать память, мышление, внимание, умение работать в коллективе и самостоятельно, развивать умение выполнять самоконтроль и взаимоконтроль.
3. Воспитывать чувство коллективизма, ответственности.
Тип урока: Урок- закрепление.
Оборудование: фотография космического корабля, макеты-рисунки планет парашюты с уравнениями. Карточки-перфокарты для фронтальной работы, песня « Крыша дома твоего».
Карточки-перфокарты для фронтальной работы, песня « Крыша дома твоего».
1.Орг. Момент.
— Какое сегодня число? (24)
-Какое число получится, если его разделить на 2? (12)
-Какой праздник отмечался 12 апреля?
-Кто первый космонавт?
-На каком корабле он взлетел?
Итак, сегодня на уроке математики мы тоже совершим космическое путешествие,
но только к математическим звёздам.
-Как называется космодром, с которого взлетают космические корабли? (Байконур)
-В какой стране он находится?
-Да, Байконур находится недалеко от нас. Но мы к своим математическим звёздам
Взлетим прямо отсюда на нашем космическом корабле.
1. Целевая установка:
В полёте нам пригодятся математические знания по нахождению неизвестного числа, по
решению задач. Мы будем учится умножать и делить трёхзначные числа на однозначные.
А также будем учиться ценить дружбу, взаимопомощь.
1. Устный счёт.
Устный счёт.
Итак! Готовы?
а) – Космические корабли взлетают со скоростью 8км/с . А сколько это метров? Почему?
-А нам надо вернуться через 45 минут, поэтому увеличим скорость до 10.000м/с.
Сколько это километров?
-А почему у космических кораблей такая большая скорость?
-Гагарин был в полёте 108 мин. Сколько это составляет асов и минут?
Молодцы!
б) Наш космический рейс- коммерческий, и мы на нём космические туристы. Вам надо
купить билеты, которые у вас на партах, т.е. правильно решить примеры.
1. 2.
18: 5= 3 ост. 3 14: 3 = 4 ост. 2
22: 4 = 5 ост .2 22: 9 = 3 ост. 1
34: 8 = 4 ост. 2 19: 2 = 9 ост.1
15:2 =7 ост.1 27: 6 = 4 ост. 3
-А теперь самопроверка (на доске ответы)
У кого всё верно, нарисуйте- поставьте
У кого поднимите руки!
Полет
В) Теперь проверим наши приборы, как они работают. Я показываю на прибор, вы называете его правильно. Если без ошибок назовёте, значит наши приборы будут работать нормально, и полёт наш пройдёт хорошо и удачно.
Если без ошибок назовёте, значит наши приборы будут работать нормально, и полёт наш пройдёт хорошо и удачно.
15× 6 = 640 ÷ 2 = 54 ÷ 18 =
83 × 3 = 96 ÷ 4 = 60 ÷ 12 =
Разрешён
Итак! Открыть бортовые журналы, записать дату полёта! Записи надо делать чётко, разборчиво, чтобы её могли прочитать другие космонавты.
– А вот и первая остановка!
а) Это-Луна. Мы можем без боязни на неё прилуниться. Она наш ближний сосед – спутник Земли. На Луне живут лунатики. ( Кто такие лунатики?)
Они такие же как и мы, только могут гулять во сне. Лунатики приготовили нам задачу. Давайте решим её вместе.
« На три костюма для лунатиков пошло 12 м ткани. Сколько метров ткани пойдёт на 5 таких костюмов?» 3 кост. -12м
5 кост. — ? м
( на доске запись : 12 ÷ 3 × 5 =20 (м) )
Составим обратные:
3 кост. – 12 м 5 кост. -20 м 5 кост. -20 м
? кост. 20 м 3 кост. — ? м. ? кост. – 12 м.
20 ÷ (12 ÷3 ) =5(к. ) 20 ÷ 5 × 3 =12 (м.) 12÷(20 ÷ 5) =3 (к.)
) 20 ÷ 5 × 3 =12 (м.) 12÷(20 ÷ 5) =3 (к.)
-Что находим первым действием?
— Как называются эти задачи?
Нам пора прощаться с Лунатиками. Нас ждёт много интересного!
б) На нашем пути неизвестная , необычная планета. Она нам загадочно мигает, как бы приглашая к себе манит своей неизвестностью.
Вот мы и решим задание на нахождение этих неизвестных чисел.
1в. 2в.
х × 6 =912 273÷ х =7
Чтобы вы были уверены в себе, не пугались неизвестности, поработайте в паре, посоветуйтесь, как найти неизвестное число, проверьте друг друга.
( взаимопроверка, взаимоконтроль )
-Давайте вышлем на неё разведчиков, можно ли на неё спускаться. Ребята выйдут в открытый космос, им нужны скафандры. Вот они.
Мы им также выдаём парашюты. Им нужно спуститься точно в заданном месте.
Самопроверка: У кого всё верно, значит вы хорошо друг другу объяснили. Это планета необитаема. Летим дальше. Но что-то слишком далеко улетели.
Пора возвращаться.
Физминутка.
Ребята, а вы знаете, что космонавты много занимаются спортом и всегда делают зарядку. Даже в полёте они находят время для спортивных упражнений.
Не зевай по сторонам!
Ты сегодня – космонавт!
Начинаем тренировку,
Чтобы сильным быть и ловким!
Повороты, подтягивание, наклоны.
Аккуратно надо сесть,
Чтоб приборы не задеть.
Вот уж и Земля! Мы входим в верхние, а затем и нижние слои атмосферы – оболочки вокруг Земли.
А) одноуровневая самостоятельная работа.
Что это? Облака! Посмотрите, какие они красивые. Но они тоже математические. Давайте попробуем их потрогать, пощупать.
Здесь примеры : Решим их самостоятельно, затем проверим в паре. Если всё верно, и вы считаете, что решено на «5» — ставьте .Если будет ошибка, то ставьте «4».
738 ÷ 6
945÷ 5
167×4
167 × 4 945÷ 5 738 ÷ 6
(на доске я сама даю ответы)
Самопроверка.
— В чьей паре обе «5», покажите сцепленные руки. Молодцы!
Б) разноуровневая самостоятельная работа
— Но, что это- грозовые тучи? Идёт дождь в нашем районе. Но мы не боимся грозы, решим на «4» и «5».
На «4» с проверкой На «5» с проверкой
128 4 576 8 7×9 3 ××2 4
*5* 9×
В) Проверка работы групп; у доски решают.
Фронтальная – самопроверка. Оценки.
Если успеем. Ну, а теперь нам надо точно приземлиться в Актобе.
Для этого нам надо вычислить координаты приземления. Мы получили радиограмму. Вот она.
Северо — западнее Байконура на произведение чисел 294 и 3 (км).
Западнее Астаны на частное чисел 1860 и 2 (км).
8.Итог урока.
Итак, в программа космического полёта к математическим звёздам выполнена.
Чему учились? (умножать и делить трёхзначные числа).
Д /з. Дома вы ещё раз вспомните наш полёт, повторите мысленно весь маршрут и решите
с. 257 № 8.
257 № 8.
Вот мы и дома.
-Что может быть лучше места, где крыша дома твоего? (песня)
Открытый урок по математике
в 3 «А» классе
Учитель нач.классов: Оспанова С.Т.
г.Актобе
операций для векторов и матриц в Stateflow — Операции MATLAB и Simulink
для векторов и матриц в Stateflow
Диаграммы Stateflow ® в моделях Simulink ® имеют свойство языка действий, которое определяет синтаксис, который вы использовать для вычислений с векторами и матрицами. Свойства языка действий:
Для получения дополнительной информации смотрите Различия Между MATLAB и C как Синтаксис Языка Действия.
Обозначение индекса
В диаграммах, использующих MATLAB в качестве языка действий, обращайтесь к элементам вектора или матрицы с помощью
с использованием индексации на основе единицы, разделенной круглыми скобками.
В диаграммах, использующих C в качестве языка действий, ссылайтесь на элементы вектора или матрица с использованием индексации с отсчетом от нуля, разделенной скобками. Приложите индексы для различные размеры в своей собственной паре скобок.
| Пример | как язык действия | C В качестве языка действия | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
. Первый элемент |
Двоичные операции
матричные операнды в соответствии с их порядком старшинства (1 = самый высокий, 3 = самый низкий). Двоичные операции ассоциативны слева, так что в любом выражении операторы с
одинаковый приоритет оценивается слева направо. За исключением матрицы
операторы умножения и деления в диаграммах, использующих MATLAB в качестве языка действий, все бинарные операторы выполняются поэлементно
операции.
Двоичные операции ассоциативны слева, так что в любом выражении операторы с
одинаковый приоритет оценивается слева направо. За исключением матрицы
операторы умножения и деления в диаграммах, использующих MATLAB в качестве языка действий, все бинарные операторы выполняются поэлементно
операции.
Operation | Precedence | MATLAB as the Action Language | C as the Action Language |
|---|---|---|---|
| 1 | Умножение матриц. | Поэлементное умножение. Для матричного умножения
использовать |
| 1 | Поэлементное умножение. | Не поддерживается. Используйте операцию |
| 1 | Матрица правое деление. | Поэлементное правое деление. Для правого деления матрицы
используйте операцию |
| 1 | Поэлементное правое деление. | Не поддерживается. Используйте операцию |
| 1 | Матрица левое деление. | Не поддерживается. Используйте операцию |
| 1 | Поэлементное левое деление. | Не поддерживается. Используйте операцию |
| 2 | Дополнение. | Дополнение. |
| 2 | Вычитание. | Вычитание. |
| 3 | Сравнение, равно. | Сравнение, равно. |
| 3 | Сравнение, не равно. | Сравнение, не равно. |
| 3 | Не поддерживается. | Сравнение, не равно. |
| 3 | Не поддерживается. Используйте операцию | Сравнение, не равно. |
Унарные операции и действия
Эта таблица суммирует интерпретацию всех унарных операций и действий на векторные и матричные операнды. Унарные операции:
Имеют более высокий приоритет, чем бинарные операторы.
Правоассоциативны, так что в любом выражении они оцениваются справа налево.
Выполнение поэлементных операций.
Пример | Matlab As Action Language | C, как язык действий | C. 0036 0036 |
|---|---|---|
| Логическое НЕ. Для побитового НЕ используйте | Дополнительные сведения см. в разделах Побитовые операции и Включение C-битных операций. |
| Не поддерживается. Используйте операцию | Логическое НЕ. |
| Отрицательный. | Отрицательный. |
| Не поддерживается. | Увеличение всех элементов вектора или матрицы. Эквивалент
до |
| Не поддерживается. | Уменьшить все элементы вектора или матрицы. Эквивалент
до |
Операции присваивания
матричные операнды.
| . | Простое назначение. | |
|---|---|---|
| Не поддерживается. Используйте выражение | Эквивалент |
| Не поддерживается. Используйте выражение | Эквивалент |
| Не поддерживается. Используйте выражение | Эквивалент |
| Не поддерживается. Используйте выражение | Эквивалент |
Присвоение значений отдельным элементам матрицы
Вы можете присвоить значение отдельному элементу вектора или матрицы, используя синтаксис индексирования, соответствующий языку действий диаграмма.
| Пример | MATLAB как язык действий | C как язык действий |
|---|---|---|
Присвойте значение 10 первому 9004
элемент вектора | В(1) = 10; | V[0] = 10; |
Присвоить значение 77 элементу в строке 2 и столбце 9
матрицы М . | М(2,9) = 77; | М[1][8] = 77; |
Присвоение значений всем элементам матрицы
В диаграммах, использующих MATLAB в качестве языка действий, можно использовать одно действие, чтобы указать все
элементов вектора или матрицы. Например, это действие назначает каждому
элемент матрицы 2 на 3 A в другой
значение:
А = [1 2 3; 4 5 6];
В диаграммах, использующих C в качестве языка действий, можно использовать скаляр .
расширение , чтобы установить все элементы вектора или матрицы в
такое же значение. Скалярное расширение преобразует скалярные данные, чтобы они соответствовали размерам
векторные или матричные данные. Например, это действие устанавливает все элементы
матрица А к 10 :
А = 10;
Скалярное расширение применяется ко всем графическим функциям, таблицам истинности, функциям MATLAB и Simulink. Предположим, что вы определяете формальные аргументы
функция
Предположим, что вы определяете формальные аргументы
функция f как скаляры. В этой таблице описаны правила
скалярное расширение для вызова функции y =
ф(и) .
Выход Y | Вход U | Результат |
|---|---|---|
| SCALAR | 8885 | |
| SCALAR | 8888 8188888888888888888. | |
| Скаляр | Вектор или матрица | Диаграмма выдает ошибку несоответствия размеров. |
| Вектор или матрица | Скаляр | Диаграмма использует скалярное расширение для назначения
скалярное выходное значение y[i][j] = f(u) |
| Вектор или матрица | Вектор или матрица | выходное значение для каждого элемента y[i][j] = f(u[i][j])Если у и у нет
имеют одинаковый размер, диаграмма генерирует несоответствие размера
ошибка.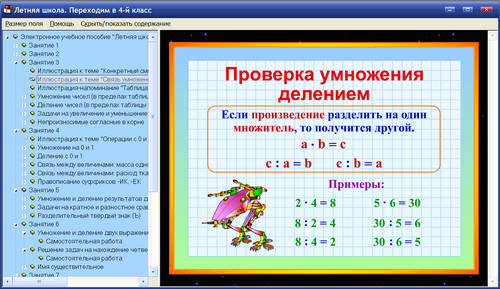 |
Для функций с несколькими выходами применяются те же правила, если только все выходы и входы являются векторами или матрицами. В этом случае график генерирует ошибку несоответствия размера, и скалярное расширение не происходит.
Диаграммы, использующие MATLAB в качестве языка действий, не поддерживают скалярное расширение.
Выполнение матричных арифметических операций с помощью функций MATLAB
В диаграммах, использующих C в качестве языка действий, операции * и / выполняют поэлементное умножение и деление. К
выполнить стандартное матричное умножение и деление в диаграмме C, используя функцию MATLAB.
Предположим, что вы хотите выполнить эти операции над квадратными матрицами и1 и и2 :
Вычисление стандартного матричного произведения
y1 = u1 * у2.
Решите уравнение
u1 * y2 = u2.Решите уравнение
y3 * u1 = u2.
Чтобы выполнить эти расчеты в диаграмме C, добавьте функцию MATLAB, которая запускает этот код:
функция [y1, y2, y3] = my_matrix_ops(u1, u2) %#codegen у1 = и1 * и2; % умножение матрицы у2 = и1 \ и2; % деление матрицы справа у3 = и1 / и2; % деление матрицы слеваДо вызывая функцию, укажите свойства для входных и выходных данных, как описано в разделе «Установка свойств данных».
В диаграммах, использующих MATLAB в качестве языка действий, операции * , / и \ выполняют стандартные матрицы
умножение и деление. Вы можете использовать эти операции непосредственно в состоянии и
переходные действия.
Похожие темы
- Векторы и матрицы в диаграммах Stateflow
- Укажите размер данных Stateflow
NumberNut.
 com: Арифметика: Операции: Сравнение
com: Арифметика: Операции: Сравнение Числа и подсчет| Арифметика |Дроби и десятичные дроби|Предварительная алгебра|Карта сайта
Вы познакомились с основными арифметическими операциями , такими как сложение, вычитание, умножение и деление. У нас есть полные разделы о том, как использовать эти операции. Мы просто хотели воспользоваться моментом, чтобы поговорить о том, как связаны эти операции. Сложение и вычитание очень близки, если посмотреть на их понятия. Начнем с того, что представим кучу орехов на столе. Когда вы отнимаете несколько, вы вычитаете. Когда вы кладете несколько в кучу, вы добавляете. Некоторые из них, а некоторые из них. Умножение — это быстрый способ сделать много сложений. Мы собираемся поговорить об операциях более подробно, и вам нужно следить за шаблонами, когда мы будем рассматривать примеры.
Мы говорили об этой идее несколько раз на предыдущих страницах. Начиная с сложения и вычитания , мы находим две противоположные идеи . Сложение объединяет, а вычитание удаляет. Словесные задачи могут заставить вас положить орехи в ведро так же быстро, как и вытащить их из этого ведра. Этими действиями являются сложение и вычитание. Каждый человек (КАЖДЫЙ человек) в мире использует сложение и вычитание каждый день. Это может быть не всегда сверхсложное сложение или вычитание, но операции есть.
Начиная с сложения и вычитания , мы находим две противоположные идеи . Сложение объединяет, а вычитание удаляет. Словесные задачи могут заставить вас положить орехи в ведро так же быстро, как и вытащить их из этого ведра. Этими действиями являются сложение и вычитание. Каждый человек (КАЖДЫЙ человек) в мире использует сложение и вычитание каждый день. Это может быть не всегда сверхсложное сложение или вычитание, но операции есть.
Пример:
7 = 5 + 2 (сложение)
7 - 5 = 2 (вычитание)
Сложение и умножение связаны, потому что они соединяют . Умножение похоже на ярлык для длинных задач на сложение. Кому захочется записывать 3+3+3+3+3+3, когда гораздо быстрее написать 6x3? Умножение экономит время при записи. Это также дает вам возможность подумать о группах . Когда мы писали его долго, у нас было шесть групп по три человека. Если вы преобразуете это в математический язык, вы получите 6 групп по 3, равных 6x3. Кстати, ответ 18.
Если вы преобразуете это в математический язык, вы получите 6 групп по 3, равных 6x3. Кстати, ответ 18.
Умножение заключается в объединении двух или более групп для получения большей группы (продукта). Если мы напишем это словами, сложение может занять одну группу из шести, добавить ее к другой группе из шести, добавить ее к другой группе из шести и закончить еще одной группой из шести (6+6+6+6). Умножение использует более короткий путь, говоря: «Составь сумму, равную четырем группам по шесть». Они оба получают один и тот же ответ, но умножение происходит намного быстрее.
Пример:
2 + 2 + 2 + 2 + 2 = 10 (Сложение)
2 х 5 = 10 (Умножение)
Умножение и деление тесно связаны друг с другом. Вы знаете, что умножение объединяет группы объектов. Сколько у вас камней, если есть пять (5) групп по семь (7) камней? За ответ вы получаете тридцать пять (35) камней. Деление подобно обратному действию умножения. Требуется большая группа, и разбивает ее на более мелкие группы . Используя те же значения, задача на деление начинается с тридцати пяти (35) камней и разбивается на более мелкие группы по семь (7). Сколько меньших групп будет? Эта задача на деление даст вам ответ пять (5). Вы должны увидеть шаблон, когда смотрите на детали примера. Как будто мы просто поменяли местами символы.
Требуется большая группа, и разбивает ее на более мелкие группы . Используя те же значения, задача на деление начинается с тридцати пяти (35) камней и разбивается на более мелкие группы по семь (7). Сколько меньших групп будет? Эта задача на деление даст вам ответ пять (5). Вы должны увидеть шаблон, когда смотрите на детали примера. Как будто мы просто поменяли местами символы.
Пример:
5 x 7 = 35 (умножение)
35 ÷ 7 = 5 (деление)
Напиши по-другому...
5 x 7 = 35
5 = 35/7
7 = 35/5
Видите, как в последних двух примерах одно число переключается на другую сторону знака равенства? Мы разделили обе стороны на семь для первого примера и обе стороны на пять во втором примере. В разделе деления мы решим еще много задач.
► СЛЕДУЮЩАЯ СТРАНИЦА ПО АРИФМЕТИКЕ
► ВЕРНУТЬСЯ НА НАЧАЛО СТРАНИЦЫ
► Или поищите на сайтах...
- Обзор
- Операции
- Заказ
- Сравнения
- Дополнение
- Вычитание
- Умножение
- Отдел
- Виды деятельности
Википедия:
https://en.
 * b
* b  См. Выполнение матричной арифметики при помощи функций MATLAB.
См. Выполнение матричной арифметики при помощи функций MATLAB. Используйте операцию
Используйте операцию