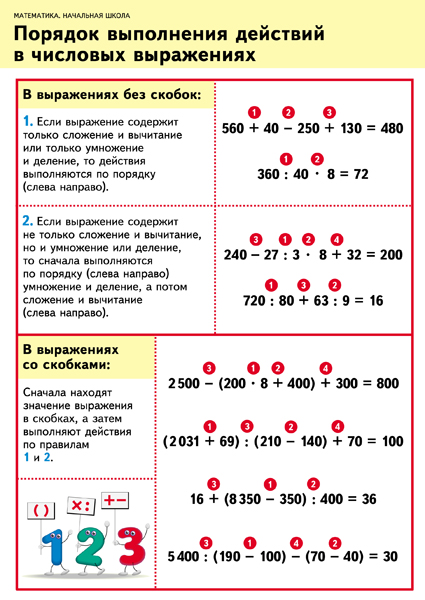
Сложение и вычитание без перехода через десяток: обучающий материал с примерами
Математика
Сложение и вычитание чисел в пределах 10 и 20 без перехода через разряд – первые ступеньки в математике. Чтобы двигаться дальше к более сложным математическим понятиям стоит убедиться, что ребёнок легко справляется с простыми арифметическими действиями.
Сложение
Сложение — это арифметическое действие, при котором два исходных числа объединяются в одно новое число. Для записи действия сложения используют знак плюс «+», который пишут между первым и вторым числом. В сложении каждое число имеет своё название.
В данном примере к 5 единицам одного числа прибавляем 3 единицы, в итоге получаем их общее количество — сумму, которая состоит из 8 единиц.
Разберём пример, в котором числа имеют два разряда: десятки и единицы.
11 + 7 = 18
К числу 11 мы добавляем семь.
Сложение без перехода через десяток – это такой случай сложения двузначных чисел, в результате которого сумма единиц меньше 10. А значит переход из разряда единиц в разряд десятков не происходит.
Наши рабочие листы на сложение без перехода через десяток помогут ребёнку закрепить умение быстро решать такие примеры.
Вот несколько примеров с решением:
16 + 3 = 10 + 6 + 3 = 10 + 9 = 19
12 + 5 = 10 + 2 + 5 = 10 + 7 = 17
5 + 23 = 20 + 5 + 3 = 20 + 8 = 28
Сложение с переходом через десяток или через разряд – это более сложный вариант сложения чисел. Узнайте, как наглядно объяснить ребёнку переход через разряд при сложении (ссылка) в обучающем материале от Логиклайк.
Когда ребёнок понял, как складывать числа, можно переходить к вычитанию.
Вычитание
Вычитание – это арифметическое действие, в результате которого первое число уменьшается на столько единиц, сколько содержит в себе второе число в записи этого примера.
Начинайте объяснять вычитание с простых примеров, где нужно вычесть один или два. Затем переходите к более сложным примерам, но без перехода через десяток.
Предложите подобные простые примеры на вычитание в пределах десяти:
3 — 1 = 2
4 — 2 = 2
7 — 3 = 4
Для обозначения вычитания используют знак минус «−», который пишут между числами, с которыми будут производить вычитание. Каждое число при вычитании имеет своё название. Для легкого старта в первом классе важно, чтобы ребёнок запомнил и не путал названия компонентов вычитания.
Ребёнок легче поймёт вычитание, если вы покажете взаимосвязь действий сложения и вычитания.
Примеры, с которых можно начать:
5 + 1 = 6
6 — 5 = 1
6 — 1 = 5
Решайте логические и математические задачи на платформе Логиклайк. Смотрите, скачивайте и распечатывайте бесплатные рабочие листы на сложение и вычитание.
Правила умножения и деления для начальной школы примеры
После того, как выучена таблица умножения, школьникам объясняют правила умножения и деления, учат использовать их при вычислении математических выражений.
Содержание
- 1 Что такое умножение? Это умное сложение
- 2 Да какая разница?
- 3 Что важнее – умножение или сложение?
- 4 Математические действия с нулем
- 5 Умножение и деление на единицу
- 6 Вычисления с дробями, степенями и сложными функциями
- 7 Главные правила по теме
Что такое умножение? Это умное сложение
При сложении и вычитании, умножении и делении чисел в простых выражениях у детей не возникает трудностей:
- 5 × 3 = 15;
- 86 – 9 = 77;
- 81 : 9 = 9.
В таких вычислениях необходимо только знать правила сложения и вычитания и таблицу умножения.
Когда начинаются более сложные упражнения, примеры состоят из двух и более действий, да еще и со скобками, при решении у детей появляются ошибки. И главная из них – неправильный порядок действий.
Математика: переместительное свойство умножения
Да какая разница?
Действительно, настолько ли это важно – какое действие в примере выполнить первым, какое вторым?
- Рассмотрим примеры:
10 – 5 + 2 = ?
Если мы будем выполнять действия по порядку, получим:
- 10 – 5 = 5;
- 5 + 2 = 7.
Попробуем иначе:
- 5 + 2 = 7;
- 10 – 7 = 3.
Получили два разных ответа. Но так быть не должно, следовательно, порядок выполнения действий имеет значение. Тем более, если в выражении имеются скобки:
25 – (18+2) = ?
Пробуем решить двумя способами:
- 25 – 18 + 2 = 9;
- 25 – 20 = 5.
Ответы разные, а для того чтобы определить порядок действий, в выражении стоят скобки – они показывают, какое действие нужно выполнить первым. Значит, правильным будет такое решение:
- 18 + 2 = 20;
- 25 – 20 = 5.
Другого решения у ответа у примера быть не должно.
Итак:
Что важнее – умножение или сложение?
При решении примеров
Расставь порядок действий.
Умножить или разделить – на первом месте.
Для выражений, в которых присутствуют не сложение либо вычитание, а умножение или деление, действует то же правило: все действия с числами выполняются по порядку, начиная с левого:
81 : 9 х 2 = ?
- 81 : 9 = 9;
- 9 х 2 = 18.
Сложнее случай – когда в одной задаче встречаются умножение или деление со сложением или вычитанием. Каков порядок вычислений тогда?
Рассмотрим пример:
8 : 2 + 2 = ?
Если выполнять все действия по порядку, сначала деление, затем сложение.
В итоге получим:
- 8 : 2 = 4;
- 4 + 2 = 6.
Значит, пример решен правильно. А если в нем будут скобки?
8 : (2 + 2) = ?
- 2 + 2 = 4;
- 8 : 4 = 2.
То, что заключено в скобки, всегда в приоритете. Для того они и стоят в выражении. Поэтому порядок вычислений в подобных выражениях будет следующим:
- Раскрываем скобки. Если их несколько, делаем вычисления для каждых.
- Умножение либо деление.
- Вычисляем конечный результат, выполняя действия слева направо.
Пример:
81 : 9 + (6 – 2) + 3 = ?
- 6 – 2 = 4;
- 81 : 9 = 9;
- 9 + 4 = 13;
- 13 + 3 = 16.
81 : 9 + (6 – 2) + 3 = 16.
А что будет приоритетным: умножение — или деление, вычитание — или сложение, если оба действия встречаются в задаче? Ничего, они равны, в таком случае действует первое правило – действия производятся одно за другим, начиная слева.
Алгоритм решения выражения:
- Анализируем задачу – есть ли скобки, какие математические действия нужно будет выполнить.
- Выполняем вычисления в скобках.
- Делаем умножение и деление.
- Выполняем сложение и вычитание.
Пример:
28 : (11 – 4) + 18 – (25 – 8) = ?
Порядок вычисления:
- 11 – 4 = 7;
- 25 – 8 = 17;
- 28 : 7 = 4;
- 4 + 18 = 22;
- 22 – 17 = 5.
Ответ: 28 : (11 – 4) + 18 – (25 – 8) = 5.
Важно! Если в выражении есть буквенные обозначения, порядок действий остается прежним.
Математические действия с нулем
Круглый нуль такой хорошенький,
Но не значит ничегошеньки.
В примерах нуль как число не встречается, но он может быть результатом какого-либо промежуточного действия, например:
5 × (8 : 2 – 4) = ?
- 8 : 2 = 4;
- 4 – 4 = 0;
- 5 × 0 = ?
При умножении на 0 правило гласит, что в результате всегда получится 0. Почему? Объяснить можно просто: что такое умножение? Это одно и то же число, сложенное с себе подобным несколько раз.
Иначе:
0 × 5 = 0 + 0 + 0 + 0 + 0 = 0;
Деление на 0 бессмысленно, а деление нуля на любое число даст в результате всегда 0:
0 : 5 = 0.
Да и как может быть иначе, когда делить-то нечего? Если у вас нет яблок, поделиться с друзьями вам нечем.
Почему нельзя делить на ноль
Напомним другие арифметические действия с нулем:
Умножение и деление на единицу
Математические действия с единицей отличаются от действий с нулем. При умножении или делении числа на 1 получается само первоначальное число:
7 × 1 = 7;
7 : 1 = 7.
Конечно, если у вас есть 7 друзей, и каждый подарил вам по конфете, у вас будет 7 конфет, а если вы их съели в одиночестве, то есть поделились лишь с самим собой, то все они и оказались в вашем желудке.
Вычисления с дробями, степенями и сложными функциями
Это сложные случаи вычислений, которые не рассматриваются в рамках начальной школы.
- Действия с дробями
Умножение простых дробей друг на друга не представляется сложными, достаточно лишь перемножить числитель на числитель, а знаменатель – на знаменатель.
Пример:
\({{2}\over{5}} × {{3}\over{8}}\) = ?
- 2 × 3 = 6 — числитель
- 5 × 8 = 40 — знаменатель
\({{2}\over{5}} × {{3}over\{8}} = {{6}over\{40}}\)
После сокращения получаем:\({{6}over\{40}}\) = \({{3}over\{20}}\).
Деление простых дробей не так сложно, как кажется на первый взгляд. Достаточно лишь преобразовать задачу – превратить ее в пример с умножением. Сделать это просто – нужно перевернуть дробь так, чтобы знаменатель стал числителем, а числитель – знаменателем.
Пример:
\({{2}\over{8}}={{2}\over{5}} : {{3}\over{5}}\)=? \({{2}\over{8}} : {{3}\over{5}} = {{2}\over{8}} × {{5}\over{3}}\)
- 2 × 5 = 10;
- 8 × 3 = 24.
\({{2}\over{8}} : {{3}\over{5}} = {{10}\over{24}}={{5}\over{12}}\)
- Действия со степенями
Если в задаче встречается число, представленное в виде степени, его значение вычисляется прежде всех остальных (можете представить, что оно заключено в скобки – а действия в скобках выполняются первыми).
Пример:
(5² – 7) : 3 = ?
- 5² = 5 х 5 = 25;
- 25 – 7 = 18;
- 18 : 3 = 6.
(5² – 7) : 3 = 6.
Преобразовав число, представленное в виде степени, в обычное выражение с действием умножения, решить пример оказалось просто: сначала умножение, затем вычитание (потому что в скобках) и деление.
- Действия с корнями, логарифмами, функциями
Поскольку такие функции изучаются только в рамках старшей школы, рассматривать их мы не будем, достаточно только сказать, что они, как и в случае со степенями, имеют приоритет при вычислении: сначала находится значение данного выражения, затем порядок вычислений обычный – скобки, умножение с делением, далее по порядку слева направо.
Главные правила по теме
Говоря о главных и неглавных математических действиях, нужно сказать, что четыре основных действия можно свести к двум: сложение и умножение. Если вычитание и деление представляется для школьников сложным, правила сложения и умножения они запоминают быстрее.
Действительно, выражение 5 – 2 можно записать иначе:
2 + х = 5.
Аналогично:
8 : 2 = у × 2 = 8.
В случаях с умножением действуют правила, схожие со свойствами сложения: от перестановки множителей произведение не изменится:
5 × 4 = 4 × 5.
При решении сложных задач первое действие — то, которое выделено скобками, затем — деление или умножение, потом все остальные действия по порядку.
Когда нужно решить примеры без скобок, вначале выполняется умножение или деление, далее — вычитание либо сложение.
Стратегии вычитания Прогресс | Департамент образования
Добро пожаловать в асинхронный модуль, Стратегии вычитания Прогресс . В своем собственном темпе читайте материалы, смотрите короткие видеоклипы и разбирайтесь в картинках. Этот модуль длится примерно 1 час и может быть завершен за один присест или небольшими частями. Когда вы пройдете модуль, щелкните ссылку на анкету в поле справа. После успешной отправки анкеты ваш сертификат часа контакта будет автоматически отправлен по электронной почте на адрес, указанный в анкете.
Если у вас есть какие-либо вопросы об этом процессе или содержании этого модуля, свяжитесь с Джен Робитайл по адресу [email protected].
Стратегии перечислены от самых ранних до стандартного алгоритма. Многие из них используются параллельно, но важно понимать, что различные стратегии используются для более глубокого концептуального понимания и перехода к более процедурной модели, основанной на концептуальном понимании вычитания. Имейте в виду, что освоение стандартного алгоритма вычитания не ожидается до 4-го класса в соответствии с результатами обучения штата Мэн и общими базовыми стандартами штата, однако учащиеся начнут практиковать стандартный алгоритм наряду с другими стратегиями намного раньше 4-го класса.
Модели
Учащиеся впервые осваивают вычитание с помощью моделей. Они могут использовать различные манипулятивные средства, такие как кубики, счетные медведи, пуговицы, пять и десять рамок, пальцы или счетчики.
Учащиеся могут также рисовать представления или картинки для моделирования математики или даже физически разыгрывать вычитание. Эти модели помогают учащимся понять действие, происходящее в самых ранних задачах на вычитание. Модели по-прежнему могут быть полезны, когда учащиеся работают над задачами «часть-часть-сумма», «изменение» и «сравнительное вычитание». Студентам также необходимо попрактиковаться в поиске пропущенных значений во всех местах задачи на вычитание — уменьшаемое, вычитаемое и разность. Дополнительные примеры ситуаций с задачами на вычитание см. в Глоссарии, таблица 1 из Общего стандарта штата по математике.
Обратный (или прямой) счет
При использовании стратегии обратного или даже прямого счета важно помнить, что вычитание означает разницу или расстояние между уменьшаемым и вычитаемым значениями. Когда ваши ученики понимают взаимосвязь значений и то, что они могут либо считать в обратном порядке от уменьшаемого, либо считать от вычитаемого, они углубляют свое понимание смысла чисел и того, как числа работают вместе.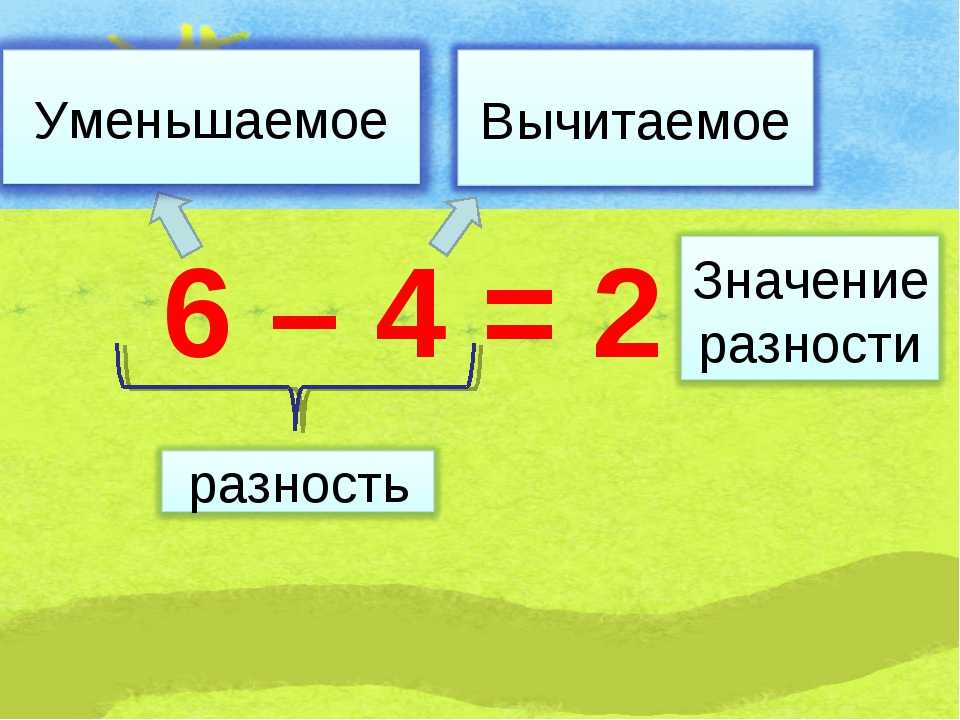
Стратегия обратного отсчета или подсчета вверх часто может сочетаться с числовой линией или открытой числовой линией, поскольку значения работают с увеличением.
Числовые сетки
Числовые сетки — отличный способ найти шаблоны для вычитания учащихся. Это начинает формировать понимание разрядности, когда учащиеся начинают смотреть на то, что они замечают в разрядах десятков и единиц. Числовые сетки уникально настроены в рядах по десять, чтобы смоделировать нашу систему счисления с основанием десять. Когда учащиеся перемещаются по строке, они должны заметить, что цифра в разряде десятков остается неизменной до конца ряда, а разряд единиц увеличивается на единицу. Двигаясь вверх или вниз по строке, они должны заметить, что разряд единиц остается прежним, а разряд десятков либо увеличивается, либо уменьшается на единицу.
Обратите внимание на разницу в этих двух сетках чисел. Одна сетка идет от 0 до 110 сверху вниз, а другая идет от 1 до 100 снизу вверх.
Тот, что слева, чаще используется в классе, однако тот, что справа, более точно соответствует действиям ученика по сложению или вычитанию. По мере того, как учащиеся продолжают считать, числа увеличиваются в таблице. По мере того, как учащийся ведет обратный отсчет при вычитании, числа идут вниз по таблице.
Базовые десять блоков
Блоки с основанием 10 — это инструмент, используемый многими способами в математике. В этом случае мы будем использовать десятичные блоки, представляющие сотни, десятки и единицы, чтобы показать действие вычитания или удаления из одной группы. Учащиеся должны начать с построения представления уменьшаемого (число, от которого отнимается), затем взять от уменьшаемого значение вычитаемого (вычитаемое число), оставив разницу. По мере того как учащиеся изучают эту стратегию, начните с чисел, где не нужно разбивать группы. По мере того, как учащиеся знакомятся с действием вычитания, начните обсуждение отдельных цифр в разрядном значении, узнайте, что, по мнению учащихся, вы могли бы сделать, если не хватает одного конкретного разрядного значения.
Затем учащиеся могут смоделировать справедливую торговлю. Когда учащиеся освоятся с физическими манипуляциями, переходите к визуальному представлению или эскизу десяти базовых блоков. Объясните учащимся, что им не нужно рисовать отдельные единицы, а использовать «стенографические» наброски основных десяти блоков (квадрат для сотен, линия для десятков и точка для единиц). Затем учащиеся могут связать свои модели с более абстрактным стандартным алгоритмом вычитания. Эта последовательность обучения смоделирована в видео.
Открытая числовая строка
Мы все знакомы с числовой строкой, которую используют маленькие дети. Обычно он начинается с нуля и увеличивается до единицы. Открытая числовая строка — это пустая числовая строка, которую можно использовать для любых значений вдоль числовой строки, которые могут быть полезны при решении задач.
Обычно галочки не включаются в открытую числовую строку, и по мере добавления числа в числовую строку они могут не соответствовать масштабу. Открытая числовая линия полезна для создания представления для записи шагов умственных вычислений. Посмотрите видео, чтобы увидеть пример использования незамкнутых числовых рядов с вычитанием.
Компенсация/отдача и получение (постоянные различия)
Компенсация — это стратегия, часто применяемая в ментальной арифметике, когда одно или несколько чисел корректируются, чтобы сделать их более удобными для ментальной арифметики. Например, некоторое значение может быть взято из уменьшаемого или вычитаемого или добавлено к нему, а затем разница корректируется, чтобы упростить решение проблемы.
В задаче 59 — 32 59 всего на единицу меньше 60, и 60 будет легче вычесть, чем 59., а разбиение 32 на 30 и 2 также облегчит мысленное вычитание, что даст нам задачу 60 — 30 — 2. 60 — 30 = 30, 30 — 2 = 28. Теперь нам нужно скорректировать задачу для дополнительной, которую мы начали с, поэтому 28 — 1 = 27. Другой способ решить ту же проблему, используя постоянные разности, состоит в том, чтобы сделать то же самое для каждого уменьшаемого и вычитаемого, виртуально перемещая их положение на числовой прямой. Подумайте о расстоянии между 32 и 59 на числовой прямой, добавляя единицу к каждому значению, делая такое же расстояние, теперь это расстояние между 33 и 60; проблемы эквивалентны только в другом месте на числовой прямой. Построение смысла чисел и использование отношений разрядных значений и цифр позволяет нам углубить наше понимание операций.
Компенсация разлагает (разбирает) или перекомпоновывает (собирает обратно) числа, чтобы упростить вычитание в уме. Учащиеся должны понять, как числа можно разбить на части и собрать вместе, чтобы укрепить свои навыки восприятия чисел.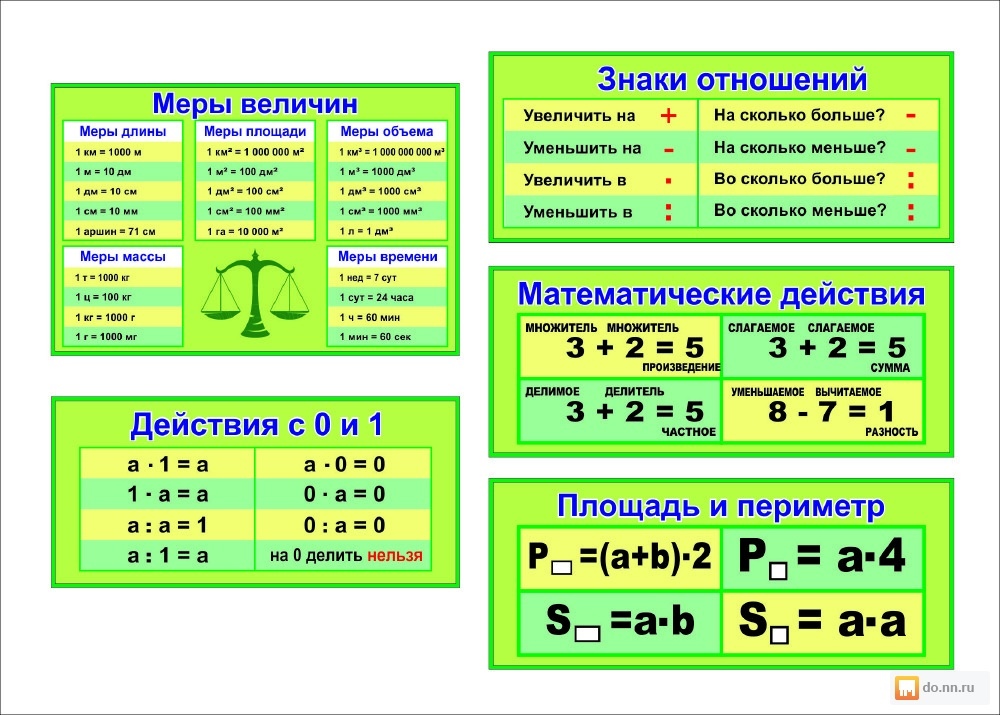
Расширенная нотация (перегруппировка)
Расширенная нотация использует разрядное значение для вычитания внутри каждого разрядного значения, а затем объединяет расширенное обозначение, чтобы получить окончательное различие. В расширенной нотации одно разрядное значение может быть перегруппировано, когда это необходимо для вычитания разрядного значения.
Стандартный алгоритм США
Стандартный алгоритм США для вычитания — это стратегия, о которой большинство взрослых думают, когда их просят вычесть числа: сложите и вычтите. Исторически сложилось так, что это набор процедур, которым нас учили в школе. Это эффективная стратегия, но строго процедурная. Когда учащиеся могут использовать более концептуальные стратегии для построения своего понимания вычитания, они могут связать процедуры с этим концептуальным пониманием.
Освоение стандартного алгоритма ожидается к концу 4 класса, однако учащиеся познакомятся с этой стратегией намного раньше, поскольку они соединяют стратегии для углубления знаний.
Видео Грэхема Флетчера — Прогресс сложения и вычитания
Чтобы узнать больше о раннем счете или о прогрессе сложения, умножения или деления, щелкните по обучающим модулям или найдите другие учебные модули по математике. здесь.
15 простых и эффективных стратегий сложения и вычитания для небольших групп
Обучение стратегиям сложения может быть легким, если вы различаете их.
Когда я впервые начал преподавать в 1-м классе, я понятия не имел, что такое стратегии сложения и вычитания…..Я знаю….звучит плохо, правда?!?! Я вырос, используя точки касания или пальцы, и это все. Поэтому в первый год обучения я предполагал, что мы будем использовать пальцы и точки касания, и в конечном итоге они просто поймут это и узнают факты. Я был так неправ, и я проделал такой долгий путь с тех пор!
Изучение основных фактов сложения и вычитания в начальных классах имеет решающее значение. Знание этих фактов будет использоваться почти в каждом математическом навыке до конца обучения каждого ученика. Как учитель первого класса, первое, что я рассказываю и убеждаюсь, что ученики овладевают различными стратегиями сложения и вычитания. Изучив эти различные стратегии сложения и вычитания на раннем этапе, учащиеся смогут использовать те из них, которые лучше всего подходят им для других навыков, в течение остальной части года.
Что такое сложение и вычитание Стратегии Существует так много разных стратегий сложения и вычитания, так каким из них вы должны научить? Стратегии обучения сложению Существует множество различных стратегий сложения и вычитания по математике, и некоторые из них немного сложнее других.
Поскольку я преподаю в 1-м классе, такие стратегии, как добавление 0 или добавление 1, уже преподавались в детском саду. Я могу быстро просмотреть эти простые стратегии, а затем перейти к более сложным. Я всегда начинаю с расчета. Этому также учат в детском саду, но это одна из стратегий сложения для 1-го класса, которую используют многие ученики. Посмотрите видео, которое я сделал, где я подробно рассказываю о том, как я учу считать в дифференцированных малых группах. Кроме того, в 1-м классе ученики работают с числами до 20, поэтому им нужна дополнительная практика с большими числами.
Посчитав, я перехожу к тому, чтобы показать им, как использовать числовую связь, рамку десятков и числовую линию или числовой путь. Опять же, этому учат в детском саду, но не в больших количествах. Кстати, если вы не слышали о числовом пути, это то же понятие, что и числовая прямая, только проще для первоклассника. На числовом пути числа представлены прямоугольниками, которые учащиеся могут считать.
На числовой прямой учащиеся должны считать единицы длины, и им трудно увидеть единицы, которые они считают. Я знаю, что когда мои первоклассники пытаются использовать числовую прямую, они начинают с 0 и заканчивают ошибкой на единицу.
Некоторые другие стратегии обучения сложению: прибавить десять, сделать десятку, удвоить и удвоить плюс один. Это следующие в моем списке для покрытия.
Стратегии вычитания После того, как мы хорошо усвоили эти стратегии сложения фактов, мы переходим к вычитанию. Большинство стратегий вычитания очень похожи на многие стратегии сложения. Сложение начинаем с обратного отсчета, а вычитание начинаем с обратного отсчета. Опять же, это наиболее часто используемая стратегия, которую я вижу со своими учениками каждый год. Затем мы начинаем вычитать с помощью таких инструментов, как числовая связь и числовые линии или числовой путь. Я также учу своих студентов, как считать, чтобы вычесть, что действительно помогает позже с семьями фактов.
Мы заканчиваем стратегии вычитания, используя то, что мы узнали о двойниках и двойниках плюс один, а также вычитании десяти.
Если учащиеся действительно овладели стратегиями обучения сложению, они обычно неплохо справляются со стратегиями вычитания. Имейте в виду, что вычитание всегда сложнее, чем сложение для большинства учащихся.
Как преподавать стратегии сложения и вычитания Есть 15 основных стратегий сложения и вычитания, которые я люблю использовать со своими первоклассниками. Большинство из тех, что я перечислил выше. У меня есть система того, что действительно работает, и я использую ее каждый год в течение первых нескольких недель в школе. Я преподаю математику ТОЛЬКО в небольших группах. Управляемая математика в 1-м классе чрезвычайно важна, на мой взгляд. Преподавание математики в группе никогда не было для меня успешным. Я не могу увидеть, осваивают ли более 20 студентов навыки, которые мне нужны, или они просто пишут число, которое написал их сосед, и показывают его мне.
Гораздо полезнее быть в небольшой группе, где я сижу прямо перед 5-6 учениками.
Я начинаю занятия в малых группах, просто быстро просматривая несколько задач, связанных с навыком, над которым мы работали в предыдущий день, а затем мы сразу приступаем к делу. У нас всего 20 минут, поэтому мы двигаемся быстро и не теряем времени. Сначала я объясняю, над чем мы будем работать в этот день, а затем использую свой рабочий коврик учителя, чтобы смоделировать для них. После того, как я смоделировал несколько примеров, ученики получают свои рабочие коврики, которые соответствуют моему коврику учителя, и они тренируются со мной. Мы следуем модели CPA (конкретно-графические-абстрактные) при работе над любым математическим навыком. Если вы не знакомы с моделью CPA, перейдите по ссылке внизу этого поста.
После того, как ученики увидели мою модель, и мы сделали несколько примеров вместе, они переворачиваются на вторую сторону своего рабочего коврика и работают независимо друг от друга, а я наблюдаю.
У меня есть список математических вопросов, которые я задаю им, чтобы убедиться, что они могут объяснить свое мышление и полностью понимают, что делают. ‘
Если вы думаете о том, чтобы попробовать заниматься математикой с гидом в классе 1-го класса, ознакомьтесь с моими 3 советами для успешного проведения групп по математике с гидом.
Стратегии сложения и вычитания для текстовых задачНа каждом уроке у меня есть набор текстовых задач, которые ученики решают, используя стратегию, которую мы отрабатывали в тот день. Итак, если мы только что провели урок по подсчету на вычитание, они должны решить свою задачу со словами, используя эту стратегию. Проблемы со словами или контекстуальные проблемы — это то, над чем нужно работать весь год. Я обнаружил, что работа над несколькими упражнениями в конце небольшой группы каждый день действительно помогает.
Мы начинаем в начале года, практикуя более простые типы ситуаций, такие как добавление и удаление.
С моей старшей группой мы начинаем пробовать запуск и изменение неизвестных проблем. Позже в этом году мы добавим другие типы задач, такие как сравнение контекстных задач.
У меня всегда есть 4 небольшие группы, и я встречаюсь с ними каждый божий день. В каждой из моих групп от 4 до 6 студентов, и мы встречаемся по 20 минут. Так как у меня нет целой группы по математике, очень важно, чтобы я видел каждого ученика каждый день. Также очень важно максимально использовать наши 20 минут. В конце нашего урока мне всегда нравится иметь игры и расширения, которые можно вытащить и использовать. Дети любят игры! Все мы знаем, что лучший способ закончить урок, чем игра.
Это никогда не подводит, хотя бы раз или два в неделю моя старшая группа просто пролетает урок за считанные минуты, и мы заканчиваем на 10 минут раньше. В эти дни у меня есть расширения задач, которые я использую.
Примером расширения задачи, которое я использую, является моделирование проблемы и намеренное совершение ошибки. Учащиеся должны понять мою ошибку и исправить ее. Другим примером может быть предоставление учащимся суммы или разности, а учащиеся придумывают числа, которые могут быть слагаемыми, уменьшаемыми или вычитаемыми. Я каждый день слежу за тем, чтобы для моих небольших групп готовилось дополнительное задание.
Самостоятельная практика после небольшой группы Стратегии вычитания и сложения для 1-го класса в моей комнате всегда включают страницы для самостоятельной практики. Когда студенты покидают мою группу, мне нравится, когда они берут страницу, чтобы попрактиковаться в навыке, который они только что выучили на своей математической станции. Они выполнят это самостоятельно и сдадут на оценку по математике. Мне нравится, когда они делают это, как только покидают мой стол, чтобы информация была свежа в их мозгу.
Я встречаюсь со своей самой высокой группой в последнюю очередь, поэтому они работают над своей практической страницей во время своего первого занятия по математике на следующий день. Иногда я могу переключать его и предлагать им работать на этой странице практики для утренней работы, домашней работы, позже в качестве обзора и т. д. Много возможностей!
Собираясь со всеми моими учениками в небольших группах, я получаю возможность различать их в зависимости от их потребностей. Когда я встречаюсь с каждой группой, я делаю все то, что упомянул выше, но на разных уровнях. Все рабочие коврики, которые используют мои группы, основаны на их уровне, а также числах, которые мы используем, страницах с независимыми упражнениями, задачах со словами и т. д.
Из всех различных стратегий сложения и вычитания, которые я использую, дифференцированные математические коврики — мои любимые! В первом классе учащиеся будут использовать эти стратегии и работать с числами до 20.
Поскольку я начинаю обучать этим стратегиям в самом начале школы, все мои группы не готовы работать с такими большими числами. Моя группа более низкого уровня обычно начинает с работы с числами только до 5, группа высокого уровня будет работать с числами до 15 (или даже 10, если им нужно), а моя группа самого высокого уровня будет практиковаться с числами до 20. Я делаю обязательно постарайтесь подтолкнуть все уровни как можно ближе к 20, поскольку это стандарт, но какой смысл заставлять их, если они не готовы.
Я преподавал, используя перечисленные выше методы, в течение многих лет, но у меня никогда не было организованного набора ежедневных планов для использования. Этим летом я решил взять все, что использовал, и организовать 15 ежедневных уроков. Необходимо было иметь все стратегии, перечисленные в том порядке, в котором они должны быть изучены, а также игры, рабочие коврики и страницы для самостоятельной практики, выровненные и скопированные на бумаге разного цвета для каждой группы.
Я хотел, чтобы проблемы со словами были уже напечатаны и дифференцированы, а вопросы, которые я задавал бы во время группы, планировались заранее.
Теперь у меня есть первые 15 дней моих математических планов, готовых к работе. Лучше всего то, что теперь, когда у меня все это напечатано, я могу использовать его долгие годы. Единственное, что мне придется копировать каждый год, это страницы независимой практики.
Я копирую все материалы нижнего уровня на оранжевый, верхнего уровня на фиолетовый и верхнего уровня на розовый. Затем я храню каждый урок вместе с фишками и карточками в сумке с номером урока. Когда я преподаю определенный урок, я вытаскиваю все для этого урока. С помощью этой стратегии цветового кодирования легко получить нужные мне страницы или карточки в зависимости от того, на какой цветной бумаге они скопированы.
Если вы хотите избавить себя от хлопот, связанных с планированием каждого из этих компонентов, а также дифференцировать их для своих учеников, ознакомьтесь с моим набором «Стратегии сложения и вычитания — Дифференцированные математические планы с подсказками».