Узнаем что сначала — сложение или умножение: правила, порядок выполнения действия и рекомендации
С самого начала следует напомнить, чтобы потом не путаться: есть цифры – их 10. От 0 до 9. Есть числа, и они состоят их цифр. Чисел бесконечно много. Точно больше, чем звезд на небе.
Математическое выражение − это записанное с помощью математических символов наставление, какие действия нужно произвести с числами, чтобы получить результат. Не «выйти» на искомый результат, как в статистике, а узнать, сколько их точно было. А вот чего и когда было − уже не входит в сферу интересов арифметики. При этом важно не ошибиться в последовательности действий, что сначала — сложение или умножение? Выражение в школе иногда называют «пример».
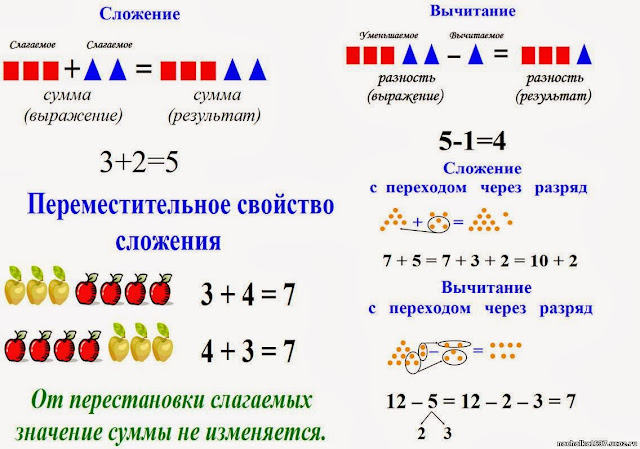
Сложение и вычитание
Какие же действия можно произвести с числами? Есть два базовых. Это сложение и вычитание. Все остальные действия построены на этих двух.
Самое простое человеческое действие: взять две кучки камней и смешать их в одну. Это и есть сложение. Для того чтобы получить результат такого действия, можно даже не знать, что такое сложение. Достаточно просто взять кучку камней у Пети и кучку камней у Васи. Сложить все вместе, посчитать все заново. Новый результат последовательного счета камней из новой кучки − это и есть сумма.
Это и есть сложение. Для того чтобы получить результат такого действия, можно даже не знать, что такое сложение. Достаточно просто взять кучку камней у Пети и кучку камней у Васи. Сложить все вместе, посчитать все заново. Новый результат последовательного счета камней из новой кучки − это и есть сумма.
Точно так же можно не знать, что такое вычитание, просто взять и разделить кучу камней на две части или забрать из кучи какое-то количество камней. Вот и останется в куче то, что называется разностью. Забрать можно только то, что есть в куче. Кредит и прочие экономические термины в данной статье не рассматриваются.
Чтобы не пересчитывать каждый раз камни, ведь бывает, что их много и они тяжелые, придумали математические действия: сложение и вычитание. И для этих действий придумали технику вычислений.
Сумма двух любых цифр тупо заучиваются без всякой техники. 2 плюс 5 равно семь. Посчитать можно на счетных палочках, камнях, рыбьих головах – результат одинаковый. Положить сначала 2 палочки, потом 5, а потом посчитать все вместе. Другого способа нет.
Другого способа нет.
Те, кто поумнее, обычно это кассиры и студенты, заучивают больше, не только сумму двух цифр, но и суммы чисел. Но самое главное, они могут складывать числа в уме, используя разные методики. Это называется навыком устного счета.
Для сложения чисел, состоящих из десятков, сотен, тысяч и еще больших разрядов, используют специальные техники − сложение столбиком или калькулятор. С калькулятором можно не уметь складывать даже цифры, да и читать дальше не нужно.
Сложение столбиком − это метод, который позволяет складывать большие (многоразрядные) числа, выучив только результаты сложения цифр. При сложении столбиком последовательно складываются соответствующие десятичные разряды двух чисел (то есть фактически две цифры), если результат сложения двух цифр превышает 10, то учитывается только последний разряд этой суммы – единицы числа, а к сумме следующих разрядов добавляется 1.
Умножение
Математики любят группировать похожие действия для упрощения расчетов. Так и операция умножения является группировкой одинаковых действий – сложения одинаковых чисел. Любое произведение N x M − есть N операций сложения чисел M. Это всего лишь форма записи сложения одинаковых слагаемых.
Так и операция умножения является группировкой одинаковых действий – сложения одинаковых чисел. Любое произведение N x M − есть N операций сложения чисел M. Это всего лишь форма записи сложения одинаковых слагаемых.
Для вычисления произведения используется такой же метод – сначала тупо заучивается таблица умножения цифр друг на друга, а потом применяется метод поразрядного умножения, что называется «в столбик».
Что сначала — умножение или сложение?
Любое математическое выражение – это фактически запись учетчика «с полей» о результатах каких-либо действий. Допустим, сбора урожая помидоров:
- 5 взрослых работников собрали по 500 помидоров каждый и выполнили норму.
- 2 школьников не ходили на уроки математики и помогали взрослым: собрали по 50 помидоров, норму не выполнили, съели 30 помидоров, надкусили и испортили еще 60 помидоров, 70 помидоров было изъято из карманов помощников. Зачем брали с собой их в поле – непонятно.
Все помидоры сдавали учетчику, он укладывал их по кучкам.
Запишем результат «сбора» урожая в виде выражения:
- 500 + 500 + 500 + 500 + 500 — это кучки взрослых работников;
- 50 + 50 – это кучки малолетних работников;
- 70 – изъято из карманов школьников (испорченное и надкусанное в зачет результата не идет).
Получаем пример для школы, запись учетчика результатов работы:
500 + 500 +500 +500 +500 + 50 +50 + 70 =?;
Здесь можно применить группировку: 5 кучек по 500 помидоров − это можно записать через операцию умножения: 5 ∙ 500.
Две кучки по 50 – это тоже можно записать через умножение.
И одна кучка 70 помидоров.
5 ∙ 500 + 2 ∙ 50 + 1 ∙ 70 =?
И что делать в примере сначала − умножение или сложение? Так вот, складывать можно только помидоры. Нельзя сложить 500 помидоров и 2 кучки. Они не складываются. Поэтому сначала нужно всегда все записи привести к базовым операциям сложения, то есть в первую очередь вычислить все операции группировки-умножения. Совсем простыми словами — сначала выполняется умножение, а сложение уже потом. Если умножить 5 кучек по 500 помидоров каждая, то получится 2500 помидоров. А дальше их уже можно складывать с помидорами из других кучек.
Если умножить 5 кучек по 500 помидоров каждая, то получится 2500 помидоров. А дальше их уже можно складывать с помидорами из других кучек.
2500 + 100 + 70 = 2 670
При изучении ребенком математики нужно донести до него, что это инструмент, используемый в повседневной жизни. Математические выражения являются, по сути (в самом простом варианте начальной школы), складскими записями о количестве товаров, денег (очень легко воспринимается школьниками), других предметов.
Соответственно, любое произведение – это сумма содержимого некоторого количества одинаковых емкостей, ящиков, кучек, содержащих одинаковое количество предметов. И что сначала умножение, а сложение потом, то есть сначала начала вычислить общее количество предметов, а затем уже складывать их между собой.
Деление
Операция деления отдельно не рассматривается, она обратная умножению. Нужно что-то распределить по коробкам, так, чтобы во всех коробках было одинаковое заданное количество предметов. Самый прямой аналог в жизни – это фасовка.
Скобки
Большое значение в решении примеров имеют скобки. Скобки в арифметике – математический знак, используемый для регулирования последовательности вычислений в выражении (примере).
Умножение и деление имеют приоритет выше, чем сложение и вычитание. А скобки имеют приоритет выше, чем умножение и деление.
Все, что записано в скобках, вычисляется в первую очередь. Если скобки вложенные, то сначала вычисляется выражение во внутренних скобках. И это непреложное правило. Как только выражение в скобках вычислено, скобки пропадают, а на их месте возникает число. Варианты раскрытия скобок с неизвестными здесь не рассматриваются. Так делают до тех пор, пока все они не исчезнут из выражения.
((25-5) : 5 + 2) : 3 =?
- Это как коробочки с конфетами в большом мешке. Сначала нужно раскрыть все коробочки и ссыпать в большой мешок: (25 – 5 ) = 20. Пять конфет из коробочки сразу заслали отличнице Люде, которая приболела и в празднике не участвует. Остальные конфеты − в мешок!
- Потом связать конфеты в пучки по 5 штук: 20 : 5 = 4.

- Потом добавить в мешок еще 2 пучка конфет, чтобы можно было поделить на троих детей без драки. Признаки деления на 3 в данной статье не рассматриваются.
(20 : 5 + 2) : 3 = (4 +2) : 3 = 6 : 3 = 2
Итого: трем детям по два пучка конфет (по пучку в руку), по 5 конфет в пучке.
Если вычислить первые скобки в выражении и переписать все заново, пример станет короче. Метод не быстрый, с большим расходом бумаги, зато удивительно эффективный. Заодно тренирует внимательность при переписывании. Пример приводится к виду, когда остается только один вопрос, сначала умножение или сложение без скобок. То есть к такому виду, когда скобок уже и нет. Но ответ на этот вопрос уже есть, и нет смысла обсуждать, что идет сначала — умножение или сложение.
«Вишенка на торте»
И напоследок. К математическому выражению не применимы правила русского языка – читать и выполнять слева направо:
5 – 8 + 4 = 1;
Это простенький пример может довести до истерики ребенка или испортить вечер его маме. Потому что именной ей придется объяснять второкласснику, что бывают отрицательные числа. Или рушить авторитет «МарьиВановны», которая сказала, что: «Нужно слева направо и по порядку».
Потому что именной ей придется объяснять второкласснику, что бывают отрицательные числа. Или рушить авторитет «МарьиВановны», которая сказала, что: «Нужно слева направо и по порядку».
«Совсем вишня»
В Сети гуляет пример, вызывающий затруднения у взрослых дяденек и тетенек. Он не совсем по рассматриваемой теме, что сначала — умножение или сложение. Он вроде как про то, что сначала выполняете действие в скобках.
От перестановки слагаемых сумма не изменяется, от перестановки множителей тоже. Нужно просто записывать выражение так, чтобы не было потом мучительно стыдно.
6 : 2 ∙ (1+2) = 6 ∙ ½ ∙ (1+2) = 6 ∙ ½ ∙ 3 = 3 ∙ 3 = 9
Теперь точно все!
Вычитание натуральных чисел | Математика | 5 класс
На уроке вы узнаете, какие бывают прямые и обратные действия в математике. Учитель расскажет обо всех компонентах вычитания, а также покажет два способа для вычитания суммы из числа.
Прямое и обратное действие
В жизни мы все время сталкиваемся с прямыми и противоположными действиями. Можно налить воду в кружку, можно вылить воду. Можно зайти в дом, потом выйти из дома. Таких примеров очень много.
Можно налить воду в кружку, можно вылить воду. Можно зайти в дом, потом выйти из дома. Таких примеров очень много.
В математике мы тоже легко найдем пару таких противоположных действий. Это сложение и вычитание.
Как устроено сложение? Добавили к 3 яблокам 2 яблока, получили 5 яблок, получилось сложение (рис. 1).
Рис. 1. Иллюстрация сложения
Вычитание: было 5 яблок, отняли 2, осталось 3. Получилось вычитание (рис. 2).
Рис. 2. Вычитание
Ясно, что добавить и отнять – это противоположные действия, таким образом, сложение и вычитание – это взаимопротивоположные действия.
Вычитание
Чтобы выполнить сложение или вычитание, мы не берем себе в помощь предметы и не складываем их в одну кучу. Мы решаем такую задачу отвлеченно, используя числа и противоположные операции.
Например, чтобы вычесть 2 из 5, мы должны понять, что останется.
А для этого нам нужно представить 5 как сумму двух частей.
И мы понимаем, что если вычесть 2, то останется 3.
Одно и то же количество можно представить и записать различными способами. Все эти способы эквивалентны:
. Мы всегда можем пользоваться тем, который нам удобен в данном случае. Сейчас нам удобно представить, что 5 – это сумма 3 и 2. Поэтому если убрать, вычесть одну часть (2), то останется вторая (3).
Как из 15 вычесть 7?
Мы сразу представляем, что
. Значит, после вычитания 7 останется 8.
Становится понятно, что вычитание – это нахождение неизвестного числа разложения.
Еще раз рассмотрим пример.
Чтобы вычесть из числа 5 число 2, нужно представить 5 в виде двух слагаемых и найти неизвестное слагаемое. Оно и будет результатом вычитания .
Определение вычитания
Если из числа
нужно вычесть число :
Значит, что число
нужно представить в виде двух слагаемых и .
Одно слагаемое нам неизвестно. Его и надо найти. Оно и есть результат вычитания.
Понятно, что взять из вазы больше яблок, чем там было, невозможно. Поэтому, когда мы говорим о вычитании натуральных чисел, мы не можем из меньшего числа вычесть большее. Потом будут и другие числа, не только натуральные, и вычитание из меньшего числа большего станет возможным.
Или еще вот такое рассуждение: вычесть – значит представить в виде двух слагаемых, но ведь слагаемые, части не могут быть больше целого.
Но пока договоренность следующая: из числа
вычитаем число , только если не меньше, чем . Результатом будет новое число .
- Число , от которого мы будем отнимать, которое мы будем уменьшать, называют «уменьшаемое».
- Число , количество, которое мы будем отнимать, вычитать, называется «вычитаемое».
- Число , результат вычитания, называется разностью.
- Сама запись тоже называется разностью (рис. 3).
Рис. 3. Названия компонентов при вычитании
3. Названия компонентов при вычитании
Слово «разность» очень похоже на слово «разница». В самом деле, какова разница, на сколько отличается число 15 от числа 7, 15 яблок от 7 яблок? На 8 яблок. То есть, разность чисел 15 и 7 – это и есть разница между ними.
Таким образом, с одной стороны разность – это результат вычитания из большего числа меньшего. С другой стороны – это то, на сколько одно число отличается от другого, разница между ними.
Задачи на вычитание. Пример 1
Папе 36 лет, а маме на 2 года меньше. Сколько маме лет?
Из 36 вычитаем 2.
Это первый тип задач, которые мы решаем при помощи вычитания: известно одно число, нужно найти второе, которое меньше на известную величину. То есть нам сразу известны уменьшаемое и вычитаемое, числа
и .
Пример 2
В классе учится 25 человек, из них 14 девочек. Сколько в классе мальчиков?
Понятно, что девочек и мальчиков всего 25 человек. Девочек 14, мальчиков – неизвестное количество.
Нужно найти неизвестное слагаемое. А поиск неизвестного слагаемого – это уже задача на вычитание. Из 25 нужно отнять 14.
В классе 11 мальчиков.
Это второй тип задач, когда складывают два числа, одно из них известно, а другое нет. Но зато известен результат, сумма.
Синим цветом выделены известные
и . Необходимо найти неизвестное слагаемое . Но поиск неизвестного слагаемого – это и есть вычитание.
Пример 3
Сестре 12 лет, а брату 9. На сколько лет сестра старше брата?
Нужно узнать разницу, а значит нужно вычитать. Итак, вычитаем из 12 число 9.
Сестра старше брата на 3 года.
Это третий тип задач – задачи на сравнение.
Задача 1
В вазе было 17 яблок. Петя взял 4 яблока, Маша взяла 3. Сколько осталось яблок в вазе?
Решение
1 способ
Петя взял 4, Маша – 3, всего они взяли
яблок. Чтобы найти, сколько осталось, вычитаем:
Если записать в одну строчку:
2 способ
Посчитаем, сколько оставалось яблок каждый раз, когда Петя и Маша брали яблоки. Петя взял 4, осталось
Петя взял 4, осталось
. Маша взяла еще 3, осталось .
Или, в одну строчку,
.
В вазе осталось 10 яблок.
Оба способа равносильны, ответ одинаковый. То есть вычесть сумму – это все равно, что вычесть каждое слагаемое этой суммы по отдельности.
Правило вычитания
Если необходимо вычесть сумму, то можно сначала вычислить сумму в скобках, после этого произвести вычитание. Либо можно вычесть каждое слагаемое по отдельности:
Пример 4
1 способ
Можно сделать сначала действия в скобках и потом из 79 вычесть результат.
2 способ
Мы видим, что 79 и 19 оканчиваются на одну цифру, на 9. Значит, удобнее вычесть из 79 первое число,19, а затем второе число 24.
Правило
Вычитание и сложение – равноправные действия.
Пусть есть ваза с яблоками. Мама туда добавила 3 яблока, а папа взял 4. Изменится ли итоговое количество яблок, если они сделают это в другой последовательности – сначала папа возьмет 4, а потом мама добавит 3?
Мама туда добавила 3 яблока, а папа взял 4. Изменится ли итоговое количество яблок, если они сделают это в другой последовательности – сначала папа возьмет 4, а потом мама добавит 3?
Нет, конечно, результат будет одинаков. То есть если к числу что-то прибавляется и вычитается, то эти действия можно менять местами. Главное – помнить, что мы не можем от меньшего отнять большее.
Пример 5
Здесь удобно сначала из 79 вычесть 19. Для этого меняем местами действия сложения и вычитания.
Имеет ли смысл переставлять местами слагаемые? Нет.
Здесь явно удобнее вычесть третье слагаемое из первого.
Заключение
Список литературы
- Дорофеев Г. В., Петерсон Л. Г. Математика. 5 класс. Учебник в 2 ч. – 2-е изд., перераб. – М.: 2011; Ч. 1 – 176 с, Ч. 2 – 240 с.
- Зубарева И. И., Мордкович А. Г. Математика. 5 класс.
 – 14-е изд., испр. и доп. – М.: 2013. – 270 с.
– 14-е изд., испр. и доп. – М.: 2013. – 270 с. - Никольский С. М., Потапов М. К. и др. Математика. 5 класс. Учебник. – 14-е изд. – М.: 2015. – 272 с.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «infourok.ru» (Источник)
Домашнее задание
Вычислите удобным способом:
5 класс. Математика. Действия с натуральными числами — Сложение и вычитание натуральных чисел
Комментарии преподавателяНа этом уроке вы познакомитесь со сложением натуральных чисел и законами, которым оно подчиняется. Выясните, что, используя эти законы, гораздо удобнее складывать числа. А также решите несколько примеров.
Пример 1
Детям, которые учатся читать и писать, дают такое задание: сложите два слога в одно слово: БАН и КА.
БАН + КА = БАНКА
Но иногда делают и наоборот: КА + БАН = КАБАН
Пример 2
Лена и Ваня наливают воду в ведро. У Лены есть двухлитровая банка с водой, а у Вани – трехлитровая. Есть разница, в какой последовательности они выльют воду? Нет. В любом случае там окажется одинаковое количество воды (5 литров).
У Лены есть двухлитровая банка с водой, а у Вани – трехлитровая. Есть разница, в какой последовательности они выльют воду? Нет. В любом случае там окажется одинаковое количество воды (5 литров).
В обоих примерах складывали две части. Но в первом случае порядок был важен, и если мы переставляли слагаемые местами, то менялся результат. Во втором случае порядок был не важен, слагаемые можно было менять местами.
Математическое сложение
Вычислите: .
Вычислите: .
То есть .
Все эти три записи означают одно и то же количество.
Вспоминая примеры со слогами и водой, приходим к предположению, что математическое сложение похоже на второй пример с водой, где менять местами слагаемые было можно.
Чтобы понять, что можно делать при сложении, а чего нельзя, нужно выяснить, что это такое. Что значит сложить 5 и 3? Это значит, что надо сложить 5 единиц и 3 единицы.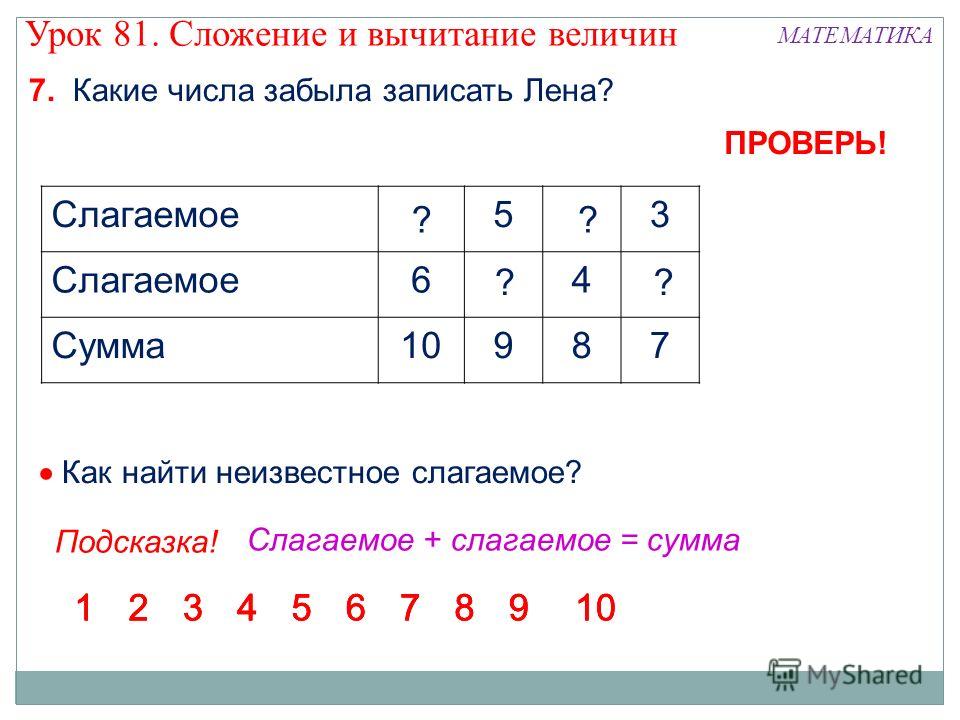 Можно представить их палочками (см. рис. 1).
Можно представить их палочками (см. рис. 1).
Рис. 1. Представление сложения
Слово «сложить» значит сложить в одну кучу. А потом посчитать, сколько там всего. Получится восемь (см. рис. 2).
Утверждение
Количество единиц, палочек в большой куче всегда можно посчитать. То есть любые две группы палочек можно сложить в одну большую. И там будет конкретное количество палочек.
На языке математики это можно сказать следующим образом: два любых натуральных числа и можно сложить. В результате получится новое натуральное число .
Числа и называются слагаемыми. Число называют суммой чисел и . Саму запись тоже называют суммой.
Переместительный закон сложения
Складывая две группы единиц в одну большую, можно поступить двумя способами:
1) к первой группе добавить вторую,
2) ко второй добавить первую.
Неважно, в какой последовательности это делать.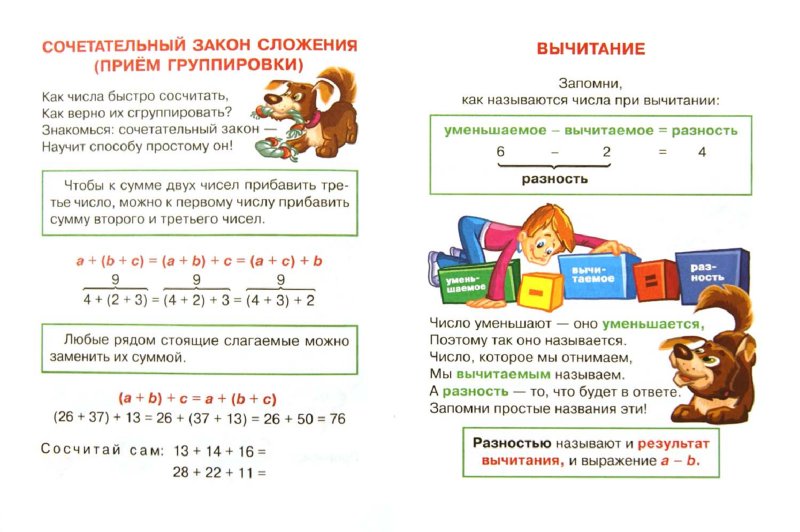 Взять сначала пять единиц и к ним добавить три или наоборот. То есть мы просто внутри большой кучки поменяли местами несколько элементов. Но от этого их количество не изменится. Результат всегда будет одинаков. Единиц, палочек в общей кучке всегда будет одно и то же количество. В данном случае восемь.
Взять сначала пять единиц и к ним добавить три или наоборот. То есть мы просто внутри большой кучки поменяли местами несколько элементов. Но от этого их количество не изменится. Результат всегда будет одинаков. Единиц, палочек в общей кучке всегда будет одно и то же количество. В данном случае восемь.
На языке математики это можно сказать следующим образом: от перестановки слагаемых сумма не изменяется.
Так , потому что и та, и другая сумма равны 8.
С большими числами этот закон тоже работает: . Эти две суммы равны друг другу. Чтобы это понять, не нужно считать. Мы знаем, что от перестановки слагаемых сумма не меняется.
Сочетательный закон сложения
Пусть теперь у нас три числа (три группы единиц) и их нужно сложить. То есть сложить в одну кучу. Есть два варианта:
1) добавить к первой сначала вторую, потом третью,
2) добавить к первой уже сложенные заранее вторую и третью.
Нет никакой разницы. Мы всегда будем получать одно и то же множество единиц, палочек. Ниоткуда новые не возьмутся, и имеющиеся не потеряются.
Если записать это с помощью чисел:
Если складывать любые три числа , то можно сложить сначала первые два числа, а можно начать с последних двух. Последовательность действий при сложении нескольких слагаемых не важна.
Эти законы очень сильно могут облегчить вычисления.
Пример
Мы можем складывать в любой последовательности. Выберем такую последовательность, чтобы было удобно. Смотрим на последние цифры. Если они дают в сумме 10, то лучше попробовать начать с них, их проще сложить. У второго слагаемого в конце 6, а у третьего 4, в сумме они дают 10, поэтому сложим сначала их, а затем прибавим первое слагаемое.
Пример
Первое и последнее числа заканчиваются на пять, значит, сумма будет заканчиваться на ноль, это удобно. Но они стоят не подряд. Поменяем местами 39 и 295.
Но они стоят не подряд. Поменяем местами 39 и 295.
Идея проста: если надо сложить сразу несколько чисел, мы можем переставлять их, как хотим, и выполнять действия в любом порядке.
Пример
Первое число удобно сложить с последним, а второе – с третьим.
Пример
Пусть у нас несколько ваз, в каждой какое-то количество яблок. Нужно узнать, сколько яблок всего. Не нужно ссыпать все яблоки в одну кучу и пересчитывать их. Просто выпишем на бумагу, сколько в каждой вазе яблоке, и сложим эти числа. Например, .
Если какая-то ваза окажется пустой, то мы напишем, что в ней ноль яблок, и общий подсчет будет выглядеть так: .
Пустая ваза не влияет на общее количество яблок. То есть добавления нуля не меняет исходное количество: .
Заключение
Подведем итог.
1)
Любые два натуральных числа и можно сложить, в итоге будет тоже натуральное число . Числа и называются слагаемыми, число суммой.
Числа и называются слагаемыми, число суммой.
2)
От перестановки слагаемых сумма не изменяется.
3)
Последовательность действий при суммировании не важна.
4)
Прибавление нуля к числу не меняет этого числа.
На уроке вы узнаете, какие бывают прямые и обратные действия в математике. Учитель расскажет обо всех компонентах вычитания, а также покажет два способа для вычитания суммы из числа.
В жизни мы все время сталкиваемся с прямыми и противоположными действиями. Можно налить воду в кружку, можно вылить воду. Можно зайти в дом, потом выйти из дома. Таких примеров очень много.
В математике мы тоже легко найдем пару таких противоположных действий. Это сложение и вычитание.
Как устроено сложение? Добавили к 3 яблокам 2 яблока, получили 5 яблок, получилось сложение (рис. 1).
Рис. 1. Иллюстрация сложения
Вычитание: было 5 яблок, отняли 2, осталось 3. Получилось вычитание (рис. 2).
Получилось вычитание (рис. 2).
Рис. 2. Вычитание
Ясно, что добавить и отнять – это противоположные действия, таким образом, сложение и вычитание – это взаимопротивоположные действия.
Вычитание
Чтобы выполнить сложение или вычитание, мы не берем себе в помощь предметы и не складываем их в одну кучу. Мы решаем такую задачу отвлеченно, используя числа и противоположные операции.
Например, чтобы вычесть 2 из 5, мы должны понять, что останется.
А для этого нам нужно представить 5 как сумму двух частей.
И мы понимаем, что если вычесть 2, то останется 3.
Одно и то же количество можно представить и записать различными способами. Все эти способы эквивалентны: . Мы всегда можем пользоваться тем, который нам удобен в данном случае. Сейчас нам удобно представить, что 5 – это сумма 3 и 2. Поэтому если убрать, вычесть одну часть (2), то останется вторая (3).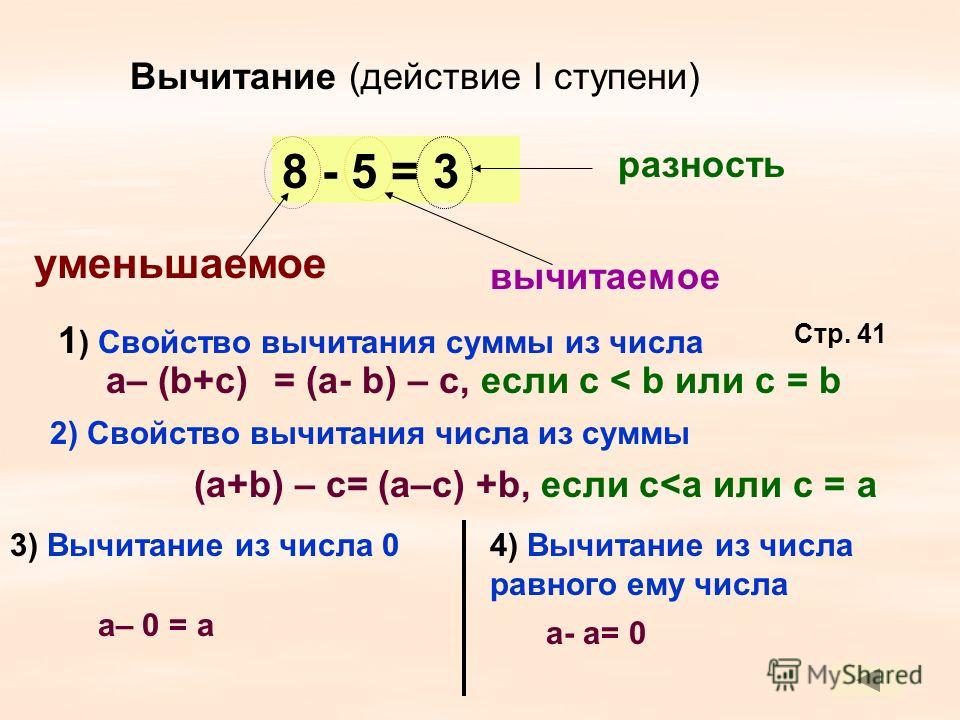
Как из 15 вычесть 7?
Мы сразу представляем, что . Значит, после вычитания 7 останется 8.
Становится понятно, что вычитание – это нахождение неизвестного числа разложения.
Еще раз рассмотрим пример. Чтобы вычесть из числа 5 число 2, нужно представить 5 в виде двух слагаемых и найти неизвестное слагаемое. Оно и будет результатом вычитания .
Определение вычитания
Если из числа нужно вычесть число :
Значит, что число нужно представить в виде двух слагаемых и .
Одно слагаемое нам неизвестно. Его и надо найти. Оно и есть результат вычитания.
Понятно, что взять из вазы больше яблок, чем там было, невозможно. Поэтому, когда мы говорим о вычитании натуральных чисел, мы не можем из меньшего числа вычесть большее. Потом будут и другие числа, не только натуральные, и вычитание из меньшего числа большего станет возможным.
Или еще вот такое рассуждение: вычесть – значит представить в виде двух слагаемых, но ведь слагаемые, части не могут быть больше целого.
Но пока договоренность следующая: из числа вычитаем число , только если не меньше, чем . Результатом будет новое число .
-
Число , от которого мы будем отнимать, которое мы будем уменьшать, называют «уменьшаемое».
-
Число , количество, которое мы будем отнимать, вычитать, называется «вычитаемое».
-
Число , результат вычитания, называется разностью.
-
Сама запись тоже называется разностью (рис. 3).
Рис. 3. Названия компонентов при вычитании
Слово «разность» очень похоже на слово «разница». В самом деле, какова разница, на сколько отличается число 15 от числа 7, 15 яблок от 7 яблок? На 8 яблок. То есть, разность чисел 15 и 7 – это и есть разница между ними.
То есть, разность чисел 15 и 7 – это и есть разница между ними.
Таким образом, с одной стороны разность – это результат вычитания из большего числа меньшего. С другой стороны – это то, на сколько одно число отличается от другого, разница между ними.
Задача
Папе 36 лет, а маме на 2 года меньше. Сколько маме лет?
Из 36 вычитаем 2.
Это первый тип задач, которые мы решаем при помощи вычитания: известно одно число, нужно найти второе, которое меньше на известную величину. То есть нам сразу известны уменьшаемое и вычитаемое, числа и .
Задача
В классе учится 25 человек, из них 14 девочек. Сколько в классе мальчиков?
Понятно, что девочек и мальчиков всего 25 человек. Девочек 14, мальчиков – неизвестное количество.
Нужно найти неизвестное слагаемое. А поиск неизвестного слагаемого – это уже задача на вычитание. Из 25 нужно отнять 14.
В классе 11 мальчиков.
Это второй тип задач, когда складывают два числа, одно из них известно, а другое нет. Но зато известен результат, сумма.
Синим цветом выделены известные и . Необходимо найти неизвестное слагаемое . Но поиск неизвестного слагаемого – это и есть вычитание.
Задача
Сестре 12 лет, а брату 9. На сколько лет сестра старше брата?
Нужно узнать разницу, а значит нужно вычитать. Итак, вычитаем из 12 число 9.
Сестра старше брата на 3 года.
Это третий тип задач – задачи на сравнение.
Задача
В вазе было 17 яблок. Петя взял 4 яблока, Маша взяла 3. Сколько осталось яблок в вазе?
Решение
1 способ
Петя взял 4, Маша – 3, всего они взяли яблок. Чтобы найти, сколько осталось, вычитаем:
Если записать в одну строчку:
2 способ
Посчитаем, сколько оставалось яблок каждый раз, когда Петя и Маша брали яблоки. Петя взял 4, осталось . Маша взяла еще 3, осталось .
Петя взял 4, осталось . Маша взяла еще 3, осталось .
Или, в одну строчку, .
В вазе осталось 10 яблок.
Оба способа равносильны, ответ одинаковый. То есть вычесть сумму – это все равно, что вычесть каждое слагаемое этой суммы по отдельности.
Правило вычитания
Если необходимо вычесть сумму, то можно сначала вычислить сумму в скобках, после этого произвести вычитание. Либо можно вычесть каждое слагаемое по отдельности:
Пример
1 способ
Можно сделать сначала действия в скобках и потом из 79 вычесть результат.
2 способ
Мы видим, что 79 и 19 оканчиваются на одну цифру, на 9. Значит, удобнее вычесть из 79 первое число,19, а затем второе число 24.
Правило
Вычитание и сложение – равноправные действия.
Пусть есть ваза с яблоками. Мама туда добавила 3 яблока, а папа взял 4. Изменится ли итоговое количество яблок, если они сделают это в другой последовательности – сначала папа возьмет 4, а потом мама добавит 3?
Нет, конечно, результат будет одинаков. То есть если к числу что-то прибавляется и вычитается, то эти действия можно менять местами. Главное – помнить, что мы не можем от меньшего отнять большее.
То есть если к числу что-то прибавляется и вычитается, то эти действия можно менять местами. Главное – помнить, что мы не можем от меньшего отнять большее.
Пример
Здесь удобно сначала из 79 вычесть 19. Для этого меняем местами действия сложения и вычитания.
Имеет ли смысл переставлять местами слагаемые? Нет.
(14 +36) – (25 + 25) = 50 – 50 = 0
3. 414 – (93 +114) =
Здесь явно удобнее вычесть третье слагаемое из первого.
414 – (93 +114) = 414 – (114 + 93) = 414 – 114 – 93 = 300 – 93 = 207
Источник конспекта: http://interneturok.ru/ru/school/matematika/5-klass/bslozhenie-i-vychitanie-naturalnyh-chiselb/slozhenie-naturalnyh-chisel-i-ego-svoystva?konspekt&chapter_id=768
http://interneturok.ru/ru/school/matematika/5-klass/bslozhenie-i-vychitanie-naturalnyh-chiselb/vychitanie?konspekt&chapter_id=768
Источник теста:https://www.youtube. com/watch?v=c2D2l8dqtng
com/watch?v=c2D2l8dqtng
Источник видео: http://www.youtube.com/watch?v=fYgpLuMdOW0
Занятия по математике для первого класса. Стратегии сложения и вычитания. Рабочие листы с числами
Вовлеките своих учащихся в эти веселые задания по математике для первого класса, основанные на чувстве чисел, со стратегиями сложения и вычитания. Рабочие листы и цифровые задания помогут им овладеть этими важными основополагающими навыками.
Эти задания для первого класса по математике, а также рабочие листы по стратегиям сложения и вычитания идеально подходят для утренней работы, выполнения домашних заданий, занятий в математических центрах, дистанционного или гибридного обучения или домашнего обучения.
Рабочие листы No Prep для печати и готовые к использованию цифровые задания дают вам множество вариантов при назначении вашим ученикам. Идеально подходит для управляемой практики, самостоятельной практики, математических центров или вмешательства.
Цифровые задания легко назначить через Google Classroom или поделившись ссылкой напрямую со своими учениками. Заполните свои планы уроков этими не требующими подготовки занятиями и отдыхайте, зная, что вы предлагаете своим ученикам увлекательную и кропотливую математическую практику.
Задания по математике для первого класса со свойствами операций Рабочие листы включают:
- Печатный формат PDF
- Цифровая версия, совместимая с Google Slides полностью ЦИФРОВАЯ версия для использования с Google Slides™ НАЖМИТЕ ЗДЕСЬ.
Для распечатки в формате PDF, идеально подходящей только для дистанционного обучения, НАЖМИТЕ ЗДЕСЬ.
Мегапрактика по математике для первого класса 1.OA.6 Много 1.OA.6 Практика по математике для первого класса для ваших учеников, работающих с различными математическими стратегиями. 1.OA.6 посвящен изучению стратегий сложения и вычитания основных фактов в пределах двадцати.
 Получение основы с этими стратегиями даст вашим ученикам преимущество в будущей математической работе. Учащимся нужно много возможностей для работы со всеми новыми математическими навыками. Эти стратегии очень важны для ваших учеников, чтобы они могли понять математические концепции более высокого уровня.
Получение основы с этими стратегиями даст вашим ученикам преимущество в будущей математической работе. Учащимся нужно много возможностей для работы со всеми новыми математическими навыками. Эти стратегии очень важны для ваших учеников, чтобы они могли понять математические концепции более высокого уровня.Этот модуль соответствует стандарту Common Core Math Standard для первого класса 1.OA.6:
Сложение и вычитание в пределах 20 с демонстрацией свободного владения языком
сложение и вычитание в пределах 10 стратегии вычитания).
Он включает в себя следующие стратегии сложения и вычитания:
1.OA.6.a: Считаем и делаем десятку, чтобы сложить. (17 страниц)
1.OA.6.b Разложение чисел, ведущих к десятке (14 страниц)
1.OA.6.c Использование связи между сложением и вычитанием (9 страниц)
1.
 OA.6.d Создание эквивалентных, но более простых сумм (5 страниц)
OA.6.d Создание эквивалентных, но более простых сумм (5 страниц) 1.OA .6 Выберите свою стратегию – беглость речи (21 страница)
Включает более шестидесяти страниц практики на круглогодичную тему. Я использую эти страницы во время нашей ротации «письменной математической практики» во время математического семинара / математического занятия с гидом. Эти страницы также можно использовать для тех, кто рано заканчивает, или для домашних заданий во время обучения математической стратегии 1.OA.6b. Смотрите еще MEGA MATH PRACTICE единиц должны быть приведены в соответствие с Едиными базовыми стандартами штата.
Обязательно ознакомьтесь с ОГРОМНЫМ набором практических упражнений по математике здесь:
Практика по мегаматематике ВСЕ СТАНДАРТЫ плюс сезонные единицы (53 ЕДИНИЦЫ)
БОЛЕЕ 2000 страниц практических занятий на основе стандартов Сезонные единицы здесь:
Мегапрактика по математике Снова в школу 1.
 NBT.2
NBT.2Мегапрактика по математике Снова в школу 1.OA.4
Мегапрактика по математике Снова в школу 1.OA.3
Мегапрактика по математике Снова в школу БЕСПЛАТНО 1.NBT.2
Мегапрактика по математике Снова в школу БЕСПЛАТНО 1.NBT.4
Мегапрактика по математике Хэллоуин 1.OA. 1
Мегапрактика по математике на Хэллоуин 1.NBT.2
Мегапрактика по математике на День Благодарения 1.OA.5
Мегапрактика по математике на День Благодарения БЕСПЛАТНО 1.OA.5
Мегапрактика по математике на День Благодарения 1.OA.6A
Мегаматематика Практические каникулы 1.OA.1
Mega Math Practice Holiday 1.OA.5
Mega Math Practice Holiday FREE 1.OA.6A
Mega Math Practice Holiday Holiday 1.OA.6A
Mega Math Practice Winter 1.OA.3
Mega Math Practice New Year 1.OA.4
Mega Math Практика Валентина 1.OA.6
Мегапрактика по математике St. Patty 1.NBT.1
Мегапрактика по математике Весна 1.NBT.2
Еще Мегапрактика по математике:
Набор чисел и операций с основанием 10 1.
 NBT
NBTСборник операций и алгебраического мышления 1.OA
Операции и ALgebraic Thinking Word Problems 1.OA.1
Комплект по геометрии 1.G
Комплект по измерениям 1.MD
Я использую математику в своих классах более десяти лет. Я начинаю свой учебный блок обучения/расширения математических концепций всей группой, но большая часть моего математического блока посвящена управляемой практике в небольших группах, за которой следует независимая практика или практика в малых группах, центры и вмешательство. Я начинаю свое математическое время каждый день со страницы из моего популярного номера дня 9.Серия 0004. Вы можете найти больше математики в этом «печатном» формате в моем магазине.
Я надеюсь, что вам и вашим детям понравится этот забавный ресурс. Загляните в мой магазин, чтобы найти множество забавных математических единиц, в том числе мои популярные единицы Number of the Day для оценок K-Second.
Советы покупателям:
Как получить кредит TPT для будущих покупок:
• Перейдите на страницу «Мои покупки» (возможно, вам потребуется войти в систему).
 Рядом с каждой покупкой вы увидите кнопку «Оставить отзыв». Просто нажмите на нее, и вы попадете на страницу, где вы можете дать быструю оценку и оставить краткий комментарий к продукту. Каждый раз, когда вы оставляете отзыв, TPT начисляет вам баллы за отзыв, которые вы используете для снижения стоимости ваших будущих покупок. Я очень ценю ваши отзывы, поскольку они помогают мне определить, какие продукты наиболее ценны для вашего класса, чтобы я мог создавать для вас больше.
Рядом с каждой покупкой вы увидите кнопку «Оставить отзыв». Просто нажмите на нее, и вы попадете на страницу, где вы можете дать быструю оценку и оставить краткий комментарий к продукту. Каждый раз, когда вы оставляете отзыв, TPT начисляет вам баллы за отзыв, которые вы используете для снижения стоимости ваших будущих покупок. Я очень ценю ваши отзывы, поскольку они помогают мне определить, какие продукты наиболее ценны для вашего класса, чтобы я мог создавать для вас больше.Узнавайте первыми о моих новых скидках, бесплатных подарках и новых продуктах:
• Найдите зеленую звездочку рядом с логотипом моего магазина и щелкните ее, чтобы стать подписчиком. Теперь вы будете получать по электронной почте обновления о моем магазине.
Эта покупка предназначена только для одного учителя.
Авторские права на этот материал принадлежат Барбаре Морган Балиус. Приобретение этого продукта, защищенного авторским правом, включает ограниченную лицензию на использование в классе.
 Он предназначен для использования одним учителем в одном классе. Вы можете использовать этот ресурс для каждого из ваших учеников в одном классе. Продукт нельзя копировать и распространять, загружать в Интернет или хранить в общедоступной поисковой системе за пределами вашего класса до получения письменного разрешения от его автора, Барбары Морган Балиус. Этот ресурс не является открытым образовательным ресурсом (OER) и поэтому не может быть загружен ни на какие веб-сайты #GoOpen, включая, помимо прочего, Amazon Inspire. Если вы собираетесь использовать его более чем для одного класса, целой школы или целого округа, дополнительные лицензии можно приобрести в магазине «Учителя платят учителям». Страницы, включенные в этот ресурс, не могут использоваться полностью или частично для создания чего-либо нового и/или распространяться каким-либо образом без письменного согласия автора, Барбары Морган Балиус.
Он предназначен для использования одним учителем в одном классе. Вы можете использовать этот ресурс для каждого из ваших учеников в одном классе. Продукт нельзя копировать и распространять, загружать в Интернет или хранить в общедоступной поисковой системе за пределами вашего класса до получения письменного разрешения от его автора, Барбары Морган Балиус. Этот ресурс не является открытым образовательным ресурсом (OER) и поэтому не может быть загружен ни на какие веб-сайты #GoOpen, включая, помимо прочего, Amazon Inspire. Если вы собираетесь использовать его более чем для одного класса, целой школы или целого округа, дополнительные лицензии можно приобрести в магазине «Учителя платят учителям». Страницы, включенные в этот ресурс, не могут использоваться полностью или частично для создания чего-либо нового и/или распространяться каким-либо образом без письменного согласия автора, Барбары Морган Балиус.Если у вас есть какие-либо вопросы, касающиеся этой ограниченной лицензии на этот продукт, пожалуйста, свяжитесь с mrsbaliusfirstgrade@aol.
 com для получения предложения.
com для получения предложения.15 простых и эффективных стратегий сложения и вычитания для небольших групп
Обучение стратегиям сложения может быть легким, если вы различаете их.Когда я впервые начал преподавать в 1-м классе, я понятия не имел, что такое стратегии сложения и вычитания… Я знаю… Звучит плохо, правда?!?! Я вырос, используя точки касания или пальцы, и это все. Поэтому в первый год обучения я предполагал, что мы будем использовать пальцы и точки касания, и в конечном итоге они просто поймут это и узнают факты. Я был так неправ, и я проделал такой долгий путь с тех пор!
Изучение основных фактов сложения и вычитания в начальных классах имеет решающее значение. Знание этих фактов будет использоваться почти в каждом математическом навыке до конца обучения каждого ученика. Как учитель первого класса, первое, что я рассказываю и убеждаюсь, что ученики овладевают различными стратегиями сложения и вычитания. Изучив эти различные стратегии сложения и вычитания на раннем этапе, учащиеся смогут использовать те из них, которые лучше всего подходят им для других навыков, в течение остальной части года.
Что такое сложение и вычитание Стратегии Существует так много различных стратегий сложения и вычитания, так каким из них вы должны научить? Стратегии обучения сложению
Существует множество различных стратегий сложения и вычитания по математике, и некоторые из них немного сложнее других. Поскольку я преподаю в 1-м классе, такие стратегии, как добавление 0 или добавление 1, уже преподавались в детском саду. Я могу быстро просмотреть эти простые стратегии, а затем перейти к более сложным. Я всегда начинаю с расчета. Этому также учат в детском саду, но это одна из стратегий сложения для 1-го класса, которую используют многие ученики. Посмотрите видео, которое я сделал, где я подробно рассказываю о том, как я учу считать в дифференцированных малых группах. Кроме того, в 1-м классе ученики работают с числами до 20, поэтому им нужна дополнительная практика с большими числами.
Посчитав, я перехожу к тому, чтобы показать им, как использовать числовую связь, рамку десятков и числовую линию или числовой путь.
 Опять же, этому учат в детском саду, но не в больших количествах. Кстати, если вы не слышали о числовом пути, это то же понятие, что и числовая прямая, только проще для первоклассника. На числовом пути числа представлены прямоугольниками, которые учащиеся могут считать. На числовой прямой учащиеся должны считать единицы длины, и им трудно увидеть единицы, которые они считают. Я знаю, что когда мои первоклассники пытаются использовать числовую прямую, они начинают с 0 и заканчивают ошибкой на единицу.
Опять же, этому учат в детском саду, но не в больших количествах. Кстати, если вы не слышали о числовом пути, это то же понятие, что и числовая прямая, только проще для первоклассника. На числовом пути числа представлены прямоугольниками, которые учащиеся могут считать. На числовой прямой учащиеся должны считать единицы длины, и им трудно увидеть единицы, которые они считают. Я знаю, что когда мои первоклассники пытаются использовать числовую прямую, они начинают с 0 и заканчивают ошибкой на единицу.Некоторые другие стратегии обучения сложению: прибавить десять, сделать десятку, удвоить и удвоить плюс один. Это следующие в моем списке для покрытия.
Стратегии вычитанияПосле того, как мы хорошо усвоили эти стратегии сложения фактов, мы переходим к вычитанию. Большинство стратегий вычитания очень похожи на многие стратегии сложения. Сложение начинаем с обратного отсчета, а вычитание начинаем с обратного отсчета. Опять же, это наиболее часто используемая стратегия, которую я вижу со своими учениками каждый год.
 Затем мы начинаем вычитать с помощью таких инструментов, как числовая связь и числовые линии или числовой путь. Я также учу своих студентов, как считать, чтобы вычесть, что действительно помогает позже с семьями фактов. Мы заканчиваем стратегии вычитания, используя то, что мы узнали о двойниках и двойниках плюс один, а также вычитании десяти.
Затем мы начинаем вычитать с помощью таких инструментов, как числовая связь и числовые линии или числовой путь. Я также учу своих студентов, как считать, чтобы вычесть, что действительно помогает позже с семьями фактов. Мы заканчиваем стратегии вычитания, используя то, что мы узнали о двойниках и двойниках плюс один, а также вычитании десяти.Если учащиеся действительно овладели стратегиями обучения сложению, они обычно неплохо справляются со стратегиями вычитания. Имейте в виду, что вычитание всегда сложнее, чем сложение для большинства учащихся.
Как преподавать стратегии сложения и вычитанияЕсть 15 основных стратегий сложения и вычитания, которые я люблю использовать со своими первоклассниками. Большинство из тех, что я перечислил выше. У меня есть система того, что действительно работает, и я использую ее каждый год в течение первых нескольких недель в школе. Я преподаю математику ТОЛЬКО в небольших группах. Управляемая математика в 1-м классе чрезвычайно важна, на мой взгляд.
Стратегии сложения и вычитания во время занятий в малых группах Преподавание математики в группе никогда не было для меня успешным. Я не могу увидеть, осваивают ли более 20 студентов навыки, которые мне нужны, или они просто пишут число, которое написал их сосед, и показывают его мне. Гораздо полезнее быть в небольшой группе, где я сижу прямо перед 5-6 учениками.
Преподавание математики в группе никогда не было для меня успешным. Я не могу увидеть, осваивают ли более 20 студентов навыки, которые мне нужны, или они просто пишут число, которое написал их сосед, и показывают его мне. Гораздо полезнее быть в небольшой группе, где я сижу прямо перед 5-6 учениками.Я начинаю занятия в малых группах, просто быстро просматривая несколько задач, связанных с навыком, над которым мы работали в предыдущий день, а затем мы сразу приступаем к делу. У нас всего 20 минут, поэтому мы двигаемся быстро и не теряем времени. Сначала я объясняю, над чем мы будем работать в этот день, а затем использую свой рабочий коврик учителя, чтобы смоделировать для них. После того, как я смоделировал несколько примеров, ученики получают свои рабочие коврики, которые соответствуют моему коврику учителя, и они тренируются со мной. Мы следуем модели CPA (конкретно-графические-абстрактные) при работе над любым математическим навыком.
 Если вы не знакомы с моделью CPA, перейдите по ссылке внизу этого поста.
Если вы не знакомы с моделью CPA, перейдите по ссылке внизу этого поста.После того, как ученики увидели мою модель, и мы сделали несколько примеров вместе, они переворачиваются на вторую сторону своего рабочего коврика и работают независимо друг от друга, а я наблюдаю. У меня есть список математических вопросов, которые я задаю им, чтобы убедиться, что они могут объяснить свое мышление и полностью понимают, что делают. ‘
Если вы думаете о том, чтобы попробовать заниматься математикой с гидом в классе 1-го класса, ознакомьтесь с моими 3 советами для успешного проведения групп по математике с гидом.
Стратегии сложения и вычитания для текстовых задачНа каждом уроке у меня есть набор текстовых задач, которые ученики решают, используя стратегию, которую мы отрабатывали в тот день. Итак, если мы только что провели урок по подсчету на вычитание, они должны решить свою задачу со словами, используя эту стратегию. Проблемы со словами или контекстуальные проблемы — это то, над чем нужно работать весь год.
 Я обнаружил, что работа над несколькими упражнениями в конце небольшой группы каждый день действительно помогает.
Я обнаружил, что работа над несколькими упражнениями в конце небольшой группы каждый день действительно помогает.Мы начинаем в начале года, практикуя более простые типы ситуаций, такие как добавление и удаление. С моей старшей группой мы начинаем пробовать запуск и изменение неизвестных проблем. Позже в этом году мы добавим другие типы задач, такие как сравнение контекстных задач.
Игры и дополнительные задания Стратегии обучения сложению и вычитанию всегда должны включать игры!У меня всегда есть 4 небольшие группы, и я встречаюсь с ними каждый божий день. В каждой из моих групп от 4 до 6 студентов, и мы встречаемся по 20 минут. Так как у меня нет целой группы по математике, очень важно, чтобы я видел каждого ученика каждый день. Также очень важно максимально использовать наши 20 минут. В конце нашего урока мне всегда нравится иметь игры и расширения, которые можно вытащить и использовать. Дети любят игры! Все мы знаем, что лучший способ закончить урок, чем игра.

Это никогда не подводит, хотя бы раз или два в неделю моя старшая группа просто пролетает урок за считанные минуты, и мы заканчиваем на 10 минут раньше. В эти дни у меня есть расширения задач, которые я использую.
Использование расширенных заданий — отличный способ вывести старшую группу на новый уровень обучения.Примером расширения задачи, которое я использую, является моделирование проблемы и намеренное совершение ошибки. Учащиеся должны понять мою ошибку и исправить ее. Другим примером может быть предоставление учащимся суммы или разности, а учащиеся придумывают числа, которые могут быть слагаемыми, уменьшаемыми или вычитаемыми. Я каждый день слежу за тем, чтобы для моих небольших групп готовилось дополнительное задание.
Самостоятельная практика после небольшой группы Стратегии вычитания и сложения для 1-го класса в моей комнате всегда включают какую-либо страницу для самостоятельной практики.Когда студенты покидают мою группу, мне нравится, когда они берут страницу, чтобы попрактиковаться в навыке, который они только что выучили на своей математической станции.
Дифференциация для сложения и вычитания Стратегии Они выполнят это самостоятельно и сдадут на оценку по математике. Мне нравится, когда они делают это, как только покидают мой стол, чтобы информация была свежа в их мозгу. Я встречаюсь со своей самой высокой группой в последнюю очередь, поэтому они работают над своей практической страницей во время своего первого занятия по математике на следующий день. Иногда я могу переключать его и предлагать им работать на этой странице практики для утренней работы, домашней работы, позже в качестве обзора и т. Д. Много возможностей!
Они выполнят это самостоятельно и сдадут на оценку по математике. Мне нравится, когда они делают это, как только покидают мой стол, чтобы информация была свежа в их мозгу. Я встречаюсь со своей самой высокой группой в последнюю очередь, поэтому они работают над своей практической страницей во время своего первого занятия по математике на следующий день. Иногда я могу переключать его и предлагать им работать на этой странице практики для утренней работы, домашней работы, позже в качестве обзора и т. Д. Много возможностей!Встреча со всеми моими учениками в небольшой группе дает мне возможность различать их в зависимости от их потребностей. Когда я встречаюсь с каждой группой, я делаю все то, что упомянул выше, но на разных уровнях. Все рабочие коврики, которые используют мои группы, основаны на их уровне, а также числах, которые мы используем, страницах с независимыми упражнениями, задачах со словами и т.
Из всех различных стратегий сложения и вычитания, которые я использую, дифференцированные математические коврики — мои любимые! д.
д.В первом классе учащиеся будут использовать эти стратегии и работать с числами до 20. Поскольку я начинаю обучать этим стратегиям в самом начале школы, все мои группы не готовы работать с такими большими числами. Моя группа более низкого уровня обычно начинает с работы с числами только до 5, группа высокого уровня будет работать с числами до 15 (или даже 10, если им нужно), а моя группа самого высокого уровня будет практиковаться с числами до 20. Я делаю обязательно постарайтесь подтолкнуть все уровни как можно ближе к 20, поскольку это стандарт, но какой смысл заставлять их, если они не готовы.
Как обучать техникам сложения и вычитания таким образомЯ много лет преподавал, используя перечисленные выше методы, но у меня никогда не было организованного набора ежедневных планов для использования. Этим летом я решил взять все, что использовал, и организовать 15 ежедневных уроков.
 Необходимо было иметь все стратегии, перечисленные в том порядке, в котором они должны быть изучены, а также игры, рабочие коврики и страницы для самостоятельной практики, выровненные и скопированные на бумаге разного цвета для каждой группы. Я хотел, чтобы проблемы со словами были уже напечатаны и дифференцированы, а вопросы, которые я задавал бы во время группы, планировались заранее.
Необходимо было иметь все стратегии, перечисленные в том порядке, в котором они должны быть изучены, а также игры, рабочие коврики и страницы для самостоятельной практики, выровненные и скопированные на бумаге разного цвета для каждой группы. Я хотел, чтобы проблемы со словами были уже напечатаны и дифференцированы, а вопросы, которые я задавал бы во время группы, планировались заранее.Теперь у меня есть первые 15 дней моих математических планов, готовых к работе. Лучше всего то, что теперь, когда у меня все это напечатано, я могу использовать его долгие годы. Единственное, что мне придется копировать каждый год, это страницы независимой практики.
Я копирую все материалы нижнего уровня на оранжевый, верхнего уровня на фиолетовый и верхнего уровня на розовый. Затем я храню каждый урок вместе с фишками и карточками в сумке с номером урока. Когда я преподаю определенный урок, я вытаскиваю все для этого урока. С помощью этой стратегии цветового кодирования легко получить нужные мне страницы или карточки в зависимости от того, на какой цветной бумаге они скопированы.

Если вы хотите избавить себя от хлопот, связанных с планированием каждого из этих компонентов, а также дифференцировать их для своих учеников, ознакомьтесь с моим набором «Стратегии сложения и вычитания — Дифференцированные математические планы с подсказками».
Я знаю, что эти методы, которые я только что обсуждал, могут не работать для всех, особенно если вы не обучаете математике в небольших группах. Так что, если вам нужен только список стратегий сложения и вычитания, которым я обучаю, и порядок, в котором я их учу, вы можете получить его здесь бесплатно! Если вы все еще задаетесь вопросом, подходит ли вам управляемая математика или почему вы должны использовать ее вместо всей групповой математики, ознакомьтесь с этим постом.
Возьмите список стратегий сложения и вычитания для математики, которые я использую, и порядок, в котором я их преподаю. Дополнительная информация о добавлении и вычитании СтратегииСтратегии для добавления и вычитания — дифференцированные планы по математике
Численные линии против номеров
Метод CPA
Интерактивные чтения вслух… Что это такое, как их использовать и почему они так важны!
Сложение, вычитание, умножение и деление: правила
Может быть полезно понять, как использовать различных математических операций , так как их можно использовать каждый день в самых разных ситуациях, точно так же, как вычислять, как можно разделить пакет со сладостями.
 поровну между группой людей.
поровну между группой людей.Определение сложения, вычитания, умножения и деления
Сложение, вычитание, умножение и деление — все типы операций, используемых в математике.
Сложение
Сложение — это тип операции, результатом которой является сумма двух или более чисел. Существует знак для обозначения операции сложения, называемый знаком плюс, который представляет собой .
Вычитание
Вычитание — это тип операции, результатом которой является нахождение разницы между двумя числами. Знак, обозначающий операцию вычитания, называется знаком минус и выглядит следующим образом.
Умножение
Умножение — это тип операции, который требует сложения равными группами, в результате умножения получается произведение. Знак, обозначающий операцию умножения, можно назвать знаком умножения и выглядит он так.
Деление
Деление — операция, обратная умножению, заключается в разбиении числа на равные части. Знак, представляющий операцию деления, называется просто знаком деления и выглядит так.

Правила сложения, вычитания, умножения и деления
Существуют различные правила и методы, которые могут быть полезны при использовании каждой из этих операций.
Сложение
При сложении двух или более чисел можно использовать метод сложения столбцов. Это включает в себя размещение чисел одно над другим в столбце, затем вы работаете справа налево, добавляя числа, которые находятся в одном столбце.
Вычислить
Решение:
Для начала вы можете расположить числа друг над другом:
Теперь, работая справа налево, сложите два горизонтальных числа вместе, начиная с 2 и 2:
Теперь перейдем к 2 и 5:
И, наконец, 5 и 1:
Следовательно,
Если два добавляемых вами числа больше 10, вы можете перенести это число.
Вычитание
При вычитании двух чисел можно также использовать метод столбца; метод вычитания столбцов. Это работает так же, как метод сложения столбцов, однако вы вычитаете числа, а не добавляете их.

Вычислить
Решение:
Для начала вы можете расположить числа друг над другом, поместив число, от которого вы вычитаете, сверху:
Теперь, работая справа налево, вычтите одно число от другого, начиная с 8 и 4:
Теперь переходим к 3 и 1:
И, наконец, 5 и 2:
Следовательно,
Если вычитаемое число больше, чем вычитаемое, вам нужно взять цифру. из столбца влево.
Умножение
При умножении двух чисел можно использовать различные методы, включая метод сетки. Это включает в себя разбиение двух чисел и размещение их в сетке. Затем вы выполняете отдельные умножения, а затем складываете их все вместе.
Calculate
Solution:
To begin with, draw out a grid, break down your numbers, and place them into the grid-like so:
20 3 40 2 .
 0389
038940 800 120 2 40 40 40 8 40 8. проще сделать это пошагово: Следовательно,
Деление
При делении одного числа на другое вы можете использовать метод, называемый коротким делением, этот метод лучше всего работает, когда вы делите число на 10. или менее. Короткое деление предполагает мысленное деление числа на более мелкие этапы.
Вычислить
Решение:
Для начала вы можете нарисовать свой расчет, записав число, на которое вы делите, слева, а число, которое вы делите, запишите справа, как показано ниже:
Теперь вам нужно проработать число, которое вы делите по одной единице за раз, начните с выяснения, сколько раз 9 может перейти в 3. Поскольку это невозможно, вам нужно перенести 3 на следующую единицу.
 :
:Теперь вы можете подумать о том, сколько раз 9 может перейти в 30. 9 входит в 30 три раза с остатком три:
Затем это можно записать в ваше деление, как показано ниже, с делимым числом, записанным над вычислением. а остаток 3 переносится на 6:
Наконец, вы можете подсчитать, сколько раз 9 входит в число 36:
Следовательно,
Сложение, вычитание, умножение и деление отношений
Операции могут иметь отношения друг с другом. Существует связь между сложением и вычитанием, а также связь между умножением и делением.
Сложение и вычитание
Сложение и вычитание можно считать обратными друг другу. Это просто означает, что операции противоположны, вы можете отменить сложение, вычитая то же число, и наоборот!
Умножение и деление
Умножение и деление также считаются обратными друг другу, если вы хотите отменить умножение, вы можете просто разделить число.
Примеры сложения, вычитания, умножения и деления
Вычислить
Решение:
Для начала вы можете расположить числа друг над другом:
Теперь, работая справа налево, сложите два горизонтальные числа вместе.
 Начиная с 7 и 8, так как они равны 15, вам нужно перенести 1 на:
Начиная с 7 и 8, так как они равны 15, вам нужно перенести 1 на:Теперь вам нужно сложить вместе 4, 7 и 1, опять же, поскольку это больше 10, вам нужно перенести единицу:
Наконец, вы можете сложить вместе 6, 2 и 1:
Вычислить
Решение:
Для начала вы можете расположить числа друг над другом, поместив число, из которого вычитаете, сверху:
Теперь, работая справа налево, вычтите одно число от другого, начиная с 2 и 6. Поскольку 6 больше двух, вам нужно позаимствовать цифру из столбца слева:Теперь из 2 можно вычесть 2:
Наконец, из 7 можно вычесть 4:
Рассчитать
your numbers, and place them into the grid-like so:
50 3 30 5 To fill out the grid you simply multiply each number in the columns:
50 3 30 1500 90 5 250 15 Теперь вы можете сложить все значения вместе, чтобы найти ответ на вопрос, может быть проще сделать это пошагово:
Вычислить
Решение:
Давайте начнем с записи суммы, используя метод короткого деления:
Теперь начнем с вычисления, сколько раз 7 входит в 4, это невозможно, так что вы можете перенести 4 на 3:
Затем вы можете посмотреть, сколько раз 7 может войти в число 43:
Это оставляет нам остаток от 1, который можно перенести на 4:
Наконец, посчитайте, как много раз 7 может перейти в 14:
Следовательно,
Применения сложения, вычитания, умножения и деления
Эти операции часто используются в повседневной жизни, давайте рассмотрим несколько примеров:
В коллекции Эми 326 наклеек, у Клэр 213 наклейки.
 Сколько наклеек у них было бы, если бы они объединили свои коллекции?
Сколько наклеек у них было бы, если бы они объединили свои коллекции?Решение:
Начните с размещения двух чисел друг над другом:
Теперь вы можете складывать их вместе, работая справа налево, начиная с 6 и 3:
Работайте по номерам:
Следовательно, если Эми и Клэр объединит свои коллекции, у них будет 539 наклейки в коллекцию.
У Сэма 142 конфеты, он отдает своему другу 54, сколько конфет осталось у Сэма?
Решение:
Чтобы узнать, сколько конфет у Сэма, мы можем вычесть 54 из 142. Для начала поместите два числа друг над другом:
Теперь, работая справа налево, вычтите одно число из другого. Не забывайте, так как 2 меньше 4, вам нужно взять единицу из столбца слева:
Теперь вы можете двигаться дальше, опять же, поскольку 3 меньше 5, вам нужно будет взять единицу из столбца слева. столбец слева:
Следовательно, у Сэма осталось 88 конфет .

Дейв готовит на 12 человек, но по его рецепту он рассчитан только на 4. Если по рецепту требуется 72 грамма пасты, сколько пасты понадобится Дейву?
Решение:
Чтобы узнать, сколько пасты понадобится Дейву для его рецепта, мы можем использовать операцию умножения. Поскольку 4 входит в 12, 3 раза, Дейву понадобится в три раза больше, чем указано в рецепте. To do this we can use the grid method:
70 2 3 210 6 Now you can add the two numbers together:
Therefore , Дейву понадобится 216 грамм пасты на 12 персон.
Барбара обедает с тремя друзьями, счет составляет 188 фунтов стерлингов, и они решают разделить его поровну. Сколько платит каждый человек?
Решение:
Для начала запишите задачу, используя метод короткого деления.


 – 14-е изд., испр. и доп. – М.: 2013. – 270 с.
– 14-е изд., испр. и доп. – М.: 2013. – 270 с.  Получение основы с этими стратегиями даст вашим ученикам преимущество в будущей математической работе. Учащимся нужно много возможностей для работы со всеми новыми математическими навыками. Эти стратегии очень важны для ваших учеников, чтобы они могли понять математические концепции более высокого уровня.
Получение основы с этими стратегиями даст вашим ученикам преимущество в будущей математической работе. Учащимся нужно много возможностей для работы со всеми новыми математическими навыками. Эти стратегии очень важны для ваших учеников, чтобы они могли понять математические концепции более высокого уровня. OA.6.d Создание эквивалентных, но более простых сумм (5 страниц)
OA.6.d Создание эквивалентных, но более простых сумм (5 страниц) 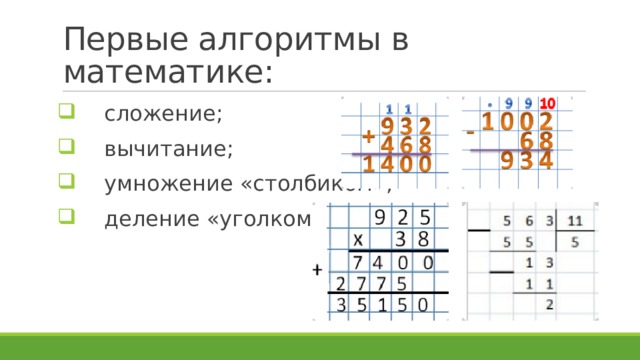 NBT.2
NBT.2 NBT
NBT Рядом с каждой покупкой вы увидите кнопку «Оставить отзыв». Просто нажмите на нее, и вы попадете на страницу, где вы можете дать быструю оценку и оставить краткий комментарий к продукту. Каждый раз, когда вы оставляете отзыв, TPT начисляет вам баллы за отзыв, которые вы используете для снижения стоимости ваших будущих покупок. Я очень ценю ваши отзывы, поскольку они помогают мне определить, какие продукты наиболее ценны для вашего класса, чтобы я мог создавать для вас больше.
Рядом с каждой покупкой вы увидите кнопку «Оставить отзыв». Просто нажмите на нее, и вы попадете на страницу, где вы можете дать быструю оценку и оставить краткий комментарий к продукту. Каждый раз, когда вы оставляете отзыв, TPT начисляет вам баллы за отзыв, которые вы используете для снижения стоимости ваших будущих покупок. Я очень ценю ваши отзывы, поскольку они помогают мне определить, какие продукты наиболее ценны для вашего класса, чтобы я мог создавать для вас больше. Он предназначен для использования одним учителем в одном классе. Вы можете использовать этот ресурс для каждого из ваших учеников в одном классе. Продукт нельзя копировать и распространять, загружать в Интернет или хранить в общедоступной поисковой системе за пределами вашего класса до получения письменного разрешения от его автора, Барбары Морган Балиус. Этот ресурс не является открытым образовательным ресурсом (OER) и поэтому не может быть загружен ни на какие веб-сайты #GoOpen, включая, помимо прочего, Amazon Inspire. Если вы собираетесь использовать его более чем для одного класса, целой школы или целого округа, дополнительные лицензии можно приобрести в магазине «Учителя платят учителям». Страницы, включенные в этот ресурс, не могут использоваться полностью или частично для создания чего-либо нового и/или распространяться каким-либо образом без письменного согласия автора, Барбары Морган Балиус.
Он предназначен для использования одним учителем в одном классе. Вы можете использовать этот ресурс для каждого из ваших учеников в одном классе. Продукт нельзя копировать и распространять, загружать в Интернет или хранить в общедоступной поисковой системе за пределами вашего класса до получения письменного разрешения от его автора, Барбары Морган Балиус. Этот ресурс не является открытым образовательным ресурсом (OER) и поэтому не может быть загружен ни на какие веб-сайты #GoOpen, включая, помимо прочего, Amazon Inspire. Если вы собираетесь использовать его более чем для одного класса, целой школы или целого округа, дополнительные лицензии можно приобрести в магазине «Учителя платят учителям». Страницы, включенные в этот ресурс, не могут использоваться полностью или частично для создания чего-либо нового и/или распространяться каким-либо образом без письменного согласия автора, Барбары Морган Балиус. com для получения предложения.
com для получения предложения.
 Опять же, этому учат в детском саду, но не в больших количествах. Кстати, если вы не слышали о числовом пути, это то же понятие, что и числовая прямая, только проще для первоклассника. На числовом пути числа представлены прямоугольниками, которые учащиеся могут считать. На числовой прямой учащиеся должны считать единицы длины, и им трудно увидеть единицы, которые они считают. Я знаю, что когда мои первоклассники пытаются использовать числовую прямую, они начинают с 0 и заканчивают ошибкой на единицу.
Опять же, этому учат в детском саду, но не в больших количествах. Кстати, если вы не слышали о числовом пути, это то же понятие, что и числовая прямая, только проще для первоклассника. На числовом пути числа представлены прямоугольниками, которые учащиеся могут считать. На числовой прямой учащиеся должны считать единицы длины, и им трудно увидеть единицы, которые они считают. Я знаю, что когда мои первоклассники пытаются использовать числовую прямую, они начинают с 0 и заканчивают ошибкой на единицу. Затем мы начинаем вычитать с помощью таких инструментов, как числовая связь и числовые линии или числовой путь. Я также учу своих студентов, как считать, чтобы вычесть, что действительно помогает позже с семьями фактов. Мы заканчиваем стратегии вычитания, используя то, что мы узнали о двойниках и двойниках плюс один, а также вычитании десяти.
Затем мы начинаем вычитать с помощью таких инструментов, как числовая связь и числовые линии или числовой путь. Я также учу своих студентов, как считать, чтобы вычесть, что действительно помогает позже с семьями фактов. Мы заканчиваем стратегии вычитания, используя то, что мы узнали о двойниках и двойниках плюс один, а также вычитании десяти. Преподавание математики в группе никогда не было для меня успешным. Я не могу увидеть, осваивают ли более 20 студентов навыки, которые мне нужны, или они просто пишут число, которое написал их сосед, и показывают его мне. Гораздо полезнее быть в небольшой группе, где я сижу прямо перед 5-6 учениками.
Преподавание математики в группе никогда не было для меня успешным. Я не могу увидеть, осваивают ли более 20 студентов навыки, которые мне нужны, или они просто пишут число, которое написал их сосед, и показывают его мне. Гораздо полезнее быть в небольшой группе, где я сижу прямо перед 5-6 учениками. Если вы не знакомы с моделью CPA, перейдите по ссылке внизу этого поста.
Если вы не знакомы с моделью CPA, перейдите по ссылке внизу этого поста. Я обнаружил, что работа над несколькими упражнениями в конце небольшой группы каждый день действительно помогает.
Я обнаружил, что работа над несколькими упражнениями в конце небольшой группы каждый день действительно помогает.
 Они выполнят это самостоятельно и сдадут на оценку по математике. Мне нравится, когда они делают это, как только покидают мой стол, чтобы информация была свежа в их мозгу. Я встречаюсь со своей самой высокой группой в последнюю очередь, поэтому они работают над своей практической страницей во время своего первого занятия по математике на следующий день. Иногда я могу переключать его и предлагать им работать на этой странице практики для утренней работы, домашней работы, позже в качестве обзора и т. Д. Много возможностей!
Они выполнят это самостоятельно и сдадут на оценку по математике. Мне нравится, когда они делают это, как только покидают мой стол, чтобы информация была свежа в их мозгу. Я встречаюсь со своей самой высокой группой в последнюю очередь, поэтому они работают над своей практической страницей во время своего первого занятия по математике на следующий день. Иногда я могу переключать его и предлагать им работать на этой странице практики для утренней работы, домашней работы, позже в качестве обзора и т. Д. Много возможностей! д.
д. Необходимо было иметь все стратегии, перечисленные в том порядке, в котором они должны быть изучены, а также игры, рабочие коврики и страницы для самостоятельной практики, выровненные и скопированные на бумаге разного цвета для каждой группы. Я хотел, чтобы проблемы со словами были уже напечатаны и дифференцированы, а вопросы, которые я задавал бы во время группы, планировались заранее.
Необходимо было иметь все стратегии, перечисленные в том порядке, в котором они должны быть изучены, а также игры, рабочие коврики и страницы для самостоятельной практики, выровненные и скопированные на бумаге разного цвета для каждой группы. Я хотел, чтобы проблемы со словами были уже напечатаны и дифференцированы, а вопросы, которые я задавал бы во время группы, планировались заранее.
 поровну между группой людей.
поровну между группой людей.

 0389
0389 :
: Начиная с 7 и 8, так как они равны 15, вам нужно перенести 1 на:
Начиная с 7 и 8, так как они равны 15, вам нужно перенести 1 на: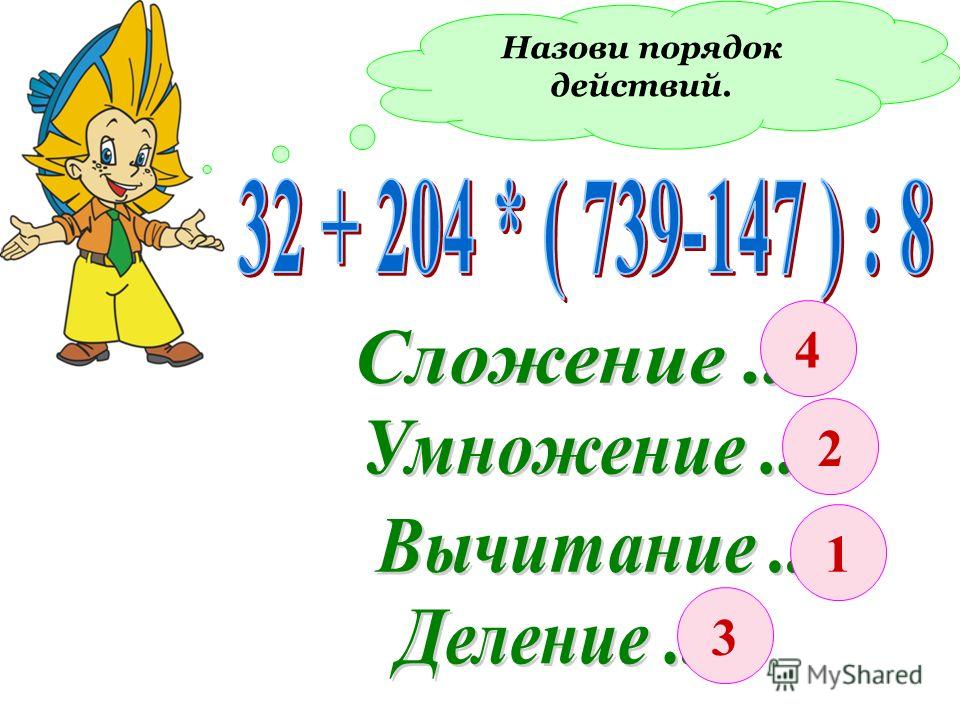 Сколько наклеек у них было бы, если бы они объединили свои коллекции?
Сколько наклеек у них было бы, если бы они объединили свои коллекции?