» Порядок выполнения действий в выражениях со скобками и без скобок»
Луханина Ирина Александровна, учитель начальных классов ГБОУ РК «Лозовская специальная школа-интернат»
Урок математики в 3 классе
Тема урока : « Порядок выполнения действий в выражениях со скобками и без скобок».
Цель урока: создать условия для закрепления умений применять знания о порядке выполнения действий в выражениях без скобок и со скобками в различных ситуациях, умений решать задачи выражением.
Задачи урока:
Образовательные:
— закрепить знания учащихся о правилах выполнения действий в выражениях без скобок и со скобками; формировать у них умение пользоваться этими правилами при вычислении конкретных выражений; совершенствовать вычислительные навыки; повторить табличные случаи умножения и деления;
Развивающие:
— развивать вычислительные навыки, логическое мышление, внимание, память, познавательные способности учащихся,коммуникативные навыки;
Воспитательные:
— воспитывать толерантное отношение друг к другу, взаимное сотрудничество,
культуру поведения на уроке,
аккуратность, самостоятельность, воспитывать интерес к занятиям
математикой.
Формируемые УУД:
Регулятивные УУД:
-работать по предложенному плану, инструкции;
-выдвигать свои гипотезы на основе учебного материала;
— осуществлять самоконтроль.
Познавательные УУД:
-знать правила порядка выполнения действий:
-уметь разъяснить их содержание;
-понимать правило порядка выполнения действий;
-находить значения выражений согласно правилам порядка выполнения
действий, используя для этого текстовые задачи;
— записывать решение задачи выражением;
— применять правила порядка выполнения действий;
-уметь применять полученные знания при выполнении контрольной работы.
Коммуникативные УУД:
-слушать и понимать речь других;
— выражать свои мысли с достаточной полнотой и точностью;
— допускать возможность различных точек зрения, стремиться понимать позицию собеседника;
-работать в команде разного наполнения (паре, малой группе, целым классом), участвовать в обсуждениях, работая в паре;
Личностные УУД:
-устанавливать связь между целью деятельности и её результатом;
-определять общие для всех правила поведения;
— уметь осознанно и внимательно читать задания;
-выражать способность к самооценке на основе критерия
успешности учебной деятельности.
Планируемый результат:
Предметные:
-Знать правила порядка выполнения действий.
-Уметь разъяснить их содержание.
-Уметь решать задачи с помощью выражений.
Личностные:
—Уметь проводить самооценку на основе
критерия успешности учебной деятельности.
Метапредметные: регулятивные УУД-
-Уметь определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по коллективно составленному плану; оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки; планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать своё предположение.
Коммуникативные УУД:
-Уметь оформлять свои мысли в устной форме; слушать и понимать
речь других; совместно договариваться о правилах поведения и общения в школе и
следовать им .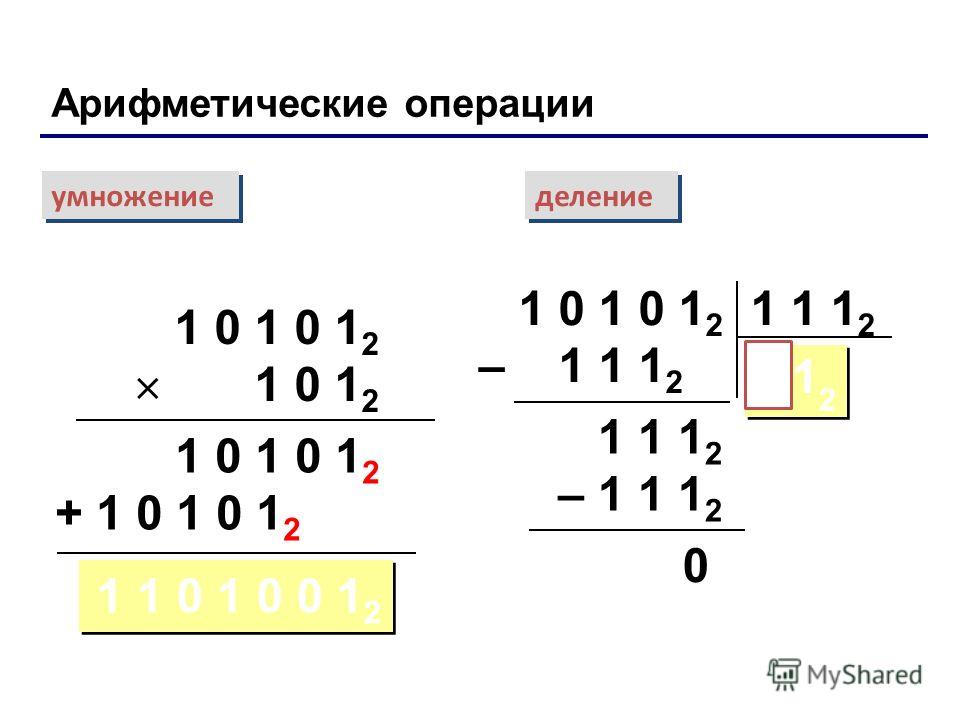
Познавательные УУД:
-Уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке .
Тип урока : Комплексное применение знаний и способов действий.
Методы и формы обучения: методы- словесный, наглядный, практический. Формы- фронтальная, индивидуальная.
Оборудование: интерактивная доска, компьютер, проектор, листы с числами
Ход урока
1. Организационный момент. Эмоционально-психологическая и мотивационная подготовка к усвоению материала.
Давайте, ребята, учиться считать,
Делить, умножать,
Прибавлять, вычитать.
Запомните все,
Что без точного счета,
Не сдвинется с места
Любая работа.
— Займите свои рабочие места.
Открыли тетради, записали число и классная работа.
2. Актуализация знаний.
— На уроке нам с вами предстоит подробно рассмотреть порядок выполнения арифметических действий в выражениях без скобок и со скобками.
2.1.Устный счёт.
Игра «Молчанка»
3 х
2 | 8 | 4 | 6 | 7 | 9 | 5 | 3 | 10 |
2.2.Игра «Найди правильный ответ».
( У каждого ученика лист с числами)
55 | 56 | 57 | 58 | 59 | 60 | 61 |
62 | 63 | 64 | 65 | 66 | 67 | 68 |
69 | 70 | 71 | 72 | 73 | 74 | 75 |
76 | 77 | 78 | 79 | 80 | 81 | 82 |
83 | 84 | 85 | 86 | 87 | 88 | 89 |
90 | 91 | 92 | 93 | 94 | 95 | 96 |
97 | 98 | 99 | 100 | 101 | 102 | 103 |
— Я читаю задания, а вы, выполнив в уме действия, должны
полученный результат, т.
1. Я задумала число, из него вычла 80, получила 18. Какое число я задумала? (98)
2. Я задумала число, к нему прибавила 12, получила 70. Какое число я задумала? (58)
3. Первое слагаемое 90, второе слагаемое 12. Найдите сумму. (102)
— Соедините полученные результаты.
— Какую геометрическую фигуру вы получили? ( Треугольник)
— Расскажите, что вы знаете о данной геометрической фигуре. (Имеет 3 стороны, 3 вершины, 3 угла)
— Продолжаем работать по карточке.
1. Найдите разность чисел 100 и 22. (78)
2. Уменьшаемое 99, вычитаемое 19. Найдите разность. (80).
3. Возьмите число 25 4 раза. (100)
— Начертите внутри треугольника еще 1 треугольник, соединяя полученные результаты.
— Сколько треугольников получилось? (5)
3. Работа над темой урока.
(Наблюдение за изменением значения выражения от порядка выполнения арифметических действий )
— В жизни мы постоянно выполняем какие-либо действия: гуляем,
учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы
выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет.
Например, собираясь утром в школу, можно сначала сделать зарядку, затем
заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом
надеть одежду.
Эти действия мы
выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет.
Например, собираясь утром в школу, можно сначала сделать зарядку, затем
заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом
надеть одежду.
— А в математике обязательно ли выполнять арифметические действия в определенном порядке?
— Давайте проверим:
Сравним выражения:
8-3+4 и 8-3+4
-Видим, что оба выражения совершенно одинаковы.
-Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий ( выведено на экран)
Порядок действий
-В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.
-Запишем.
8-3+4=5+4=9
-Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.
8-3+4=8-7=1
— Почему результаты получились разные ?
— Отчего зависит порядок действий?
— Давайте сделаем вывод: порядок выполнения
арифметических действий менять нельзя.
— Каков же порядок выполнения действий в выражениях без скобок ?
— Узнаем правило выполнения арифметических действий в выражениях без скобок.
— Учебник, страница 24. Читаем правило.
— Какая же тема нашего урока и цель?
4. Закрепление знаний.
— Рассмотрим выражение :38-10+6
— В этом выражении имеются только действия сложения и вычитания. Эти действия называют
-Выполняем действия слева направо по порядку ( на экране).
Порядок действий
— Рассмотрим второе выражение
24:3*2
— В этом выражении имеются только действия умножения и деления – это действия второй ступени.
— Выполняем действия слева направо по порядку ( на экране).
Порядок действий
— В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?
Вывод: Если в выражение без скобок входят не только
действия сложения и вычитания, но и умножения и деления, или оба этих действия,
то сначала выполняют по порядку (слева направо) умножение и деление, а затем
сложение и вычитание. Сначала выполняем по порядку (слева направо) умножение и деление, а затем
сложение и вычитание. Расставим порядок действий.
Сначала выполняем по порядку (слева направо) умножение и деление, а затем
сложение и вычитание. Расставим порядок действий.
1 4 2 5 3
18:2-2*3+12:3
— Давайте вычислим значение выражения ( один ученик работает у доски, остальные в тетрадях)
1 4 2 5 3
18:2-2*3+12:3=9-6+4=3+4=7
— Давайте сделаем вывод, в каком порядке выполняются арифметические действия, если в выражении имеются скобки? (Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках).
Работа у доски с объяснением: рассмотрим выражение- 30 + 6 * (13 — 9) ( все действия комментируются учеником сч помощью учителя)
-Какие действия имеются в данном выражении? ( в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение.
— Расставим порядок действий.
3 2 1
30 + 6 * (13 — 9)
-Вычислим значение выражения.
3 2 1
30+6*(13-9)=30+6*4=30+24=54
— Как вы думаете ,как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении? (Надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:
1. действия, записанные в скобках;
действия, записанные в скобках;
2. умножение и деление;
3. сложение и вычитание.
( На интерактивную доску выводится порядок выполнения арифметических действий) :
Порядок действий
ФИЗМИНУТКА
Раз, два — выше голова.
Три, четыре — руки шире.
Пять, шесть — всем присесть.
Семь, восемь — встать попросим.
Девять, десять — сядем вместе.
5. Выполнение тренировочных заданий на изученное правило . (Работа у доски с комментированием).
(*Учащиеся устанавливают порядок действий и выполняют вычисления).
43 — (20 — 7) +15
32 + 9 * (19 — 16)
2 * 9 — 18:3
— По какому правилу надо действовать? ( Комментированное
объяснение ученика: Будем действовать по правилу. В выражении 43 — (20 — 7) +15
имеются действия в скобках, а также действия сложения и вычитания. Установим
порядок действий. Первым действием выполним действие в скобках, а затем по
порядку слева направо вычитание и сложение).
43 — (20 — 7) +15 =43 — 13 +15 = 30 + 15 = 45
— Решение выражений с комментированием учениика : В выражении 32 + 9 * (19 — 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.
32 + 9 * (19 — 16) =32 + 9 * 3 = 32 + 27 = 59
(В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание).
2*9-18:3=18-6=12
6. Самостоятельная работа ( со взаимопроверкой):
— Узнайте ,правильно ли определен порядок действий в следующих выражениях.
4 3 1 2
37 + 9 — 6 : 2 * 3 =
3 1 2
18 : (11 — 5) + 47=
1 3 2
7 * 3 — (16 + 4)=
— Проверяем работу. Как вы рассуждали при решении выражений .
Как вы рассуждали при решении выражений .
— Кто повторит правило выполнения действий в выражениях со скобками и без скобок?
( Вспоминаем правило и повторяем хором).
7. Решение задачи. ( На экран выведена текстовая задача).
В книге 48 страниц. Даша читала 3 дня по 9 страниц. Сколько страниц книги осталось прочитать Даше?
— Задача простая или составная?
— Что надо еще найти, прежде, ответить на главный вопрос задачи?
— После этого можно узнать,сколько страниц осталось прочитать Даше? ( Оформляют решение и ответ самостоятельно).
— А теперь проверим как вы справились с задачей ( порядок действий комментируют).
8. Подведение итогов. Рефлексия.
— Какие знания вы получили на
уроке? ( Сегодня на уроке мы познакомились с правилом
порядка выполнения действий в выражениях без скобок и со скобками. В ходе
выполнения заданий определяли, зависит ли значение выражений от порядка
выполнения арифметических действий, узнали, отличается ли порядок
арифметических действий в выражениях без скобок и со скобками, потренировались
в применении изученного правила, искали и исправляли ошибки, допущенные при
определении порядка действий).
— Какой момент на уроке был для вас удачным?
— Где испытывали трудности?
9. Домашнее задание: рабочая тетрадь с.13, № 16-17.
Как правильно решить пример без скобок?
Как правильно решить пример без скобок?
Запомните правило:
- Если в примере нет скобок, сначала выполняем действия умножения и деления по порядку, слева направо. …
- Если в примере есть скобки, то сначала мы выполняем действия в скобках, затем умножение и деление, и затем — сложение и вычитание начиная слева направо.
Какое первое действие в примере без скобок?
Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.
Какие первые действия в математике?
Сначала умножение и деление, затем сложение и вычитание В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок: действия выполняются по порядку слева направо, причем сначала выполняется умножение и деление, а затем – сложение и вычитание.
Что сначала делается сложение или умножение?
При умножении двух разных единиц измерения получается новая единица измерения, при сложении единицы измерения не меняются. При умножении мы получаем эту самую новую единицу измерения. Если она такая же, как и у первого слагаемого, тогда мы можем выполнить сложение. Это просто правило.
Что это вычитание?
Вычитание — операция обратная сложению. Вычитание возможно только, если оба аргумента принадлежат одному множеству элементов (имеют одинаковый тип).
Что такое сложение и вычитание?
Сложение – это объединение объектов в одно целое. Результатом сложения чисел является число, называемое суммой чисел (слагаемых). Вычитание – это такое действие, в котором отнимают меньшее число от большего. Большее число называется уменьшаемым, меньшее – вычитаемым, результат вычитания – разностью.
Как решать дроби Сложение и вычитание?
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить без изменений. Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель опять же оставить без изменений.
Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель опять же оставить без изменений.
Как называется сложение в математике?
Сложение чисел Результат сложения двух или более чисел называется суммой, а сами числа — слагаемыми. … Складываем числа, аналогично положительным, записываем результат со знаком «минус». Например, (-6)+(-5,3)=-(6+5,3)=-11,3. От перестановки мест слагаемых сумма не изменяется a+b=b+a.
Как называется в математике плюс?
Знаки «плюс» и «минус» (+ и −) — математические символы, используемые для обозначения операций сложения и вычитания, а также положительных и отрицательных величин.
Как называется математическое действие Если стоит знак плюс?
В стране математики живут не только цифры и числа, но и разные математические знаки. Сегодня вы с Лисёнком познакомитесь с ними. … В математике это действие называется сложением и ставится знак плюс.
Как называется действие с минусом?
Вычитание – действие обратное сложению. Уменьшаемое – число, из которого вычитают. Вычитаемое – число, которое вычитают. Разность – результат вычитания.
Как называется при умножении?
Так же, как и при сложении и вычитании, числа при умножении имеют свое название. Первое число при умножении называется множитель. Второе число при умножении тоже называется множитель. Результат умножения называют произведение.
Что такое результат умножения?
Умноже́ние — одна из основных математических операций над двумя аргументами (множителями или сомножителями). Иногда первый аргумент называют множимым, а второй множителем; результат умножения двух аргументов называется их произведением.
Как умножить два отрицательных числа?
Умножение отрицательных чисел Правило умножения отрицательных чисел: чтобы умножить два отрицательных числа, нужно перемножить их модули. Это значит, что для любых отрицательных чисел -a, -b верно равенство: (-а) * (-b) = a * b.
Это значит, что для любых отрицательных чисел -a, -b верно равенство: (-а) * (-b) = a * b.
Как умножить натуральное число на отрицательное?
Правило умножения отрицательных чисел заключается в том, что для того, чтобы умножить два отрицательных числа, необходимо перемножить их модули. Данное правило записывается так: для любых отрицательных чисел –a, −b данное равенство считается верным. (−а)⋅(−b)=a⋅b.
Правило БОДМАС | Что такое правило БОДМАСА?
В соответствии с правилом BODMAS , мы должны сначала вычислить выражения, данные в скобках. Полная форма BODMAS — скобки, порядки, деление, умножение, сложение и вычитание. Следовательно, второе предпочтение в BODMAS отдается здесь порядкам или показателям (x n ). Позже мы выполняем арифметические операции (÷, ×, +, -). Мы будем решать примеры на основе этого правила в следующих разделах.
Содержание:
|
Арифметическое выражение, включающее в себя несколько операций, таких как сложение, вычитание, умножение и деление, решить сложнее, чем операции с двумя числами. Операция над двумя числами проста, но как решить выражение со скобками и несколькими операциями и как упростить скобку? Давайте вспомним BODMAS правило и узнать об упрощении скобок.
Операция над двумя числами проста, но как решить выражение со скобками и несколькими операциями и как упростить скобку? Давайте вспомним BODMAS правило и узнать об упрощении скобок.
Подробнее: Математика
Что такое ПРАВИЛО БОДМА?
BODMAS — это аббревиатура, обозначающая скобки, порядок, деление, умножение, сложение и вычитание. В некоторых регионах используется PEMDAS (скобки, экспоненты, умножение, деление, сложение и вычитание), что является синонимом BODMAS. Таким образом, порядок работы BODMAS и PEMDAS показан на рисунке ниже.
Объяснение правила BODMAS
Объясняет порядок выполнения операций при решении выражения. Согласно правилу BODMAS, если выражение содержит скобки ((), {}, []), мы должны сначала решить или упростить скобку, а затем «порядок» (это означает степени и корни и т. д.), затем деление, умножение , сложение и вычитание слева направо. Решение задачи в неправильном порядке приведет к неправильному ответу.
Правило BODMAS можно применять, если в выражении участвует более одного оператора. В этом случае, во-первых, мы должны упростить члены внутри скобки от самой внутренней скобки до самой внешней скобки [{()}] и упростить корни или показатели степени, если они есть. Затем выполните операцию умножения или деления слева направо. Наконец, выполните операцию сложения или вычитания, чтобы получить точный ответ.
Примечание: Буква «O» в полной форме BODMAS также называется «Порядок», что относится к числам, включающим степени, квадратные корни и т. д. Ознакомьтесь с приведенными ниже примерами, чтобы лучше понять, как использовать правило BODMAS.
Правило BODMAS Полная форма
Как мы упоминали ранее, полная форма BODMAS — это Скобки, Порядок, Деление, Умножение, Сложение, Вычитание. Применяя правило BODMAS, мы должны соблюдать порядок этих операций.
| Б | Кронштейны | ( ), { }, [ ] |
| О | Приказ | Квадратные корни, индексы, показатели степени и степени |
| Д | Подразделение | ÷, / |
| М | Умножение | ×, * |
| А | Дополнение | + |
| С | Вычитание | – |
Этот порядок необходимо соблюдать для получения точных результатов.
Видеоурок по правилу BODMAS
В этом видео объясняется правилоBODMAS вместе с различными примерами. Посмотрите это видео, чтобы полностью ознакомиться с правилом BODMAS или PEDMAS и эффективно решить любое математическое уравнение.
Что такое правило БОДМАС?
BODMAS расшифровывается как скобка, деление, умножение, сложение и вычитание. BODMAS используется для объяснения порядка работы математического выражения. В некоторых регионах BODMAS также известен как PEDMAS, что означает скобки, показатели степени, деление, умножение, сложение и вычитание.
В соответствии с правилом BODMAS сначала нужно решить скобки, затем степени или корни (т. е. из), затем деление, умножение, сложение и, наконец, вычитание. Решение любого выражения считается правильным только в том случае, если для его решения соблюдается правило BODMAS или правило PEDMAS.
Пример вопроса с использованием правила BODMAS:
Возьмите следующие вопросы:
(3+5)-5+2
Чтобы решить это, нужно решить первую скобку, что даст следующее:
(8)-5+2
Теперь нужно решить сложение:
(8)-7 = 1.
Иногда вы также можете встретить проценты при упрощении числового выражения с помощью этого правила BODMAS.
Условия и правила
Несколько условий и правил для общего упрощения приведены ниже:
| Состояние | Правило |
| х + (у + г) ⇒ х + у + г | Откройте скобку и добавьте условия. |
| х – (у + г) ⇒ х – у – г | Откройте скобку и умножьте знак минус на каждое слагаемое внутри скобки. (Все положительные члены будут отрицательными и наоборот) |
| х(у + г) ⇒ ху + хг | Умножить внешний член на каждый член в скобках |
Советы, которые следует помнить Правило BODMAS:
Правила упрощения выражения с использованием правила BODMAS следующие:
- Сначала упростите скобки
- Решить экспоненту или корень
- Выполнить операцию деления или умножения (слева направо)
- Выполнить операцию сложения или вычитания (слева направо)
Примеры решения правила BODMAS
Пример 1:
\(\begin{array}{l}Решить\\left (\frac{1}{2} + \frac{1}{4}\right)\ of\ 16\end{array} \)
Решение-
\(\begin{array}{l}Дано:\ \left ( \frac{1}{2} + \frac{1}{4}\right )\ of\ 16\end{array} \)
Шаг 1: Сначала решить дробь в скобках-
\(\begin{array}{l}\frac{1}{2} + \frac{1}{4} = \frac{3}{4}\end{array} \)
Шаг 2: Теперь выражение будет (3/4) от 16
\(\begin{array}{l}=\frac{3}{4} \times 16\end{array} \)
\(\начало{массив}{l}= 12\конец{массив} \)
Упрощение кронштейнов
Упрощение терминов в скобках можно сделать напрямую. Это означает, что мы можем выполнять операции внутри скобки в порядке деления, умножения, сложения и вычитания.
Это означает, что мы можем выполнять операции внутри скобки в порядке деления, умножения, сложения и вычитания.
Примечание: Порядок скобок для упрощения следующий: (), {}, [].
Пример 2:
Упростить: 14 + (8 – 2 × 3)
Решение:
14 + (8 – 2 × 3)
= 14 + (8 – 6)
= 14 + 2
= 16
Следовательно, 14 + (8 – 2 × 3) = 16.
Пример 3:
Упростите следующее.
(i) 1800 ÷ [10{(12−6)+(24−12)}]
(ii) 1/2[{−2(1+2)}10]
Решение:
(i) 1800 ÷ [10{(12−6)+(24−12)}]
Шаг 1. Упростите термины внутри {}.
Шаг 2. Упростите {} и работайте с терминами за скобками.
1800 ÷ [10{(12−6)+(24−12)}]
= 1800 ÷ [10{6+12}]
= 1800 ÷ [10{18}]
Шаг 3: Упростите термины внутри [ ].
= 1800 ÷ 180
= 10
(ii) 1/2[{−2(1+2)}10]
Шаг 1: Упростите термины внутри (), за которыми следует {}, а затем [].
Шаг 2: Работайте с терминами вне квадратных скобок.
1/2[{−2(1+2)}10]
= 1/2 [{-2(3)} 10]
= 1/2 [{-6} 10]
= 1/2 [-60]
= -30
Правило BODMAS без скобок
Правило БОДМАС можно применять и для решения математического выражения без скобок. Рассмотрим следующий вопрос для проверки.
Пример 4:
Упрощение: 17 – 24 ÷ 6 × 4 + 8
Решение:
17 – 24 ÷ 6 × 4 + 8
Согласно правилу BODMAS, мы должны сначала выполнить деление.
17 – 4 × 4 + 8
Выполним умножение.
17 – 16 + 8
Наконец, сложение и вычитание.
25 – 16 = 9
Пример 5:
Упростите выражение: 1/7 от 49 + 125 ÷ 25 – 12
Решение:
1/7 от 49 + 125 ÷ 25 – 12
= (1/7) × 49 + 125 ÷ 25 – 12
= 7 + 125 ÷ 25 – 12
= 7 + 5 – 12
= 12 – 12
= 0
Решенные проблемы с Bodmas
Вопрос 1: Решите 8 + 9 ÷ 9 + 5 × 2 − 7.
Решение:
Дана задача на 8 + 9 ÷ 9 + 5 × 2 − 7.
Сначала выполняется операция деления.
9 ÷ 9 = 1
Итак, выражение сводится к 8 + 1 + 5 × 2 − 7
Далее выполняется операция умножения,
5 × 2 = 10
Итак, выражение сводится к 8 + 1 + 10 − 7
Операция сложения
8 + 1 + 10 = 19
Окончательный ответ: 19 – 7 = 12.
Вопрос 2: Упростите выражение [25 – 3 (6 + 1)] ÷ 4 + 9.
Решение:
Дана задача [25 – 3 (6 + 1)] ÷ 4 + 9.
Круглая скобка (6 + 1) = 7.
Следующая скобка 3 (7) = 21
Возьми [25 – 21] ÷ 4 + 9
(25 – 21) = 4
Затем выполняется операция деления,
4 ÷ 4 = 1
Тогда 1 + 9 = 10
Окончательный ответ 10.
Вопрос 3: Решите (1/4 + 1/8) числа 64.
Решение:
На первом шаге рассмотрим (1/4 + 1/8) = (2 + 1)/8 = 3/8
Возьми (3 / 8) из 64
Здесь термин «из» относится к операции умножения.
(3/8) из 64 = (3/8) * 64
= 24
Вопрос 4: Упростите данное выражение: 180 ÷ 15 {(12 – 6) – (14 – 12)}.
Решение:
Изначально первые скобки ( ) упрощены,
180 ÷ 15 {(12 – 6) – (14 – 12)}
= 180 ÷ 15 (6 − 2) (решить круглую скобку)
= 180 ÷ 15 (4) (решить фигурную скобку)
= 12 (4) (180 разделить на 15 = 12)
= 12 × 4 (если за какой-либо скобкой не указан оператор, можно выполнить операцию умножения)
= 48
Окончательный ответ: 48.
Вопрос 5: Упростите следующее выражение 3 + 2 4 × (15 ÷ 3), используя правило BODMAS.
Решение:
Полученное выражение равно 3 + 2 4 × (15 ÷ 3).
Сначала берется скобка.
(15 ÷ 3) = 5
Затем 3 + 2 4 × 5
Расчет производится по порядку 2 4 = 2 × 2 × 2 × 2 = 16
16 × 5 = 80
Далее выполняется операция сложения.
3 + 80 = 83
Окончательный ответ: 83.
Вопрос 6:
\(\begin{array}{l} Решить\ 16[8-\{5-2(\overline{2-1}+1)\}] с помощью\ правила BODMAS\.\ конец {массив} \)
Решение:
\(\begin{array}{l}Дано:\ 16[8-\{5-2(\overline{2-1}+1)\}]\end{массив} \)
Сначала рассмотрим винкулум или линейную скобку 16 [8 – {5 – 2 (1 + 1)}]
= 16 [8 – {5 – 2 * 2}] (решаем кривую скобку)
= 16 [8 — {5 — 4}] (умножить фигурную скобку)
= 16 [8 — 1] (решить фигурную скобку)
= 16 * 7 (решить внутреннюю часть квадратной скобки)
= 112
Следовательно, окончательный ответ равен 112.
Вопрос 7: Решите выражение, используя правило БОДМАС{50 – (2 + 3) + 15}.
Решение:
Входное уравнение:
= {50 – (2 + 3) + 15}
= {50 – (5) + 15}
= {50 – 5 + 15}
= {45 + 15}
= {60}
= 60
Вопрос 8: Упростите выражение, используя правило BODMAS [18 – 2 (5 + 1)] ÷ 3 + 7.
Решение:
Входное уравнение можно переписать:
= [18 – 2 * (5 + 1)] / 3 + 7
= [18 – 2 * (6)] / 3 + 7
= [18 – 2 * 6] / 3 + 7
= [18 – 12] / 3 + 7
= [6] / 3 + 7
= (6 / 3) + 7
= 2 + 7
= 9
Проблемы с правилом BODMAS
Попробуйте решить вопросы по правилу BODMAS, приведенные ниже, чтобы понять применение правила в упрощениях.
- Чему равно 28 – [26 – {2 + 5 × (6 – 3)}]?
- Упростить: 2 + 5(4 + 2) + 32 – (1 + 6 × 3)
- Найдите значение 7 + {8 – 3 из (√4 + 2)}.
Чтобы решить больше текстовых задач на арифметические операции, загрузите BYJU’S — The Learning App и смотрите интерактивные видеоролики.
Часто задаваемые вопросы о правиле 9 BODMAS0052
Что такое Математическое правило БОДМАСА?
BODMAS — это аббревиатура, обозначающая последовательность операций, выполняемых при упрощении математических выражений.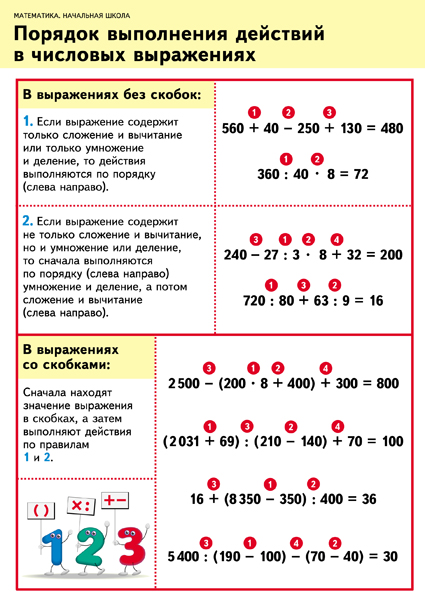 Таким образом, BODMAS означает скобки, порядок, деление, умножение, сложение и вычитание.
Таким образом, BODMAS означает скобки, порядок, деление, умножение, сложение и вычитание.
Можно ли использовать правило BODMAS, если скобок нет?
Да, мы можем использовать правило BODMAS и при отсутствии скобок.
Что представляет S в правиле BODMAS?
Буква S обозначает вычитание в математическом правиле БОДМАС.
Какие арифметические операции используются в правиле BODMAS?
Основными арифметическими операциями, используемыми в правиле BODMAS, являются:
Сложение
Вычитание
Умножение
Деление
Квадратные корни или индексы
Для чего используется правило BODMAS?
Правило BODMAS помогает точно упростить математическое выражение. Используя это правило, мы можем правильно вычислить заданное выражение, чтобы ответ был правильным.
Правильно ли Бодмас?
BODMAS — это аббревиатура, помогающая детям запомнить порядок математических операций — правильный порядок решения математических задач. BODMAS означает B-скобки, O-порядки (степени/показатели или корни), D-деление, M-умножение, A-сложение, S-вычитание.
BODMAS означает B-скобки, O-порядки (степени/показатели или корни), D-деление, M-умножение, A-сложение, S-вычитание.
|
Посмотреть полный ответ на сайте Thirdspacelearning.com
Всегда ли прав Бодмас?
Да, даже если скобок нет, все равно используется правило BODMAS. Нам нужно решить другие операции в том же порядке. Следующим шагом после скобок (B) является порядок степеней или корней, за которым следует деление, умножение, сложение и затем вычитание.
Запрос на удаление |
Посмотреть полный ответ на cuemath.com
Что правильнее Бодмас или Пемдас?
Термин PEMDAS используется в основном в США, но в Индии и Великобритании мы называем его BODMAS. Но между ними нет никакой разницы. Порядок действий для скобок, порядков, сложения, вычитания, умножения и деления одинаков для обоих правил.
|
Посмотреть полный ответ на byjus.com
Есть ли у Bodmas недостатки?
Он не содержит скобок, степеней, деления или умножения, поэтому мы будем следовать BODMAS и делать сложение с последующим вычитанием: это ошибочно. Правильное значение — 3. BODMAS подвел нас.
Запрос на удаление |
Полный ответ можно найти на сайте Teachwire.net
Какая самая сложная операция в математике?
Сегодняшние математики, вероятно, согласятся с тем, что гипотеза Римана — самая важная открытая проблема во всей математике. Это одна из семи задач премии тысячелетия, за решение которой назначено вознаграждение в 1 миллион долларов.
Запрос на удаление |
Просмотреть полный ответ на PopularMechanics.com
Как использовать BODMAS (порядок действий) #2
youtube.com/embed/70cAYYCJBuQ?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Бодмас британец?
Наиболее распространенным в Великобритании, Пакистане, Индии, Бангладеш и Австралии, а также в некоторых других англоязычных странах является БОДМАС, означающий скобки, порядок, деление/умножение, сложение/вычитание или скобки, деление/умножение, сложение/вычитание.
Запрос на удаление |
Посмотреть полный ответ на en.wikipedia.org
Каков наиболее правильный порядок действий?
Мы можем запомнить порядок, используя PEMDAS: скобки, экспоненты, умножение и деление (слева направо), сложение и вычитание (слева направо).
Запрос на удаление |
Посмотреть полный ответ на сайте khanacademy.org
Был ли заменен Пемдас?
Пожалуйста, извините, моя дорогая тетя Салли (PEMDAS — круглые скобки, показатели степени, умножение/деление, сложение/вычитание) уступает место новой мненомике — GEMDAS.
|
Посмотреть полный ответ на middleboro.k12.ma.us
Учат ли Пемдаса в Англии?
И BODMAS, и PEMDAS верны и используются в разных регионах мира. BODMAS распространен в Великобритании, а PEMDAS используется в США. BODMAS означает скобки, порядок, деление, умножение, сложение, вычитание.
Запрос на удаление |
Посмотреть полный ответ на сайте Thirdspacelearning.com
Знают ли калькуляторы Bidmas?
BODMAS/BIDMAS на калькуляторе
BODMAS или BIDMAS также должны использоваться при использовании калькулятора. Научные калькуляторы автоматически применяют операции в правильном порядке, однако могут потребоваться дополнительные скобки.
Запрос на удаление |
Посмотреть полный ответ на bbc.co.uk
Какую скобку следует решить в первую очередь?
Согласно этому правилу, если в выражении присутствует несколько квадратных скобок, сначала начните упрощать самую внутреннюю круглую скобку или круглую скобку, затем квадратную скобку и фигурную скобку, а затем решите в соответствии с арифметическими операциями приоритета.
|
Просмотреть полный ответ на embibe.com
Как долго Бодмас преподается в школах?
Порядок операций, например BODMAS, был введен в 1800-х годах.
Запрос на удаление |
Посмотреть полный ответ на twitter.com
Что они тоже изменили в Пемдасе?
Чтобы помочь учащимся в Соединенных Штатах запомнить этот порядок операций, учителя заучивают в них аббревиатуру PEMDAS: круглые скобки, показатели степени, умножение, деление, сложение, вычитание. Другие учителя используют эквивалентную аббревиатуру БОДМАС: скобки, порядок, деление и умножение, сложение и вычитание.
Запрос на удаление |
Полный ответ на nytimes.com
Является ли Python Пемдасом?
Правило приоритета операторов Python — PEMDAS
Приоритет операторов в python соответствует правилу PEMDAS для арифметических выражений. Приоритет операторов указан ниже в порядке возрастания. Сначала будут оцениваться круглые скобки, затем возведение в степень и так далее.
Приоритет операторов указан ниже в порядке возрастания. Сначала будут оцениваться круглые скобки, затем возведение в степень и так далее.
|
Посмотреть полный ответ на scaler.com
Кто изобрел Bodmas?
Ахиллес Реселфельт — математик, который изобрел БОДМАС. Это мнемоника, которая помогает нам запомнить, как оценивать математические операторы в математическом утверждении, включающем более одной математической операции.
Запрос на удаление |
Посмотреть полный ответ на vedantu.com
Используют ли математики Pemdas?
PEMDAS помогает математикам запомнить порядок операций при решении задач с несколькими видами функций. Функции внутри круглых скобок всегда идут первыми. Далее идут любые показатели степени за пределами круглых скобок.
Запрос на удаление |
Посмотреть полный ответ на сайте Study. com
com
Люди все еще используют Pemdas?
Большинство людей следуют правилу PEMDAS. Потому что их так учили. Существует также правило BEDMAS, согласно которому деление предшествует умножению.
Запрос на удаление |
Посмотреть полный ответ на people.math.harvard.edu
Когда они изменили порядок операций в математике?
В 1907 году в High School Algebra, Elementary Course Слота и Леннеса рекомендуется сначала выполнять умножение в любом порядке, а затем деление слева направо.
Запрос на удаление |
Посмотреть полный ответ на hsm.stackexchange.com
Какие операции мы должны решить в первую очередь?
Сначала мы решаем любые операции внутри скобок или скобок. Во-вторых, мы решаем любые показатели. В-третьих, мы решаем все умножение и деление слева направо. В-четвертых, мы решаем все операции сложения и вычитания слева направо.
В-четвертых, мы решаем все операции сложения и вычитания слева направо.
|
Посмотреть полный ответ на сайте khanacademy.org
Какая операция должна быть первой?
Порядок операций говорит вам сначала выполнить умножение и деление слева направо, прежде чем выполнять сложение и вычитание.
Запрос на удаление |
Полный ответ см. на content.nroc.org
Если скобок нет, сначала умножаете?
Поскольку 4 × 4 = 16, и когда скобок не осталось, мы выполняем умножение перед сложением.
Запрос на удаление |
Посмотреть полный ответ на hmhco.com
Почему Бодмас поменяли на Бидмас?
Правило BIDMAS — это аббревиатура, альтернативная BODMAS, помогающая запомнить порядок операций. Разница только в том, что вместо О стоит И. Смысл тот же. Бидмас — это термин, который сегодня чаще используется в начальных школах.
Смысл тот же. Бидмас — это термин, который сегодня чаще используется в начальных школах.
|
Посмотреть полный ответ на сайте Thirdspacelearning.com
Использует ли Австралия Bodmas или Pemdas?
BODMAS в национальной учебной программе Австралии
В Австралии BODMAS и порядок действий обычно вводятся в 6 классе. Он преподается как часть следующей цели национальной учебной программы: Изучить использование скобок и порядок действий для написания числовых предложений (ACMNA134).
Запрос на удаление |
Посмотреть полный ответ на twinkl.com.au
Почему в Англии математика во множественном числе?
Математика — это аббревиатура от математики, которая является исчисляемым существительным в британском английском языке, потому что существуют различные типы математики (геометрия, алгебра, исчисление и т.