Что такое порядок действий и почему люди без него все время путаются / Бери и делай
С порядком действий в математике каждый из нас знакомится в школе. Постепенно мы забываем эти правила, из-за чего легко допускаем ошибки в расчетах, которые совершаем в повседневной жизни.
«Бери и Делай» объясняет, чему учит порядок действий в математике, из-за которого даже взрослые часто допускают ошибки в «детских» задачках, и почему его важно знать в любом возрасте.
Зачем соблюдать правильный порядок действий
Основные арифметические операции в математике — это:
- сложение (+)
- вычитание (-)
- умножение (×)
- деление (÷)
Если в числовом выражении используется одна операция, то решить такой пример не составит труда. Например, 3 + 2 = 5 или 6 ÷ 3 = 2. Когда операций 2 или более, то, чтобы получить верный ответ, необходимо выполнять действия в определенном порядке.
Выше изображены 3 примера, каждый из которых легко решить неправильно, если забыть о правильном порядке действий в математике. Попробуйте решить эти примеры самостоятельно, а затем сверьте полученные результаты с правильными ответами в конце статьи. Если хотя бы в одном из них вы ошиблись, возможно, вам стоит повторить вместе с нами правила, касающиеся порядка действий.
Попробуйте решить эти примеры самостоятельно, а затем сверьте полученные результаты с правильными ответами в конце статьи. Если хотя бы в одном из них вы ошиблись, возможно, вам стоит повторить вместе с нами правила, касающиеся порядка действий.
Правило № 1. Действия выполняются слева направо по очереди
✅ Выполняя основные арифметические операции над числами, принято двигаться слева направо.
Обратите внимание на картинку выше. Чтобы вычислить результат выражения 6 ÷ 3 × 2, необходимо выполнить действия поочередно слева направо, сначала разделив число 6 на 3, а затем умножив результат на 2. Выполнив операции в ином порядке (сначала умножение, а потом деление), мы получим неверный ответ.
❗ Если выражение состоит только из операций умножения или операций сложения, то, согласно переместительному закону, результат выражения не зависит от того, в какой последовательности выполнены операции.
Правило № 2. Сначала выполняются умножение и деление, затем сложение и вычитание
Одно выражение может содержать несколько разных арифметических операций, как на картинке выше. Запишем это выражение как 2 + 2 × 2. Если выполнить все действия по очереди слева направо, то получим 2 + 2 × 2 = 4 × 2 = 8. Этот ответ неверный (в этом можно удостовериться, пересчитав единичные квадратики на фотографии). Почему так получилось?
Запишем это выражение как 2 + 2 × 2. Если выполнить все действия по очереди слева направо, то получим 2 + 2 × 2 = 4 × 2 = 8. Этот ответ неверный (в этом можно удостовериться, пересчитав единичные квадратики на фотографии). Почему так получилось?
✅ Выше мы говорили о 4 основных арифметических операциях. Они неравнозначны по приоритету, что влияет на порядок, в котором нужно решать пример. Умножение и деление имеют больший приоритет, чем сложение и вычитание. Если действие имеет больший приоритет, то оно выполняется в первую очередь.
Применим это на практике и решим пример еще раз: 2 + 2 × 2 = 2 + 4 = 6. Ответ верный.
❗ Если в выражении есть 2 и более равнозначные операции, то их выполняют по порядку слева направо. Таким образом, умножение и деление — это равнозначные операции и порядок их выполнения зависит только от порядка появления в выражении. То же самое касается сложения и вычитания.
Выше показан пример решения выражения 12 ÷ 3 × 6 — 12 ÷ 6 × 3. По правилам, сначала необходимо выполнить деление и умножение, двигаясь слева направо, затем снова деление и умножение в правой части выражения, а только в конце перейти к вычитанию. Если порядок нарушить, ответ будет неверным.
По правилам, сначала необходимо выполнить деление и умножение, двигаясь слева направо, затем снова деление и умножение в правой части выражения, а только в конце перейти к вычитанию. Если порядок нарушить, ответ будет неверным.
Правило № 3. Возвести число в степень или извлечь корень нужно до перехода к другим операциям
✅ Если в выражении есть число, которое нужно возвести в степень, или произвести обратную операцию (извлечь корень), то это необходимо сделать перед тем, как выполнять основные арифметические операции.
К примеру, попробуем решить, чему равно 4 + 2 +22 + 32. Для этого нужно сначала поочередно возвести в степень тройку и двойку, получив 4 + 2 + 4 + 9, а затем сложить все числа и получить в ответе 19.
❌ Здесь легко допустить ошибку, сложив между собой числа с одинаковыми показателями степени (то есть 22 и 32), а затем возведя полученную сумму в степень.
Правило № 4. Действия в скобках всегда выполняются в первую очередь
✅ Если часть выражения заключена в скобки, ее нужно решить в первую очередь. Затем вычислить степень или корень числа, после выполнить остальные операции, соблюдая приоритет и двигаясь слева направо.
Затем вычислить степень или корень числа, после выполнить остальные операции, соблюдая приоритет и двигаясь слева направо.
На картинке выше изображен простой пример. Слева ход решения, где соблюдаются правильный порядок действий: сначала получаем результат в скобках, затем выполняем умножение по очереди слева направо, в конце — операцию сложения. Справа неверный ход решения, где все операции выполняются поочередно слева направо, а в результате получается неправильный ответ.
✅ Между операциями в скобках действуют правила приоритета и очередности решений слева направо.
В длинных выражениях можно проставлять над операциями числа, соответствующие очередности выполнения действий, как в примере выше. Это облегчает процесс решения.
Как запомнить порядок действий
1. Если в выражении есть скобки, сначала выполните действия внутри них.
2. Если в выражении число нужно возвести в степень или извлечь из него корень, сделайте это перед тем, как выполнять другие операции.
3 и 4. Среди 4 элементарных арифметических действий умножение и деление имеют больший приоритет, чем сложение и вычитание, поэтому выполняются в первую очередь. Равнозначные по приоритету операции выполняются по очереди, в порядке слева направо.
Ответы на примеры в начале статьи
- 8 ÷ 4 × 2 = 2 × 2 = 4
Это достаточно простой пример. Вы вряд ли допустили ошибку, так как решали его, инстинктивно выполняя действия по очереди, двигаясь слева направо.
- 6 ÷ 2(1 + 3) = ?
Этот пример выглядит простым, но способен поставить в тупик даже профессоров математики. Это связано с тем, что вы можете получить разные ответы в зависимости от того, как именно решаете его. Например, можно решить так: 6 ÷ 2(1 + 3) = 6 ÷ 2(4) = 3 * 4 = 12. Но если опереться на свойство дистрибутивности (где a(b+c) равняется a × b + a × c), то получается 6 ÷ 2(1 + 3) = 6 ÷ ((2 × 1) + (2 × 3)) = 6 ÷ (2 + 6) = 6 ÷ 8 = 3/4. Это возникает из-за того, что выражение можно интерпретировать по-разному, в результате чего ответы тоже получаются разными. В каком-то смысле это похоже на ситуации, когда из-за некорректной формулировки и порядка слов в предложении оно приобретает разные смыслы, например, «Как удивили его слова брата!» может означать, как его удивили слова брата, или как его слова удивили брата.
В каком-то смысле это похоже на ситуации, когда из-за некорректной формулировки и порядка слов в предложении оно приобретает разные смыслы, например, «Как удивили его слова брата!» может означать, как его удивили слова брата, или как его слова удивили брата.
- 3(4 + 1) + 62 ÷ 3 — 7 = 3 × 5 + 62 ÷ 3 — 7 = 3 × 5 + 36 ÷ 3 — 7 = 15 + 36 ÷ 3 — 7 = 15 + 12 — 7 = 20
В этом выражении легко допустить разные ошибки, но правильный алгоритм следующий: сначала выполняется операция в скобках, затем число 6 возводится во 2-ю степень, после нужно выполнить умножение, затем деление, после чего остаются сложение и вычитание. Аналогичный результат получится, если вспомнить свойство дистрибутивности (где a(b+c) равняется a × b + a × c) и решать пример следующим образом: 3(4 + 1) + 62 ÷ 3 — 7 =
((3 × 4) + (3 × 1)) + 62 ÷ 3 — 7 = (12 + 3) + 62 ÷ 3 — 7 = 15 + 36 ÷ 3 — 7 = 15 + 12 — 7 = 20.
Бери и делай/Наука/Что такое порядок действий и почему люди без него все время путаются
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 31 из 39Следующая ⇒ Цель работы на данном этапе — опираясь на практические умения учащихся, обратить их внимание на порядок выполнения действий в таких выражениях и сформулировать соответствующее правило. Работа ведется в такой последовательности: 1. Рассматривается правило о порядке выполнения действий в выражениях без скобок, когда над числами производят либо только сложение и вычитание, либо только умножение и деление. Вывод: если в выражении без скобок указаны только действия сложения и вычитания (или только действия умножения и деления), то их выполняют в том порядке, в каком они записаны (т. е. слева направо). 2. Аналогично изучают порядок действий в выражениях со скобками вида: 85-(46-14),60: (30-20), 90: (2*5). С такими выражениями учащиеся также знакомы и умеют их читать, записывать и вычислять их значение. 3. Наиболее трудным является правило порядка выполнения действий в выражениях без скобок, когда в них содержатся действия первой и второй ступени. Вывод: порядок действий принят по договоренности: сначала выполняется умножение, деление, затем сложение, вычитание слева на право. 4. Упражнения на вычисления значения выражений, когда ученику приходится применять все изученные правила. Ознакомление с тождественными преобразованиями выражений. Тождественное преобразование выражения — это замена данного выражения другим, значение которого равно значению заданного выражения. Учащиеся выполняют такие преобразования выражений, опираясь на свойства арифметических действий и следствия, вытекающие из них (как прибавить сумму к числу, как вычесть число из суммы, как умножить число и, произведение и др. Ознакомление с буквенными выражениями. Уже в I классе возникает необходимость введения символа, обозначающего неизвестное число. В учебной и методической литературе с этой целью для учащихся предлагались самые разнообразные знаки: многоточие, обведенная пустая клетка, звездочки, вопросительный знак и т. п. Но так как все эти знаки полагается использовать в другом назначении, то для записи неизвестного числа следует использовать общепринятый для этих целей знак — букву. В дальнейшем буква как математический символ используется в начальном обучении математике также для записи обобщенных чисел, то есть когда имеются в виду не одно какое-либо целое неотрицательное число, а любое число. В I классе учащиеся применяют букву с целью — обозначения неизвестного искомого числа. Учащиеся знакомятся с написанием и чтением некоторых латинских букв, применяя их сразу для записи примеров с неизвестным числом (простейшие уравнения). Учащимся показывается, как перевести на язык математических символов задание, выраженное словесно: «К неизвестному числу прибавили 2 и получили 6. Найти неизвестное число». Учитель объясняет, как записать эту задачу: обозначить неизвестное число буквой х, затем показать при помощи знака +. что к неизвестному числу прибавили 2 и получили число, равное 6, что и записать, используя знак равенства: х + 2 = 6. Теперь надо выполнять действие вычитания, чтобы по сумме двух слагаемых и одному из них найти другое слагаемое. Основная работа с использованием буквы как математического символа выполняется в последующих классах. При введении буквенных выражений важную роль в системе упражнений играет умелое комбинирование индуктивного и дедуктивного методов. В соответствии с этим упражнения предусматривают переходы от числовых выражений к буквенным и, обратно, от буквенных выражений к числовым. а + Ъ (а плюс Ъ) также математическое выражение, только в нем слагаемые обозначены буквами: каждая из букв обозначает любые числа. Придавая буквам различные числовые значения, можно получить много, сколько угодно числовых выражений. В работе над такими выражениями раскрывается понятие постоянной. Использование буквенной символики способствует повышению уровня обобщения знаний, приобретаемых учащимися начальных классов, и готовит их к изучению систематического курса алгебры в следующих классах. Равенства, неравенства. В практике обучения в начальных классах числовые выражения с самого начала рассматриваются в неразрывной связи с числовыми равенствами и неравенствами. В математике числовые равенства и неравенства делятся на истинные и ложные. В начальных классах вместо этих терминов употребляют слова «верные» и «неверные». Задачи изучения равенств и неравенств в начальных классах заключаются в том, чтобы научить учащихся практически оперировать равенствами и неравенствами: сравнивать числа, сравнивать арифметические выражения, решать простейшие неравенства с одним неизвестным, переходить от неравенства к равенству и от равенства к неравенству. Понятия о равенствах, неравенствах раскрываются во взаимосвязи. При изучении, арифметического материала. Знаками «>», «<», « = » соединяются не любые два числа, не любые два выражения, а лишь те, между которыми существуют указанные отношения. Сравнение чисел осуществляется сначала на основе сравнения множеств, которое выполняется, с помощью установления взаимно однозначного соответствия. Далее при изучении нумерации чисел в пределах 100, 1000, а также нумерации многозначных чисел сравнение чисел осуществляется либо на основе сопоставления их по месту в натуральном ряду, либо на основе разложения чисел по десятичному составу и сравнения соответствующих разрядных чисел. Сравнение величин сначала выполняется с опорой на сравнение самих предметов по данному свойству, а потом осуществляется на основе сравнения числовых значений величин. Переход к сравнению выражений осуществляется постепенно. Сначала в процессе изучения сложения и вычитания в пределах 10 учащиеся упражняются в сравнении выражения и числа (числа и выражения). Выражение и число (число и выражение) учащиеся сравнивают, не прибегая к операциям над множествами (подумай — поставь знак — объясни — проверь вычислением). Сравнить два выражения — значит, сравнить их значения. Сначала выполняются вычисления, затем рассматриваются задания на основе рассуждений с опорой на обобщение. Термины «решить неравенство», «решение неравенства» не вводятся в начальных классах. Уравнения. Впервые с уравнением учащиеся знакомятся в первом классе после того, как они познакомились с зависимостью между компонентами сложения. Здесь учащийся воспринимает уравнение как равенство, которое справедливо при определенном значении пока неизвестного числа. В соответствии с программой в начальных классах рассматриваются уравнения первой степени с одним неизвестным вида: 7+х=10,х-3=10 + 5,х*(17-10) = 70,х:2-г10 = 30. Неизвестное число сначала находят подбором, а позднее на основе знания связи между результатом и компонентами арифметических действий (т.е. знания способов нахождения неизвестных компонентов). Найти неизвестное число (корень) — значит решить уравнение. С целью формирования умений решать уравнения предлагают разнообразные упражнения: 1) Решите уравнения и выполните проверку. 2) Выполните проверку решенных уравнений, объясните ошибки в неверно решенных уравнениях. 3) Составьте уравнения с числами х, 7, 10, решите и проверьте решение. 4) Из заданных уравнений выберите и решите те, в которых неизвестное число находят вычитанием (делением). После того как учащиеся освоят решение простейших уравнений, уравнения усложняются в том отношении, что: 1) в правой части дается выражение: х+10=30-7; 2) один из компонентов задан выражением к + (18— 15) = 24; 3) один из компонентов задан выражением, причем в него входит неизвестное (73 — В) + 31 = 85 Для решения таких уравнений необходимы знания порядка действий в выражении, а также умения выполнять простейшие преобразования выражений. Далее вводятся уравнения, содержащие действия первой и второй ступени. Для овладения приемом решения этих уравнений в начальных классах учащемуся необходимо в первую очередь научиться левую часть представить в виде двух компонентов, в результате действий с которыми была получена правая часть, и разобрать состав каждого компонента. При обучении решения уравнений важно вырабатывать навык проверки его корня, то есть найденного значения буквы. Здесь учащиеся должны в уравнение вместо буквы подставить ее значение, отдельно вычислить левую и правую части и сравнить полученные результаты. ⇐ Предыдущая26272829303132333435Следующая ⇒ Читайте также: Где возникла философия и почему? Относительная высота сжатой зоны бетона Сущность проекции Гаусса-Крюгера и использование ее в геодезии Тарифы на перевозку пассажиров |
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 2195; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. |
Что сначала выполняется умножение или сложение. Примеры со скобками, урок с тренажерами
Составление выражения со скобками
1. Составь из следующих предложений выражения со скобками и реши их.
Из числа 16 вычти сумму чисел 8 и 6.
Из числа 34 вычти сумму чисел 5 и 8.
Сумму чисел 13 и 5 вычесть из числа 39.
Разность чисел 16 и 3 прибавь к числу 36
Разность чисел 48 и 28 прибавь к числу 16.
2. Реши задачи, сперва составив правильно выражения, а за тем последовательно их решив:
2.1. Папа принёс из леса мешок с орехами. Коля взял из мешка 25 орешков и съел. За тем Маша взяла из мешка 18 орешков. Мама то же взяла из мешка 15 орешков, но положила обратно 7 из них. Сколько осталось в итоге орешков в мешке, если в начале их было 78?
2.2. Мастер ремонтировал детали. В начале рабочего дня их было 38. В первой половине дня он смог отремонтировать 23 из них. После полудня ему принесли еще столько же, сколько было в самом начале дня. Во второй половине он отремонтировал еще 35 деталей. Сколько деталей ему осталось отремонтировать?
Во второй половине он отремонтировал еще 35 деталей. Сколько деталей ему осталось отремонтировать?
3. Реши примеры правильно выполняя последовательность действий:
45: 5 + 12 * 2 -21:3
56 — 72: 9 + 48: 6 * 3
7 + 5 * 4 — 12: 4
18: 3 — 5 + 6 * 8
Решение выражений со скобками
1. Реши примеры правильно раскрывая скобки:
1 + (4 + 8) = | 8 — (2 + 4) = | 3 + (6 — 5) = | 59 + 25 = |
82 + 14 = | 29 + 52 = | 18 + 47 = | 39 + 53 = |
37 + 53 = | 25 + 63 = | 87 + 17 = | 19 + 52 = |
2. Реши примеры правильно выполняя последовательность действий:
Реши примеры правильно выполняя последовательность действий:
2.1. 36: 3 + 12 * (2 — 1) : 3
2.2. 39 — (81: 9 + 48: 6) * 2
2.3. (7 + 5) * 2 — 48: 4
2.4. 18: 3 + (5 * 6) : 2 — 4
3. Реши задачи, сперва составив правильно выражения, а за тем последовательно их решив:
3.1. На складе было 25 упаковок стирального порошка. В один магазин увезли 12 упаковок. За тем во второй магазин увезли столько же. После этого на склад привезли в 3 раза больше упаковок, чем было раньше. Сколько упаковок порошка стало на складе?
3.2. В гостинице проживало 75 туристов. За первый день из гостиницы уехали 3 группы по 12 человек, а заехали 2 группы по 15 человек. На второй день уехали еще 34 человека. Сколько туристов осталось в гостинице к концу 2 дня?
3.3. В химчистку привезли 2 мешка одежды по 5 вещей в каждом мешке. За тем забрали 8 вещей. После полудня привезли ещё 18 вещей на стирку. А забрали только 5 выстиранных вещей. Сколько вещей в химчистке к концу дня, если в начале дня там было 14 вещей?
ФИ _________________________________
21: 3 * 6 — (18 + 14) : 8 = | 63: (81: 9) + (8 * 7 — 2) : 6 = | 64:2: 4+ 9*7-9*1= |
37 *2 + 180: 9 – 36: 12 = | 52 * 10 – 60: 15 * 1 = | 72: 4 +58:2= |
5 *0: 25 + (72: 1 – 0) : 9 = | 21: (3 * 7) – (7* 0 + 1)*1 = | 6:6+0:8-8:8= |
91: 7 + 80: 5 – 5: 5 = | 64:4 — 3*5 +80:2= | (19*5 – 5) : 30 = |
19 + 17 * 3 – 46 = | (39+29) : 4 + 8*0= | (60-5) : 5 +80: 5= |
54 – 26 + 38: 2 = | 63: (7*3) *3= | (160-70) : 18 *1= |
200 – 80: 5 + 3 * 4 = | (29+25): (72:8)= | 72:25 + 3* 17= |
80: 16 + 660: 6 = | 3 * 290 – 800= | 950:50*1-0= |
(48: 3) : 16 * 0 = | 90-6*6+29= | 5* (48-43) +15:5*7= |
54: 9 *8 — 14: 7 * 4 = | 63: 7*4+70:7 * 5= | 24: 6*7 — 7*0= |
21: 7 * 8 + 32: 8 * 4 = | 27: 3* 5 + 26-18 *4= | 54: 6*7 — 0:1= |
45: 9 * 6 + 7 * 5 – 26 = | 28: 7 *9 + 6 * (54 – 47)= | 6*(9: 3) — 40:5 = |
21 * 1 — 56: 7 – 8 = | 9 * (64: 8) — 18:18 | 3 *(14: 2) — 63:9= |
4 * 8 + 42: 6 *5 = | 0*4+0:5 +8* (48: 8)= | 56:7 +7*6 — 5*1= |
31 * 3 — 17 – 80: 16 * 1 = | 57:19 *32 — 11 *7= | 72-96:8 +60:15 *13= |
36 + 42: 3 + 23 + 27 *0 = | 56:14 *19 — 72:18= | (86-78:13)* 4= |
650 – 50 * 4 + 900: 100 = | 630: 9 + 120 * 5 + 40= | 980 – (160 + 20) : 30= |
940 — (1680 – 1600) * 9 = | 29* 2+26 – 37:2= | 72:3 +280: (14*5)= |
300: (5 *60) * (78: 13) = | 63+ 100: 4 – 8*0= | 84:7+70:14 – 6:6= |
45: 15 – 180: 90 + 84: 7 = | 32+51 + 48:6 * 5= | 54:6 ?2 – 70:14= |
38: 2 – 48: 3 + 0 * 9 = | 30:6 * 8 – 6+3*2= | (95:19) *(68:2)= |
(300 — 8 * 7) * 10 = | 1:1 — 0*0 + 1*0 — 1*1= | (80: 4 – 60:30) *5 = |
2 * (120: 6 – 80: 20) = | 56:4+96:3- 0*7= | 20+ 20: 4 — 1*5= |
(18 + 14) : 8 – (7 *0 + 1) *1 = | (8*7-2):6 +63: (7*3)= | (50-5) : 5+21: (3*7)= |
19 + 17 * 3 – 60: 15 * 1 = | 80: 5 +3*5 +80:2= | 54: 9 *8-64:4 +16*0= |
72 * 10 — 64: 2: 4 = | 84 – 36 + 38:2 | 91:13+80:5 – 5:5 |
300 – 80: 5 + 6 * 4 = | 950:190 *1+14: 7*4= | (39+29) : 17 + 8*0= |
(120 — 30) : 18 * 1- 72: 25 = | 210:30*60-0:1= | 90-6*7+3* 17= |
240: 60 *7 – 7 * 0 = | 60:60+0:80-80:80= | 720: 40 +580:20= |
9 *7 – 9 *1 + 5 * 0: 25 = | 21: 7 * 6 +32: 4 *5= | 80:16 +66:6 -63:(81:9)= |
(19 * 5 – 5) : 30 + 70: 7 = | 15:5*7 + 63: 7 * 5= | 54: 6 * 7 — (72:1-0):9= |
3 *290 – 600 – 5 * (48 – 43) = | (300-89*7)*10 — 3?2= | (80: 4) +30*2+ 180: 9= |
30: 6 * 8 – 6 + 48: 3 + 0 *9 = | (95:19) *(68:34) — 60:30*5= | 27: 3*5 — 48:3= |
3* 290 – 800 + 950: 50 = | 80:16 +660:6*1-0= | 90-6*6+ 15:5*7= |
5*(48 — 43) + (48: 3) :16*0= | 280: (14*5) +630: 9*0= | 300: (50*6)* (78: 6)= |
Если в примерах встретится вопросительный знак (?), следует его заменить на знак * — умножение.
1. РЕШИ ВЫРАЖЕНИЯ:
35: 5 + 36: 4 — 3
26 + 6 х 8 – 45: 5 24: 6 + 18 – 2 х 6
9 х 6 – 3 х 6 + 19 – 27:3
2. РЕШИ ВЫРАЖЕНИЯ:
48: 8 + 32 – 54: 6 + 7 х 4
17 + 24: 3 х 4 – 27: 3 х 2 6 х 4: 3 + 54: 6: 3 х 6 + 2 х 9
100 – 6 х 2: 3 х 9 – 39 + 7 х 4
3. РЕШИ ВЫРАЖЕНИЯ:
100 – 27: 3 х 6 + 7 х 4
2 х 4 + 24: 3 + 18: 6 х 9 9 х 3 – 19 + 6 х 7 – 3 х 5
7 х 4 + 35: 7 х 5 – 16: 2: 4 х 3
4. РЕШИ ВЫРАЖЕНИЯ:
32: 8 х 6: 3 + 6 х 8 – 17
5 х 8 – 4 х 7 + 13 — 11 24: 6 + 18: 2 + 20 – 12 + 6 х 7
21: 3 – 35: 7 + 9 х 3 + 9 х 5
5. РЕШИ ВЫРАЖЕНИЯ:
42: 7 х 3 + 2 + 24: 3 – 7 + 9 х 3
6 х 6 + 30: 5: 2 х 7 — 19 90 — 7 х 5 – 24: 3 х 5
6 х 5 – 12: 2 х 3 + 49
6. РЕШИ ВЫРАЖЕНИЯ:
32: 8 х 7 + 54: 6: 3 х 5
50 – 45: 5 х 3 + 16: 2 х 5 8 х 6 + 23 – 24: 4 х 3 + 17
48: 6 х 4 + 6 х 9 – 26 + 13
7. РЕШИ ВЫРАЖЕНИЯ:
42: 6 + (19 + 6) : 5 – 6 х 2
60 – (13 + 22) : 5 – 6 х 4 + 25 (27 – 19) х 4 + 18: 3 + (8 + 27) :5 -17
(82 – 74) : 2 х 7 + 7 х 4 — (63 – 27): 4
8. РЕШИ ВЫРАЖЕНИЯ:
РЕШИ ВЫРАЖЕНИЯ:
90 – (40 – 24: 3) : 4 х 6 + 3 х 5
3 х 4 + 9 х 6 – (27 + 9) : 4 х 5
(50 – 23) : 3 + 8 х 5 – 6 х 5 + (26 + 16) : 6
(5 х 6 – 3 х 4 + 48: 6) +(82 – 78) х 7 – 13
54: 9 + (8 + 19) : 3 – 32: 4 – 21: 7 + (42 – 14) : 4 – (44 14) : 5
9. РЕШИ ВЫРАЖЕНИЯ:
9 х 6 – 6 х 4: (33 – 25) х 7
3 х (12 – 8) : 2 + 6 х 9 — 33 (5 х 9 — 25) : 4 х 8 – 4 х 7 + 13
9 х (2 х 3) – 48: 8 х 3 + 7 х 6 — 34
10. РЕШИ ВЫРАЖЕНИЯ:
(8 х 6 – 36: 6) : 6 х 3 + 5 х 9
7 х 6 + 9 х 4 – (2 х 7 + 54: 6 х 5) (76 – (27 + 9) + 8) : 6 х 4
(7 х 4 + 33) – 3 х 6:2
11. РЕШИ ВЫРАЖЕНИЯ:
(37 + 7 х 4 – 17) : 6 + 7 х 5 + 33 + 9 х 3 – (85 – 67) : 2 х 5
5 х 7 + (18 + 14) : 4 – (26 – 8) : 3 х 2 – 28: 4 + 27: 3 – (17 + 31) : 6
12. РЕШИ ВЫРАЖЕНИЯ:
(58 – 31) : 3 – 2 + (58 – 16) : 6 + 8 х 5 – (60 – 42) : 3 + 9 х 2
(9 х 7 + 56: 7) – (2 х 6 – 4) х 3 + 54: 9
13. РЕШИ ВЫРАЖЕНИЯ:
(8 х 5 + 28: 7) + 12: 2 – 6 х 5 + (13 – 5) х 4 + 5 х 4
(7 х 8 – 14: 7) + (7 х 4 + 12: 6) – 10: 5 + 63: 9
Тест «Порядок арифметических действий» (1 вариант)
1(1б)
2(1б)
3(1б)
4(3б)
5(2б)
6(2б)
7(1б)
8(1б)
9(3б)
10(3б)
11(3б)
12(3б)
110 – (60 +40) :10 х 8
а) 800 б) 8 в) 30
а) 3 4 6 5 2 1 4 5 6 3 2 1
3 4 6 5 1 2
5. В каком из выражений последнее действие умножение?
В каком из выражений последнее действие умножение?
а) 1001:13 х (318 +466) :22
в) 10000 – (5 х 9+56 х 7) х2
6. В каком из выражений первое действие вычитание?
а) 2025:5 – (524 – 24:6) х45
б) 5870 + (90-50 +30) х8 -90
в) 5400:60 х (3600:90 -90)х5
Выбери верный ответ:
9. 90 – (50- 40:5) х 2+ 30
а) 56 б) 92 в) 36
10. 100- (2х5+6 — 4х4) х2
а) 100 б) 200 в) 60
11. (10000+10000:100 +400) : 100 +100
а) 106 б) 205 в) 0
12. 150: (80 – 60:2) х 3
а) 9 б) 45 в) 1
Тест «Порядок арифметических действий»
1(1б)
2(1б)
3(1б)
4(3б)
5(2б)
6(2б)
7(1б)
8(1б)
9(3б)
10(3б)
11(3б)
12(3б)
1. Какое действие в выражении сделаешь первым?
560 – (80+20) :10 х7
а) сложение б) деление в) вычитание
2. Какое действие в этом же выражении сделаешь вторым?
а) вычитание б) деление в) умножение
3. Выбери правильный вариант ответа данного выражения:
а) 800 б) 490 в) 30
4. Выбери верный вариант расстановки действий:
Выбери верный вариант расстановки действий:
а) 3 4 6 5 2 1 4 5 6 3 2 1
320: 8 х 7 + 9 х (240 – 60:15) в) 320:8 х 7+9х(240 – 60:15)
3 4 6 5 2 1
б) 320: 8 х 7 + 9 х (240 – 60:15)
5. В каком из выражений последнее действие деление?
а) 1001:13 х (318 +466) :22
б) 391 х37:17 х (2248:8 – 162)
в) 10000 – (5 х 9+56 х 7) х2
6. В каком из выражений первое действие сложение?
а) 2025:5 – (524 + 24 х6) х45
б) 5870 + (90-50 +30) х8 -90
в) 5400:60 х (3600:90 -90)х5
7. Выбери верное высказывание: «В выражении без скобок действия выполняются:»
а) по порядку б) х и: , затем + и — в) + и -, затем х и:
8. Выбери верное высказывание: «В выражении со скобками действия выполняются:»
а) сначала в скобках б)х и:, затем + и — в) по порядку записи
Выбери верный ответ:
9. 120 – (50- 10:2) х 2+ 30
а) 56 б) 0 в) 60
10. 600- (2х5+8 — 4х4) х2
а) 596 б) 1192 в) 60
11. (20+20000:2000 +30) : 20 +200
а) 106 б) 203 в) 0
12. 160: (80 – 80:2) х 3
160: (80 – 80:2) х 3
а) 120 б) 0 в) 1
Октябрь 24th, 2017 admin
Лопатко Ирина Георгиевна
Цель: формирование знаний о порядке выполнения арифметических действий в числовых выражениях без скобок и со скобками, состоящих из 2-3 действий.
Задачи:
Образовательная: формировать у учащихся умение пользоваться правилами порядка выполнения действий при вычислении конкретных выражений, умение применять алгоритм действий.
Развивающая: развивать навыки работы в паре, мыслительную деятельность учащихся, умение рассуждать, сопоставлять и сравнивать, навыки вычисления и математическую речь.
Воспитательная: воспитывать интерес к предмету, толерантное отношение друг к другу, взаимное сотрудничество.
Типа: изучение нового материала
Оборудование: презентация, наглядности, раздаточный материал, карточки, учебник.
Методы: словесный, наглядно- образный.
ХОД УРОКА
- Организационный момент
Приветствие.
Мы сюда пришли учиться,
Не лениться, а трудиться.
Работаем старательно,
Слушаем внимательно.
Маркушевич сказал великие слова: “Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели .” Добро пожаловать на урок математики!
- Актуализация знаний
Предмет математики столь серьезен, что не следует упускать ни одной возможности сделать его более занимательным. (Б. Паскаль)
Предлагаю выполнить логические задания. Вы готовы?
Какие два числа, если их перемножить, дают такой же результат, что и при их сложении? (2 и 2)
Из-под забора видно 6 пар лошадиных ног. Сколько этих животных во дворе? (3)
Петух, стоя на одной ноге весит 5кг. Сколько он будет весить, стоя на двух ногах? (5кг)
На руках 10 пальцев. Сколько пальцев на 6 руках? (30)
У родителей 6 сыновей. Каждый имеет сестру. Сколько всего детей в семье? (7)
Сколько всего детей в семье? (7)
Сколько хвостов у семи котов?
Сколько носов у двух псов?
Сколько ушей у 5 малышей?
Ребята, именно такой работы я и ждала от вас: вы были активны, внимательны, сообразительны.
Оценивание: словесное.
Устный счет
КОРОБКА ЗНАНИЙ
Произведение чисел 2 * 3, 4 * 2;
Частные чисел 15: 3, 10:2;
Сумма чисел 100 + 20, 130 + 6, 650 + 4;
Разность чисел 180 – 10, 90 – 5, 340 – 30.
Компоненты умножения, деления, сложения, вычитания.
Оценивание: ученики самостоятельно оценивают друг друга
- Сообщение темы и цели урока
“Чтобы переварить знания, надо поглощать их с аппетитом.” (А.Франц)
Вы готовы поглощать знания с аппетитом?
Ребята, Маше и Мише была предложена такая цепочка
24 + 40: 8 – 4=
Маша её решила так:
24 + 40: 8 – 4= 25 правильно? Ответы детей.
А Миша решил вот так:
24 + 40: 8 – 4= 4 правильно? Ответы детей.
Что вас удивило? Вроде и Маша и Миша решили правильно. Тогда почему ответы у них разные?
Они считали в разном порядке, не договорились, в каком порядке будут считать.
От чего зависит результат вычисления? От порядка.
Что вы видите в этих выражениях? Числа, знаки.
Как в математике называют знаки? Действия.
О каком порядке не договорились ребята? О порядке действий.
Что мы будем изучать на уроке? Какая тема урока?
Мы будем изучать порядок арифметических действий в выражениях.
Для чего нам нужно знать порядок действий? Правильно выполнять вычисления в длинных выражениях
«Корзина знаний» . (Корзина висит на доске)
Ученики называют ассоциации связанные с темой.
- Изучение нового материала
Ребята, послушайте, пожалуйста, что говорил французский математик Д.Пойя: “Лучший способ изучить что-либо — это открыть самому”. Вы готовы к открытиям?
180 – (9 + 2) =
Прочитайте выражения. Сравните их.
Сравните их.
Чем похожи? 2 действия, числа одинаковые
Чем отличаются? Скобки, разные действия
Правило 1.
Прочитайте правило на слайде. Дети читают вслух правило.
В выражениях без скобок, содержащих только сложение и вычитание или умножение и деление, действия выполняются в том порядке, как они записаны: слева направо.
О каких действиях здесь говорится? +, — или : , ·
Из данных выражений найдите только те, которые соответствуют правилу 1. Запишите их в тетрадь.
Вычислите значения выражений.
Проверка.
180 – 9 + 2 = 173
Правило 2.
Прочитайте правило на слайде.
Дети читают вслух правило.
В выражениях без скобок сначала выполняются по порядку слева направо умножение или деление, а потом сложение или вычитание.
:, · и +, — (вместе)
Есть скобки? Нет.
Какие действия будем выполнять сначала? ·, : слева направо
Какие действия будем выполнять потом? +, — слева, направо
Найдите их значения.
Проверка.
180 – 9 * 2 = 162
Правило 3
В выражениях со скобками, сначала вычисляют значение выражений в скобках, затем выполняются по порядку слева направо умножение или деление, а потом сложение или вычитание.
А здесь какие арифметические действия указаны?
:, · и +, — (вместе)
Есть скобки? Да.
Какие действия будем выполнять сначала? В скобках
Какие действия будем выполнять потом? ·, : слева направо
А затем? +, — слева, направо
Выпишите выражения, которые относятся ко второму правилу.
Найдите их значения.
Проверка.
180: (9 * 2) = 10
180 – (9 + 2) = 169
Еще раз все вместе проговариваем правило.
ФИЗМИНУТКА
- Закрепление
“Много из математики не остается в памяти, но когда поймешь ее, тогда легко при случае вспомнить забытое.” , говорил М.В. Остроградский. Вот и мы сейчас вспомним, что мы только что изучили и применим новые знания на практике.
Страница 52 №2
(52 – 48) * 4 =
Страница 52 №6 (1)
Учащиеся собрали в теплице 700 кг овощей: 340 кг огурцов, 150 кг помидоров, а остальные – перец. Сколько килограммов перца собрали учащиеся?
О чем говорится? Что известно? Что нужно найти?
Давайте попробуем решить эту задачу выражением!
700 – (340 + 150) = 210 (кг)
Ответ: 210 кг перца собрали учащиеся.
Работа в парах.
Даны карточки с заданием.
5 + 5 + 5 5 = 35
(5+5) : 5 5 = 10
Оценивание:
- быстрота – 1 б
- правильность — 2 б
- логичность – 2 б
- Домашнее задание
Страница 52 № 6 (2) решить задачу, записать решение в виде выражения.
- Итог, рефлексия
Кубик Блума
Назови тему нашего урока?
Объясни порядок выполнения действий в выражениях со скобками.
Почему важно изучать эту тему?
Продолжи первое правило.
Придумай алгоритм выполнения действий в выражениях со скобками.
“Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе.” (М.И. Калинин)
Спасибо за работу на уроке!!!
ПОДЕЛИТЬСЯ Вы можете
И вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий .
В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.
Навигация по странице.
Сначала умножение и деление, затем сложение и вычитание
В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок :
- действия выполняются по порядку слева направо,
- причем сначала выполняется умножение и деление, а затем – сложение и вычитание.
Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.
Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.
Пример.
Выполните действия 7−3+6 .
Решение.
Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7
отнимаем 3
, получаем 4
, после чего к полученной разности 4
прибавляем 6
, получаем 10
.
Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7
отнимаем 3
, получаем 4
, после чего к полученной разности 4
прибавляем 6
, получаем 10
.
Кратко решение можно записать так: 7−3+6=4+6=10 .
Ответ:
7−3+6=10 .
Пример.
Укажите порядок выполнения действий в выражении 6:2·8:3 .
Решение.
Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.
Ответ:
Сначала 6 делим на 2 , это частное умножаем на 8 , наконец, полученный результат делим на 3.
Пример.
Вычислите значение выражения 17−5·6:3−2+4:2 .
Решение.
Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5
умножаем на 6
, получаем 30
, это число делим на 3
, получаем 10
. Теперь 4
делим на 2
, получаем 2
. Подставляем в исходное выражение вместо 5·6:3
найденное значение 10
, а вместо 4:2
— значение 2
, имеем 17−5·6:3−2+4:2=17−10−2+2
.
Так 5
умножаем на 6
, получаем 30
, это число делим на 3
, получаем 10
. Теперь 4
делим на 2
, получаем 2
. Подставляем в исходное выражение вместо 5·6:3
найденное значение 10
, а вместо 4:2
— значение 2
, имеем 17−5·6:3−2+4:2=17−10−2+2
.
В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7 .
Ответ:
17−5·6:3−2+4:2=7 .
На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: .
Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями.
Действия первой и второй ступени
В некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим.
Разберемся с этим.
Определение.
Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени .
В этих терминах правило из предыдущего пункта, определяющее порядок выполнения действий, запишется так: если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание).
Порядок выполнения арифметических действий в выражениях со скобками
Выражения часто содержат скобки, указывающие порядок выполнения действий . В этом случае правило, задающее порядок выполнения действий в выражениях со скобками , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.
Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.
Рассмотрим решения примеров для большей ясности.
Пример.
Выполните указанные действия 5+(7−2·3)·(6−4):2 .
Решение.
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3 . В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1 . Переходим ко второму выражению в скобках 6−4 . Здесь лишь одно действие – вычитание, выполняем его 6−4=2 .
Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2 . В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6 . На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2 .
Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6 .
Ответ:
5+(7−2·3)·(6−4):2=6 .
Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.
Покажем решение примера.
Пример.
Выполните действия в выражении 4+(3+1+4·(2+3)) .
Решение.
Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3) . Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5 . Подставив найденное значение, получаем 3+1+4·5 . В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24 . Исходное значение, после подстановки этого значения, принимает вид 4+24 , и остается лишь закончить выполнение действий: 4+24=28 .
Ответ:
4+(3+1+4·(2+3))=28 .
Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.
Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1
. Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1
, то после этого исходное выражение примет вид (4+(4+1)−1)−1
. Опять выполняем действие во внутренних скобках, так как 4+1=5
, то приходим к следующему выражению (4+5−1)−1
. Опять выполняем действия в скобках: 4+5−1=8
, при этом приходим к разности 8−1
, которая равна 7
.
Опять выполняем действие во внутренних скобках, так как 4+1=5
, то приходим к следующему выражению (4+5−1)−1
. Опять выполняем действия в скобках: 4+5−1=8
, при этом приходим к разности 8−1
, которая равна 7
.
На данном уроке подробно рассмотрен порядок выполнения арифметических действий в выражениях без скобок и со скобками. Учащимся предоставляется возможность в ходе выполнения заданий определить, зависит ли значение выражений от порядка выполнения арифметических действий, узнать отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренироваться в применении изученного правила, найти и исправить ошибки, допущенные при определении порядка действий.
В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.
Но нельзя сначала уйти в школу, а потом надеть одежду.
А в математике обязательно ли выполнять арифметические действия в определенном порядке?
Давайте проверим
Сравним выражения:
8-3+4 и 8-3+4
Видим, что оба выражения совершенно одинаковы.
Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).
Рис. 1. Порядок действий
В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.
Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.
Видим, что значения выражений получаются разные.
Сделаем вывод: порядок выполнения арифметических действий менять нельзя .
Узнаем правило выполнения арифметических действий в выражениях без скобок.
Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.
Потренируемся.
Рассмотрим выражение
В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени .
Выполняем действия слева направо по порядку (рис. 2).
Рис. 2. Порядок действий
Рассмотрим второе выражение
В этом выражении имеются только действия умножения и деления — это действия второй ступени.
Выполняем действия слева направо по порядку (рис. 3).
Рис. 3. Порядок действий
В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?
Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.
Рассмотрим выражение.
Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.
Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.
Вычислим значение выражения.
18:2-2*3+12:3=9-6+4=3+4=7
В каком порядке выполняются арифметические действия, если в выражении имеются скобки?
Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.
Рассмотрим выражение.
30 + 6 * (13 — 9)
Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.
30 + 6 * (13 — 9)
Вычислим значение выражения.
30+6*(13-9)=30+6*4=30+24=54
Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?
Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:
1. действия, записанные в скобках;
действия, записанные в скобках;
2. умножение и деление;
3. сложение и вычитание.
Схема поможет запомнить это несложное правило (рис. 4).
Рис. 4. Порядок действий
Потренируемся.
Рассмотрим выражения, установим порядок действий и выполним вычисления.
43 — (20 — 7) +15
32 + 9 * (19 — 16)
Будем действовать по правилу. В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.
43 — (20 — 7) +15 =43 — 13 +15 = 30 + 15 = 45
В выражении 32 + 9 * (19 — 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.
32 + 9 * (19 — 16) =32 + 9 * 3 = 32 + 27 = 59
В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие — умножение, второе — деление, третье — вычитание.
Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие — умножение, второе — деление, третье — вычитание.
2*9-18:3=18-6=12
Узнаем, правильно ли определен порядок действий в следующих выражениях.
37 + 9 — 6: 2 * 3 =
18: (11 — 5) + 47=
7 * 3 — (16 + 4)=
Рассуждаем так.
37 + 9 — 6: 2 * 3 =
В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие — деление, второе — умножение. Третье действие должно быть сложение, четвертое — вычитание. Вывод: порядок действий определен верно.
Найдем значение данного выражения.
37+9-6:2*3 =37+9-3*3=37+9-9=46-9=37
Продолжаем рассуждать.
Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие — в скобках, второе — деление, третье — сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
Проверяем: первое действие — в скобках, второе — деление, третье — сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
18:(11-5)+47=18:6+47=3+47=50
В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие — в скобках, второе — умножение, третье — вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
7*3-(16+4)=7*3-20=21-20=1
Выполним задание.
Расставим порядок действий в выражении, используя изученное правило (рис. 5).
Рис. 5. Порядок действий
Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.
Действуем по алгоритму.
В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.
Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого — вычитание.
Проверим себя (рис. 6).
Рис. 6. Порядок действий
Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками.
Список литературы
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
- Нормативно-правовой документ. Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.
- «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
- С.И. Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.

- В.Н. Рудницкая. Тесты. — М.: «Экзамен», 2012.
- Festival.1september.ru ().
- Sosnovoborsk-soobchestva.ru ().
- Openclass.ru ().
Домашнее задание
1. Определи порядок действий в данных выражениях. Найди значение выражений.
2. Определи, в каком выражении такой порядок выполнения действий:
1. умножение; 2. деление;. 3. сложение; 4. вычитание; 5. сложение. Найди значение данного выражения.
3. Составь три выражения, в которых такой порядок выполнения действий:
1. умножение; 2. сложение; 3. вычитание
1. сложение; 2. вычитание; 3. сложение
1. умножение; 2. деление; 3. сложение
Найди значение этих выражений.
В пятом веке до нашей эры древнегреческий философ Зенон Элейский сформулировал свои знаменитые апории, самой известной из которых является апория «Ахиллес и черепаха». Вот как она звучит:
Допустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.
За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.
Это рассуждение стало логическим шоком для всех последующих поколений. Аристотель, Диоген, Кант, Гегель, Гильберт… Все они так или иначе рассматривали апории Зенона. Шок оказался настолько сильным, что «… дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось… к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса… » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.
С точки зрения математики, Зенон в своей апории наглядно продемонстрировал переход от величины к . Этот переход подразумевает применение вместо постоянных. Насколько я понимаю, математический аппарат применения переменных единиц измерения либо ещё не разработан, либо его не применяли к апории Зенона. Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.
Этот переход подразумевает применение вместо постоянных. Насколько я понимаю, математический аппарат применения переменных единиц измерения либо ещё не разработан, либо его не применяли к апории Зенона. Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.
Если перевернуть привычную нам логику, всё становится на свои места. Ахиллес бежит с постоянной скоростью. Каждый последующий отрезок его пути в десять раз короче предыдущего. Соответственно, и время, затрачиваемое на его преодоление, в десять раз меньше предыдущего. Если применять понятие «бесконечность» в этой ситуации, то правильно будет говорить «Ахиллес бесконечно быстро догонит черепаху».
Как избежать этой логической ловушки? Оставаться в постоянных единицах измерения времени и не переходить к обратным величинам. На языке Зенона это выглядит так:
На языке Зенона это выглядит так:
За то время, за которое Ахиллес пробежит тысячу шагов, черепаха в ту же сторону проползёт сто шагов. За следующий интервал времени, равный первому, Ахиллес пробежит ещё тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес на восемьсот шагов опережает черепаху.
Этот подход адекватно описывает реальность без всяких логических парадоксов. Но это не полное решение проблемы. На Зеноновскую апорию «Ахиллес и черепаха» очень похоже утверждение Эйнштейна о непреодолимости скорости света. Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения.
Другая интересная апория Зенона повествует о летящей стреле:
Летящая стрела неподвижна, так как в каждый момент времени она покоится, а поскольку она покоится в каждый момент времени, то она покоится всегда.
В этой апории логический парадокс преодолевается очень просто — достаточно уточнить, что в каждый момент времени летящая стрела покоится в разных точках пространства, что, собственно, и является движением. Здесь нужно отметить другой момент. По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
Здесь нужно отметить другой момент. По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
среда, 4 июля 2018 г.
Очень хорошо различия между множеством и мультимножеством описаны в Википедии . Смотрим.
Как видите, «во множестве не может быть двух идентичных элементов», но если идентичные элементы во множестве есть, такое множество называется «мультимножество». Подобную логику абсурда разумным существам не понять никогда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова «совсем». Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи.
Подобную логику абсурда разумным существам не понять никогда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова «совсем». Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи.
Когда-то инженеры, построившие мост, во время испытаний моста находились в лодке под мостом. Если мост обрушивался, бездарный инженер погибал под обломками своего творения. Если мост выдерживал нагрузку, талантливый инженер строил другие мосты.
Как бы математики не прятались за фразой «чур, я в домике», точнее «математика изучает абстрактные понятия», есть одна пуповина, которая неразрывно связывает их с реальностью. Этой пуповиной являются деньги. Применим математическую теорию множеств к самим математикам.
Мы очень хорошо учили математику и сейчас сидим в кассе, выдаем зарплату. Вот приходит к нам математик за своими деньгами. Отсчитываем ему всю сумму и раскладываем у себя на столе на разные стопки, в которые складываем купюры одного достоинства. Затем берем с каждой стопки по одной купюре и вручаем математику его «математическое множество зарплаты». Поясняем математику, что остальные купюры он получит только тогда, когда докажет, что множество без одинаковых элементов не равно множеству с одинаковыми элементами. Вот здесь начнется самое интересное.
Затем берем с каждой стопки по одной купюре и вручаем математику его «математическое множество зарплаты». Поясняем математику, что остальные купюры он получит только тогда, когда докажет, что множество без одинаковых элементов не равно множеству с одинаковыми элементами. Вот здесь начнется самое интересное.
В первую очередь, сработает логика депутатов: «к другим это применять можно, ко мне — низьзя!». Дальше начнутся уверения нас в том, что на купюрах одинакового достоинства имеются разные номера купюр, а значит их нельзя считать одинаковыми элементами. Хорошо, отсчитываем зарплату монетами — на монетах нет номеров. Здесь математик начнет судорожно вспоминать физику: на разных монетах имеется разное количество грязи, кристаллическая структура и расположение атомов у каждой монеты уникально…
А теперь у меня самый интересный вопрос: где проходит та грань, за которой элементы мультимножества превращаются в элементы множества и наоборот? Такой грани не существует — всё решают шаманы, наука здесь и близко не валялась.
Вот смотрите. Мы отбираем футбольные стадионы с одинаковой площадью поля. Площадь полей одинакова — значит у нас получилось мультимножество. Но если рассматривать названия этих же стадионов — у нас получается множество, ведь названия разные. Как видите, один и тот же набор элементов одновременно является и множеством, и мультимножеством. Как правильно? А вот здесь математик-шаман-шуллер достает из рукава козырный туз и начинает нам рассказывать либо о множестве, либо о мультимножестве. В любом случае он убедит нас в своей правоте.
Чтобы понять, как современные шаманы оперируют теорией множеств, привязывая её к реальности, достаточно ответить на один вопрос: чем элементы одного множества отличаются от элементов другого множества? Я вам покажу, без всяких «мыслимое как не единое целое» или «не мыслимое как единое целое».
воскресенье, 18 марта 2018 г.
Сумма цифр числа — это пляска шаманов с бубном, которая к математике никакого отношения не имеет. Да, на уроках математики нас учат находить сумму цифр числа и пользоваться нею, но на то они и шаманы, чтобы обучать потомков своим навыкам и премудростям, иначе шаманы просто вымрут.
Вам нужны доказательства? Откройте Википедию и попробуйте найти страницу «Сумма цифр числа». Её не существует. Нет в математике формулы, по которой можно найти сумму цифр любого числа. Ведь цифры — это графические символы, при помощи которых мы записываем числа и на языке математики задача звучит так: «Найти сумму графических символов, изображающих любое число». Математики эту задачу решить не могут, а вот шаманы — элементарно.
Давайте разберемся, что и как мы делаем для того, чтобы найти сумму цифр заданного числа. И так, пусть у нас есть число 12345. Что нужно сделать для того, чтобы найти сумму цифр этого числа? Рассмотрим все шаги по порядку.
1. Записываем число на бумажке. Что же мы сделали? Мы преобразовали число в графический символ числа. Это не математическое действие.
2. Разрезаем одну полученную картинку на несколько картинок, содержащих отдельные цифры. Разрезание картинки — это не математическое действие.
3. Преобразовываем отдельные графические символы в числа. Это не математическое действие.
Это не математическое действие.
4. Складываем полученные числа. Вот это уже математика.
Сумма цифр числа 12345 равна 15. Вот такие вот «курсы кройки и шитья» от шаманов применяют математики. Но это ещё не всё.
С точки зрения математики не имеет значения, в какой системе счисления мы записываем число. Так вот, в разных системах счисления сумма цифр одного и того же числа будет разной. В математике система счисления указывается в виде нижнего индекса справа от числа. С большим числом 12345 я не хочу голову морочить, рассмотрим число 26 из статьи про . Запишем это число в двоичной, восьмеричной, десятичной и шестнадцатеричной системах счисления. Мы не будем рассматривать каждый шаг под микроскопом, это мы уже сделали. Посмотрим на результат.
Как видите, в разных системах счисления сумма цифр одного и того же числа получается разной. Подобный результат к математике никакого отношения не имеет. Это всё равно, что при определении площади прямоугольника в метрах и сантиметрах вы получали бы совершенно разные результаты.
Ноль во всех системах счисления выглядит одинаково и суммы цифр не имеет. Это ещё один аргумент в пользу того, что . Вопрос к математикам: как в математике обозначается то, что не является числом? Что, для математиков ничего, кроме чисел, не существует? Для шаманов я могу такое допустить, но для ученых — нет. Реальность состоит не только из чисел.
Полученный результат следует рассматривать как доказательство того, что системы счисления являются единицами измерения чисел. Ведь мы не можем сравнивать числа с разными единицами измерения. Если одни и те же действия с разными единицами измерения одной и той же величины приводят к разным результатам после их сравнения, значит это не имеет ничего общего с математикой.
Что же такое настоящая математика? Это когда результат математического действия не зависит от величины числа, применяемой единицы измерения и от того, кто это действие выполняет.
Открывает дверь и говорит:
Ой! А это разве не женский туалет?
— Девушка! Это лаборатория по изучению индефильной святости душ при вознесении на небеса! Нимб сверху и стрелочка вверх. Какой еще туалет?
Какой еще туалет?
Женский… Нимб сверху и стрелочка вниз — это мужской.
Если у вас перед глазами несколько раз в день мелькает вот такое вот произведение дизайнерского искусства,
Тогда не удивительно, что в своем автомобиле вы вдруг обнаруживаете странный значок:
Лично я делаю над собой усилие, чтобы в какающем человеке (одна картинка), увидеть минус четыре градуса (композиция из нескольких картинок: знак минус, цифра четыре, обозначение градусов). И я не считаю эту девушку дурой, не знающей физику. Просто у неё дугой стереотип восприятия графических образов. И математики нас этому постоянно учат. Вот пример.
1А — это не «минус четыре градуса» или «один а». Это «какающий человек» или число «двадцать шесть» в шестнадцатеричной системе счисления. Те люди, которые постоянно работают в этой системе счисления, автоматически воспринимают цифру и букву как один графический символ.
| Табличка на двери |
Какое действие в математике выполняется первым сложение или умножение
Что сначала — сложение или умножение: правила, порядок выполнения действия и рекомендации
С самого начала следует напомнить, чтобы потом не путаться: есть цифры – их 10. От 0 до 9. Есть числа, и они состоят их цифр. Чисел бесконечно много. Точно больше, чем звезд на небе.
От 0 до 9. Есть числа, и они состоят их цифр. Чисел бесконечно много. Точно больше, чем звезд на небе.
Математическое выражение − это записанное с помощью математических символов наставление, какие действия нужно произвести с числами, чтобы получить результат. Не «выйти» на искомый результат, как в статистике, а узнать, сколько их точно было. А вот чего и когда было − уже не входит в сферу интересов арифметики. При этом важно не ошибиться в последовательности действий, что сначала — сложение или умножение? Выражение в школе иногда называют «пример».
Сложение и вычитание
Какие же действия можно произвести с числами? Есть два базовых. Это сложение и вычитание. Все остальные действия построены на этих двух.
Самое простое человеческое действие: взять две кучки камней и смешать их в одну. Это и есть сложение. Для того чтобы получить результат такого действия, можно даже не знать, что такое сложение. Достаточно просто взять кучку камней у Пети и кучку камней у Васи. Сложить все вместе, посчитать все заново. Новый результат последовательного счета камней из новой кучки − это и есть сумма.
Сложить все вместе, посчитать все заново. Новый результат последовательного счета камней из новой кучки − это и есть сумма.
Точно так же можно не знать, что такое вычитание, просто взять и разделить кучу камней на две части или забрать из кучи какое-то количество камней. Вот и останется в куче то, что называется разностью. Забрать можно только то, что есть в куче. Кредит и прочие экономические термины в данной статье не рассматриваются.
Чтобы не пересчитывать каждый раз камни, ведь бывает, что их много и они тяжелые, придумали математические действия: сложение и вычитание. И для этих действий придумали технику вычислений.
Сумма двух любых цифр тупо заучиваются без всякой техники. 2 плюс 5 равно семь. Посчитать можно на счетных палочках, камнях, рыбьих головах – результат одинаковый. Положить сначала 2 палочки, потом 5, а потом посчитать все вместе. Другого способа нет.
Те, кто поумнее, обычно это кассиры и студенты, заучивают больше, не только сумму двух цифр, но и суммы чисел. Но самое главное, они могут складывать числа в уме, используя разные методики. Это называется навыком устного счета.
Но самое главное, они могут складывать числа в уме, используя разные методики. Это называется навыком устного счета.
Для сложения чисел, состоящих из десятков, сотен, тысяч и еще больших разрядов, используют специальные техники − сложение столбиком или калькулятор. С калькулятором можно не уметь складывать даже цифры, да и читать дальше не нужно.
Сложение столбиком − это метод, который позволяет складывать большие (многоразрядные) числа, выучив только результаты сложения цифр. При сложении столбиком последовательно складываются соответствующие десятичные разряды двух чисел (то есть фактически две цифры), если результат сложения двух цифр превышает 10, то учитывается только последний разряд этой суммы – единицы числа, а к сумме следующих разрядов добавляется 1.
Умножение
Математики любят группировать похожие действия для упрощения расчетов. Так и операция умножения является группировкой одинаковых действий – сложения одинаковых чисел. Любое произведение N x M − есть N операций сложения чисел M. Это всего лишь форма записи сложения одинаковых слагаемых.
Это всего лишь форма записи сложения одинаковых слагаемых.
Для вычисления произведения используется такой же метод – сначала тупо заучивается таблица умножения цифр друг на друга, а потом применяется метод поразрядного умножения, что называется «в столбик».
Что сначала — умножение или сложение?
Любое математическое выражение – это фактически запись учетчика «с полей» о результатах каких-либо действий. Допустим, сбора урожая помидоров:
- 5 взрослых работников собрали по 500 помидоров каждый и выполнили норму.
- 2 школьников не ходили на уроки математики и помогали взрослым: собрали по 50 помидоров, норму не выполнили, съели 30 помидоров, надкусили и испортили еще 60 помидоров, 70 помидоров было изъято из карманов помощников. Зачем брали с собой их в поле – непонятно.
Все помидоры сдавали учетчику, он укладывал их по кучкам.
Запишем результат «сбора» урожая в виде выражения:
- 500 + 500 + 500 + 500 + 500 — это кучки взрослых работников;
- 50 + 50 – это кучки малолетних работников;
- 70 – изъято из карманов школьников (испорченное и надкусанное в зачет результата не идет).

Получаем пример для школы, запись учетчика результатов работы:
500 + 500 +500 +500 +500 + 50 +50 + 70 =?;
Здесь можно применить группировку: 5 кучек по 500 помидоров − это можно записать через операцию умножения: 5 ∙ 500.
Две кучки по 50 – это тоже можно записать через умножение.
И одна кучка 70 помидоров.
5 ∙ 500 + 2 ∙ 50 + 1 ∙ 70 =?
И что делать в примере сначала − умножение или сложение? Так вот, складывать можно только помидоры. Нельзя сложить 500 помидоров и 2 кучки. Они не складываются. Поэтому сначала нужно всегда все записи привести к базовым операциям сложения, то есть в первую очередь вычислить все операции группировки-умножения. Совсем простыми словами — сначала выполняется умножение, а сложение уже потом. Если умножить 5 кучек по 500 помидоров каждая, то получится 2500 помидоров. А дальше их уже можно складывать с помидорами из других кучек.
2500 + 100 + 70 = 2 670
При изучении ребенком математики нужно донести до него, что это инструмент, используемый в повседневной жизни. Математические выражения являются, по сути (в самом простом варианте начальной школы), складскими записями о количестве товаров, денег (очень легко воспринимается школьниками), других предметов.
Математические выражения являются, по сути (в самом простом варианте начальной школы), складскими записями о количестве товаров, денег (очень легко воспринимается школьниками), других предметов.
Соответственно, любое произведение – это сумма содержимого некоторого количества одинаковых емкостей, ящиков, кучек, содержащих одинаковое количество предметов. И что сначала умножение, а сложение потом, то есть сначала начала вычислить общее количество предметов, а затем уже складывать их между собой.
Деление
Операция деления отдельно не рассматривается, она обратная умножению. Нужно что-то распределить по коробкам, так, чтобы во всех коробках было одинаковое заданное количество предметов. Самый прямой аналог в жизни – это фасовка.
Скобки
Большое значение в решении примеров имеют скобки. Скобки в арифметике – математический знак, используемый для регулирования последовательности вычислений в выражении (примере).
Умножение и деление имеют приоритет выше, чем сложение и вычитание. А скобки имеют приоритет выше, чем умножение и деление.
А скобки имеют приоритет выше, чем умножение и деление.
Все, что записано в скобках, вычисляется в первую очередь. Если скобки вложенные, то сначала вычисляется выражение во внутренних скобках. И это непреложное правило. Как только выражение в скобках вычислено, скобки пропадают, а на их месте возникает число. Варианты раскрытия скобок с неизвестными здесь не рассматриваются. Так делают до тех пор, пока все они не исчезнут из выражения.
- Это как коробочки с конфетами в большом мешке. Сначала нужно раскрыть все коробочки и ссыпать в большой мешок: (25 – 5 ) = 20. Пять конфет из коробочки сразу заслали отличнице Люде, которая приболела и в празднике не участвует. Остальные конфеты − в мешок!
- Потом связать конфеты в пучки по 5 штук: 20 : 5 = 4.
- Потом добавить в мешок еще 2 пучка конфет, чтобы можно было поделить на троих детей без драки. Признаки деления на 3 в данной статье не рассматриваются.
(20 : 5 + 2) : 3 = (4 +2) : 3 = 6 : 3 = 2
Итого: трем детям по два пучка конфет (по пучку в руку), по 5 конфет в пучке.
Если вычислить первые скобки в выражении и переписать все заново, пример станет короче. Метод не быстрый, с большим расходом бумаги, зато удивительно эффективный. Заодно тренирует внимательность при переписывании. Пример приводится к виду, когда остается только один вопрос, сначала умножение или сложение без скобок. То есть к такому виду, когда скобок уже и нет. Но ответ на этот вопрос уже есть, и нет смысла обсуждать, что идет сначала — умножение или сложение.
«Вишенка на торте»
И напоследок. К математическому выражению не применимы правила русского языка – читать и выполнять слева направо:
Это простенький пример может довести до истерики ребенка или испортить вечер его маме. Потому что именной ей придется объяснять второкласснику, что бывают отрицательные числа. Или рушить авторитет «МарьиВановны», которая сказала, что: «Нужно слева направо и по порядку».
«Совсем вишня»
В Сети гуляет пример, вызывающий затруднения у взрослых дяденек и тетенек. Он не совсем по рассматриваемой теме, что сначала — умножение или сложение. Он вроде как про то, что сначала выполняете действие в скобках.
Он не совсем по рассматриваемой теме, что сначала — умножение или сложение. Он вроде как про то, что сначала выполняете действие в скобках.
От перестановки слагаемых сумма не изменяется, от перестановки множителей тоже. Нужно просто записывать выражение так, чтобы не было потом мучительно стыдно.
интернет проект BeginnerSchool.ru
Сегодня мы поговорим о порядке выполнения математических действий. Какие действия выполнять первыми? Сложение и вычитание, или умножение и деление. Странно, но у наших детей возникают проблемы с решением, казалось бы, элементарных выражений.
Порядок выполнения действий:Читаем выражение слева направо и выбираем порядок действий по приоритету. Сначала выполняем действия в скобках. Затем умножение и/или деление. Далее складываем и вычитаем.
Если скобки имеют несколько вложений, то есть если внутри скобок есть ещё скобки, то сначала выполняем действия во внутренних скобках. Для простоты понимания, выражение в скобках можно воспринимать как самостоятельное выражение, то есть как отдельный пример, который надо решить. Внутри скобок действия выполняются согласно тому же порядку: Действия в скобках, затем умножение/деление, затем сложение/вычитание.
Для простоты понимания, выражение в скобках можно воспринимать как самостоятельное выражение, то есть как отдельный пример, который надо решить. Внутри скобок действия выполняются согласно тому же порядку: Действия в скобках, затем умножение/деление, затем сложение/вычитание.
Умножение и деление не имеет между собой приоритета и выполняются слева направо, также как и сложение с вычитанием.
38 – (10 + 6) = 22;Итак, вспомним о том, что сначала вычисляются выражения в скобках
1) в скобках: 10 + 6 = 16 ;
2) вычитание: 38 – 16 = 22 .
Если в выражение без скобок входит только сложение и вычитание, или только умножение и деление, то действия выполняются по порядку слева направо.
10 ÷ 2 × 4 = 20;Порядок выполнения действий:
1) слева направо, сначала деление: 10 ÷ 2 = 5 ;
2) умножение: 5 × 4 = 20 ;
10 + 4 – 3 = 11 , т.е.:
Если в выражении без скобок есть не только сложение и вычитание, но и умножение или деление, то действия выполняются по порядку слева направо, но преимущество имеет умножение и деление, их выполняют в первую очередь, а за ними и сложение с вычитанием.
Порядок выполнения действий:
4) 9 – 6 = 3 ; т.е. слева направо – результат первого действия минус результат второго;
5) 3 + 4 = 7 ; т.е. результат четвертого действия плюс результат третьего;
Если в выражении есть скобки, то сначала выполняются выражения в скобках, затем умножение и деление, а уж потом сложение с вычитанием.
30 + 6 × (13 – 9) = 54 , т.е.:1) выражение в скобках: 13 – 9 = 4 ;
2) умножение: 6 × 4 = 24 ;
3) сложение: 30 + 24 = 54 ;
Итак, подведем итоги. Прежде чем приступить к вычислению, надо проанализировать выражение: есть ли в нем скобки и какие действия в нем имеются. После этого приступать к вычислениям в следующем порядке:
1) действия, заключенные в скобках;
2) умножение и деление;
3) сложение и вычитание.
Если вы хотите получать анонсы наших статей подпишитесь на рассылку “Новости сайта“.
- Продолжаем рубрику «основные содержательные линии курса математики начальной школы».
 В.Продолжаем тему «основные содержательные линии курса математики начальной школы». В.Продолжим изучение предметов, которые изучают наши дети в начальной школе.Продолжим изучение программы математики в начальной школе и на этот.Одним из простых арифметических действий является деление. Мы знаем, что.
В.Продолжаем тему «основные содержательные линии курса математики начальной школы». В.Продолжим изучение предметов, которые изучают наши дети в начальной школе.Продолжим изучение программы математики в начальной школе и на этот.Одним из простых арифметических действий является деление. Мы знаем, что.Понравилась статья — поделитесь с друзьями:
Оставляйте пожалуйста комментарии в форме ниже
Отзывов (60)
Полезная статья. Спасибо!
Очень все понятно. Для детей важна такая разъяснительная работа. Где Вы были, когда я пошла в школу?
)) Покажу сыну, пусть изучает. Я это вроде все помню. Спасибо )
Спасибо, сайт нужный. Честно говоря, уже кое – что подзабыла, а уроки с внучкой делаем. Вот, вспомнилось…
Очень необычная тематика сайта. Но тем, наверное, он и интересен. Иногда не знаешь, как объяснить ребенку тот или иной материал школьной программы.
Какое подспорье для родителей. И полезности для деток. Не всегда они материал усваивают в школе.
Сам учитель. Сайт очень полезный. Детям и родителям – хорошее подспорье
Вы взяли пример из головы, в начальной школе не изучают отрицательных чисел, а также не оперируют такими большими числами. Результат пятого действия будет отрицательным.
Но попробуем решить данный пример:
1) Выражение в скобках: 64385 – 39288 = 25097
Далее умножение:
2) 4217 * 4 = 16868
3) 25097 * 3 = 75291
4) 321 * 1000 = 321000
Теперь слева на право
5) 16868 – 75291 = -58423 (. )
Это уже шестой класс, тема “Сложение положительных и отрицательных чисел”
6) -58423 + 321000
От перемены мест слагаемых сумма не меняется:
321000 + (-58423) = 321000 – 58423 = 262577
Помогите люди добрые.
Я тут читал кое где в иностранной литературе, что если в выражении есть действия двух уроовней 1(сложение и вычитание) и 2 (умножение и деление)
к примеру 20-6:3х2+2=
то в первую очередь должно выполнятся действия 2-ого уровня, потом 1-го. Но загвоздка с тем, что говорится – надо выполнить сперва умножение а потом деление, а не как нас учили по правилу слева направо.
Но загвоздка с тем, что говорится – надо выполнить сперва умножение а потом деление, а не как нас учили по правилу слева направо.
Объясните плз.
Обязательно слева на право, так как умножение и деление равноценны. Но, если представить умножение в виде дроби:
тогда 2 перенесется в числитель и первым выполняется умножение
(6 * 2)/3 = (6:3)*2 = 4.
То есть порядок выполнения важен!
Помогите решить пример у всех расходятся ответы
6/2*(1+2)
ответь пожалуйста
Если 6 : 2 * (1 + 2) =
1) 1 + 2 = 3
2) 6 : 2 = 3
3) 3 * 3 = 9
Если
6
———-
2 * (1 + 2)
то есть 6 : (2 * (1 + 2))
1) 1 + 2 = 3
2) 2 * 3 = 6
3) 6 : 6 = 1
Это два разных примера.
Если
6 * (1 + 2)
———–
2
1) 1 + 2 = 3
2) 6 * 3 = 18
3) 18 : 2 = 9
Это тот же первый вариант
Если Вы правильно написали, то это первый вариант и ответ 9
Очень жаль, если вы этому детей учите.. Примеры 6:2*(1+2) и 6/2*(1+2) одинаковые… никогда не было такого, чтобы черта дроби и двоеточие означали разные действия или определяли порядок действий.
В данном случае необходимо также учесть правило раскрытия скобок:
6:2*(1+2) = 6:(2*1 + 2*2) = 6:(2+4) = 6:6 = 1 – единственный верный ответ.
6:2*(1+2) и 6/2*(1+2) это абсолютно эквивалентные записи (то есть одинаковые).
Порядок действий следующий:
1) 1+2 = 3
2) 6:2 = 3
3) 3*3 = 9
Ваш вариант с раскрытием скобок будет верен, если запись выражения будет следующей:
6:(2*(1+2)) = 1;
Ваше недоумение понятно, оно имеет глубокие исторические корни, в старых учебниках по алгебре можно встретить упоминание о именно такой последовательности действий, как предлагаете вы. Это связанно с неоднозначностью интерпретации записи. Но в наше время это разночтение устранено. Так что не надо забивать людям голову неверной информацией, а тем более забивать этими пережитками прошлого головы детей.
Простой пример. Ребенок на уроке информатики на языке Паскаль запишет y:=6:2*(1+2) и, поверьте мне, получит y=9. Не ломайте детскую психику.
В связи с порядком действий бывают забавные ситуации когда человеку в руки попадает калькулятор с обратной польской записью, а он и понятия не имеет об этом. И начинается “Святая Война за Истину”. Будьте проще, меньше пафоса, мы все люди и нам свойственно ошибаться. Добра Вам.
И начинается “Святая Война за Истину”. Будьте проще, меньше пафоса, мы все люди и нам свойственно ошибаться. Добра Вам.
Математика для блондинок
Математикой должны заниматься блондинки — они врать не умеют.
Страницы
- Главная страница
- Новая математика
- Словарик
четверг, 29 марта 2012 г.
Почему умножение первое?
Вот какой интересный вопрос о порядке выполнения математических действий мне задали:
меня зовут Александр. меня подруга замучала вопросом почему умножение делается раньше сложения? например почему 1+2*3=7 а не 9 я просто не знаю как объяснить, просто знаю что 7 и всё!!))))
Традиционный ответ на этот вопрос будет звучать приблизительно так: правила математики гласят — сперва выполняется умножение, потом сложение. Нам нужно просто делать то, чему нас учат наши учителя, соблюдать математические правила и мы получим правильный результат. В математике абстрагирование от конкретных условий приводит к потере смысла выполняемых действий.
Так всё же почему умножение выполняется первое, а только потом сложение? Ответ довольно прост. При умножении двух разных единиц измерения получается новая единица измерения, при сложении единицы измерения не меняются. При умножении мы получаем эту самую новую единицу измерения. Если она такая же, как и у первого слагаемого, тогда мы можем выполнить сложение.
Вот задача, которая хорошо иллюстрирует сказанное. У нас имеется геометрическая фигура площадью 1 квадратный сантиметр. К ней прибавили прямоугольник размером 2 на 3 сантиметра. Какая общая площадь двух фигур? Если вы захотите к одному квадратному сантиметру прибавить два сантиметра стороны прямоугольника, то у вас ничего не получится. Нельзя сложить две величины с разными единицами измерения. Если вы умножите стороны прямоугольника, тогда вы получите его площадь. Площадь с площадью можно сложить и получить результат — 7 квадратных сантиметров составляет общая площадь двух фигур.
По умолчанию, в математике считается, что если между числами записан знак математического действия, значит это действие можно выполнять. Отсутствие единиц измерения превращает математику в бессмысленную детскую игру в числа.
Отсутствие единиц измерения превращает математику в бессмысленную детскую игру в числа.
Порядок действий в вычислениях доклад, проект
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация на тему Порядок действий в вычислениях, предмет презентации: Математика. Этот материал в формате pptx (PowerPoint) содержит 13 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Этот материал в формате pptx (PowerPoint) содержит 13 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Математика это- гимнастика для ума.(М. Калинин)
500-328 (е)
(56+77)+44 (ц)
61:61 (е)
451* 0 (в)
1313:13 (н)
23 * 10 (и)
4500 : 10 (я)
Расположив ответы примеров в порядке возрастания, вы получите название города, единственного в своем роде, другого такого нет на свете. Он стоит в море, на 118 островах, расположенных в 4 км. от суши. В этом городе нет автобусов, троллейбусов, а средством передвижения являются речные трамваи – катера и гондолы
Венеция
Вспомним пройденный материал.
Назовите наименьшее натуральное число
Какие числа чередуются в натуральном ряду?
Назовите компоненты сложениям
Назовите компоненты вычитания
Назовите компоненты деления
Продолжите: Если число разделить на единицу, то..
Продолжите: Если число умножить на ноль, то…
Найдите значение этого выражения
37-7*(18-6 * 2):7+9
Что нужно знать, чтобы выполнить это задание без ошибок?
Порядок действий в вычислениях
Цели урока
Повторить основные арифметические действия
Вспомнить порядок выполнения действий
Совершенствовать свои вычислительные навыки
Порядок действий в вычислениях.
Арифметические действия
Действия 1 ступени:
Сложение и вычитание
Действия 2 ступени:
Умножение и деление
Порядок действий в вычислениях.
Порядок выполнения действий определяется следующими правилами:
1. Если в выражении нет скобок, и оно содержит только действия одной ступени, то они выполняются по порядку слева направо.
2. Если выражение содержит действия 1 и 2 ступени и в нем нет скобок, то сначала выполняются действия второй ступени, а потом действия первой ступени по порядку слева направо.
3. Если в выражении есть скобки, то сначала выполняются действия в скобках, учитывая при этом правила 1 и 2.
Порядок действий в вычислениях.
Самостоятельная работа
I вариант
Решив пример, вы узнаете, в каком году Петр I завез в Россию картофель.
631-224:16+18*60
II вариант
Решив пример, вы получите массу черепахи-гиганта, живущей на островах Тихого океана. Она такой величины, что дети могут кататься, сидя на ее панцире.
39*15+180:12
Порядок действий в вычислениях.
1697 год Дермохелис ее масса 600кг
Порядок действий в вычислениях.
тест
1.В выражении 200 — (20+10:2)*8 последним выполняется:
1)Вычитание п 2)Сложение я 3)Умножение р 4)Деление с
2. В выражении (120+50):17*15 — 65 первым выполняется
1)Вычитание п 3) Сложение я 2)Умножение р 4)Деление с
3. Указать в каком из примеров указанный порядок действий приведет к неправильному результату:
4. Вычислить: (35+25):15+45
1)1 э 2)49 ь 3)48 ю 4)0 я
Порядок действий в вычислениях.
Поработаем с учебником.
Стр. 62 № 224-226,№ 230.
Порядок действий в вычислениях.
Подведение итогов
Продолжите предложение:
Сегодня на уроке я повторил…
Материал урока мне … (понятен/ непонятен )
Порядок действий в вычислениях.
Скачать презентацию
Что такое shareslide.ru?
Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Для правообладателей
Обратная связь
Email: Нажмите что бы посмотреть
Некоторые недоразумения относительно порядка операций
В этой статье я опишу некоторые недоразумения относительно порядка операций и предложу лучший способ осмысления этой темы. Пожалуйста, добавляйте свои идеи в комментарии.
Порядок операций — это набор правил, которые мы используем для вычисления математических выражений. Правила следующие:
- Выполнять все операции внутри круглых скобок.
- Применить показатели.
- Выполнить все операции умножения и деления слева направо.
- Выполняйте все операции сложения и вычитания слева направо.

Мне нравится начинать тему, показывая своим ученикам два способа расчета и спрашивая их, какой из них правильный. Я также показываю им, что разные калькуляторы дадут разные ответы на одну и ту же задачу в зависимости от типа логики, которую они используют. Калькулятор с четырьмя функциями дает ответ 35, а научный калькулятор дает 23. На самом деле, калькулятор Windows дает оба ответа, в зависимости от режима (стандартный или научный).
Многие ученики и некоторые учителя неправильно понимают эти правила. Есть некоторые тонкости правил, которые опускаются во многих книгах, и эти упущения приводят к путанице. Вот некоторые из этих недоразумений.
1. Порядок операций указан в скобках.
Некоторые учащиеся знают, что сначала им следует упрощать в скобках, но они не понимают, что порядок операций также применяется при работе внутри скобок. Например, в выражении
ученик может не знать, что сначала нужно выполнить умножение.
2. Упрощение в круглых скобках не означает удаление круглых скобок.
Некоторые учителя описывают первый шаг как избавление от круглых скобок. Это вызывает путаницу, когда студентов просят упростить такие выражения, как или . В этих случаях выражения внутри круглых скобок уже были упрощены, но круглые скобки по-прежнему служат полезной цели.
3. Группировка иногда обозначается другими средствами, кроме скобок.
Круглые скобки часто используются для группировки, но мы также используем квадратные скобки [ ] или фигурные скобки { }. Столетие назад также было распространено использование vinculum, представляющего собой вертикальную черту, написанную над частью выражения. Винкулум сегодня редко используется, но он сохраняется в обозначении квадратных корней.
Иногда подразумевается группировка. Когда выражение записывается в виде вертикальной дроби, подразумевается, что члены в числителе сгруппированы вместе, как и члены в знаменателе. Например,
Например,
Выражения в показателе степени также содержат круглые скобки. Эти скобки необходимо вводить явно при использовании калькулятора.
4. Умножение и деление имеют одинаковый приоритет и должны выполняться слева направо. То же самое верно для сложения и вычитания.
Этот момент обсуждается в отличном блоге Дэвида Гинзбурга, поэтому я не буду обсуждать его в этом посте. Пожалуйста, прочитайте его пост!
5. Порядок операций является чрезмерным упрощением.
Если мы задумаемся над тем, как мы на самом деле упрощаем выражения, то поймем, что не всегда строго следуем порядку операций. Иногда мы выполняем вычисления параллельно и можем даже сначала выполнить операцию с более низким приоритетом. Например:
Это нарушение правил операций, так как мы сначала выполнили сложение. И все же мы знаем, что это нарушение безобидно; ответ по-прежнему правильный. Есть ли хороший способ сформулировать правила порядка операций, чтобы обеспечить эту гибкость?
6. Математические выражения рекурсивны.
Математические выражения рекурсивны.
Рекурсия — сложная тема, но она имеет решающее значение для понимания математических выражений. Наша нотация вынуждает нас записывать математические выражения в линейном порядке, но истинная структура лучше отражается деревом. Например, вот древовидная структура для .
Дерево выражений для 1 + 2 − 3 × 4.
Важно, чтобы учащиеся научились видеть эту рекурсивную структуру. Структуру можно показать и другими способами, например, обведя кружком 1+2 и 3×4.
7. Последняя операция является самой важной.
В начальной алгебре каждое выражение представляет собой либо одно число, либо сумму, либо разность, либо произведение, либо частное, либо степень. Тип выражения определяется последней выполняемой операцией. Эта операция находится в корневом узле дерева выражений.
Мы используем последнюю операцию, когда решаем линейное уравнение. Чтобы решить уравнение
, мы сначала вычтем 3 из обеих частей, потому что мы должны отменить последнюю операцию, которая заключалась в добавлении 3.
Последняя операция является ключом к применению правил для производных в исчислении. Если последней операцией является сложение, мы используем правило сумм, а если последней операцией является умножение, то используем правило произведения.
Нравится:
Нравится Загрузка…
Неявное умножение? – The Math Doctors
Я хочу завершить эту серию темой, которая постоянно возникает как в классах, так и в социальных сетях: как вы оцениваете выражение типа \(a\div bc\) или \(8\div 4( 3-1)\), где умножение указано без специального символа? Есть несколько причин, по которым можно интерпретировать это иначе, чем правило, которое мы обсуждали, согласно которому умножение и деление выполняются слева направо. Сначала мы рассмотрим это с точки зрения студентов и преподавателей, а затем (в следующий раз) исследуем некоторые исторические вопросы, чтобы завершить серию.
Два способа оценки ax÷by
Давайте сначала рассмотрим один из предыдущих вопросов, которые у нас были по этой проблеме, в 1999 году, чтобы подготовить почву:
Порядок действий Проблема была представлена так: а = 1,56 б = 1,2 х = 7,2 у = 0,2 топор / по = ? Вот два способа, которыми я это решил: 1) Сначала я переписал задачу как [1.56(7.2)/1.2](0.2). Во-вторых, а умножается на х. Продукт был 11,232. Затем, поскольку скобок не было, я следовал порядку операций и разделил 11,232 на b, что равнялось 1,2. Частное было 9.36. Затем я умножил 9,36 на y, что составило 0,2. Окончательный ответ был 1,872. 2) С другой стороны, первое, что я сделал, это умножил а на х. Продукт, который был 11,232, пока отложили. Затем b умножили на y, что дало произведение 0,24. Теперь проблема была решена путем деления 11,232 (или ax) на 0,24 (или на), чтобы получить окончательный ответ 46,8. Скажите, пожалуйста, какой ответ правильный и почему?
(Обратите внимание, что в то время единственным способом ввести деление в нашей электронной почте было использование косой черты \(a/b\), которая, как я обычно полагаю, представляет собой выражение, на самом деле написанное как \(a\div b\) , Я буду время от времени вставлять обелус, ÷, где мы сделали грубые попытки смоделировать его.)
Первый способ буквально следует за PEMDAS, как обычно учат и как я представил его здесь, вычисляя слева направо как \(a\cdot x\div b\cdot y = ((a\cdot x)\div б)\cdot у\).
Второй видит это как \(ax\div by = (ax)\div (by)\). Это не объясняется тем, что следует какому-то выученному правилу, а просто делает то, что выглядит правильно, либо потому, что деление читается, как если бы это была дробная черта, либо просто потому, что « на » выглядит так, как будто оно принадлежит друг другу как единое целое. Мы увидим несколько причин, по которым учащиеся сделали это.
Хотя я был с Спросите доктора Математики меньше года, это был уже знакомый вопрос, на который я хотел подробно ответить ради архива:
Вы не одиноки, задаваясь этим вопросом. У нас было несколько других вопросов о выражениях, подобных вашему, от сбитых с толку учителей и учеников, которые обнаружили, что разные книги или учителя дают разные ответы, и даже калькуляторы расходятся во мнениях.
Обратите внимание, что не только ученики делают то, что им кажется правильным, но и некоторые учебники и калькуляторы следуют второму методу.
Новое правило или то, что кажется правильным?
Я подробно остановился на двух методах, приняв версию PEMDAS за правильную (хотя у меня есть некоторые сомнения по этому поводу):
Как написано, ваше выражение
топор / по
должно оцениваться слева направо : a умножить на x, разделить на b, умножить на y. Умножение не выполняется перед делением, но оба выполняются в том порядке, в котором они появляются. Ваше первое решение верное.
Некоторые тексты составляют правило , как во втором решении, что умножение без символа («подразумеваемое умножение») должно выполняться перед любыми другими операциями в выражении [кроме возведения в степень], включая «явное умножение» с использованием символа. Следуя этому правилу, вы должны умножить a на x, затем умножить b и y, а затем разделить одно на другое. В некоторых (вероятно, в большинстве) текстах такое правило не упоминается, но некоторые из них могут использовать его, не говоря об этом, что гораздо хуже .
Умножение не выполняется перед делением, но оба выполняются в том порядке, в котором они появляются. Ваше первое решение верное.
Некоторые тексты составляют правило , как во втором решении, что умножение без символа («подразумеваемое умножение») должно выполняться перед любыми другими операциями в выражении [кроме возведения в степень], включая «явное умножение» с использованием символа. Следуя этому правилу, вы должны умножить a на x, затем умножить b и y, а затем разделить одно на другое. В некоторых (вероятно, в большинстве) текстах такое правило не упоминается, но некоторые из них могут использовать его, не говоря об этом, что гораздо хуже . Кажется, я придумал термин « подразумевающий или неявный умножение », когда я ответил на свой первый вопрос по этой теме за несколько месяцев до этого, чтобы сослаться на умножение, обозначенное простым помещением двух чисел, переменных или выражений в скобках друг рядом с другом — « сопоставление », как это называют другие — например \( ab\) или \( 2b\) или \( a(b+c)\), в отличие от явного написания \( a\times b\) или \( a\cdot b\).
Мы видели несколько вопросов от студентов, чьи учебники учили только обычному PEMDAS, но оценивали второй способ в примерах или решениях без комментариев. Возможно, это произошло из-за того, что ответы в конце были написаны кем-то другим, а не автором, но это непростительное несоответствие.
Зачем автору вводить это дополнительное правило? В разное время у меня были разные мнения о том, является ли это правило хорошей идеей, но я всегда признавал, что это не то, чему обычно учат:
Я не знаю общего правила среди математиков, согласно которому умножение следует выполнять до явное умножение. Насколько я понимаю, все умножения помещаются в одно и то же место в порядке операций. Однако это не является необоснованным правилом , так как кажется, что подразумеваемое умножение более тесно связывает операнды вместе, хотя бы визуально ; но идея Порядка Операций (или приоритета, как это называется в компьютерном мире) должна гарантировать, что все будут одинаково интерпретировать двусмысленное выражение — так что , если некоторые тексты изменят правила, или если люди делай то, что кажется естественным, цель потеряна .
Правило, которое не является правилом, бесполезно, каким бы разумным оно ни было. Да, «новое правило» — это естественный способ чтения \(ax\div by\), потому что \(by\) выглядит как единое целое; но пока этому не научат все, мы не можем этого делать и ожидать, что нас поймут все читатели.
В частности, многие студенты предполагают, что оно представляет собой горизонтальную версию \(\displaystyle\frac{ax}{by}\):
Проблема здесь в том, что выражение выглядит так, как будто оно должно быть
топор
----
по
В часто задаваемых вопросах доктора математики о написании математики в электронной почте одна из наших рекомендаций состоит в том, чтобы использовать круглые скобки везде, где это возможно, чтобы избежать двусмысленности , даже там, где правила должны прояснять это, потому что в некоторых ситуациях их можно легко забыть. .
Поэтому в электронной почте мы бы написали это так:
ax/(by) или (ax/b)*y
в зависимости от того, что задумано.
Используя круглые скобки, мы можем избежать написания того, что люди, которых учили другим правилам или которые игнорируют правила, которым их учили, могли бы воспринять иначе, чем мы предполагали.
Проблемы с калькулятором
В моем исследовании для другого «пациента» доктора математики я обнаружил, что некоторые калькуляторы экспериментировали с этим правилом. Калькуляторы имеют несколько иные потребности, чем математики, поскольку они должны вводить данные линейно, один символ за другим, поэтому они вынуждены принимать решение об этом. На веб-сайте TI я узнал, что они преднамеренно добавили эту «функция» в TI 82, а затем убрали ее из TI 83, вероятно, потому, что решили, что это не стандартное правило и оно будет путать людей.
Связь там давно вышла из строя; но когда в 2008 году возник конкретный вопрос о калькуляторе, я процитировал слова TI из их базы знаний:
Подразумеваемое умножение и калькуляторы TI. ... Решение 11773. Подразумеваемое умножение по сравнению с явным умножением в графических калькуляторах TI.Имеют ли подразумеваемое умножение и явное умножение одинаковый приоритет в графических калькуляторах TI? Неявное умножение имеет более высокий приоритет, чем явное умножение , чтобы пользователи могли вводить выражения таким же образом, как они были бы написаны. Например, TI-80, TI-81, TI-82 и TI-85 оценивают 1/2X как 1/(2*X), в то время как другие продукты могут оценивать то же выражение как 1/2*X слева направо. Правильно. Без этой функции было бы необходимо группировать 2X в круглых скобках, что обычно не делается при написании выражения на бумаге. Этот порядок приоритета был изменен для семейства TI-83, семейства TI-84 Plus, семейства TI-89, TI-92 Plus, Voyage™ 200 и портативного устройства TI-Nspire™ в режиме TI-84 Plus. Неявное и явное умножение имеют одинаковый приоритет.
Это ясно показывает, что разработчики калькуляторов должны устанавливать свои собственные правила, которые не обязательно должны совпадать с правилами письма на бумаге; но педагоги, кажется, убедили их оставить все как можно более одинаковым ради учеников.
В заключение (назад к ответу 1999 года):
Итак, отвечая на ваш вопрос, я думаю оба ответа можно считать правильными - значит, конечно, что сам вопрос неверен . Я предпочитаю стандартный способ (ваш первый ответ) в общении со студентами, , если их собственный текст не содержит правила «сначала неявное умножение» ; но на практике, если бы я встретил это выражение, я, вероятно, сначала проверил бы, откуда оно взялось, чтобы увидеть, могу ли я сказать, что имелось в виду. Главный урок, который нужно усвоить, заключается не в том, какому правилу следовать, а в том, как избежать двусмысленности в том, что вы пишете сами. Не доставляй другим людям таких хлопот.
Впоследствии у нас было еще много вопросов по этому поводу; Я просто процитирую несколько уникальных фрагментов из некоторых из этих ответов.
Старомодная математика?
Вот типичный пример школьного конфликта, начиная с 2000 года:
Порядок Операции Спор Задача гласит: N ÷ ml, где n=12, m=6 и l=3.Я считаю, что правильный ответ должен быть 0,6666, так как 12 разделить на 18 равно этому. Муж со мной согласен. Мой сын пришел домой очень расстроенный из школы, с запиской от учителя, что ответ был неправильным. Она указала, что я должен был разделить 6 (m) на 12 (n), прежде чем разделить 3 (l) на уравнение. Ее ответ был 6. Мой сын очень расстроен мной; его учитель сказал ему, что я занимаюсь "старомодной математикой". Мне нужно вернуться в школу?
Проблема в \(N\div ml\), и родители сначала выполняют умножение. Я частично ответил:
Я могу сообщить вам хорошие и плохие новости. Во-первых, плохие новости: в соответствии с обычным порядком выполнения правил, которые сейчас изучаются, ваш ответ неверен. ...
Я объяснил стандартные правила и добавил:
НО... Вы не одиноки в своем мнении. Эта часть правила — совместное выполнение умножения и деления — вероятно, является последним правилом, которое стабилизировалось; Я знаю, что в 1920-х, по крайней мере, договоренности не было.Кажется, соглашение сложилось, но сейчас оно рушится, как я слышал от многих студентов, чьи тексты отвечают на подобные вопросы так же, как и вы. Похоже, что они добавляют неустановленное правило, которое кажется вполне разумным в данном контексте , что подразумеваемое умножение (обозначаемое простым помещением двух переменных или выражений вместе, как в «ml») должно быть выполнено первым. Конечно, выглядит как , как будто это должно означать это. Проблема в том, что, хотя я слышал, что это правило равно часто следовал за , я почти никогда не слышал, чтобы обучал , поэтому эти тексты не следуют их собственным установленным правилам.
В следующий раз я расскажу больше об истории.
Так как этот тип выражения настолько двусмыслен, люди расходятся во мнениях по поводу правил, а правила легко упустить из виду, я считаю, что ни ваш ответ, ни ответ учителя неверны: вопрос неверен . Ни один ответственный математик не стал бы писать такое выражение; мы бы просто сказали
н
---
м л
так что не было бы вопроса о его значении. В конце концов, цель правил — позволить нам ясно общаться, а не помогать нам обманывать учеников и устраивать ссоры между семьями.
Так что на самом деле вы можете быть «старомодным»; или вы можете быть на переднем крае. В любом случае, боюсь, вам просто нужно узнать, как они это делают в классе, и следовать за ними. Не должно быть больше таких проблем, о которых нужно беспокоиться.
В конце концов, цель правил — позволить нам ясно общаться, а не помогать нам обманывать учеников и устраивать ссоры между семьями.
Так что на самом деле вы можете быть «старомодным»; или вы можете быть на переднем крае. В любом случае, боюсь, вам просто нужно узнать, как они это делают в классе, и следовать за ними. Не должно быть больше таких проблем, о которых нужно беспокоиться. В последнее время драки, как правило, происходят в социальных сетях!
Неправильное использование свойства дистрибутива
Я закончу последним архивным обсуждением. Этот вопрос от 2017 года:
Еще больше о порядке операций Мне любопытно узнать, какой ответ на это: 8/4(3 - 1) Строго следуя PEMDAS, ответ равен 4: 8/4(2) 2*2 4 Однако, если вы будете следовать дистрибутивному свойству, вы получите 1: 8/((4*3) - (4*1)) 8/(12 - 4) 8/8 1 Какой из них будет правильным и почему? Оба варианта действительны, поэтому я не уверен, какой ответ будет правильным.Это должно быть правильно или неправильно, а не два разных ответа.
Я ответил набором своих стандартных ответов на такого рода вопросы; даже мой первый заархивированный ответ на эту тему в 1999 году был в значительной степени стандартным ответом, который я давал другим раньше. Здесь я просто рассмотрю несколько сделанных мною замечаний, которые не были полностью освещены выше.
Сначала я подытожил происходящее:
Проблема не в конфликте между PEMDAS и дистрибутивом; дело в том, что строгая интерпретация PEMDAS противоречит естественному впечатлению человека значения выражения, так что вы неосознанно применяете альтернативную интерпретацию, когда думаете, что просто применяете распределительное свойство.
Если вы вспомните более ранние заявления о том, что PEMDAS (а) находится в гармонии со свойствами операций и (б) соответствует визуальному впечатлению от наших обозначений, то некоторые тревожные звоночки уже должны звучать!
Когда вы распределяли, вы ПРЕДПОЛАГАЛИ, что это 4, а не 8/4 умножает (3 - 1).При этом вы нарушали правила и всего делал то, что считал нужным . Если бы вы следовали правилам И распространяли, вы бы получили это: (((8/4)*3) - ((8/4)*1)) ((2*3) - (2*1)) 6 - 2 4
На самом деле не свойство распределения привело к «неправильному» результату, а тот факт, что при распределении 4 рассматривалось как множитель.
Те, кто говорят, что вы должны распространять сначала , ставят телегу впереди лошади: вы не можете применять трюки для оценки выражения, прежде чем вы сначала не узнаете, что оно ОЗНАЧАЕТ, но они думают, что свойство распределения влияет на значение. (На самом деле свойство дистрибутивности здесь — пустая трата времени, потому что оно заставляет вас делать два умножения там, где нужно только одно!) Смысл определяется порядком действий. Умножение должно производиться до или после деления? 92\div 4b + c\):На самом деле есть несколько разных причин, которые люди приводят (это очень популярный вопрос), некоторые из которых лучше, чем другие.Как утверждает ваш друг, правила, как обычно учат, говорят нам выполнять все умножения и деления слева направо (в пределах любого их кластера) и не делать исключений, из-за которых 4b будет оцениваться первым. Многие из нас здесь согласятся с этим и покончат с этим. Некоторые люди сначала оценили бы 4b из-за неправильного понимания PEMDAS, думая, что это означает, что умножение должно быть выполнено до деления . Я думаю, вы знаете, что они ошибаются. Еще одна неверная причина, примененная к выражению несколько иного типа, — это неправильное понимание скобок : правило, согласно которому скобки «предшествуют» всему остальному, приводит их к мысли, что в таком выражении, как 12/4(4-1), умножение 4 (4-1) должно быть сделано первым. Но правило о скобках на самом деле говорит только о том, что то, что находится ВНУТРИ скобок, должно быть оценено в первую очередь; результат обрабатывается как любое другое число. (Я иногда называю это " липкие скобки "вид.
) Другая причина, связанная с этим вторым типом выражений, заключается в том, что дистрибутивное свойство вынуждает вас сначала выполнять умножение, потому что сначала вычисляется 4(4-1) = 4*4-4*1 = 12, а затем разделять; но это вызывает вопрос, потому что единственная причина, по которой они взяли 4, а не 12/4, в качестве множителя слева, заключается в том, что им это показалось именно так. И, конечно же, свойство дистрибутивности — это всего лишь способ, которым вы можете, если хотите, переписать выражение так, чтобы оно давало то же самое значение; это вне вопроса о том, что само по себе ЗНАЧИТ это выражение. В конце концов, большинство людей, вероятно, делают это всего лишь , потому что это кажется правильным : 4b выглядит ближе друг к другу, поэтому мы, естественно, хотим сделать это в первую очередь. Но они не могут указать ни на одно правило, оправдывающее это; и поскольку математика — это доказательство и то, что вы ЗНАЕТЕ правильно, а не только то, что кажется правильным, это нехорошо.

Пример «липких скобок» см. в разделе
Связана ли цифра 2 с числами в скобках?Пример отображения знака деления в виде дробной черты (и долгое обсуждение того, как не поддаваться влиянию внешнего вида) см. в разделе 9.0003
Порядок операций и дробейНазад к ответу 2017 года …
Избегание — лучшая политика
В книгах и рукописной математике за пределами элементарного уровня мы почти никогда не используем символ горизонтального деления, а вместо этого используем дроби, которые не оставляет двусмысленности. В результате математическому сообществу никогда не приходилось делать выбор в этой ситуации! По сути, он остался неопределенным , и именно авторы учебников придумали явные «правила» для описания того, что на самом деле является просто языком, который развивался органически, основано не на тщательно сформулированных правилах, а на молчаливом соглашении . Так что «правильный» способ прочтения такого выражения зависит от того, какие правила действуют в конкретном сообществе (математический класс, журнал и т.д.) — и что имел в виду автор.
Я закрыл призывом к миру:
В результате в таких задачах ошибаются в первую очередь не те, кто дает "неправильные" ответы, а те, кто ставит задачу в первую очередь ( или передать дальше). Любой, кто действительно хочет правильно заниматься математикой, захочет четко об этом сообщить и будет избегать двусмысленности или неопределенности. Они должны либо полностью заключаться в круглые скобки, либо использовать горизонтальную дробную черту, которая проясняет порядок: 6 6 -------- или ---(2 + 1) 2(2 + 1) 2Споры о подобных вещах в соцсетях — пустая трата времени. Но размышление о наших соглашениях может быть очень поучительным. В следующий раз я завершу все рассмотрением истории и некоторыми вескими причинами считать, что «новое правило» на самом деле правильное.
Правило PEMDAS: понимание порядка действий
Каждый, кто когда-либо посещал уроки математики в США, уже слышал аббревиатуру «PEMDAS».
Но что это означает? Здесь мы подробно объясним значение PEMDAS и его использование , прежде чем дать вам несколько примеров задач PEMDAS, чтобы вы могли попрактиковаться в том, что узнали.
PEMDAS Значение: что это значит?
PEMDAS — это аббревиатура, призванная помочь вам запомнить порядок операций, используемых для решения математических задач. Обычно произносится как "пем-дасс", "пем-доз" или "пем-досс".
Вот что означает каждая буква в PEMDAS:
- P арентезы
- E компоненты
- M умножение и D ivision
- Дополнение A и удаление S
Порядок букв показывает порядок, в котором вы должны решать различные части математической задачи , причем выражения в скобках идут первыми, а сложение и вычитание - последними.
Многие ученики используют этот мнемонический прием, чтобы запомнить каждую букву: Пожалуйста, извините, моя дорогая тетя Салли .
В Соединенном Королевстве и других странах 9Студенты 0021 обычно изучают PEMDAS как BODMAS . Значение BODMAS такое же, как и значение PEMDAS, просто используется пара разных слов. В этой аббревиатуре буква B означает «скобки» (то, что мы в США называем круглыми скобками), а буква O — «порядки» (или показатели степени).
Теперь, как именно вы используете правило PEMDAS? Давайте взглянем.
Как вы используете PEMDAS?
PEMDAS — это аббревиатура, используемая для напоминания людям о порядке операций.
Это означает, что вы не просто решаете математические задачи слева направо; скорее вы решаете их в заранее определенном порядке, который дается вам через аббревиатуру PEMDAS . Другими словами, вы начнете с упрощения любых выражений в круглых скобках, прежде чем упростить экспоненты и перейдете к умножению и т. д.
Но это еще не все. Вот что именно означает PEMDAS для решения математических задач:
- Круглые скобки: Все, что в скобках, должно быть сначала упрощено
- Экспоненты: Все, что имеет экспоненту (или квадратный корень), должно быть упрощено после все в скобках упрощено
- Умножение и деление: Разобравшись со скобками и показателями степени, решите любое умножение и деление слева направо
- Сложение и вычитание: После того, как вы разобрались со скобками, показателями степени, умножением и делением, выполните любое сложение и вычитание слева направо
Если какой-либо из этих элементов отсутствует (например, у вас есть математическая задача без показателей степени), вы можете просто пропустить этот шаг и перейти к следующему.
Теперь давайте рассмотрим пример задачи, чтобы помочь вам лучше понять правило PEMDAS:
4 (5 − 3)² − 10 ÷ 5 + 8
У вас может возникнуть соблазн решить эту математическую задачу слева направо, но это приведет к неправильному ответу! Итак, вместо этого давайте воспользуемся PEMDAS, чтобы помочь нам подойти к этому правильно .
Мы знаем, что скобки должны быть обработаны в первую очередь. В этой задаче один набор скобок: (5 − 3). Упрощение дает нам 2 , так что теперь наше уравнение выглядит так:
4 (2)² − 10 ÷ 5 + 8
Следующая часть PEMDAS — это показатели степени (и квадратные корни). В этой задаче есть один показатель степени, который возводит в квадрат число 2 (то есть то, что мы нашли, упростив выражение в скобках).
Это дает нам 2 × 2 = 4. Теперь наше уравнение выглядит так:
4 (4) − 10 ÷ 5 + 8 ИЛИ 4 × 4 − 10 ÷ 5 + 8
Далее следует умножение и деление слева направо . Наша задача содержит и умножение, и деление, которые мы будем решать слева направо (то есть сначала 4 × 4, а затем 10 ÷ 5). Это упрощает наше уравнение следующим образом:
Наша задача содержит и умножение, и деление, которые мы будем решать слева направо (то есть сначала 4 × 4, а затем 10 ÷ 5). Это упрощает наше уравнение следующим образом:
16 − 2 + 8
Наконец, все, что нам нужно сделать сейчас, это решить оставшееся сложение и вычитание слева направо :
16 − 2 + 8
14 + 8
= 22
Окончательный ответ: 22. Не верите? Вставьте все уравнение в свой калькулятор (написанное точно так, как оно указано выше), и вы получите тот же результат!
David Goehring/Flickr
Примеры математических задач с использованием PEMDAS + ответы
Проверьте, сможете ли вы правильно решить следующие четыре задачи, используя правило PEMDAS. Мы пройдемся по ответам после.
Примеры задач PEMDAS
- 11 − 8 + 5 × 6
- 8 ÷ 2 (2 + 2)
- 7 × 4 − 10 (5 − 3) ÷ 2²
- √25 (4 + 2)² − 18 ÷ 3 (3 − 1) + 2³
Ответы
- 33
- 16
- 23
- 176
Объяснение ответов
Здесь мы рассмотрим каждую задачу выше и то, как вы можете использовать PEMDAS, чтобы получить правильный ответ.
#1 Ответ Объяснение
11 − 8 + 5 × 6
Эта математическая задача является довольно простым примером PEMDAS, в котором сложение, вычитание и умножение используются только , поэтому здесь не нужно беспокоиться о скобках или показателях степени.
Мы знаем, что умножение предшествует сложению и вычитанию , поэтому вам нужно начать с умножения 5 на 6, чтобы получить 30:
11 − 8 + 30
Теперь мы можем просто работать слева направо на сложение и вычитание:
11 − 8 + 30
3 + 30
= 33
Это приводит нас к правильному ответу , который равен 33 .
#2 Ответ Объяснение
8 ÷ 2 (2 + 2)
Если эта математическая задача кажется вам знакомой, это, вероятно, потому, что стала вирусной в августе 2019 года из-за неоднозначной настройки . Многие люди спорили о том, какой правильный ответ: 1 или 16, но, как мы все знаем, в математике (почти всегда!) только одно действительно 9. 0108 правильный ответ.
0108 правильный ответ.
Так что это: 1 или 16?
Давайте посмотрим, как PEMDAS может дать нам правильный ответ. В этой задаче есть скобки, деление и умножение. Итак, мы начнем с упрощения выражения в скобках согласно PEMDAS:
8 ÷ 2 (4)
В то время как большинство людей в Интернете соглашались до этого момента, многие не соглашались с тем, что делать дальше: умножить ли 2 на 4 или разделить 8 на 2?
PEMDAS может ответить на этот вопрос: когда дело доходит до умножения и деления, вы всегда работаете слева направо. Это означает, что вы действительно разделите 8 на 2, прежде чем умножать на 4.
Это может помочь взглянуть на проблему таким образом, так как люди часто путаются в скобках (помните, что все, что рядом со скобкой, равно , умноженному на то, что в скобках):
8 ÷ 2 × 4
Теперь решаем уравнение слева направо:
8 ÷ 2 × 4
4 × 4
= 16
Правильный ответ: 16. Любой, кто утверждает, что 1, определенно неправильно — и явно неправильно использует PEMDAS!
Любой, кто утверждает, что 1, определенно неправильно — и явно неправильно использует PEMDAS!
Если бы эти примеры задач PEMDAS были такими простыми...
#3 Ответ Объяснение
7 × 4 − 10 (5 − 3) ÷ 2²
9000 bit хитрее сейчас.В этой математической задаче есть скобки, показатель степени, умножение, деление, и вычитание. Но не перегружайтесь — давайте работать с уравнением шаг за шагом.
Во-первых, согласно правилу PEMDAS, мы должны упростить то, что в скобках :
7 × 4 − 10 (2) ÷ 2²
Легко, правда? Далее, давайте упростим показатель степени :
7 × 4 − 10 (2) ÷ 4
Теперь осталось только умножение, деление и вычитание. Помните, что с умножением и делением мы просто работаем слева направо:
7 × 4 − 10 (2) ÷ 4
28 − 10 (2) ÷ 4
28 − 20 ÷ 4
28 − 5
умножали и делили, вам просто нужно сделать вычитание , чтобы решить это:
28 − 5
= 23
Это дает нам правильный ответ 23 .
#4 Ответ Объяснение
√25 (4 + 2)² − 18 ÷ 3 (3 − 1) + 2³
Эта задача может показаться пугающей, но я обещаю, что это не так! Пока вы будете подходить к ней шаг за шагом, используя правило PEMDAS , вы сможете решить ее в кратчайшие сроки.
Сразу видно, что эта задача содержит все компонентов PEMDAS : круглые скобки (два набора), показатели степени (два и квадратный корень), умножение, деление, сложение и вычитание. Но на самом деле это ничем не отличается от любой другой математической задачи, которую мы решали.
Во-первых, мы должны упростить то, что находится в двух скобках:
√25 (6)² − 18 ÷ 3 (2) + 2³
Затем мы должны упростить все показатели степени — сюда входят и квадратные корни. :
5 (36) − 18 ÷ 3 (2) + 8
Теперь мы должны выполнить умножение и деление слева направо:
5 (36) − 18 ÷ 3 (2) + 8
180 − 18 ÷ 3 (2) + 8
180 − 6 (2) + 8
180 − 12 + 8
Наконец, решаем оставшееся сложение и вычитание слева направо:
180 - 12 + 8
168 + 8
= 176
Это приводит нас к правильному ответу 176 .
Что дальше?
Еще одна математическая аббревиатура, которую вы должны знать, это SOHCATOA. В нашем экспертном руководстве вы узнаете, что означает аббревиатура SOHCAHTOAH и как вы можете использовать ее для решения задач, связанных с треугольниками.
Готовитесь к секции SAT или ACT по математике? Тогда вам определенно стоит ознакомиться с нашим исчерпывающим руководством по математике SAT/ACT, в котором вы найдете множество советов и стратегий для этого сложного раздела.
Заинтересованы в действительно больших числах? Узнайте, что такое гугол и гуголплекс, а также почему невозможно записать одно из этих чисел.
Нужна дополнительная помощь по этой теме? Проверьте Tutorbase!
Наша проверенная база данных репетиторов включает ряд опытных преподавателей, которые могут помочь вам отшлифовать эссе по английскому языку или объяснить, как производные работают для исчисления. Вы можете использовать десятки фильтров и критериев поиска, чтобы найти идеального человека для ваших нужд.
Вы можете использовать десятки фильтров и критериев поиска, чтобы найти идеального человека для ваших нужд.
У вас есть друзья, которым тоже нужна помощь в подготовке к экзамену? Поделись этой статьей!
Ханна Муниз
Об авторе
Ханна получила степень магистра японоведения в Мичиганском университете и степень бакалавра в Университете Южной Калифорнии. С 2013 по 2015 год преподавала английский язык в Японии по программе JET. Она увлечена образованием, писательством и путешествиями.
Сложение, вычитание, умножение и деление значений в элементе управления
InfoPath 2010 InfoPath 2013 Больше...Меньше
Вы можете помочь своим пользователям заполнять формы на основе вашего шаблона формы, используя формулы для вычисления значения элемента управления на основе данных, которые пользователь вводит в другие элементы управления. Вычисления могут включать сложение, вычитание, умножение и деление значений. Например, если вы разрабатываете шаблон формы, который подрядчики по электроснабжению будут использовать для подачи заявок на получение разрешений, вы можете добавить формулу в элемент управления, который автоматически вычисляет общую стоимость, которую подрядчик должен заплатить за заявку, путем умножения количества разрешений в приложение по цене каждого разрешения.
Например, если вы разрабатываете шаблон формы, который подрядчики по электроснабжению будут использовать для подачи заявок на получение разрешений, вы можете добавить формулу в элемент управления, который автоматически вычисляет общую стоимость, которую подрядчик должен заплатить за заявку, путем умножения количества разрешений в приложение по цене каждого разрешения.
В этой статье
Что такое формула?
Использование двух и более операторов в формуле
Вставка математической формулы в элемент управления
Что такое формула?
Формула — это выражение XPath, состоящее из значений, полей или групп, функций и операторов, используемых для вычисления и отображения других значений. Формулы можно использовать для решения следующих задач:
Формулы можно использовать для решения следующих задач:
Расчет математических значений на основе значений, указанных при разработке шаблона формы, или значений, которые пользователи вводят в элементы управления при заполнении форм на основе вашего шаблона формы..
Показать определенные даты и время.
Отображение значений, которые пользователи вводят в один элемент управления, в другой элемент управления.
Установите значение по умолчанию для поля или элемента управления.
org/ListItem">
Запустить правило на основе значения, рассчитанного по формуле.
Каждое выражение XPath, используемое в формуле, представляет собой комбинацию значений, функций и операторов, результатом которой является одно значение. Формула может содержать несколько выражений. Вы можете думать о формуле как о предложении, состоящем из одной или нескольких фраз, где каждая фраза представляет одно выражение в формуле.
На следующем рисунке показана связь между формулой и выражением.
Функция — это выражение, возвращающее значение на основе результатов вычисления. Значения, используемые в функциях, называются аргументами. Вы можете использовать стандартные функции XPath 1.0, включенные в InfoPath, а также некоторые функции, специфичные для InfoPath. Найдите ссылки на дополнительные сведения о функциях InfoPath в разделе См. также .
Верх страницы
Использование двух или более операторов в формуле
Если формула содержит два или более математических оператора, InfoPath выполняет расчет в соответствии с приоритетом оператора. В следующем списке показан порядок выполнения операций:
В следующем списке показан порядок выполнения операций:
Вычисления в скобках
Вычисления умножения и деления
Вычисления сложения и вычитания
Если формула содержит два оператора с одинаковым приоритетом, вычисления выполняются слева направо.
Например, представьте, что вы создаете шаблон формы заявки на получение разрешения, в котором есть текстовое поле, отображающее общую стоимость всех разрешений, представленных в заявке. Значения, требуемые этой формулой, берутся из других текстовых полей формы. Текстовое поле, отображающее общую стоимость, содержит следующую формулу:
Текстовое поле, отображающее общую стоимость, содержит следующую формулу:
txtPermit1Qty * txtPermitCost1 + txtPermit2Qty * txtPermitCost2 /txtNumberOfPermits
Эта формула включает операторы сложения (+), умножения (*) и деления (/). В соответствии с приоритетом операторов вычисления умножения и деления выполняются перед вычислением сложения. Поскольку операторы умножения и деления имеют одинаковый приоритет, вычисление умножения выполняется перед оператором деления, поскольку оператор умножения расположен слева от оператора деления. Формула рассчитывается таким образом:
Значение в txtPermit1Qty умножается на значение в txtPermitCost1 .
org/ListItem">Результат расчета на шаге 1 добавляется к результатам расчета на шаге 2.
Значение в txtPermit2Qty умножается на значение в txtPermitCost2 , а затем этот результат делится на значение в txtNumberOfPermits .
Чтобы управлять порядком вычислений, заключите вычисление, которое вы хотите выполнить первым, в круглые скобки. Вычисления в скобках выполняются перед вычислениями вне скобок. Помещайте вычисления со скобками слева от вычислений без скобок. Вычисления во вложенных скобках выполняются от внутренних к внешним скобкам.
Например, рассмотрим следующую формулу:
((txtPermit1Qty * txtPermitCost1) + (txtPermit2Qty * txtPermitCost2))/txtNumberOfPermits
В этом вычислении значение, полученное в результате умножения значений в txtPermit1Qty и txtPermitCost1 , добавляется к значению, полученному в результате умножения значений в txtPermit2Qty и txtPermitCost2 . Затем сумма этого расчета делится на значение в txtNumberOfPermits 9.0739 .
Затем сумма этого расчета делится на значение в txtNumberOfPermits 9.0739 .
Верх страницы
Вставить математическую формулу в элемент управления
Дважды щелкните элемент управления или поле, для которого вы хотите создать формулу.
Перейдите на вкладку Данные .
Щелкните Вставить формулу .
Чтобы вставить значение или математический оператор в формулу, введите значение или символ математической операции в поле Формула .

Список математических операций
Операция
Символ
Добавить
+
Вычесть
-
Умножить
*
Разделить
/
Примечание.
 Если в формуле используется оператор деления (/), убедитесь, что перед ним и после него есть пробел. Если перед оператором деления и после него нет пробела, InfoPath может интерпретировать «/» как разделитель шагов расположения XPath, а не как оператор деления.
Если в формуле используется оператор деления (/), убедитесь, что перед ним и после него есть пробел. Если перед оператором деления и после него нет пробела, InfoPath может интерпретировать «/» как разделитель шагов расположения XPath, а не как оператор деления.Совет: Математические формулы обычно используют целые или десятичные значения в качестве аргументов. Чтобы избежать пустых значений в формуле, установите флажок Считать пустые значения равными нулю в категории Расширенные в диалоговом окне Параметры формы .
Чтобы проверить правильность синтаксиса формулы, в диалоговом окне Вставить формулу щелкните Проверить формулу .
Моя формула содержит ошибки
Щелкните Показать подробности в диалоговом окне Microsoft Office InfoPath , чтобы просмотреть ошибки в формуле.
 Ниже приведены некоторые предложения по устранению этих ошибок:
Ниже приведены некоторые предложения по устранению этих ошибок:Если вы используете функцию в своей формуле, убедитесь, что вы используете правильные аргументы для функции. Некоторым функциям требуются поля или группы, в то время как другим функциям требуются указанные значения в качестве аргументов. Найдите ссылки на дополнительную информацию о функциях в См. также раздел .
Удалите формулу и введите ее заново, чтобы убедиться, что она введена правильно.
Чтобы проверить изменения, щелкните Preview на панели инструментов Standard или нажмите CTRL+SHIFT+B.

Верх страницы
Почему учителям математики пора выбросить БОДМАС
SecondaryMaths
Практически каждый учащийся средней школы в Великобритании сталкивался с аббревиатурой порядка операций, но есть проблема; не всегда получается...
- по Оуэн Элтон
Что означает БОДМАС?
Аббревиатура BODMAS означает скобки, порядок, деление, умножение, сложение, вычитание.
Иногда его называют BIDMAS (с «Индексами», используемыми вместо «Порядков»), или правилом PEMDAS в Америке (с «Скобками» и «Экспонентами»).
БОДМАС правило
Это математическое правило диктует правильный порядок операций, которым необходимо следовать, когда вы выполняете задание на математическое числовое предложение с различными операциями.
Первый шаг - сделать что-нибудь в скобках, затем порядки (например, квадратный корень или индексы). Деление и умножение находятся на одном уровне, что означает, что они имеют одинаковый приоритет и должны выполняться слева направо, а не все деление, а затем все умножение. Точно так же сложение и вычитание находятся на одном уровне и должны выполняться слева направо.
Я начал свою преподавательскую деятельность в школе Highgate. Молодой, неподготовленный и еще не лысеющий, я столкнулся с самой крутой кривой обучения в своей жизни.
Еженедельные встречи с моим начальником отдела были жизненно важны для обсуждения педагогики, и я верно следовал его инструкциям: «Никогда не сокращайте кумулятивную частоту», «Мы всегда подбрасываем монеты и получаем решку, мы никогда не подбрасываем монеты и выпадаем орлом», и самое главное , «Мы никогда, никогда не используем BODMAS».
Не использовать BODMAS было не так просто, как вы можете себе представить. Студенты приехали хорошо разбирающиеся в его применении.
Нам пришлось научить этому и . Нам пришлось убедить комнаты, полные подростков, что они должны изменить фундаментальные принципы своей арифметической системы убеждений. Это было трудно, потому что подростки ненавидят перемены и ненавидят прозелитизм взрослых.
Так с какой стати нам беспокоиться? Что убедило весь отдел в том, что нужно направить столько усилий на такое, казалось бы, тривиальное дело?
БОДМАС неправильный. Это то что.
Неправильный ответ
Его буквы обозначают Скобки, Порядок (значение сил), Деление, Умножение, Сложение, Вычитание. Таким образом, предполагается, что в этой последовательности происходит упрощение любого заданного математического выражения.
Например, чтобы оценить 3 + (3 + 3) 3 ÷ 3 – 3 x 3 , мы действуем в указанном выше порядке:
Это был бы действительно полезный алгоритм, если бы он работал в любой ситуации, но рассмотрим гораздо более простое выражение 1 – 2 + 4 . Он не содержит скобок, степеней, деления или умножения, поэтому мы будем следовать BODMAS и делать сложение с последующим вычитанием:
Он не содержит скобок, степеней, деления или умножения, поэтому мы будем следовать BODMAS и делать сложение с последующим вычитанием:
Это ошибка. Правильное значение — 3. BODMAS подвел нас. Позор BODMAS!
Математические задачи
У нас не может быть волшебной мнемоники, которая не работает все время; предположим, что он решил не работать в важный момент. Представьте, что вы пытаетесь объяснить своему ученику, что причина, по которой он потерял оценку на экзамене, заключалась в том, что то, о чем вы говорили ему, всегда работает, на самом деле не работает во всех случаях, и на самом деле один из таких случаев произошел в эта бумага GCSE.
Это не новая проблема. Я не первый, кто об этом пишет. Даже Википедия решает эту проблему и предлагает некоторые альтернативы. Студенты любят Википедию! Так почему же BODMAS все еще актуален?
В Хайгейте это было окружено таким клеймом, что некоторые стороны высмеивали меня более десяти лет после того, как мой коллега пережил обмен мнениями в классе, который проходил примерно так:
Учитель: Как нам упростить это выражение? Студент: БОДМАС, сэр. Учитель: Мы не используем здесь BODMAS. Студент: Но именно этому нас научил мистер Элтон в прошлом году, сэр.
Учитель: Мы не используем здесь BODMAS. Студент: Но именно этому нас научил мистер Элтон в прошлом году, сэр.
После этого мне несправедливо присвоили прозвище «БОДМАС», которое преследовало меня повсюду. У меня не было защиты; платный студент сделал заявление, так что это должно быть правдой. По крайней мере, один человек (он знает, кто он такой) до сих пор называет меня БОДМАСом чаще, чем использует мое настоящее имя.
Несмотря на то, что я абсолютно не виновен в том, что оскверняю умы невинных учеников, я чувствую себя обязанным загладить свою вину, поэтому я использую эту платформу. Думайте об этом как о общественной работе.
Правильный ответ
Однако нет смысла ругать BODMAS, не предлагая альтернативы. Ошибка, показанная выше, вызвана тем фактом, что сложение и вычитание не обязательно должны происходить в указанном порядке. Если у нас есть строка из этих двух операций, она называется суммой, и мы должны работать слева направо:
. Точно так же деление не более важно, чем умножение. Если у нас есть строка из этих двух операций, она называется произведением, и мы снова будем работать слева направо:
Если у нас есть строка из этих двух операций, она называется произведением, и мы снова будем работать слева направо:
Теперь у нас следующий порядок: Скобки, Порядок, Произведения, Суммы.
Это дает нам BOPS, который на целый слог короче, чем BODMAS, и имеет значительное преимущество в том, что он надежен.
Уверен, что если бы кто-то предложил БОПС до БОДМАСа, то последний был бы предан забвению. Даже сейчас еще не поздно избавиться от двусложных арифметических сокращений.
Я призываю своих коллег по всему миру запретить BIDMAS и очистить PEMDAS. Не оставляй от них следов. Пусть БОПС нанесет везде победный удар юным математикам.
Оуэн Элтон — учитель математики, сочинитель/исполнитель глупых песенок и автор математических минут. Вы можете следить за его новостями в Твиттере @owenelton.
Что такое порядок операций? - Определение, правила и примеры
При решении уравнения порядок операций представляет собой набор правил, которым необходимо следовать в определенном порядке.
Все мы хорошо знаем четыре основных математических действия: сложение, умножение, деление и вычитание. С детства мы постоянно репетируем задачи, связанные с этими четырьмя операциями. Эти операции используются, от добавления счета за вашу покупку в торговом центре до разделения пиццы на четыре равные части. Но до сих пор мы решали проблемы, связанные с каждой операцией в отдельности. Что, если у нас есть выражение, в котором все четыре операции работают вместе? Мы сначала умножаем или сначала вычитаем? Это может быть проблематично, если вы будете следовать неправильному подходу. Это может привести к неправильным ответам. Поэтому порядок действий вступил в действие.
Анализ любого математического утверждения с использованием арифметических операций, таких как деление, умножение, сложение и вычитание, в математике называется операциями. Давайте посмотрим на законы порядка операций и посмотрим, насколько хорошо мы можем их вспомнить, используя простые стратегии. В этой статье вы узнаете порядок операций, правила порядка операций, математический порядок операций и решите задачи на порядок операций.
Почему выполняется Порядок операций?
При вычислении уравнений в арифметике может потребоваться выполнение множества операций, и упрощение, в конце концов, дает разные результаты. Однако на каждую фразу может быть только один правильный ответ. Мы используем принципы, чтобы упростить любое данное математическое выражение, чтобы найти правильный ответ. Эти принципы основаны на всех основных математических операторах.
С единственной целью всегда получать правильные ответы на любое математическое уравнение, был реализован порядок операций.
Каков порядок действий?
В математике такие операторы, как сложение (+), вычитание (-), умножение (×) и деление (÷), имеют приоритет друг над другом. Мы не можем самостоятельно решить выражение, содержащее любой из двух операторов. Мы должны следовать правилам порядка операций, которые гласят, что в любом выражении, как арифметическом, так и алгебраическом, первыми будут оцениваться скобки. Заказ будет рассчитываться во вторую очередь. Умножение и деление будут оцениваться третьими и, наконец, сложение и вычитание будут упрощены.
Умножение и деление будут оцениваться третьими и, наконец, сложение и вычитание будут упрощены.
Приоритет решения любого выражения упоминается в таблице ниже:
| Приоритет | Операция |
| Первые | Бркеки (), {{{{rake), {{), {rake rakes |
| , | |
| , | |
| . | Порядки (Экспоненты, Квадратный корень, Кубический корень, Логарифмический и т. д.) |
| Третьи | Деление или умножение (Любая операция, расположенная слева от выражения, будет оцениваться первой) |
| Четвертый | Сложение или вычитание (какая бы операция ни находилась в левой части выражения, будет оцениваться первой) |
Определение порядка операций принципы приоритета, которые мы используем при решении любого математического уравнения, включающего множество операций.
 Когда между двумя операторами существует подвыражение, должен быть реализован оператор, который появляется первым в таблице, упомянутой в предыдущем разделе.
Когда между двумя операторами существует подвыражение, должен быть реализован оператор, который появляется первым в таблице, упомянутой в предыдущем разделе.Давайте теперь разберемся с порядком операций, правило за правилом, в соответствии с установленным приоритетом: операторы, применяемые к выражению. При решении любого выражения всегда двигайтесь от левой стороны к правой. Это поможет вам облегчить упрощение этого выражения. Теперь прочитайте правила, упомянутые ниже, чтобы полностью понять концепцию порядка операций:
Правило 1: Необходимо всегда проверять наличие скобок или круглых скобок в выражении. Чаще всего в математических выражениях встречаются скобки «()», «{}» и «[]». Если терм содержит все три квадратных скобки, решите уравнение следующим образом:
- Сначала решите термины внутри круглой скобки «()» или круглых скобок.
- Решите условия внутри фигурных скобок '{}' секунду.
- Наконец, решите условия в квадратных скобках «[ ]».

Кроме того, помните, что если в любой из скобок есть несколько операций, обязательно используйте порядок операций для их решения.
Правило 2: После того, как вы решите числа в скобках, найдите любые термины в следующем порядке, такие как возведенные в степень термины, корневые термины, логарифмические термины, тригонометрические термины и т. д., и решите их.
Правило 3: Осталось расставить четыре основных оператора в правильном порядке. Вы можете выполнять умножение или деление в зависимости от того, какой оператор стоит первым с левой стороны выражения.
Правило 4: Последним шагом является добавление или вычитание элементов в том же порядке слева направо.
Если вы помните эти пять правил, значит, вы усвоили порядок действий. Каким бы длинным ни было выражение, вы легко сможете решить его, не задумываясь. Если вы не уверены, что запомните эти правила, есть два простых способа их запомнить. Они известны как BODMAS и PEMDAS. В следующих разделах вы узнаете об этих двух аббревиатурах для порядка операций.
Они известны как BODMAS и PEMDAS. В следующих разделах вы узнаете об этих двух аббревиатурах для порядка операций.
Способы запоминания порядка операций – BODMAS и PEMDAS
Существует два очень важных способа запоминания порядка операций. Они сокращенно называются правилом PEMDAS и правилом BODMAS. Буквы в этих аббревиатурах определяют математические операции. Буква, которая присутствует первой, применяется первой к любому уравнению.
Давайте теперь узнаем, что означает каждая из букв в этих аббревиатурах:
BODMAS
BODMAS — наиболее распространенная аббревиатура для порядка операций. Многие из вас наверняка слышали об этом где-то в своей жизни. В развернутом виде это означает:
- B – Brackets ( ), { }, [ ]
- O – Order
- D – Division (÷)
- M – Multiplication (×)
- A – Сложение (+)
- S – Вычитание (-)
PEMDAS
PEMDAS также является аббревиатурой порядка операции. Тем не менее, его меньше слышно в нашей повседневной жизни, но он столь же эффективен, как и БОДМАС.
Тем не менее, его меньше слышно в нашей повседневной жизни, но он столь же эффективен, как и БОДМАС.
- P – Скобки (), {}, [].
- E - Экспоненты (A2) (например, здесь, A - это число с показателем 2 )
- M - Умножение (×)
- D - . )
- A – означает сложение (+)
- S – означает вычитание (-)
Это наиболее эффективный метод запоминания последовательности событий. Забавная фраза « Пожалуйста, извините, моя дорогая тетя Салли »- хороший способ запомнить PEMDAS.
Оба эти метода используются для упрощения нашего понимания порядка операций. Мы увидим пример порядка операций, чтобы прояснить эту тему.
Пример порядка операций
Давайте рассмотрим различные примеры, упомянутые ниже, чтобы понять точность правил, используемых в порядке операций.
- Для оценки арифметических операций
Выражение 1: 2 + 3 x 5
- Правильный способ: Правильный способ решить это выражение — сначала умножить 3 x 5 = 15, а затем добавить 2 к результату. 15 + 2 = 17.
- Неправильный способ: Если сначала добавить 2 + 3. Получаем 6 х 5 = 30, что неверно для решения этого выражения.
Выражение 2: 15 ÷ 3 x 2 – 6
- Правильный способ: Правильный способ решить это выражение – сначала разделить 15 и 3 = 5, потому что оно ближе к левой части выражения. Затем умножьте 5 на 2 = 10 и вычтите из этого 6, что дает 10 – 6 = 4.
- Неверный способ: Если умножить 3 х 2 = 6, то вычесть из него 6, то получим 15 ÷ 0 = не определено. Это неправильный способ решения этого выражения.
- Для оценки заказов
Выражение 1: 6 x 32
- Правильный способ: Теперь правильно решить это выражение порядка 3.
 умножьте это на 6. 9 x 6 = 54.
умножьте это на 6. 9 x 6 = 54. - Неправильно: Если умножить 6 х 3 = 18, то возведем в квадрат ответ, получим 182 = 324, что неверно.
Выражение 2: 2 x sin 30
- Правильный способ: Сначала оцените порядок sin 30 = ½. Теперь умножаем 2 на ответ. 2 x ½ = 1
- Неправильный способ: Если умножить 30 на 2 = 60 и решить порядок, то получим sin 60 = 3/2. Какой ответ неверен
- Для оценки скобок
Выражение 1: (12 + 3) x 4
Решение: Мы видим, что в этом выражении присутствуют круглые скобки; следовательно, мы сначала решим содержимое в скобках. Следовательно, 12 + 3 = 15. Теперь умножаем 15 на 4 = 60.
Примечание: Мы должны соблюдать шаблон операторов при выполнении порядка операций над любой заданной фразой.
Из вышеупомянутых правил мы узнаем, как выполнять несколько операций, если они входят в одно уравнение.
 Все правила по сольфеджио
Все правила по сольфеджио






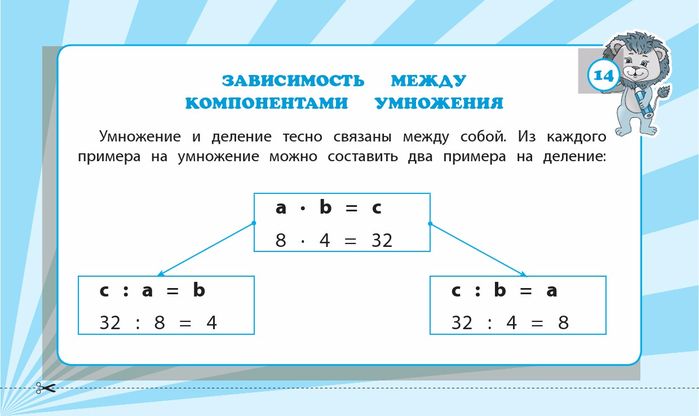

 Отношение равенства этих результатов является основанием для заключения, что найденное число удовлетворяет условиям уравнения.
Отношение равенства этих результатов является основанием для заключения, что найденное число удовлетворяет условиям уравнения. Обратная связь — 176.9.44.166 (0.006 с.)
Обратная связь — 176.9.44.166 (0.006 с.)

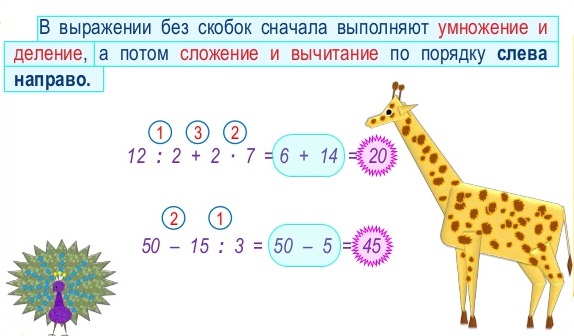 А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.
А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.
 Для предыдущего примера это выглядело бы так: .
Для предыдущего примера это выглядело бы так: . В этом случае правило, задающее порядок выполнения действий в выражениях со скобками , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.
В этом случае правило, задающее порядок выполнения действий в выражениях со скобками , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание. На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2
.
На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2
.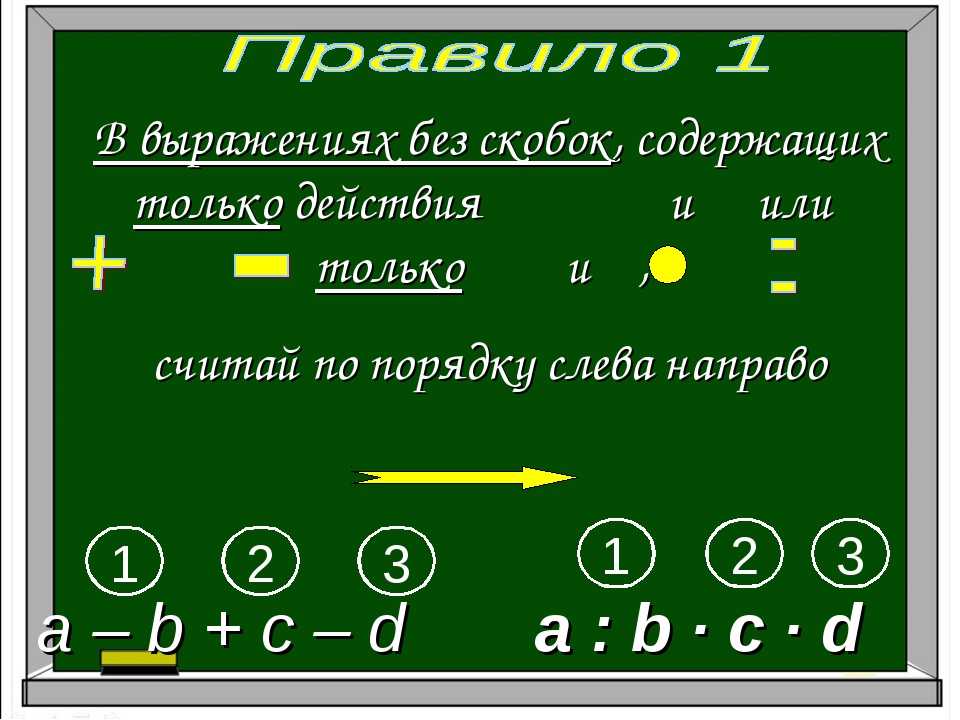
 Это происходит потому, что во втором и третьем примере есть скобки.
Это происходит потому, что во втором и третьем примере есть скобки. Тренажер
Тренажер Для этого находим свободные знаки «+» и «–» (свободные — значит не в скобках, на рисунке показаны стрелочками).
Для этого находим свободные знаки «+» и «–» (свободные — значит не в скобках, на рисунке показаны стрелочками).
 Учащиеся самостоятельно решают подобранные учителем примеры и объясняют, в каком порядке выполняли; действия в каждом примере. Затем формулируют сами или читают по учебнику вывод: если в выражении без скобок указаны только действия сложения и вычитания (или только действия умножения и деления), то их выполняют в том порядке, в каком они записаны (т.е. слева направо).
Учащиеся самостоятельно решают подобранные учителем примеры и объясняют, в каком порядке выполняли; действия в каждом примере. Затем формулируют сами или читают по учебнику вывод: если в выражении без скобок указаны только действия сложения и вычитания (или только действия умножения и деления), то их выполняют в том порядке, в каком они записаны (т.е. слева направо). Но при первом знакомстве со скобками важно нацелить учащихся на то, что сначала выполняется действие в скобках.
Но при первом знакомстве со скобками важно нацелить учащихся на то, что сначала выполняется действие в скобках. Поскольку правила порядка действий приняты по договоренности, учитель сообщает их детям или же учащиеся знакомятся с ними по учебнику. Чтобы учащиеся усвоили введенные правила, наряду с тренировочными упражнениями включают решение примеров с пояснением порядка выполнения их действий. Эффективны также упражнения в объяснении ошибок на порядок выполнения действий. Например, из заданных пар примеров предлагается выписать только те, где вычисления выполнены по правилам порядка действий:
Поскольку правила порядка действий приняты по договоренности, учитель сообщает их детям или же учащиеся знакомятся с ними по учебнику. Чтобы учащиеся усвоили введенные правила, наряду с тренировочными упражнениями включают решение примеров с пояснением порядка выполнения их действий. Эффективны также упражнения в объяснении ошибок на порядок выполнения действий. Например, из заданных пар примеров предлагается выписать только те, где вычисления выполнены по правилам порядка действий: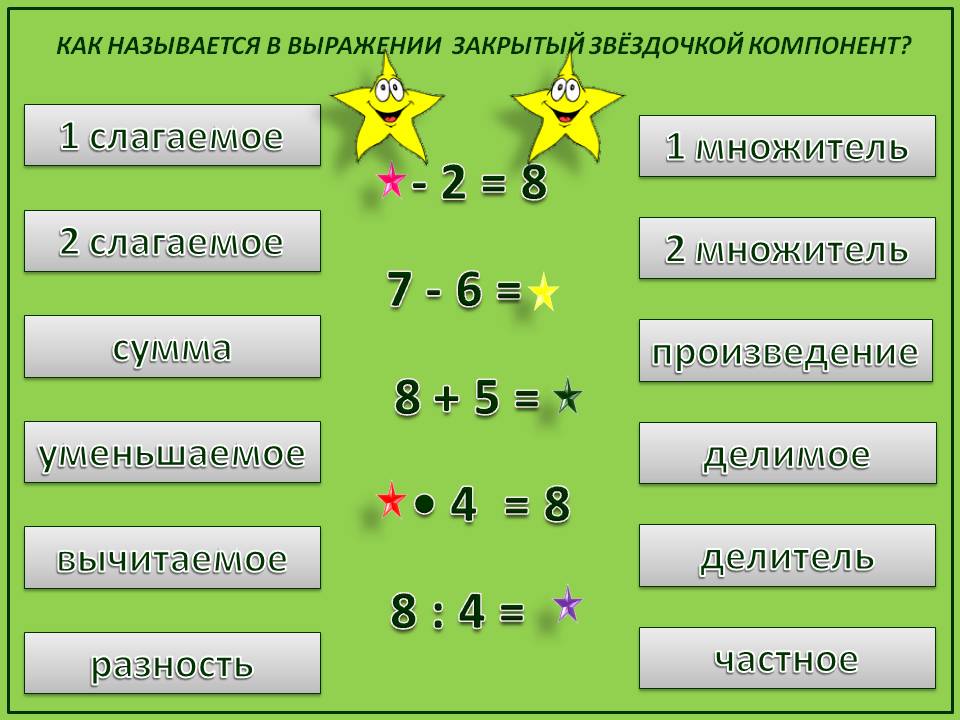 Расставьте скобки так, чтобы равенства были верными:
Расставьте скобки так, чтобы равенства были верными: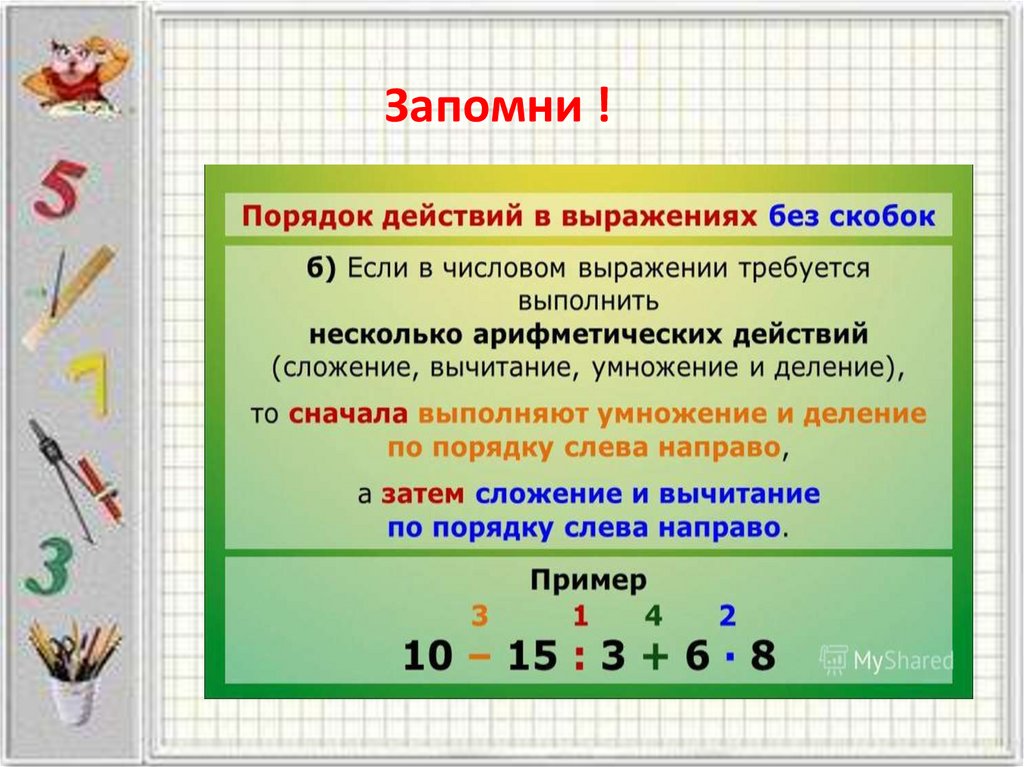
 Вы должны обязательно потренироваться в применении изученных правил, а если понадобиться, то найти и исправить ошибки в установлении порядка действий в числовых выражениях. Помните, пожалуйста, что порядок важен в любом деле, но в математике он имеет особое значение!
Вы должны обязательно потренироваться в применении изученных правил, а если понадобиться, то найти и исправить ошибки в установлении порядка действий в числовых выражениях. Помните, пожалуйста, что порядок важен в любом деле, но в математике он имеет особое значение! Аристотель, Диоген, Кант, Гегель, Гильберт… Все они так или иначе рассматривали апории Зенона. Шок оказался настолько сильным, что «… дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось… к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса… » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.
Аристотель, Диоген, Кант, Гегель, Гильберт… Все они так или иначе рассматривали апории Зенона. Шок оказался настолько сильным, что «… дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось… к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса… » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.
С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху. Теперь Ахиллес на восемьсот шагов опережает черепаху.
Теперь Ахиллес на восемьсот шагов опережает черепаху.  Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования. Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи.
Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи. Вот здесь начнется самое интересное.
Вот здесь начнется самое интересное. Как видите, один и тот же набор элементов одновременно является и множеством, и мультимножеством. Как правильно? А вот здесь математик-шаман-шуллер достает из рукава козырный туз и начинает нам рассказывать либо о множестве, либо о мультимножестве. В любом случае он убедит нас в своей правоте.
Как видите, один и тот же набор элементов одновременно является и множеством, и мультимножеством. Как правильно? А вот здесь математик-шаман-шуллер достает из рукава козырный туз и начинает нам рассказывать либо о множестве, либо о мультимножестве. В любом случае он убедит нас в своей правоте. Её не существует. Нет в математике формулы, по которой можно найти сумму цифр любого числа. Ведь цифры — это графические символы, при помощи которых мы записываем числа и на языке математики задача звучит так: «Найти сумму графических символов, изображающих любое число». Математики эту задачу решить не могут, а вот шаманы — элементарно.
Её не существует. Нет в математике формулы, по которой можно найти сумму цифр любого числа. Ведь цифры — это графические символы, при помощи которых мы записываем числа и на языке математики задача звучит так: «Найти сумму графических символов, изображающих любое число». Математики эту задачу решить не могут, а вот шаманы — элементарно.
 Это ещё один аргумент в пользу того, что . Вопрос к математикам: как в математике обозначается то, что не является числом? Что, для математиков ничего, кроме чисел, не существует? Для шаманов я могу такое допустить, но для ученых — нет. Реальность состоит не только из чисел.
Это ещё один аргумент в пользу того, что . Вопрос к математикам: как в математике обозначается то, что не является числом? Что, для математиков ничего, кроме чисел, не существует? Для шаманов я могу такое допустить, но для ученых — нет. Реальность состоит не только из чисел. Какой еще туалет?
Какой еще туалет?