Порядок действий в математике. Действия первой, второй ступеней в выражениях. Что первое умножение или деление в 2022 году

Действия первой и второй ступени с натуральными числами. Порядок действий

Мы уже рассмотрели арифметические действия сложения и вычитания. Эти действия называются действиями первой ступени. Умножение и деление принято считать действиями второй ступени. Если в математическом выражении есть несколько действий, включая действия и первой, и второй ступени, есть разные числа, соответственно результат зависит от порядка совершенных действий. Поэтому при решении примеров следует соблюдать правильный порядок действий.

Если в выражении нет скобок и присутствуют только действия второй ступени, то действия выполняются в том порядке, в котором они написаны, слева направо.

Например, 80 : 4 ⋅ 2 : 10 = 20 ⋅ 2 : 10 = 40 : 10 = 4

Если в выражении нет скобок и присутствуют только действия первой ступени, то действия выполняются в том порядке, в котором они написаны, слева направо.

Например, 56 + 10 – 25 + 30 = 66 – 25 + 30 = 41 + 30 = 71

Если в выражении нет скобок и случаются действия разных степеней, то сначала выполняют действия  второй ступени, а затем действия первой ступени. Напомним, умножение и деление считаются действиями второй ступени, сложение и вычитание – действиями первой ступени.

Например, 43 + 25 ⋅ 4 – 10. Сначала выполним умножение 25 ⋅ 4 = 100, 43 + 100 – 10 = 133.

Если в выражении есть скобки, сначала выполняем действия в скобках, а затем все остальные согласно порядку действий. Если в скобках записано выражение из нескольких действий первой и второй ступеней, то в скобках также сначала выполняем действия второй ступени.

То есть порядок действий в выражении будет следующим:

1. действия в скобках
2. умножение и деление,
3. сложение и вычитание.

Действия в пределах одной ступени выполняются поочередно слева направо.

Сначала сложение или вычитание?

Сложение и вычитание являются действиями первой ступени, если нет скобок, то они выполняются поочередно слева направо.

Какое первое действие – умножение или деление?

И умножение, и деление – это действия второй степени, они «равноправны». Поэтому, если нет скобок, действия выполняются поочередно слева направо.

Сначала умножение или сложение?

Поскольку умножение является действием высшей степени, а сложение – действием низшей степени, если нет скобок, то сначала выполняем умножение.

Что сначала – деление или вычитание?

Поскольку деление является действием высшей степени, а вычитание – действием низшей степени, если нет скобок, сначала выполняем деление.

Алгоритм вычисления числового выражения

Перед вычислением числового выражения следует определить порядок действий и только после этого приступать к расчетам.

Рассмотрим выражение с несколькими действиями и скобками.

(53 – 42 : 7) ⋅ (22 ⋅ 2 +36 — 12) + 30

Первоочередность действий в данном выражении будет такой:

• 42 разделить на 7 (42 : 7 = 6)
• Из 53 вычесть результат первого действия: 53 – 6 = 47
• Во вторых скобках сначала нужно выполнить умножение 22 на 2: 22 ⋅ 2 = 44
• К результату умножения прибавляем 36: 44 + 36 = 80
• Из полученной суммы вычитаем 12: 80 – 12 = 68
• Умножим множители, которые являются результатами выполнения действий в первых и вторых скобках: 47 ⋅ 68 = 3196
• К произведению прибавляем 30: 3196 + 30 = 3226

Ответ: (53 – 42 : 7) ⋅ (22 ⋅ 2 +36 -12) + 30 = 3226

Порядок действий с круглыми, квадратными и фигурными скобками

В математических выражениях встречаются не только круглые () скобки, но и квадратные —  [ ]  и фигурные  { }. Фигурные и квадратные скобки используют тогда, когда у скобки необходимо взять выражение в скобках. Порядок действий со скобками следующий: сначала выполняем действия внутри круглых скобок согласно правилам последовательности, второй этап – действия в квадратных скобках, третий этап – действия в фигурных скобках согласно правилам последовательности.

Рассмотрим выражение с круглыми и квадратными скобками

100 — 4 ⋅ [14 + 45 : (10 + 5)] + 6 ⋅ (30 + 4 ⋅ 5 + 10).

1. Выполним действия в круглых скобках:

10 + 5 = 15

30 + 4 ⋅ 5 + 10 = 30 + 20 + 10 = 60

2. Выполним действия в квадратных скобках: 14 + 45 : 15 = 17
3. Выполним остальные действия: 100 – 4 ⋅ 17 + 6 ⋅ 60 = 100 – 68 + 360 = 32 + 360 = 392

Последовательность действий в решении примера 4 класса

1. Форум
2. Архив
3. Школы, Олимпиады, Вузы

Евочки, подскажите, пожалуйста, ребенку задали пример :
(345-45)*(222:3)+(123*4).
Вопрос : каков порядок действий ? Я говорю, что сначала делается первая скобка, потом вторая, третья, умножение результатов первой и второй скобки и сложение. Ребенок говорит, что нужно делать сначала деление и умножение ( во второй и третьей скобке), а потом первую скобку, и умножение и сложение результатов. Так как деление и умножение делается в первую очередь.

Но это же все же скобки! Почему нельзя делать первым вычитание ? Это принципиально и важно, так все же — каков порядок действий,кто может подсказать ? Спасибо!

И вы правы. И ребенок прав. Какая разница в какой последовательности делать действия в скобках? Можете сначала решить первую скобку, потом вторую, а затем третью (а можете наоборот, но проще последовательно, чтобы не запутаться, а можете в произвольном порядке). Затем у вас 300*74+492. Сначала делается умножение, а затем сложение.

Да без разницы совершенно, если ребенку так удобнее, то смысл упираться? Сын вообще может сначала третьи скобки посчитать, потом первые, а потом вторые

В принципе, без разницы. Но для выработки автоматического навыка определения порядка действий я бы согласилась с Вашим ребенком. Раз учат сперва делать умножение/деление, а потом сложение/вычитание, пусть так и делает, чтоб не путаться ))

Скобки считаются последовательно(первая, вторая, третья). Вы правильно сказали ребенку. Другой вопрос, как их учитель научил это делать. Посмотрите в тетради, как они в классе решают подобные примеры, и делайте по аналогии.

вы правы математически
но ребенок скорее всего лучше вас знаете правила игры — учебной игры
для умножения-деления скобки не нужны вообще, потому здесь видимо учебный пример, подчеркнута приоритетность умножения и деления
с математической точки зрение нет разницы какую скобку рассчитать первой — они независимы друг от друга

Дальше будет ещё интереснее. Учитель сына требовал всегда сперва делать умножение и деление, поэтому когда в скобках появилось несколько действий (345-45*7+30:5)*(222:3-7)+(123*4+256:2), требовалось скакать по всем скобкам, выполняя сначала умножение и деление, но целиком скобку сразу считать нельзя было ни в коем случае. Это засчитывалось, как ошибка.

Без разницы, наши тоже не как мы решают, а блоками, ответы сходятся.

В школе моих тоже учат сначала там где деление-умножение, потом все остальное. Хотя в примере не важно какую скобку будут решать и в какой последовательности. А вот что стоим между ними это по стандартному правилу.

Ребенок прав. Видимо, это в вашем примере пока действительно важно — для отработки последовательности действий в скобках. Иначе совсем теряется смысл последней скобки (123*4). Если было бы неважен порядок действий со скобками, то и последняя скобка была бы не нужна. Результат-то один и тот же.

«1) сначала выполняются действия, заключенные в скобки; при этом умножение и деление делаются в порядке их следования, но раньше, чем сложение и вычитание;
2) затем выполняются остающиеся действия, причем опять умножение и деление делаются в порядке их следования, но раньше сложения и вычитания.»

В математике принято выполнять действия слева направо с учетом старшинства операций.
1. действия в скобках
2. возведение в степень
3. умножение/деление
4. сложение/вычитание.
По этому правилу скобки раскрываются слева направо, каждая из них обрабатывается по общему правилу. Я нигде не видела, чтобы у скобок был какой-то «вес» (там может быть 2+7*6).
http://math-prosto.ru/?page=pages/order_of_action/order_of_action.php
Учителя объясняют по-разному, надо классные работы в тетради посмотреть. Беда еще в том, что придет ребенок к другому учителю, а тот трактует иначе.

А зачем здесь вторые и третьи скобки?

Вторые-то понятно, иначе сначала надо было бы выполнить умножение. А третьи лишние, об этом тоже выше написала.

И вторые скобки не нужны. Без них результат был бы тот же.

Для отработки навыка.

Их так учат, чтоб запомнили раз и навсегда. Надо делать так, как требует учитель, хотя с точки зрения взрослого — смысла в этом не больше, чем во второй и третьей паре скобок.

И потом ребенок не будет знать, что делать, когда в скобках 2*3+4

Какого? Для отработки навыка выполнять сначала умножение и деление скобки то зачем?

Наверное это будет следующая тема урока .

Скобки как раз и меняют порядок выполнения операций, из значения вычисляются слева направо.

А если бы их не было, тогда бы умножение сначала выполнялось.

Зачем здесь вторые и третьи скобки???? Их наличие ничего не меняет.

Это следующим шагом проходят.

Выполнять сначала действия в скобках. Вы зря волнуетесь, это короткий период, его отрабатывают, и все.

Вторые скобки нужны. Этот пример просто частный случай. Было перед вторыми скобками не умножение, а деление- результат был бы другой. Вот в третьих скобках без разницы, умножение или деление, отсутствие скобок ничего бы не изменило

Именно в этом примере отсутствие вторых скобок ничего не изменило бы. Поэтому с математической точки зрения в этом примере вторые скобки НЕ нужны.

Ну это к составителю примера вопрос. Ребенок все равно должен правильно определить порядок действий. Подозреваю, что если порядок будет нарушен, ответ могут не засчитать, даже если результат с математической точки зрения верный. Это из той же оперы, когда посадили 5 рядов берез по 7 берез в каждом ряду, сколько всего берез? Решение 5×7 неверное в рамках школьной программы началки, хотя математически результат тот же, что и 7×5.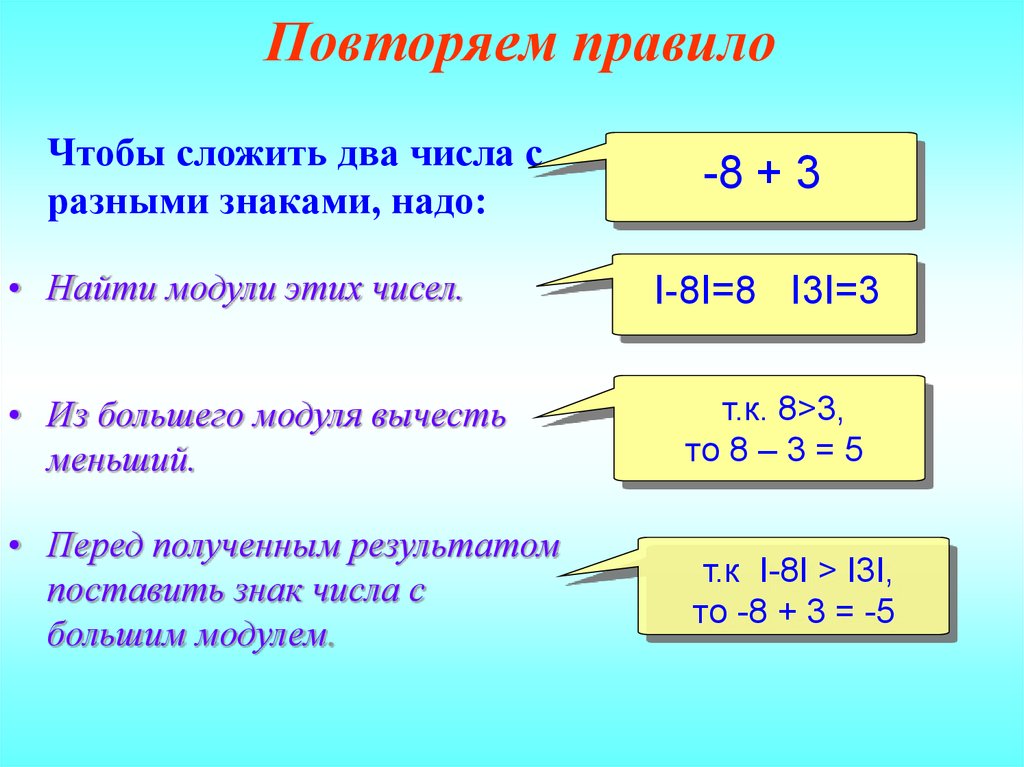

Это понятно, что расставить порядок действий нужно с учетом этих скобок.
Но в этой ветке разговор не об этом совсем

Да? Ну сорри, я так поняла, что в ветке обсуждают последовательность действий при умножении, делении и скобках, даже если наличие этих скобок ничего не меняет. Разве нет? Просто есть правила, которые на уроке обозначили ребенку, и если он выполнит действия в другой последовательности, а не так как озвучил в классе учитель, то ответ не засчитают. Аргумент, что результат математически такой же, будет не аргумент. Это же школа.

Да я вообще не волнуюсь. Просто поинтересовалась — зачем бессмысленная информация детям.

Не могут так учить. Ребенок не понял. Учат — сначала скобки в том порядке, в каком записаны.С остальным согласна.

Скажите, кто учит ваших детей? Наверное, «сильные» учителя в «сильных» школах?

Такие скобки считаются просто слева направо.

Это был учитель началки. Заслуженный, увешанный званиями и регалиями, регулярно пишущий статьи и обучающий других учителей, о котором с придыханием говорили и говорят и мамы учеников и коллеги. В итоге сын дома решал одним способом, в школе другим, полностью удовлетворявшим требованиям учителя.

Мне жаль вашего ребенка, что вы не уверены в таком примере для 2 класса

У вас есть собственная эффективная методика преподавания основ математики детям?

Мне в свое время многое в школьной программе казалось лишним и бессмысленным, особенно с колокольни моего высшего математического образования. Потом посмотрела внимательно, в том числе на собственного ребенка, как он осваивает с нуля то, что мне кажется очевидным, как доводит до автоматизма навыки, которыми я уже владею, и поняла, что в общем глупо считать идиотами составителей школьной программы. Лучше или не вмешиваться, или попытаться понять, чего они хотели добиться в конкретном случае. Обычно смысл находится.

Открыть тему в окнах

Порядок операций

Порядок операций — это определенный порядок или набор правил, согласованных математиками, которым необходимо следовать при выполнении арифметических операций для упрощения выражений.

Правила порядка операций

Вот порядок выполнения операций, который необходимо соблюдать в порядке, указанном ниже, чтобы избежать разных ответов при упрощении выражений. Если используются символы группировки, такие как скобки, скобки или фигурные скобки, сначала выполните операции внутри символов группировки. Затем переходите к показателям и т. д….

1. Упростите любое выражение в круглых и квадратных скобках или символах группировки: (  ) [  ] {  }

2. Упростите степени или выражения, включающие показатели степени: 4 ² , 2 ⁵ или 5 ^{332 . Умножьте и разделите слева направо: × и ÷}

4. Сложите и вычтите слева направо: + и —

Задачи на порядок действий

Внимательно изучите пример на рисунке ниже, чтобы понять понять, как использовать порядок операций!

Другие примеры, показывающие, как использовать порядок операций

Пример #1:

4 ² — 6 × 2 ÷ 4 × 3 + 5

Показатель степени: 6 —

2 100003

÷ 4 × 3 + 5

Умножить и разделить слева направо

16 — 12 ÷ 4 × 3 + 5

16 — 3 × 3 + 5

16 — 2 Сложить 9003

16 — 9 + 3 900 слева направо

16 — 9 + 5

7 + 5

12

Пример № 2:

(2 + 5 ² ) + 4 × 3 — 10

DO СКАК:

(2 + 25) + 4 × 3 — 10

27 + 4 × 3 — 10

DO Умножение

27 + 12 — 10

Добавить

39 — 10

Пример

29

#3:

0 39002

#3:

0 39002

#3:

03

. 14 ÷ 2 = 10 — 7 = 3 (деление предшествует вычитанию)

Помните, что если вы видите умножение и деление одновременно, выполняйте операцию слева направо.

Пример №4:

4 + 5 ÷ 5 × 6 = 4 + 1 × 6 = 4 + 6 = 10

Как запомнить порядок операций вам запомнить порядок действий.

• PEMDAS (используется в основном в Соединенных Штатах Америки, а также во Франции)

• BODMAS (используется в основном в Великобритании, Австралии и Индии)

• BEDMAS (used in Canada and New Zealand)

• BIDMAS

The following mnemonic may help you remember the PEMDAS rule:

PEMDAS (Please Excuse My Dear Aunt Sally)

• The P stands для круглых скобок

• E означает степень

• M означает умножение

• D означает деление

• A означает сложение

• S означает вычитание

Несмотря на то, что M стоит перед D в PEMDAS, эти две операции имеют одинаковый приоритет. Тот же приоритет означает, что умножение не более важно, чем деление. Точно так же, хотя A предшествует S, обе операции имеют одинаковый приоритет. Сложение не более важно, чем вычитание.

На мой взгляд, гораздо лучший способ написать PEMDAS — это P-E-MD-AS.

В P-E-MD-AS операции с одинаковым приоритетом не имеют дефисов между собой.

Например, поскольку сложение и вычитание имеют одинаковый приоритет, между ними нет необходимости ставить дефис.

Однако между P и E стоит дефис, поскольку P имеет более высокий приоритет, чем E.

Все четыре буквы в MDAS, DMAS, DMAS и DMAS относятся к умножению, делению, сложению и вычитанию.

• В правиле BODMAS буква B означает скобку, а буква O — порядок. Порядок может быть силами или корнями.

• В правиле BEDMAS буква B обозначает квадратную скобку, а буква E — показатель степени.

• В правиле BIDMAS буква B обозначает скобку, а буква I — индексы. Индексы представляют собой такие степени, как 6 ²

. Имейте в виду также, что PEMDAS, BODMAS, BEDMAS и BIDMAS являются правильными способами выполнения операций с ордерами. Ни один из них не лучше другого. Это просто названия, которые используются в зависимости от страны, чтобы упростить запоминание правил.

Как насчет вложенных скобок в порядке операций?

Пример №5:

Упростить √4 + 1 + {2 — [(6 — 2) × 5] + 13}.

Сначала работайте с самым внутренним набором скобок или (6 — 2).

√4 + 1 + {2 + [(6 — 2) × 5] + 13} = √4 + 1 + {2 — [4 × 5] + 13}

Далее снова поработайте сначала с внутренним набором скобок или [4 × 5].

√4 + 1 + {2 + [(6 — 2) × 5] + 13} = √4 + 1 + {2 — 20 + 13}

Оставайтесь в скобках, пока не закончите. Работая внутри скобок, обратите внимание, что вам нужно складывать и вычитать слева направо.

√4 + 1 + {2 + [(6 — 2) × 5] + 13} = √4 + 1 + {-18 + 13}

√4 + 1 + {2 + [(6 — 2) × 5] + 13} = √4 + 1 + -5

Согласно правилу BODMAS, сначала нужно выполнить root.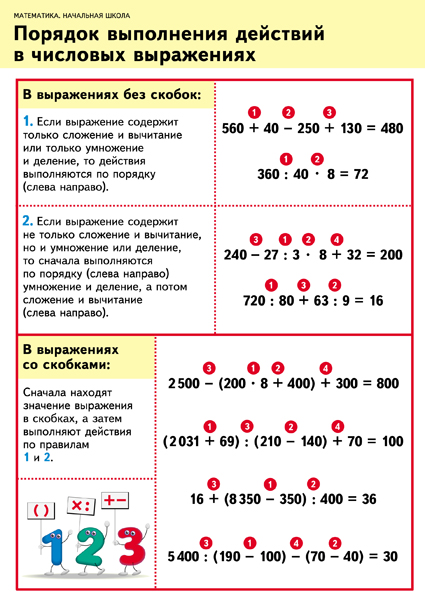

√4 + 1 + {2 + [(6 — 2) × 5] + 13} = 2 + 1 + -5

Снова сложить и вычесть слева направо

√4 + 1 + {2 + [(6 — 2) × 5] + 13} = 3 + -5

√4 + 1 + {2 + [(6 — 2) × 5] + 13} = -2

Окончательный ответ — 2

Реальный пример PEMDAS

Порядок действий — очень важный навык, поскольку вы используете его каждый день, даже если не осознаете этого.

Например, вы идете в супермаркет. Предположим, арахис стоит 3 доллара за фунт, а бутылка воды — 1 доллар. Вы получаете 2 фунта арахиса и 1 бутылку воды.

Сколько денег вы платите?

Поскольку 1 фунт арахиса стоит 3 доллара, а вы купили 2 фунта, арахис стоит 6 долларов. Добавьте это к сумме, которую вы платите за воду (1 доллар), вы заплатили в общей сложности 7 долларов.

Возможно, вы разобрались с этим без особых проблем. Однако, если я представлю вам следующее уравнение, которое является моделью вышеописанной проблемы, у вас может возникнуть тенденция прибавлять 3 к 1 и умножать результат на 2. Это будет неправильный способ сделать это!

2 × 3 + 1

Это даст 8 и не будет равно 7.

Правильный способ — сначала выполнить умножение, а затем прибавить произведение к 1.

Тест на порядок действий. Посмотрите, как вы понимаете этот урок.

1. Типы треугольников

   03, 22 декабря 12:47

   Научитесь определять 6 типов треугольников по их сторонам или углам и еще 7 типов по сторонам и углам.

   Подробнее

2. График прямоугольников и усов

   18, 22 ноября 08:20

   Легко научитесь строить график прямоугольников и усов для набора данных, используя средние и экстремальные значения.

   Подробнее

Порядок операций — Идентификаторы триггеров

Порядок действий: Порядок действий — это правила, которым мы следуем при выполнении операций над математической формулой. Когда в любом выражении есть более одной операции, мы используем порядок операций.

Когда в уравнении есть несколько арифметических операций, мы используем правило DOMAS .

В правиле BODMAS

1. Всегда сначала решать скобки
2. Затем решить порядок операций
3. Подразделение
4. Умножение
5. Дополнение
6. Вычитание

• Скобки
• Экспоненты
• Умножение
• Подразделение
• Дополнение
• Вычитание

Если кто-то попросит вас упростить уравнение типа «3 – 2 × 4», то возникает общий вопрос, что я могу сделать в первую очередь. Должен ли я сначала вычесть, а затем умножить «(3-2) × 4 = 1 × 4 = 4»?

Или сначала умножить, а затем вычесть «3 -2 × 4=3 – 8 = -5»?

Какой ответ правильный?

Кажется, что ответ зависит от того, под каким углом вы смотрите на проблему. В математике один вопрос имеет один точный ответ и не может дать несколько ответов одной задачи, поэтому для решения этой задачи мы используем « порядок операции ». Порядок работы: круглые скобки, показатели степени (корень, степень), деление, умножение, сложение и вычитание. В уравнениях, где присутствуют все операции, правильный порядок решения уравнений сначала раскройте круглые скобки, затем решите показатели степени, затем вы должны решить деление, затем вы должны решить умножение, а затем вы должны решить сложение, а затем вычитание.

Примечание: для умножения или деления ( всегда решать вопросы слева направо).

Сложение и вычитание ( всегда решать уравнения слева направо ).

Как запомнить порядок действий

Обычный способ запомнить порядок действий PEMDAS — использовать сокращения (« ПОЖАЛУЙСТА, ИЗВИНИТЕ МОЮ ДОРОГУЮ ТЕТУ САЛЛИ »).

1. Сначала решить скобки.

Всегда обращайте внимание на круглые скобки в уравнении. Если в уравнении есть круглые скобки, сначала решите их, потому что они имеют более высокий приоритет, чем операции другого порядка.

• Правильный путь:

Правильный способ решения уравнений — сначала решить скобки, затем степени, умножение, деление, сложение и вычитание. Вы всегда будете использовать правило DOMAS для решения алгебраических уравнений.

 

5 × (8 + 4) (сначала раскройте скобки)

5 × 12 = 60   (затем умножьте уравнение)

• Неправильно:

Если вы не следуете правилу DOMAS, ваш ответ неверен.

                            5× (8 + 4) = 40 + 4 = 44

 

2. Решение показателей степени (степень, корень) перед сложением, вычитанием, умножением и делением.

• Правильный путь

Правильный способ решения уравнений — сначала решить скобки, затем степени, умножение, деление, сложение и вычитание. Вы всегда будете использовать правило DOMAS для решения алгебраических уравнений.

4 × 3 ²   (сначала решить показатели)

4 × 9 = 36 (затем умножить выражение)

 

• Неверный путь
• 13

Если сначала решить умножение, а затем показатель степени, то ответ будет неверным. Если вы не следуете правилу DOMAS, ваш ответ неверен.

4 × 3 ² = 12 ² = 144

Умножение и деление

Теперь посмотрите на любой оператор деления и умножения в уравнении. Необязательно, чтобы деление всегда предшествовало умножению, эти операторы решаются слева направо. Посмотрите слева направо, если какой-либо оператор (умножение или деление) идет первым, решите их. Они имеют более низкий приоритет, чем экспонента и круглые скобки.

• Правильный путь

Правильный способ решения уравнений — сначала решить скобки, затем степени, умножение, деление, сложение и вычитание. Вы всегда будете использовать правило DOMAS для решения алгебраических уравнений.