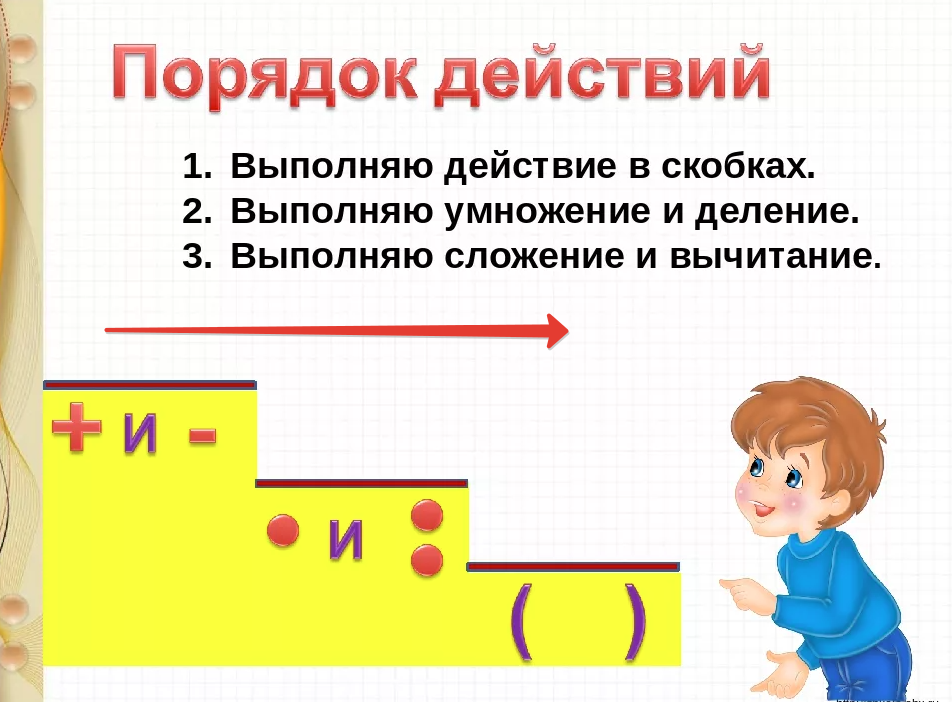
Порядок действий в математике. Действия первой, второй ступеней в выражениях. Что первое умножение или деление в 2023 году

Действия первой и второй ступени с натуральными числами. Порядок действий

Мы уже рассмотрели арифметические действия сложения и вычитания. Эти действия называются действиями первой ступени. Умножение и деление принято считать действиями второй ступени. Если в математическом выражении есть несколько действий, включая действия и первой, и второй ступени, есть разные числа, соответственно результат зависит от порядка совершенных действий. Поэтому при решении примеров следует соблюдать правильный порядок действий.

Если в выражении нет скобок и присутствуют только действия второй ступени, то действия выполняются в том порядке, в котором они написаны, слева направо.

Например, 80 : 4 ⋅ 2 : 10 = 20 ⋅ 2 : 10 = 40 : 10 = 4

Если в выражении нет скобок и присутствуют только действия первой ступени, то действия выполняются в том порядке, в котором они написаны, слева направо.

Например, 56 + 10 – 25 + 30 = 66 – 25 + 30 = 41 + 30 = 71

Если в выражении нет скобок и случаются действия разных степеней, то сначала выполняют действия  второй ступени, а затем действия первой ступени. Напомним, умножение и деление считаются действиями второй ступени, сложение и вычитание – действиями первой ступени.

Например, 43 + 25 ⋅ 4 – 10. Сначала выполним умножение 25 ⋅ 4 = 100, 43 + 100 – 10 = 133.

Если в выражении есть скобки, сначала выполняем действия в скобках, а затем все остальные согласно порядку действий. Если в скобках записано выражение из нескольких действий первой и второй ступеней, то в скобках также сначала выполняем действия второй ступени.

То есть порядок действий в выражении будет следующим:

1. действия в скобках
2. умножение и деление,
3. сложение и вычитание.

Действия в пределах одной ступени выполняются поочередно слева направо.

Сначала сложение или вычитание?

Сложение и вычитание являются действиями первой ступени, если нет скобок, то они выполняются поочередно слева направо.

Какое первое действие – умножение или деление?

И умножение, и деление – это действия второй степени, они «равноправны». Поэтому, если нет скобок, действия выполняются поочередно слева направо.

Сначала умножение или сложение?

Поскольку умножение является действием высшей степени, а сложение – действием низшей степени, если нет скобок, то сначала выполняем умножение.

Что сначала – деление или вычитание?

Поскольку деление является действием высшей степени, а вычитание – действием низшей степени, если нет скобок, сначала выполняем деление.

Алгоритм вычисления числового выражения

Перед вычислением числового выражения следует определить порядок действий и только после этого приступать к расчетам.

Рассмотрим выражение с несколькими действиями и скобками.

(53 – 42 : 7) ⋅ (22 ⋅ 2 +36 — 12) + 30

Первоочередность действий в данном выражении будет такой:

• 42 разделить на 7 (42 : 7 = 6)
• Из 53 вычесть результат первого действия: 53 – 6 = 47
• Во вторых скобках сначала нужно выполнить умножение 22 на 2: 22 ⋅ 2 = 44
• К результату умножения прибавляем 36: 44 + 36 = 80
• Из полученной суммы вычитаем 12: 80 – 12 = 68
• Умножим множители, которые являются результатами выполнения действий в первых и вторых скобках: 47 ⋅ 68 = 3196
• К произведению прибавляем 30: 3196 + 30 = 3226

Ответ: (53 – 42 : 7) ⋅ (22 ⋅ 2 +36 -12) + 30 = 3226

Порядок действий с круглыми, квадратными и фигурными скобками

В математических выражениях встречаются не только круглые () скобки, но и квадратные —  [ ]  и фигурные  { }. Фигурные и квадратные скобки используют тогда, когда у скобки необходимо взять выражение в скобках. Порядок действий со скобками следующий: сначала выполняем действия внутри круглых скобок согласно правилам последовательности, второй этап – действия в квадратных скобках, третий этап – действия в фигурных скобках согласно правилам последовательности.

Рассмотрим выражение с круглыми и квадратными скобками

100 — 4 ⋅ [14 + 45 : (10 + 5)] + 6 ⋅ (30 + 4 ⋅ 5 + 10).

1. Выполним действия в круглых скобках:

10 + 5 = 15

30 + 4 ⋅ 5 + 10 = 30 + 20 + 10 = 60

2. Выполним действия в квадратных скобках: 14 + 45 : 15 = 17
3. Выполним остальные действия: 100 – 4 ⋅ 17 + 6 ⋅ 60 = 100 – 68 + 360 = 32 + 360 = 392

Что выполняется вперед, деление или умножение?

Что выполняется вперед, деление или умножение?

Рассмотрим примеры.20/4*2. Понятно, что если выполнять сначала деление, потом умножение мы получим правильный результат 20/4 = 5. 5*2 = 10.Если же выполнить сначала умножение, а потом деление то, ответ будет совершенно иным и конечно же неправильным. 4*2 = 8. 20/8 = 2,5. Причина такой ошибки в том, что операции деления умножения и деления выполняются в порядке их расположения, то есть слева направо.Второй пример. 20*5/4. Проверяем правило.

По порядку расположения сначала умножение. Умножаем 20*5=100, 100/4=25. Правильно.Если же выполним сначала деление, а потом умножение, то получим: 5/4 = 1,25. Далее 20/1,25 = 16.Ответ неверный. Вывод: все зависит от порядка расположения этих операций.

Чтобы ответить на данный вопрос необходимо вспомнить последовательность выполнения математических операций. Если в примере есть выражение в скобках, то оно делается в первую очередь. Если выбирать между действиями «сложение», «вычитание», «умножение» и «деление», то в первую очередь делаем «умножение» или «»деление».Если же в примере только деление и умножение, то действия выполняются последовательно слева направо.

Мы должны при присутствии только деления и умножения в примере, и без участия скобок, действовать по порядку. Если сначала действие с делением, а потом с умножением, то делим, результат далее умножаем. Если сначала умножение, потом деление, то умножаем, результат далее делим. Когда есть действие в скобках, вроде такого (5*2):(2*1), то умножаем что в скобках сначала, а результаты делим, 10(результат первой скобки):2(результат второй скобки). Если знаки вычитания и прибавления есть, все равно, сначала слева направо выполняем деление или умножение, или умножение или деление, что стоит первым среди этих действий. Просто так принято по правилам. Если бы правило было иным, справа налево, то тогда ответы принимались бы те за верные, что даются при подобном порядке. А так у нас априори верные именно

слева направо. И для расчетов берутся именно они. Поэтому даже если в решении справа налево и получается целое «вполне нормальное» число, это не признак того, что пример решен верно.

действия выполняются по порядку, слева направо. но если в примере присутствуют еще и сложение и вычитание, то в начале выполняют деление с умножением, потом уже сложение и вычитание. а если присутствуют еще и скобки, то в первую очередь решают то, что в скобках.

Слева направо если есть сложение и вычитания они делаются в последний очередь

Это часто встречаемый вопрос у ребят и они часто допускают ошибки. Это в заданиях по информатике и математике часто встречается. Деление и умножение равноправны, поэтому они выполняются по порядку. Так в примере 1+250*5/10 сначала 250*5, потом делим на 10 и только потом прибавляем один. Если будет наоборот 15- 250/5*10, то сначала 250/5, потом умножаем на десять по порядку и только потом из 15 вычитаем полученный результат. По приоритету операций у нас 1 возведение в степень, 2 умножение и деление, 3 вычитание и сложение. Если есть скобки, то сначала они.

Очень важно, чтобы правильно решать задачи по математике, знать порядок выполнения вычислений.Рассмотрим пример:20:4*5 (двадцать разделить на четыре и умножить на пять). Решаем такой пример, по порядку выполняя действия (слева направо).Получится вот что: двадцать разделить на четыре — будет пять, теперь пять умножаем на пять, получится двадцать пять. То есть, и деление, и умножение имеют одинаковую первоочередность, преимуществом обладает то действие. которое стоит первым в примере.

Share on facebook

Facebook

Share on twitter

Twitter

Share on vk

VK

Share on odnoklassniki

OK

Share on tumblr

Tumblr

Share on telegram

Telegram

Экспоненты, умножение и сложение – MathFour

Рубрики: Алгебра; Будьте первым, кто поделится своими мыслями — оставьте комментарий ниже!

Это четвертая книга из серии Объяснение порядка действий.
Чтобы ознакомиться с другими статьями этой серии, нажмите здесь, чтобы перейти к введению.

Изображение из Википедии

Порядок операций можно свести к трем «настоящим» операциям.

Скобки — это просто способ сгруппировать элементы, а не настоящая операция. Поэтому они не считаются реальной операцией.

Поскольку деление — это просто умножение, перевернутое с ног на голову, нам не нужно включать его отдельно. Точно так же вычитание — это сложение на слуху. Так что его тоже выкидываем.

Теперь у нас есть только три: показатели степени, умножение и сложение.

Экспоненты — это ярлык для умножения.

В предыдущей статье о запоминании правил экспоненты я записал это видео о экспонентах:

Вы видите, что 3 x 3 x 3 x 3 равно 3 ⁴ . Экспонента — это сокращение для умножения.

Умножение — это быстрый способ сложения.

Точно так же, когда мы перегружены сложением одних и тех же чисел снова и снова, как в видео, 4 + 4 + 4 + 4 + 4, мы можем использовать умножение, чтобы сократить это: 5 x 4.

Следуйте сокращению эволюция.

Эволюция быстрого доступа выглядит следующим образом:

1. Сначала появилось дополнение.
2. Затем мы создали умножение, чтобы упростить сложение.
3. Затем мы создали показатели степени, чтобы упростить умножение.

Итак, когда вы занимаетесь арифметикой, мы должны сначала использовать «недавние» сокращения (возведение в степень), затем «старые» сокращения (умножение), а затем «обычные» арифметические действия (сложение). Помните, что вычитание — это сложение, а деление — это умножение.

И имейте в виду, что нам нужно следить за группировкой или чем-либо изолированным скобками, барами абсолютного значения или дробью. Инструменты группировки/изоляции всегда важнее других правил работы.

Изображение из Википедии

Что, если ваш ответ не совпадает с ответом на обратной стороне книги?

В некоторых учебниках умножение выполняется перед делением. Это означает, что задача 9  3 x 2 будет показывать другой ответ (3/2) на страницах решения этого учебника, чем тот, который вы получили бы после ОоО, которое я здесь описываю (6). Эти тексты редки, но я их видел. Так что держите глаза открытыми.

Порядок операций — это набор правил, которые мы согласовали. Это означает, что пока учебник четко определяет их порядок, которому они будут следовать, они могут делать такие вещи.

Если вы не знаете, что делать первым, потребуйте скобки. (Да, вы можете это сделать.) Или поставьте круглые скобки в учебнике вашего ребенка, чтобы помочь ему.

Наборы задач должны быть там, чтобы обеспечивать, а не путать.

Что вы думаете? Это помогает или мешает тому, как вы всегда относились к порядку операций? Поделитесь своими мыслями в комментариях.

Статьи по теме

Этот пост может содержать партнерские ссылки. Когда вы используете их, вы поддерживаете нас, чтобы мы могли продолжать предоставлять бесплатный контент!

Порядок операций (PEMDAS) – значение, правила, аббревиатура и примеры

Мы выполняем различные математические операции для решения задач, связанных с нашей повседневной жизнью. Некоторые общие операции, которые мы регулярно выполняем в арифметике, — это сложение, вычитание, умножение, деление и возведение в квадрат.

Порядок операций описывает шаги, в которых мы выполняем операции в выражении. Рассмотрим данное выражение целыми числами:

6 × (3 + 6 ² – 5) ÷ 5

Какую часть нужно вычислить первой?

Нам необходимо следовать порядку операций или правилу приоритета операторов, известному как PEMDAS, когда мы идем слева направо в выражении.

Что такое порядки операций

Математические порядки операций — это правила, описывающие последовательность, в которой выполняются операции в выражении.

Он был изобретен в 1913 году Вебстером Уэллсом и Уолтером У. Хартом.

Как я это помню

Способ запомнить порядок операций — это PEMDAS. Шаги:

Шаг 1: P для круглых скобок

Первый — решить все операции в круглых скобках ( ), { }, [ ]. Все выражения в скобках считаются группой.

Шаг 2: E для степени

Следующим шагом является решение выражений с показателем степени (степень и показатель степени).

Шаг 3: MD для умножения и деления

Эти две операции (×) и (÷) имеют одинаковый ранг и должны выполняться на третьем шаге. Выполните операцию, которая придет первой.

Шаг 4: AS для сложения и вычитания

Наконец, подобно умножению и делению, сложение (+) и вычитание (-) также имеют одинаковый ранг и должны выполняться рядом с ними.

Заказ операций PEMDAS

Некоторые другие Mnemonics:

• P Lease E AT M OM D Electiou onday D onuts A LWAY S UNDAY
• P EOPE E Семейство M ADE D ECISSES A BOUT S UMS

В Соединенном Королевстве вместо этого.

B для квадратных скобок, O для заказов, D для деления, M для умножения, A для сложения и S для вычитания

В Канаде они следуют BEDMAS.

B для квадратных скобок, E для степени, D для деления, M для умножения, A для сложения и S для вычитания

Теперь давайте решим выражение, данное нам в начале этой статьи: 6 × (3 + 6 ² – 5) ÷ 5 с помощью PEMDAS.

Здесь в выражении 6 × (3 + 6 ² – 5) ÷ 5

(3 + 6 ² – 5) заключено в скобки и должно выполняться первым. Однако есть две отдельные операции + и – . По правилу PEMDAS первым должен выполняться показатель степени 6 ² . Таким образом, выражение принимает вид

= 6 × (3 + 36 – 5) ÷ 5

. Затем следует выполнить операцию сложения в скобках, а затем вычитание.

= 6 × (40 – 5) ÷ 5

= 6 × 35 ÷ 5

Теперь мы выполним деление с последующим умножением или умножение с последующим делением, поскольку они оба имеют одинаковый ранг.

= 6 × 7

= 42

Давайте решим еще несколько задач, которые немного сложно решить, используя порядок операций PEMDAS.

Решенные примеры

Решите данное выражение с целыми числами, используя PEMDAS
a) 5 × 4 – 2
b) 16 ÷ 4 + 6
C) (4 × 5 ² ) + 6

Решение:

Оценка (4 × 2 ÷ 1) — 2

Решение:

x (5 + 7) ÷ 3 – 7 с использованием PEMDAS.

Решение:

Упростить выражение алгебраии (8x — 2x) ÷ 3x с использованием Pemdas

Решение:

Использование заказа с выражением.

Решите данное выражение (5/2 × 7/2) + (7/3 × 5/3)

Решение:

Используя порядок решения ВЫРАЖЕНИЕ с АБСОЛЮТНЫМ ЗНАЧЕНИЕМ

Решите данное выражение (-9 – (-3) x 7) ÷ |-3 ²  + 5|

Решение:

Почему порядок операций важен

Он важен, потому что предлагает универсальное правило, которому мы все можем следовать, чтобы выполнить выражение и получить одинаковый результат.

Мы используем PEMDAS всякий раз, когда нам нужно решить повседневную проблему. Давайте рассмотрим простую текстовую задачу.

Предположим, мы купили 6 пицц по 15 долларов каждая. Если мы распределим 6 кусочков поровну между 6 вашими друзьями, каждый получит по одному кусочку. Если мы намерены найти стоимость каждой части, мы применяем PEMDAS для решения выражения.

Общее количество людей = 6

Количество кусочков пиццы = 6

Стоимость каждого кусочка = 15 долларов США

Выражение принимает вид (15 + 15 + 15 + 15 + 15 +15) ÷ 6 или (6 × 15) ÷ 6

Согласно PEMDAS,

(6 × 15) ÷ 6

Экспрессия	Оценка
3 9000). : (6 × 15) = 90 Шаг 2 : 90 ÷ 6 = 15	Круглая скобка Деление

Точно так же мы используем PEMDAS для решения многих подобных задач в нашей повседневной жизни.