Что выполняется вперед, деление или умножение?
Что выполняется вперед, деление или умножение?
Рассмотрим примеры.20/4*2. Понятно, что если выполнять сначала деление, потом умножение мы получим правильный результат 20/4 = 5. 5*2 = 10.Если же выполнить сначала умножение, а потом деление то, ответ будет совершенно иным и конечно же неправильным. 4*2 = 8. 20/8 = 2,5. Причина такой ошибки в том, что операции деления умножения и деления выполняются в порядке их расположения, то есть слева направо.Второй пример. 20*5/4. Проверяем правило. По порядку расположения сначала умножение. Умножаем 20*5=100, 100/4=25. Правильно.Если же выполним сначала деление, а потом умножение, то получим: 5/4 = 1,25. Далее 20/1,25 = 16.Ответ неверный. Вывод: все зависит от порядка расположения этих операций.
Чтобы ответить на данный вопрос необходимо вспомнить последовательность выполнения математических операций. Если в примере есть выражение в скобках, то оно делается в первую очередь.
Мы должны при присутствии только деления и умножения в примере, и без участия скобок, действовать по порядку. Если сначала действие с делением, а потом с умножением, то делим, результат далее умножаем. Если сначала умножение, потом деление, то умножаем, результат далее делим. Когда есть действие в скобках, вроде такого (5*2):(2*1), то умножаем что в скобках сначала, а результаты делим, 10(результат первой скобки):2(результат второй скобки). Если знаки вычитания и прибавления есть, все равно, сначала слева направо выполняем деление или умножение, или умножение или деление, что стоит первым среди этих действий. Просто так принято по правилам. Если бы правило было иным, справа налево, то тогда ответы принимались бы те за верные, что даются при подобном порядке.
действия выполняются по порядку, слева направо. но если в примере присутствуют еще и сложение и вычитание, то в начале выполняют деление с умножением, потом уже сложение и вычитание. а если присутствуют еще и скобки, то в первую очередь решают то, что в скобках.
Слева направо если есть сложение и вычитания они делаются в последний очередь
Это часто встречаемый вопрос у ребят и они часто допускают ошибки. Это в заданиях по информатике и математике часто встречается. Деление и умножение равноправны, поэтому они выполняются по порядку. Так в примере 1+250*5/10 сначала 250*5, потом делим на 10 и только потом прибавляем один. Если будет наоборот 15- 250/5*10, то сначала 250/5, потом умножаем на десять по порядку и только потом из 15 вычитаем полученный результат.
Очень важно, чтобы правильно решать задачи по математике, знать порядок выполнения вычислений.Рассмотрим пример:20:4*5 (двадцать разделить на четыре и умножить на пять). Решаем такой пример, по порядку выполняя действия (слева направо).Получится вот что: двадцать разделить на четыре — будет пять, теперь пять умножаем на пять, получится двадцать пять.То есть, и деление, и умножение имеют одинаковую первоочередность, преимуществом обладает то действие. которое стоит первым в примере.
Share on facebook
Share on twitter
Share on vk
VK
Share on odnoklassniki
OK
Share on tumblr
Tumblr
Share on telegram
Telegram
Порядок действий в примерах: ответы пользователей удивляют
Метки
Действия Логика Математика Правила ПримерыБывает, что самым сложным неожиданно оказывается самое простое. И мы сейчас говорим не о рецепте человеческого счастья и тайнах атомных ядер. Возьмем порядок действий в примерах. Его проходят в начальных классах школы и, по идее, должны помнить всю жизнь.
И мы сейчас говорим не о рецепте человеческого счастья и тайнах атомных ядер. Возьмем порядок действий в примерах. Его проходят в начальных классах школы и, по идее, должны помнить всю жизнь.
Но тем не менее миллионы людей в Сети снова и снова ломают копья вокруг довольно незатейливых математических выражений. Причем удивительное разнообразие ответов ставит под сомнение сам статус математики как царицы точных наук. Предлагаем и тебе возможность проверить себя, назвать верный ответ и освежить в памяти подзабытые знания из старых школьных учебников.
Порядок действий в примерах
Увидев предлагаемый пример в Facebook, я, честно говоря, растерялся. Почти 8 миллионов комментариев под задачкой на три действия? О чём тут спорить? Это же математика!
Однако реальность часто превосходит даже самые смелые фантазии. А ответы пользователей соцсети просто ставят в тупик. Рассмотрим самые распространенные, сохраняя логику и написание их авторов.
«Я думаю, что все комментирующие хотя бы доучились до 4-го класса.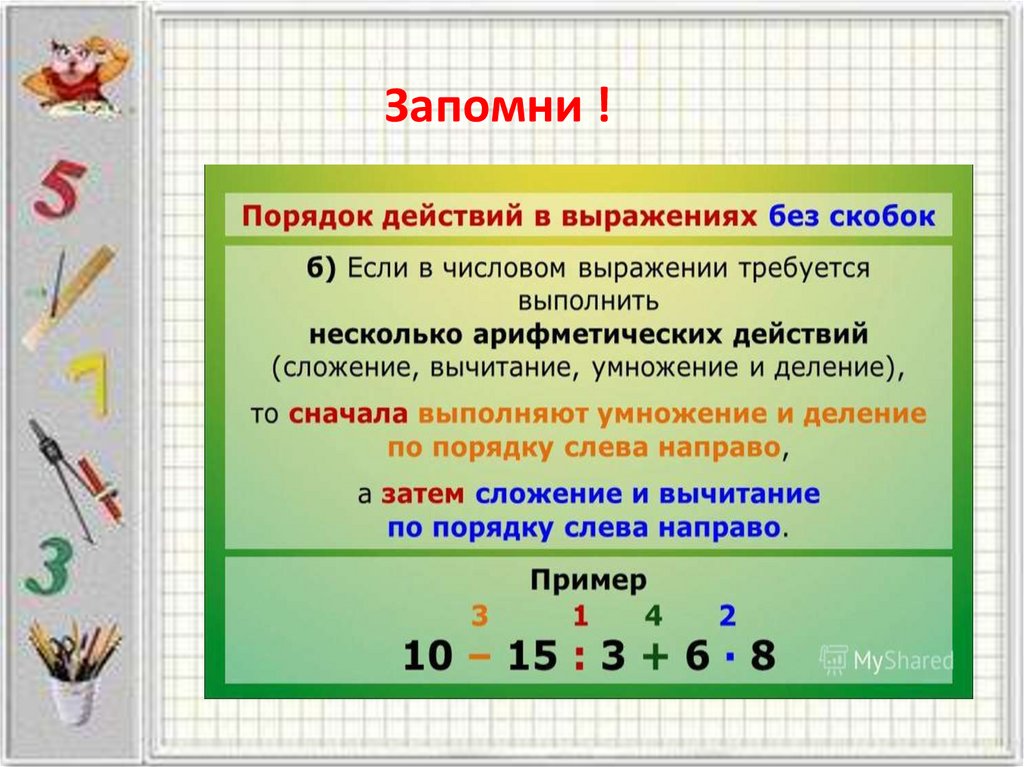 Слава богу, я проходил. 10 − 10 × 10 + 10 = 0 × 10 + 10 = 0 + 10 = 10»
Слава богу, я проходил. 10 − 10 × 10 + 10 = 0 × 10 + 10 = 0 + 10 = 10»
© Depositphotos
«Хороший ответ 10», — утверждает один из комментаторов. Согласны, в нумерологии 10 – хорошее число, обещающее удачу и счастье. Вот только подходит ли 10 на роль правильного ответа?
Прокручиваем ленту дальше. «Это очень просто. Чтобы решить проблему, мы делаем (10 – 10) × (10 + 10) = 0 × 20 = 0, тогда как любое число × на 0 = 0. Результат — 0!»
«По правилам в первую очередь 10 × 10 = 100. 10 – 100, так как 100 больше = 90 и 90 + 10 = 100». Хм… С первой частью сложно не согласиться, но потом логика машет нам ручкой и полностью теряется из виду. А мы продолжаем дальше.
Опытные пользователи пошли особенным путем и спросили совета у Калькулятора Google. Умная программа сразу заключила 10 × 10 в скобки и выдала ответ «–80».
Что говорят правила?
Порядок вычисления выражений определяется двумя простыми правилами. Во-первых, при отсутствии скобок действия выполняются по порядку слева направо. Во-вторых, сначала выполняется умножение и деление, а затем — сложение и вычитание.
Во-первых, при отсутствии скобок действия выполняются по порядку слева направо. Во-вторых, сначала выполняется умножение и деление, а затем — сложение и вычитание.
© Depositphotos
Если в выражении есть скобки, то сначала выполняются действия в скобках, следом в установленном порядке — умножение и деление, затем — сложение и вычитание. В этом примере нет скобок, но есть вычитание, умножение и сложение. Помня о приоритете умножения, начнем с него.
10 – 10 × 10 + 10 = 10 – 100 + 10
Теперь всё, что осталось, — это сложение и вычитание, которые выполняем слева направо. Вычитание стоит первым, когда мы смотрим на уравнение слева направо, поэтому сначала вычитаем.
10 – 10 × 10 + 10 = 10 – 100 + 10 = –90 + 10
Наконец, последний шаг — сложение.
10 – 10 × 10 + 10 = 10 – 100 + 10 = –90 + 10 = –80
Ответ: –80. А какой результат получился у тебя? Возможно, мы где-то просчитались и допустили ошибку? Выскажи свое мнение на этот счет.
© Depositphotos
Напомним, что не так давно настоящий переполох в Интернете вызвал еще один пример: 8 / 2 (2 + 2) = ? Одни пользователи уверяют, что в итоге должно получиться шестнадцать. Другие же правильным ответом считают единицу. И те и другие приводят свои доводы. Но кто из них прав?
Поделиться
Умножение и деление целых чисел
Умножение и деление целых чиселУмножение и деление целых чисел
УМНОЖЕНИЕ
ПРАВИЛО 1: Произведение положительного целого числа на отрицательное число отрицательно.
ПРАВИЛО 2: Произведение двух положительных целых чисел положительно.
ПРАВИЛО 3: Произведение двух отрицательных целых чисел положительно.
Примеров:
Правило 1: 1. (+4) x (-2) = -8 2. (-2) x (+5) = -10
Правило 2: 1. (+6) x (+8) = +48 2. (+6) x (+2) = +12
Правило 3: 1. (-6) x (-8) = +48 2.
(-2) x (-4) = +8
ОТДЕЛ
ПРАВИЛО 1: Частное положительного целого числа и отрицательного целого числа отрицательно.
ПРАВИЛО 2: Частное двух положительных целых чисел положительно.
ПРАВИЛО 3: Частное двух отрицательных целых чисел положительно.
Примеры:
Правило 1: 1. (-8) / (+4) = -2 2. (-12) / (+6) = -2
Правило 2: 1. (+6) / (-3) = -2 2. (+24) / (-6) = -4
Правило 3. 1. (+9) / (+3) = +3 2. (+16) / (+4) = +4
Правило 4: 1. (-6) / (-2) = +3 2. (-42) / (-7) = +6
ОБЗОР ПРАВИЛ УМНОЖЕНИЯ И ДЕЛЕНИЯ
- Если знаки разные, то ответ отрицательный.
- Если знаки одинаковые, ответ положительный .
Проблемы:
- (+3) х (-1) = __________
- (+7) х (+6) = __________
- (-5) х (-5) = ___________
- (-8) х (-6) = ___________
- (-12) х (+5) = _________
- (+16) х (0) = __________
- (-30) х (-3) = __________
- (-18) х (+23) = ________
- (-11) х (+4) = _________
- (+3) х (-8) = __________
- (+15) х (0) = __________
- (-7) х (-4) = ___________
- (+9) х (+8) = __________
- (+9) / (+3) = __________
- (+10) /(-5) = __________
- (-12) / (-3) = __________
- (-25) / (+5) = __________
- (-45) / (+15) = _________
- (-18) / (-6) = __________
- (+52) / (13) = __________
- (-30) / (+10) = _________
- (+14) / (-2) = __________
- (+16) / (-4) = __________
- (-42) / (+7) = __________
- (4) / (2) = _____________
- 0 / (-7) = ______________
- 0 / (6) = ______________
Ключ ответа Умножение и деление целых чисел
- 42
- 25
- 48
- 60
- 0
- 90
- 414
- 160
- 44
- 24
- 0
- 28
- 72
- 3
- 2
- 4
- 5
- 3
- 3
- 4
- 3
- 7
- 4
- 6
- 2
- 0
- 0
Стандартный алгоритм | CoolMath5Kids
Страница 1 из 5 Я собираюсь идти очень медленно и покажу каждый шаг. После того, как вы увидите несколько примеров, это начнет обретать смысл!
После того, как вы увидите несколько примеров, это начнет обретать смысл!
Первое, что мы делаем, это меняем способ написания задачи…
Первый математический шаг — посмотреть на первое число парня, на которого мы делим… на 6. Это шаг деления!
| Мы хотим посмотреть, как много раз 2 будет входить в 6… 2 три раза войдёт в 6, верно? Итак, мы поместим эту 3 прямо над 6: |
Это было совсем не сложно, не так ли?
Вот и второй шаг… Это шаг умножения!
| Умножьте 3 на 2 и поместите ответ прямо под 6: |
Вот и третий шаг… Это шаг вычитания!
Вычитание. .. .. Это 6 — 6 = 0 |
Эй, мы только что закончили первую часть шагов! И это было не так уж плохо!
Деление, потом умножение, потом вычитание.
Давайте назовем это петлей DMS!
Эй, эти буквы идут по алфавиту!! Вы можете использовать это, чтобы запомнить это!
Хорошо, теперь мы проделаем то же самое, но с другим номером…
| Прежде всего: Перетащите 8 вниз. |
Теперь вернемся к нашему циклу деления, умножения и вычитания с использованием числа 8!
| Подразделение: Мы хотим увидеть, как |
| Умножение: Умножьте 4 на 2 и поставьте ответ прямо под 8: |
| Вычитание: Это 8 — 8 = 0 |
Угадайте, что? Мы сделали! (Ни за что.
 (-2) x (-4) = +8
(-2) x (-4) = +8