«Чему равно 6÷2(1+2)?» — Яндекс Кью

Александр Кульков  · 25 янв 2016  ·

404,1 K

Степан Лисовский

Философия

Физтех, М Ф Т И   · 22 июн 2017

Если считать, что знак умножения допустимо опускать в любом случае, то выражение очевидно преобразуется в 6/2*(2+1) = 9 (в соответствии с классическим порядком действий, где умножение и деление обладают равным приоритетом).

Однако так считают не все. Достаточно интуитивным является, что знак умножения допустимо опускать не во всех случаях, а только непосредственно между двумя сомножителями. Соответственно, ориентируясь на то, что знак умножения по факту опущен, считаем произведение 2(1+2) неразрывным и равным 6 и уже на него делим 6/6 = 1 (т.е. приоритет скрытого умножения признаётся более высоким по отношению к делению).

В качестве примера, где скрытое умножение обладает повышенным приоритетом по отношению к обычным умножению и делению можно считать «Курс теоретической физики» Ландау-Лифшица и другую физическую литературу.

125 оценили

  ·

63,1 K

Степан Лисовский

9 июн 2018

В физике есть не только mg, но и k(T1+T2) и т.п. Скобки никогда не были помехой для восприятия записи слитно… Читать дальше

Комментировать ответ…Комментировать…

Andrei Novikov

Математика

кандидат физико-математических наук, математик, ис…  · 13 апр 2021

Вот поэтому математики не пишут дроби в строчку, потому что найдется умник который скажет, что это не так считается. Математик запишет это выражение как 6 —— 2(1+2) И все сразу же станет ясно. Или запишет как 6 —… Читать далее

23 оценили

  ·

11,3 K

Николай Глаголев

16 авг 2021

Согласен с мыслью, что запись могла быть проще для понимания. Однако, если стоит задача прочитать этот пример, то… Читать дальше

Комментировать ответ…Комментировать…

Дмитрий Ушаков

Математика

Студент ВМК Московского Государственного Университ…  · 21 мар 2021

Не думайте об этом слишком много. Данный пример был придуман кем-то нехорошим, просто чтобы позлить комментаторов. Ответ зависит от того, в каком порядке выполнять действия. Лично я уверен в том, что данное выражение — именно в… Читать далее

13 оценили

  ·

11,2 K

Askar Imanakunov

21 мар 2021

Шесть делим на два, умножаем на три

Комментировать ответ…Комментировать…

Вадим Румянцев

Программирование

Специалист в области разработки систем…  · 9 нояб 2019

Это вопрос правил синтаксиса той нотации, в которой записано это математическое выражение. Не зная, в контексте какого формального языка употреблено это выражение, ответить невозможно. Как мне помнится, в школьной математике… Читать далее

51 оценил

  ·

39,9 K

Надежда Д.

11 июл

Даже страшно становится , сколько людей, пытаясь показать свой ум, скатываются к банальному абсурду. Это пример из… Читать дальше

Комментировать ответ…Комментировать…

Риэлтор в Москве Рощина Елена, Агентство недвижимости

Частный риэлтор в Москве, специалист по купле-прод…  · 31 мая 2021

Отвечает

Рощина Елена

Здесь может быть два ответа и зависит от соглашений ( нотации/правил) заложенных при написании. В математике написание направленно на упрощение ( записать сложные вещи простым языком ). В обычной школе принято опускать знак.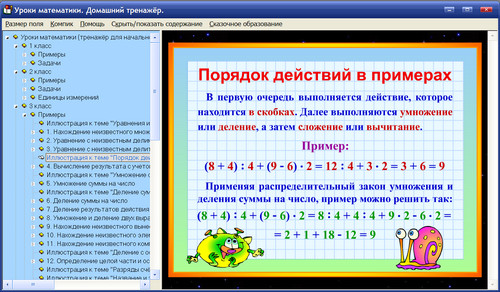 .. Читать далее

Практикующий частный риэлтор в Москве

Перейти на uslugi.yandex.ru/profile/RoshhinaElena-15400437 оценили

  ·

5,0 K

Николай Глаголев

13 сент 2021

Не соглашусь вот с этим предложением: «Но можно Просто заменить пропуск умножением то получится 6/2*(1+2)=9» 6/2… Читать дальше

Комментировать ответ…Комментировать…

Макс Евтишкин

Программирование

Математик и программист Python.  · 15 июл

Знак умножения между 2 и 1+2 опускается. 6/2*(1+2). Дальше по действиям: 1) 1+2=3 2) 6/2=3 3) 3*3=9. Ответ 1 получается из неверных соображений, что опущенный знак умножения выполняется первым и получается 6/6 (это мое мнение) П… Читать далее

Нет оценок  ·

425

Николай Глаголев

3 нояб

После первого действия вы поменяете произведение 2(2+1) умножением 2 на (2+1). Согласно правилу «деление числа на… Читать дальше

Комментировать ответ…Комментировать…

Вега

10 сент 2020

Отвечает

Леха В

раз пошла такая математика, то мне больше нравится ответ 18! и я сейчас объясню как его получить. упрощаем выражение выносим 3 за скобки 3(2:1)(1+2) теперь делаем действия в скобках 3(2)(3) раскрываем скобки 3*2*3 все, мы… Читать далее

17 оценили

  ·

7,4 K

Максим Балакирев

29 июн 2021

Ну, настроение подняли, спасибо!))
6/2≠3(2/1)
6/2=3(2/2)=3×1=3

Комментировать ответ…Комментировать…

Инесса Спиркина

инженер, увлекаюсь комментариями в соцсетях  · 9 окт 2021

Сначала нужно выполнить действие в скобках: 1+2=3.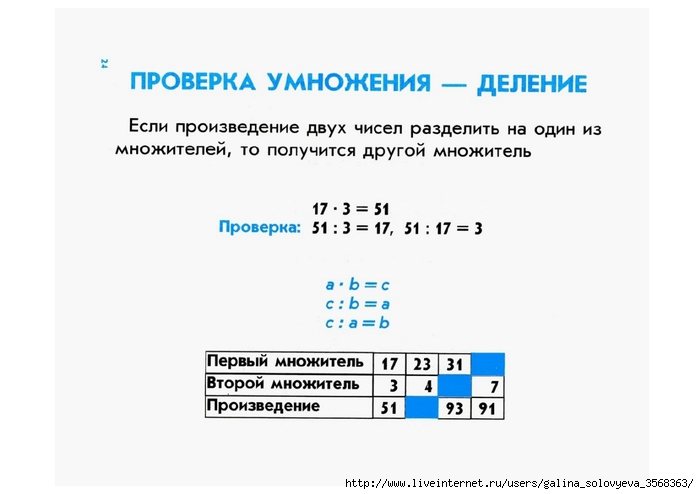

Затем действия выполняются по порядку слева направо.
Второе действие 6:2=3 .
Нам остаëтся 3 умножить на то, что получилось в скобках : 3*3=9
Ответ: 9.

13 оценили

  ·

1,7 K

Сергей Чабовский

подтверждает

15 дек 2021

Арифметика

Комментировать ответ…Комментировать…

Николай Глаголев

Просят написать какую нибудь хрень. Вот пожалуйста  · 28 мар 2021

Знак умножения пропускать можно в определенных случаях, поэтому запись верная, но в первую очередь важно определить порядок действий. Рассуждаем так: для решения этой задачи в первую очередь нужно раскрыть скобочки, однако ТК… Читать далее

13 оценили

  ·

2,3 K

Комментировать ответ…Комментировать…

Денис Кутушев

Интересуюсь иногда чем-то .   · 21 сент 2020

Запись 6:2(1+2)=1 Запись 6:2*(1+2)=9 Именно такие записи с такими ответами не нарушают ни одно правило Так было, так есть и так будет. Хоть в математике, хоть в алгебре, Про порядок действий. 6:2(1+2)= ? Заменим a=6, b=2… Читать далее

14 оценили

  ·

6,1 K

виктор чеботарев

23 сент 2020

Денис. Запись 6:2(1+2)=1 – нарушает правила: 1- порядок действий со скобками: — сначала выполняются действия в… Читать дальше

Комментировать ответ…Комментировать…

В чем проблема изучения математики в современной школе

Почему школьники ошибаются в счете? И почему, проучившись несколько лет в школе,  дети не могут сложить 17 + 18 или 28 + 17? Даже в таких примерах, как 7 + 8, дети ошибаются.

Взрослые недоумевают: “Как так можно? Ведь это 7 + 8?”

Мы с вами знаем «на автомате», что 7+8=15, или понимаем, что к семёрке до 10 надо добавить число 3, а потом 5, т. к. 8 — это 3 и 5. И легко считаем что 7+8 = 15 (7+3+5). Этому учат и в школе:  сначала состав числа, например, 15 — это 7 и 8 и т.д., а потом озвученный выше прием.

Дети, базируясь на вычислительных навыках в пределах 20, далее начинают использовать этот прием с числами более высокого порядка, в более сложных вычислениях. Например, 28 + 17: мы складываем десятки с десятками, единицы с единицами 20 + 10=30, дальше у нас остаётся снова 8 + 7 =15, и получается 30+15 = 45.

Но… есть огромное НО…

Эта  техника счета в пределах 20 отрабатывается в школе всего лишь полтора месяца из всей (!) программы начальной школы, в 1 классе с середины апреля + май. Затем начинаются летние каникулы, за которые дети успешно все забывают…

Далее, во втором классе, когда уже подразумевается, что вышеназванный навык освоен и автоматизирован, дети сразу переходят к сложению и вычитанию в пределах 20, а затем и в пределах 100 и т.д.

Но проблема заключается в том, что если числа в пределах 10 дети легко могут раскладывать на составляющие, например, 7 — это 5 + 2, 6 + 1, 3 + 4, т. к. этот навык автоматизируется  с сентября до середины апреля, то составу чисел в пределах 20 (этому самому важному навыку!) — уделяется всего лишь 1,5 месяца!

И что мы имеем в итоге? 

У многих детей сам алгоритм вычисления, когда мы считаем 7+8 или 15 — 7 — не усвоен. Таким образом получается, что мы имеем ошибки сначала в пределах 20, затем — 100 и, конечно же, в вычислениях с многозначными числами. Т.к. любые вычисления многозначных чисел базируются на счете в пределах 10 и 20.

Как видите, ситуация, в которой ребенок допускает множество ошибок в вычислениях, заключается в неусвоенном базовом алгоритме, стратегии счета в пределах 20 с переходом через десяток или в отсутствии автоматизации этого навыка.

Почему же она не усваивается? Это происходит по нескольким причинам. 

1. Обучаясь в школе, ребёнок много фокусного внимания уделяет счёту в пределах 10 и мало  счету в пределах 20.
2. По школьной программе, когда мы изучаем с детьми новые навыки счета, мы осваиваем  почти одновременно и сложение, и вычитание, не фокусируясь на одной задаче (только сложение, только вычитание).

А теперь сравним: в Сингапурской системе, которая легла в основу Школы спецагентов “Агент Суперсчет”, освоение счета в пределах 20 происходит за 10 последовательных шагов, на каждом из которых изолированно усваивается определенная стратегия счета.

Какие это шаги:

1. Сложение числа с 0: если мы к любому числу прибавим 0, то число не изменится.

И ребёнок решает 10, 20, 30 примеров типа 3 + 0, 12 + 0, 0+5 и т.д. для того, чтобы усвоилась базовая стратегия “если к какому-то числу прибавить 0 — число не меняется”.

2. Сложение в пределах 10: 3+5, 2+1, 4+6 и т.д.

Только сложение. И таких примеров может быть снова великое множество. Но суть заключается в том, что отрабатывается только сложение, и только в пределах 10. Когда ребёнок начинает “щелкать” такие примеры как орешки, мы переходим к 3 стратегии.

3. Вычитание в пределах 10: 10-2, 7-1, 8-4 и т.д.

И снова навык изолированно отрабатывается до автоматизма. И только после этого переходят к следующему навыку.

4. Сложение и вычитание в пределах 10: 3+5, 2-1, 6+3, 9-4 и т.д

Здесь уже ребенок учится переключаться между сложением и вычитанием и решает примеры и на сложение, и на вычитание. Получается, что по отдельности примеры на сложение и вычитание ребенком уже усвоены. А благодаря тому, что только на 4 этапе происходит их одновременное решение — происходит усиление навыка счета в пределах 10 путем многократной его отработки.

5. Сложение в пределах 20 без перехода через 10: 11+2, 13+5, 12+4, 3+16.

3 + 5  ребенок уже складывать умеет, а на этом этапе просто добавляется еще 10 к результату. (Учителя могут возразить сейчас: мы же тоже так учим, тоже разделяем этапы! Согласна. Но вопрос только в том, сколько времени уделяется каждому этапу — как правило, у нас один день разобрали сложение в пределах 20, через день — вычитание, а еще на следующий день — все примеры вместе. Мы же следуем программе!!!)

6. Вычитание в пределах 20 без перехода через 10: 18-3, 19-6, 15-4, 17-6.

Здесь то же самое — счет 8-3, 9-6 и т.д. ребенком уже усвоен, а десятки в таких примерах остаются без изменений.

7. Сложение и вычитание вместе в пределах 20 без перехода через десяток.

8. Сложение в пределах 20 с переходом через десяток: 9+3, 7+4, 7+8. До тех пор, пока навык не будет усвоен.

9. Вычитание в пределах 20 с переходом через десяток: 14-9, 12-7, 11-2. До тех пор, пока навык не будет усвоен.

10. Сложение и вычитание одновременно в пределах 20 с переходом через десяток.

За счет этой разницы в программах по математике мы и имеем сейчас такую ситуацию, что ребенок, когда выполняет какое-то математическое действие, путается, теряется и соответственно, ошибается — путается в десятках, единицах и в вычислениях между ними.

Просто у него НЕ АВТОМАТИЗИРОВАН НАВЫК!!!!

Поэтому именно разделение на этапы, именно отдельная отработка каждого навыка очень и очень важна.

Вернемся к классической математике, но с использованием техник эффективного обучения:  счету дети обучаются легко, и также легко могут применять его в дальнейшем.

Они просто начинают считать. Начинают считать в уме, начинают считать легко, а значит и в дальнейшем вычисления в столбик типа 13456+8264 или 13456-8264 для ребенка тоже будут несложными, потому что автоматизированы навыки сложения и вычитания в пределах 10 и 20.

Поэтому так важны правильная стратегия, правильная последовательность подачи материала, плюс материалы для тренировки и отработки, мотивация, а самое главное — понимание основных математических концепций. 

Этому мы обучаем детей в курсе Школы спецагентов “Агент Суперсчет”. (В этой программе дети проходят обучение, конечно, не только в пределах 20)

Программа состоит из ТРЁХ ступеней:

1 Ступень. Овладение стратегиями сложения и вычитания в пределах 1000 (базовая ступень).

Примерно 2/3 программы на этой ступени дети занимаются овладением навыков счета в пределах 20, 100. Потому что именно здесь и есть основная проблема. И если ребенок в пределах 100 сможет в уме раскладывать числа, он будет их видеть, он научится складывать и вычитать десятки с десятками, единицы с единицами, делать переходы, то никаких проблем в дальнейших письменных вычислениях  в пределах миллиона у него тоже не случится.

При этом из периода “от 0 до 100” около 2/3 времени мы отрабатываем навык счета в пределах 20.

Данная ступень длится 30 дней. Ежедневно ребенок получает один из  навыков и тренируется в его отработке. В итоге у него срабатывает понимание стратегии, формируется автоматизация этого навыка и ребенок готов к переходу к следующему шагу, на следующую ступень.

Благодаря программе курса, над которым работали лучшие методисты проекта “Обучение с удовольствием”, ребенок, пройдя все этапы, без проблем освоит основные математические принципы, которые будет использовать для счета уже не только  в пределах 100, 1000, но и миллиона, и это на самом деле легко и просто.

2 Ступень. Умножение и деление.

Когда ребенок приходит во второй класс, начинаются вычисления в пределах 100, тут же добавляется умножение и деление, дети часто не видят связи между этими действиями, путаются, допускают ошибки, а самое главное — даже не в таблице умножения, а во внетабличном умножении, которому мы и уделяем максимальное внимание.

В курсе вы узнаете, что можно сделать, например, чтобы ребенок спокойно умножил 93 на 95, или 7 на 8. И даже, если он забыл таблицу умножения, он мог бы с легкостью сам  себе подсказать. Этому способствуют различные математические фокусы и математические приемы, встроенные в курс, но самое главное — это стратегии, выполняя которые, ребенок шаг за шагом научится умножать и делить без ошибок легко без калькулятора. Даже будет вас обгонять в вычислениях. Но кроме того, он сможет с помощью разложения чисел дать правильный ответ, и самое главное — объяснить, как он его получил. 

3 Ступень. Дроби.

На самом деле, научившись складывать и вычитать, умножать и делить, можно совершенно не разбираться в том, что делать с дробями. Как работают дроби? Что такое смешанная дробь? Что такое обыкновенная дробь? А десятичная? 

Обратите внимание: эта ступень курса не всегда нужна ученикам начальной школы. Но начиная с 4-5 класса и далее, 6-9 — она необходима, потому что дроби, на самом деле — это основа в дальнейшем всей математики, которая изучается в средней школе. И в данном случае ребенок без проблем научится всем действиям с дробями — сложение, вычитание, умножение, деление и сравнение.

Ребенок не просто познакомится с понятием «дроби», у него придет полное понимание темы, потому что в рамках курса Школы спецагентов “Агент Суперсчет” ребенок с помощью простых стратегий и коротких миссий достигает потрясающих результатов.

Следует отметить, что 1 и 2 ступень помогают закрыть около 80% всех проблем, которые ребенок может испытывать в математике начальной и средней школы.

А, соответственно, ступень 3 — идеальна для того, чтобы научить ребенка работать с дробями.

Записывайтесь на курс!
Вы можете выбрать одну или сразу несколько ступеней, которые будут вам открываться последовательно, чтобы гарантировано помочь вашим детям решить проблемы со счетом.

Регистрируйтесь и действуйте прямо сейчас.

Записаться в школу спецагентов. Агент суперсчет

Вам понравилась статья? Сохраните себе на стену, чтобы не потерять

Математика на основе запросов: зачем умножать перед сложением?

Продолжая наше исследование того, почему у нас есть правила для порядка операций, мы начали с того, что вспомнили, что мы узнали и задавались вопросом о

вчера  используя нашу аналогию со сверхспособностями:

Одним из наших вопросов было: «Зачем нам нужны правила для порядка операций в математике?»

Это отличный вопрос, и сегодня мы его рассмотрели.

Когда дети узнают, ПОЧЕМУ математика (а не только КАК), они глубже узнают и ценят.

Конечно, гораздо проще просто объяснить БОДМАС / правила порядка работы, но мы должны хотеть, чтобы дети понимали, почему это так.

Мы начали с того, что использовали наши калькуляторы, чтобы ответить:

Некоторые из наших калькуляторов сказали, что ответ будет 19, а другие сказали 35.

Как это может быть?!?!?

Это нас озадачило.

Поделились некоторыми теориями.

Так какой же правильный ответ? / Есть ли правильный ответ?

Чтобы выяснить это, мы подумали о том, как мы могли бы интерпретировать числовое предложение, если бы не было правил.

Вспомнив, что умножение — это многократное сложение, мы обнаружили, что более разумно умножать перед сложением, потому что умножение — это многократное сложение. Чтобы разобраться в числовом предложении, мы можем разбить его на сложение:

Ученик предложил попробовать еще одно числовое предложение, и поэтому это числовое предложение было предложено одноклассником:

Нам показалось интересным, как мы пришли к этому. с таким количеством различных возможных ответов.

Что это говорит нам о математике?

— Должны быть специальные правила, иначе будет более одного ответа, и это не работает с математикой.

— Представьте, если бы эти числа представляли деньги. Мы бы закончили с разными суммами!

— В математике должна быть какая-то грамматика, как в языках. Мы можем путать слова, но нам нужно следовать правилам грамматики, иначе нас могут неправильно понять. Я думаю, что в математике должны быть правила, чтобы мы все могли понять, что делаем.

Что мы должны сделать в первую очередь?

— скобки

Почему?

— Потому что мы не знаем его стоимости. Нам нужно сначала выяснить это, прежде чем мы сможем что-то сделать с числовым предложением.

Итак, после скобок, что нам делать дальше?

— Вычислить 3 в квадрате.

Почему?

Потому что это тоже неизвестное значение. Нам нужно знать его стоимость.

Но почему бы не решить это перед раскрытием скобок?

— я думаю, это потому, что когда мы смотрим на 3 в квадрате, мы можем получить представление о его значении, но со скобками нам действительно нужно больше думать о том, какое значение оно представляет.

Эта теория показалась нам логичной.

Итак, что нам делать дальше?

— Умножить 4 на 7

Почему?

— Потому что умножение сильнее, чем сложение. Мы всегда сначала делаем то, что мощнее.

Любые другие идеи, чтобы добавить к этому?

— Это повторяющееся добавление, чтобы мы могли разбить его на более простой для понимания способ. Это еще один способ узнать его истинную стоимость.

Интересно.

Затем мы могли увидеть, как мы нашли все неизвестные значения в нашем числовом предложении.

Итак?

— Теперь мы можем добавить их вообще.

Давайте посмотрим на это по-другому. Можем ли мы рассматривать все это числовое предложение как полностью сложение?

Пары поиграли с этим, а затем мы поделились своим открытием:

Нам показалось, что это помогло нам понять, почему мы выполняем одни операции раньше других.