Что делается первым деление или вычитание: Урок 10. порядок выполнения действий в числовых выражениях — Математика — 3 класс

Содержание

Урок 10. порядок выполнения действий в числовых выражениях — Математика — 3 класс

Математика, 3 класс

Урок №10. Порядок выполнения действий в числовых выражениях

Перечень вопросов, рассматриваемых в теме:

— В какой последовательности выполняются действия в выражениях без скобок?

— В какой последовательности выполняются действия в выражениях со скобками?

Глоссарий по теме:

Если в выражение без скобок входят только сложение и вычитание или умножение и деление, то действия выполняются по порядку: слева направо.

Если в выражение без скобок входят не только сложение и вычитание, но и умножение или деление, то сначала выполняются по порядку умножение и деление, а затем сложение и вычитание также по порядку.

Если в выражение есть скобки, то сначала выполняются действия в скобках, а затем в установленном порядке сначала умножение и деление, затем сложение и вычитание

Основная и дополнительная литература по теме урока:

1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 24.

2. Моро М. И., Волкова С. И. Математика. Рабочая тетрадь 3 класс. Часть 1. М.; Просвещение, 2016. – с. 15.

Теоретический материал для самостоятельного изучения

Выполним вычисления устно и расставим значения выражений в порядке возрастания.

Подсказка: Он должен быть в доме, в шкафу, на столе и даже в портфеле ученика.

В результате вычислений получилось:

Действительно во всём должен быть порядок и в математике тоже.

Выполняя задания, мы пользуемся законами и правилами математики. Эти правила и законы и поддерживают математический порядок.

Выполняя устные вычисления, мы выполняли действия по порядку. В выражениях использовали действия умножения и деления.

Рассмотрим выражения:

6 ∙ 3 + 4 : 2; 27 : 3 — 2 ∙ 2; 2 ∙ (5 + 4).

Это числовые выражения. Для их составления использовали числа и знаки действий.

Использовали не только умножение и деление, но и сложение, вычитание. В каком порядке будем выполнять действия?

В выражении 76 – 27 + 9 – 10 использовали знаки сложения и вычитания. Выполнять действия нужно по порядку: слева направо.

В выражении 80 : 8 ∙ 2 использовали знаки умножения и деления. Выполнять действия нужно также по порядку: слева направо.

Вывод: Если в выражениях только сложение и вычитание или умножение и деление, то действия выполняются по порядку слева направо.

Выражения могут содержать сложение и вычитание, и умножение, и деление. В этом случае сначала выполняются деление и умножение по порядку. В математике эти действия считаются сильными. А затем сложение и вычитание тоже по порядку.

В математике есть способ, который позволяет выделить какое-то действие. Это постановка скобок. Скобки показывают, что действие внутри них, выполняется в первую очередь.

Действия в числовых выражениях выполняются в следующем порядке:

Действия записанные в скобках;
Умножение иделение по порядку: слева направо;
Сложение и вычитание по порядку: слева направо.

Знания этих математических правил позволит правильно находить значения выражений и не нарушать порядок.

Порядок действий в выражениях особый.
И в каждом случае, помните, он свой.
В порядке все действия выполняйте.

Сначала в скобках все посчитайте.

Потом чередом, умножайте или делите.

И, наконец, вычитайте или сложите.

Тренировочные задания.

1. Выберите действие, которое будет в выражение первым.

38 + 4 ∙ 7 + 19

Правильный ответ: умножение.

2. Выберите действие, которое в выражение будет последним.

40 : 5 + 12 – 8 : 2

Правильный ответ: вычитание.

Порядок выполнения действий без скобок и со скобками

Для правильного вычисления значений числовых выражений, в которых нужно произвести более одного действия, необходимо знать установленный порядок выполнения арифметических действий.

Порядок действий без скобок

Установленный порядок арифметических действий без скобок:

Если выражение содержит только действия на сложение и вычитание, то они выполняются в порядке следования — слева направо:
Если выражение содержит только действия на умножение и деление, то действия выполняются в порядке следования — слева направо:
Если в выражении присутствуют и умножение с делением, и сложение с вычитанием, то сначала выполняются умножение и деление в порядке их следования (слева направо), а затем сложение и вычитание в порядке их следования (слева направо):

Порядок действий со скобками

Если выражение содержит скобки, то сначала выполняются все действия внутри скобок, а затем все действия, находящиеся за скобками.

В числовых выражениях со скобками порядок выполнения арифметических действий такой же, как и в выражениях без скобок.

Скобки применяются для обозначения действий, которые нужно произвести раньше остальных. Скобки не влияют на порядок остальных действий в выражении, остальные действия выполняются в указанном порядке.

Дробная черта

Дробная черта в выражении может быть заменена на знак деления, в этом случае, всё что было над и под дробной чертой надо взять в скобки. Например:

13 + 2	= (13 + 2) : (10 — 7).
10 — 7

Знак деления в выражении можно заменить дробной чертой только в том случае, если это не нарушает порядок действий. Например, выражение:

20 : 4(2 + 3)

нельзя заменить на

потому что такая замена нарушит порядок действий в данном выражении.

20 : 4(2 + 3) ≠	20	;
	4(2 + 3)

20	= 20 : (4(2 + 3)).
4(2 + 3)

Дробная черта в выражении заменяет скобки и означает, что надо вычислить отдельно выражение, стоящее в числителе, и отдельно выражение, стоящее в знаменателе, и первый результат разделить на второй.

Порядок выполнения действий: правила, примеры.

Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.

В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.

Порядок вычисления простых выражений

Определение 1

В случае выражений без скобок порядок действий определяется однозначно:

Все действия выполняются слева направо.
В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.

Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.

Пример 1

Условие: вычислите, сколько будет 7−3+6.

Решение

В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:

7−3+6=4+6=10

Ответ: 7−3+6=10.

Пример 2

Условие: в каком порядке нужно выполнять вычисления в выражении

6:2·8:3?

Решение

Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.

Пример 3

Условие: подсчитайте, сколько будет 17−5·6:3−2+4:2.

Решение

Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30, потом 30 разделить на 3 и получить 10. После этого делим 4 на 2, это 2. Подставим найденные значения в исходное выражение:

17−5·6:3−2+4:2=17−10−2+2

Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:

17−10−2+2=7−2+2=5+2=7

Ответ: 17−5·6:3−2+4:2=7.

Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:

Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.

Что такое действия первой и второй ступени

Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.

К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.

Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:

Определение 2

В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).

Порядок вычислений в выражениях со скобками

Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:

Определение 3

Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.

Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание Пример 4

Условие: вычислите, сколько будет 5+(7−2·3)·(6−4):2.

Решение

В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7−2·3. Здесь нам надо умножить 2 на 3 и вычесть результат из 7:

7−2·3=7−6=1

Считаем результат во вторых скобках. Там у нас всего одно действие: 6−4=2.

Теперь нам нужно подставить получившиеся значения в первоначальное выражение:

5+(7−2·3)·(6−4):2=5+1·2:2

Начнем с умножения и деления, потом выполним вычитание и получим:

5+1·2:2=5+2:2=5+1=6

На этом вычисления можно закончить.

Ответ: 5+(7−2·3)·(6−4):2=6.

Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.

Пример 5

Условие: вычислите, сколько будет 4+(3+1+4·(2+3)).

Решение

У нас есть скобки в скобках. Начинаем с 3+1+4·(2+3), а именно с 2+3. Это будет 5. Значение надо будет подставить в выражение и подсчитать, что 3+1+4·5. Мы помним, что сначала надо умножить, а потом сложить: 3+1+4·5=3+1+20=24. Подставив найденные значения в исходное выражение, вычислим ответ: 4+24=28.

Ответ: 4+(3+1+4·(2+3))=28.

Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.

Допустим, нам надо найти, сколько будет (4+(4+(4−6:2))−1)−1. Начинаем с выражения во внутренних скобках. Поскольку 4−6:2=4−3=1, исходное выражение можно записать как (4+(4+1)−1)−1. Снова обращаемся к внутренним скобкам: 4+1=5. Мы пришли к выражению (4+5−1)−1. Считаем 4+5−1=8 и в итоге получаем разность 8-1, результатом которой будет 7.

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.

Разберем пример такого вычисления.

Пример 6

Условие: найдите, сколько будет (3+1)·2+62:3−7.

Решение

У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 62=36. Теперь подставим результат в выражение, после чего оно примет вид (3+1)·2+36:3−7.

Дальше действуем по знакомому алгоритму: считаем, сколько у нас получится в скобках, потом в оставшемся выражении выполняем умножение и деление, а следом – сложение и вычитание.

(3+1)·2+36:3−7=4·2+36:3−7=8+12−7=13

Ответ: (3+1)·2+62:3−7=13.

В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.

Порядок выполнения математических действий

В математике установлен определенный порядок выполнения математических действий при любой записи действий над числами. Для основных арифметических действий установлен следующий порядок: сначала выполняется возведение числа в степень, затем выполняется умножение и деление и в самую последнюю очередь выполняется сложение и вычитание.

Если необходимо выполнить несколько действий умножения и деления, то выполняются они слева на право в том порядке, в котором записаны.

Точно так же выполняются несколько действий сложения и вычитания: слева на право в том порядке, в котором действия сложения и вычитания записаны.

Если хотят, чтобы порядок арифметических действий в какой-нибудь записи отличался от установленного, то употребляют скобки. Математические выражения заключают последовательно в круглые ( … ), квадратные [ . .. ( … ) … ] и фигурные { … [ … ( … ) … ] … } скобки. Действия над числами выполняются последовательно: сначала в круглых, затем в квадратных и, наконец, в фигурных скобках. Если в скобках заключены несколько различных математических действий, установленный порядок выполнения действий необходимо соблюдать: сначала выполняется умножение и деление, после этого сложение и вычитание внутри скобок. После получения результатов математических действий, заключенных в скобки, приступают к выполнению математических действий, записанных за скобками, соблюдая установленный порядок выполнения математических действий.

Если деление обозначено чертой, необходимо сократить дробь, если это возможно. Деление, обозначенное чертой, выполняют после вычисления выражений, стоящих в числителе и в знаменателе.

Знак извлечения корня рассматривается как запись при помощи скобок.

При возведении в степень сначала выполняют все математические действия, указанные в показателе степени. Если требуется указать иной порядок действий, то употребляют скобки. В этом случае сперва выполняются все действия внутри скобок, только после этого приступают к выполнению действий за скобками.

18 сентября 2009 года — 22 сентября 2019 года.

© 2006 — 2021 Николай Хижняк. Все права защишены.

Порядок выполнения действий / Справочник по математике для начальной школы

Главная
Справочники
Справочник по математике для начальной школы
Порядок выполнения действий

В данном разделе мы познакомимся с порядком действий, с выражениями со скобками и без них.

1) Если тебе нужно выполнить только сложение и вычитание или только умножение и деление, то все действия выполняют по порядку слева направо.

Например,

В числовом выражении 3 арифметических действия: сложение, вычитание и вычитание.

Определим порядок действий и запишем их над арифметическими знаками: так как нет ни умножения ни деления, действия выполняют по порядку слева направо:

Вычисляем:

1) 10 + 15 = 25

2) 25 — 6 = 19

3) 19 — 8 = 11

Полностью пример записываем так:

10 + 15 — 6 — 8 = 25 — 6 — 8 = 19 — 8 = 11

Например,

В числовом выражении 3 арифметических действия: деление, умножение и деление.

Определим порядок действий и запишем их над арифметическими знаками: так как нет ни сложения ни вычитания, действия выполняют по порядку слева направо:

Вычисляем:

1) 15 : 5 = 3

2) 3 • 4 = 12

3) 12 : 6 = 2

Полностью пример записываем так:

15 : 5 • 4 : 6 = 3 • 4 : 6 = 12 : 6 = 2

2) Если тебе нужно выполнить несколько арифметических действий (сложение, вычитание, умножение и деление), то сначала выполняют умножение и деление по порядку слева направо, а затем сложение и вычитание по порядку слева направо.

Например,

В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.

Определим порядок действий и запишем их над арифметическими знаками: сначала производим деление, потом умножение, затем вычитание и сложение.

1)15 : 3 = 5

2) 6 • 8 = 48

3) 10 — 5 = 5

4) 5 + 48 = 53

Полностью пример записываем так:

10 — 15 : 3 + 6 • 8 = 10 — 5 + 6 • 8 = 10 — 5 + 48 = 5 + 48 = 53

3) Если в выражении есть скобки, то сначала выполняют действия в скобках, но обязательно учитывать первое и второе правила.

Например,

В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.

Определим порядок действий и запишем их над арифметическими знаками: сначала производим вычитание в скобках, затем деление, потом умножение и сложение.

1) 25 — 10 = 15

2) 15 : 3 = 5

3) 6 • 8 = 48

4) 5 + 48 = 53

Полностью пример записываем так:

(25 — 10) : 3 + 6 • 8 = 15 : 3 + 6 • 8 = 5 + 6 • 8 = 5 + 48 = 53

Например,

В числовом выражении 4 арифметических действия: сложение, деление, сложение и деление.

Определим порядок действий и запишем их над арифметическими знаками: сначала производим действия в скобках (деление, затем сложение), затем деление, потом сложение.

1) 12 : 4 = 3

2) 6 + 3 = 9

3) 18 : 9 = 2

4) 42 + 2 = 44

Полностью пример записываем так:

42 + 18 : (6 + 12 : 4) = 42 + 18 : (6 + 3) = 42 + 18 : 9 = 42 + 2 = 44

Вывод:

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Скобки

Правило встречается в следующих упражнениях:

2 класс

Страница 10, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 15, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 23, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 53, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 106, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 110, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 31, Моро, Волкова, Рабочая тетрадь, часть 2

Страница 40, Моро, Волкова, Рабочая тетрадь, часть 2

Страница 50, Моро, Волкова, Рабочая тетрадь, часть 2

Страница 68, Моро, Волкова, Рабочая тетрадь, часть 2

3 класс

Страница 28, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 41, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 74, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 97, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 100, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 30. Вариант 1. № 1, Моро, Волкова, Проверочные работы

Страница 11, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 92, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 107, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 110, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

4 класс

Страница 29, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 62, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 69, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 73, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 75, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 47, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 46, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 80, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 89, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 48, Моро, Волкова, Рабочая тетрадь, часть 2

5 класс

Задание 22, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 86, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 449, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 548, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Номер 136, Мерзляк, Полонский, Якир, Учебник

Номер 163, Мерзляк, Полонский, Якир, Учебник

Номер 253, Мерзляк, Полонский, Якир, Учебник

Номер 365, Мерзляк, Полонский, Якир, Учебник

Номер 368, Мерзляк, Полонский, Якир, Учебник

Номер 5, Мерзляк, Полонский, Якир, Учебник

6 класс

Задание 18, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 73, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 85, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 373, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 378, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 411, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 417, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 422, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 425, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 454, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Пользовательское соглашение

Первое действие сложение. Примеры на порядок действий

Числовые и буквенные выражения могут содержать знаки различных арифметических действий. При преобразовании выражений и вычислении значений выражений действия выполняются в определенной очередности, так как существует строгий порядок выполнения математических действий

Сначала умножение и деление, затем сложение и вычитание

Порядок выполения действий в выражениях без скобок:

— действия выполняются по порядку слева направо,

— причем сначала выполняется умножение и деление, а затем – сложение и вычитание .

1. Рассмотрим пример: выполните действия 17−3+6

Исходное выражение не содержит умножения и деления и не содержит скобок. Поэтому нам следует выполнить все действия по порядку слева направо , то есть, сначала мы от 17 отнимаем 3, получаем 14, после чего к полученной разности 14 прибавляем 6, получаем 20.

Кратко решение можно записать так: 17 − 3 + 6 = 14 + 6 = 20

2. Вычислите значение выражения 17 − 5 · 6: 3 − 2 + 4: 2

Сначала определим, в каком порядке следует выполнять действия в выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление .

4: 2 теперь 4 делим на 2, получаем 2.

Подставляем в исходное выражение вместо 5 · 6: 3 найденное значение 10, а вместо 4: 2 — значение 2, получаем следующее выражение 17 − 5 · 6: 3 − 2 + 4: 2 = 17 − 10 − 2+ 2 .

В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7.

Действия первой и второй ступени

Для удобства принятия решения о последовательности выполнения действий их разделили на две ступени:

первая ступень — сложение и вычитание,

вторая ступень — умножение и деление.

Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание)

Порядок выполнения арифметических действий в выражениях со скобками

Правило, задающее порядок выполнения действий в выражениях со скобками, формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.

Рассмотрим пример: 99: (45 – 39 + 5) – 25: 5

Порядок вычисления такой. Сначала выполним действия в скобках:

45 – 39 = 6 ; 6 + 5 = 11 ,

затем действия второй ступени

Для правильного вычисления выражений, в которых нужно произвести более одного действия, нужно знать порядок выполнения арифметических действий. Арифметические действия в выражении без скобок условились выполнять в следующем порядке:

Если в выражении присутствует возведение в степень, то сначала выполняется это действие в порядке следования, т. е. слева направо.
Затем (при наличии в выражении) выполняются действия умножения и деления в порядке их следования.
Последними (при наличии в выражении) выполняются действия сложения и вычитания в порядке их следования.

В качестве примера рассмотрим следующее выражение:

Сначала необходимо выполнить возведение в степень (число 4 возвести в квадрат и число 2 в куб):

3 · 16 — 8: 2 + 20

Затем выполняются умножение и деление (3 умножить на 16 и 8 разделить на 2):

И в самом конце, выполняются вычитание и сложение (из 48 вычесть 4 и к результату прибавить 20):

48 — 4 + 20 = 44 + 20 = 64

Действия первой и второй ступени

Арифметические действия делятся на действия первой и второй ступени. Сложение и вычитание называются действиями первой ступени , умножение и деление — действиями второй ступени .

Если выражение содержит действия только одной ступени и в нём нет скобок, то действия выполняются в порядке их следования слева направо.

Пример 1.

15 + 17 — 20 + 8 — 12

Решение. Данное выражение содержит действия только одной ступени — первой (сложение и вычитание). Надо определить порядок действий и выполнить их.

Ответ: 42.

Если выражение содержит действия обеих ступеней, то первыми выполняются действия второй ступени, в порядке их следования (слева направо), а затем действия первой ступени.

Пример. Вычислить значение выражения:

24: 3 + 5 · 2 — 17

Решение. Данное выражение содержит четыре действия: два первой ступени и два второй. Определим порядок их выполнения: согласно правилу первым действием будет деление, вторым — умножение, третьим — сложение, а четвёртым — вычитание.

Теперь приступим к вычислению.

Начальная школа подходит к концу, скоро ребёнок шагнёт в углубленный мир математики. Но уже в этот период школьник сталкивается с трудностями науки. Выполняя простое задание, ребёнок путается, теряется, что в результате приводит к отрицательной отметке за выполненную работу. Чтобы избежать подобных неприятностей, нужно при решении примеров, уметь ориентироваться в порядке, по которому нужно решать пример. Не верно распределив действия, ребёнок не правильно выполняет задание. В статье раскрываются основные правила решения примеров, содержащих в себе весь спектр математических вычислений, включая скобки. Порядок действий в математике 4 класс правила и примеры.

Перед выполнением задания попросите своё чадо пронумеровать действия, которые он собирается выполнить. Если возникли затруднения – помогите.

Некоторые правила, которые необходимо соблюдать при решении примеров без скобок:

Если в задании необходимо выполнить ряд действий, нужно сначала выполнить деление или умножение, затем . Все действия выполняются по ходу письма. В противном случае, результат решения будет не верным.

Если в примере требуется выполнить , выполняем по порядку, слева направо.

27-5+15=37 (при решении примера руководствуемся правилом. Сначала выполняем вычитание, затем – сложение).

Научите ребёнка всегда планировать и нумеровать выполняемые действия.

Ответы на каждое решённое действие записываются над примером. Так ребёнку гораздо легче будет ориентироваться в действиях.

Рассмотрим ещё один вариант, где необходимо распределить действия по порядку:

Как видим, при решении соблюдено правило, сначала ищем произведение, после — разность.

Это простые примеры, при решении которых, необходима внимательность. Многие дети впадают в ступор при виде задания, в котором присутствует не только умножение и деление, но и скобки. У школьника, не знающего порядок выполнения действий, возникают вопросы, которые мешают выполнить задание.

Как говорилось в правиле, сначала найдём произведение или частное, а потом всё остальное. Но тут же есть скобки! Как поступить в этом случае?

Решение примеров со скобками

Разберём конкретный пример:

При выполнении данного задания, сначала найдём значение выражения, заключённого в скобки.
Начать следует с умножения, далее – сложение.
После того, как выражение в скобках решено, приступаем к действиям вне их.
По правилам порядка действий, следующим шагом будет умножение.
Завершающим этапом станет .

Как видим на наглядном примере, все действия пронумерованы. Для закрепления темы предложите ребёнку решить самостоятельно несколько примеров:

Порядок, по которому следует вычислять значение выражения уже расставлен. Ребёнку останется только выполнить непосредственно решение.

Усложним задачу. Пусть ребёнок найдёт значение выражений самостоятельно.

7*3-5*4+(20-19) 14+2*3-(13-9)
17+2*5+(28-2) 5*3+15-(2-1*2)
24-3*2-(56-4*3) 14+12-3*(21-7)

Приучите ребёнка решать все задания в черновом варианте. В таком случае, у школьника будет возможность исправить не верное решение или помарки. В рабочей тетради исправления не допустимы. Выполняя самостоятельно задания, дети видят свои ошибки.

Родители, в свою очередь, должны обратить внимание на ошибки, помочь ребёнку разобраться и исправить их. Не стоит нагружать мозг школьника большими объёмами заданий. Такими действиями вы отобьёте стремление ребёнка к знаниям. Во всём должно быть чувство меры.

Делайте перерыв. Ребёнок должен отвлекаться и отдыхать от занятий. Главное помнить, что не все обладают математическим складом ума. Может из вашего ребёнка вырастет знаменитый философ.

На данном уроке подробно рассмотрен порядок выполнения арифметических действий в выражениях без скобок и со скобками. Учащимся предоставляется возможность в ходе выполнения заданий определить, зависит ли значение выражений от порядка выполнения арифметических действий, узнать отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренироваться в применении изученного правила, найти и исправить ошибки, допущенные при определении порядка действий.

В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.

А в математике обязательно ли выполнять арифметические действия в определенном порядке?

Давайте проверим

Сравним выражения:
8-3+4 и 8-3+4

Видим, что оба выражения совершенно одинаковы.

Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).

Рис. 1. Порядок действий

В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.

Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.

Видим, что значения выражений получаются разные.

Сделаем вывод: порядок выполнения арифметических действий менять нельзя .

Узнаем правило выполнения арифметических действий в выражениях без скобок.

Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.

Потренируемся.

Рассмотрим выражение

В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени .

Выполняем действия слева направо по порядку (рис. 2).

Рис. 2. Порядок действий

Рассмотрим второе выражение

В этом выражении имеются только действия умножения и деления — это действия второй ступени.

Выполняем действия слева направо по порядку (рис. 3).

Рис. 3. Порядок действий

В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?

Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.

Рассмотрим выражение.

Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.

Вычислим значение выражения.

18:2-2*3+12:3=9-6+4=3+4=7

В каком порядке выполняются арифметические действия, если в выражении имеются скобки?

Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.

Рассмотрим выражение.

30 + 6 * (13 — 9)

Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.

30 + 6 * (13 — 9)

Вычислим значение выражения.

30+6*(13-9)=30+6*4=30+24=54

Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?

Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:

1. действия, записанные в скобках;

2. умножение и деление;

3. сложение и вычитание.

Схема поможет запомнить это несложное правило (рис. 4).

Рис. 4. Порядок действий

Потренируемся.

Рассмотрим выражения, установим порядок действий и выполним вычисления.

43 — (20 — 7) +15

32 + 9 * (19 — 16)

Будем действовать по правилу. В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.

43 — (20 — 7) +15 =43 — 13 +15 = 30 + 15 = 45

В выражении 32 + 9 * (19 — 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.

32 + 9 * (19 — 16) =32 + 9 * 3 = 32 + 27 = 59

В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие — умножение, второе — деление, третье — вычитание.

2*9-18:3=18-6=12

Узнаем, правильно ли определен порядок действий в следующих выражениях.

37 + 9 — 6: 2 * 3 =

18: (11 — 5) + 47=

7 * 3 — (16 + 4)=

Рассуждаем так.

37 + 9 — 6: 2 * 3 =

В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие — деление, второе — умножение. Третье действие должно быть сложение, четвертое — вычитание. Вывод: порядок действий определен верно.

Найдем значение данного выражения.

37+9-6:2*3 =37+9-3*3=37+9-9=46-9=37

Продолжаем рассуждать.

Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие — в скобках, второе — деление, третье — сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

18:(11-5)+47=18:6+47=3+47=50

В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие — в скобках, второе — умножение, третье — вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

7*3-(16+4)=7*3-20=21-20=1

Выполним задание.

Расставим порядок действий в выражении, используя изученное правило (рис. 5).

Рис. 5. Порядок действий

Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.

Действуем по алгоритму.

В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.

Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого — вычитание.

Проверим себя (рис. 6).

Рис. 6. Порядок действий

Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками.

Список литературы

М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
М.И. Моро, М. А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.
М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
Нормативно-правовой документ. Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.
«Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
С.И. Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
В.Н. Рудницкая. Тесты. — М.: «Экзамен», 2012.

Festival.1september.ru ().
Sosnovoborsk-soobchestva.ru ().
Openclass.ru ().

Домашнее задание

1. Определи порядок действий в данных выражениях. Найди значение выражений.

2. Определи, в каком выражении такой порядок выполнения действий:

1. умножение; 2. деление;. 3. сложение; 4. вычитание; 5. сложение. Найди значение данного выражения.

3. Составь три выражения, в которых такой порядок выполнения действий:

1. умножение; 2. сложение; 3. вычитание

1. сложение; 2. вычитание; 3. сложение

1. умножение; 2. деление; 3. сложение

Найди значение этих выражений.

Yandex.RTB R-A-339285-1

Определение 1

В случае выражений без скобок порядок действий определяется однозначно:

Все действия выполняются слева направо.
В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.

Пример 1

Условие: вычислите, сколько будет 7 − 3 + 6 .

Решение

7 − 3 + 6 = 4 + 6 = 10

Ответ: 7 − 3 + 6 = 10 .

Пример 2

Условие: в каком порядке нужно выполнять вычисления в выражении 6: 2 · 8: 3 ?

Решение

Пример 3

Условие: подсчитайте, сколько будет 17 − 5 · 6: 3 − 2 + 4: 2 .

Решение

Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30 , потом 30 разделить на 3 и получить 10 . После этого делим 4 на 2 , это 2 . Подставим найденные значения в исходное выражение:

17 − 5 · 6: 3 − 2 + 4: 2 = 17 − 10 − 2 + 2

Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:

17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7

Ответ: 17 − 5 · 6: 3 − 2 + 4: 2 = 7 .

Что такое действия первой и второй ступени

К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.

Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:

Определение 2

Порядок вычислений в выражениях со скобками

Определение 3

Пример 4

Условие: вычислите, сколько будет 5 + (7 − 2 · 3) · (6 − 4) : 2 .

Решение

В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7 − 2 · 3 . Здесь нам надо умножить 2 на 3 и вычесть результат из 7:

7 − 2 · 3 = 7 − 6 = 1

Считаем результат во вторых скобках. Там у нас всего одно действие: 6 − 4 = 2 .

Теперь нам нужно подставить получившиеся значения в первоначальное выражение:

5 + (7 − 2 · 3) · (6 − 4) : 2 = 5 + 1 · 2: 2

Начнем с умножения и деления, потом выполним вычитание и получим:

5 + 1 · 2: 2 = 5 + 2: 2 = 5 + 1 = 6

На этом вычисления можно закончить.

Ответ: 5 + (7 − 2 · 3) · (6 − 4) : 2 = 6 .

Пример 5

Условие: вычислите, сколько будет 4 + (3 + 1 + 4 · (2 + 3)) .

Решение

У нас есть скобки в скобках. Начинаем с 3 + 1 + 4 · (2 + 3) , а именно с 2 + 3 . Это будет 5 . Значение надо будет подставить в выражение и подсчитать, что 3 + 1 + 4 · 5 . Мы помним, что сначала надо умножить, а потом сложить: 3 + 1 + 4 · 5 = 3 + 1 + 20 = 24 . Подставив найденные значения в исходное выражение, вычислим ответ: 4 + 24 = 28 .

Ответ: 4 + (3 + 1 + 4 · (2 + 3)) = 28 .

Допустим, нам надо найти, сколько будет (4 + (4 + (4 − 6: 2)) − 1) − 1 . Начинаем с выражения во внутренних скобках. Поскольку 4 − 6: 2 = 4 − 3 = 1 , исходное выражение можно записать как (4 + (4 + 1) − 1) − 1 . Снова обращаемся к внутренним скобкам: 4 + 1 = 5 . Мы пришли к выражению (4 + 5 − 1) − 1 . Считаем 4 + 5 − 1 = 8 и в итоге получаем разность 8 — 1 , результатом которой будет 7 .

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Разберем пример такого вычисления.

Пример 6

Условие: найдите, сколько будет (3 + 1) · 2 + 6 2: 3 − 7 .

Решение

У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 6 2 = 36 . Теперь подставим результат в выражение, после чего оно примет вид (3 + 1) · 2 + 36: 3 − 7 .

(3 + 1) · 2 + 36: 3 − 7 = 4 · 2 + 36: 3 − 7 = 8 + 12 − 7 = 13

Ответ: (3 + 1) · 2 + 6 2: 3 − 7 = 13 .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Порядок действий

В уроке выражения мы узнали, что они бывают числовые и буквенные. Мы рассмотрели несколько числовых и буквенных выражений. Это были самые простейшие выражения.

Настало время сдвинуться с мёртвой точки и рассмотреть более сложные выражения. В данном уроке мы познакомимся с порядком выполнения действий.

Выражения могут состоять из нескольких чисел. Таковыми к примеру являются следующие выражения:

10 − 1 + 2 + 3
(3 + 5) + 2 × 3
5 × 2 + (5 − 3) : 2 + 1

Такие выражения нельзя вычислить сразу, то есть поставить знак равенства и записать значение выражения.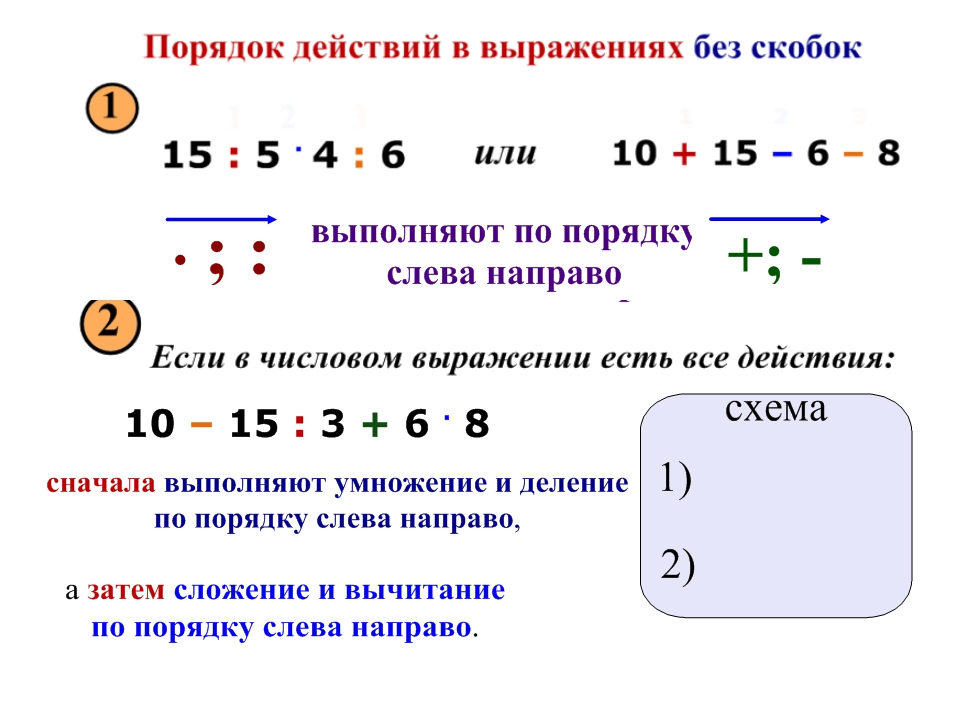 Да и выглядят они не так просто, как 2 + 2 или 9 − 3.

Для подобных выражений принято соблюдать так называемый порядок действий. Суть в том, что выражение вычисляется кусочками по определённому порядку.

Когда нам требуется решить подобные примеры, мы сразу должны мысленно прочитать следующее правило:

Сначала вычислить то, что находится в скобках!

Посмотрим на выражение 10 − 1 + 2 + 3. Видим, что в нём нет никаких скобок. Тогда переходим к следующему правилу, которое выглядит так:

Читаем выражение слева направо. Если встретится умножение или деление, то сразу же выполняем эту операцию!

Читаем наше выражение 10 − 1 + 2 + 3 слева направо. Видим, что в нём нет никакого умножения или деления. Тогда переходим к следующему правилу:

Читаем выражение слева направо. Если встретится сложение или вычитание, то сразу же выполняем эту операцию!

Читаем наше выражение 10 − 1 + 2 + 3 слева направо. Встречаем вычитание 10 − 1. Сразу выполняем эту операцию: 10 − 1 = 9. Полученную девятку запишем в главном выражении вместо 10 − 1

Затем снова читаем те, правила, которые мы прочитали выше. Читать их нужно в следующем порядке:

1. Сначала вычислить то, что находится в скобках!

2. Читаем выражение слева направо. Если встретится умножение или деление, то сразу же применяем эту операцию!

3. Читаем выражение слева направо. Если встретится сложение или вычитание, то сразу же применяем эту операцию!

Сейчас у нас имеется выражение 9 + 2 + 3 Читаем его слева направо и встречаем сложение 9 + 2. Выполняем эту операцию: 9 + 2 = 11. Запишем число 11 в главном выражении вместо 9 + 2:

Осталось простейшее выражение 11 + 3, которое вычисляется легко:

11 + 3 = 14

Таким образом, значение выражения 10 − 1 + 2 + 3 равно 14

10 − 1 + 2 + 3 = 14

Иногда удобно расставить порядок действий над самим выражением. Для этого над операцией, которую необходимо выполнить, указывают её очередь. К примеру, в выражении 10 − 1 + 2 + 3 все действия выполняются последовательно слева направо, поэтому для него можно определить следующий порядок:

И далее можно выполнить действия по отдельности, что очень удобно:

1) 10 − 1 = 9

2) 9 + 2 = 11

3) 11 + 3 = 14

Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий. Например, решение для выражения 10 − 1 + 2 + 3 можно записать следующим образом:

Но если человек не научился быстро считать в уме, то не рекомендуется использовать такой способ.

Пример 2. Найти значение выражения (3 + 5) + 2 × 3

Применим правила порядка действий. Прочитаем правила в порядке их приоритета.

Сначала вычислить то, что находится в скобках!

Посмотрим на выражение (3 + 5) + 2 × 3. Видим, что в нём есть выражение в скобках (3 + 5). Вычислим то, что в этих скобках: 3 + 5 = 8. Запишем полученную восьмёрку в главном выражении вместо выражения в скобках:

8 + 2 × 3

Снова читаем первое правило:

Сначала вычислить то, что находится в скобках!

Видим, что в выражении 8 + 2 × 3 нет никаких скобок. Тогда читаем следующее правило:

Читаем выражение слева направо. Если встретится умножение или деление, то сразу же выполняем эту операцию!

Посмотрим на наше выражение 8 + 2 × 3. Видим, что в нём есть умножение 2 × 3. Выполним эту операцию: 2 × 3 = 6. Запишем полученную шестёрку в главном выражении вместо 2 × 3

8 + 6

Осталось простейшее выражение 8 + 6, которое вычисляется легко:

8 + 6 = 14

Таким образом, значение выражения (3 + 5) + 2 × 3 равно 14

(3 + 5) + 2 × 3 = 14

Также, этот пример можно решить, расставив порядок действий над самим выражением. Действие в скобках будет первым действием, умножение — вторым действием, а сумма — третьим:

И далее можно выполнить действия по отдельности, что очень удобно:

1) 3 + 5 = 8

2) 2 × 3 = 6

3) 8 + 6 = 14

Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:

Но опять же, используя такой способ, нужно быть очень внимательным.

Пример 3. Найти значение выражения 5 × 2 + (5 − 3) : 2 + 1

Расставим порядок действий над выражением. Действие в скобках будет первым действием, умножение — вторым действием, деление — третьим действием, четвёртое и пятое действие являются суммами и они будут выполнены в порядке их следования:

1) 5 − 3 = 2

2) 5 × 2 = 10

3) 2 : 2 = 1

4) 10 + 1 = 11

5) 11 + 1 = 12

Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:

Четвёртое и пятое действие заключалось в том, чтобы вычислить оставшееся простейшее выражение 10 + 1 + 1. Мы не стали тратить время на выполнение каждого из этих действий, а поставили знак равенства и записали ответ 12.

Пример 4. Найти значение выражения (3250 − 2905) : 5

Расставим порядок действий над выражением. Действие в скобках будет первым действием, а деление — вторым

1) 3250 − 2905 = 345

2) 345 : 5 = 69

В скобках могут выполняться два и более действия. Бывает даже так, что в скобках встречаются другие скобки. В таких случаях нужно применять те же правила, которые мы изучили ранее.

Пример 5. Найти значение выражения (6 411 × 8 − 40799) × 6

Расставим порядок действий над выражением. Действие в скобках будет первым действием. При этом в скобках выполняется умножение и вычитание. Согласно порядку действий, умножение выполняется раньше вычитания.

В данном случае сначала нужно 6 411 умножить на 8, и из полученного результата вычесть 40 799. Полученный результат будет значением выражения, содержащегося в скобках. Этот результат будет умножен на 6.

В результате будем иметь следующий порядок:

1) 6 411 × 8 = 51 288

2) 51 288 − 40 799 = 10 489

3) 10 489 × 6 = 62 934

Пример 6. Найти значение выражения: 1 657 974 : 822 × 106 − (50 377 + 20 338)

Расставим порядок действий над выражением. Действие в скобках будет первым действием, деление будет вторым действием, умножение — третьим, вычитание — четвёртым.

1) 50 377 + 20 338 = 70 715

2) 1 657 974 : 822 = 2 017

3) 2 017 × 106 = 213 802

4) 213 802−70 715 = 143 087

Пример 7. Найти значение выражения: 14 026 − (96 : 4 + 3680)

Расставим порядок действий над выражением. Действие в скобках будет первым действием. При этом в скобках выполняется деление и сложение. Согласно порядку действий деление выполняется раньше сложения.

В данном случае сначала нужно 96 разделить на 4, и полученный результат сложить с 3 680. Полученный результат будет значением выражения, содержащегося в скобках. Этот результат нужно вычесть из 14 026. В результате будем иметь следующий порядок:

1) 96 : 4 = 24

2) 24 + 3 680 = 3 704

3) 14026 − 3 704 = 10 322

Задания для самостоятельного решения

Задание 1. Найдите значение выражения:

5 + 2 − 2 − 1

Решение

Задание 2. Найдите значение выражения:

14 + (6 + 2 × 3) − 6

Решение

Задание 3. Найдите значение выражения:

486 : 9 − 288 : 9

Решение

Задание 4. Найдите значение выражения:

756 : 3 : 4 × 28

Решение

Задание 5. Найдите значение выражения:

807 : 3 − (500 − 58 × 4)

Решение

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Порядок операций — PEMDAS

Операции

«Операции» означают такие вещи, как сложение, вычитание, умножение, деление, возведение в квадрат и т. Д. Если это не число, это, вероятно, операция.

Но, когда вы видите что-то вроде …

7 + (6 × 5 ² + 3)

… какую часть нужно рассчитать в первую очередь?

Начать слева и пойти направо?
Или идти справа налево?

Предупреждение: вычислите их в неправильном порядке, и вы можете получить неправильный ответ!

Итак, давным-давно люди согласились соблюдать правила при расчетах, а это:

Порядок действий

Действия, указанные в скобках, сначала

		4 × (5 + 3)	=	4 × 8	=	32
		4 × (5 + 3)	=	20 + 3	=	23	(неправильно)

Показатели (степени, корни) перед умножением, делением, сложением или вычитанием

		5 × 2 ²	=	5 × 4	=	20
		5 × 2 ²	=	10 ²	=	100	(неправильно)

Умножьте или разделите перед сложением или вычитанием

		2 + 5 × 3	=	2 + 15	=	17
		2 + 5 × 3	=	7 × 3	=	21	(неправильно)

В противном случае просто идите слева направо

		30 ÷ 5 × 3	=	6 × 3	=	18
		30 ÷ 5 × 3	=	30 ÷ 15	=	2	(неправильно)

Как я все это помню.

..? ПЕМДАС!

пол	P первые скобки
E	E xponents (т.е. степени, квадратные корни и т. Д.)
MD	M ultiplication и D ivision (слева направо)
AS	A ddition и S ubtraction (слева направо)

Разделение и Умножение ранжируются одинаково (и идут слева направо).

Сложить и вычесть ранг одинаково (и идти слева направо)

Так сделай так:

После того, как вы сделали «P» и «E», просто идите слева направо, выполняя любую «M» или «D», как вы их найдете.

Затем идите слева направо, выполняя любые «A» или «S», когда найдете их.

	Вы можете вспомнить, сказав: « P lease E xcuse M y D ear A Unt S ally».
Или …	Пухлые эльфы могут потребовать перекус Попкорн Каждый понедельник Пончики Всегда воскресенье Ешьте, пожалуйста, вкусные яблочные штрудели мамы Везде приняли решения по суммам

Примечание: в Великобритании говорят BODMAS (скобки, заказы, деление, умножение, сложение, вычитание), а в Канаде говорят BEDMAS (скобки, экспоненты, разделить, умножить, сложить, вычесть). Все это означает одно и то же! Неважно, как вы это запомните, главное, чтобы вы все поняли правильно.

Примеры

Пример: как вычислить

3 + 6 × 2 ?

M Ультипликация до A ddition:

Сначала 6 × 2 = 12 , затем 3 + 12 = 15

Пример: как вычислить

(3 + 6) × 2 ?

P первая цифра:

Сначала (3 + 6) = 9 , затем 9 × 2 = 18

Пример: как вы работаете

12/6 × 3/2 ?

M ultiplication и D ivision ранжируются одинаково, поэтому просто идите слева направо:

Сначала 12/6 = 2 , затем 2 × 3 = 6 , затем 6/2 = 3

Практический пример:

Пример: Сэм бросил мяч прямо вверх со скоростью 20 метров в секунду, как далеко он улетел за 2 секунды?

Сэм использует эту особую формулу, которая учитывает эффекты гравитации:

высота = скорость × время — (1/2) × 9. 8 × время ²

Сэм устанавливает скорость 20 метров в секунду и время 2 секунды:

высота = 20 × 2 — (1/2) × 9,8 × 2 ²

Теперь о расчетах!

Начать с: 20 × 2 — (1/2) × 9,8 × 2 ²

Сначала скобки: 20 × 2 — 0,5 × 9,8 × 2 ²

Тогда экспоненты (2 ² = 4): 20 × 2 — 0,5 × 9,8 × 4

Затем умножается: 40 — 19,6

Вычесть и СДЕЛАНО! 20.4

Мяч достигает 20,4 метра за 2 секунды

Показатели экспоненты …

А как насчет этого примера?

4 ^{3 ²}

Экспоненты особые: идут сверху вниз (сначала экспонента сверху). Итак, вычисляем так:

Начать с:		4 ^{3 ²}
3 ² = 3 × 3:		4 ⁹
4 ⁹ = 4 × 4 × 4 × 4 × 4 × 4 × 4 × 4 × 4:		262144

Так 4 ^{3 ²} = 4 ^{(3 ²)}, а не (4 ³) ^²

И, наконец, как насчет примера с самого начала?

Начать с: 7 + (6 × 5 ² + 3)

Скобки сначала , а затем Показатели : 7 + (6 × 25 + 3)

Затем Умножить : 7 + (150 + 3)

Затем Добавьте : 7 + (153)

Скобки завершены: 7 + 153

Последняя операция — Добавить : 160

ПОРЯДОК РАБОТЫ

Как рассчитать 2 + 3 x 7? Ответ 35 или 23? Чтобы знать правильный ответ, нужно знать правильный порядок операций относительно сложения, вычитания, умножения, деления и т. Д.

Правило 20:: Умножение и деление должны быть выполнены до сложение и вычитание.
2 + 3 x 7 = 2 + 21 = 23 — правильный ответ на поставленный выше вопрос.

Как вы вычисляете (2 + 3) x (7 — 3)? Ответ 32, 20 или ответ 14? Чтобы узнать правильный ответ, нужно знать правильный порядок операций относительно сложения, вычитания, умножения, деления и скобок.

Правило 21:: Выражения в скобках обрабатываются как одно число и должны быть рассчитаны в первую очередь.
(2 + 3) x (7-3) = 5 x 4 = 20 — правильный ответ на предыдущий проблема

Как бы вы вычислили [3 + 7 — (2 + 3 x 6) +2 x 5-7 +1]?

Правило 22:

Если круглые скобки заключены в другие круглые скобки, работайте изнутри.

В выражении выражение (2 + 3 x 6) является самой внутренней круглой скобкой и должно быть вычислено в первую очередь.2 + 3 х 6 = 2 + 18 = 20.

Выражение теперь изменено на. Следующая скобка для вычисления: 7-20 + 2 x 5 = 7-20 + 10 = — 13 + 10 = — 3.

Теперь выражение сокращается до [3 + {-3} — 7 + 1] = 0 — 7 + 1 = — 6.

Как бы вы посчитали.

Правило 23:: Скобки указывают на необходимость упрощения выражение в скобках, прежде чем продолжить. Отдел символ имеет ту же роль, что и скобка.Он поручает вам относиться к количеству над числителем, как если бы оно было заключено в скобки и обрабатывать количество под числителем, как если бы оно были заключены в еще одну круглую скобку. Когда вы закончите это задача, у вас есть что-то вроде двух добавляемых дробей. Не так! может быть написано и умножение должно быть завершено перед сложением в каждом скобка ..
= Оба скобки были упрощены. Теперь выполните умножение на урожай .Последнее, что нужно делать это дополнение.

Если вы хотите, чтобы другие примеры и задачи работали, щелкните соответствующее слово.

: Правило 20
: Правило 21
: Правило 22
: Правило 23

Меню Назад к простым дробям [Идентификация] [Факторинг целых чисел] [Уменьшение дробей] [Умножение] [Разделение] [Строительные фракции] [Добавление] [Вычитание] [Порядок работы] С.

Домашняя страница O.S MATHematics

Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard.

Автор: Нэнси Маркус

— ChiliMath

Правило PEMDAS (сокращение от «Прошу прощения, дорогая тетя Салли») представляет собой набор правил, определяющих порядок вычислений в первую очередь.В противном случае можно получить несколько или разные ответы. Мы не хотим, чтобы это произошло.

Ниже показан пример, в котором есть два возможных ответа. Первое решение дает неправильный ответ, поскольку вычисляет числовое выражение слева направо. В то время как второе решение является правильным, потому что оно следует правилам Порядка операций.

Упростите числовое выражение.

Неправильное решение:

Правильное решение:

Порядок операций

Шаг 1 : В верхней части списка помните: ВСЕГДА упрощайте все внутри символов группировки.Примерами символов группировки являются круглые скобки (), квадратные скобки и фигурные скобки {}. Для вложенных группирующих символов проработайте это изнутри и снаружи.

Шаг 2 : Экспоненциальные выражения вычисляются или оцениваются перед выполнением любой из четырех основных арифметических операций, а именно: сложение, вычитание, умножение и деление.

Шаг 3 : Затем умножьте и / или разделите слева направо в зависимости от того, что наступит раньше, перед выполнением сложения и вычитания.Это говорит нам о том, что умножение и деление имеют более высокий уровень важности, чем сложение и вычитание.

Шаг 4 : Наконец, сложите и / или вычтите слева направо в зависимости от того, что произойдет раньше.

PEMDAS

PEMDAS — это мнемоническое устройство, которое может помочь нам запомнить порядок операций, который, как мы уже знаем, означает « P lease E xcuse M y D ear A Unt S . союзник».

P — Круглые скобки

E — Показатели

M — Умножение

D — Раздел

A — Добавление

S операции умножения и деления имеют одинаковый уровень приоритета.Чтобы решить, когда умножать или делить, всегда выполняйте первое слева направо.

Таким же образом сложение и вычитание равны по важности. Выполните первую операцию слева направо.

Примеры применения правила PEMDAS

Пример 1 : Упростите следующее выражение, используя Порядок операций.

Решение : Обратите внимание, что здесь задействованы три операции.В зависимости от порядка операций умножение имеет приоритет перед сложением и вычитанием, поэтому мы будем умножать в первую очередь. Затем вычтите, затем добавьте, так как операция вычитания выполняется перед сложением слева направо.

Пример 2 : Упростите следующее выражение, используя Порядок операций.

Решение : символ группировки имеет наивысший приоритет, что означает, что мы должны сначала упростить все внутри. В скобках указаны операции деления и умножения.Поскольку они имеют одинаковую важность, порядок их появления слева для записи будет определять, что будет первым. В этом случае мы сначала делим, а затем умножаем.

После упрощения выражения внутри скобок у нас останется вычитание и деление. Очевидно, что деление должно быть вычислено перед вычитанием.

Пример 3 : Упростите следующее выражение, используя Порядок операций.

Решение : Упростите выражение в скобках, затем оцените степени (члены с показателями).После этого у нас будет более простое выражение, включающее сложение, умножение и деление. Просматривая слева направо, мы видим, что сначала нужно умножить, затем разделить и, наконец, сложить.

Вас также может заинтересовать:

Порядок операций

Темы алгебры: Порядок операций

Урок 1: Порядок действий

Введение в порядок работы

Как бы вы решили эту проблему?

12–2 ⋅ 5 + 1

Ответ, который вы получите, будет во многом зависеть от порядка , в котором вы решаете проблему.Например, если вы решите задачу от слева до справа —12-2, затем 10⋅5, затем прибавьте 1, вы получите 51.

12-2 ⋅ 5 + 1
10 5 + 1
50 + 1
51

С другой стороны, если вы решите задачу в направлении , противоположном направлению — от вправо до слева — ответ будет 0.

12–2 ⋅ 5 + 1
12–2 ⋅ 6
12–12
0

Наконец, что, если бы вы выполняли вычисления в несколько другом порядке? Если вы сначала умножите на , а затем на прибавите , ответ будет 3.

12 — 2 ⋅ 5 + 1
12 — 10 + 1
2 + 1
3

Оказывается, 3 на самом деле — это правильный ответ, потому что это ответ, который вы получите, если будете следовать стандартному порядку операций . Порядок операций — это правило, которое сообщает вам правильный порядок для решения различных частей математической задачи. ( Операция — это просто другой способ выразить вычисление . Вычитание, умножение и деление — все это примеры операций.)

Порядок операций важен, потому что он гарантирует, что все люди могут читать и решать проблему одинаково. Без стандартного порядка действий формулы для реальных расчетов в финансах и науке были бы бесполезны — и было бы трудно понять, правильно ли вы получили ответ на тесте по математике!

Использование порядка операций

Стандартный порядок операций:

Круглые скобки
Показатели
Умножение и деление
Сложение и вычитание

Другими словами, в любая математическая задача вы должны начать с вычисления скобок сначала, затем показателей умножения , затем показателей , затем и деление , затем сложение и вычитание .Для операций на том же уровне решите от слева до справа . Например, если ваша задача содержит более одного показателя степени, вы должны сначала решить крайнюю левую, а затем работать вправо.

Давайте более внимательно посмотрим на порядок операций и попробуем другую задачу. Это может показаться сложным, но в основном это простая арифметика. Вы можете решить ее, используя порядок действий и некоторые навыки, которые у вас уже есть.

4/2 ⋅ 3 + (4 + 6 2) + 18/3 ² — 8

Круглые скобки

Всегда начинайте с операций, заключенных в круглые скобки.Скобки используются для группировки частей выражения.

Если скобок несколько, сначала найдите те, которые указаны слева. В этой задаче у нас только один набор:

4/2 ⋅ 3 + (4 + 6 2) + 18/3 ² — 8

В любых скобках вы следуете порядку операций, как и в любой другой части математической задачи.

Здесь у нас есть две операции: сложение и умножение . Поскольку умножение всегда идет первым, мы начнем с умножения 6 ⋅ 2.

4/2 ⋅ 3 + (4 + 6 2) + 18/3 ² — 8

6 ⋅2 равно 12.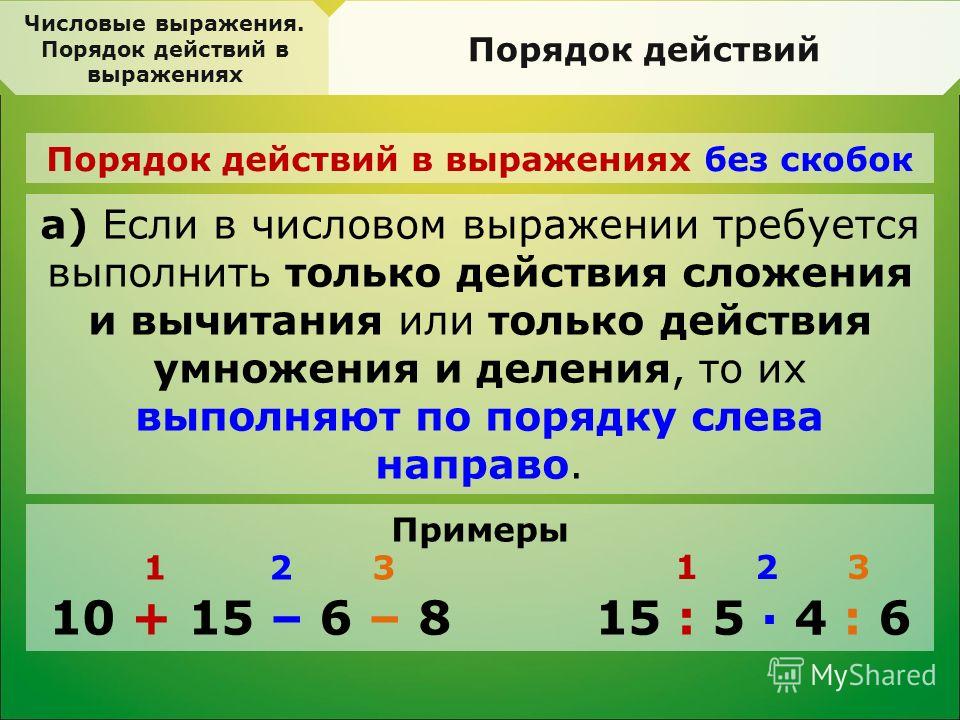 Затем мы прибавим 4 .

4/2 ⋅ 3 + (4 + 12) + 18/3 ² — 8

4 + 12 равно 16. Итак, мы упростили скобки до 16 . Поскольку в скобках указано только одно число, мы можем избавиться от них всех вместе — теперь они не , объединяющие вместе.

4/2 ⋅ 3 + 16 + 18/3 ² — 8

Экспоненты

Во-вторых, решите любые показатель степени .Экспоненты — это способ умножения числа на само себя. Например, 2 ³ — это 2 , умноженное само на себя три раза, поэтому вы можете решить его, умножив 2 ⋅2 ⋅2 . (Чтобы узнать больше об экспонентах, просмотрите наш урок здесь).

В этой задаче только одна экспонента : 3 ² . 3 ² — это 3 , умноженное на себя дважды — другими словами, 3 ⋅ 3 .

4/2 ⋅ 3 + 16 + 18/3 ² — 8

3 ⋅ 3 равно 9, поэтому 3 ² можно упростить как 9 .

4/2 ⋅ 3 + 16 + 18/9 — 8

Умножение и деление

Затем найдите любые операции умножения или деления операции. Помните, что умножение не обязательно предшествует делению — вместо этого эти операции решаются от слева до справа .

Начало слева означает, что нам нужно сначала решить 4/2 .

4/2 ⋅ 3 + 16 + 18/9 — 8

4 делится на 2 равно 2. Таким образом, наша следующая задача составляет 2 ⋅ 3 .

2 ⋅ 3 + 16 + 18/9 — 8

2 ⋅ 3 равно 6. Наконец, осталась только одна задача умножения или деления: 18/9 .

6 + 16 + 18/9 — 8

18/9 равно 2. Нечего умножать или делить, поэтому мы можем перейти к следующей и последней части Порядка операций: сложение и вычитание .

6 + 16 + 2 — 8

Сложение и вычитание

Теперь решить нашу проблему стало намного проще. Осталось только сложение и вычитание.

Так же, как мы делали с умножением и делением, мы будем складывать и вычитать от слева до справа . Это означает, что сначала мы добавим 6 и 16.

6 + 16 + 2 — 8

6 + 16 равно 22. Далее нам нужно добавить 22 к 2.

22 + 2 — 8

22 + 2 это 24.Осталась всего одна операция: 24 — 8.

24–8

24-8 это 16. Вот и все!

Готово! Мы решили всю проблему, и ответ — 16 . Другими словами, 4/2 ⋅ 3 + (4 + 6 ⋅ 2) + 18/3 ²-8 равно 16.

4/2 ⋅ 3 + (4 + 6 ⋅ 2) + 18/3 ² — 8 = 16

Уф! Об этом было много сказать, но как только мы разложили его в правильном порядке, решить его было уже не так сложно.Когда вы впервые изучаете порядок операций, вам может потребоваться некоторое время, чтобы решить подобную проблему. Однако при достаточной практике вы привыкнете решать проблемы в правильном порядке.

Запоминание порядка операций

Если вы будете его часто использовать, то со временем разберетесь с порядком операций. А пока может быть полезно запомнить слово или фразу. Двумя популярными из них являются бессмысленное слово PEMDAS (круглые скобки, экспоненты, умножение и деление, сложение и вычитание) и фраза , пожалуйста, извините мою дорогую тетю Салли .

/ ru / algebra-themes / exponents / content /

Упорядочивание математических операций, BODMAS | SkillsYouNeed

Для вычисления, которое включает только одну математическую операцию с двумя числами, это простой случай сложения, вычитания, умножения или деления, чтобы найти свой ответ.

А что делать, если есть несколько номеров и разные операции? Может быть, вам нужно делить и умножать или складывать и делить. Что вы делаете тогда?

К счастью, математика — дисциплина, основанная на логике.Как это часто бывает, есть несколько простых правил, которые помогут вам определить порядок выполнения расчетов. Они известны как «Порядок действий» .

Правила упорядочивания в математике — BODMAS

BODMAS — полезная аббревиатура, которая сообщает вам порядок, в котором вы решаете математические задачи. Важно, чтобы вы следовали правилам BODMAS, потому что без них ваши ответы могут быть неправильными.

Аббревиатура BODMAS означает:

B ракетки (части расчета внутри скобок всегда идут на первом месте).
O rders (числа, содержащие степени или квадратные корни).
D ivision.
M повторение.
A доп.
S убирание.

BODMAS, BIDMAS или PEMDAS?

Вы можете часто видеть BIDMAS вместо BODMAS. Они точно такие же. В BIDMAS буква «I» относится к индексам, которые аналогичны заявкам. Для получения дополнительной информации см. Нашу страницу «Специальные числа и понятия».

PEMDAS

PEMDAS обычно используется, в США он работает так же, как BODMAS. Акроним PEMDAS:

P аренца,

E xponents (степени и корни),

M ultiplication и D ivision,

A ddition и S ubtraction.

Использование BODMAS

Кронштейны

Начните с чего-нибудь внутри скобок слева направо.

Пример:

4 × (3 + 2) =?

Вам нужно выполнить операцию, сначала в скобках 3 + 2, а затем умножить ответ на 4.

3 + 2 = 5.
4 × 5 = 20

Если вы проигнорируете скобки и произведете расчет слева направо 4 × 3 + 2, вы получите 14. Вы можете увидеть, как скобки влияют на ответ.

Заказы

Далее выполните все, что связано с степенью или квадратным корнем (они также известны как заказы ), снова работая слева направо, если их больше одного.

Пример:

3 ² + 5 =?

Прежде чем прибавить 5, необходимо вычислить мощность.

3 ² = 3 × 3 = 9
9 + 5 = 14

Деление и умножение

После того, как вы выполнили какие-либо части вычислений с использованием скобок или степеней, следующим шагом будет деление и умножение .

Умножение и деление ранжируются одинаково, поэтому вы работаете с суммой слева направо, выполняя каждую операцию в том порядке, в котором она появляется.

Пример:

6 ÷ 2 + 7 × 4 =?

Сначала вам нужно выполнить деление и умножение, но у вас есть по одному.

Начните слева и двигайтесь вправо, что означает, что вы начинаете с 6 ÷ 2 = 3. Затем выполните умножение, 7 × 4 = 28.

Теперь ваш расчет 3 + 28.

Завершите сложение, чтобы найти ответ: 31 .

Смотрите наши страницы: Умножение и Деление , чтобы узнать больше.

Сложение и вычитание

Последний шаг — вычислить любое прибавление или вычитание . Опять же, вычитание и сложение равны, и вы просто работаете слева направо.

Пример:

4 + 6-7 + 3 =?

Вы начинаете слева и продвигаетесь вперед.

4 + 6 = 10
10-7 = 3
3 + 3 = 6
Ответ: 6 .

Смотрите наши страницы: Сложение и Вычитание , чтобы узнать больше.

Собираем все вместе

Этот последний рабочий пример включает все элементы BODMAS.

Пример:

4 + 8 ² × (30 ÷ 5) =?

Начнем с расчета в скобках.

30 ÷ 5 = 6
Это дает вам 4 + 8 ² × 6 =?

Затем рассчитайте заказы — в данном случае квадрат 8.

8 ² = 64
Теперь ваш расчет 4 + 64 × 6

Затем переходим к умножению 64 × 6 = 384

Наконец, выполните сложение.4 + 384 = 388

Ответ: 388 .

Контрольные вопросы BODMAS

Правила BODMAS легче всего понять с помощью некоторой практики и примеров.

Попробуйте эти вычисления самостоятельно, а затем откройте окно (щелкните символ + слева), чтобы увидеть работу и ответы.

3 + 20 × 3

В этом расчете нет скобок или порядков.

Умножение предшествует сложению, поэтому начните с 20 × 3 = 60.
Расчет теперь показывает 3 + 60

Следовательно, ответ 63 .

25-5 ÷ (3 + 2)

Начните с скобок. (3 + 2) = 5.
Расчет теперь показывает 25-5 ÷ 5
Деление предшествует вычитанию.5 ÷ 5 = 1.
Расчет теперь показывает 25 — 1

Следовательно, ответ 24 .

10 + 6 × (1 + 10)

Начните с скобок. (1 + 10) = 11.
Расчет теперь показывает 10 + 6 × 11
Умножение предшествует сложению. 6 × 11 = 66.
Расчет теперь показывает 10 + 66.

Следовательно, ответ 76 .

5 (3 + 2) + 5 ²

Если в этом вычислении нет знака, подобного этому, оператор представляет собой умножение, то же самое, что и запись 5 × (3 + 2) + 5 ².

Сначала завершите расчет в скобках: (3 + 2) = 5.
Это дает вам 5 × 5 + 5 ².
Следующий шаг — заказы, в данном случае квадрат. 5 ² = 5 × 5 = 25.Теперь у вас 5 × 5 + 25.
Деление и умножение предшествуют сложению и вычитанию, поэтому следующий шаг — 5 × 5 = 25. Теперь вычисление показывает 25 + 25 = 50.

Ответ: 50 .

(105 + 206) — 550 ÷ 5 ² + 10

В этом есть все! Но не паникуйте. BODMAS по-прежнему применяется, и все, что вам нужно сделать, это отменить расчет.

Начните с скобок.(105 + 206) = 311.
Расчет теперь показывает 311-550 ÷ 5 ² + 10
Далее, приказы или полномочия. В данном случае это 5 ² = 25.
Расчет теперь показывает 311-550 ÷ 25 + 10
Далее, деление и умножение. Умножения нет, но деление 550 ÷ 25 = 22.
Теперь расчет показывает 311 — 22 + 10.
Хотя у вас еще остались две операции, сложение и вычитание ранжируются одинаково, поэтому вы просто идете слева направо.311 — 22 = 289 и 289 + 10 = 299.

Ответ: 299 .

7 + 7 ÷ 7 + 7 × 7-7 =?

Подобные проблемы часто появляются на сайтах социальных сетей с такими заголовками, как «90% людей ошибаются». Просто следуйте правилам BODMAS, чтобы получить правильный ответ.

Здесь нет скобок или порядков, поэтому начните с деления и умножения.
7 ÷ 7 = 1 и 7 × 7 = 49.
Расчет теперь показывает 7 + 1 + 49-7
Теперь выполните сложение и вычитание. 7 + 1 + 49 = 57-7 = 50

Следовательно, ответ будет 50 .

Как у вас дела?

Надеюсь, вам удалось правильно ответить на все вопросы. Если нет, вернитесь и проверьте, где вы ошиблись, и еще раз прочтите правила.

Чем больше вы практикуетесь, тем легче становится БОДМА, и в конечном итоге вам даже не придется об этом думать.

Порядок операций — Джеймс Бреннан

Порядок действий

Когда мы сталкиваемся с таким выражением, как 3 + 15 ÷ 3 + 5 × 2 ^{2 + 3}, то имеет большое значение, как мы выбираем, какие операции выполнять в первую очередь. Нам нужен набор правил, которые направят любого к одному уникальному значению для такого рода выражений. Некоторые из этих правил просто основаны на соглашении, в то время как другие навязаны нам математической логикой. В главе о свойствах действительных чисел вы увидите, как закон распределения согласуется с этими правилами.Общепризнанный порядок вычисления математического выражения следующий:

1. Круглые скобки наизнанку

Под «круглыми скобками» мы подразумеваем все, что действует как символ группировки, включая все, что находится внутри символов, например [], {}, | | и . Любое выражение в числителе или знаменателе дроби или в показателе степени также считается сгруппированным и должно быть упрощено перед выполнением дальнейших операций.

· Если есть вложенные круглые скобки (скобки внутри скобок), вы работаете от самых внутренних скобок наружу.

2. Показатели

Также другие специальные функции, такие как log, sin, cos и т. Д.

3. Умножение и деление слева направо

Порядок слева направо не имеет значения, если используется только умножение, но имеет значение для деления.

4. Сложение и вычитание слева направо

Порядок слева направо не имеет значения, если используется только сложение, но он имеет значение для вычитания.

Пример: Возвращаясь к нашему исходному примеру, 3 + 15 ÷ 3 + 5 × 2 ^{2 + 3}

Дано:	3 + 15 ÷ 3 + 5 × 2 ^{2 + 3}
Показатель степени — это подразумеваемая группировка, , поэтому сначала нужно вычислить 2 + 3:	= 3 + 15 ÷ 3 + 5 × 2 ⁵
Сейчас проводится экспонента:	= 3 + 15 ÷ 3 + 5 × 32
Теперь умножение и деление, слева направо, используя 15 ¸ 3 = 5 и 5 ´ 32 = 160: .	= 3 + 5 + 160
Теперь сложение слева направо:	= 168

Калькулятор Примечание. Большинство современных калькуляторов «знают» порядок операций, и вы можете вводить выражения практически в том виде, в каком они написаны.Некоторые старые калькуляторы будут выполнять каждую операцию при нажатии клавиши, что может привести к выполнению операций в неправильном порядке. Попробуйте несколько примеров, если вы не знаете, как ведет себя ваш калькулятор.

Например, если вы введете

3 + 4 × 5 =
Правильный ответ должен быть 23, потому что умножение должно выполняться перед сложением, что дает 3 + 20. Но если ваш калькулятор выполняет «3 + 4» до перехода к «× 5» , он покажет результат 35, потому что он будет видеть его как 7 × 5.

Калькулятор Примечание. Используйте скобки для принудительного группирования. Если вы оцениваете такое выражение, как

знаменатель необходимо упростить перед делением. Если вы введете его в свой калькулятор как 4 ÷ 3 + 5, он сначала оценит «4 ÷ 3», а затем прибавит 5 к результату, дав неправильный ответ 6.3333. Чтобы он сначала выполнил сложение, используйте круглые скобки:

4 ÷ (3 + 5) = 0,5

В нашем примере задачи, приведенном выше, «2 + 3» в показателе степени является подразумеваемой группировкой, и вам нужно будет использовать круглые скобки.», А на других -« y ^x »)

Упрощение выражений с помощью порядка операций

Результаты обучения

Используйте порядок операций для упрощения математических выражений
Упростите математические выражения, включающие сложение, вычитание, умножение, деление и показатели

Упростите выражения, используя порядок операций

Мы ввели большинство символов и обозначений, используемых в алгебре, но теперь нам нужно уточнить порядок операций. В противном случае выражения могут иметь разное значение и давать разные значения.

Например, рассмотрим выражение:

[латекс] 4 + 3 \ cdot 7 [/ латекс]

[latex] \ begin {array} {cccc} \ hfill \ text {Некоторые студенты говорят, что это упрощается до 49.} \ Hfill & & & & \ hfill \ text {Некоторые студенты говорят, что это упрощается до 25.} \ hfill \\ \ begin {array} {ccc} & & \ hfill 4 + 3 \ cdot 7 \ hfill \\ \ text {Поскольку} 4 + 3 \ text {дает 7.} \ hfill & & \ hfill 7 \ cdot 7 \ hfill \\ \ text {And} 7 \ cdot 7 \ text {равно 49.} \ hfill & & \ hfill 49 \ hfill \ end {array} & & & \ begin {array} {ccc} & & \ hfill 4 + 3 \ cdot 7 \ hfill \\ \ text {Since} 3 \ cdot 7 \ text {равно 21.} \ hfill & & \ hfill 4 + 21 \ hfill \\ \ text {And} 21 + 4 \ text {составляет 25.} \ hfill & & \ hfill 25 \ hfill \ end {array} \ hfill \ end {array} [/ latex]

Представьте себе путаницу, которая могла бы возникнуть, если бы для каждой проблемы было несколько разных правильных ответов. Одно и то же выражение должно дать тот же результат. Таким образом, математики установили некоторые правила, называемые порядком операций, которые определяют порядок, в котором части выражения должны быть упрощены.

Порядок операций

При упрощении математических выражений выполняйте операции в следующем порядке:
1. P аренсы и другие символы группировки

Упростите все выражения внутри скобок или других группирующих символов, работая в первую очередь с самыми внутренними скобками.

2. E xponents

Упростите все выражения с показателями степени.

3. M ultiplication и D ivision

Выполняйте все операции умножения и деления слева направо.Эти операции имеют равный приоритет.

4. A ddition и S ubtraction

Все операции сложения и вычитания выполняются слева направо. Эти операции имеют равный приоритет.

Студенты часто спрашивают: «Как мне запомнить заказ?» Вот способ помочь вам запомнить: возьмите первую букву каждого ключевого слова и замените глупую фразу. P аренда E xcuse M y D ухо A Unt S союзник.

Порядок работы
P аренда	P арентезов
E xcuse	E компоненты
M y D ухо	M ultiplication и D ivision
A Unt S союзник	A ddition и S ubtraction

Хорошо, что « M y D ear» идут вместе, поскольку это напоминает нам, что m ultiplication и d ivision имеют равный приоритет.Мы не всегда выполняем умножение перед делением или всегда делаем деление перед умножением. Делаем их слева направо.
Точно так же « A Unt S союзник» идет вместе и напоминает нам, что ddition и s ubtraction также имеют равный приоритет, и мы выполняем их в порядке слева направо.

пример

Упростите выражения:

[латекс] 4 + 3 \ cdot 7 [/ латекс]
[латекс] \ влево (4 + 3 \ вправо) \ cdot 7 [/ латекс]

Решение:

On the next line it states are there any parentheses in the expression? No. The line below that states are there any exponents in the expression? No. The next line states is there any multiplication or division in the expression? Yes. The next line states Multiply first and is followed by the expression of four plus three times seven. The expression is now four plus twenty-one. The last operation is addition. Add four and twenty-one to get twenty-five.» data-label=»»>

1.
	[латекс] 4 + 3 \ cdot 7 [/ латекс]
Есть ли какие-нибудь арентезы p ? №
Есть ли компоненты e ? №
Есть ли ультипликация m или d ivision? да.
Сначала умножить.	[латекс] 4+ \ color {красный} {3 \ cdot 7} [/ латекс]
Доп.	[латекс] 4 + 21 [/ латекс]
	[латекс] 25 [/ латекс]

2.
	[латекс] (4 + 3) \ cdot 7 [/ латекс]
Есть ли какие-нибудь арентезы p ? да.	[латекс] \ color {красный} {(4 + 3)} \ cdot 7 [/ латекс]
Упростите в скобках.	[латекс] (7) 7 [/ латекс]
Есть ли компоненты e ? №
Есть ли ультипликация m или d ivision? да.
Умножить.	[латекс] 49 [/ латекс]

пример

Упростить:

[латекс] \ text {18} \ div \ text {9} \ cdot \ text {2} [/ latex]
[латекс] \ text {18} \ cdot \ text {9} \ div \ text {2} [/ latex]

Показать решение

Решение:

Are there any parentheses? No. Are there any exponents? No. Is there any multiplication or division? Yes, there is both multiplication and division. Perform multiplication and division from left to right so, divide first. Divide eighteen by nine to get two. The expression is now two times two. The last operation is multiplication. Multiply two by two to get four.» data-label=»»>

1.
	[латекс] 18 \ div 9 \ cdot 2 [/ латекс]
Есть ли какие-нибудь арентезы p ? Нет.
Есть ли компоненты e ? №
Есть ли ультипликация m или d ivision? да.
Умножайте и делите слева направо. Делить.	[латекс] \ color {красный} {2} \ cdot 2 [/ латекс]
Умножить.	[латекс] 4 [/ латекс]

2.
	[латекс] 18 \ cdot 9 \ div 2 [/ латекс]
Есть ли какие-нибудь арентезы p ? Нет.
Есть ли компоненты e ? №
Есть ли ультипликация m или d ivision? да.
Умножайте и делите слева направо.
Умножить.	[латекс] \ color {красный} {162} \ div 2 [/ латекс]
Разделить.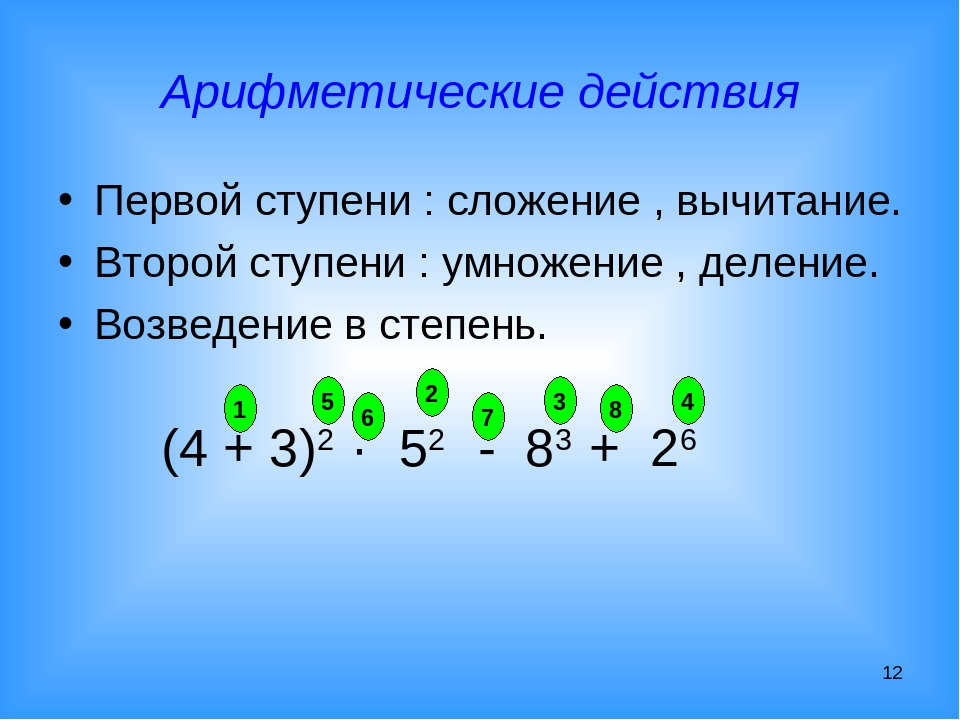	[латекс] 81 [/ латекс]

пример

Упростить: [латекс] 18 \ div 6 + 4 \ left (5-2 \ right) [/ latex].

Показать решение

Решение:

	[латекс] 18 \ div 6 + 4 (5-2) [/ латекс]
Скобки? Да, сначала вычтите.	[латекс] 18 \ div 6 + 4 (\ color {red} {3}) [/ латекс]
Показатели? №
Умножение или деление? да.
Сначала разделите, потому что мы умножаем и делим слева направо.	[латекс] \ color {красный} {3} +4 (3) [/ латекс]
Любое другое умножение или деление? да.
Умножить.	[латекс] 3+ \ color {красный} {12} [/ латекс]
Любое другое умножение или деление? №
Любое сложение или вычитание? да.	[латекс] 15 [/ латекс]

В видео ниже мы показываем еще один пример того, как использовать порядок операций для упрощения математического выражения.

Когда имеется несколько символов группировки, мы сначала упрощаем самые внутренние круглые скобки и работаем наружу.