Деятельность учащихся | ||||
— Для успешной работы на уроке нам необходимы следующее: учебник, рабочая тетрадь, ручка, карандаш, линейка. Если все необходимое на парте, садитесь | Ученики проверяют необходимое на уроке оборудование, если все в наличии садятся, если нет достают все необходимое | Умею находить первое промежуточное делимое и определить количество цифр в неполном частном | Умею находить результат деления и правильно записать цифру в неполном частном и остаток (если остаток равен 0, то его не записывать) | Умею находить второе промежуточное делимое. | Умею находить результат деления и правильно записать цифру в неполном частном и остаток (если остаток равен 0, то его не записывать) |
Всё умею, всё получается! | ||||
Умею, но допускаю ошибки | ||||
Материал плохо понял, испытываю трудности. | Умею находить первое промежуточное делимое и определить количество цифр в неполном частном | Умею находить результат деления и правильно записать цифру в неполном частном и остаток (если остаток равен 0, то его не записывать) | Умею находить второе промежуточное делимое. | Умею находить результат деления и правильно записать цифру в неполном частном и остаток (если остаток равен 0, то его не записывать) |
Всё умею, всё получается! | ||||
Умею, но допускаю ошибки | ||||
Материал плохо понял, испытываю трудности. | Умею находить первое промежуточное делимое и определить количество цифр в неполном частном | Умею находить результат деления и правильно записать цифру в неполном частном и остаток (если остаток равен 0, то его не записывать) | Умею находить второе промежуточное делимое. | Умею находить результат деления и правильно записать цифру в неполном частном и остаток (если остаток равен 0, то его не записывать) |
Всё умею, всё получается! | ||||
Умею, но допускаю ошибки | ||||
Материал плохо понял, испытываю трудности. | ||||
Правильно записать пример деления в столбик | ||||
Правильно записать пример деления в столбик | ||||
Правильно записать пример деления в столбик | ||||
Правильно записать пример деления в столбик | ||||
Правильно записать пример деления в столбик | ||||
Правильно записать пример деления в столбик | ||||
Правильно записать пример деления в столбик | ||||
Правильно записать пример деления в столбик |
простой принцип с примерами — «Семья и Школа»
Содержание
Содержание статьи
- Как правильно делить в столбик?
- Что нужно знать ребенку для понимания деления столбиком?
- Методика обучения детей делению столбиком
- Работа с многозначными числами
- Как объяснить деление с остатком?
Чтобы упростить деление чисел, традиционно используется метод деления в столбик. Не все дети понимают принцип с первого раза, а многие взрослые уже успели его забыть. Давайте разберемся, как без лишних слов объяснить ребенку деление «уголком», чтобы он научился решать примеры с двузначными, трехзначными и даже четырехзначными числами.
Не все дети понимают принцип с первого раза, а многие взрослые уже успели его забыть. Давайте разберемся, как без лишних слов объяснить ребенку деление «уголком», чтобы он научился решать примеры с двузначными, трехзначными и даже четырехзначными числами.
Как правильно делить в столбик?
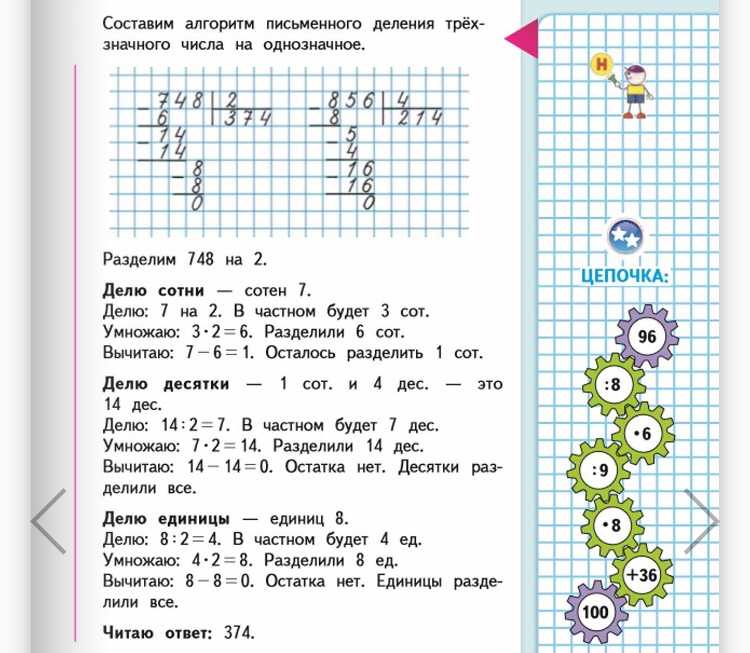
Удобнее рассмотреть сам процесс на несложной иллюстрации (№1).
Как найти частное двух чисел – 35 и 5?
- Пишем числа, участвующие в делении, так:
Делимое в данном случае – 35, делитель – 5. Под делителем пишется частное.
- Находим неполное частное. Посмотрим на первую цифру слева. В нашем случае это 3, и оно меньше 5 – значит, добавляем следующую цифру слева и будем работать с этой величиной (у нас 35).
- Определяем, какое количество пятерок (5) поместится в 35. Вспоминаем таблицу умножения и заключаем, что в 35 поместиться 7 пятерок. Значит, в графе частное записываем 7.
- Проверяем правильность действий путем умножения: 7 X 5=35.
 Все верно, решение выполнено точно.
Все верно, решение выполнено точно.
Что нужно знать ребенку для понимания деления столбиком?
Чтобы любимое чадо освоило, как делить уголком (в столбик), нужно два условия:
- умение быстро считать в уме.
В конце 3 класса ученики усваивают, как разделить простые двузначные числа.
При переходе в 4 класс дети учатся делить многозначные числа (больше, чем 100). Также происходит обучение делению уголком чисел с двузначным и трехзначным делителем, решение примеров с остатком.
Методика обучения детей делению столбиком
Если школьник пропустил занятия по математике либо не смог усвоить знания на уроке, то родители должны сами донести до него нужную информацию. Спешка в таком деле неуместна – быстро не значит хорошо. Следует проявить терпение. Деление чисел – простое дело для взрослого, а для школьника задача весьма сложная.
Проверьте знание таблицы умножения.
Если ребенок не умножает «автоматически», позвольте подсматривать в табличку.
Первый пример можно взять простейший, с делением без остатка на однозначное число (как в иллюстрации №1).
Когда малыш понял принцип и успешно справился с несложным заданием, пора научить его делению трехзначных чисел. Выполним пример №2.
Работа с многозначными числами
Задание 2: разделим 372 на 6. Для этого на листке бумаги производим следующие действия:
- Определяем делимое (372) и делитель (6), оформляем запись в уголок:
- Неполное частное в нашем варианте, конечно, 37 (т. к. в 3 не поместится 6 ни разу, берем следующую цифру).
- Считаем, много ли шестерок уместится в 37. Если 36:6, то получим 6. Получившееся 6 пишем в графе «частное», а 36 пишем под делителем.
- Вычитаем из 37-36=1.
 Пишем единичку слева внизу под чертой:
Пишем единичку слева внизу под чертой: - В единичке не поместится ни одной шестерки, значит, берем оставшуюся цифру из делимого (2). Получилось 12. Нужно определить, сколько в 12 поместится 6 (12 больше 6 ровно в два раза). Получаем 2. Записываем в частное получившуюся величину:
Пример решен, можно проверить правильность путем умножения: 62X6=372.
Как объяснить деление с остатком?
Иногда разделить на равные доли невозможно. Легче всего объяснить такую ситуацию школьнику на несложной задаче. Например:
В группе 8 учеников, на обед им выдали 18 ватрушек на подносе. Когда каждый получит по 2 ватрушки (18:8=2 и ост. 2), на подносе останутся лишние 2 штуки. Это и есть остаток.
Решение столбиком с остатком, по математическому правилу, записывается точно так же, как и без него. Разница лишь в том, что в конце остаток будет. В этом варианте правильно прописать количество целых единиц и количество единиц в остатке (пример: 4 целых и 9 в остатке).
Обучение школьника должно проходить поэтапно, от простых примеров к более сложным. Если нет понимания простых действий в делении, значит, нужно повторить информацию еще раз. Постепенно решение примеров начнет происходить быстрее и увереннее. Главное – поверить в силы маленького человека, быть терпеливым, и тогда делить числа методом столбца станет интересным занятием для школьника.
Умножение и деление. Часть вторая. Алгоритмы
← Умножение и деление. Часть первая. Развитие концепции и навыков
Буктрейлеры! →
19 март
После того, как учащиеся решили многие задачи разными способами, мы переходим к алгоритмам (процедуре вычислений).
Стратегии разделения используют распределительное свойство умножения. Не волнуйтесь, я тоже не слышал об этом до того, как начал преподавать математику. Хотел бы я, потому что это действительно важно понять (даже если вы не знаете этот термин). Это важно для алгебры, а также удобно для ментальной математики. Я говорил об этом в своем посте о математических беседах здесь, потому что мы можем использовать его и для наших фактов о таблице умножения. Это видео действительно хорошо объясняет это с помощью визуальных эффектов.
Хотел бы я, потому что это действительно важно понять (даже если вы не знаете этот термин). Это важно для алгебры, а также удобно для ментальной математики. Я говорил об этом в своем посте о математических беседах здесь, потому что мы можем использовать его и для наших фактов о таблице умножения. Это видео действительно хорошо объясняет это с помощью визуальных эффектов.
Я обнаружил, что некоторые учащиеся могут найти метод умножения двузначного числа на однозначное самостоятельно и когда они делятся своей стратегией с классом! Ух ты! Глаза других детей широко раскрываются в момент Эврики! Что такое метод разрыва? Вы разбиваете одно или несколько чисел на части, чтобы упростить умножение. Это также демонстрирует, почему вы «переносите» число в следующий столбец.
Когда я продолжу учить студентов традиционному способу умножения, они смогут понять, почему они «несут» 2 (на самом деле это 2 десятка в 25, и они должны быть в столбце десятков). Над этим сейчас работают учащиеся 4 класса.
Раздел
В пятом классе мы работали над разделом. Мы начали с задач, и пары решали деление так, как им хотелось. Затем мы перешли к альтернативному алгоритму длинного деления. Мне нравится этот метод, потому что он подтверждает, что деление — это операция, обратная умножению (они отменяют друг друга) и что это повторяющееся вычитание. Вот пример:
Сначала я начал с 10 групп, потому что 10 — хорошее число, на которое легко умножать, но многие дети быстро понимают, что умножать на более крупные «дружественные» числа проще и быстрее).
Мне нравится это видео, объясняющее метод, за исключением того, что в нем нет звука, и чтение может быть проблемой для некоторых детей, но мы можем прочитать его им.
Умножение и деление требуют долгого обучения. Учащимся нужно время, чтобы решать задачи, изучать различные способы решения задач, практиковаться в таблице умножения, практиковать алгоритмы. Я думаю, что всем учащимся будет полезно решать одну задачу на вычитание в день (и проверять свой ответ на сложение) и одну задачу на деление в день (проверять свой ответ на умножение), пока они не станут свободно говорить.
Учащимся нужно время, чтобы решать задачи, изучать различные способы решения задач, практиковаться в таблице умножения, практиковать алгоритмы. Я думаю, что всем учащимся будет полезно решать одну задачу на вычитание в день (и проверять свой ответ на сложение) и одну задачу на деление в день (проверять свой ответ на умножение), пока они не станут свободно говорить.
Нравится:
Нравится Загрузка…
Теги: разбить умножение, альтернативный алгоритм деления
← Умножение и деление – Часть первая – Развитие концепции и навыков
Буктрейлеры! →
Что такое алгоритм в математике? Определение, свойства, примеры
Что такое алгоритм?
Алгоритм — это пошаговый процесс решения конкретной проблемы.
Думайте об этом как о математическом «рецепте», позволяющем добраться до сути проблемы. Если вы будете следовать инструкциям, вы сможете получить ответ в кратчайшие сроки!
Пример алгоритма: Простым примером алгоритма, который вы используете каждый день, является ваша утренняя рутина. Скажем, вы встаете в 6:30 утра, чтобы идти в школу. Если вы всегда встаете, чистите зубы, пьете воду, идете в ванную, а затем принимаете ванну, это может быть алгоритмом, которому следует ваше тело! Алгоритмы вокруг нас. Важно обнаружить их, чтобы узнать, как они функционируют, а затем создать свои собственные.
Скажем, вы встаете в 6:30 утра, чтобы идти в школу. Если вы всегда встаете, чистите зубы, пьете воду, идете в ванную, а затем принимаете ванну, это может быть алгоритмом, которому следует ваше тело! Алгоритмы вокруг нас. Важно обнаружить их, чтобы узнать, как они функционируют, а затем создать свои собственные.
В повседневной жизни мы применяем множество процедур, которые, как мы не понимаем, являются алгоритмами.
Сюда входят:
Завязывание шнурков
Расписание дня, которому вы следуете в школе
Правила алгебраических формул, такие как сложение и вычитание
Техника, которой вы пользуетесь во время занятий спортом
Правила игр с друзьями
Алгоритмы в математике
Определение математического алгоритма
Алгоритм в математике — это процедура, описание набора шагов, которые можно использовать для решения математических вычислений.
Например, пошаговая процедура, используемая в длинных делениях, является распространенным примером математического алгоритма.
Пример математического алгоритма: Процесс решения математической задачи, такой как «Сколько 82 разделить на 3?» можно получить, выполнив следующий алгоритм:
Сколько раз 3 входит в 8?
Ответ: 2.
Сколько осталось? 2
Поставьте 2 (десятки) перед 3.
Сколько раз 3 входит в число 22?
Ответ: 7 с остатком 1.
И, конечно же, ответ равен 27 с остатком 1.
Стандартный алгоритм сложения
Стандартный алгоритм сложения состоит из четырех простых шагов:
Шаг 1. Выровняйте числа по вертикали, сопоставляя места ценности.
Шаг 2. Сложите числа с одинаковым разрядом, начиная со столбца единиц.
Шаг 3: Запишите сумму под каждым столбцом.
Шаг 4: Если сумма в столбце больше 9, перенесите цифру десятков в следующий столбец.
Стандартный алгоритм вычитания
Стандартный алгоритм сложения состоит из четырех простых шагов:
Шаг 1. Выровняйте числа по вертикали, сопоставив разряды.
Шаг 2. Вычтите числа с одинаковым разрядом, начиная со столбца единиц.
Шаг 3: Запишите разницу под каждым столбцом.
Шаг 4: Если число в верхней части столбца меньше числа в нижней части, перегруппируйте перед вычитанием.
Стандартный алгоритм умножения
Перейдите по ссылке , чтобы проверить стандартный алгоритм умножения.
Преимущества алгоритмов
Алгоритмы необходимы из-за большого разнообразия приложений, в которых они используются. Понимание того, как работают алгоритмы, также имеет решающее значение для развития навыков решения проблем и построения логических рассуждений. Ниже перечислены некоторые преимущества алгоритма:
- Процесс создания алгоритма позволяет вам смотреть на что-то рациональным и расчетливым образом, что очень помогает, когда дело доходит до решения различного рода проблем.
- Алгоритмы помогают преодолеть разрыв в общении, когда следование процедуре поможет вам найти необходимое решение, не повторяя процесс повторно.
 Вы можете следовать заранее установленным правилам, чтобы быстрее найти решение.
Вы можете следовать заранее установленным правилам, чтобы быстрее найти решение. - Алгоритмы используют определенную процедуру, и, используя и оптимизируя их, люди могут решать проблемы гораздо быстрее.
- Алгоритмы легко отлаживать, поскольку каждый шаг имеет свою логическую последовательность.
- Когда мы используем алгоритмы, мы можем разбить задачи на более мелкие шаги или части, поэтому программист может легко преобразовать их в настоящую программу.
Как только вы поймете основы алгоритмов, вы сможете создавать свои собственные, сэкономив себе много времени. С веселыми заданиями и играми SplashLearn вы можете проверить свои математические способности и найти алгоритмы в решаемых вами вопросах.
Свойства алгоритмов
Алгоритмы должны использоваться для решения трех задач:
- Правильное выполнение задачи: Работа, которую вы хотите выполнить, должна быть выполнена с ожидаемыми результатами.
- Эффективно обработайте предоставленную информацию: Время и ресурсы вашей системы должны использоваться надлежащим образом для понимания и последующего решения проблемы.

- Быть понятным: Алгоритмы предназначены для облегчения работы и в идеале должны поддерживаться на базовом уровне понимания.
Примеры алгоритмов в реальном мире
Многие компании в реальном мире используют алгоритмы, чтобы помочь своим клиентам или развивать свой бизнес, и часто пытаются улучшить их каждый день.
- YouTube : Посмотрев несколько видео определенного канала, вы заметите, что вам рекомендуют все больше и больше видео этого канала. Это связано с алгоритмом рекомендаций YouTube, который собирает информацию из вашей предыдущей истории для представления видео того же типа в вашей ленте, чтобы вы продолжали смотреть видео на платформе.
- Социальные сети : Если вы перейдете на страницу «Обзор» в Instagram, вы заметите, что многие из отображаемых сообщений связаны с теми, которые вы обычно ищете или ставите лайки/комментарии. Алгоритм здесь идентифицирует сообщения, с которыми вы взаимодействуете, и показывает вам больше таких сообщений, потому что считает, что вам нравятся такие сообщения.

- Google : Google использует очень известный алгоритм под названием PageRank для сортировки результатов поиска в порядке, который показывает наиболее посещаемые и достоверные сайты вверху. Этот алгоритм учитывает десятки параметров и быстро предоставляет сайты, которые вы хотите найти.
- Lyft/Uber : компании по совместному использованию такси, такие как Lyft или Uber, используют алгоритмы позиционирования, чтобы помочь клиентам находить автомобили рядом с ними для оптимального опыта. Эти глобальные алгоритмы позиционирования также помогают водителям находить самые быстрые маршруты для достижения определенного пункта назначения. Алгоритмы также помогают таким приложениям решить, какого клиента они должны выбрать первым или отказаться от него.
- Распознавание лиц : Всякий раз, когда компании требуют проверки пользователей, они могут перейти от таких методов, как идентификаторы пользователей и пароли, к более безопасным методам аутентификации, таким как распознавание лиц.
 Здесь алгоритмы используются для идентификации человека и проверки наличия у него доступа к вещам, к которым он хочет получить доступ.
Здесь алгоритмы используются для идентификации человека и проверки наличия у него доступа к вещам, к которым он хочет получить доступ.
Советы по освоению алгоритмов
Вы можете освоить алгоритмы, научившись замечать их в повседневной жизни. После этого вы можете разбить алгоритм на шаги размером с укус. Возможно, вам придется проверить это несколько раз, чтобы заметить закономерность в том, как что-то происходит, но как только вы ее найдете, вы сможете обнаруживать ее снова и снова.
Попытайтесь понять, почему происходит каждый шаг в процессе. Как только вы поймете, почему что-то происходит, вам будет легче соединить точки и выяснить логическую последовательность событий. Кроме того, это очень удобно для того, чтобы понять, как создавать алгоритмы для себя. С помощью веселых занятий и игр на SplashLearn вы сможете быстро освоить основы алгоритмов!
Решенные примеры
Пример 1 : Запишите этапы приготовления бутерброда с арахисовым маслом и желе.
Ответ: Этапы приготовления бутерброда с арахисовым маслом и желе:
Шаг 1: Возьмите 2 ломтика хлеба.
Шаг 2: Нанесите арахисовое масло на одну сторону ломтика.
Шаг 3: Нанесите желе на одну сторону другого ломтика.
Шаг 4: Сожмите оба ломтика хлеба вместе.
Пример 2: Запишите шаги стандартного алгоритма вычитания.
Ответ: Стандартный алгоритм вычитания состоит из следующих 4 шагов:
Шаг 1: Выровняйте числа по вертикали, сопоставляя разряды.
Шаг 2. Вычтите числа с одинаковым разрядом, начиная со столбца единиц.
Шаг 3: Запишите разницу под каждым столбцом.
Шаг 4: Если число в верхней части столбца меньше числа в нижней части, перегруппируйте перед вычитанием.
Пример 3: Напишите алгоритм, определяющий, является ли число четным или нечетным.
Ответ: Алгоритм определения четности или нечетности числа:
Шаг 1. Разделите число на 2.
Разделите число на 2.
Шаг 2: Если число полностью делится на 2, оно четное, иначе — нечетное.
Пример 4: Напишите алгоритм для нахождения площади прямоугольника.
Ответ: Алгоритм нахождения площади прямоугольника:
Шаг 1: Запишите длину меньшей стороны как «b».
Шаг 2: Запишите длину большей стороны как «l».
Шаг 3: Площадь прямоугольника будет произведением «l» и «b».
Практические задачи
1
Какая последовательность даст правильное изображение совы?
2,4,1,3
2,1,4,3
2,1,3,4
2,4,1,3
Правильный ответ: 2,1,4,3
Данная последовательность расставляет сову в правильной последовательности.
2
Какая последовательность даст правильный алгоритм кипячения воды?
1. Нагрейте кастрюлю, пока вода не закипит
2. Включите плиту
3. Возьмите пустую кастрюлю
4. Поставьте наполненную водой кастрюлю на огонь
Поставьте наполненную водой кастрюлю на огонь
5. Налейте воду в пустую кастрюлю
2,3,5,4,1
3,5,4,2,1
3,5,2,4,1
2,3,4,5,1
Правильный ответ: 3,5,2,4,1
Данная последовательность дает правильный алгоритм кипячения воды.
3
Каким будет первый шаг алгоритма сложения
Добавление цифр любого столбца
Добавление цифр столбца единиц
Вертикальное размещение цифр в столбцах
Перенос цифр столбца Правильный ответ:
900 цифры вертикально в столбцах
Первый шаг при сложении любых чисел — расположить их вертикально в столбцах.
4
Что из следующего правильно умножает 45 ✕ 7 с использованием стандартного алгоритма?
A
B
C
D
Правильный ответ: D




 )
) 64 , 33, 24, 18, 53, 82, 16, 48, 56, 67.
64 , 33, 24, 18, 53, 82, 16, 48, 56, 67.
 Один в паре читает вопрос, другой отвечает на него. В алгоритме записано как необходимо действовать, ваша задача ещё составить пошаговый план, что необходимо делать. Необходимые предложения вы найдете в конверте.
Один в паре читает вопрос, другой отвечает на него. В алгоритме записано как необходимо действовать, ваша задача ещё составить пошаговый план, что необходимо делать. Необходимые предложения вы найдете в конверте.  )
) )
) Этап контроля результатов деятельности учащихся или хода усвоения нового материала
Этап контроля результатов деятельности учащихся или хода усвоения нового материала

 Все верно, решение выполнено точно.
Все верно, решение выполнено точно. Если ребенок не умножает «автоматически», позвольте подсматривать в табличку.
Если ребенок не умножает «автоматически», позвольте подсматривать в табличку.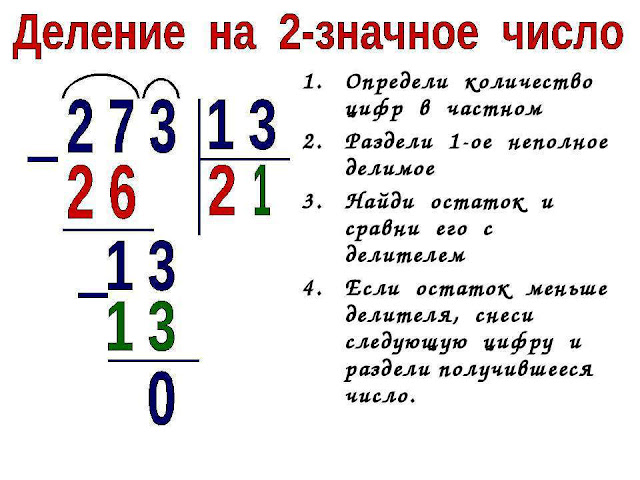 Пишем единичку слева внизу под чертой:
Пишем единичку слева внизу под чертой: Вы можете следовать заранее установленным правилам, чтобы быстрее найти решение.
Вы можете следовать заранее установленным правилам, чтобы быстрее найти решение.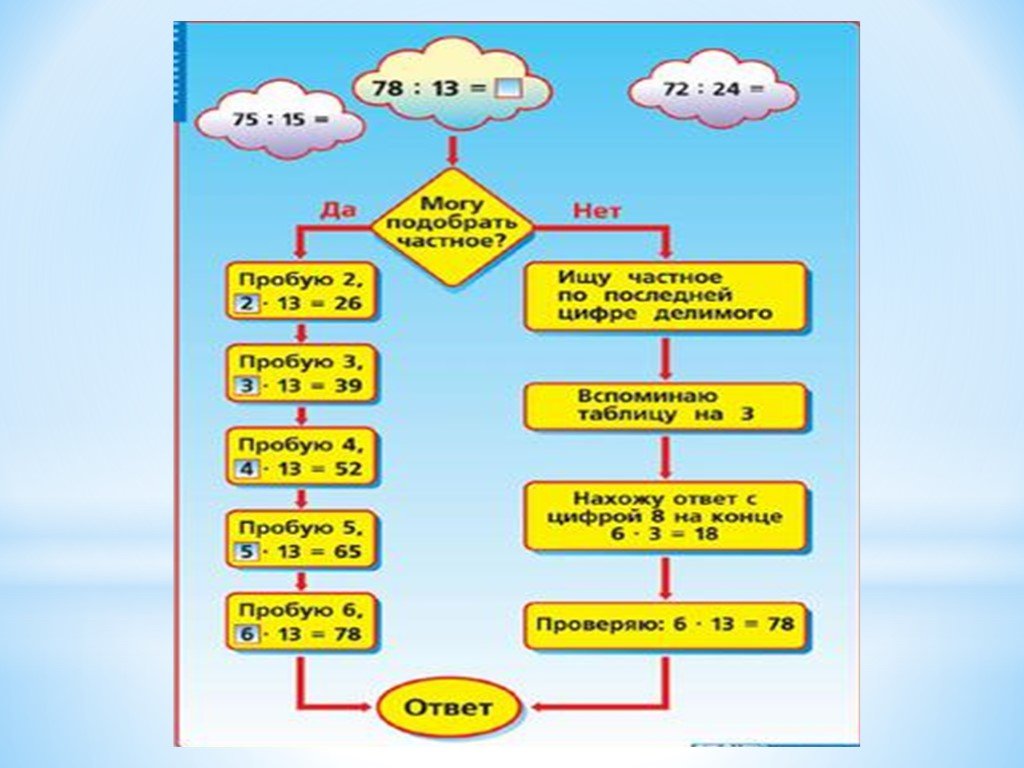

 Здесь алгоритмы используются для идентификации человека и проверки наличия у него доступа к вещам, к которым он хочет получить доступ.
Здесь алгоритмы используются для идентификации человека и проверки наличия у него доступа к вещам, к которым он хочет получить доступ.