Арифметические действия: сложение и вычитание. 4 класс
1. Тема урока в 4 –А классе: «Арифметические действия: сложение и вычитание».
урок математикиТема урока
в 4 –А классе:
«Арифметические
действия: сложение и
вычитание».
Прочитайте числа
8 900 207
41 095 204
905 003 020
Назовите единицы ΙΙΙ, ΙΙ, Ι классов.
Какое из чисел самое большое?
4. задание без ошибок балла задание с ошибкой – 1 балл «5» — 10 баллов «4» — 8 – 9 баллов «3» — 6 – 7 баллов
Тема: «Повторение.Арифметические действия:
сложение и вычитание».
5. +309.045 8.244 317.289
Письменное сложение ивычитание многозначных чисел
+309.045
8.244
317.289
-470.205
129.108
431.097
6. 1. Решение задачи на нахождение нескольких долей числа. 2. Сложение и вычитание многозначных чисел. 3. Выполнение
Запишите в тетрадь:15 мая.
Повторение. Арифметические
действия: сложение и
вычитание
(тема урока).
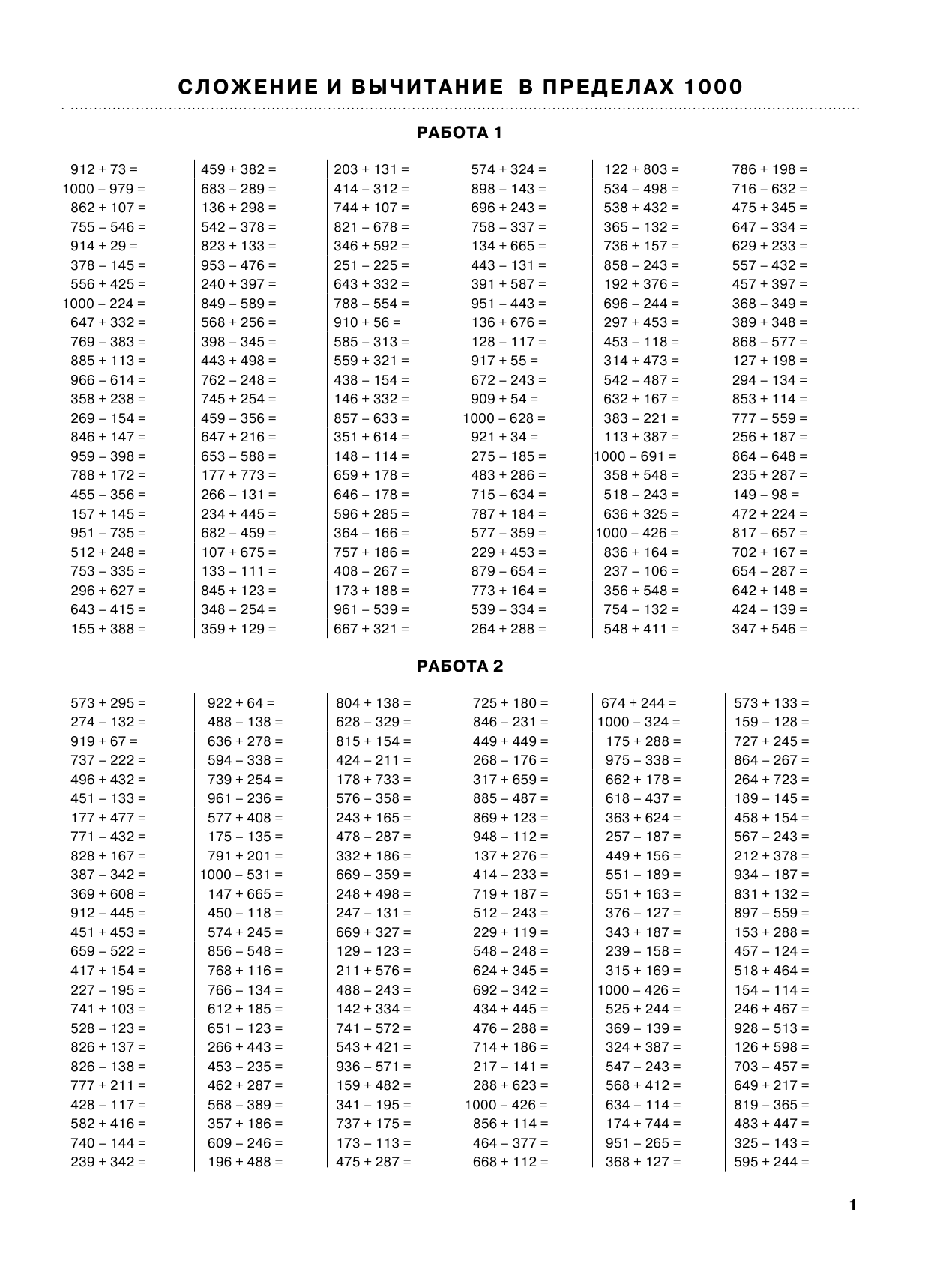
Сложение и вычитание величин,
запишите в тетрадь:
Задание 1.
9. 3ч 40 мин + 28 мин = 2 ц 30 кг + 64 кг = 105 км 40м + 24 км =
Сложение и вычитание величин.Выполните в тетради:
Задание 2.
3ч 40 мин + 28 мин =
2 ц 30 кг + 64 кг =
105 км 40м + 24 км =
Заполни пропуски и запиши в тетрадь:
8 ц 05 кг = … кг
83 т = …кг
4 км 035м = … м
2ч 25мин =… мин
Найди ошибку!
12. В ателье было 240 м ситца. Из него сшили рубашки, платья и простыни. Одну третью часть потратили на пошив рубашек, из 140 м
Реши задачу в тетради, записавданные в таблицу:
Задача 4.
В ателье было 240 м ситца. Из
него сшили рубашки, платья и
простыни. Одну третью часть
потратили на пошив рубашек, из
140 м сшили платья. Сколько
метров ситца потратили на
пошив простыней?
рубашки
платья
простыни
израсходовали
решение
одна третья часть
всей ткани
140м
?
?
?
всего
240м
14.
 1. Решение задачи на нахождение нескольких долей числа. 2. Сложение и вычитание многозначных чисел. 3. Выполнение Примеры 7 (2),(стр.90)
1. Решение задачи на нахождение нескольких долей числа. 2. Сложение и вычитание многозначных чисел. 3. Выполнение Примеры 7 (2),(стр.90)(решите примеры в столбик и
сделайте проверку).
Примеры 12 (стр. 91).
15. Спасибо за работу!
Этап мотивации (самоопределение) к учебной деятельности. Этап актуализации и фиксации индивидуального затруднения в пробном действии.
Этап открытия нового знания Этап динамической паузы. Этап включения нового знания в систему знаний, повторение и систематизации знаний
Этап самостоятельной работы с самопроверкой по эталону Этап рефлексии учебной деятельности на уроке. Домашнее задание | Положительный настрой на работу, установление контакта между учениками Создание условия для появления мотива к изучению нового. Закрепить:- приёмы письменного сложения и вычитания любых многозначных чисел Научить: — соотносить полученный результат с поставленной целью; — оценивать результат своей деятельности; — оценивать результат учебной деятельности Обеспечить активный отдых организму в процессе учебной деятельности Установить правильность и осознанность учащимися рассматриваемого материала. Выявить пробелы и провести коррекцию Перенос полученных знаний в практическую деятельность
Выявить качества знаний учащими, определить пробелы, установить их причины
Научить: — соотносить полученный результат с поставленной целью; — оценивать результат своей деятельности; — оценивать результат учебной деятельности
| Слайд 1 — Вслушайтесь внимательно в слова песни, в ней есть слова, связанные с математикой. (Звучит музыка, слова песни: «Я, ты, он…» — Какое слово вы услышали? (1000000). — В песне ещё поётся о том, что наша Родина богата полями, лесами. Площадь её составляет (17098246 кв.км). — Наша Россия многонациональная страна, на конец 2018 года численность населения составляет (146880432 чел). — Но, к сожалению, на доске только лишь граница, силуэт России. Давайте сделаем её к концу нашего занятия богатой, яркой, красивой. — Вернёмся к нашим числам. Как одним словом можно назвать все эти числа? — Какие действия вы уже умеете делать с многозначными числами? — Новый материал это для вас? — Значит какова тема нашего урока?
Слайд 2 — Какую цель мы перед собой поставим? Цель урока: создание условий для усвоения алгоритма письменного сложения и вычитания многозначных чисел. Слайд 3 — Значит, какие мы перед собой поставим задачи, чтобы добиться цели урока?
и применять полученные знания на практике. — А для реализации этих задач, что мы с вами должны сделать? — Откройте тетради, запишите дату. — В учебнике на стр. 16 № 2. Выполним 1-й столбик по вариантам. — Кто забыл алгоритм сложения и вычитания многозначных чисел, я вам раздала памятки на парты, можете посмотреть (здесь, кто справился быстрее можно дать дополнительное задание) (взаимопроверка, проверка по эталону). Слайд 5,6 — Оцените на полях в тетради -Заполните лист самооценки за 1 –е задание — Какая первая задача стояла перед нами. _ — — Справились мы с ней? (Учитель заполняет контур карты 1 листком) — Наша страна богата лесами, полями, реками, озёрами. Давайте выполним следующее задание, чтобы заполнилась наша карта. — А работать мы будем в группах. Разделимся на 6 групп. — О чём нужно помнить, когда работаешь в группе. ( Работать дружно, определить ответственного за группу, уметь выслушивать мнение товарища и показать умение приходить к общему мнению. — Выберите себе ответственного в группе, который в конце урока должен отчитаться за работу группы Слайд 7 — Задание № 2. Самая высокая гора Уральских гор – гора Народная, её вершина – 1895 м. А вершина самой высокой горы Кавказских гор – гора Эльбрус, её вершина – 5642 м. На сколько метров больше вершина самой высокой горы Кавказских гор, чем вершина самой высокой горы Уральских гор? — Прочитайте задание. — Что требуется узнать? Каким арифметическим действием будем выполнять? — Выполняем в группах, записываем в тетрадь Слайд 8 (проверка). — Какой приём отработали?(алгоритм вычитания многозначных чисел) — Заполняем лист самооценки за 2 задание — Какая группа первая выполнила задание, заполняем нашу карту 2 м листком. — Какая задача у нас решена? ( Учитель вешает 3 картинку на карту) Физминутка — Много пустого места ещё на нашей карте, продолжим работать над нашей темой?
— Задание № 3 Слайд 9 В озеро Байкал впадает много рек. — Прочитайте задание. — Что требуется узнать? Каким арифметическим действием будем выполнять? — Выполняем в группах, записываем в тетрадь Слайд 10 (проверка). Какой приём отработали?(алгоритм сложения многозначных чисел) — Заполняем лист самооценки за 3 задание — Какая группа первая выполнила задание, заполняем нашу карту 4 м листком. — Какая задача у нас выполнена? ( Учитель вешает 5 картинку на карту) — Какая задача у нас осталась нерешённая? -Выполним следующее задание — Задание № 4 Слайд 11 Берега России омывают 13 морей разной площадью. Запишите цифрами площадь морей, омывающих берега России, в порядке возрастания. — Что необходимо сделать? Слайд 12 (проверка). — Заполняем лист самооценки за 4 задание — Какая группа первая выполнила задание, заполняем нашу карту 6 м листком. — В течении урока вы заполняли лист самооценки. Давайте подведём итог. Посчитайте баллы и поставьте себе отметки. — Давайте посмотрим, что получилось. Поднимите руки, у кого 5, 4. — Мы многое узнали сегодня на уроке о нашей стране. Сейчас руководителей групп попрошу отчитаться за проделанную работу на уроке. Кто как работал в группе, согласны ли с выставленными отметками и заполним нашу карту. — Итак, цель нашего урока достигнута? -Задачи выполнены? — Скажите для чего нам нужны многозначные числа? Где мы можем ещё применять многозначные числа? — Будете применять изученный материал в жизни. — На столах стоят флажки, возьмитесь за белый цвет те, кому на уроке было интересно и у него всё получилось. — Возьмитесь за синий цвет те, кому на уроке было интересно, но некоторые задания вызывали затруднения. — А за красный цвет возьмитесь те, которым было скучно на уроке и трудно выполнять задания. — Домашнее задание вам будет на стр. 1. № 2 доделать – это на «3» 2.№ 4 – на «4» 3. № 5 – на «5» -Спасибо вам, ребята, за урок. | Отвечают на вопросы учителя. Читают числа Формулируют тему и цели урока Читают задания и выполняют Работа в парах, в группах Выполняют задание на листочках Участие в оценки результативности и процессуальной стороной работы класса и отдельных учащихся | Принятие социальной роли ученика, осознание личностного смысла учения и интерес к изучению темы Спокойное отношение к ошибке как рабочей ситуации, требующей коррекции, вера в себя. Навыки сотрудничества, умение находить выход из спорных ситуаций Внутренняя позиция школьника, самоуважение и самооценка Навыки сотрудничества в предложенной ситуации Самооценка на основе критериев успешности | Познавательные: определять взаимосвязь между действием сложения и вычитания многозначных чисел, обосновывать своё суждение; Регулятивные: учитывать правило при выполнении учебного задания; Коммуникатив ные: формулировать коррективные высказывания в рамках учебного диалога; Познавательные: — определять связь между действием сложения и вычитания любых многозначных чисел, обосновать своё суждение; — использовать ранее полученные знания, применять приобретенные умения при решении примеров на сложение и вычитание многозначных чисел. Регулятивные: — выполнять учебное задание в соответствии с правилом. Коммуникатив ные : — выполнять учебные задания в паре; — формулировать высказывания, используя математические термины. Регулятивные: Выполнять учебные действия и осуществлять контроль по результату Коммуникатив ные : адекватно воспринимать предложения товарищей по исправлению ошибок Познавательные: использовать приобретенные знания в практической деятельности Регулятивные: -выполнять учебное действие в соответствии с заданием. Коммуникативные: адекватно использовать речь для представления результата. Регулятивные: Адекватно судить о причинах своего успеха или неуспеха в учении Коммуникативные: формулировка собственного мнения и позиции | Анализировать способы вычисления Работать по алгоритмусложения и вычитания многозначных чисел. Систематизи ровать вычислительные навыки Вычислять арифметичес кие выражения |
4 класс.
 Моро. Учебник №2. Ответы к стр. 90
Моро. Учебник №2. Ответы к стр. 90Числа от 1 до 1000
Итоговое повторение всего изученного
Арифметические действия
Сложение и вычитание
Повтори всё, что ты знаешь об арифметических действиях. Отвечай на вопросы и выполняй задания, а в случае затруднений пользуйся справочным материалом (с. 118-124).
1. Составь и реши задачи на сложение и вычитание, используя слова: «Сколько всего …?», «Сколько осталось?», «… больше, чем …», «… меньше, чем …», «На сколько … больше, чем …?».
1) Автобус выехал из деревни и проехал до посёлка 100 км. Затем он проехал 150 км до города. Сколько всего километров проехал автобус?
100 + 150 = 250 (км)
О т в е т: всего 250 км.
2) На склад привезли 80 ящиков с яблоками. В магазин забрали со склада 30 ящиков. Сколько осталось на складе ящиков с яблоками?
80 – 30 = 50 (ящ. )
)
О т в е т: осталось 50 ящиков.
3) В первом ящике 20 кг яблок, а во втором – на 2 кг больше, чем в первом. Сколько килограмм яблок во втором ящике?
20 + 2 = 22 (кг)
4) В первом ящике 20 кг яблок, а во втором – на 2 кг меньше, чем в первом. Сколько килограмм яблок во втором ящике?
20 – 2 = 18 (кг)
О т в е т: во втором ящике 18 кг яблок.
5) В первом автобусе ехало 35 человек, а во втором – 45. На сколько во втором автобусе ехало человек больше, чем в первом?
45 – 35 = 10 (ч.)
О т в е т: на 10 человек.
2. Вспомни, как называются знаки, которые обозначают сложение и вычитание, и выражения, в которых числа соединены знаком сложения; знаком вычитания. Приведи примеры.
Знак сложения: + (плюс), знак вычитания: – (минус).
Знак сложения определяет сумму, знак вычитания – разность: 3 + 4 – сумма, 10 – 7 – разность.
3. Как называются при сложении и вычитании данные числа и число, которое получается в результате выполнения действия?
3 (первое слагаемое) + 4 (второе слагаемое) = 7 (сумма).
10 (уменьшаемое) – 7 (вычитаемое) = 3 (разность).
4. Прочитай, используя различные словесные формулировки, следующие равенства:
26 + 8 = 34 72 – 14 = 58
26 + 8 = 34
Сумма 26 и 8 равна 34.
26 плюс 8 равно 34
Если к 26 прибавить 8, то получится 34.
Первое слагаемое 26, второе 8, сумма 34.
72 – 14 = 58
Разность 72 и 14 равна 58.
72 минус 14 равно 58.
Если из 72 вычесть 14, то получится 58.
Уменьшаемое 72, вычитаемое 14, разность 58.
5. Рассмотри примеры и ответь на вопросы: 1) Что получится, если из суммы двух слагаемых вычесть одно из них? 2) Что получится, если к разности прибавить вычитаемое? 3) Что получится, если из уменьшаемого вычесть разность?
1) 37 + 48 = 85 2) 93 – 26 = 67
85 – 37 = 48 67 + 26 = 93
1) Получится другое слагаемое.
2) Получится уменьшаемое.
3) Получится вычитаемое.
6. После того как из числа 600 вычли задуманное число, получили 170. Какое число задумали?
600 – х = 170
х = 600 – 170
х = 430
Задумали число 430.
7. 1) Объясни два способа проверки сложения и вычитания.
+375 Проверка:
123 _498 _498
498 123 375
375 123
_867 Проверка:
482 +482 _867
385 385 385
867 482
2) Вычисли и сделай проверку.
79108 + 21892 200100 – 109678
3) Найди сумму и проверь различными способами.
1386 + 20049 + 63108 + 732
1) Сложение проверяется вычитанием, а вычитание проверяется сложением и вычитанием.
2) + 79108 Проверка:
21892 _101000 _101000
101000 21892 79108
79108 21892
_200100 Проверка:
109678 +109678 _200100
90422 90422 90422
79108 109678
3) 1386 + 20049 + 63108 + 732 = 85275
Проверка:
85275 – 1386 – 20049 – 63108 = 732
85275 – 1386 – 20049 – 732 = 63108
85275 – 1386 – 63108 – 732 = 20049
85275 – 20049 – 63108 – 732 = 1386
ЗАДАНИЕ НА ПОЛЯХ
РЕБУСЫ
306
+123
773
428
1630
_ 2507
1438
1069
Ответы по математике.
Математика. 4 класс
4.6 / 5 ( 30 голосов )
Сложение и вычитание числа 4. Приёмы вычислений.
Тема: «Сложение и вычитание числа 4. Приёмы вычислений».
Цель: создать условия для открытия способа сложения и вычитания числа 4.
Формируемые УУД:
личностные:
— способность к самооценке на основе критерия успешности учебной деятельности.
регулятивные:
— уметь определять и формулировать цель на уроке с помощью учителя, проговаривать последовательность действий на уроке; уметь высказывать свое предположение на основе работы с материалом учебника; планировать свое действие в соответствии с поставленной задачей.
коммуникативные:
— уметь оформлять свои мысли в устной форме; слушать и понимать речь других; учиться работать в паре, формулировать собственное мнение и позицию.
познавательные:
— уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке.
Тип (вид урока): открытие нового знания.
Ход урока.
1.Организационный момент.
Звенит звонок! Ты входишь в класс!
Кто любит знанья получать?
Кто любит тайны открывать?
СТРЕМИСЬ ПОЗНАТЬ,
ДЕРЗАЙ УЗНАТЬ,
Учись века,
Ведь жизнь совсем уж нелегка!
— Сегодня на уроке, ребята, мне бы хотелось увидеть , как вы сами умеете добывать знания!
А, чтобы урок был удачным — мы будем внимательны, активны и точны! Пожелаем друг другу успеха!
II. Актуализация знаний.
Актуализация знаний.
1. Минута чистописания.
Спишите числа, запишите ещё 2 числа, продолжив закономерность.
2 4 6 … …
1 3 5 … …
2.Устный счёт.
— Ребята, приготовьте карточки с числами. Карточки с ответами располагайте слева направо.
— Какое число идет при счете перед числом 2? (1)
— Какое число называют после числа 8? (9)
— 5 уменьши на 3. (2)
— К трем прибавь такое же число. (6)
-5 без 2. (3)
— Первое слагаемое 2, второе слагаемое 3. Сумма? (5)
— Найди сумму чисел 4 и 3. (7)
— 5 да еще 5. (10)
— Какое число находится между числами 3 и 5? (4)
— Какое число меньше 9 на 1? (8)
— Прочитайте получившийся ряд чисел.
— Как можно расположить данные числа? (в порядке возрастания и убывания).
— 1 вариант расположите в порядке убывания, 2 вариант – в порядке возрастания.
— Проверьте себя. (самопроверка, самооценка)
(самопроверка, самооценка)
кот. Сколько воробьёв осталось? ( 0)
III. Самоопределение к деятельности. (Определение знания и незнания на данном этапе)
На доске:
6+2 5+3
9-2 7+3
8+1 6-3
5-2 5+4
Учитель: — Найдите значения выражений в 1-ом столбике. Игра «Молчанка».
(Учитель показывает на выражение, ученики — блок-сигналами показывают ответ.)
а) -В 1-ом столбике найдите «лишнее» выражение.
Ученики: — 8+1 -лишнее, так как остальные выражения на сложение и
вычитание числа 2.
Учитель:- Что значит — прибавить 1? (Назвать следующее число)
— Что значит — вычесть 1?(Назвать предыдущее число )
— Чем похожи остальные выражения? (Во всех нужно + или — 2 ).
— Вспомните, как можно прибавить число 2?(Сначала 1,а затем ещё 1).
— Как можно вычесть число 2?(Сначала 1 ,затем ещё 1).
б). Учитель:- Найдите значения выражений во 2-ом столбике
, комментируя способ решения.
(Дети, рассуждая, не могут прокомментировать способ решения в выражении 5+4 )
Учитель: — Чему же будем учиться на уроке?
Ученики: — Будем учиться прибавлять и вычитать число 4.
Учитель: — Назовите тему урока.
Ученики: — Прибавить и вычесть число 4.
Научимся сложению с 4 и вычитанию 4.
(Идёт целеполагание. Ученики сами называют тему и цель урока)
IV.Открытие новых знаний.
Учитель: — Подумайте в паре, каким способом можно прибавить число 4? Мы еще не все умеем это делать. Как вы предлагаете облегчить эту работу?
— Что вам может помочь сделать это открытие? ( Работа с кружками )
— Положите на стол 5 красных кружков. Возьмите ещё 4 синих кружка.
— Поработайте в паре.
(Дети работают в паре. Пара, которая готова сигналит о готовности)
— Какое открытие сделали?
— Как по частям можно прибавить число 4?
( Ученики на доске ставят 5 кружков и практически демонстрируют своё открытие, которое наработали в паре )
Ученики: — К 5 ,прибавим сначала 2 , получится 7 , а затем к 7 прибавим ещё 2 — получится 9.
— Можно иначе. Сначала к 5 прибавим 3, получится 8 , а затем к 8 прибавим 1.
— Можно, наоборот — к 5 сначала прибавим 1 ,получится 6 ,а к 6 прибавим 3 ,то получится 9.
(Учитель на доске фиксирует приёмы прибавления числа 4)
5+4=5+2+2=9
5+4=5+3+1=9
5+4=5+1+3=9
Учитель: -А теперь подумайте, как можно из 7 вычесть 4?
Поработайте в паре, используя числовой ряд.
(На экране ряд чисел от 1 до 10 .)
Учитель: — Кто готов рассказать о своём открытии?
(Ученики объясняют самостоятельно с опорой на числовой ряд приёмы вычитания числа 4, делая запись на доске и в тетрадях. Учитель пояснения сопровождает стрелками)
Запись на доске:
7-4=7-2-2= 3
7-4=7-3-1=3
7-4=7-1-3=3
— Вы замечательно поработали!
V. Физминутка.
Мы решали, все решали
И немножко подустали.
Наш дежурный выходи,
И зарядку проведи!
(Выходит дежурный, проводит зарядку. )
)
Раз подняться…
VI. Закрепление изученного материала.
1. Работа с учебником.
А) Задание №2 стр.-8. (Комментированное упражнение. Ученики объясняют способы сложения и вычитания числа 4 в устной форме)
Б) Найдите номер 3. Прочитайте задачу. Вслух прочитает …, остальные поставили пальчики и следим.
— Докажите, что это задача (есть условие и вопрос).
— Прочитайте только условие задачи.
-Прочитайте вопрос задачи.
-О чём задача?
— Что известно?
-Как понимаете на 4 года старше? ( Больше лет)
-Что означает «больше на 4»? (Столько же и ещё 4.)
— Что надо найти в задаче?
-Какое выбираете действие?
— Вспомните порядок работы над задачей. Что мы выполняем сначала? (схему)
— Дальше? (решение, ответ.) Кто желает у доски?
-Сделайте схему и запишите решение и ответ к задаче.
Самопроверка
— У кого так же, как у ….?
— Кто по-другому решил задачу?
… объясни, как к 6 прибавил 4? (по числовой ленте) – у доски
2. Самостоятельная работа.
Самостоятельная работа.
Задание № 4 стр.8. (Примеры решают по вариантам. Затем учащиеся меняются тетрадями, проводя взаимопроверку).
Встаньте, у кого безошибочная работа. Молодцы! Остальные – будьте внимательны!
VII. Рефлексия. (Работа по электронному приложению)
VIII. Итог урока.
Учитель: — Какой была тема урока?
Ученик: — Сложение и вычитание числа 4.
Учитель: — Как можно прибавить и вычесть число 4?
(Ученики повторяют приёмы сложения и вычитания числа 4)
Учитель: — Какое задание было для вас интересным?
-А какое задание было трудным?
(Дети отвечают на вопросы)
Рефлексия.
Самооценка. Раскрась себе смайлик.
Учитель: — Урок окончен! Спасибо!
Оценка: 4 — Алгебраическое мышление 1
Особенности специального образования
Рекомендации по специальному образованию, написанные учителями специального образования штата Индиана, предназначены для повышения вовлеченности и поддержки роста учащихся в рамках специального образования. Это не исчерпывающий список стратегий, но эта поддержка поможет вам сделать обучение математике более доступным для учащихся. Педагоги должны адаптировать стратегии к потребностям ваших учеников и убедиться, что вы создаете возможности для всех учеников, чтобы они могли взаимодействовать с строгим содержанием.
Это не исчерпывающий список стратегий, но эта поддержка поможет вам сделать обучение математике более доступным для учащихся. Педагоги должны адаптировать стратегии к потребностям ваших учеников и убедиться, что вы создаете возможности для всех учеников, чтобы они могли взаимодействовать с строгим содержанием.
| Универсальные стратегии для отстающих учащихся | |
|---|---|
Использование манипуляторов |
|
Модель / Рисование рисунка |
|
Строительные леса |
|
Ежедневное подкрепление |
|
Карты памяти |
|
Взаимодействие с точками соприкосновения | |
Визуальные подсказки |
|
Несколько способов доставки |
|
% PDF-1. 4
%
3503 0 объект
>
эндобдж
xref
3503 72
0000000016 00000 н.
0000006112 00000 п.
0000006307 00000 н.
0000006440 00000 н.
0000007172 00000 н.
0000007210 00000 н.
0000007466 00000 н.
0000008142 00000 п.
0000008280 00000 н.
0000008943 00000 н.
0000009020 00000 н.
0000009090 00000 н.
0000009519 00000 п.
0000010324 00000 п.
0000011851 00000 п.
0000013031 00000 н.
0000014604 00000 п.
0000016145 00000 п.
0000016539 00000 п.
0000016595 00000 п.
0000016931 00000 п.
0000017952 00000 п.
0000019073 00000 п.
0000019600 00000 п.
0000019708 00000 п.
0000019935 00000 п.
0000020514 00000 п.
0000023025 00000 п.
0000034824 00000 п.
0000038876 00000 п.
0000187589 00000 н.
0000353820 00000 н.
0000354040 00000 н.
0000354131 00000 п.
0000354230 00000 н.
0000354330 00000 н.
0000354397 00000 н.
0000354492 00000 н.
0000354515 00000 н.
0000354620 00000 н.
0000354649 00000 н.
0000354736 00000 н.
0000354779 00000 н.
0000354814 00000 н.
0000354844 00000 н.
0000354869 00000 н.
4
%
3503 0 объект
>
эндобдж
xref
3503 72
0000000016 00000 н.
0000006112 00000 п.
0000006307 00000 н.
0000006440 00000 н.
0000007172 00000 н.
0000007210 00000 н.
0000007466 00000 н.
0000008142 00000 п.
0000008280 00000 н.
0000008943 00000 н.
0000009020 00000 н.
0000009090 00000 н.
0000009519 00000 п.
0000010324 00000 п.
0000011851 00000 п.
0000013031 00000 н.
0000014604 00000 п.
0000016145 00000 п.
0000016539 00000 п.
0000016595 00000 п.
0000016931 00000 п.
0000017952 00000 п.
0000019073 00000 п.
0000019600 00000 п.
0000019708 00000 п.
0000019935 00000 п.
0000020514 00000 п.
0000023025 00000 п.
0000034824 00000 п.
0000038876 00000 п.
0000187589 00000 н.
0000353820 00000 н.
0000354040 00000 н.
0000354131 00000 п.
0000354230 00000 н.
0000354330 00000 н.
0000354397 00000 н.
0000354492 00000 н.
0000354515 00000 н.
0000354620 00000 н.
0000354649 00000 н.
0000354736 00000 н.
0000354779 00000 н.
0000354814 00000 н.
0000354844 00000 н.
0000354869 00000 н. Ӯ | > 6 / EW u1HkT $ YӞ 䯬 @ {$ Gϒ | HC {ӪGL5 \:% JKD +% u {) 0rw1 {$ Wϩin / ɾ 䞨 U.b (o` ݮ AsnN + 3jdmJ ejL ׀ afD ը nıt; Y
Ӯ | > 6 / EW u1HkT $ YӞ 䯬 @ {$ Gϒ | HC {ӪGL5 \:% JKD +% u {) 0rw1 {$ Wϩin / ɾ 䞨 U.b (o` ݮ AsnN + 3jdmJ ejL ׀ afD ը nıt; Y
Учебная программа по математике для 4-го класса — Общие основные уроки и оценки
Что такое математика для 4-го класса?
4 класс фокусируется на трех ключевых достижениях предыдущих лет: (1) развитие понимания с помощью многозначного умножения и деления; (2) развитие понимания эквивалентности дробей и некоторых случаев сложения, вычитания и умножения дробей; и (3) понимание того, что геометрические фигуры можно анализировать и классифицировать на основе их свойств, включая их угловую меру и симметрию.
Как мы заказывали агрегаты?
Блок 1, Разрядная стоимость, Округление, Сложение и Вычитание , год начинается с основного содержания, на котором основывается большая часть оставшихся единиц — разряда. Учащиеся начинают видеть структуру разрядной системы в контексте мультипликативного сравнения — например, 1 тысяча в 10 раз больше, чем 1 сотня. Затем они используют это понимание места для сравнения, округления, сложения и вычитания чисел до 1 000 000.Они также решают многоступенчатые задачи со словами, включая сложение и вычитание, используя округление для оценки обоснованности своих ответов.
Затем они используют это понимание места для сравнения, округления, сложения и вычитания чисел до 1 000 000.Они также решают многоступенчатые задачи со словами, включая сложение и вычитание, используя округление для оценки обоснованности своих ответов.
В , Блок 2, Многозначное умножение , учащиеся используют это понимание разряда, чтобы начать развивать понимание многозначного умножения (включая 2-значное, 3-значное и 4-значное на 1-значное, а также как двузначное умножение на двузначное). Хотя учащиеся познакомились с идеей мультипликативного сравнения в Блоке 1 в контексте структуры нашей системы разметки, они более глубоко вникают в эти типы задач рассказа в этом блоке. Раздел 3, Многозначный Дивизион , аналогично полагается на понимание разряда, чтобы познакомить учащихся с многозначным делением (включая 4-значное, 3-значное и 2-значное на однозначное деление). Студенты продолжают свою работу над многоступенчатыми задачами со словами, работая с остатками, интерпретируя их в контексте задачи.
В , Блок 4, Углы , студенты получают формальное введение в углы после многих лет неформальной категоризации форм в соответствии с их углами.Учащиеся измеряют углы и находят неизвестные меры углов, а затем используют это более глубокое понимание для классификации форм и изучения симметрии отражения.
В Блок 5, Эквивалентность дробей и упорядочение учащихся работают с эквивалентностью и сравнением дробей, разрабатывая общий метод генерации эквивалентных дробей и исследуя несколько стратегий для сравнения дробей. Это готовит их к Блоку 6, Операциям с дробями , где они начинают изучать операции с дробями (а именно сложение, вычитание и умножение на целое число).Студенты также начинают решать задачи со словами, включающие сложение, вычитание и умножение дробей. Затем это распространяется на блок , блок 7, десятичные дроби , в котором учащиеся изучают десятичные дроби, которые особенно важны, поскольку они являются расширением системы разметки. Они находят эквивалентные десятичные дроби, складывают и вычитают десятичные дроби (включая десятые и сотые, требующие общего знаменателя) и используют десятичную систему счисления.
Они находят эквивалентные десятичные дроби, складывают и вычитают десятичные дроби (включая десятые и сотые, требующие общего знаменателя) и используют десятичную систему счисления.
Курс завершается блоком 8 , преобразование единиц , в котором студенты применяют большую часть своего понимания четырех операций, а также дробей и десятичных дробей для решения задач со словами, включающих преобразование большей единицы в меньшую единицу в той же системе. .
Этот курс соответствует рамкам учебной программы штата Массачусетс 2017 года, которые включают Общие основные государственные стандарты 2010 года. Кроме того, мы полагаем, что ежедневная беглость речи и практика применения являются важной частью обучения элементарной математике, но не включены в наши математические единицы. Все ученики 4-х классов получают около 45 минут практики в этих областях во время других блоков.
открытых учебников | Сиявула
Математика
Наука
- Читать онлайн
Учебники
Английский
Класс 7A
Марка 7Б
Оценка 7 (вместе A и B)
Африкаанс
Граад 7А
Граад 7Б
Граад 7 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
класс 8A
Марка 8Б
Оценка 8 (вместе A и B)
Африкаанс
Граад 8А
Граад 8Б
Граад 8 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 9А
Марка 9Б
9 класс (A и B вместе)
Африкаанс
Граад 9А
Граад 9Б
Граад 9 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Класс 4A
Класс 4Б
Класс 4 (вместе A и B)
Африкаанс
Граад 4А
Граад 4Б
Граад 4 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 5А
Марка 5Б
Оценка 5 (вместе A и B)
Африкаанс
Граад 5А
Граад 5Б
Граад 5 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Класс 6A
класс 6Б
6 класс (A и B вместе)
Африкаанс
Граад 6А
Граад 6Б
Граад 6 (A en B saam)
Пособия для учителя
Наша книга лицензионная
Эти книги не просто бесплатные, они также имеют открытую лицензию! Один и тот же контент, но разные версии (брендированные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий. Вы можете делать ксерокопии, распечатывать и распространять их сколько угодно раз. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственным ограничением является то, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.
Вы можете делать ксерокопии, распечатывать и распространять их сколько угодно раз. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственным ограничением является то, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.
Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (версии без марочного знака)
Эти небрендированные версии одного и того же контента доступны для вас, чтобы вы могли делиться ими, адаптировать, трансформировать, модифицировать или дополнять их любым способом, с единственным требованием — дать соответствующую оценку Siyavula. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Сложение и вычитание, часть 1: задачи рассказа
сюжетные ситуацииКак мы упоминали ранее, учащиеся развивают свое понимание операций сложения и вычитания, когда они используют их для решения задач рассказа.Существует несколько категорий сюжетных задач, известных как типов ситуаций , которые описывают отношения между количествами в сюжетных задачах. Четыре типа ситуаций, которые согласно Общим основным государственным стандартам (CCSS) должны изучать учащиеся в классах K-1:
- Дополнение к
- Взять из
- Сборка / разборка
- Сравнить
Учителя, которые понимают типы ситуаций (а также то, что в них нового и сложного) могут лучше поддержать своих учеников в развитии сильного концептуального понимания сложения и вычитания.По этой причине мы хотим посвятить оставшуюся часть этого ресурса ознакомлению вас с четырьмя сюжетными ситуациями сложения и вычитания.
Ситуации сложения и вычитания
Чтобы лучше понять, что мы подразумеваем под «типом ситуации», давайте вернемся к нашему примеру задачи сложения, которая представляет собой добавление к ситуации . В этой задаче одно количество (3 рыбы) добавляется к существующему количеству (5 рыб), в результате чего получается новое количество (что мы обнаруживаем как 8 рыб).Детали проблемы могут измениться (например, это может быть печенье вместо рыбы), как и неизвестное количество (например, возможно, мы знали, сколько рыбы у нас было в итоге, но не сколько мы начали), но соотношение между количествами одинаково для всех дополнительных задач.
Ниже мы представляем ситуацию добавления в виде диаграммы и помечаем каждое количество так, как CCSS относится к ним ( начало увеличивается на изменение становится результат ).Мы не рекомендуем представлять диаграмму в качестве модели учащимся, но учителям может быть полезно визуально увидеть, какой тип ситуации представлен.
Еще одна важная вещь, которую следует понять, заключается в том, что тип ситуации сам по себе не дает нам определения, использовать ли сложение или вычитание . Скорее, мы определяем необходимую операцию, основываясь на том, какое количество неизвестно. В нашем примере выше 3 рыбы добавляются в аквариум с 5 рыбками, и неизвестным является общее количество рыб (5 + 3 =?), Поэтому это требует добавления.Но если мы добавим 3 рыбок в аквариум, в котором теперь 8 рыб, это все равно «дополнительная» ситуация:? + 3 = 8), но мы использовали бы вычитание, чтобы найти неизвестное (8 — 3 =?).
В таблице ниже мы приводим пример проблемы для каждого типа сюжетной ситуации и диаграмму, которая представляет взаимосвязь каждой ситуации между количествами.
Урок четвертого класса с использованием обратной операции для сложения и вычитания
В этом вводном видео с использованием обратной операции я объясняю нашу цель на сегодня.
Учащиеся уже научились складывать и вычитать с помощью разряда. На сегодняшнем уроке они учатся находить недостающее число в задаче сложения или вычитания с помощью обратной операции. Это согласуется с 4.NBT.4, потому что учащиеся складывают и вычитают многозначные целые числа, используя стандартный алгоритм.
На сегодняшнем уроке они учатся находить недостающее число в задаче сложения или вычитания с помощью обратной операции. Это согласуется с 4.NBT.4, потому что учащиеся складывают и вычитают многозначные целые числа, используя стандартный алгоритм.
Это очень важный навык для студентов. Им нужно знать, что если у вас отсутствует номер, вы можете взять числа, которые они вам дают, и выполнить операцию, которая поможет вам определить недостающий номер.Эта операция является «обратной».
Я сообщаю студентам, что сегодня мы изучаем стратегию, которая поможет нам добавить, если есть недостающее слагаемое, и даже найти разницу, если одно из наших чисел отсутствует.
Мне нравится использовать свою доску Smart для обсуждения всего класса. Студенты подходят к ковру, чтобы они могли быть рядом, пока мы вместе обсуждаем навык. Мои ученики знают, что они могут задавать вопросы или вносить свой вклад во время прямого обучения всего класса.Обсуждая этот навык, я задаю вопросы на протяжении всего урока.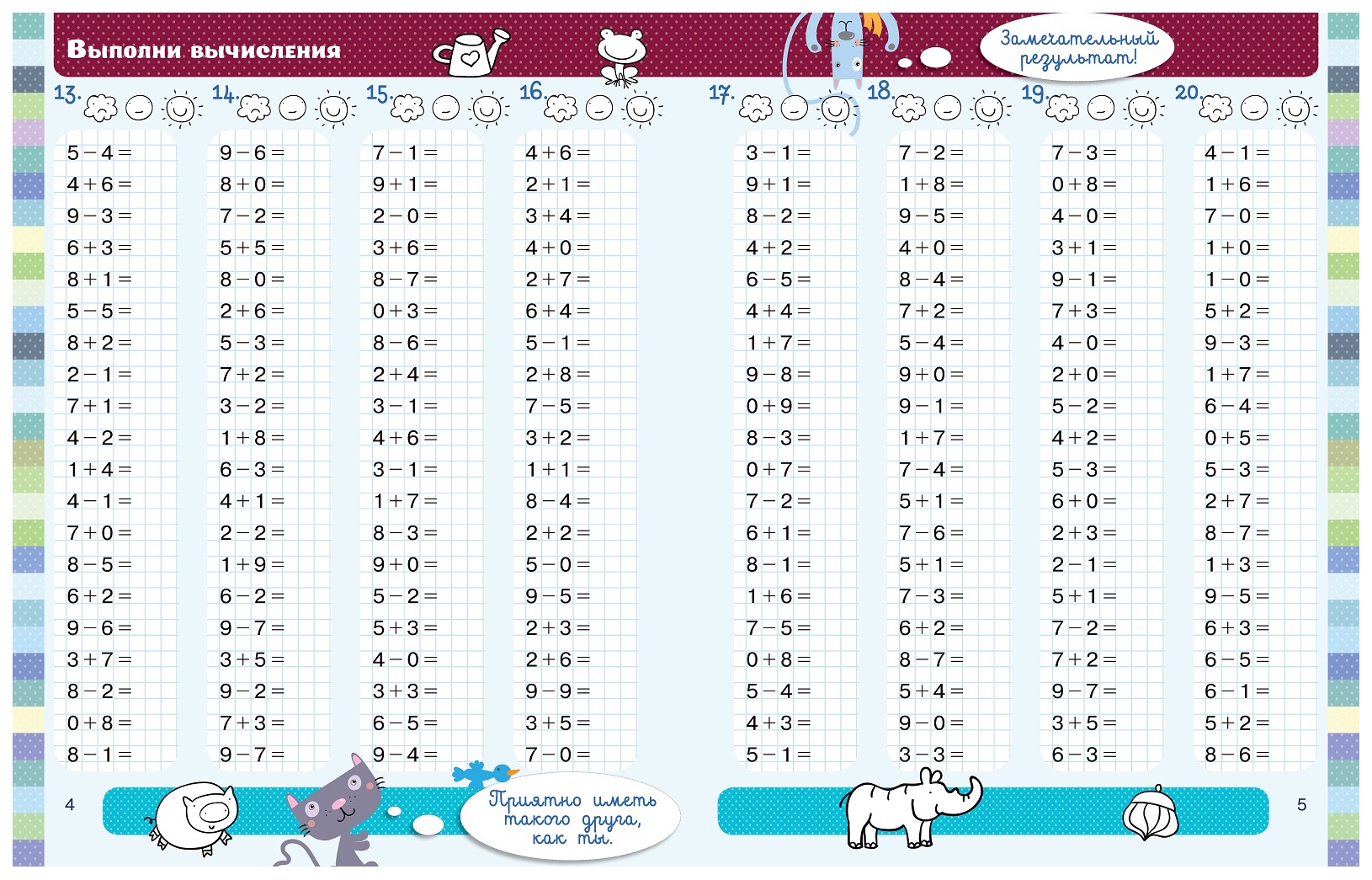 Делая это, это позволяет студентам думать над ответом, вместо того, чтобы я просто давал им много информации. Я чувствую, что студенты учатся лучше, когда они придумывают что-то самостоятельно.
Делая это, это позволяет студентам думать над ответом, вместо того, чтобы я просто давал им много информации. Я чувствую, что студенты учатся лучше, когда они придумывают что-то самостоятельно.
Точка мощности с использованием инверсной операции отображается на интеллектуальной плате. В этом конкретном уроке я начну с обзора стоимости места и того, как мы используем ее для сложения и вычитания.
Обзор:
1. Когда мы складываем или вычитаем, мы выстраиваем наши числа в соответствии с разрядными значениями.Цифры в разряде единиц должны совпадать друг с другом, разряды десятков и т. Д.
2. Некоторые номера нужно перегруппировать. Когда мы перегруппировываемся, мы помещаем число в разряды единиц внизу и перегруппируем число в разрядах десятков вверху разряда десятков. Например, с числом 15 5 будет стоять на месте единиц, а 1 будет перегруппировано в разряд десятков, потому что оно оценивается в 10
. 3. Когда мы вычитаем, нам, возможно, также придется перегруппироваться. Если верхнее число меньше нижнего числа, нам нужно убрать 1 с места слева и добавить его к месту справа.Например, 17-8. 7 меньше, чем 8, поэтому мы убираем единицу из разряда десятков (которая становится нулем), затем добавляем эту единицу к разряду единиц. Теперь у нас есть 17.
Если верхнее число меньше нижнего числа, нам нужно убрать 1 с места слева и добавить его к месту справа.Например, 17-8. 7 меньше, чем 8, поэтому мы убираем единицу из разряда десятков (которая становится нулем), затем добавляем эту единицу к разряду единиц. Теперь у нас есть 17.
Давай попрактикуемся!
45 + ___ = 87
Чтобы найти недостающее слагаемое для этой задачи сложения, мы можем использовать обратную операцию вычитания.
Поскольку у нас есть два числа, мы можем взять эти два числа и решить математическую задачу.
87–45 = 42
Отсутствует добавление 42.
Давай попробуем с вычитанием!
___ — 53 = 28
Чтобы найти недостающее число, мы можем использовать обратное вычитание. Давайте добавим, чтобы найти недостающий номер.
28 + 53 = 81
Как использование обратной операции помогает находить недостающие числа?
Сложение и вычитание: Введение в сложение
Урок 1: Введение в Дополнение
Что такое сложение?
Дополнение — это способ соединить вещи. Когда вы прибавляете к двум суммам, вы считаете их вместе как одну большую сумму. В реальной жизни сложение происходит постоянно.
Когда вы прибавляете к двум суммам, вы считаете их вместе как одну большую сумму. В реальной жизни сложение происходит постоянно.
Что, если бы было еще , четыре, еще кроликов?
Как видите, если у вас есть 4 кроликов и добавить еще 4 , у вас будет всего 8 кроликов. Вы могли бы написать это так:
4 + 4 = 8
4 + 4 = 8 — это математическое уравнение . Вы могли прочитать это так: четыре плюс четыре равняются восьми.Математическое уравнение — это, по сути, математическое предложение . Вместо слов используются числа и символов, . Когда мы записываем уравнения со сложением, мы используем два символа: + и = .
Знак плюс ( + ) означает, что две вещи складываются. Вот почему мы поместили его между кроликами — у нас было 4 кролика и добавили еще 4.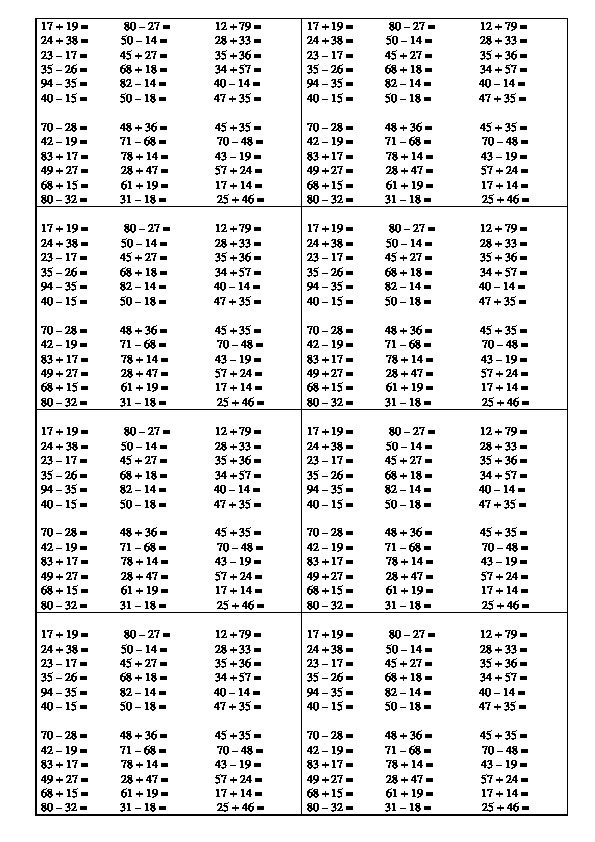
Другой символ в нашем уравнении — равно знак ( = ).Когда вы видите знак равенства в уравнении, это означает, что два больше: равно или эквивалентно . Эквивалентные вещи не всегда выглядят или кажутся абсолютно одинаковыми, но они означают одно и то же.
Например, когда вы видите кого-то, кого знаете, вы можете сказать несколько вещей:
Эти слова не совсем похожи, но означают одно и то же. Это все способы поприветствовать кого-то.
В математике знак равенства показывает, что два числа или выражения означают одно и то же, , даже если они могут выглядеть по-разному.Помните наших кроликов? Поскольку всего кроликов было 8, мы написали 8 справа от знака равенства.
Видите, как каждая сторона означает 8? Слева 8 кроликов, а справа цифра 8. Обе стороны равны .
Попробуй!
Заполните пропуски, чтобы завершить уравнения.
Написание выражений
На последней странице мы рассмотрели некоторые математические выражения.Выражения полезны, поскольку они помогают отслеживать добавляемые вами суммы.
Любую задачу сложения можно превратить в письменное выражение. Например, предположим, что вы планировали пригласить на ужин троих друзей. В последний момент вы приглашаете еще двоих. Чтобы узнать общее количество друзей, которые приходят к вам домой, вы можете написать такое выражение:
3 + 2
Выражение — это просто другой способ описания ситуации: трое друзей плюс двое еще приходят на обед.
Попробуй!
Запишите эти ситуации в виде математических выражений. Пока не решайте проблемы — просто установите их.
Вы съели на обед трех кусочков пиццы. За ужином вы съели , два, еще :
Вы уже ждали пять минут, чтобы обратиться к врачу. Медсестра говорит вам подождать пять еще минут:
Медсестра говорит вам подождать пять еще минут:
На вашем пальто четыре пуговицы с правой стороны и три пуговицы с левой стороны:
Решение проблем
Теперь, когда вы знаете, как писать задачи сложения, давайте решим некоторые из них.Когда вы только начинаете, вам может быть проще использовать , считая , для решения проблем.
Попробуй!
Например, можете ли вы использовать счет, чтобы написать и решить эту задачу?
С этой проблемой вы смогли подсчитать добавляемые вами объекты. В реальной жизни некоторые люди любят считать пальцами. Другие люди используют мелкие предметы, такие как пуговицы или пенни. Другие могут делать небольшие отметки на листе бумаги. Когда учишься складывать, можно считать! Чем больше вы практикуетесь, тем легче будет складывать без счета.
Способы подсчета
Давайте рассмотрим два способа решения задач сложения со счетом.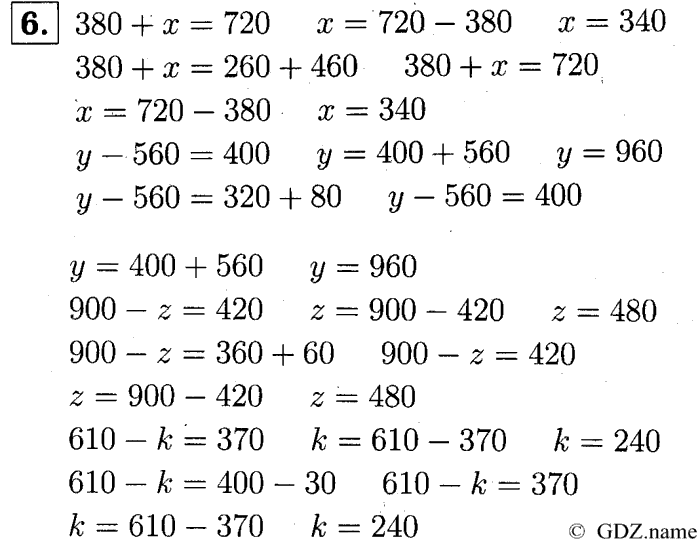 Сначала мы посчитаем с объектами .
Сначала мы посчитаем с объектами .
Для подсчета с помощью объектов используйте объекты, чтобы отобразить каждое число в выражении. Давайте попробуем это с этим выражением, 2 + 3.
Первое число — 2, поэтому нам понадобится 2 объекта.
Первое число — 2, поэтому нам понадобится 2 объекта.
Первое число — 2, поэтому нам понадобится 2 объекта.
Следующее число — 3. Возьмем еще 3 объекта.
Следующее число — 3. Возьмем еще 3 объекта.
Следующее число — 3. Возьмем еще 3 объекта.
Теперь мы можем закончить наше уравнение. Все, что нам нужно сделать, это сосчитать !
Теперь мы можем закончить наше уравнение. Все, что нам нужно сделать, это сосчитать !
Теперь мы можем закончить наше уравнение. Все, что нам нужно сделать, это сосчитать !
Теперь мы можем закончить наше уравнение.
 Все, что нам нужно сделать, это сосчитать !
Все, что нам нужно сделать, это сосчитать !Теперь мы можем закончить наше уравнение. Все, что нам нужно сделать, это сосчитать !
Всего объектов пять, поэтому наш ответ: 5
В завершение напишем 5 справа от знака равенства.
Другой способ решить проблемы сложения — использовать строку номера .
Практика!
Попрактикуйтесь в добавлении этих задач. Всего 5 наборов задач, по 3 задач в каждом наборе.
Набор 1
Набор 2
Набор 3
Набор 4
Набор 5
/ ru / addsubtraction / сложение двух- и трехзначных-чисел / content /
.

 (вывешиваю на доску).
(вывешиваю на доску).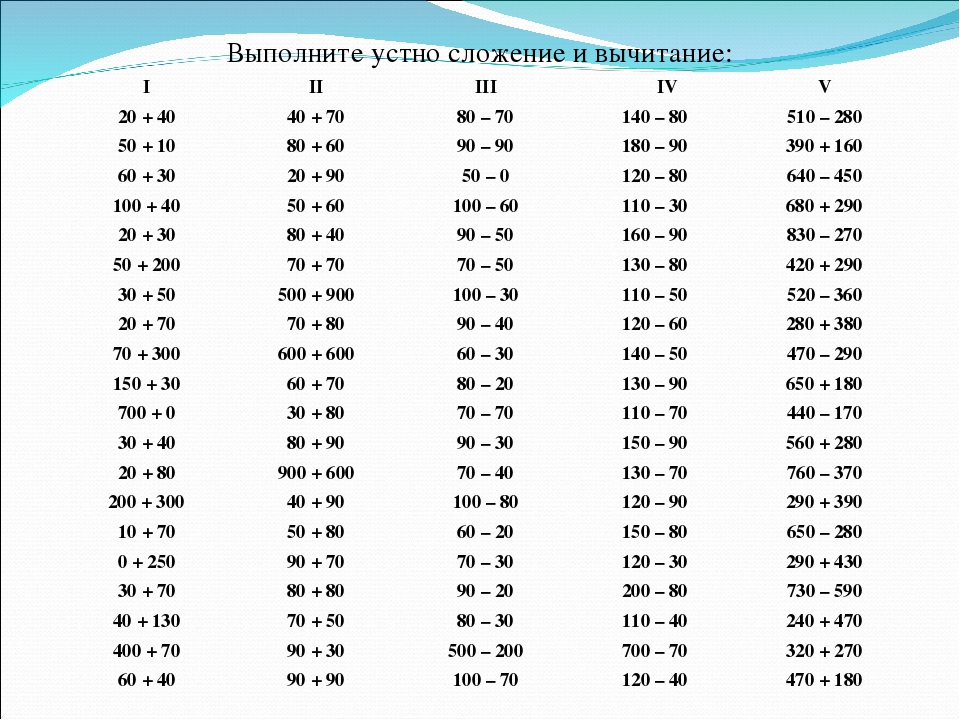
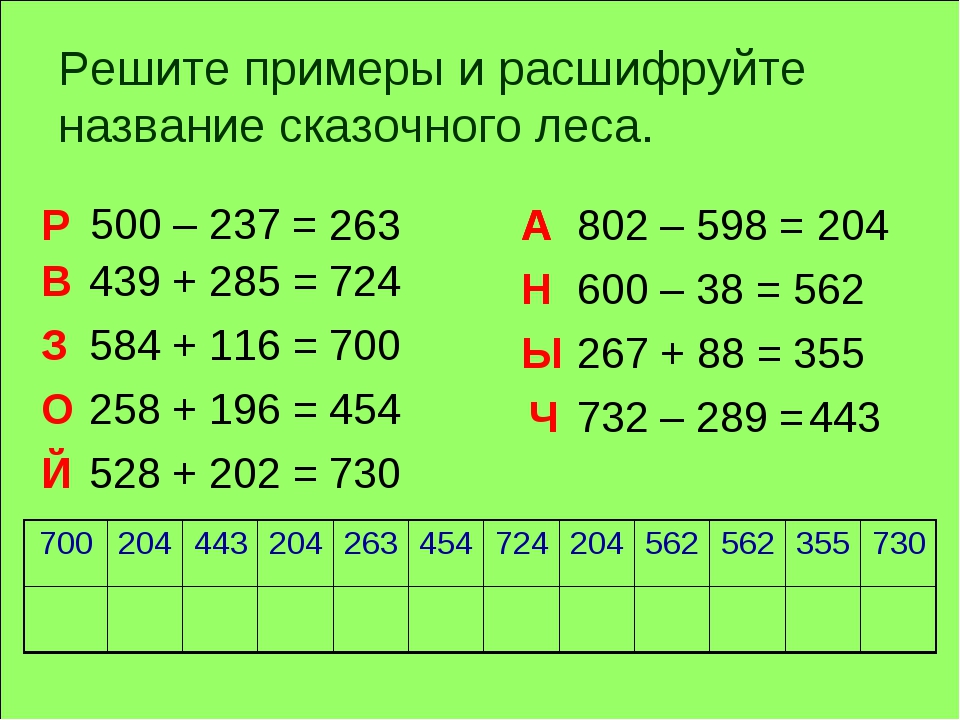 )
)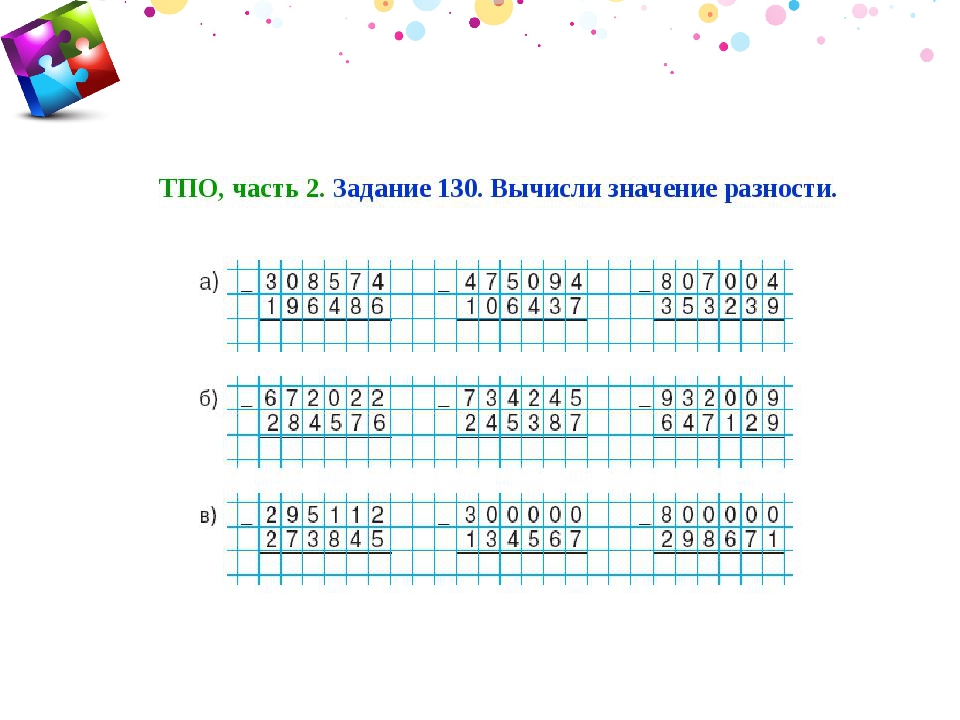 Например, длина реки Баргузин – 480000 м, реки Селенга – 1024000 м, реки Тыя – 120000 м. Найдите общую длину этих рек? Длину рек выразите в метрах?
Например, длина реки Баргузин – 480000 м, реки Селенга – 1024000 м, реки Тыя – 120000 м. Найдите общую длину этих рек? Длину рек выразите в метрах?
 16. Разноуровневое:
16. Разноуровневое:
 Все, что нам нужно сделать, это сосчитать !
Все, что нам нужно сделать, это сосчитать !