Страница 23 — ГДЗ Математика 1 класс. Моро, Волкова. Учебник часть 2

1. Главная
2. ГДЗ
3. 1 класс
4. Математика
5. Моро, Волкова. Учебник
6. Что узнали. Чему научились
7. Страница 23. Часть 2

Вернуться к содержанию учебника

Что узнали. Чему научились

Вопрос

2. 

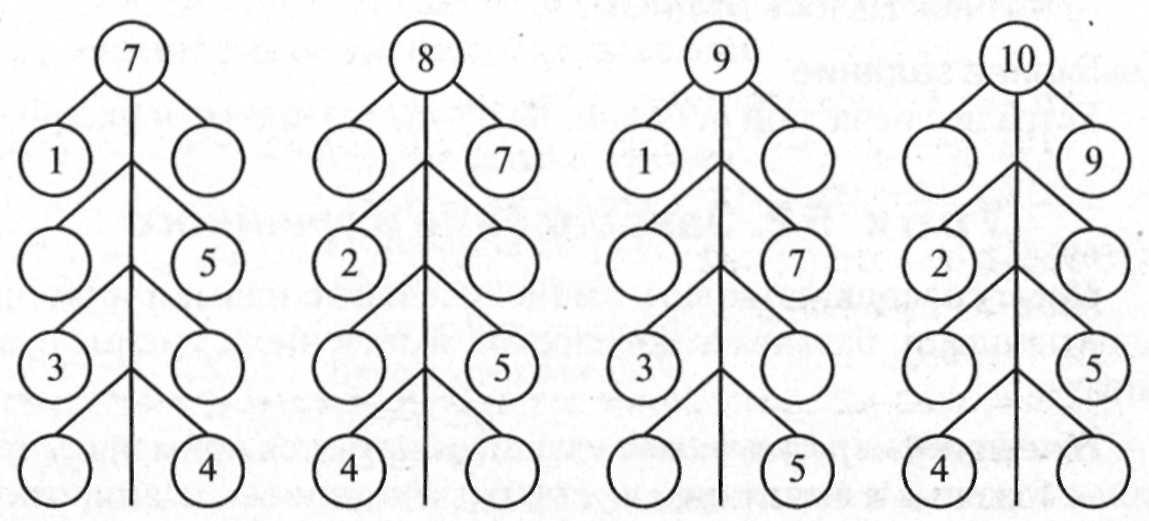
1)  Повтори состав числа 6, рассматривая ряды кругов справа от линии.

2) Покажи карандашом и линейкой, как узнать состав чисел 5, 10, 9 и оставших­ся чисел от 2 до 8.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

3.

 Составь по рисунку задачу и реши её.

6 страниц.	На 2 меньше.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

4. На тарелке лежали 6 помидоров. За обедом съели 4 помидора. Поставь вопрос и реши задачу.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

5. Лена знает 3 песни, а Валя — на 2 пес­ни больше. Сколько песен знает Валя?

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

6.  Павлик забил 4 гола, а Серёжа — 1 гол. На сколько меньше голов забил Серёжа, чем Павлик?

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

7.

6 + 3	9 — 4	10 — 3	3 + 5 — 3
9 — 3	4 + 5	10 — 4	8 — 3 + 4

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

Цепочка:

Ответ

Поделись с друзьями в социальных сетях:

Вернуться к содержанию учебника

---

Открытый урок по математике в 1 классе «Состав числа 10»

МБОУ г. Керчи РК «Школа № 23»

Открытый урок

по математике

на тему

«Состав чисел в пределах 10»

в 1 – Г классе

Подготовила и провела учитель начальных классов: Рассказова И.В.

2022г.

Цели урока:

• Закрепить знание таблицы сложения и умение выполнять вычитание чисел в пределах десяти.

• Повторить состав чисел первого десятка.

• Закрепить знания последовательности натуральных чисел от 1 до 10.

• Проверить умение учащихся выбирать нужное арифметическое действие (сложение, вычитание) для решения задач.

• Развивать интерес к изучению предмета.

УУД на уроке:

Регулятивные: принимать и сохранять учебную задачу и активно включаться в деятельность, направленную на её решение в сотрудничестве с учителем и одноклассниками; адекватно оценивать свои достижения, осознавать возникающие трудности и искать способы их преодоления;

Познавательные: использовать знаково – символические средства, в том числе модели и схемы; осуществлять синтез, как составление целого из частей;

Коммуникативные: выражать  свои мысли и   действия; использовать речь  для регуляции своего действия; строить понятные для партнёра  высказывания; работать в паре, оценивать себя и своего товарища.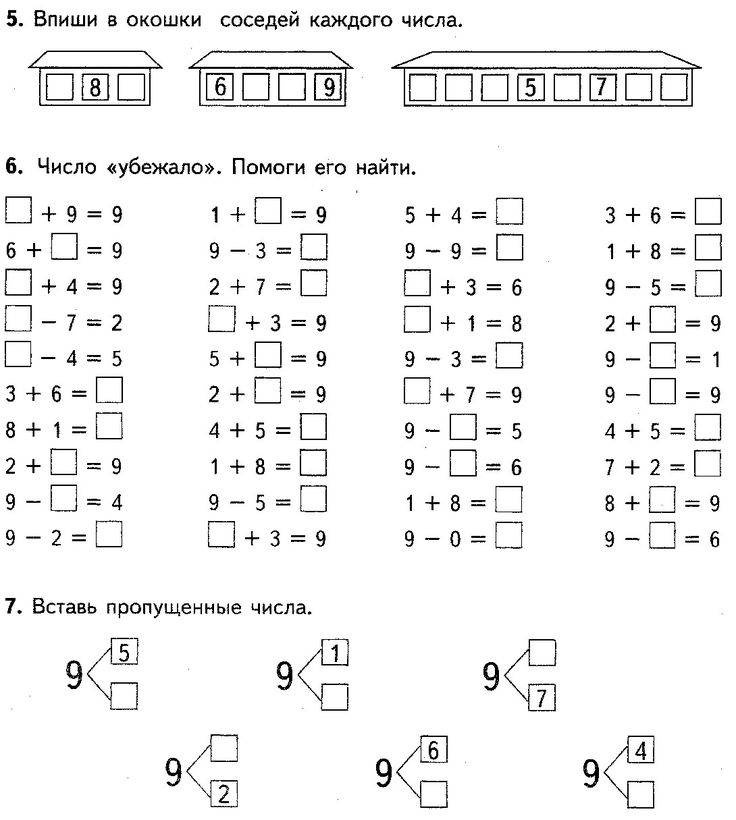

Предметные: читать, записывать числа в пределах 10;  решать примеры, сравнивать числовые выражения.

Оборудование: карточки с цифрами для устного счета,

геометрические фигуры,

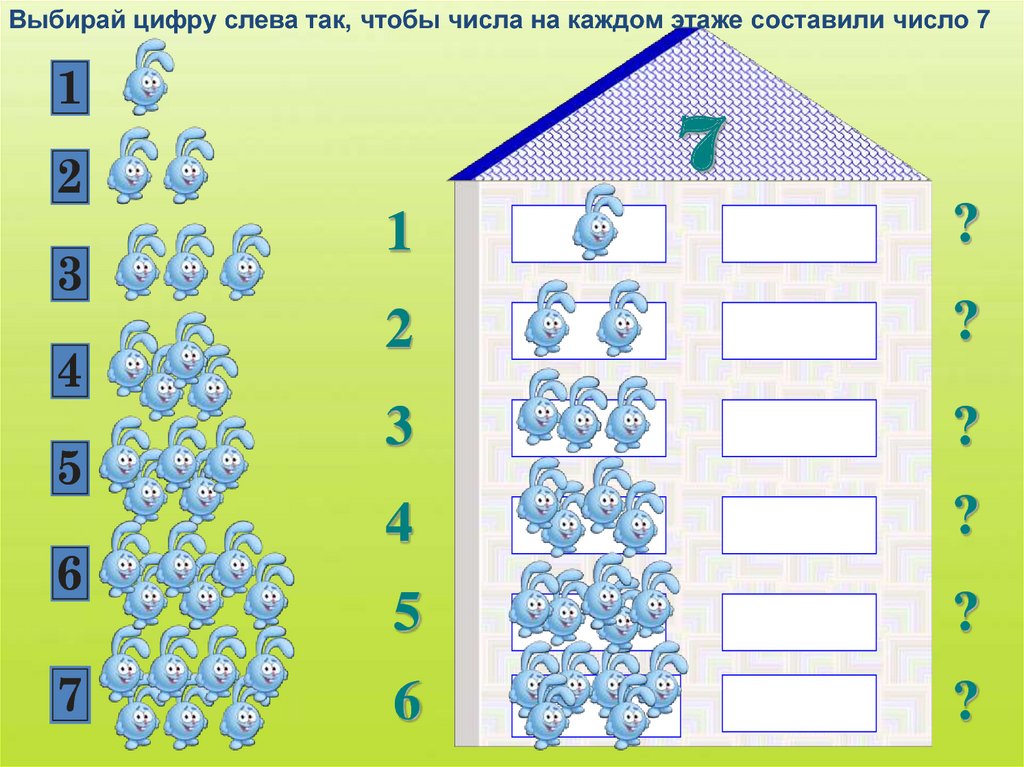
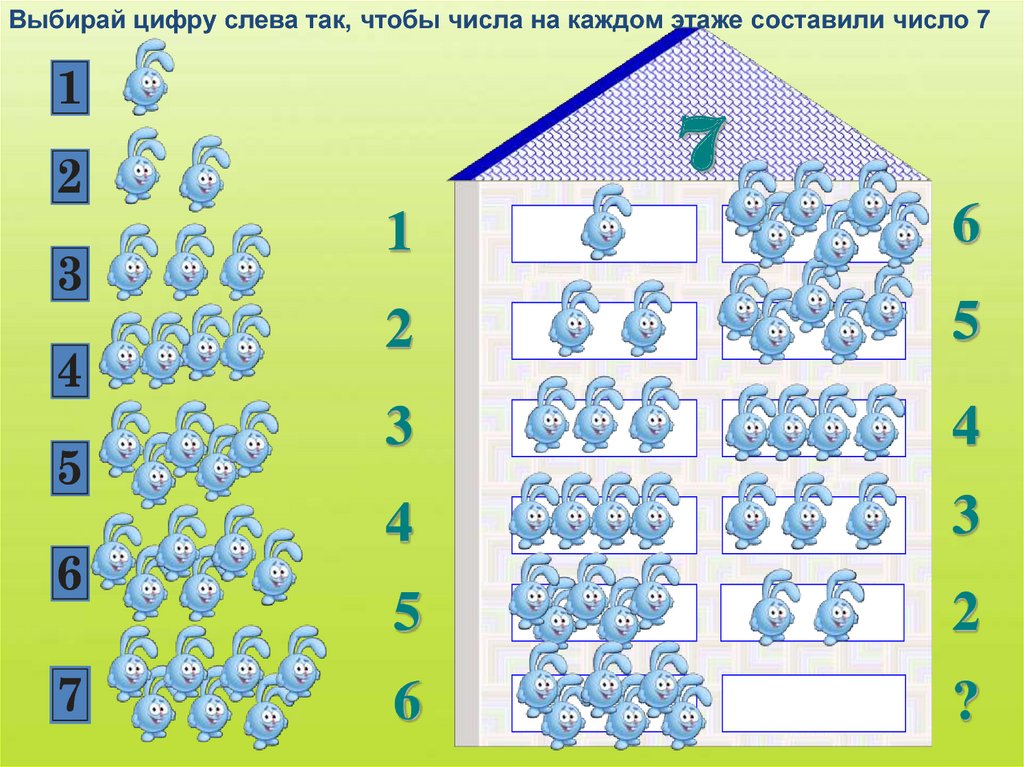
числовой домик,

герои Незнайка, Лунтик, Кузя, Мила и Пчелёнок,

билетики с числами,

мячик,

слова для решения задачи,

смайлики,

домино с числами,

портрет Н.Носова,

сигнальные карточки

Ход урока

№ п/п	Этап урока	Содержание	Оборудование
1	Организационный момент	Ребята, сегодня к нам на урок математики пришли гости, чтобы посмотреть, чему мы с Вами уже научились в 1 классе. Ребята, можете поприветствовать наших гостей и подарите улыбки друг другу. Приятного вам  учебного дня!! А девизом нашего урока служат следующие строки: МЫ – умные, мы – дружные!  Мы – внимательные! Мы – старательные! В первом классе учимся! Всё у нас получится! – Покажите, с каким настроением вы пришли на урок. – Что вы ждёте от сегодняшнего урока?	На экране Смайлики Ответы детей
2.	Целевая установка	— Сегодня на уроке мы совершим математическое путешествие на Планету Чисел. Ваша задача во время этого путешествия вспомнить всё, что узнали о числах. Мы познакомимся с составом числа 10, будем складывать и вычитать, а также задачи решать. Вспомним геометрические фигуры. — Вместе с нами отправится в математическое путешествие герой одного из самых популярных и любимых произведений Н. Н.Носова… Отгадайте его имя. Он, конечно, самый главный Озорник – шалун забавный. Он в огромной синей шляпе Неумеха и растяпа. (Незнайка) — Молодцы! Конечно, это он. А ещё – Лунтик и наши любимые друзья помогут вам в подготовке к полёту. Ну, что, вперёд!	Портрет Н.Н. Носова Незнайка Лунтик
3	Актуализация знаний	— Настоящие космонавты тщательно готовятся к полёту. И вам необходимо совершить предполётную подготовку. Но ребята, нам чего-то не хватает для путешествия? (Ракеты) Каждое выполненное задание поможет нам построить ракету из геометрических фигур. Готовы? Вперёд!
	1. Восстановление числового ряда.  2. Найти значение выражения.  3. Сравнение выражений 4.  Проверить работу своих товарищей.	Кузнечик Кузя рассыпал фишки домино и не может вспомнить: в каком порядке они были расположены. Два члена вашей космической команды должны ему помочь. Восстановить последовательность фишек. Мила и Пчелёнок приготовили настоящие математико-космические испытания, они очень хотят, чтобы вы с ними справились и смогли совершить путешествие. Попробуем? 2+3 8-1 4-3 4+3 8+1 6-3 7+1 5+2 — Сравните выражение и число. Поставьте знаки “” или “=” (В то время, когда дети работают у доски, идёт фронтальная работа с классом) 1) Логическая разминка Сколько лап у двух медвежат? (8) Курица, когда стоит на двух ногах весит-5 килограмм. Сколько она будет весить, если встанет на одну ногу? (5) Одно яйцо варится 5 минут, сколько минут будут вариться 5 яиц? (5) Сколько углов будет у квадрата, если отпилить один угол? (5) 2) Работа с числовым рядом. (На партах у детей выложен числовой ряд от 1 до 9 (используется мяч с небольшими шипами для массажа рук) — Назвать предыдущее число для числа 3 — Назвать последующее число для числа 5 — Назвать соседей числа 8 — На сколько 4 больше, чем 3? — Какое число при счёте идёт раньше 6 или 7? — Какое число при счёте идёт позже 9 или 8? (Обучающиеся проверяют работу своих одноклассников) Выставляем прямоугольник, треугольник и два маленьких треугольника	Выложены на доске Примеры записаны на доске выставляем два маленьких треугольника Карточки с числами на партах Мячик с шипами Сигнальные карточки красного и зеленого цвета
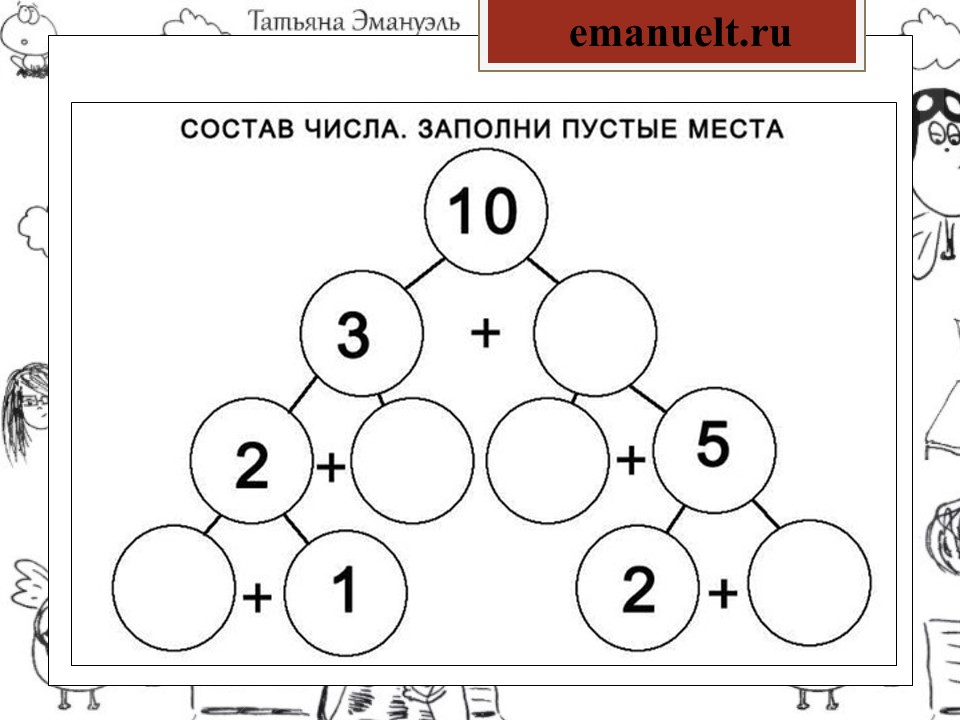
4	Изучение нового материала Натуральный ряд чисел Минутка чистописания Игра «Числовые домики» Работа в тетради и на доске	Ребята, считаю, что вы полностью подготовлены к полету и мы отправляемся. И вот, мы добрались с вами до Планеты Чисел. — А вот и жители этой планеты. Кто они? (Числа от 1 до 10) — Как называется ряд чисел, выложенный у вас на партах, на доске? (Натуральный ряд чисел от 1 до 10) — Как называется порядок: счёта слева – направо? (Прямой порядок) справа – налево? (Обратный порядок) — Что происходит с числами: при прямом порядке? (Увеличиваются на 1) при обратном порядке? (Уменьшаются на 1) — Все ли числа на доске стоят на своём месте? (Нет, числа 6 и 4 заблудились) — Восстановите ряд чисел. (Необходимо число 4 поставить после числа 3, так как оно на 1 больше, чем 3. А число 6 поставить в натуральном ряду после числа 5, так как оно на 1 больше чем 5 и меньше на 1, чем 7) — Числа очень рады видеть вас и Незнайку. Они предлагают совершить экскурсию по планете. Согласны? Тогда в путь. И первую остановку сделаем на минутке чистописания Я тетрадь свою открою и наклонно положу. Я друзья от вас не скрою, ручку я вот так держу. Сяду прямо, не согнусь. За работу я возьмусь. — Ребята в ваших тетрадях уже записана дата и поставлена точка, откуда вам нужно будет писать. Цифра вроде буквы О Это ноль иль ничего Круглый ноль, такой хорошенький, Но не значит ничегошеньки! Если ж слева рядом с ним Единицу примостим, Он побольше станет весить Потому, что это – десять. -Ребята, для начала, давайте потренируемся в написании этого числа на файликах по моему образцу. А теперь записываем в своих тетрадках. Запись числа 10. — Дети мы с вами остановились у необычного домика, где нам местные жители предлагают поиграть в игру «Числовой домик». — Какое число вы видите на крыше? (10) Чтобы узнать состав числа 10, мы заселим числа на свои этажи. Найдите пару числу, чтобы в сумме получилось число 10. Я буду показывать пустое окошко в домике, а вы должны показать карточку с цифрой так, чтобы значение суммы чисел на одном этаже было равно 10. И записать в своих домиках в тетради. Начнём заселять жителей с первого этажа. Ребята, какое число нам нужно заселить на первый этаж, чтобы получилось число 10? Покажите карточку с цифрой. 5 + … = 10 А теперь нам нужно заселить число на второй этаж. Какое число нам необходимо взять, чтобы получить в сумме с числом 6, число 10? Покажите карточку с цифрой. … + 6 = 10 Что мы сейчас с вами повторили? (состав числа 10) Итак, хором повторим 10 это: 5+5, 4+6, 3+7, 2+8, 1+9. Я показываю на строчку, а вы читаете. Молодцы! -Дети, в нашем космическом домике спрятались геометрические фигуры, кто может их назвать? Пришло время немного отдохнуть.	Видео отсчета на экране телевизора На доске числа выставлены в ряд от 1 до 10 Тетради Учитель пишет на доске число 10 Файлы с числом 10 Домик на доске с закрытыми числами Название геометрических фигур
	Музыкальная физминутка
5.	Работа с учебником, с.17 з.2 Рефлексия. Итог урока	-Ребята, вернемся к нашим числам. — Вы справились с заданиями и многому научили Незнайку. Жители Планеты Чисел решили пригласить вас к себе домой. Откройте учебник на стр. 17, задача под номером 2. (Решаем по числовой линейке на доске и в тетради.) 3. Составь по рисунку задачу, в вопросе ко­торой было бы слово меньше, и реши её. Например, Саша вырезал 7 синих квадратиков, а красных на 4 меньше. Сколько красных квадратиков вырезал Саша? 7 – 4 = 3 (кв.) (Записываем решение и ответ) — Вы сегодня настоящие Молодцы! Мы заканчиваем наше математико-космическое путешествие. Прощаемся с жителями Планеты Чисел и возвращаемся на планету Земля. Скажите, чему мы научили сегодня Незнайку? А вы какие знания вспомнили? (Сегодня на уроке мы восстанавливали натуральный ряд чисел от 1 до 10, решали задачи, вспомнили геометрические фигуры, состав числа 10. Незнайку научили считать и записывать цифры). — На память о сегодняшнем путешествии вам останутся билеты на математико-космическое путешествие. (У каждого в конце терадочки лежит лицевой стороной вниз цветной билетик с изображением “жителей Планеты Чисел”). Возьмите цветные листочки и переверните их. Это и есть ваши билеты. — Урок окончен. Спасибо!	Билетики с изображением “жителей Планеты Чисел”

Управляемая математика в 1-м классе

Ежедневные занятия 3 и Управляемая математика — это подход к изучению математики в малых группах, точно так же, как мы ежедневно встречаемся с учащимися во время управляемого чтения, мы встречаемся со школьниками как математиками. Это отклонение от группового обучения математике.

Всей командой мы решили совершить скачок с управляемой математикой — смоделировать наш математический блок после блока чтения, и трансформация была УДИВИТЕЛЬНОЙ! Впервые я почувствовал, что знаю своих учеников как математиков так же, как знал их как читателей. Если бы родитель, учитель или администратор спросил меня о математике, я мог бы продолжать и продолжать. Ежедневные встречи с моими друзьями позволяют мне прилагать больше усилий и углублять наше обучение. Как вы организуете свой математический блок?

Управляемый математический вопрос: какой длины ваш математический блок?

При использовании формата управляемой математики остается время для всей группы, но вы вкладываете свои усилия и ресурсы в ежедневные встречи с небольшими группами учащихся. Преподавая 1-й класс в первый раз, я использовал математику для всей группы с одним математическим центром в конце нашего математического блока. Затем во время зимних каникул наша команда почувствовала, что что-то не работает. В то время как наши ученики росли в математике, это было определенно не с той же скоростью, с которой они читали. Итак, мы начали сравнивать 2 блока. Для чтения мы используем модель Daily 5, поэтому 80% моих инструкций приходилось на небольшие группы во время чтения под руководством. Скорее, по математике 80% моих занятий составляла целая группа с достаточным количеством времени для посещения математического центра 3-4 раза в неделю.

При занятиях по математике в малых группах наш математический блок занимает немного больше времени (около 75-90 минут), но оно того стоит! Наша математическая программа выглядит так: «Разговоры о числах» (5-7 минут), 3 смены малых групп/Технология/Центры (17-20 минут/каждая), Рефлексия (5 минут).

Как вы группируете учащихся?

На основе общих оценок нашего округа я разделяю учащихся на три математические группы: зеленые (проблемные), желтые (на уровне класса), голубые (выше класса). Это система, которую наша команда 1-го класса использует для чтения и математики, и это потрясающе! (Подробнее читайте здесь) Я всегда начинаю встречу со своей зеленой группой первой, чтобы гарантировать, что они никогда не будут пропущены — независимо от неожиданной пожарной тревоги, изменения в расписании или собраний. Кроме того, я стараюсь добавить 4-5 минут учебного времени в эту группу. (Возьмите бесплатную редактируемую версию этой вращающейся доски здесь). Каждая единица, эти групповые изменения меняются, и у меня не всегда есть по одной из каждой группы. К концу прошлого года у меня было 2 синие группы и 1 желтая группа, что было ОЧЕНЬ интересно!

Чему вы учите в малых группах?

При планировании и организации занятий по математике в малых группах я использую цветные библиотечные корзины – по одной для каждой из моих математических групп. Часто манипуляторы перемещаются из корзины в корзину, но оценки и материалы мини-уроков зависят от группы. Мне нравится, когда мои материалы всегда под рукой, и их легко пополнить в конце дня.

Как правило, каждая из моих групп работает над одним и тем же стандартом навыков или содержания, но каждая группа работает с материалом по-разному, в самый раз. Как учителя математики, мы намеренно продвигаем учащихся, используя модель обучения CSA (конкретную, полуконкретную и абстрактную). Моя высшая группа (синяя) тратит гораздо больше времени на работу с абстрактом; в то время как моя зеленая группа нуждается в более конкретном опыте работы с контентом.

В моих малых группах мы работаем над целевыми практическими навыками. Мы пытаемся создать конкретный учебный опыт, который в конечном итоге разветвляется на полуконкретное и абстрактное понимание. От составления и разложения чисел на рекенреках до уравнений баланса на числовой шкале, чтобы освоить часть-часть-целое с помощью жезлов, мы используем манипулятивы каждый.один.день.

Честно говоря, там определенно грязно. Мой учительский стол обычно выглядит вот так — груды стержней с порядковыми значениями, десять рамок и числовые ряды, разбросанные вокруг… но это нормально! Мы так много успеваем за 17-20 минут вместе, и мне нравится обучать целевым навыкам мои небольшие группы. Для моего класса и моей группы детей ответом является управляемая математика!

Как выглядит математический блок?

Чтобы запустить каждый блок управляемой математики, мы начинаем с произнесения чисел с помощью математических подсказок. Это короткие (около 10 минут) ежедневные упражнения, направленные на развитие чувства числа. Пока мы говорим о цифрах, учащиеся думают, задают вопросы своим сверстникам и объясняют свое мышление, пока учитель записывает ход мыслей. Вы можете прочитать больше о наших Number Talks здесь и получить годовой объем Number Talks здесь.

Упражнение по математике под руководством гида – мини-уроки для всей группы

После разговора с числами мы остаемся на ковре в классе, чтобы объявить нашу цель на день. Затем я провожу быстрый 7-8-минутный мини-урок. Во время этих мини-уроков я сосредотачиваю наше время в малых группах, делюсь важной лексикой, моделирую математическое мышление и знакомлю с базовыми знаниями (вещами, которые должны знать ВСЕ учащиеся, независимо от математической группы). Некоторые из моих любимых мини-уроков включают в себя фотографии и онлайн-математические манипуляции. Мы также регулярно вытаскиваем некоторые из наших любимых математических чтений вслух! Все три отлично подходят для моделирования математического мышления учащихся!

Математическое задание под руководством учителя — стол для учителя

Когда ученики подходят к моему учительскому столу, я не хочу, чтобы они беспокоились о том, чтобы взять с собой принадлежности. Я так и сделал, когда впервые начал заниматься математикой в ​​малых группах, и это убило ТОННУ времени. С таким коротким временем для мини-урока я теперь храню все наши материалы (карандаши, маркеры, экспомаркеры) в тройном контейнере, который я нашел в Ikea. Все учащиеся должны принести свою папку Blue Math.

Честно говоря, математика в малых группах определенно запутана. Мой учительский стол обычно выглядит так — груды стержней, десять рамок и числовые ряды, разбросанные вокруг… но это нормально! Мы так много успеваем за 17-20 минут вместе. Это время практическое и увлекательное. Учащиеся строят концептуальное понимание чисел, и это критично !

Наше время, проведенное за столом учителя, обычно разбито на быструю игру на беглость/навыки (разминка 2-3), мини-урок (5-6 минут), управляемую практику (4-5 минут), самостоятельная практика (4-5 минут) и быстрая оценка (2-3 минуты). Ниже приведен пример нашей независимой практики «Создание 10 дополнений», которая почти всегда основана на манипуляциях и конкретном обучении!

Что делают ученики, когда они не с учителем?

Пока я работаю с группой студентов (6-8 студентов одновременно), другие мои друзья занимаются другими частями Daily 3 – математикой я и математикой с другом. Я заменил Math By Myself на DreamBox (окружная математическая программа, основанная на технологиях), поскольку ожидается, что мои друзья будут ежедневно записывать время на эту программу. ЗДЕСЬ вы можете посмотреть БЕСПЛАТНОЕ видео о том, как я организую и провожу математические центры в своем классе.

Во время занятий по математике с другом я предлагаю ученикам 5 центров в неделю. Студенты выбирают, какой центр посещать каждый день, но к концу недели им нужно посетить все пять. Один центр всегда математическая тетрадь, один центр всегда Versatiles или Solve the Room. Каждую неделю я открываю только 3 новых центра (хотя в какой-то момент мы практиковали эти занятия в небольших группах, так что они не совсем новые). Как правило, 2 центра относятся к спиральному обзору, а 3-й центр относится к нашему текущему обучению.

Я храню наши математические центры в больших контейнерах Sterilite (я покупаю их наборами по 6 штук) со всеми материалами, которые могут понадобиться учащимся.

Я знаю, что для того, чтобы заниматься математикой под руководством учителя, мне нужно максимизировать время, проводимое учителем за столом. Так что, если ученики в центрах задают мне вопросы или перебивают, мои друзья за учительским столом теряют свое основное время по математике. Поэтому очень важно, чтобы учащиеся знали, где найти ресурсы в классе, и знали, как их использовать. Наши манипуляторы хранятся слева от математических ванн для быстрого доступа. Учащиеся знают, что они могут взять любой математический инструмент, необходимый им для работы. (Ярлыки можно найти здесь.)

Кроме того, наши номерные строки висят в передней части комнаты с помощью командного крючка. Это держит числовые строки организованными и легко доступными для моих маленьких друзей.

Как сделать так, чтобы ученики не мешали учителю?

Чтобы помочь развить независимость, я также добавляю визуальные указания на каждую из наших математических корзин. Эти визуальные указания включают в себя утверждение «Я могу», а также центр в действии. Эти визуальные указания помогают учащимся узнать, как настроить свои материалы, а также какие материалы им понадобятся. (Вы можете получить визуальные указания для 1-го класса здесь и для 2-го класса здесь.)

Эти математические головоломки «Создание чисел» и «120-ые диаграммы» станут двумя из наших первых пяти математических центров в этом году. мы будем практиковать эти упражнения с партнерами (всей группой) до того, как мы начнем центры, а затем, когда мы будем готовы начать ротацию, студенты будут практиковаться с партнером.

Учащихся учат доставать необходимые им материалы из корзин, а затем переворачивать корзины на бок. Большие контейнеры Sterilite будут стоять сами по себе, и это станет идеальным фокусом для учащихся. Ниже учащиеся работают с треугольниками семейства фактов (от Amazon) и дифференцированными игральными костями в зависимости от их математической группы.

Как вы отличаете свои математические центры?

Другим компонентом независимости в The Daily 5 и The Daily 3 является обеспечение того, чтобы учащиеся активно участвовали в важной работе, которая бросает им вызов. Дифференциация является ключевой частью этой независимости. Когда они посещают отдельные центры/выбирают ванну, они знают, что нужно брать свою цветную папку. Каждая ячейка содержит одно и то же действие, просто другой набор чисел или другую колоду игральных костей. (Зеленый = приближающийся уровень, желтый = уровень на уровне, синий = уровень выше)

Я также использую эти игральные кости, которые я купил на Amazon за 20 долларов, и складываю их в контейнер для бусинок. Мой фунт кубиков состоял из более чем 80 кубиков, каждый с разным количеством граней и цветов — от 3-гранных до 20-гранных, у меня есть подходящие кубики для всех моих групп.

Ниже вы видите мою группу друзей на уровне, работающих с семействами фактов. Они используют 2 желтых кубика (6-гранный и 8-гранный). Моя зеленая группа (приблизительный уровень) выполняла то же задание с той же страницей записи и теми же треугольниками семейства фактов, просто используя 2 шестигранных кубика, а моя синяя группа (выше уровня) использовала два 12-гранных кубика.

При планировании математических центров я хочу убедиться, что учащиеся вовлечены и работают с практическими материалами. Наши планы на уровне классов вместе, и мы полностью привержены тому, чтобы наши центры не были одноразовыми мероприятиями по печати / вырезанию / ламинированию. Мы работаем над созданием занятий, которые позволяют проводить повторение по спирали, использовать их в течение года и обеспечивают фантастическую практику. Ниже вы видите двух друзей, которые учатся находить недостающие дополнения с помощью рекенреков.

Студенты посещают один и тот же центр 2-3 раза в год (в зависимости от навыков и необходимости). В качестве числового обзора мы часто перестраиваем диаграмму 120s. Я копирую диаграммы на цветной картон, а затем разрезаю их на части. Я пометил головоломки ROY-G-BIV цветом, при этом красный — самый сложный, а фиолетовый — самый простой (чем больше кусочков/чем сложнее разрез, тем сложнее). Мои дети такие «игривые», что им нравится идея повышения уровня!

Нам также нравится использовать наш набор домино из пенопласта для разных видов. Они идеально подходят для добавления и сортировки типов стратегий, которые мы могли бы использовать для решения предложений на сложение. Для моих друзей старшего уровня они часто используют двойные домино, а затем создают текстовые задачи, чтобы сопровождать сортировку.

 

В этой записи блога я рассказал о некоторых других моих любимых центрах добавления в 10.

В некоторых наших центрах обслуживания используются стойки для бусинок, но они предлагают такое великолепное визуальное представление цифр! Вы можете увидеть, как мы используем рекенрекс, в этом сообщении в блоге.

В этом блоге вы можете узнать больше о других моих любимых центрах стоимости и увидеть их!

Управляемый математический вопрос: как вы обогащаете/расширяете возможности одаренных учащихся?

Для меня очень важно, чтобы у каждого друга в моем классе был доступ к материалам, которые подталкивают и бросают им вызов. Используя трехцветную систему дифференциации, я намеренно планирую и выбираю занятия, которые подходят всем моим ученикам. Позже в этом году, однако, я предпочитаю выходить за рамки своего пакета математических центров и предлагать другие варианты обогащения — ведение дневника по математике и математические головоломки — для моих успешных летчиков. Это друзья, которые работают на уровень (или два) выше 1-го класса, и те, кто иногда изо всех сил пытается показать рост в программах оценки округа (STAR, MAP и т. д.).

 

Как учителя, наша первая реакция — сказать: «Эй, эти друзья знают содержание первого класса. Мне пора двигаться дальше». — только для того, чтобы неоднократно слышать от тренеров по математике и администраторов: «Не учите математику другого уровня!» Итак, вопрос на века — если я не могу преподавать материалы для 2-го или 3-го класса, как мне бросить вызов этим ученикам и продвинуть их вперед?

Математические журналы делают наше математическое мышление более гибким и бросают вызов моим высокопоставленным ученикам продумывать свои математические процессы. Кроме того, многие из наших математических журналов требуют, чтобы учащиеся рассмотрели, как кто-то другой решил задачу, и объяснили/защитили/критиковали свой процесс.

Я также достану математические головоломки. Эти головоломки требуют, чтобы ученики применяли свои математические навыки гибкими и нетрадиционными способами. Кроме того, все три направления требуют, чтобы учащиеся задавали себе вопрос: «Имеет ли смысл мой ответ?» а также уметь аргументировать свои ответы.

Итак, подскажите, друзья, как вы организуете свой математический блок? Используете ли вы модель управляемой математики, когда основная часть мини-урока проходит в небольших группах, или вы делаете больше со всей группой? Что работает в вашем классе? А до тех пор вы можете подписаться здесь, чтобы идеи и бесплатные предложения по управляемой математике ежемесячно приходили вам в почтовый ящик.
Для получения дополнительной информации и фотографий о управляемой математике и дифференциации в моем классе, ознакомьтесь с этими сообщениями!

Дифференциация математических центров с помощью кубиков

Запуск математических центров

СМОТРЕТЬ Математические центры в классе математики (БЕСПЛАТНОЕ ВИДЕО)

Необходимые материалы для управляемой математики

Построение концептуального понимания с помощью Rekenreks 9000 Инструменты дома

Math at You Can Make 3 9000

Number Talks: как и почему?

Онлайн математические манипуляции

Учебные задачи по математике для 1-го класса

Математика, 1

ALT 1 — Решать и представлять сложение-подчинение

Я могу изучать, представлять и решать задачи на сложение и вычитание, и я понимаю взаимосвязь между ними.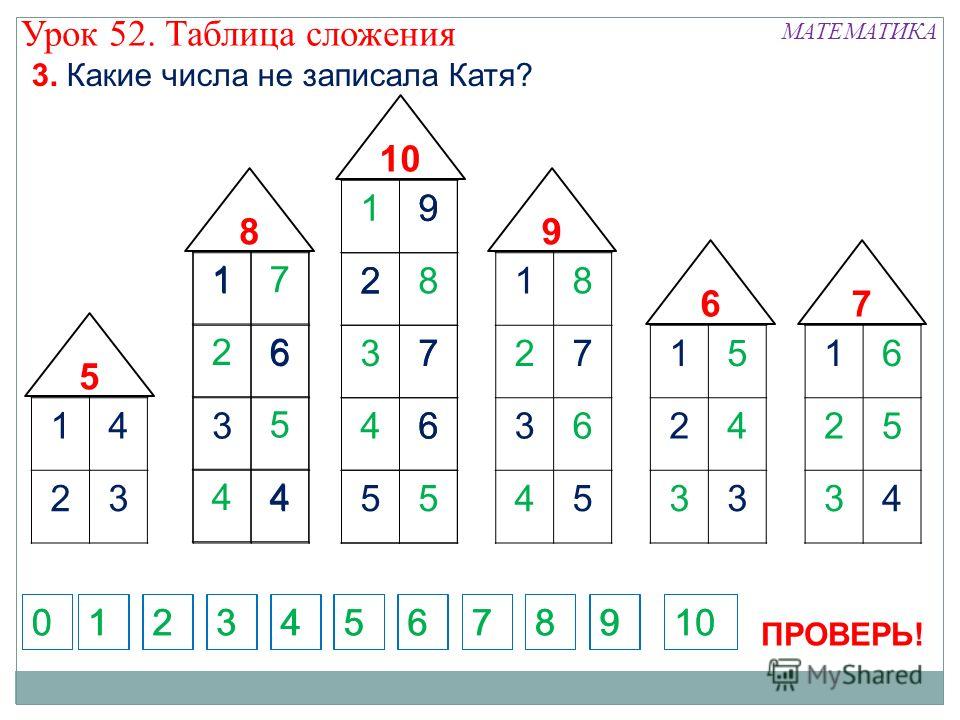

AST 1.1 — Решение текстовых задач   :  Я могу складывать и/или вычитать, чтобы решать текстовые задачи, используя объекты, рисунки и уравнения. OA.1

AST 1.2 — Словесные задачи до 20 с использованием 3 чисел   :  Я могу решать словесные задачи на сложение с 3 числами в пределах 20, используя предметы, рисунки и уравнения. ОА.2

AST 1.3 — Факты оборота   :  Я могу использовать факты оборота в качестве стратегии для решения задач на сложение. (пример: 8+3=11 и 3+8=11) OA.3

AST 1.4 — Групповые числа   :  Я могу группировать числа вместе, чтобы составить простую сумму. (пример: 2+6+4=2+10=12) OA.3

AST 1.5 — Вычитание чисел   :  Я могу вычитать такие числа, как 10-8, определяя, какое число, добавленное к 8, равно 10 (__+8= 10) ОА.4

АСТ 1.6 — Счет вверх и вниз для решения задач   :  Я умею считать вверх и вниз, чтобы решать задачи на сложение и вычитание.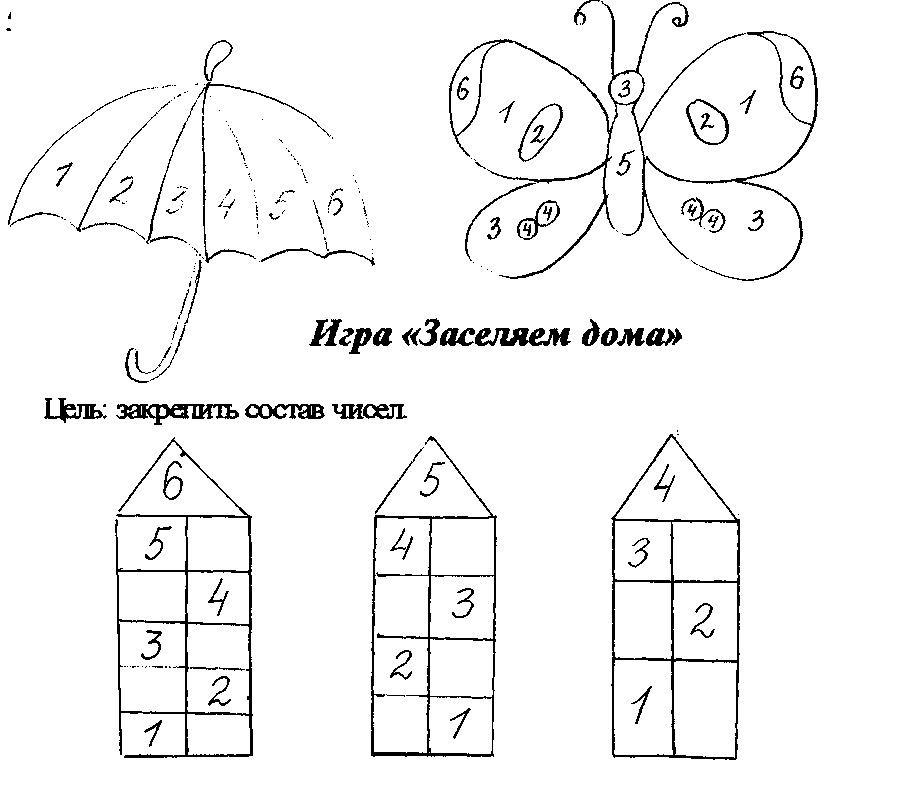 OA.5

AST 1.7 — Добавить с помощью подсчета   :  Я могу добавить, используя стратегию подсчета. OA.5

AST 1.8 — Сложение путем составления десятков   :  Я могу сложить, составив десять (пример: 8+6=8+2+4=10+4=14). OA.6

AST 1.9 — Вычитание путем составления десяти

  :  Я могу вычитать, делая десять (13-4=13-3-1) OA.6

AST 1.10 — Использование семейств фактов для сложения и вычитания   : Я могу использовать свои знания о семействах фактов для сложения и вычитания. ОА.6

AST 1.11 — Создание эквивалентных, но более простых сумм   :  Я могу составить эквивалентные, но более простые суммы для решения задач на сложение (например, 6+7 может быть 6+6+1) OA.6

AST 1.12 — Значение равенства Знак   :  Я могу сказать, что означает = (знак равенства). OA.7

AST 1.13 — Верные или ложные числовые предложения   :  Я могу сказать, является ли числовое предложение истинным или ложным. OA.7

AST 1.14 — Определение неизвестного числа   :  Я могу определить неизвестное число в числовом предложении, чтобы сделать его истинным (8+ __ = 11). ОА.8

ALT 2 — Свободно складывать и вычитать до 10

Я могу свободно складывать и вычитать до 10. OA.6

ALT 3 — Считать, читать, записывать до 120

Я умею считать, читать и записывать 120, начиная с любого числа меньше 120.

AST 3.1 — Счет, начиная с числа меньше 120   :  Я могу считать, начиная с любого числа меньше 120. NBT.1

AST 3.2 — Чтение-запись чисел до 120   :  Я могу читать и записывать числа до 120. NBT.1

ALT 4 — Разместить значение до двух цифр и сравнить

Я понимаю разрядность до двузначных чисел и могу сравнивать в пределах 100.

AST 4.1 — 10 — это группа из 10 единиц    :  Я знаю, что «десятка» — это группа из 10 «единиц». NBT.2

AST 4.2 — Десятки и единицы в двузначном числе   :  Я могу сказать, какая цифра представляет десятки, а какая — единицы в двузначном числе.

NBT.2

AST 4.3 — Количество десятков и единиц в двузначном числе   :  Я могу сказать, сколько десятков и сколько единиц в двузначном числе. НБТ.2

AST 4.4 — Сравнить больше, меньше, равно — 2 цифры

  :  Я могу использовать <,> и = для сравнения двух двузначных чисел. NBT.3

ALT 5 — Размещение значения для сложения и подсчета в пределах 100

Я использую понимание разрядности и свойства операций для сложения и вычитания со 100.

AST 5.1 — Сложение двузначных и однозначных чисел :  Я могу добавить двухзначное число и однозначное число, используя модели и чертежи. NBT.4

AST 5.2 — Сложение двузначных чисел и чисел, кратных десяти   :  Я могу добавить двузначное число, кратное 10, используя модели и чертежи. NBT.4

AST 5.3 — Сложение десятков и единиц и составление десятков   :  Я понимаю, что могу складывать десятки и десятки, а также единицы и единицы, и что иногда необходимо составить десятку. НБТ.4

АСТ 5.4 — 10 Больше-10 Меньше   :  Я могу без счета найти число на 10 больше и на 10 меньше, и рассказать, как это было сделано. NBT.5

AST 5.5 — Вычитание кратных 10   :  Я могу вычитать кратные 10 (10-90) от кратных 10 (10-90) и расскажите, как это было сделано. (пример: 80-20 равно 8 десяткам -2 десятка = 6 десяткам=60)

ALT 6 — Измерение длины

Я умею измерять длину объектов и называть единицу измерения длины.

AST 6.1 — 3 объекта в порядке   :  Я могу расположить 3 объекта в порядке длины. MD.1

AST 6.2 — Сравнение длин   :  Я могу сравнить длину двух объектов, используя третий объект (например, нить длиннее ручки, но лента короче ручки). МД.1

AST 6.3 — Измерение с помощью другого объекта   :  Я могу определить длину чего-либо, измерив его с помощью другого объекта. MD.2

AST 6.4 — Измерение от начала до конца   :  Я могу измерить от начала до конца без пробелов или перекрытий.

MD.2

ALT 7 — Сказать и записать время

Я могу сказать и записать время.

AST 7.1 — Определение времени в часах и получасах   :  Я могу сказать и написать, который час в часах и ½ часа, используя цифровые и аналоговые часы. МД.3

ALT 8 — Понимание данных

Я могу организовывать, представлять и интерпретировать данные. (Нет в табеле успеваемости)

AST 8.1 — Создание графиков с 3 группами   :  Я могу строить графики с тремя группами. MD.4

AST 8.2 — Точки данных   :  Я могу сказать общее количество точек данных, сколько в каждой категории и на сколько больше или меньше в одной категории, чем в другой. MD.4

ALT 9 — Формы и равные части

Я могу рассуждать о формах и их свойствах.

AST 9.1 — Описание формы с использованием атрибутов

  :  Я могу описать форму, используя определяющие атрибуты (стороны, углы) и неопределяющие атрибуты (цвет, размер, ориентация). G.1

AST 9.2 — Использование определяющих признаков   :  Я могу строить и рисовать фигуры, используя определяющие признаки. G.1

AST 9.3 — Преобразование 2D и 3D в другие формы   :  Я могу преобразовать двух- и трехмерные фигуры в другие формы. (пример: используйте 2 треугольника, чтобы сделать квадрат). Г.2

AST 9.4 — Разделить круги-прямоугольники на 2-4 части   :  Я могу разделить круги и прямоугольники на 2 и 4 равные части. G.3

AST 9.5 — Части круга или прямоугольника   :  Я могу описать части круга или прямоугольника, используя слова «половинки», «четверти» и «четверти». G.3

AST 9.6 — Части круга или прямоугольника-Pt 2   :  Я могу описать части круга или прямоугольника, используя фразы «половина», «четверть» и «четверть». G.3s

AST 9.7 — Круг-прямоугольник как 2 или 4 части   :  Я могу описать весь круг или прямоугольник как две части или четыре части.