Где можно делить на 0. Почему делить на ноль нельзя? Примеры, когда необходимо сдвинуть запятую, а цифр уже не осталось

В математике число ноль занимает особое место. Дело в том, что оно, по сути дела, означает «ничто», «пустоту», однако его значение действительно трудно переоценить. Для этого достаточно вспомнить хотя бы то, что именно с нулевой отметк и начинается отсчет координат положения точки в любой системе координат.

Ноль широко используется в десятичных дробях для определения значений «пустых» разрядов, находящихся как до, так и после запятой. Кроме того, именно с ним связано одно из основополагающих правил арифметики, гласящее о том, что на ноль делить нельзя. Его логика, собственно говоря, проистекает из самой сути этого числа: действительно, невозможно представить, чтобы некая отличное от него значение (да и само оно – тоже) было разделено на «ничто».

Примеры вычисления

С нулем осуществляются все арифметические действия, причем в качестве его «партнеров» по ним могут использоваться целые числа, обычные и десятичные дроби, причем все они могут иметь как положительное, так и отрицательное значение.

Приведем примеры их осуществления и некоторые пояснения к ним.

Сложение

При прибавлении нуля к некоторому числу (как целому, так и к дробному, как к положительному, так и к отрицательному) его значение остается абсолютно неизменным.

Пример 1

Двадцать четыре плюс ноль равняется двадцать четыре.

Пример 2

Семнадцать целых три восьмых плюс ноль равняется семнадцать целых три восьмых.

Умножение

При умножении любого числа (целого, дробного, положительного или отрицательного) на ноль получается ноль .

Пример 1

Пятьсот восемьдесят шесть умножить на ноль равняется ноль .

Пример 2

Ноль умножить на сто тридцать пять целых шесть седьмых равняется ноль .

Пример 3

Ноль умножить на ноль равняется ноль .

Деление

Правила деления чисел друг на друга в тех случаях, когда одно из них представляет собой ноль, различаются в зависимости от того, в какой именно роли выступает сам ноль: делимого или делителя?

В тех случаях, когда ноль представляет собой делимое, результат всегда равен ему же, причем вне зависимости от значения делителя.

Пример 1

Ноль разделить на двести шестьдесят пять равняется ноль .

Пример 2

Ноль разделить на семнадцать пятьсот девяносто шестых равняется ноль .

0:

= 0

Делить ноль на ноль согласно правилам математики нельзя. Это означает, что при совершении такой процедуры частное является неопределенным. Таким образом, теоретически оно может представлять собой абсолютно любое число.

0: 0 = 8 ибо 8 × 0 = 0

В математике такая задача, как

деление нуля на ноль , не имеет никакого смысла, поскольку ее результат представляет собой бесконечное множество. Это утверждение, однако, справедливо в том случае, если не указаны никакие дополнительные данные, которые могут повлиять на итоговый результат.

Таковые, при их наличии, должны состоять в том, чтобы указывать на степень изменения величины как делимого, так и делителя, причем еще до наступления того момента, когда они превратились в ноль . Если это определено, то такому выражению, как ноль разделить на ноль , в подавляющем большинстве случаев можно придать некий смысл.

В курсе школьной арифметики все математические операции проводятся с вещественными числами. Множество этих чисел (или непрерывное упорядоченное поле) имеет ряд свойств (аксиом): коммутативность и ассоциативность умножения и сложения, существование нуля, единицы, противоположного и обратного элементов. Также аксиомы порядка и непрерывности, применяемые для сравнительного анализа, позволяют определить все свойства вещественных чисел.

Поскольку деление является операцией, обратной умножению, при делении на ноль вещественных чисел неизбежно возникновение двух неразрешимых проблем. Во-первых, проверка результата деления на ноль при помощи умножения не имеет числового выражения. Каким бы числом не было частное, если его умножить на ноль, делимое получить невозможно. Во-вторых, в примере 0:0 ответом может служить абсолютно любое число, которое при перемножении с делителем всегда обращается в ноль.

Деление на ноль в высшей математике

Перечисленные трудности деления на ноль привели к наложению табу на эту операцию, по крайней мере, в рамках школьного курса. Однако в высшей математике находят возможности обойти этот запрет.

Например, за счет построения другой алгебраической структуры, отличной от знакомой всем числовой прямой. Примером такой структуры является колесо. Здесь существуют свои законы и правила. В частности, деление не привязано к умножению и превращается из бинарной операции (с двумя аргументами) в унарную (с одним аргументом), обозначается символом /х.

Расширение поля вещественных чисел происходит за счет введения гиперреальных чисел, которое охватывает бесконечно большие и бесконечно малые величины. Такой подход позволяет рассматривать термин «бесконечность» как некое число. Причем это число при расширении числовой прямой теряет свой знак, превращаясь в идеализированную точку, соединяющую два конца этой прямой. Такой подход можно сравнить с линией смены дат, когда при переходе между двумя часовыми поясами UTC+12 и UTC-12 можно оказаться в следующем дне или же в предыдущем. При этом становится верным утверждение х/0=∞ для любых х≠0.

Чтобы устранить неопределенность 0/0, для колеса вводится новый элемент ⏊=0/0. При этом в данной алгебраической структуре есть свои нюансы: 0·х≠0; х-х≠0 в общем случае. Также х·/х≠1, поскольку деление и умножение больше не считаются обратными операциями. Но данные особенности колеса хорошо объясняются с помощью тождеств дистрибутивного закона, действующего в такой алгебраической структуре несколько иначе. Более подробные разъяснения можно найти в специализированной литературе.

Алгебра, к которой все привыкли, является, по сути, частным случаем более сложных систем, например, того же колеса. Как видим, делить на ноль в высшей математике можно. Для этого требуется выйти за границы привычных представлений о числах, алгебраических операциях и законах, которым они подчиняются. Хотя это вполне естественный процесс, сопровождающий любой поиск новых знаний.

Число 0 можно представить, как некую границу, отделяющую мир реальных чисел от мнимых или отрицательных.

Благодаря двусмысленному положению, многие операции с этой числовой величиной не подчиняются математической логике. Невозможность деления на нуль — яркий тому пример. А разрешенные арифметические действия с нулем могут быть выполнены с помощью общепринятых определений.

История нуля

Ноль является точкой отсчета во всех стандартных системах исчисления. Европейцы стали использовать это число сравнительно недавно, но мудрецы Древней Индии пользовались нулем за тысячу лет до того, как пустое число стало регулярно использоваться европейскими математиками. Ещё раньше индийцев ноль являлся обязательной величиной в числовой системе майя. Этот американский народ использовал двенадцатеричную систему исчисления, а нулем у них начинался первый день каждого месяца. Интересно, что у майя знак, обозначающий «ноль», полностью совпадал со знаком, определяющим «бесконечность». Таким образом, древние майя делали вывод о тождественности и непознаваемости этих величин.

Математические действия с нулем

Стандартные математические операции с нулем можно свести к нескольким правилам.

Сложение: если к произвольному числу добавить ноль, то оно не изменит своего значения (0+x=x).

Вычитание: при вычитании нуля из любого числа значение вычитаемого остается неизменным (x-0=x).

Умножение: любое число, умноженное на 0, дает в произведении 0 (a*0=0).

Деление: ноль можно разделить на любое число, не равное нулю. При этом значение такой дроби будет 0. А деление на ноль запрещено.

Возведение в степень. Это действие можно выполнить с любым числом. Произвольное число, возведенное в нулевую степень, даст 1 (x 0 =1).

Ноль в любой степени равен 0 (0 а =0).

При этом сразу возникает противоречие: выражение 0 0 не имеет смысла.

Парадоксы математики

О том, что деление на ноль невозможно, многие знают со школьной скамьи. Но объяснить причину такого запрета почему-то не получается. В самом деле, почему формула деления на ноль не существует, а вот другие действия с этим числом вполне разумны и возможны? Ответ на этот вопрос дают математики.

Все дело в том, что привычные арифметические действия, которые школьники изучают в начальных классах, на самом деле далеко не так равноправны, как нам кажется. Все простые операции с числами могут быть сведены к двум: сложению и умножению. Эти действия составляют суть самого понятия числа, а остальные операции строятся на использовании этих двух.

Сложение и умножение

Возьмем стандартный пример на вычитание: 10-2=8. В школе его рассматривают просто: если от десяти предметов отнять два, останется восемь. Но математики смотрят на эту операцию совсем по-другому. Ведь такой операции, как вычитание, для них не существует. Данный пример можно записать и другим способом: х+2=10. Для математиков неизвестная разность — это просто число, которое нужно добавить к двум, чтобы получилось восемь. И никакого вычитания здесь не требуется, нужно просто найти подходящее числовое значение.

Умножение и деление рассматриваются так же. В примере 12:4=3 можно понять, что речь идет о разделении восьми предметов на две равные кучки. Но в действительности это просто перевернутая формула записи 3х4=12.Такие примеры на деление можно приводить бесконечно.

Примеры на деление на 0

Вот тут и становится понемногу понятным, почему нельзя делить на ноль. Умножение и деление на ноль подчиняется своим правилам. Все примеры на деление этой величины можно сформулировать в виде 6:0=х. Но это же перевернутая запись выражения 6 * х=0. Но, как известно, любое число, умноженное на 0, дает в произведении только 0. Это свойство заложено в самом понятии нулевой величины.

Выходит, что такого числа, которое при умножении на 0 дает какую-либо осязаемую величину, не существует, то есть данная задача не имеет решения. Такого ответа бояться не следует, это естественный ответ для задач такого типа. Просто запись 6:0 не имеет никакого смысла, и она ничего не может объяснить. Кратко говоря, это выражение можно объяснить тем самым бессмертным «деление на ноль невозможно».

Существует ли операция 0:0? Действительно, если операция умножения на 0 законна, можно ли ноль разделить на ноль? Ведь уравнение вида 0х 5=0 вполне легально. Вместо числа 5 можно поставить 0, произведение от этого не поменяется.

Действительно, 0х0=0. Но поделить на 0 по-прежнему нельзя. Как было сказано, деление — это просто обратная операция умножения. Таким образом, если в примере 0х5=0, нужно определить второй множитель, получаем 0х0=5. Или 10. Или бесконечность. Деление бесконечности на ноль — как вам это понравится?

Но если в выражение подходит любое число, то оно не имеет смысла, мы не можем из бесконечного множества чисел выбрать какое-то одно. А раз так, это значит и выражение 0:0 не имеет смысла. Получается, что на ноль нельзя делить даже сам ноль.

Высшая математика

Деление на ноль — это головная боль для школьной математики. Изучаемый в технических вузах математический анализ немного расширяет понятие задач, которые не имеют решения. Например, к уже известному выражению 0:0 добавляются новые, которые не имеют решения в школьных курсах математики:

• бесконечность, разделенная на бесконечность: ∞:∞;
• бесконечность минус бесконечность: ∞−∞;
• единица, возведенная в бесконечную степень: 1 ∞ ;
• бесконечность, умноженная на 0: ∞*0;
• некоторые другие.

Элементарными методами решить такие выражения невозможно. Но высшая математика благодаря дополнительным возможностям для ряда подобных примеров дает конечные решения. Особенно это видно в рассмотрении задач из теории пределов.

Раскрытие неопределенности

В теории пределов значение 0 заменяется условной бесконечно малой переменной величиной. А выражения, в которых при подставлении нужного значения получается деление на ноль, преобразовываются. Ниже представлен стандартный пример раскрытия предела при помощи обычных алгебраических преобразований:

Как видно в примере, простое сокращение дроби приводит ее значение к вполне рациональному ответу.

При рассмотрении пределов тригонометрических функций их выражения стремятся свести к первому замечательному пределу. При рассмотрении пределов, в которых знаменатель обращается в 0 при подставлении предела, используют второй замечательный предел.

Метод Лопиталя

В некоторых случаях пределы выражений можно заменить пределом их производных. Гийом Лопиталь — французский математик, основоположник французской школы математического анализа. Он доказал, что пределы выражений равны пределам производных этих выражений. В математической записи его правило выглядит следующим образом.

Математическое правило относительно деления на ноль всем людям рассказывали еще в первом классе общеобразовательной школы. «Делить на ноль нельзя», — учили всех нас и запрещали под страхом подзатыльника делить на ноль и вообще обсуждать эту тему. Хотя некоторые учителя младших классов все-таки пробовали объяснить на простейших примерах, почему нельзя делить на ноль, но эти примеры были настолько нелогичны, что проще было просто запомнить это правило и не задавать лишних вопросов. Но все эти примеры были нелогичными по той причине, что логически объяснить это в первом классе нам учителя не могли, так как в первом классе мы и близко не знали, что такое уравнение, а логически это математическое правило объяснить можно только с помощью уравнений.

Все знают, что при делении любого числа на ноль выйдет пустота. Почему именно пустота, мы рассмотрим потом.

Вообще в математике только две процедуры с числами признаются независимыми. Это сложение и умножение. Остальные же процедуры считаются производные от этих двух процедур. Рассмотрим это на примере.

Скажите, сколько будет, например, 11-10? Мы все моментально ответим, что это будет 1. А как мы нашли такой ответ? Кто-то скажет, что это и так понятно, что будет 1, кто-то скажет, что от 11 яблок отнял 10 и посчитал, что получилось одно яблоко. С точки зрения логики все правильно, но вот по законам математики эта задача решается по-другому. Нужно вспомнить, что основными процедурами считаются сложение и умножение, поэтому нужно составить такое уравнение: х+10=11, а только потом х=11-10, х=1. Заметим, что сложение идет на первом месте, а только потом на основе уравнения мы можем отнимать. Казалось бы, зачем столько процедур? Ведь ответ и так очевиден. Но только такими процедурами можно объяснить невозможность деления на ноль.

Например, мы делаем такую математическую задачу: хотим 20 поделить на ноль. Итак, 20:0=х. Чтобы узнать, сколько же будет, нужно вспомнить, что процедура деления вытекает из умножения. Другими словами, деление-это производная процедура от умножения. Поэтому нужно составить уравнение из умножением. Итак, 0*х=20. Вот тут и тупик. Какое бы число мы не множили на ноль, все равно будет 0, но не 20. Вот отсюда и вытекает правило: делить на ноль нельзя. Ноль делить на любое число можно, а вот число на ноль — увы, нельзя.

Отсюда появляется еще один вопрос: а можно ли ноль делить на ноль? Итак, 0:0=х, значит 0*х=0. Это уравнение можно решить. Возьмем, например, х=4, значит 0*4=0. Получается, что если разделить ноль на ноль, получится 4. Но и здесь все не так просто. Если мы возьмем, например, х=12 или х=13, то выйдет тот же ответ (0*12=0). Вообще, какое бы мы число не подставляли, все равно выйдет 0. Поэтому, если 0:0, то получится бесконечность. Вот такая нехитрая математика. К сожалению, процедура деления ноль на ноль тоже бессмысленна.

Вообще, цифра ноль в математике самая интересная. К примеру, все знают, что любое число в нулевой степени дает единицу. Конечно, с таким примером в реальной жизни мы не встречаемся, но вот с делением на ноль жизненные ситуации попадаются очень часто. Поэтому запомним, что делить на ноль нельзя.

Линия УМК А. Г. Мерзляка. Математика (5-6)

Математика

Информация о том, что на ноль делить нельзя, известна нам со школьной скамьи. Мы усваиваем это правило раз и навсегда. Однако лишь некоторые из нас задаются вопросом, а почему собственно нельзя это делать. Но ведь знать и понимать причины невозможности этого действия важно, так оно раскрывает принципы «работы» и других математических операций.

Все математические действия равны, но некоторые равнее других

Начнём с того, что четыре арифметических действия — сложение, вычитание, умножение и деление — не являются равноправными. И разговор идёт не о порядке выполнения действий при решении какого-нибудь примера или уравнения. Нет, имеется в виду само понятие числа. И согласно ему, наиболее важными являются сложение и умножение. А уже вычитание и деление «вытекают» из них тем или иным образом.

Сложение и вычитание

Например, разберём простую операцию: «3 — 1». Что это означает? Школьник легко объяснит эту задачку: это означает, что было три предмета (например, три апельсина), один вычли, оставшееся количество предметов и есть верный ответ. Верно описано? Верно. Мы и сами объяснили бы точно так же. Но математики рассматривают процесс вычитания иначе.

Операция «3 — 1» рассматривается не с позиции вычитания, а только со стороны сложения. Согласно этому нет никаких «три минус один», есть «какое-то неизвестное число, которое при прибавлении одного даёт три». Таким образом, простое «три минус один» превращается в уравнение с одним неизвестным: «х + 1 = 3». Причём появление уравнения изменило знак — вычитание поменялось на сложение. Осталась только одна задача — отыскать подходящее число.

Справочное пособие содержит все основные формулы школьного курса математики: алгебры, геометрии и начал анализа. Для удобства пользования справочником составлен предметный указатель. Пособие предназначено для школьников 5-11 классов и абитуриентов.

Умножение и деление

Аналогичные метаморфозы происходят с таким действием, как деление. Задачу «6: 3» математики отказываются воспринимать как некие шесть предметов, разбитых на три части. «Шесть разделить на три» не что иное, как «неизвестное число, умноженное на три, в результате чего получилось шесть»: «х · 3».

Делим на ноль

Выяснив принцип математических действий по отношению к задачам с вычитанием и делением, рассмотрим наше деление на ноль.

Задача «4: 0» превращается в «х · 0». Получается, нам нужно найти такое число, умножение с которым даст нам 4. Известно, что умножение на ноль всегда даёт ноль. Это уникальное свойство нуля и, собственно, его суть. Числа, умноженного на ноль и выдающего любое другое число кроме нуля, не существует. Мы пришли к противоречию, значит задача не имеет решения. Следовательно, записи «4: 0» не соответствует никакое определённое число, а отсюда уже вытекает её бессмысленность. Поэтому, чтобы кратко подчеркнуть непродуктивность такого процесса, как деление на ноль, и говорят, что «на ноль делить нельзя».

Больше интересных материалов:

• Типичные ошибки учителей при проведении уроков математики в начальной школе
• Внеурочная деятельность по математике в начальной школе
• Формирование математической грамотности в начальной школе

А что получится, если ноль разделить на ноль?

Представим такое уравнение: «0 · x = 0». С одной стороны, выглядит вполне справедливо. Представляем вместо неизвестного числа ноль и получаем готовое решение: «0 · 0 = 0». Из этого вполне логично вывести, что «0: 0 = 0».

Однако теперь давайте в это же уравнение с неизвестным вместо «x = 0» подставим любое другое число, например «x = 7». Получившееся выражение выглядит теперь как «0 · 7 = 0». Вроде бы, всё верно. Делаем обратную операцию и получаем «0: 0 = 7». Но тогда, получается, что можно взять абсолютно любое число и вывести 0: 0 = 1, 0: 0 = 2. .. 0: 0 = 145… — и так до бесконечности.

Если при любом числе х уравнение будет справедливо, то мы не имеем права выбрать лишь одно, исключив остальные. Значит, мы так и не можем ответить, какому числу соответствует выражение «0: 0». Снова оказавшись в тупике, мы признаём, что и эта операция тоже бессмысленна. Получается, что ноль нельзя делить даже на самого себя.

Оговоримся, что в математическом анализе иногда бывают специальные условия задачи — так называемое «раскрытие неопределенности». В подобных случаях разрешается отдавать предпочтение одному из возможных решений уравнения «0 · x = 0». Однако в арифметике таких «допусков» не происходит.

Решение (корни) квадратного уравнения

• Определение квадратного уравнения и общее понятие о его корнях
• Геометрический смысл решения квадратного уравнения
• Три случая после нахождения дискриминанта квадратного уравнения
• Решение полных квадратных уравнений
• Теорема Виета
• Решение неполных квадратных уравнений
• Разложение квадратного трёхчлена на множители с применением корней квадратного уравнения
• Из истории решения квадратных уравнений
• Различные прикладные задачи на квадратные уравнения
• Онлайн калькулятор квадратных уравнений

Квадратным уравнением называется уравнение вида ax² + bx + c = 0, где x — переменная, которая в уравнении присутствует в квадрате, a, b, c — некоторые числа, причём a ≠ 0.

Например, квадратным является уравнение

2x² — 3x + 1 = 0,

в котором a = 2, b = — 3, c = 1.

В квадратном уравнении ax² + bx + c = 0 коэффициент a называют первым коэффициентом, b — вторым коэффициентом, c — свободным членом.

Уравнения вида ax² + bx = 0,

где c =0,

ax² + c = 0,

где b =0, и

ax² = 0,

где a =0 и b =0,

называются неполными квадратными уравнениями.

Найти корни квадратного уравнения значит решить квадратное уравнение.

Для вычисления корней квадратного уравния служит выражение b² — 4ac, которое называется дискриминантом квадратного уравнения и обозначается буквой D.

Корни квадратного уравнения имеют следующие сферы применения:

— для разложении квадратного трёхлена на множители, что, в свою очередь, является приёмом упрощения выражений (например, сокращения дробей, вынесение за скобки общего знаменателя и т.д.) в частности, при нахождении пределов, производных и интегралов;

— для решения задач на соотношения параметров меняющегося объекта (корни квадратного уравнения, чаще всего один, являются обычно конечным решением).

График квадратичного трёхлена ax² + bx + c — левой части квадратного уравнения — представляет собой параболу, ось симметрии которой параллельна оси 0y. Число точек пересечения параболы с осью 0x определяет число корней квадратного уравнения. Если точек пересечения две, то квадратное уравнение имеет два действительных корня, если точка пересечения одна, то квадратное уравнение имеет один действительный корень, если парабола не пересекает ось 0x, то квадратное уравнение не имеет действительных корней.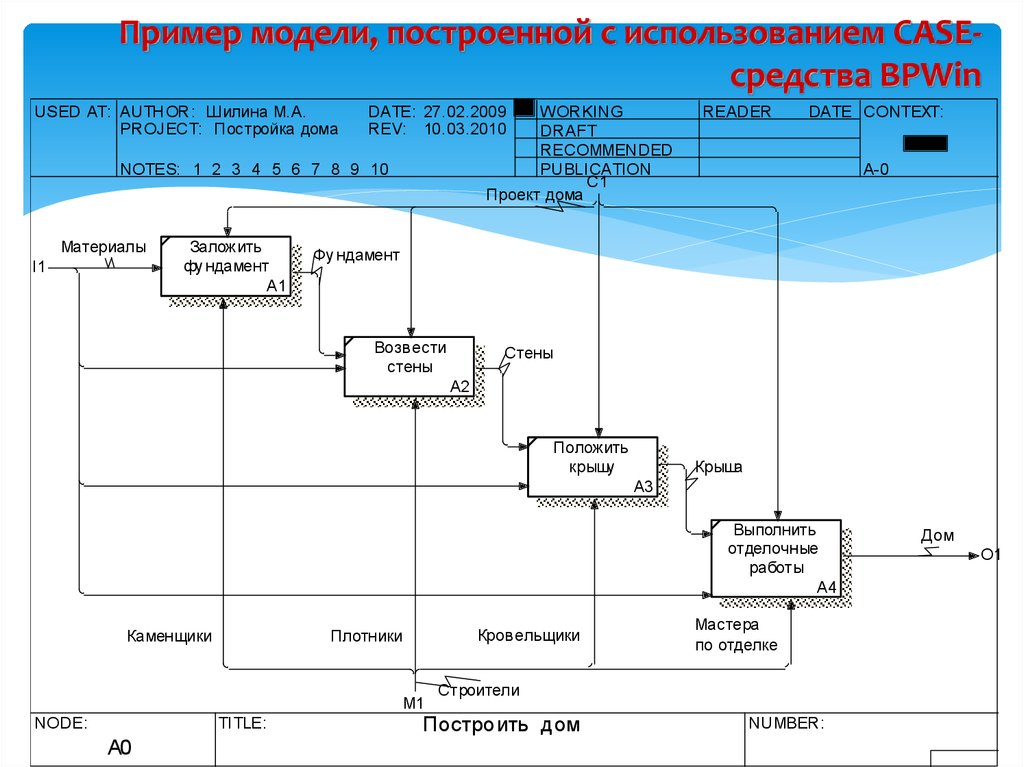 На рисунке ниже изображены три упомянутых случая.

Как видно на рисунке, красная парабола пересекает ось 0x в двух точках, зелёная — в одной точке, а жёлтая парабола не имеет точек пересечения с осью 0x.

1. Если дискриминант больше нуля (), то квадратное уравнение имеет два различных действительных корня.

Они вычисляются по формулам:

и

.

Часто пишется так: .

2. Если дискриминант равен нулю (), то квадратное уравнение имеет только один действительный корень, или, что то же самое — два равных действительных корня, которые равны .

3. Если дискриминант меньше нуля (), то квадратное уравнение не имеет действительных корней, а имеет комплексные корни, но нахождение комплексных корней в этой статье рассматривать не будем. В общем случае правильным решением является констатация того, что квадратное уравнение не имеет действительных корней.

Пример 1. Определить, сколько действительных корней имеет квадратное уравнение:

.

Решение. Найдём дискриминант:

.

Дискриминант больше нуля, следовательно, квадратное уравнение имеет два действительных корня.

Путём преобразования в квадратное уравнение следует решать и дробные уравнения, в которых хотя бы одно из слагаемых — дробь, в знаменателе которой присутствует неизвестное, например, . О том, как это делается — в материале Решение дробных уравнений с преобразованием в квадратное уравнение.

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Пример 2. Определить, сколько действительных корней имеет квадратное уравнение:

.

Решение. Найдём дискриминант:

.

Дискриминант равен нулю, следовательно, квадратное уравнение имеет один действительный корень.

Пример 3. Определить, сколько действительных корней имеет квадратное уравнение:

.

Решение. Найдём дискриминант:

.

Дискриминант меньше нуля, следовательно, квадратное уравнение не имеет действительных корней.

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Находить корни квадратного уравнения требуется при решении многих задач высшей математики, например, при нахождении пределов, интегралов, исследовании функций на возрастание и убывание и других.

Пример 4. Найти корни квадратного уравнения:

.

В примере 1 нашли дискриминант этого уравнения:

,

Решение квадратного уравнения найдём по формуле для корней:

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Пример 5. Найти корни квадратного уравнения:

.

В примере 2 нашли дискриминант этого уравнения:

.

Применим формулу корней квадратного уравнения . Отсюда , . Найденные корни квадратного уравнения равны друг другу, а это значит, что уравнение имеет единственный корень:

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Находить корни квадратного уравнения требуется при решении многих задач высшей математики, например, при нахождении пределов, интегралов, исследовании функций на возрастание и убывание и других.

Корни приведённого квадратного уравнения

Пусть дано квадратное уравнение . Так как , то разделив обе части данного уравнения на a, получим уравнение . Полагая, что и , приходим к уравнению , в котором первый коэффициент равен 1. Такое уравнение называется приведённым.

Формула корней приведённого уравнения имеет вид:

.

Существуют формулы, связывающие корни квадратного уравнения с его коэффициентами. Они впервые были получены французским математиком Ф.Виетом.

Теорема Виета. Если квадратное уравнение ax² + bx + c = 0 имеет действительные корни, то их сумма равна — b/a, а произведение равно с/a:

Следствие. Если приведённое квадратное уравнение x² + px + q = 0 имеет действительные корни и , то

Пояснение формул: сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Следовательно, теорему Виета можно применять и для поиска корней приведённого квадратного уравнения.

Пример 6. Написать приведённое квадратное уравнение, корнями которого являются числа 1 и -3.

Иначе говоря, надо найти числа p и q такие, чтобы квадратное уравнение

имело корни и .

По формулам Виета , . Требуемое в условии задачи уравнение имеет вид

---

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Пример 7. Решить квадратное уравнение .

Решение. Чтобы решить данное неполное квадратное уравнение, разложим его левую часть на множители. Получим

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю: или . Решая уравнение , находим .

Следовательно, произведение обращается в нулю при и при . Поэтому числа 0 и 1/2 являются корнями неполного квадратного уравнения .

Пример 8. Решить квадратное уравнение .

Решение. Чтобы решить данное неполное квадратное уравнение, перенесём в его правую часть свободный член с противоположным знаком и разделим обе части уравнения на 3. Получим уравнение

.

Так как , то уравнение не имеет действительных корней. Следовательно, не имеет действительных корней и эквивалентное ему неполное квадратное уравнение .

Если известны корни квадратного уравнения, то трёхчлен, представляющий собой левую часть уравнения, можно разложить на множители по следующей формуле:

.

Этот приём часто используется для упрощения выражений, особенно сокращения дробей.

Пример 9. Упростить выражение:

.

Решение. Числитель данной дроби можем рассматривать как квадратный трёхчлен в отношении x и разложить его на множители, предварительно найдя его корни. Найдём дискриминант квадратного уравнения:

.

Корни квадратного уравнения будут следующими:

.

Разложим квадратный многочлен на множители:

.

Упростили выражение, проще не бывает:

.

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Пример 10. Упростить выражение:

.

Решение. И числитель, и знаменатель — квадратные трёхчлены. Значит, их можно разложить на множители, предварительно найдя корни соответствующих квадратных уравнений. Находим дискриминант первого квадратного уравнения:

.

Корни первого квадратного уравнения будут следующими:

.

Находим дискриминант второго квадратного уравнения:

.

Так как дискриминант равен нулю, второе квадратное уравнение имеет два совпадающих корня:

.

Подставим корни квадратных уравнений, разложим числитель и знаменатель на множители и получим:

.

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Упрощать выражения путём решения квадратных уравнений требуется при решении многих задач высшей математики, например, при нахождении пределов, интегралов, исследовании функций на возрастание и убывание и других.

Разумеется, квадратного трёхчлена может может и не быть в выражении в первоначальном виде, он может быть получен в процессе предварительных преобразований выражения.

Формула корней квадратного уравнения «переоткрывалась» неоднократно. Один из первых дошедших до наших дней выводов этой формулы принажлежит индийскому математику Брахмагупте (около 598 г.). Среднеазиатский учёный аль-Хорезми (IX в.) получил эту формулу методом выделения полного квадрата с помощью геометрической иллюстрации. Суть его рассуждений видна из рисунка ниже (он рассматривает уравнение x² + 10x = 39).

Площадь большого квадрата равна (x + 5)². Она складывается из площади x² + 10x заштрихованной фигуры, равной левой части рассматриваемого уравнения, и площади четырёх квадратов со стороной 5/2, равной 25. Получается следующее уравнение и его решение:

Пример 11. Отрезок ткани стоит 180 у.ед. Если бы ткани в отрезке было на 2,5 м больше и цена отрезка оставалась бы прежней, то цена 1 м ткани была бы на 1 у.ед. меньше. Сколько ткани в отрезке?

Решение. Примем количество ткани в отрезке за x и получим уравнение:

Приведём обе части уравнения к общему знаменателю:

Произведём дальнейшие преобразования:

Получили квадратное уравнение, которое и решим:

Ясно, что количество ткани не может быть отрицательным, поэтому в качестве ответа из двух корней квадратного уравнения подходит лишь один корень — положительный.

Ответ: в отрезке 20 м ткани.

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Пример 12. Товар, количество которого 187,5 кг, взвешивают в одинаковых ящиках. Если в каждом ящике количество товара уменьшить на 2 кг, то следовало бы использовать на 2 ящика больше и при этом 2 кг товара остались бы невзвешенными. Сколько кг товара взвешивают в каждом ящике?

Решение. Примем за x количество товара, взвешиваемого в одном ящике. Тогда получим уравнение:

Приведём обе части уравнения к общему знаменателю, произведём дальнейшие преобразования и получим квадратное уравнение. Процесс записывается так:

Найдём дискриминант:

Найдём корни квадратного уравнения:

Количество товара не может быть отрицательным, поэтому в качестве ответа из двух корней квадратного уравнения подходит лишь положительный корень.

Ответ: в одном ящике взвешивают 12,5 кг ткани.

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Назад

Листать

Вперёд>>>

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Другие темы в блоке «Школьная математика»

Действия со степенями и корнями

Действия с дробями

Решение дробных уравнений с преобразованием в квадратное уравнение

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

Справочник по математике

Алгебра

Уравнения, сводящиеся к квадратным уравнениям

      Существует ряд уравнений, которые удается решить при помощи сведения их к квадратным уравнениям.

      К таким уравнениям, в частности, относятся уравнения следующих типов:

	Трёхчленные уравнения
	Уравнения 4-ой степени, левая часть которых равна произведению четырёх последовательных членов арифметической прогрессии
	Возвратные (симметричные) уравнения 3-ей степени
	Возвратные (симметричные) уравнения 4-ой степени
	Обобщенные возвратные уравнения 4-ой степени

      Замечание. Уравнения, носящие название «Биквадратные уравнения», относятся к типу «Трехчленные уравнения».

Возвратные (симметричные) уравнения 3-ей степени

      Возвратным уравнением 3-ей степени называют уравнение вида

ax3 + bx2 + bx + a = 0,

(1)

где a, b – заданные числа.

      Решение уравнения (1) осуществляется при помощи разложения левой части уравнения (1) на множители:

      Для завершения решения уравнения (1) остаётся лишь решить квадратное уравнение

ax² + (b – a) x + a = 0.

      Пример 1. Решить уравнение

2x3 + 7x2 + 7x + 2 = 0.

(2)

      Решение. Разложим левую часть уравнения (2) на множители:

      Ответ:.

Возвратные (симметричные) уравнения 4-ой степени

      Возвратными (симметричными) уравнениями 4-ой степени называют уравнения вида

ax4 + bx3 + cx2 + + bx + a = 0,

(3)

а также уравнения вида

ax4 + bx3 + cx2– – bx + a = 0,

(4)

где a, b, c – заданные числа.

      Для того, чтобы решить возвратное уравнение (3), разделим его на  x². В результате получится уравнение

(5)

      Преобразуем левую часть уравнения (5):

      В результате этого преобразования уравнение (5) принимает вид

(6)

      Если теперь обозначить

(7)

то уравнение (6) станет квадратным уравнением:

ay2 + by + c – 2a = 0.

(8)

     Найдем корни уравнения (8), а после этого, подставив каждый из найденных корней в равенство (7), решим полученное уравнение относительно  x.

      Описание метода решения уравнений вида (3) завершено.

      Для того, чтобы решить возвратное уравнение (4), разделим его на  x². В результате получится уравнение

(9)

      Преобразуем левую часть уравнения (9):

      В результате этого преобразования уравнение (9) принимает вид

(10)

      Если теперь обозначить

(11)

то уравнение (10) станет квадратным уравнением:

ay2 + by + c + 2a = 0.

(12)

      Найдем корни уравнения (13), а после этого, подставив каждый из найденных корней в равенство (11), решим полученное уравнение относительно  x.

      Описание метода решения уравнений вида (4) завершено.

      Пример 2. Решить уравнение

2x4 – 3x3 – x2 – – 3x + 2 = 0.

(13)

      Решение. Уравнение (13) является возвратным и относится к виду (3). Разделим его на  x². В результате получится уравнение

(14)

      Преобразуем левую часть уравнения (14):

      В результате этого преобразования уравнение (14) принимает вид

(15)

      Если теперь обозначить

(16)

то уравнение (15) станет квадратным уравнением:

2y2 – 3y – 5 = 0.

(17)

      Решим уравнение (17):

(18)

      В первом случае из равенства (16) получаем уравнение:

которое решений не имеет.

      Во втором случае из равенства (16) получаем:

      Ответ:

      Пример 3. Решить уравнение

6x4 – 25x3 + 12x2 + + 25x + 6 = 0.

(19)

      Решение. Уравнение (19) является возвратным и относится к виду (4). Разделим его на  x². В результате получится уравнение

(20)

      Преобразуем левую часть уравнения (20):

      В результате этого преобразования уравнение (20) принимает вид

(21)

      Если теперь обозначить

(22)

то уравнение (21) станет квадратным уравнением:

6y2 – 25y + 24 = 0.

(23)

      Решим уравнение (23):

(24)

      В первом случае из равенства (22) получаем:

      Во втором случае из равенства (22) получаем:

      Ответ:

Обобщенные возвратные уравнения 4-ой степени

      Обобщенным возвратным уравнением 4-ой степени назовём уравнение вида

(25)

где  a, b, c, d  – заданные числа.

      Для того, чтобы решить уравнение (25), разделим его на  x². В результате получится уравнение

(26)

      Преобразуем левую часть уравнения (26):

      В результате этого преобразования уравнение (26) принимает вид

      Если теперь обозначить

(28)

то уравнение (27) станет квадратным уравнением:

(29)

      Найдем корни уравнения (29), а после этого, подставив каждый из найденных корней в равенство (28), решим полученное уравнение относительно  x.

      Описание метода решения уравнений вида (25) завершено.

      Пример 4. Решить уравнение

2x4 – 15x3 + 35x2 – – 30 x + 8 = 0.

(30)

      Решение. Введем для коэффициентов уравнения (30) следующие обозначения

a = 2 ,      b =– 15,      
c = 35,       d = – 30,

и найдем значение выражения

      Поскольку

то уравнение (30) является обобщенным возвратным уравнением 4-ой степени. В соответствии с изложенным выше, разделим его на x². В результате получится уравнение

(31)

      Преобразуем левую часть уравнения (31):

      В результате этого преобразования уравнение (31) принимает вид

(32)

      Если теперь обозначить

(33)

то уравнение (32) станет квадратным уравнением:

2y2 – 15y + 27 = 0.

(34)

      Решим уравнение (34):

      В первом случае из равенства (33) получаем:

      Во втором случае из равенства (33) получаем:

      Ответ:

 

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Функция нуля — значение, график, примеры

LearnPracticeDownload

Существуют различные виды функций, которые мы изучаем в математике. Функция — это отношение, которое сопоставляет элементы домена с элементами содомена таким образом, что каждый элемент домена отображается только в один элемент содомена. Нулевая функция — это функция, область определения которой состоит из всех действительных чисел, а диапазон состоит из одного элемента, т. е. 0. Нулевая функция также является постоянной функцией, поскольку ее значение никогда не меняется при изменении входных данных. В этой статье мы исследуем свойства нулевой функции и ее природу.

1.	Что такое нулевая функция?
2.	График нулевой функции
3.	Характеристики нулевой функции
4.	Нулевая функция четная или нечетная?
5.	Часто задаваемые вопросы о нулевой функции

Что такое нулевая функция?

Нулевая функция — это постоянная функция, для которой выходное значение всегда равно нулю, независимо от входных данных. Вход нулевой функции может принимать любое значение из действительных чисел, тогда как выход нулевой функции фиксирован, то есть 0. Поскольку изображение каждого элемента в области равно 0, поэтому нулевая функция не является однозначной. -одна функция.

Нулевая функция Значение

Функция f: R → R, определяемая как f(x) = 0 для всех значений x в R, называется нулевой функцией. Диапазон нулевой функции — это одноэлементный набор, то есть {0}. Как и любой другой график постоянной функции, параллельный оси x, график нулевой функции является самой осью x, поскольку значение координаты y равно 0 на всем графике. Это функция «многие к одному», так как все элементы домена имеют одно и то же изображение, то есть 0,9.0003

График нулевой функции

График нулевой функции f(x) = 0 аналогичен графикам других постоянных функций, которые параллельны оси x. Любую функцию можно рассматривать как постоянную, если она имеет вид y = k, где k — константа, а k — любое действительное число. Это также записывается как f(x) = k. Поскольку для нулевой функции диапазон равен нулю, а значение координаты y всегда равно нулю, поэтому график нулевой функции представляет собой саму ось X. Другими словами, можно сказать, что график нулевой функции является горизонтальной осью.

Характеристики нулевой функции

Функции имеют различные характеристики, такие как наклон, область определения, диапазон, дифференцируемость, предел и непрерывность. Давайте теперь исследуем различные характеристики нулевой функции. Будучи типом постоянной функции, нулевая функция имеет свойства, аналогичные постоянным функциям.

• Функция наклона нуля: Функция нуля также может быть записана как y = 0x + 0. Сравнивая эту форму с формой пересечения наклона линии y = mx + b, где m — наклон линии и b — точка пересечения с осью y, мы получаем, что наклон нулевой функции равен 0,9.0070
• Домен и диапазон нулевой функции: Нулевая функция — это линейная функция, диапазон которой содержит только один элемент независимо от количества элементов в домене. Поскольку нулевая функция определена для всех значений x, поэтому областью определения являются все действительные числа R, а диапазон нулевой функции равен {0}.
• Производная нулевой функции: Дифференциация нуля любой постоянной функции. Производной считается наклон функции в любой заданной точке, а мы уже знаем, что наклон нулевой функции всегда равен 0. Следовательно, производная нулевой функции равна 0,9.0070
• Предел нулевой функции: Согласно свойствам пределов предел постоянной функции равен той же константе. Следовательно, предел нулевой функции равен 0,
.
• Непрерывность нулевой функции: Постоянные функции являются непрерывными, поскольку они представляют собой горизонтальные линии, непрерывно продолжающиеся в обе стороны без каких-либо разрывов. Поскольку нулевая функция является постоянной функцией, поэтому нулевая функция является непрерывной функцией без каких-либо разрывов во всей области.

Нулевая функция четная или нечетная?

Функция f называется четной, если f(-x) = f(x) для всех значений x в области определения f, и функция называется нечетной, если f(-x) = -f(x ) для всех значений x в области определения f. Нулевая функция — единственная функция, которая удовлетворяет обоим этим условиям вместе для всех значений x в области определения f. Следовательно, нулевая функция одновременно четна и нечетна. Если f(x) = 0 является нулевой функцией, то f(-x) = f(x) = -f(x) = 0, поскольку выход всегда остается одним и тем же.

Важные замечания по функции установки нуля

• Выход (диапазон) функции установки нуля всегда равен 0.
• Функция нуля является как четной, так и нечетной.
• График нулевой функции представляет собой ось X и представляет собой непрерывную функцию.

Темы, связанные с функцией нуля

• Типы функций
• Постоянная функция
• Функция идентификации
• Нули квадратного полинома

 

Примеры нулевой функции

1. Пример 1: Определите, является ли функция f(x) = 6 нулевой функцией.

   Решение: f(x) = 6 — постоянная функция, диапазон которой всегда равен 6, а 6 не равно 0. Для нулевой функции диапазон равен {0} и имеет вид f(x) = 0 для всех х. Следовательно, f(x) = 6 не является нулевой функцией.

   Ответ: Нет, f(x) = 6 не является нулевой функцией.

2. Пример 2: Каков предел нулевой функции f(x) = 0 при стремлении x к бесконечности?

   Решение:  Предел постоянной функции всегда равен значению константы (выходу) при всех значениях x. Следовательно, предел нулевой функции f(x) = 0 равен 0, когда x стремится к бесконечности.

   Ответ: Предел нулевой функции 0 при стремлении x к бесконечности.

перейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы по нулевой функции

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы по нулевой функции

Что такое нулевая функция в математике?

Функция f: R → R, определенная как f(x) = 0 для всех значений x в R, называется нулевой функцией. Диапазон нулевой функции — это одноэлементный набор, то есть {0}. Нулевая функция — это постоянная функция, для которой выходное значение всегда равно нулю независимо от входных данных.

Что такое ненулевая функция?

Функция, выход которой не равен нулю при всех значениях входов, называется ненулевой функцией. Ненулевая функция может иметь 0 в качестве выхода для некоторых значений в домене, но если она равна нулю для всех элементов в домене, то это нулевая функция.

Является ли нулевая функция четной или нечетной?

Нулевая функция — это единственная функция, которая одновременно является четной и нечетной, поскольку она удовлетворяет обоим условиям f(-x) = f(x) и f(-x) = -f(x) для всех значений x в домен ф.

Что такое интеграл нулевой функции?

Интеграл нулевой функции f(x) = 0 – это произвольная константа C, которая может принимать любые значения действительных чисел. Поскольку производная любой константы равна нулю, следовательно, интеграл от нулевой функции является произвольной константой.

Как найти нули функции?

Нули функции можно вычислить с помощью различных методов, таких как квадратичная формула и разложение полинома на множители.

Рабочие листы по математике и
наглядная программа

1.10. Деревья решений — документация scikit-learn 1.1.2

Деревья решений (DT) — это используемый непараметрический контролируемый метод обучения для классификации и регрессии. Цель состоит в том, чтобы создать модель, которая предсказывает значение целевая переменная, изучая простые правила принятия решений, полученные на основе данных Особенности. Дерево можно рассматривать как кусочно-постоянную аппроксимацию.

Например, в приведенном ниже примере деревья решений обучаются на основе данных для аппроксимировать синусоиду набором решающих правил «если-то-иначе». Чем глубже дерево, тем сложнее правила принятия решений и лучше модель.

Некоторые преимущества деревьев решений:

• Простота для понимания и интерпретации. Деревья можно визуализировать.

• Требуется небольшая подготовка данных. Другие методы часто требуют данных нормализация, необходимо создать фиктивные переменные и пустые значения для удалить. Обратите внимание, однако, что этот модуль не поддерживает отсутствующие ценности.

• Стоимость использования дерева (т. е. прогнозирования данных) является логарифмической в количество точек данных, используемых для обучения дерева.

• Способен обрабатывать как числовые, так и категориальные данные. Тем не менее, scikit-learn реализация пока не поддерживает категориальные переменные. Другой методы обычно специализируются на анализе наборов данных, которые имеют только один тип переменной. Подробнее об алгоритмах см. Информация.

• Возможность решения задач с несколькими выходами.

• Использует модель белого ящика. Если данная ситуация наблюдаема в модели, объяснение условия легко объясняется булевой логикой. Напротив, в модели черного ящика (например, в искусственном нейронном сеть), результаты могут быть труднее интерпретировать.

• Можно проверить модель с помощью статистических тестов. Это делает это можно объяснить надежность модели.

• Работает хорошо, даже если его предположения несколько нарушаются истинная модель, из которой были сгенерированы данные.

К недостаткам деревьев решений относятся:

• Изучающие деревья решений могут создавать сверхсложные деревья, которые не хорошо обобщать данные. Это называется переоснащением. Механизмы такие как обрезка, установка минимального количества необходимых образцов на листовом узле или установка максимальной глубины дерева. необходимо, чтобы избежать этой проблемы.

• Деревья решений могут быть нестабильными из-за небольших изменений в данные могут привести к созданию совершенно другого дерева. Эта проблема смягчается за счет использования дерева решений в ансамбль.

• Прогнозы деревьев решений не являются ни гладкими, ни непрерывными, но кусочно-постоянные приближения, как показано на рисунке выше. Следовательно, они не умеют экстраполировать.

• Известно, что задача изучения оптимального дерева решений NP-полным по нескольким аспектам оптимальности и даже для простых концепции. Следовательно, практические алгоритмы обучения дерева решений основаны на эвристических алгоритмах, таких как жадный алгоритм, где в каждом узле принимаются локально оптимальные решения. Такие алгоритмы не может гарантировать возвращение глобально оптимального дерева решений. Этот можно смягчить, обучив несколько деревьев в обучающем ансамбле, где функции и образцы выбираются случайным образом с заменой.

• Существуют концепции, которые трудно выучить, поскольку деревья решений не выражайте их легко, например XOR, проблемы с четностью или мультиплексором.

• Обучающиеся дерева решений создают деревья с ошибками, если некоторые классы доминируют. Поэтому рекомендуется сбалансировать набор данных перед подгонкой. с деревом решений.

1.10.1. Классификация

DecisionTreeClassifier — это класс, способный выполнять классификация по набору данных.

Как и другие классификаторы, DecisionTreeClassifier принимает на вход два массива: массив X, разреженный или плотный, формы (n_samples, n_features) , содержащий обучающие образцы и массив Y целочисленных значений формы (n_samples,) , наличие меток класса для обучающих образцов:

 >>> из дерева импорта sklearn
>>> Х = [[0, 0], [1, 1]]
>>> Y = [0, 1]
>>> clf = tree.DecisionTreeClassifier()
>>> clf = clf.fit(X, Y)
 

После подгонки модель можно использовать для прогнозирования класса образцов:

 >>> clf.predict([[2., 2.]])
массив ([1])
 

В случае, если существует несколько классов с одинаковым и самым высоким вероятность, классификатор предскажет класс с наименьшим индексом среди этих классов.

В качестве альтернативы выводу определенного класса вероятность каждого класса можно предсказать, что является долей обучающих выборок класса в лист:

 >>> clf.predict_proba([[2., 2.]])
массив([[0., 1.]])
 

DecisionTreeClassifier поддерживает как двоичные (где метки [-1, 1]) классификация и мультикласс (где метки [0, …, K-1]) классификации.

Используя набор данных Iris, мы можем построить дерево следующим образом:

 >>> из sklearn.datasets импортировать load_iris
>>> из дерева импорта sklearn
>>> диафрагма = load_iris()
>>> X, y = iris.data, iris.target
>>> clf = tree.DecisionTreeClassifier()
>>> clf = clf.fit(X, y)
 

После обучения вы можете построить дерево с помощью функции plot_tree :

 >>> tree.plot_tree(clf)
[...]
 

Мы также можем экспортировать дерево в формате Graphviz, используя export_graphviz экспортер. Если вы используете диспетчер пакетов conda, двоичные файлы graphviz и пакет python можно установить с помощью conda install python-graphviz .

В качестве альтернативы двоичные файлы для graphviz можно загрузить с домашней страницы проекта graphviz, и оболочка Python, установленная из pypi с пункт установить графвиз .

Ниже приведен пример графического экспорта приведенного выше дерева, обученного на всем набор данных по радужной оболочке; результаты сохраняются в выходной файл iris.pdf :

 >>> импорт графвиза
>>> dot_data = tree.export_graphviz(clf, out_file=Нет)
>>> graph = graphviz.Source(dot_data)
>>> graph.render("радужная оболочка")
 

Экспортер export_graphviz также поддерживает различные эстетические параметры, включая раскраску узлов по их классу (или значению для регрессии) и используя явные имена переменных и классов, если это необходимо. Ноутбуки Jupyter также отображать эти графики автоматически:

 >>> dot_data = tree.export_graphviz(clf, out_file=Нет,
... feature_names=радужная оболочка.feature_names,
... class_names=iris. target_names,
... заполнено=Истина, округлено=Истина,
... special_characters=Истина)
>>> graph = graphviz.Source(dot_data)
>>> график
 

Кроме того, дерево можно также экспортировать в текстовом формате с функция экспорт_текст . Этот метод не требует установки внешних библиотек и компактнее:

 >>> из sklearn.datasets импортировать load_iris
>>> из sklearn.tree импортировать DecisionTreeClassifier
>>> из sklearn.tree импортировать export_text
>>> диафрагма = load_iris()
>>> дерево_решений = класс_дерева_решений(случайное_состояние=0, максимальная_глубина=2)
>>> дерево_решений = дерево_решений.fit(iris.data, iris.target)
>>> r = export_text(decision_tree, feature_names=радужная оболочка['feature_names'])
>>> напечатать(р)
|--- ширина лепестка (см) <= 0,80
| |--- класс: 0
|--- ширина лепестка (см) > 0,80
| |--- ширина лепестка (см) <= 1,75
| | |--- класс: 1
| |--- ширина лепестка (см) > 1,75
| | |--- класс: 2
 

Примеры:

• Постройте поверхность решений деревьев решений, обученных на наборе данных радужной оболочки

• Понимание структуры дерева решений

1.

10.2. Регрессия

Деревья решений также можно применять к задачам регрессии, используя Класс DecisionTreeRegressor .

Как и в настройке классификации, метод подгонки будет принимать в качестве аргументов массивы X и y, только то, что в этом случае ожидается, что y будет иметь значения с плавающей запятой вместо целочисленных значений:

 >>> из дерева импорта sklearn
>>> Х = [[0, 0], [2, 2]]
>>> у = [0,5, 2,5]
>>> clf = tree.DecisionTreeRegressor()
>>> clf = clf.fit(X, y)
>>> clf.predict([[1, 1]])
массив ([0,5])
 

Примеры:

• Регрессия дерева решений

1.10.3. Проблемы с несколькими выходами

Задача с несколькими выходами — это контролируемая задача обучения с несколькими выходами. чтобы предсказать, то есть когда Y представляет собой двумерный массив формы (n_выборок, n_выходов) .

При отсутствии корреляции между выходами очень простой способ решить такая задача состоит в том, чтобы построить n независимых моделей, т. е. по одной на каждую вывод, а затем использовать эти модели для независимого прогнозирования каждого из n выходы. Однако, поскольку вполне вероятно, что выходные значения, относящиеся к одни и те же входные данные сами коррелируют друг с другом, зачастую лучший способ — создать единый модель, способная предсказывать одновременно все n выходов. Во-первых, требуется меньшее время обучения, так как строится только одна оценка. Во-вторых, точность обобщения результирующей оценки часто может быть увеличена.

Что касается деревьев решений, эту стратегию можно легко использовать для поддержки задачи с несколькими выходами. Для этого требуются следующие изменения:

Этот модуль предлагает поддержку задач с несколькими выходами, реализуя этот стратегия как в DecisionTreeClassifier , так и в DecisionTreeRegressor . Если дерево решений подходит для выходного массива Y формы (n_samples, n_outputs) , то результирующая оценка будет:

Использование деревьев с несколькими выходами для регрессии продемонстрировано в Регрессия дерева решений с несколькими выходами. В этом примере ввод X — единственное действительное значение, а выходные значения Y — синус и косинус X.

Использование многовыходных деревьев для классификации продемонстрировано в Завершение грани с многовыходными оценщиками. В этом примере входы X — пиксели верхней половины граней, а выходные данные Y — пиксели нижняя половина этих граней.

Примеров:

• Регрессия дерева решений с несколькими выходами

• Завершение грани с многовыходными оценщиками

Каталожные номера:

• М. Дюмон и др., Быстрое мультиклассовое аннотирование изображений со случайными подокнами и несколько выходных рандомизированных деревьев, Международная конференция по Теория и приложения компьютерного зрения 2009

1.10.4. Сложность

В общем случае стоимость времени выполнения для построения сбалансированного бинарного дерева составляет \(O(n_{samples}n_{features}\log(n_{samples}))\) и время запроса \(O(\log(n_{выборки}))\). {2}\log(n_{выборки}))\).

1.10.5. Советы по практическому использованию

• Деревья решений, как правило, подходят для данных с большим количеством признаков. Очень важно получить правильное соотношение выборок к количеству признаков, поскольку дерево с несколькими образцами в многомерном пространстве, скорее всего, переобучится.

• Рассмотрите возможность уменьшения размерности (PCA, ICA, или выбор функции) заранее, чтобы дайте вашему дереву больше шансов найти признаки, которые являются дискриминационными.

• Понимание структуры дерева решений поможет получить больше информации о том, как дерево решений делает прогнозы, что важно для понимания важных особенностей данных.

• Визуализируйте свое дерево во время обучения с помощью экспорта функция. Используйте max_depth=3 в качестве начальной глубины дерева, чтобы почувствовать насколько дерево соответствует вашим данным, а затем увеличьте глубину.

• Помните, что количество выборок, необходимых для заполнения дерева, удваивается за каждый дополнительный уровень, до которого растет дерево. Используйте max_depth для управления размер дерева для предотвращения переобучения.

• Используйте min_samples_split или min_samples_leaf , чтобы убедиться, что несколько выборки информируют каждое решение в дереве, контролируя, какие расщепления будут быть на рассмотрении. Очень маленькое число обычно означает, что дерево будет переобучать, тогда как большое число не позволит дереву изучить данные. Пытаться min_samples_leaf=5 в качестве начального значения. Если размер выборки варьируется в значительной степени в этих двух параметрах можно использовать число с плавающей запятой в процентах. Пока min_samples_split может создавать сколь угодно маленькие листья, min_samples_leaf гарантирует, что каждый лист имеет минимальный размер, избегая листовые узлы с низкой дисперсией и чрезмерным соответствием в задачах регрессии. За классификация с несколькими классами, min_samples_leaf=1 часто является лучшим выбор.

  Обратите внимание, что min_samples_split рассматривает сэмплы напрямую и независимо от sample_weight , если указано (например, узел с m взвешенными выборками по-прежнему рассматривается как имеющий ровно m выборок). Рассмотрим min_weight_fraction_leaf или min_impurity_decrease , если требуется учитывать вес выборки при разделении.

• Сбалансируйте набор данных перед тренировкой, чтобы предотвратить смещение дерева к господствующим классам. Балансировка классов может быть выполнена с помощью отбор равного количества образцов из каждого класса или, что предпочтительнее, путем нормализация суммы весов выборки ( sample_weight ) для каждого класс на одно и то же значение. Также обратите внимание, что критерии предварительной обрезки, основанные на весе, например min_weight_fraction_leaf , тогда будет менее смещено в сторону доминирующие классы, чем критерии, которые не знают веса выборки, как min_samples_leaf .

• Если выборки взвешены, будет проще оптимизировать дерево структура с использованием критерия предварительной обрезки на основе веса, такого как min_weight_fraction_leaf , которые гарантируют, что конечные узлы содержат не менее часть общей суммы весов выборки.

• Все деревья решений используют np.float32 внутренних массивов. Если обучающие данные не в этом формате, будет сделана копия набора данных.

• Если входная матрица X очень разреженная, рекомендуется преобразовать ее в разреженную csc_matrix перед вызовом fit and sparse csr_matrix перед вызовом предсказывать. Время обучения может быть на несколько порядков меньше для разреженных матричный ввод по сравнению с плотной матрицей, когда функции имеют нулевые значения в большинство образцов.

1.10.6. Алгоритмы дерева: ID3, C4.5, C5.0 и CART

Каковы все различные алгоритмы дерева решений и чем они отличаются друг от друга? Какой из них реализован в scikit-learn?

ID3 (Итеративный дихотомайзер 3) был разработан в 1986 году Россом Куинланом. Алгоритм создает многоходовое дерево, находя для каждого узла (т.е. в жадным образом) категориальный признак, который даст наибольшую прирост информации для категориальных целей. Деревья вырастают до своих максимальный размер, а затем обычно применяется шаг обрезки, чтобы улучшить способность дерева обобщать невидимые данные.

C4.5 является преемником ID3 и убрал ограничение, должны быть категориальными путем динамического определения дискретного атрибута (на основе числовых переменных), который разбивает непрерывное значение атрибута в дискретный набор интервалов. C4.5 преобразует обученные деревья (т. е. результат алгоритма ID3) в наборы правил «если-то». Затем оценивается точность каждого правила, чтобы определить порядок в которых они должны быть применены. Сокращение выполняется путем удаления правила предварительное условие, если точность правила улучшается без него.

C5.0 — это последняя версия Quinlan, выпущенная под частной лицензией. Он использует меньше памяти и создает меньшие наборы правил, чем C4. 5, в то же время будучи более точным.

CART (деревья классификации и регрессии) очень похож на C4.5, но отличается тем, что поддерживает числовые целевые переменные (регрессия) и не вычисляет наборы правил. CART строит бинарные деревья, используя функцию и порог, который дает наибольший прирост информации в каждом узле.

scikit-learn использует оптимизированную версию алгоритма CART; Тем не менее Реализация scikit-learn пока не поддерживает категориальные переменные. 9*)\) до достижения максимально допустимой глубины, \(n_m <\min_{выборки}\) или \(n_m = 1\).

1.10.7.1. Критерии классификации

Если целью является результат классификации, принимающий значения 0,1,…,K-1, для узла \(m\) пусть

\[p_{mk} = \frac{1}{n_m} \sum_{y \in Q_m} I(y = k)\]

— доля наблюдений класса k в узле \(m\). Если \(m\) является терминальный узел, predict_proba для этого региона имеет значение \(p_{mk}\). Общие меры загрязнения следующие.

Джини:

\[H(Q_m) = \sum_k p_{mk} (1 — p_{mk})\]

Журнал потерь или энтропии:

\[H(Q_m) = — \sum_k p_{mk} \log(p_{mk})\]

Примечание

Критерий энтропии вычисляет энтропию Шеннона возможных классов. Это берет частоты класса точек обучающих данных, которые достигли заданного лист \(m\) как их вероятность. Использование энтропии Шеннона в качестве узла дерева Критерий расщепления эквивалентен минимизации логарифмической потери (также известной как кросс-энтропия и полиномиальное отклонение) между истинными метками \(y_i\) и вероятностные прогнозы \(T_k(x_i)\) модели дерева \(T\) для класса \(k\).

Чтобы увидеть это, сначала вспомните, что логарифмическая потеря модели дерева \(T\) вычисляется на наборе данных \(D\) определяется следующим образом:

\[\mathrm{LL}(D, T) = -\frac{1}{n} \sum_{(x_i, y_i) \in D} \sum_k I(y_i = k) \log(T_k(x_i))\]

, где \(D\) — обучающий набор данных из \(n\) пар \((x_i, y_i)\).

В дереве классификации предсказанные вероятности классов в листовых узлах постоянны, то есть: для всех \((x_i, y_i) \in Q_m\) имеем: \(T_k(x_i) = p_{mk}\) для каждого класса \(k\).

Это свойство позволяет переписать \(\mathrm{LL}(D, T)\) как сумма энтропий Шеннона, вычисленных для каждого листа \(T\), взвешенного количество точек обучающих данных, достигших каждого листа:

\[\mathrm{LL}(D, T) = \sum_{m \in T} \frac{n_m}{n} H(Q_m)\]

1.

10.7.2. Критерии регрессии

Если целью является непрерывное значение, то для узла \(m\) Критерии минимизации при определении мест будущих расколов: Среднее Квадрат ошибки (MSE или ошибка L2), отклонение Пуассона, а также среднее абсолютное значение Ошибка (MAE или ошибка L1). MSE и отклонение Пуассона оба устанавливают прогнозируемое значение конечных узлов к изученному среднему значению \(\bar{y}_m\) узла тогда как MAE устанавливает прогнозируемое значение терминальных узлов в медиану \(медиана(y)_m\). 92\конец{выравнивание}\конец{выравнивание} \]

Полупуассоновское отклонение:

\[H(Q_m) = \frac{1}{n_m} \sum_{y \in Q_m} (y \log\frac{y}{\bar{y}_m} — у + \бар{у}_м)\]

Установка критерия = "poisson" может быть хорошим выбором, если вашей целью является количество или частота (количество на некоторую единицу). В любом случае \(y >= 0\) является необходимое условие для использования этого критерия. Обратите внимание, что он подходит намного медленнее, чем критерий МСЭ.

Средняя абсолютная ошибка:

\[ \begin{align}\begin{align}median(y)_m = \underset{y \in Q_m}{\mathrm{median}}(y)\\H(Q_m) = \frac{1}{ n_m} \sum_{y \in Q_m} |y — медиана(y)_m|\end{aligned}\end{align} \]

Обратите внимание, что он подходит намного медленнее, чем критерий MSE.

1.10.8. Отсечение с минимальной стоимостью и сложностью

Обрезка с минимальной стоимостью и сложностью — это алгоритм, используемый для обрезки дерева, чтобы избежать переобучение, описанное в главе 3 [BRE]. Этот алгоритм параметризован на \(\alpha\ge0\), известный как параметр сложности. Сложность Параметр используется для определения показателя сложности затрат, \(R_\alpha(T)\) заданное дерево \(T\):

\[R_\alpha(T) = R(T) + \alpha|\widetilde{T}|\]

, где \(|\widetilde{T}|\) — количество конечных узлов в \(T\) и \(R(T)\) традиционно определяется как общий коэффициент неправильной классификации терминала узлы. В качестве альтернативы, scikit-learn использует общую взвешенную примесь выборки конечные узлы для \(R(T)\). Как показано выше, примесь узла зависит от критерия. Отсечение с минимальной стоимостью и сложностью находит поддерево \(T\), который минимизирует \(R_\alpha(T)\).

Мера сложности стоимости одного узла равна \(R_\alpha(t)=R(t)+\alpha\). Ветвь \(T_t\) определяется как дерево, где узел \(t\) является его корнем. В общем, примесь узла больше суммы примесей его концевых узлов, \(R(T_t) Параметр ccp_alpha .

Примеры:

• Деревья решений после сокращения с сокращением сложности затрат

Каталожные номера:

[БРЕ]

Л. Брейман, Дж. Фридман, Р. Олшен и К. Стоун. Классификация и деревья регрессии. Уодсворт, Белмонт, Калифорния, 1984 г.

.

• https://en.wikipedia.org/wiki/Decision_tree_learning

• https://en.wikipedia.org/wiki/Predictive_analytics

• Дж. Р. Куинлан. С4. 5: программы для машинного обучения. Морган Кауфманн, 1993.

• Т. Хасти, Р. Тибширани и Дж. Фридман. Элементы статистического Обучение, Springer, 2009.

Исчисление I. Пределы вычислений

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 2-5: Расчетные пределы

В предыдущем разделе мы видели, что существует большой класс функций, который позволяет нам использовать

. \[\ mathop {\lim }\limits_{x \to a} f\left( x \right) = f\left(a \right)\]

для вычисления лимитов. Тем не менее, есть также много ограничений, для которых это не будет легко работать. Цель этого раздела — разработать методы работы с некоторыми из этих ограничений, которые не позволят нам просто использовать этот факт.

Давайте сначала вернемся назад и посмотрим на один из первых пределов, которые мы рассмотрели, вычислим его точное значение и проверим наше предположение относительно предела. 92} — 2x}} & = \mathop {\lim }\limits_{x \to 2} \frac{{\left({x — 2} \right)\left({x + 6} \right)}} {{x\left( {x — 2} \right)}}\\ & = \mathop {\lim }\limits_{x \to 2} \frac{{x + 6}}{x}\end{align *}\]

Итак, разложив на множители, мы увидели, что можем сократить \(x — 2\) как в числителе, так и в знаменателе. После этого у нас теперь есть новое рациональное выражение, в которое мы можем подставить \(x = 2\), потому что мы потеряли проблему деления на ноль. Следовательно, предел равен 9.2} — 2x}} = \ mathop {\ lim } \ limit_ {x \ to 2} \ frac {{x + 6}} {x} = \ frac {8} {2} = 4 \]

Обратите внимание, что на самом деле это то, что мы предполагаем.

Прежде чем закончить этот пример, давайте обсудим тот факт, что мы не могли подставить \(x = 2\) в наш первоначальный предел, но как только мы сделали упрощение, мы просто подставили \(x = 2\), чтобы получить ответ. На первый взгляд может показаться, что это противоречие.

В исходном пределе мы не могли подставить \(x = 2\), потому что это давало нам ситуацию 0/0, с которой мы ничего не могли сделать. Сделав упрощение, мы можем заметить, что 92} — 2x}} = \frac{{x + 6}}{x}\hspace{0,25 дюйма}{\mbox{при условии}}x \ne 2\]

Другими словами, два уравнения дают одинаковые значения, за исключением точки \(x = 2\), а поскольку пределы касаются только того, что происходит вокруг точки \(x = 2\), предел двух уравнений будет равен равный. Что еще более важно, в упрощенной версии мы получаем «достаточно хорошее» уравнение, и поэтому то, что происходит вокруг \(x = 2\), идентично тому, что происходит при \(x = 2\).

Таким образом, мы можем взять предел упрощенной версии, просто подставив \(x = 2\), даже если мы не смогли подставить \(x = 2\) в исходное уравнение, а значение предела упрощенной версии уравнение будет таким же, как предел исходного уравнения.

Кстати, 0/0, которое мы изначально получили в предыдущем примере, называется неопределенной формой . Это означает, что мы на самом деле не знаем, что это будет, пока не проделаем дополнительную работу. Как правило, ноль в знаменателе означает, что он не определен. Однако это будет верно только в том случае, если числитель не равен нулю. Кроме того, ноль в числителе обычно означает, что дробь равна нулю, если только знаменатель также не равен нулю. Точно так же все, что делится само на себя, равно 1, если только мы не говорим о нуле.

Итак, здесь действительно три конкурирующих «правила», и непонятно, какое из них победит. Также возможно, что ни один из них не выиграет, и мы получим что-то совершенно отличное от undefined, нуля или единицы. Мы могли бы, например, получить из этого значение 4, чтобы выбрать число совершенно случайно.

При простом вычислении уравнения 0/0 не определено. Однако, принимая предел, если мы получаем 0/0, мы можем получить множество ответов, и единственный способ узнать, какой из них правильный, — это фактически вычислить предел. 92}}}{h}\\ & = \mathop {\lim }\limits_{h \to 0} \frac{{h\left( { — 12 + 2h} \right)}}{h}\\ & = \ mathop {\ lim} \ limit_ {h \ to 0} \, \, — 12 + 2h = — 12 \ end {align *} \]

Пример 3 Оцените следующий предел. \[\ mathop {\lim }\limits_{t \to 4} \frac{{t — \sqrt {3t + 4}}}}{{4 — t}}\]

Показать решение

Этот предел требует немного больше работы, чем два предыдущих. Однако еще раз обратите внимание, что мы получаем неопределенную форму 0/0, если пытаемся просто оценить предел. Также обратите внимание, что ни один из двух примеров здесь не поможет, по крайней мере, на начальном этапе. Мы не можем разложить уравнение на множители и не можем просто что-то умножить, чтобы упростить уравнение. 92}\]

Итак, если в первом и/или втором члене есть квадратный корень, рационализация устранит корень(и). Этот может помочь в оценке предела.

Попробуем рационализировать числитель в этом случае.

\[\ mathop {\lim }\limits_{t \to 4} \frac{{t — \sqrt {3t + 4}}}}{{4 — t}} = \mathop {\lim }\limits_{t \ до 4} \frac{{\left( {t — \ sqrt {3t + 4}} \right)}}{{\left( {4 — t} \right)}}\,\frac{{\left( {t + \sqrt {3t + 4}} \right)}}{{\left( {t + \sqrt {3t + 4}} \right)}}\] 92} — 3t — 4}}{{\left( {4 — t} \right)\left( {t + \sqrt {3t + 4} } \right)}}\end{align*}\]

Обратите внимание, что мы также не умножали знаменатель. Большинство студентов заканчивают занятия по алгебре с вбитой в голову мыслью всегда умножать этот материал. Однако в этом случае умножение сделает задачу очень сложной, и в конце концов вы все равно просто разложите ее на множители.

На этом этапе мы почти закончили. Обратите внимание, что мы можем разложить числитель на множители, так что давайте сделаем это.

\[\ mathop {\lim }\limits_{t \to 4} \frac{{t — \sqrt {3t + 4}}}}{{4 — t}} = \mathop {\lim }\limits_{t \ до 4} \frac{{\left( {t — 4} \right)\left( {t + 1} \right)}}{{\left( {4 — t} \right)\left( {t + \sqrt {3t + 4} } \справа)}}\]

Теперь все, что нам нужно сделать, это заметить, что если мы вычитаем «-1» из первого члена в знаменателе, мы можем сделать некоторое сокращение. В этот момент проблема деления на ноль исчезнет, ​​и мы сможем оценить предел.

\[\begin{align*}\mathop {\lim}\limits_{t \to 4} \frac{{t — \sqrt {3t + 4}}}}{{4 — t}} & = \mathop {\ lim }\limits_{t \to 4} \frac{{\left( {t — 4} \right)\left( {t + 1} \right)}}{{ — \left( {t — 4} \ right)\left( {t + \sqrt {3t + 4} } \right)}}\\ & = \mathop {\lim }\limits_{t \to 4} \frac{{t + 1}}{{ — \left( {t + \sqrt {3t + 4} } \right)}}\\ & = — \frac{5}{8}\end{align*}\]

Заметим, что если бы мы умножили знаменатель, мы бы не смогли сделать это сокращение и, по всей вероятности, даже не увидели бы, что какое-то сокращение можно было бы сделать. 92} + 5 & \hspace{0.25in}{\mbox{if }}y < - 2\\ 1 - 3y & \hspace{0.25in}{\mbox{if }}y \ge - 2\end{align *} \Правильно.\]

Вычислите следующие пределы.

1. \(\ mathop {\lim }\limits_{y \to 6} g\left(y\right)\)
2. \(\ mathop {\lim }\limits_{y \to — 2} g\left( y \right)\)

Показать все решения Скрыть все решения

a \(\mathop {\lim }\limits_{y \to 6} g\left( y \right)\) Показать решение

В этом случае делать особо нечего. При выполнении ограничений помните, что мы всегда должны смотреть на то, что происходит по обе стороны от рассматриваемой точки, когда мы приближаемся к ней. В этом случае \(y = 6\) полностью находится внутри второго интервала функции, поэтому по обе стороны от \(y = 6\) есть значения \(y\), которые также находятся внутри этого интервала. Это означает, что мы можем просто использовать этот факт для оценки этого предела.

\[\begin{align*}\mathop {\lim}\limits_{y \to 6} g\left(y\right) & = \mathop {\lim}\limits_{y \to 6}( 1 — 3y )\\ & = — 17\end{align*}\]

b \(\mathop {\lim }\limits_{y \to — 2} g\left( y \right)\) Показать решение

Эта часть является реальной причиной этой проблемы. В этом случае точка, для которой мы хотим взять предел, является точкой отсечки для двух интервалов. Другими словами, мы не можем просто подставить \(y = — 2\) во вторую часть, потому что этот интервал не содержит значений \(y\) слева от \(y = — 2\) и нам нужно знать, что происходит по обе стороны точки.

Чтобы выполнить эту часть, нам нужно вспомнить факт из раздела об односторонних пределах, в котором говорится, что если два односторонних предела существуют и одинаковы, то нормальный предел также будет существовать и иметь такое же значение.

Обратите внимание, что оба односторонних ограничения могут быть выполнены здесь, так как мы будем рассматривать только одну сторону рассматриваемой точки. 2} + 5 & \hspace{0.25in}{\mbox{if}}y < - 2\\ 3 - 3y & \hspace{0.25in}{ \mbox{if }}y \ge - 2\end{align*} \right.\] 9+ }{\mbox{ подразумевает }}y > — 2\\ & = 9\end{align*}\]

Односторонние пределы одинаковы, поэтому мы получаем

\[\ mathop {\lim}\limits_{y \to — 2} g\left( y \right) = 9\]

Есть еще один предел, который нам нужно сделать. Однако нам понадобится новый факт о пределах, который поможет нам в этом.

Факт

Если \(f\left( x \right) \le g\left( x \right)\) для всех \(x\) на \([a, b]\) (за исключением, возможно, \ (x = c\)) и \(a \le c \le b\), тогда

\[\ mathop {\lim }\limits_{x \to c} f\left( x \right) \le \ mathop {\lim }\limits_{x \to c} g\left(x \right)\]

Обратите внимание, что этот факт должен иметь для вас некоторый смысл, если мы предположим, что обе функции достаточно хороши. Если обе функции «достаточно хороши», чтобы использовать факт вычисления предела, то мы имеем

. \[\ mathop {\lim}\limits_{x \to c} f\left(x\right) = f\left(c\right) \le g\left(c\right) = \mathop {\lim} \limits_{x \to c} g\left( x \right)\]

Неравенство верно, потому что мы знаем, что \(c\) находится где-то между \(a\) и \(b\), и в этом диапазоне мы также знаем \(f\left( x \right) \le g\ влево( х \вправо)\).

Обратите внимание, что нам на самом деле не нужно, чтобы две функции были достаточно хорошими, чтобы факт был правдой, но он обеспечивает хороший способ дать быстрое «обоснование» факту.

Также обратите внимание, что мы сказали, что предполагали, что \(f\left( x \right) \le g\left( x \right)\) для всех \(x\) на \([a, b]\ ) (за исключением, возможно, точки \(x = c\)). Поскольку пределы не заботятся о том, что на самом деле происходит в \(x = c\), нам на самом деле не нужно, чтобы неравенство выполнялось в этой конкретной точке. Нам нужно только, чтобы он держался вокруг \(x = c\), так как это то, о чем заботится предел.

Мы можем развить этот факт еще на один шаг, чтобы получить следующую теорему.

Теорема сжатия

Предположим, что для всех \(x\) на \([a, b]\) (кроме, возможно, на \(x = c\)) имеем

\[f\влево( x \вправо) \le h\влево( x \вправо) \le g\влево( x \вправо)\]

Также предположим, что

\[\ mathop {\ lim} \ limit_ {x \ to c} f \ left ( x \ right) = \ mathop {\ lim } \ limits_ {x \ to c} g \ left ( x \ right) = L \ ]

для некоторых \(a \le c \le b\). Затем

\[\ mathop {\lim}\limits_{x \to c} h\left( x \right) = L\]

Как и в случае с предыдущим фактом, нам нужно только знать, что \(f\left( x \right) \le h\left( x \right) \le g\left( x \right)\) верно вокруг \( x = c\), потому что мы работаем с ограничениями, и они касаются только того, что происходит вокруг \(x = c\), а не того, что на самом деле происходит в \(x = c\).

Теперь, если мы снова предположим, что все три функции достаточно хороши (опять же, это не требуется, чтобы сделать теорему о сжатии верной, это только помогает с визуализацией), тогда мы можем получить быстрый набросок того, что говорит теорема о сжатии. нас. На следующем рисунке показано, что происходит в этой теореме.

Из рисунка видно, что если пределы \(f(x)\) и \(g(x)\) равны в \(x = c\), то значения функции также должны быть равны в \ (x = c\) (здесь мы используем тот факт, что мы предполагали, что функции «достаточно хороши», что на самом деле не требуется для теоремы). Однако, поскольку \(h(x)\) «зажато» между \(f(x)\) и \(g(x)\) в этой точке, то \(h(x)\) должно иметь то же значение . Следовательно, предел \(h(x)\) в этой точке также должен быть таким же.

Теорема сжатия также известна как 92} \ cos \ влево ( {\ гидроразрыва {1} {х}} \ вправо) \]

Показать решение

В этом примере ни один из предыдущих примеров нам не поможет. Здесь нет факторинга или упрощения. Мы не можем рационализировать, и односторонние ограничения не сработают. Возникает даже вопрос, будет ли существовать этот предел, поскольку у нас есть деление на ноль внутри косинуса при \(x=0\).